Random Graph Embeddings with General Edge Potentials

Clayton Shonkwiler

Colorado State University

http://shonkwiler.org

10.02.21

/css21

This talk!

Collaborators

Jason Cantarella

U. of Georgia

Tetsuo Deguchi

Ochanomizu U.

Erica Uehara

Ochanomizu U.

Funding: Simons Foundation

Linear polymers

A linear polymer is a chain of molecular units with free ends.

Polyethylene

Nicole Gordine [CC BY 3.0] from Wikimedia Commons

Shape of linear polymers

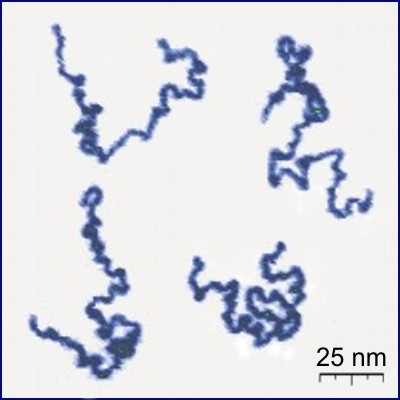
In solution, linear polymers become crumpled:

Protonated P2VP

Roiter–Minko, J. Am. Chem. Soc. 127 (2005), 15688-15689

[CC BY-SA 3.0], from Wikimedia Commons

Topological polymers

A topological polymer joins monomers in some graph type:

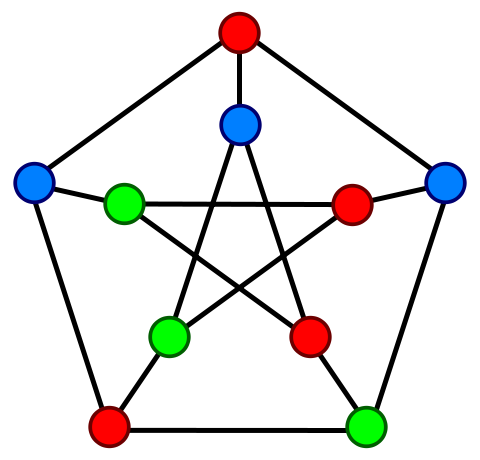
Petersen graph

Synthetic topological polymers

The Tezuka lab in Tokyo can now synthesize many topological polymers in usable quantities

Y. Tezuka, Acc. Chem. Res. 50 (2017), 2661–2672

Main Question

What is the probability distribution on the shapes of topological polymers in solution?

Ansatz

Linear polymers

Topological polymers

Random walks with independent steps

Random walks with steps conditioned on ???

Graphs and the Graph Laplacian

Suppose \(\mathcal{G}\) is a directed graph with \(\mathbf{v}\) vertices and \(\mathbf{e}\) edges.

\(L:\mathbb{R}^{\mathbf{v}}\to \mathbb{R}^{\mathbf{v}}\) given by \(L = \partial \partial^T\) is the graph Laplacian.

\mathbb{R}^{\mathbf{e}} \stackrel{\partial}{\longrightarrow} \mathbb{R}^{\mathbf{v}}
\partial(e_4)=v_4-v_2
L(v_4)=3v_4-v_1-v_2-v_5

Think of \(x=(x_1,\dots,x_{\mathbf{v}})\in \mathbb{R}^{\mathbf{v}}\) as a realization of \(\mathcal{G}\) in \(\mathbb{R}\).

E=\frac{1}{2}\sum_{j=1}^{\mathbf{e}}\|x(\operatorname{head}(e_j))-x(\operatorname{tail}(e_j))\|^2 = \frac{1}{2}\langle x, L x\rangle
p(x) \propto e^{-\frac{1}{2} \langle x, L x\rangle}

Harmonic bonds \(\Rightarrow\) Gaussian vertex distribution:

Realizations

This is James–Guth–Flory phantom network theory!

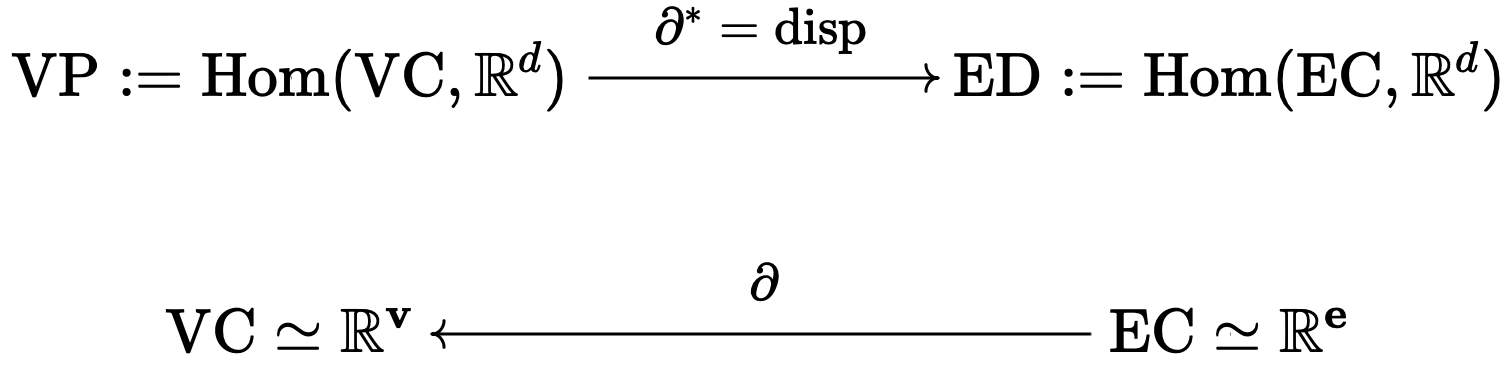
Some More Careful Linear Algebra

Define \(\widetilde{L}:=L+\frac{1}{\mathbf{v}} \mathbf{1}\mathbf{1}^T\).

Proposition.

  1. \(\partial:(\operatorname{EC},\langle \cdot,\cdot\rangle) \to (\operatorname{VC},\langle \cdot,\widetilde{L}^{-1}\cdot\rangle)\) is a partial isometry.
  2. \(\partial:(\operatorname{VP},\langle \cdot,\widetilde{L}^*\cdot\rangle)\to(\operatorname{ED},\langle\cdot,\cdot\rangle)\) is a partial isometry.

Radius of Gyration

\(\mu_{\mathcal{G}}\): \(O(d)\)-invariant measure concentrated on \(\operatorname{im}\partial^* \subset \operatorname{ED}\)

\(\nu_{\mathcal{G}}=(\partial^{*+})_\sharp \mu_{\mathcal{G}}\), its pushforward to \(\operatorname{VP}\).

\operatorname{VP} \stackrel{\partial^*}{\longrightarrow} \operatorname{ED}

\(\Sigma_{\mathbf{v}}:=\) matrix of expectations of products of a fixed coordinate of the vertices of \(\mathcal{G}\)

\(\Sigma_{\mathbf{e}}\) likewise for edges.

Theorem. The expected radius of gyration is

\(\langle \operatorname{R}_g^2\rangle_{\nu_{\mathcal{G}}} = \frac{d}{\mathbf{v}}\operatorname{tr}(\Sigma_{\mathbf{v}}) = \frac{d}{\mathbf{v}} \operatorname{tr}(\partial^{T+}\Sigma_{\mathbf{e}}\partial^+)\)

When \(\mu_{\mathcal{G}}\) is a standard Gaussian on \(\operatorname{im}\partial^*\),

\(\langle\operatorname{R}_g^2\rangle_{\nu_{\mathcal{G}}}= \frac{d}{\mathbf{v}}\operatorname{tr}\partial^{T+}(\partial^T\partial^{T+})\partial^T = \frac{d}{\mathbf{v}} \operatorname{tr} \partial^{T+}\partial^T = \frac{d}{\mathbf{v}} \operatorname{tr}L^+\).

Subdivisions

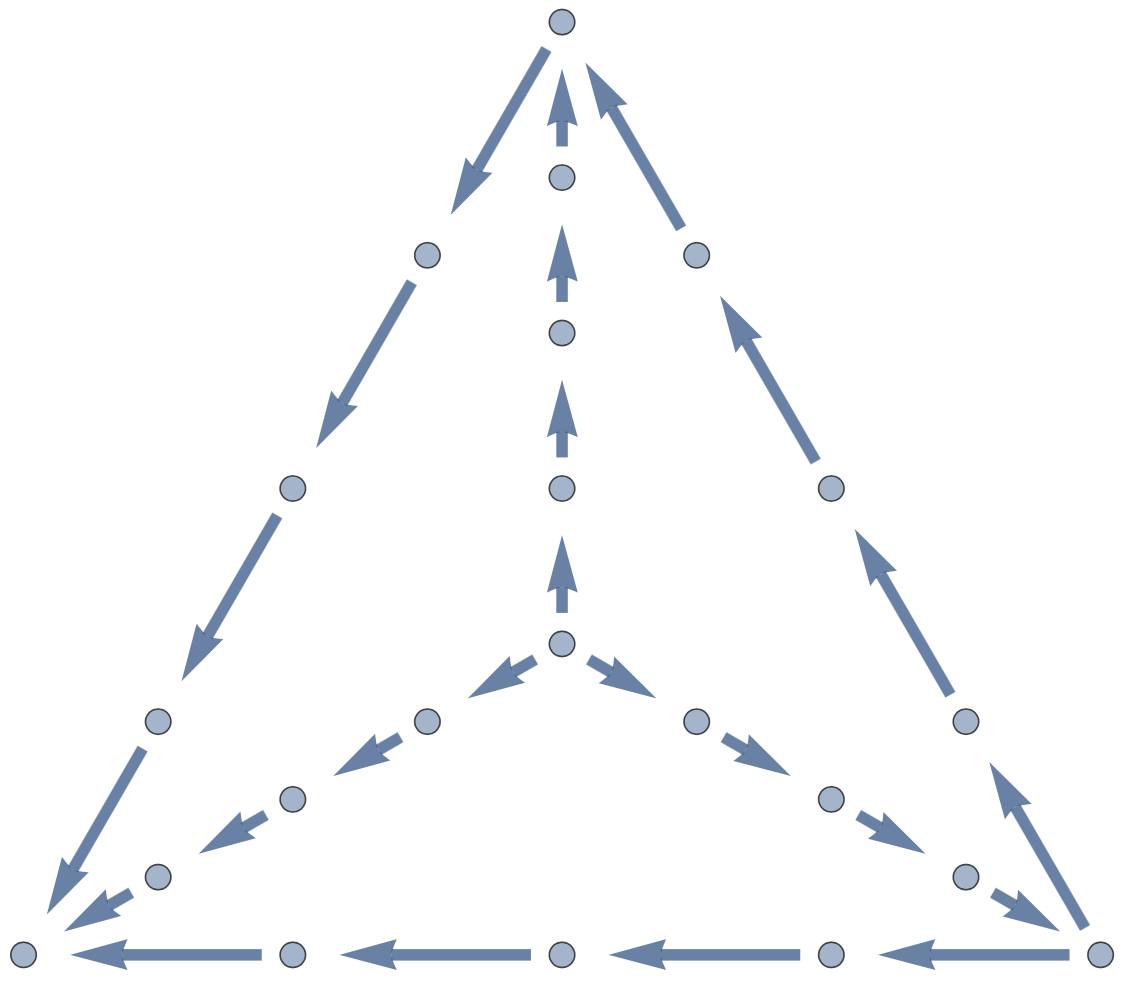
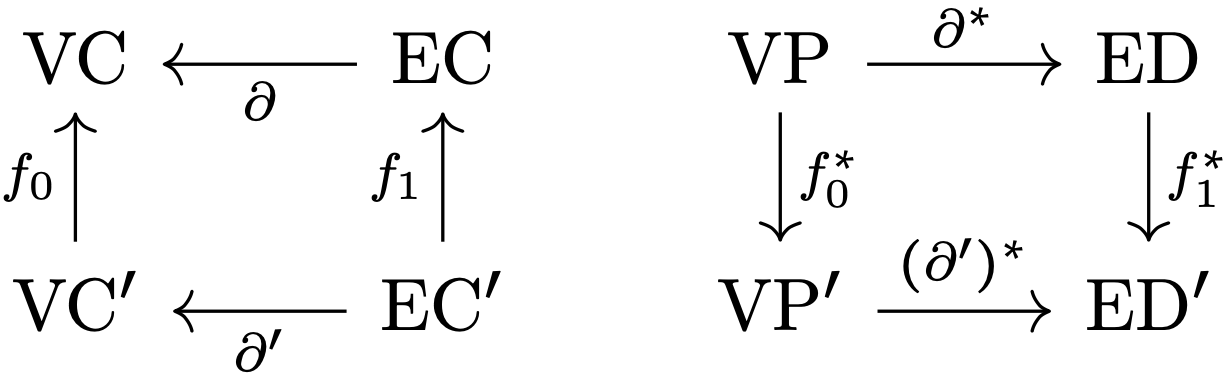
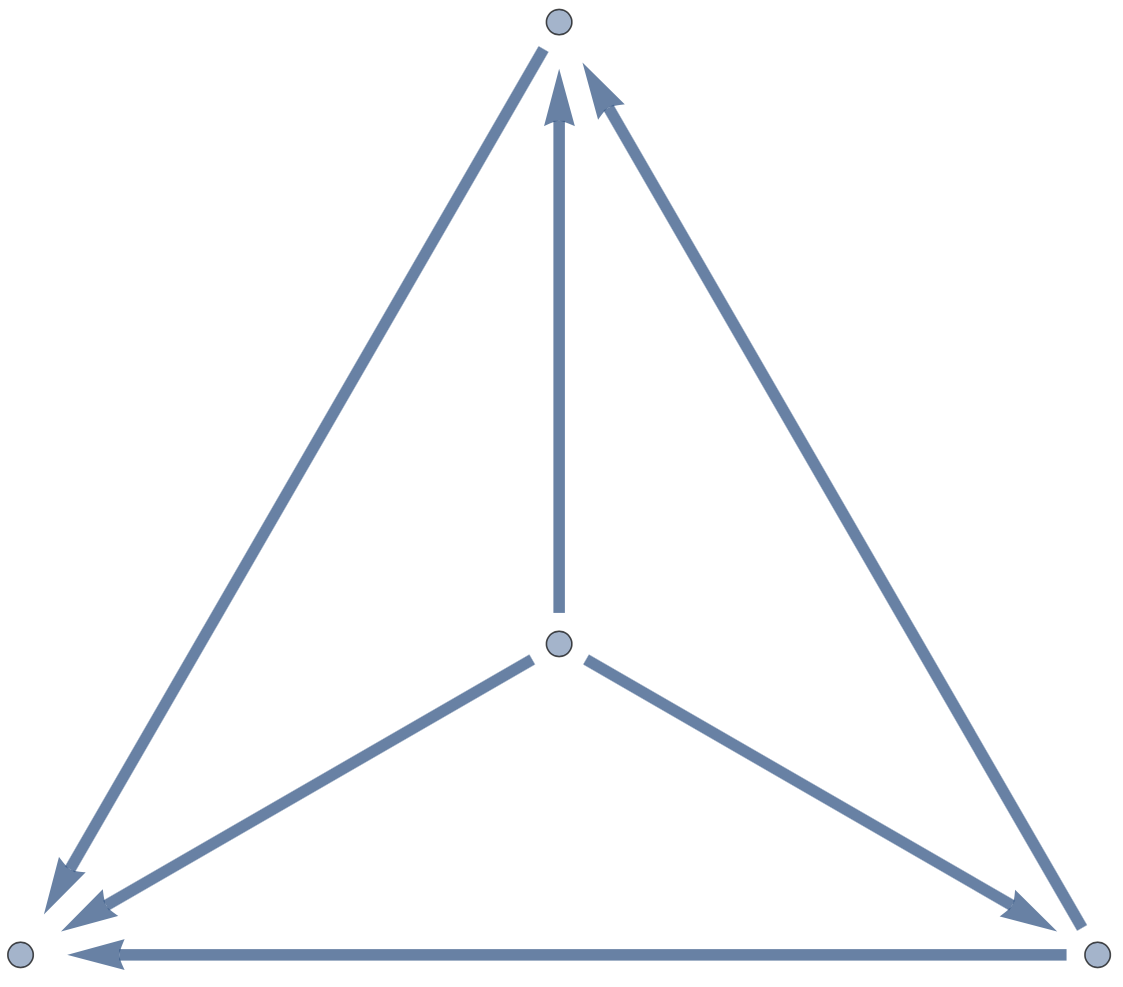
Chain Maps

Main Theorem

Theorem. Suppose \(f_0\) and \(f_1\) are injective chain maps between graphs \(\mathcal{G}'\) and \(\mathcal{G}\) of the same cycle rank. Given \(O(d)\)- and translation-invariant \(g:\operatorname{VP} \to \mathbb{R}\) which is expressible in terms of \(\mathcal{G}'\), then 

\(\mathcal{E}_{\nu_{\mathcal{G}}}(g) = \mathcal{E}_{\nu'_{\mathcal{G}'}}(g')\).

Consequences

\(\mathcal{G}\)

\(\mathcal{G}_n\)

Proposition. In phantom network theory, the joint distribution of squared distances between junction vertices in \(\mathcal{G}_n\) is the joint distribution of \(n\) times the squared distances between vertices in \(\mathcal{G}\).

Consequences

In the freely-jointed chain, each edge is a unit vector.

\(\langle \operatorname{squared\, junction-junction\, distance}\rangle_{\nu_{\mathcal{G}_n}}\) is in principle an \((18n-12)\)-dimensional integral

Using the theorem, can reduce to a \(6\)-dimensional integral.

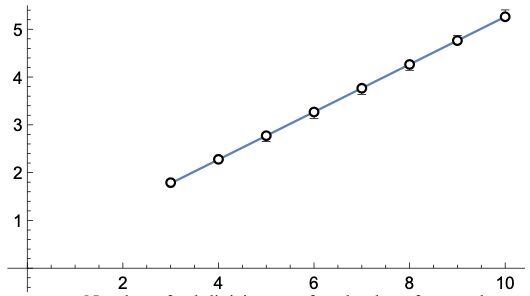
Questions

What about including distributions on bond angles in addition to bond lengths?

Sampling algorithms?

Steric constraints and the complete graph?

Thank you!

References

J. Cantarella, T. Deguchi, C. Shonkwiler, E. Uehara, Gaussian random embeddings of multigraphs, preprint, 2020, arXiv:2001.11709​

J. Cantarella, T. Deguchi, C. Shonkwiler, E. Uehara, Radius of gyration, contraction factors, and subdivisions of topological polymers, preprint, 2020, arXiv:2004.06199

J. Cantarella, T. Deguchi, C. Shonkwiler, E. Uehara, Random graph embeddings with general edge potentials, preprint, 2021, on arXiv soon!