Finding Good Coordinates for Sampling The Importance of Geometry
/cu24
this talk!
September 13, 2024

Random points on a line
Random points on a circle
Polar/angular coordinates!

Random points in a square
Rectangular coordinates!

Random points in a disk
Random points in a disk
Rectangular coordinates, sorta
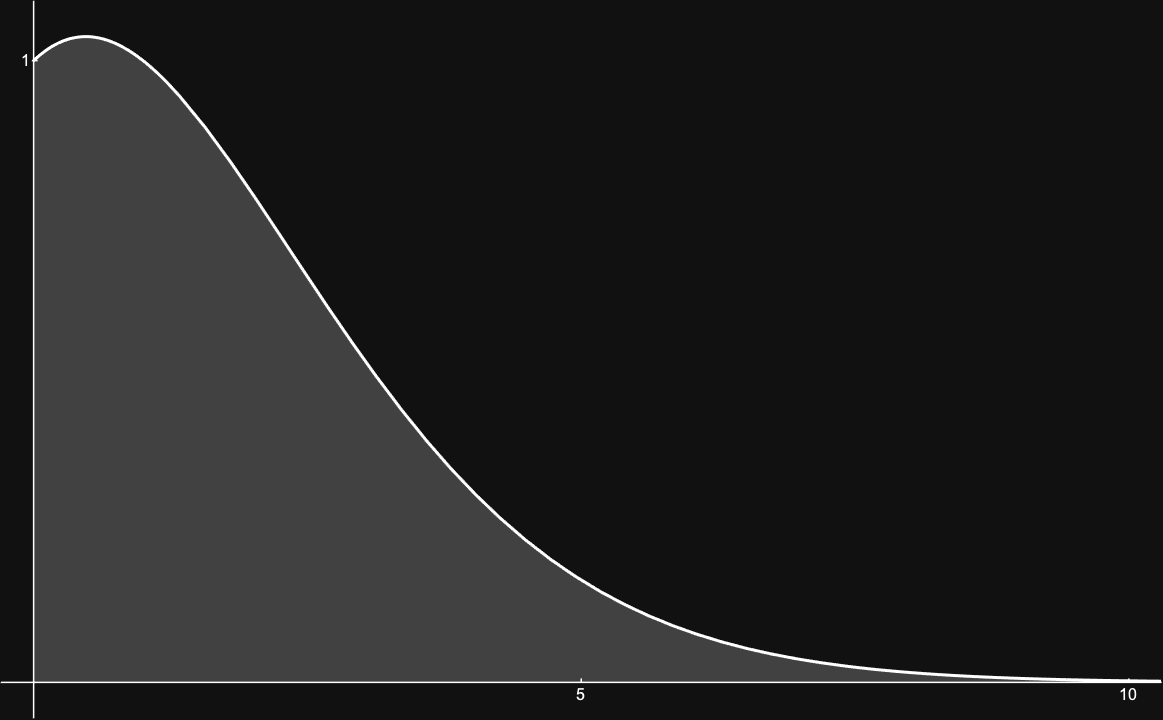
Probability that a random point in an \(n\)-dimensional cube lies inside the inscribed sphere

Random points in a disk
Random points in a disk
Polar coordinates?


Random points in a disk
Polar coordinates?
Polar coordinates, non-uniformly

Random points on a sphere
Random points on a sphere
Spherical coordinates?

Random points on a circle (or sphere)
2D standard Gaussian points
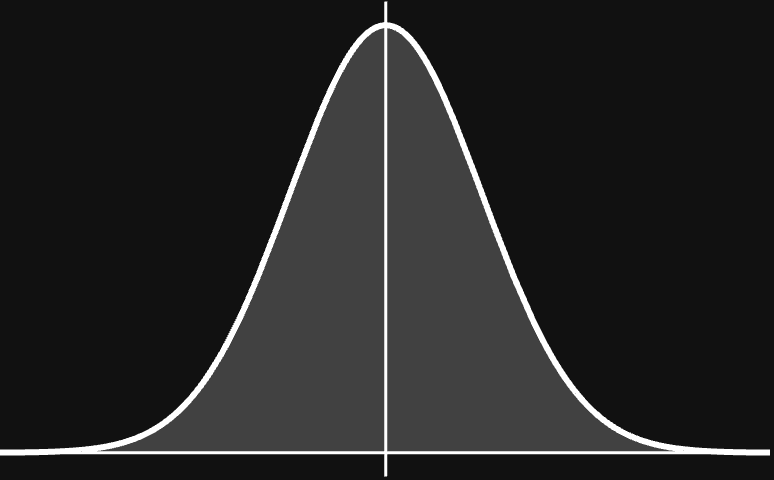
Normalized 2D standard Gaussian points
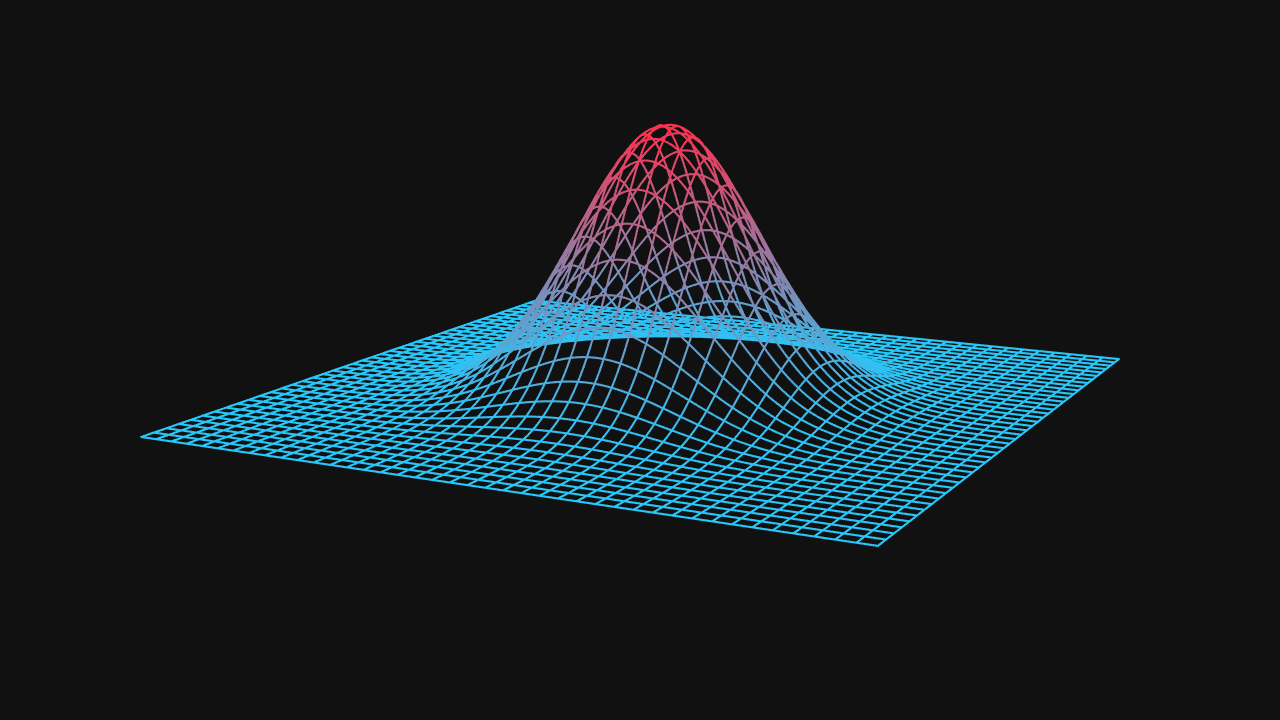
Multivariate Gaussian
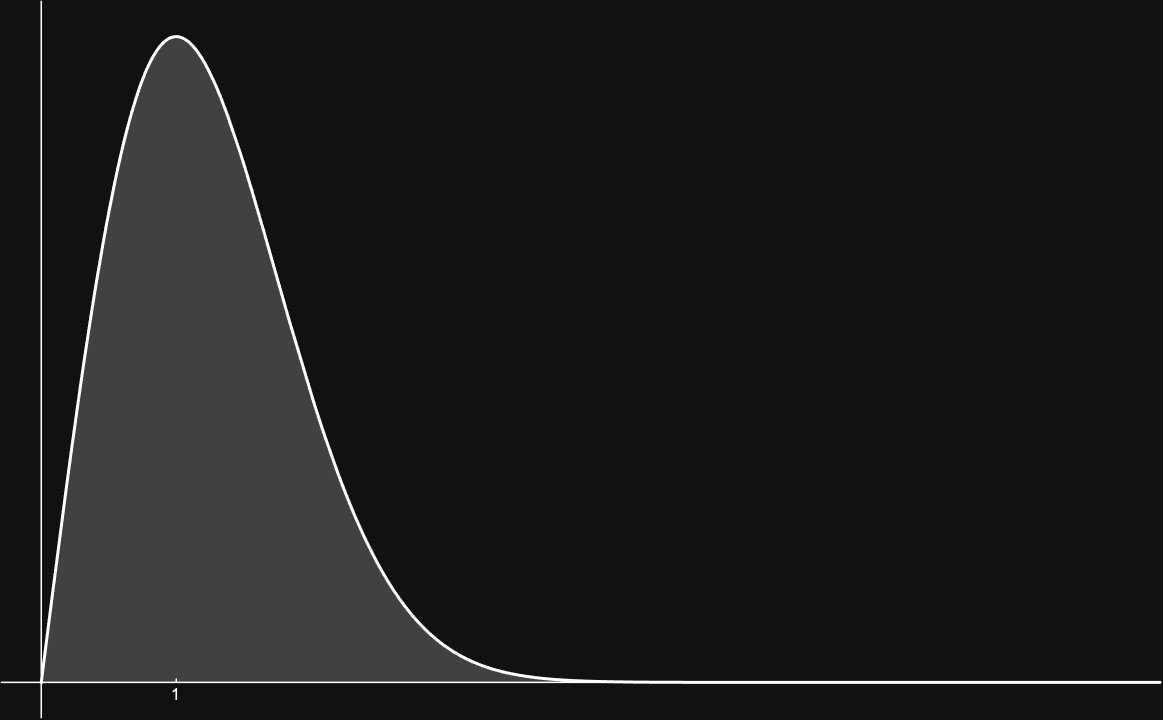
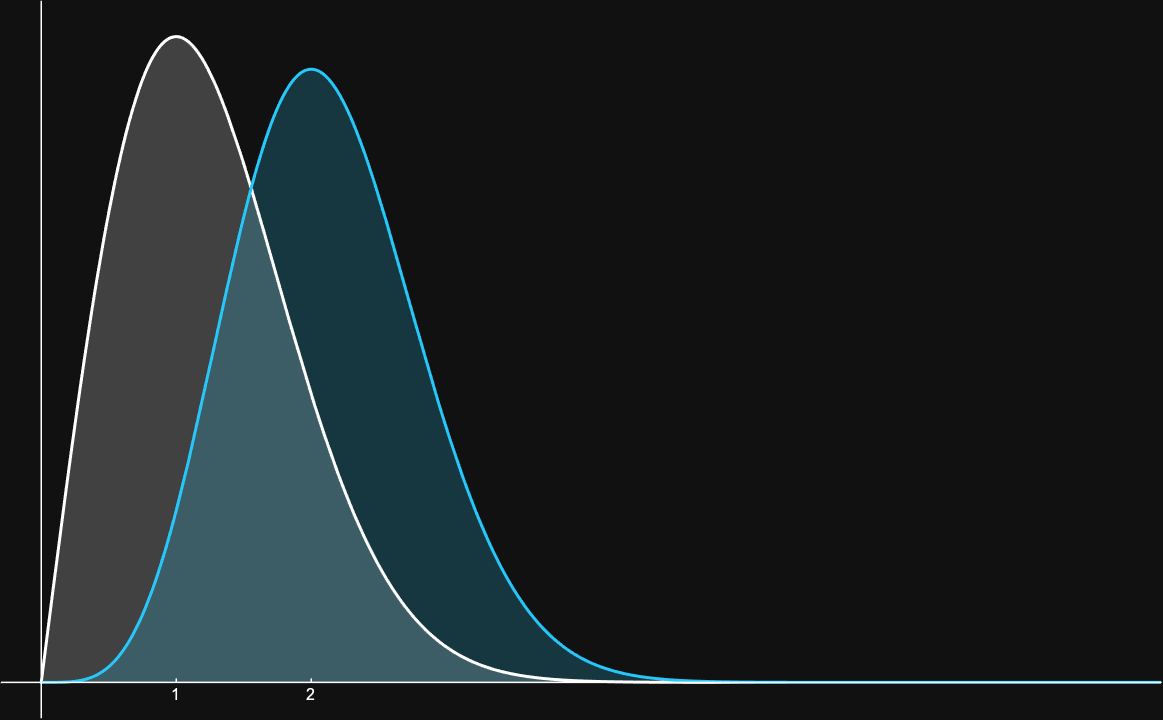
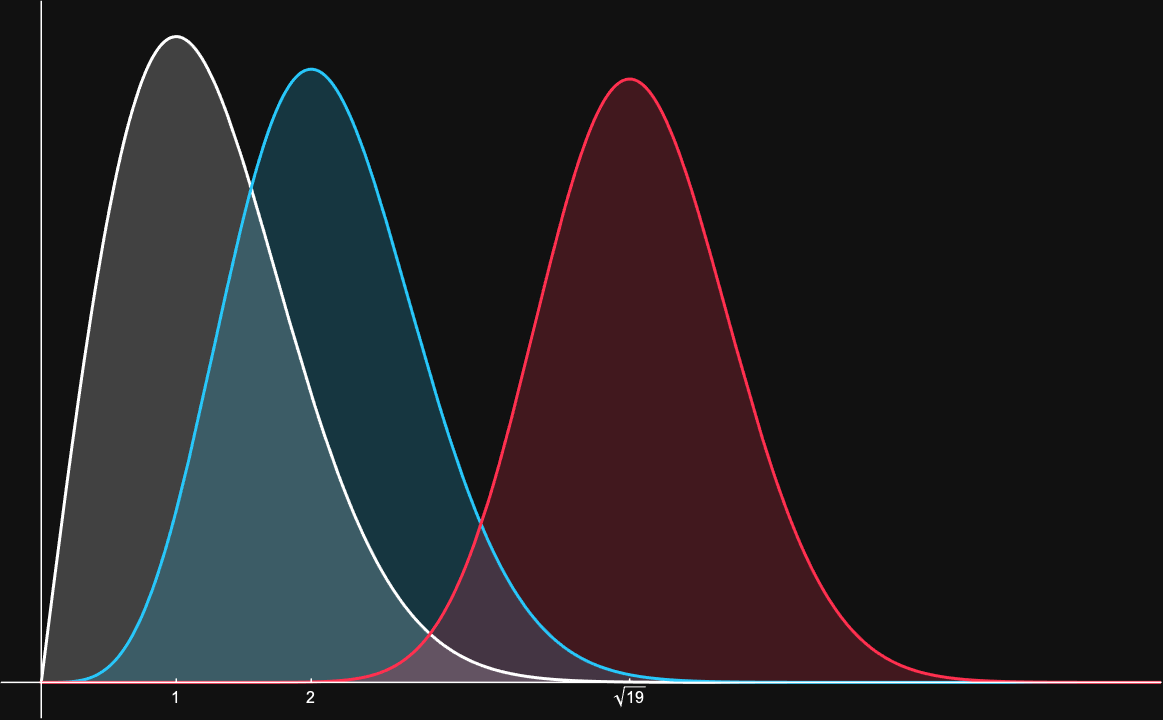
Distance distribution for 2D Gaussian
Distance distribution for 5D Gaussian
Distance distribution for 20D Gaussian

Random points on a sphere
Cylindrical coordinates?
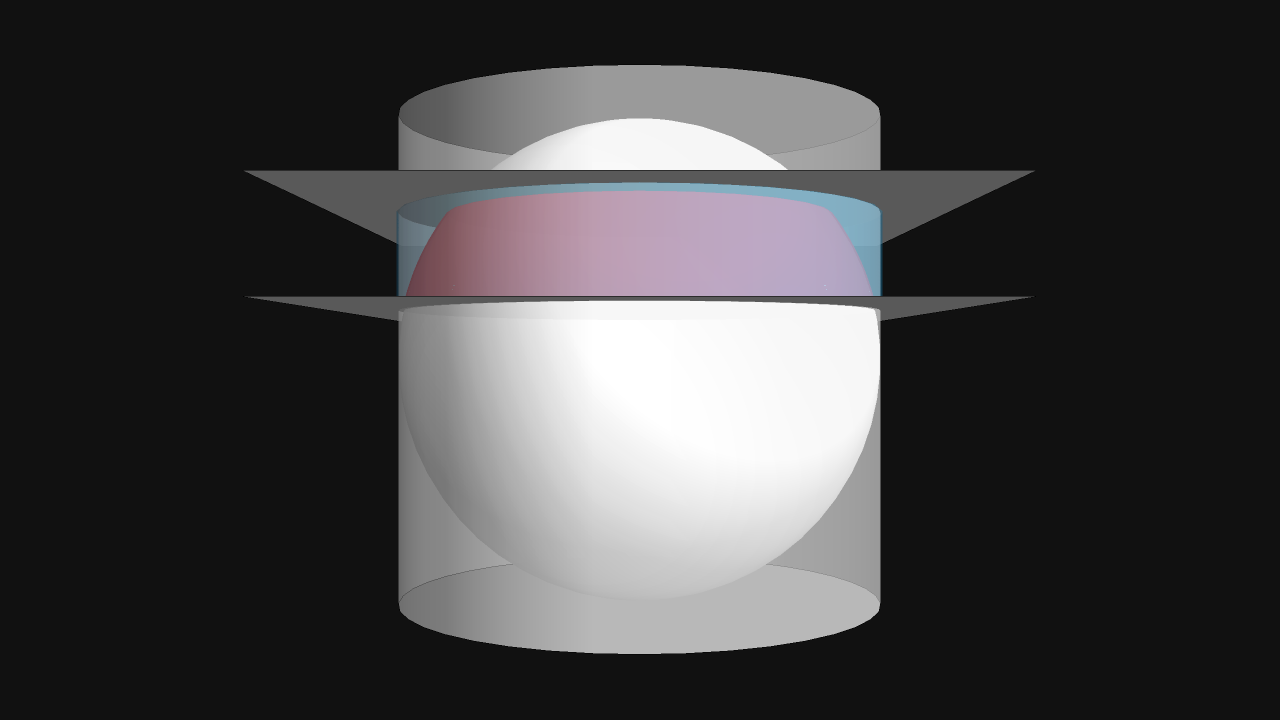
Archimedes’ Theorem:
The red and blue areas are equal!
Random points on a sphere
Cylindrical coordinates!
Lewis Carroll’s Pillow Problem #58
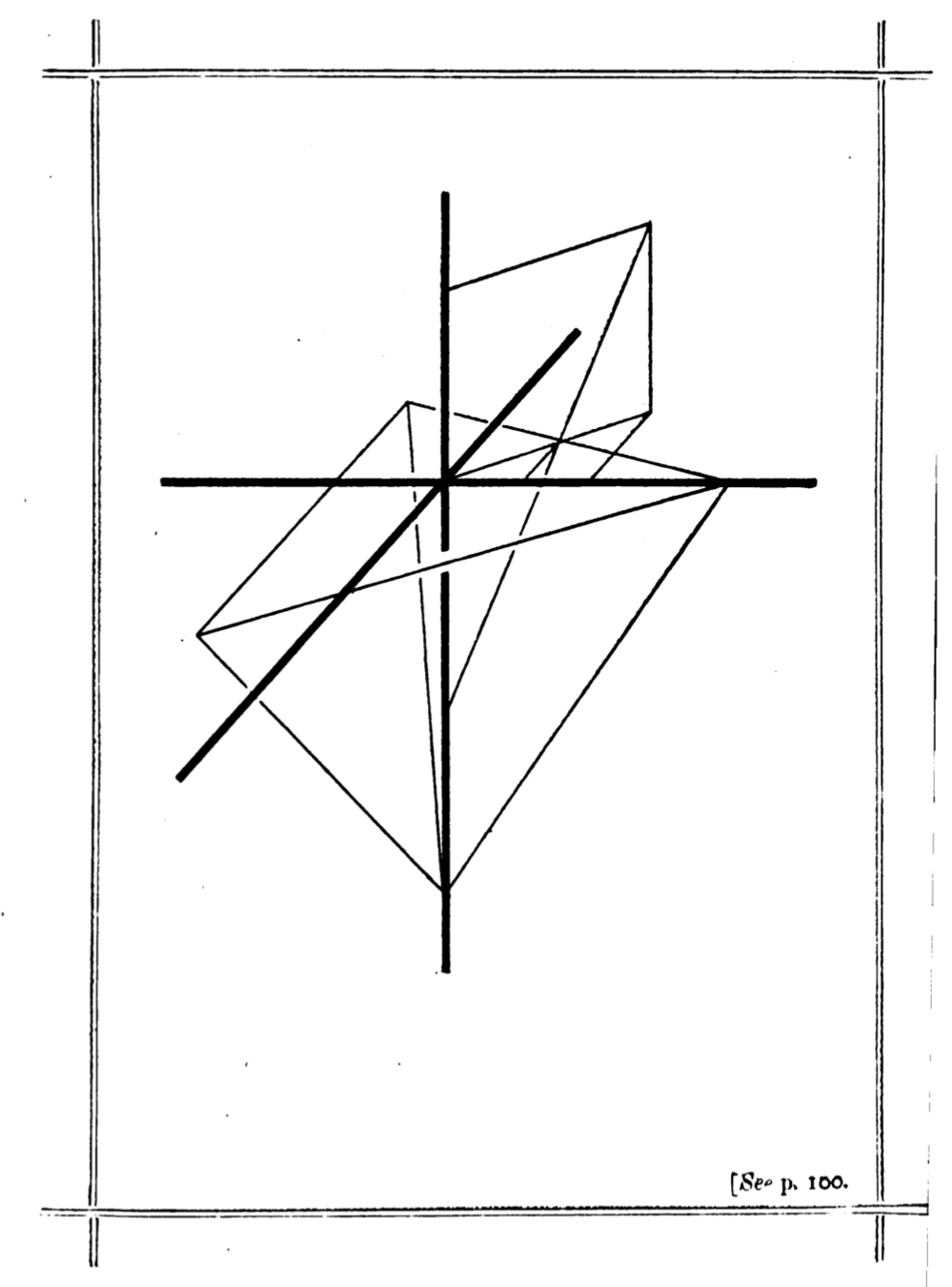


Earlier versions
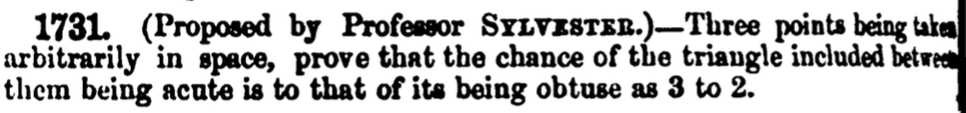

W. S. B. Woolhouse, Educational Times 18 (1865), p. 189
J. J. Sylvester, Educational Times 18 (1865), p. 68

W. S. B. Woolhouse, The Lady's and Gentleman's Diary 158 (1861), p. 76
Random Points on an Infinite Plane
Probability \(p\)
\(p\)
\(p\)
\(p\)
\(p\)
Uh oh!
A probabilist’s answer
Proposition [Portnoy]
If the vertices of the triangle are chosen from the standard Gaussian on \(\mathbb{R}^2\), then
\(\mathbb{P}(\text{obtuse}) = \frac{3}{4}\)

Choose three vertices uniformly in the disk:
\(\mathbb{P}(\text{obtuse})=\frac{9}{8}-\frac{4}{\pi^2}\approx 0.7197\)
Restricted domain?
Choose three vertices uniformly in the square:
\(\mathbb{P}(\text{obtuse})=\frac{97}{150}-\frac{\pi}{40}\approx 0.7252\)
Side Lengths?!
Sidelengths \((a,b,c)\) uniquely determine a triangle (SSS).
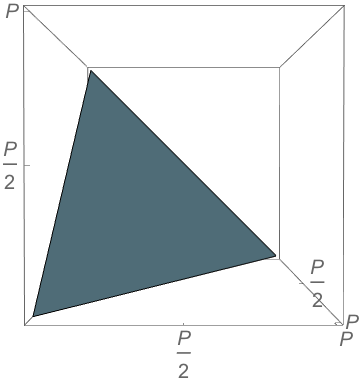
Obtuseness is scale-invariant, so pick a perimeter \(P\) and we have \(a+b+c=P\).
\(b+c<a\)
\(a+b<c\)
\(a+c<b\)
\(\mathbb{P}(\text{obtuse})=9-12\ln 2 \approx 0.68\)
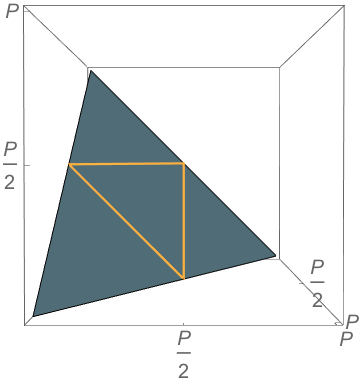
\(b^2+c^2=a^2\)
\(a^2+b^2=c^2\)
\(a^2+c^2=b^2\)
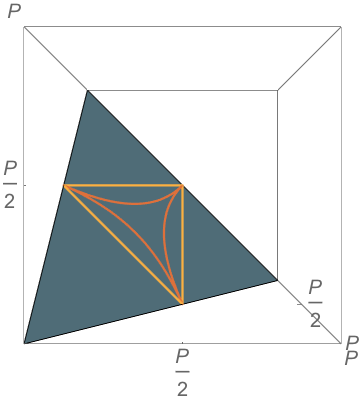
Carroll’s answer
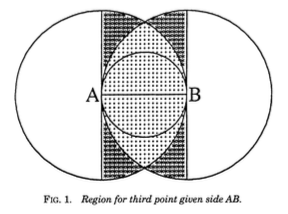
Suppose \(AB\) is the longest side. Then
\(\mathbb{P}(\text{obtuse})=\frac{\pi/8}{\pi/3-\sqrt{3}/4} \approx 0.64\)
But if \(AB\) is the second longest side,
\(\mathbb{P}(\text{obtuse}) = \frac{\pi/2}{\pi/3+\sqrt{3}/2} \approx 0.82\)

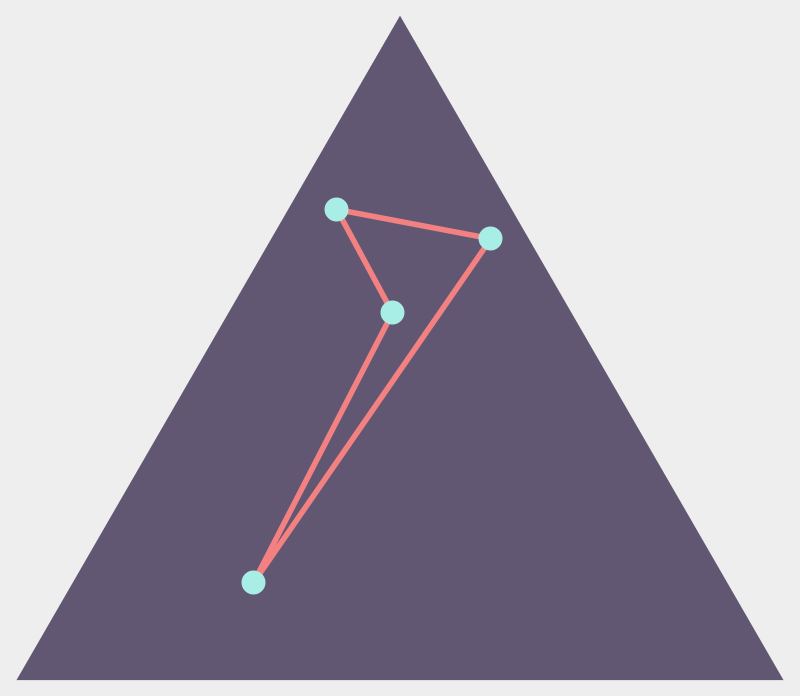
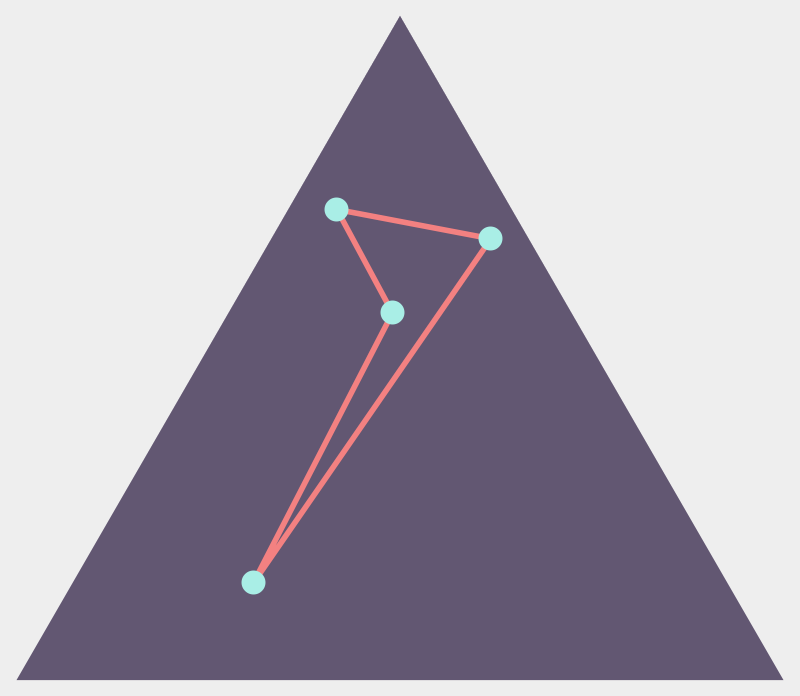
reentrant
J.J. Sylvester, Educational Times, April 1864
Sylvester’s four point problem
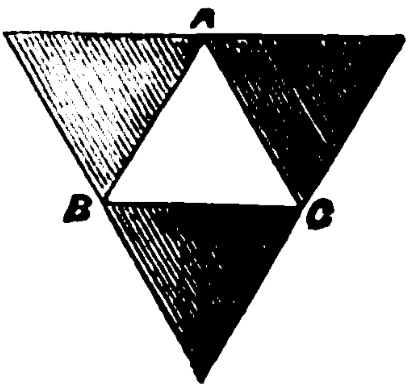
Sylvester and Cayley’s solution

J.J. Sylvester, Phil. Trans. R. Soc. London 154 (1864), p. 654, footnote 64(b)
W.S.B. Woolhouse, Mathematical Questions with Their Solutions VII (1867), p. 81
A. De Morgan’s solution

A. De Morgan, Trans. Cambridge Phil. Soc. XI (1871), pp. 147–148
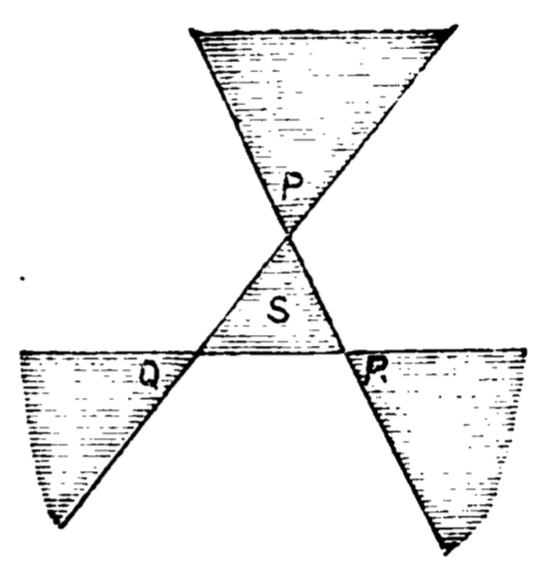
W.S.B. Woolhouse, Mathematical Questions with Their Solutions VI (1866), p. 52

C.M. Ingleby, Mathematical Questions with Their Solutions V (1865), p. 82
C.M. Ingleby’s solution
G. C. De Morgan’s solution

G.C. De Morgan, Mathematical Questions with Their Solutions V (1865), p. 109

W.S.B. Woolhouse’s solution

W.S.B. Woolhouse, Mathematical Questions with Their Solutions VI (1866), p. 52
W.S.B. Woolhouse’s solutions
W.S.B. Woolhouse, Mathematical Questions with Their Solutions VIII (1868), p. 105
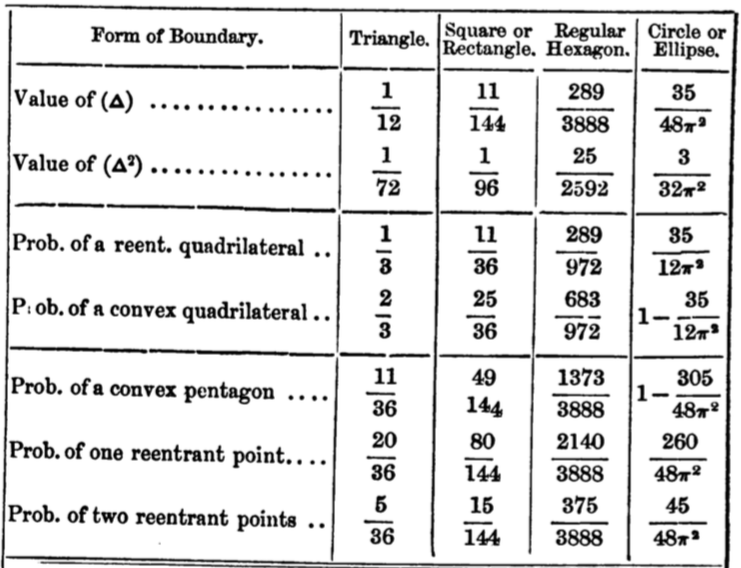
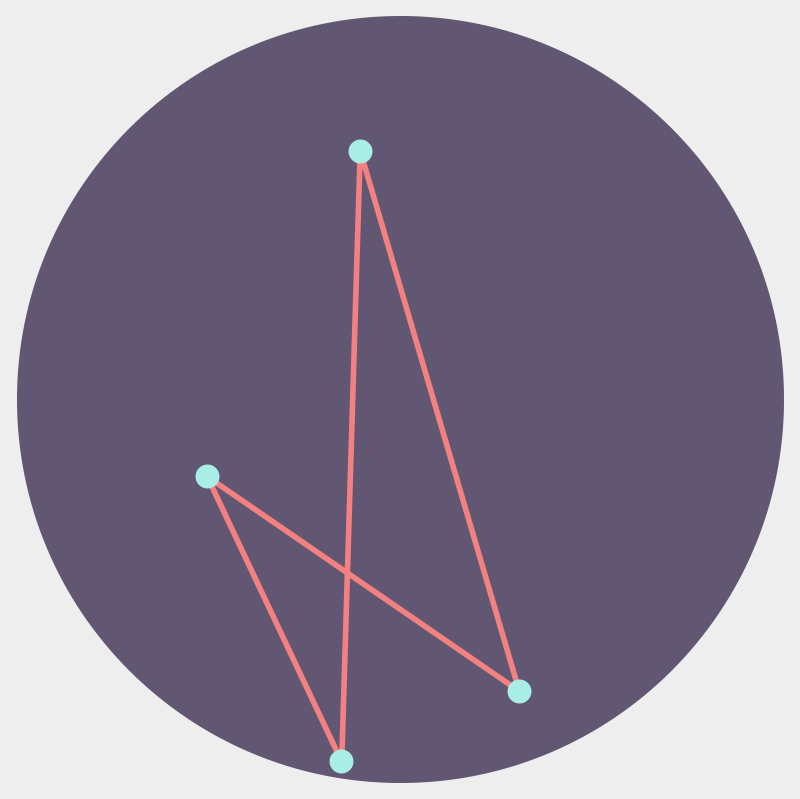
Quadrilaterals in convex bodies
\(\mathbb{P}(\text{reflex})=\frac{1}{3}\)
\(\mathbb{P}(\text{reflex})=\frac{35}{12\pi^2}\approx 0.296\)
Theorem [Blaschke, 1917]
\(\frac{35}{12\pi^2}\leq\mathbb{P}(\text{reflex})\leq\frac{1}{3}\)
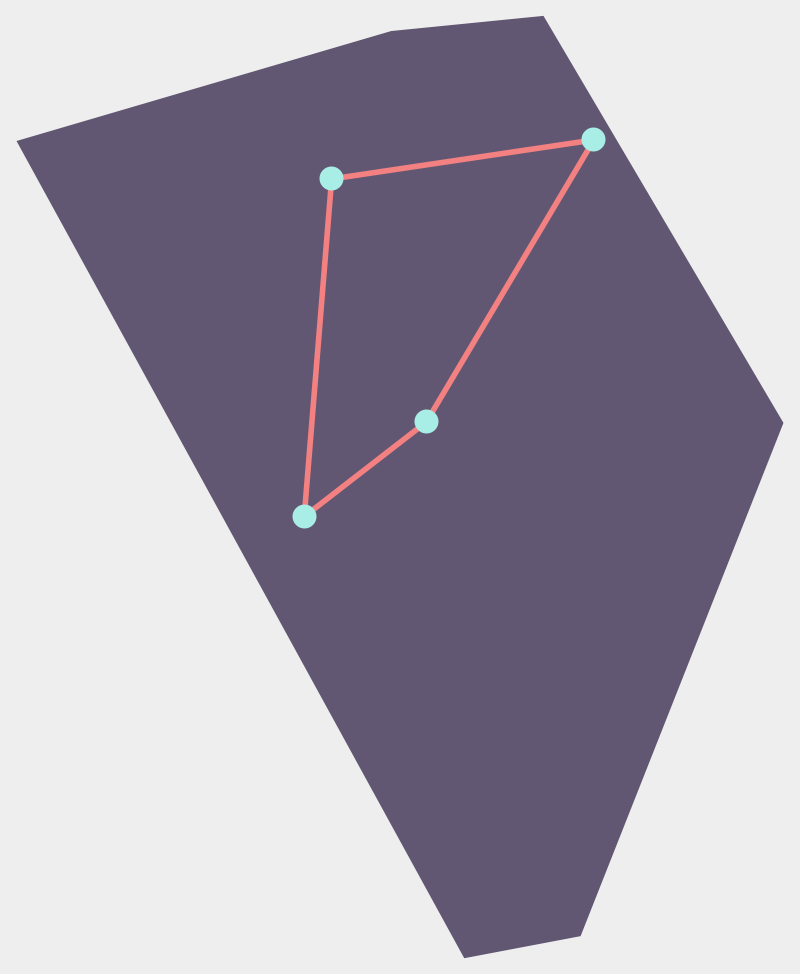
J.M. Wilson’s solution

J.M. Wilson, Mathematical Questions with Their Solutions V (1866), p. 81


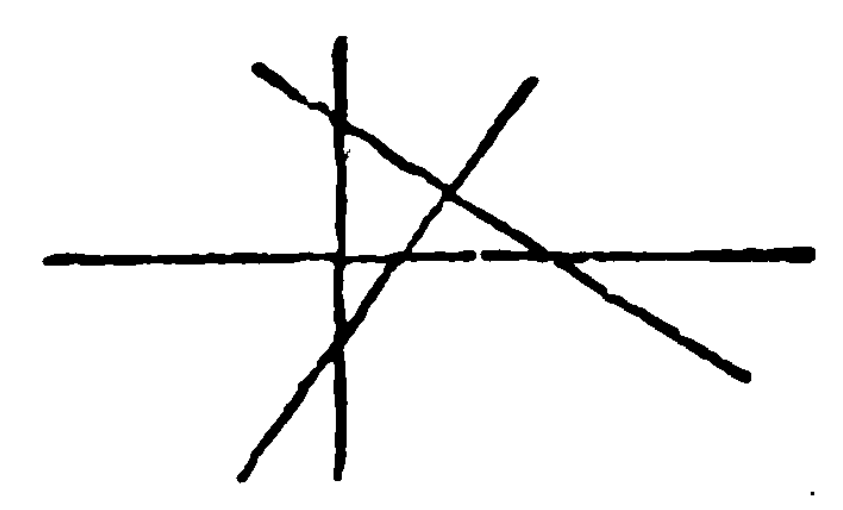



We need measure theory!
W.A. Whitworth, Mathematical Questions with Their Solutions VIII (1868), p. 36

Report on J.J. Sylvester’s presentation of his paper “On a Special Class of Questions on the Theory of Probabilities” to the British Association for the Advancement of Science, 1865
We need geometry!
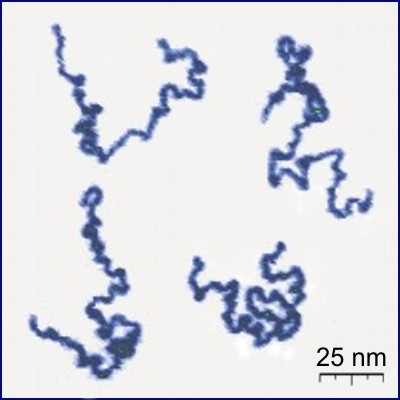
Protonated P2VP
Polymers in solution
Random flight model
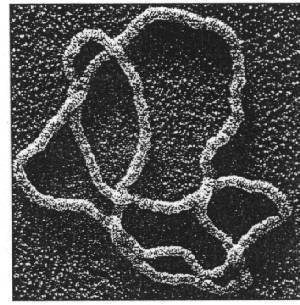
Ring Polymers
Knotted DNA
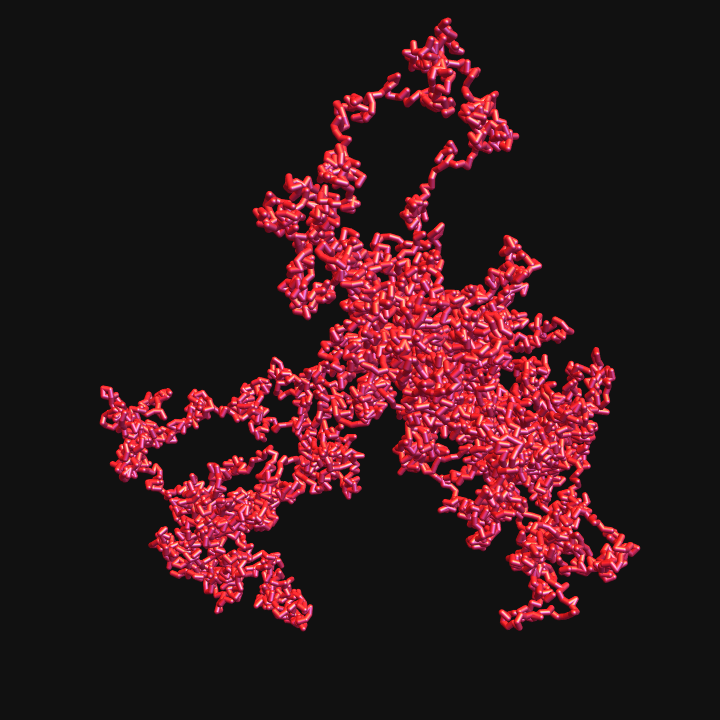
Random polygon model

Symmetries \(\Rightarrow\) Coordinates
Action-angle coordinates
Action Coordinates
Polytope determined by triangle inequalities
Action-Angle Coordinates
Angle Coordinates
Action-Angle Coordinates are Good
Theorem [with Cantarella]
Sampling action-angle coordinates uniformly is equivalent to sampling equilateral polygons uniformly.
Theorem [with Cantarella and Schumacher]
We can generate random equilateral \(n\)-gons in expected time \(\Theta(n^2)\).

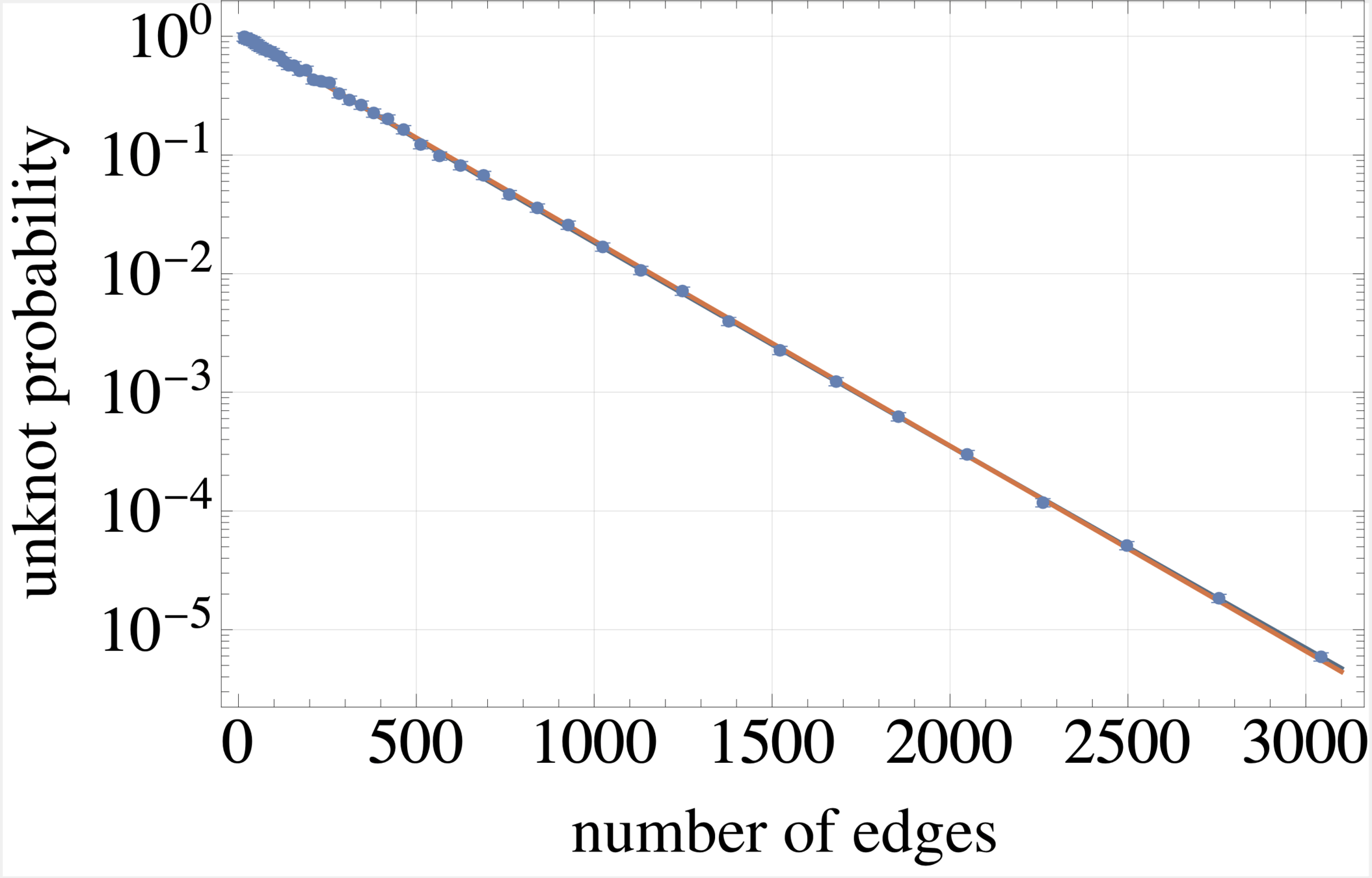
What is the Probability of Knotting?
Frisch–Wasserman–Delbrück Conjecture
In any reasonable model of random knots parametrized by a “size,” the probability of knotting goes to 1 as the size goes to infinity.

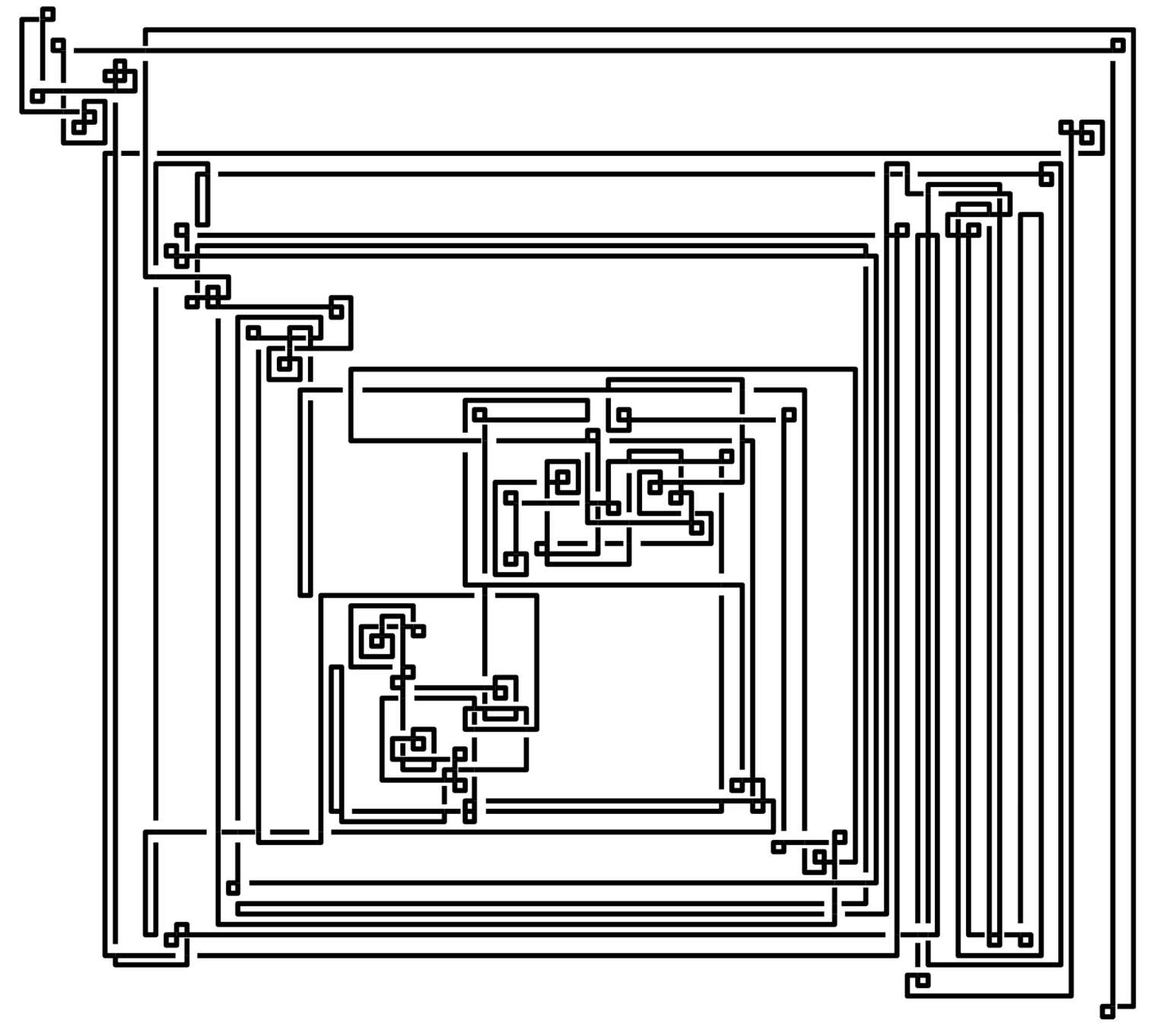
Random polygon
Random diagram
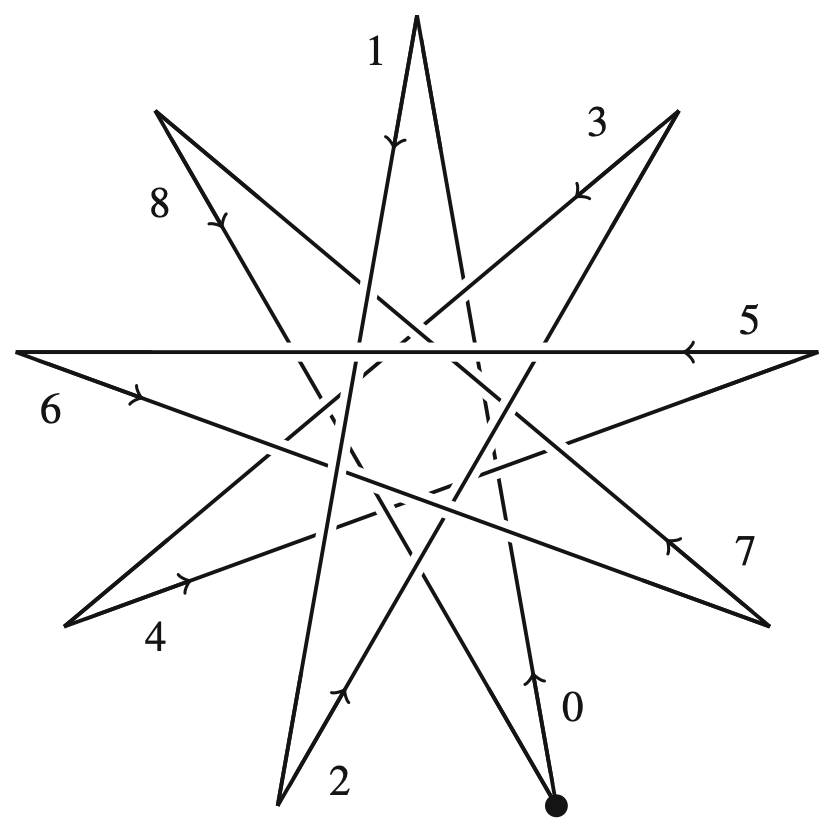
Random petal knot
What is the Probability of Knotting?
Frisch–Wasserman–Delbrück Conjecture
In any reasonable model of random knots parametrized by a “size,” the probability of knotting goes to 1 as the size goes to infinity.

Random polygon
Theorem [Diao]
For random equilateral \(n\)-gons, the probability of knotting is
\(\geq 1-e^{-n^{\epsilon}}\) for some \(\epsilon > 0\).
What About More Complicated Topological Polymers?
Synthetic chemists can now produce simple topological polymers in usable quantities.

\(\theta\)-curves in solution at the Tezuka lab
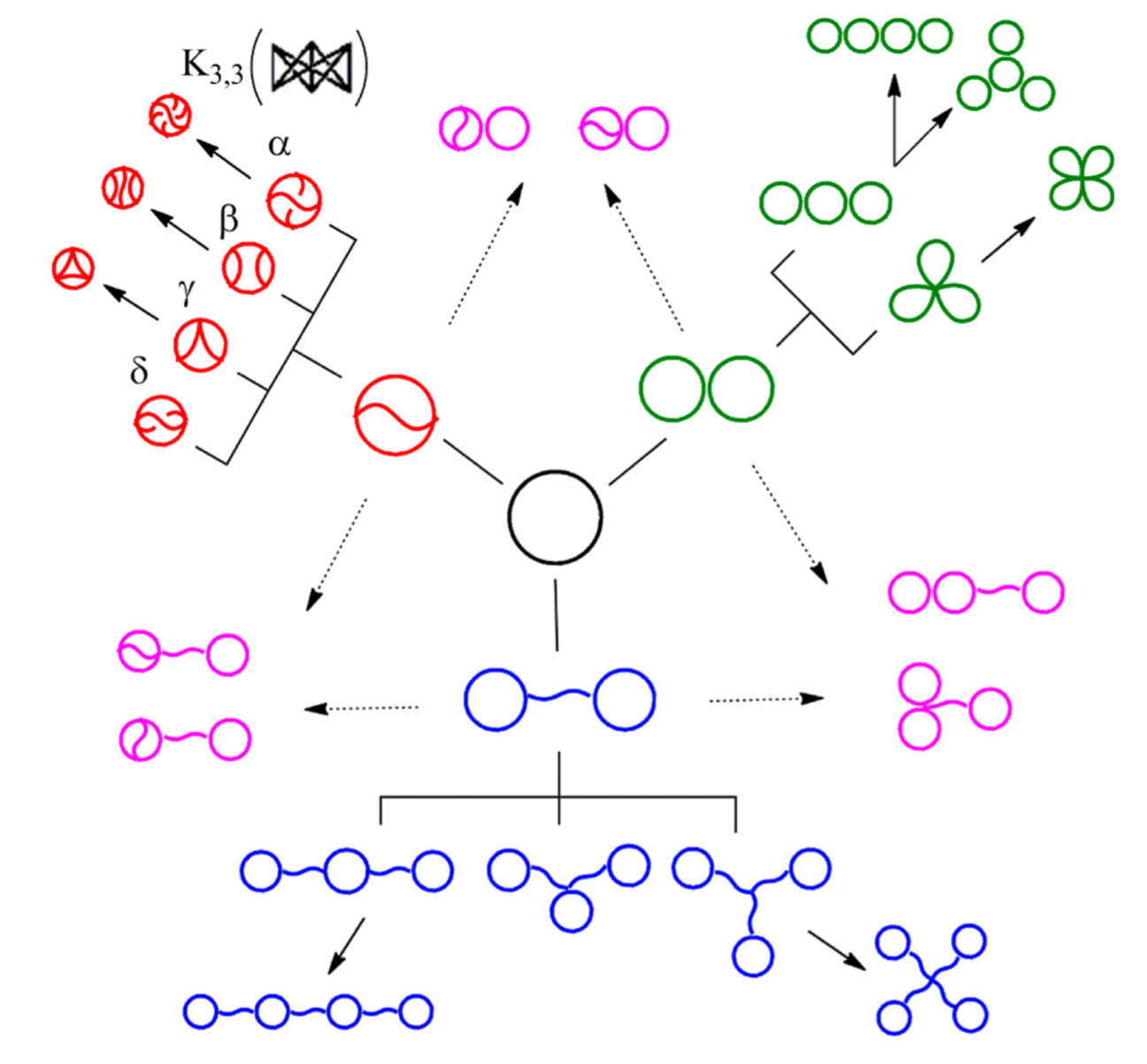
What are good coordinates for random embeddings of graphs?
Thank You!
shonkwiler.org/cu24
References
The symplectic geometry of closed equilateral random walks in 3-space
Jason Cantarella and Clayton Shonkwiler
Annals of Applied Probability 26 (2016), no. 1, 549–596
New stick number bounds from random sampling of confined polygons
Thomas D. Eddy and Clayton Shonkwiler
Experimental Mathematics 31 (2022), no. 4, 1373–1395
Random triangle and polygons in the plane
Jason Cantarella, Tom Needham, Clayton Shonkwiler, and Gavin Stewart
The American Mathematical Monthly 126 (2019), no. 2, 113–134
A faster direct sampling algorithm for equilateral closed polygons and the probability of knotting
Jason Cantarella, Henrik Schumacher, and Clayton Shonkwiler
Journal of Physics A: Mathematical and Theoretical 57 (2024), no. 28, 28205