Frames, Optimization, and Geometric Invariant Theory
/cvg23
this talk!
Special Session on Harmonic Analysis and its Applications to Signals and Information, Apr. 15, 2023
Collaborators
Florida State University
Funding
National Science Foundation (DMS–2107700)
Simons Foundation (#709150)
(The) Ohio State University
Johns Hopkins University
Finite Frames
\(\mathbb{K} = \mathbb{R}\) or \(\mathbb{C}\). A (finite) frame in \(\mathbb{K}^d\) is a spanning set \(f_1, \dots, f_N \in (\mathbb{K}^d)^N\).

\(F = [f_1 \, f_2 \, \ldots \, f_N ] \in \mathbb{K}^{d \times N}\)
Frame operator \(FF^* = \sum f_if_i^*\)
Frames and Projectors
If \(\|f_i\|^2 = 1\) for all \(i\), the \(P_i := f_if_i^*\) are orthogonal projectors.
\(FF^* = \sum f_if_i^* = \sum P_i\)
More generally, (unweighted) fusion frames are sequences of subspaces \(S_1, \ldots , S_N \subseteq \mathbb{K}^d\) so that \(\sum P_i\) is invertible.
Unit-norm frames \(\Longleftrightarrow\) (certain) points in \(\prod_{i=1}^N \mathbb{KP}^{d-1}\)
(certain) points in \(\prod_{i=1}^N \operatorname{Gr}(k_i,d)\)
These (fusion) frames are tight if \(\sum P_i = \lambda \mathbb{I}_{d \times d}\).
\(\Longleftrightarrow\)
FUNTFs
TFFs
Frame Potential
Definition [Benedetto–Fickus, Casazza–Fickus]
The (fusion) frame potential is
\(\operatorname{FP}(P_1,\ldots,P_N) = \|\sum P_i\|_{\operatorname{Fr}}^2\)
Proposition [cf. Welch]
When they exist, the FUNTFs/TFFs are exactly the global minima of \(\operatorname{FP}\).
Theorem [Benedetto–Fickus]
As a function on unit-norm frames with fixed \(d\) and \(N\), \(\operatorname{FP}\) has no spurious local minima.
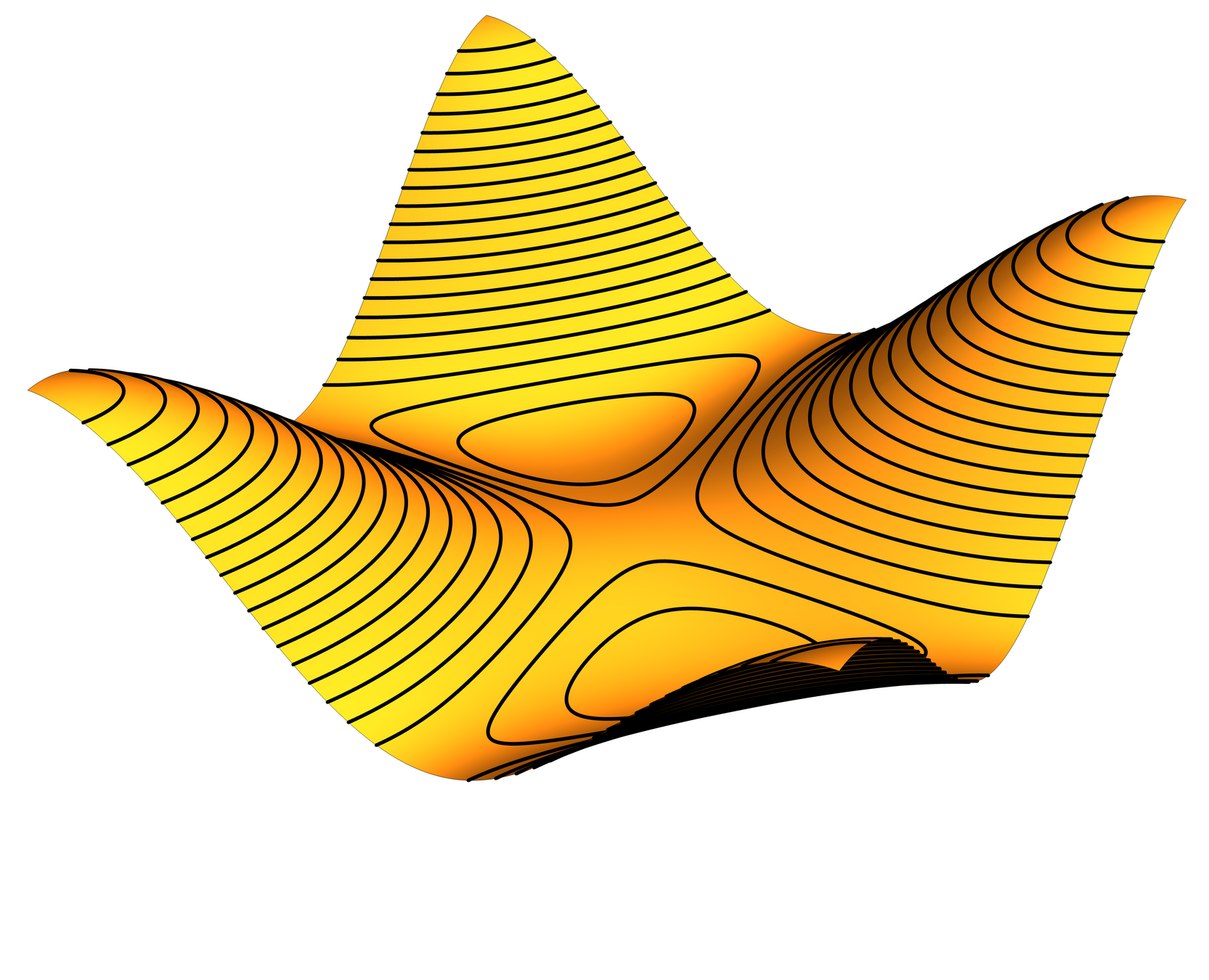
Optimization

Theorem [with Mixon, Needham, and Villar]
Consider the initial value problem
\(\Gamma(F_0,0) = F_0, \qquad \frac{d}{dt}\Gamma(F_0,t) = -\operatorname{grad}\operatorname{FP}(\Gamma(F_0,t))\).
If \(F_0\) has full spark, then \(\lim_{t \to \infty} \Gamma(F_0,t)\) is a FUNTF.
Theorem [with Needham]
Same for fusion frames.
Some Symplectic Geometry
\(F \mapsto FF^*\) is the momentum map of the diagonal \(SU(d)\) action on \(\prod_{i=1}^N \mathbb{CP}^{d-1}\).
\(\Longrightarrow\) \(\operatorname{FP}(F) = \|FF^*\|_{\operatorname{Fr}}^2\) is the squared norm of a momentum map.

Frances Kirwan
Gert-Martin Greuel [CC BY-SA 2.0 DE], from Oberwolfach Photo Collection
Image by rawpixel.com on Freepik
Theorem [Kirwan]
Reductive algebraic group action on Kähler manifold \(\Longrightarrow\) semistable points flow to global minima.

This kind of function is really nice!
Geometric Invariant Theory (GIT)
The GIT quotient consists of group orbits which can be distinguished by \(G\)-invariant (homogeneous) polynomials.
\(\mathbb{C}^* \curvearrowright \mathbb{CP}^2\)
\(t \cdot [z_0:z_1:z_2] = [z_0: tz_1:\frac{1}{t}z_2]\)

Roughly: identify orbits whose closures intersect, throw away orbits on which all polynomials vanish.
\( \mathbb{CP}^2/\!/\,\mathbb{C}^* \cong\mathbb{CP}^1\)
Stability
Definition.
Given a reductive group \(G\) acting algebraically on a vector space \(V\), a vector \(v \in V\) is unstable if \(0 \in \overline{G \cdot v}\); otherwise, \(v\) is semi-stable.
Example.
For UNFs, \(G = \operatorname{SL}(d)\), \(V = (\mathbb{K}^d)^{\otimes N}\),
\(g \cdot (v_1 \otimes \cdots \otimes v_N) = (gv_1) \otimes \cdots \otimes (gv_N)\)
Metatheorem [cf. Kirwan]
- Gradient flow stays in the \(G\) orbit.
- Gradient flow preserves semi-stability.
- Non-minimizing critical points are unstable.
Key Technical Tool
Hilbert–Mumford Criterion.
\(v \in V\) is semi-stable \(\Longleftrightarrow\) there exists a 1-parameter subgroup \(\lambda: \mathbb{C}^* \to G\) so that
\(\lim_{t \to 0}\lambda(t) \cdot v = 0\).
Example.
Question
What other functions of interest arise as squared norms of momentum maps?
Thank you!
References
Fusion frame homotopy and tightening fusion frames by gradient descent
Tom Needham and Clayton Shonkwiler
Journal of Fourier Analysis and Applications, to appear
Three proofs of the Benedetto–Fickus theorem
Dustin Mixon, Tom Needham, Clayton Shonkwiler, and Soledad Villar
Sampling, Approximation, and Signal Analysis (Harmonic Analysis in the Spirit of J. Rowland Higgins), Stephen D. Casey, M. Maurice Dodson, Paulo J. S. G. Ferreira and Ahmed Zayed, eds., to appear