Generating (and Computing with) Very Large Ensembles of Random Polygonal Knots
/davis21
this talk!
Key Points
- Symplectic tools lead to efficient algorithms for sampling random polygonal knots (in confinement).
- Confinement boosts the likelihood of complicated knots: enriched sampling.
Elementary Knot Invariants
Definition.
The stick number of a knot \(K\), denoted \(\operatorname{stick}[K]\), is the minimum number of segments needed to create a polygonal version of \(K\).
\(\operatorname{stick}[3_1]=6\)


Elementary Knot Invariants
If \(v \in S^2\) and \(\gamma\) a closed curve, let \(\operatorname{b}_v(\gamma)\) be the number of local maxima of the projection of \(\gamma\) to the line through \(v\).
\(\operatorname{b}_{v_1}(\gamma)=2\)
\(v_1\)
\(v_2\)
\(\operatorname{b}_{v_2}(\gamma)=3\)
Elementary Knot Invariants
Definition.
If \(\gamma\) is a closed curve, its bridge number is
and its superbridge number is
The bridge index of a knot \(K\) is
and the superbridge index is

\(\operatorname{b}[4_1]=2\) and \(\operatorname{sb}[4_1]=3\).
(Most of) What is Known
Theorem [Jeon–Jin]
Every knot except \(3_1\) and \(4_1\) and possibly \(5_2\), \(6_1\), \(6_2\), \(6_3\), \(7_2\), \(7_3\), \(7_4\), \(8_4\), and \(8_9\) has superbridge index \(\geq 4\).
Theorem [Calvo]
Every knot except \(3_1\), \(4_1\), \(5_1\), \(5_2\), \(6_1\), \(6_2\), \(6_3\), \(8_{19}\), \(8_{20}\), \(3_1 \# 3_1\), and \(3_1\# -3_1\) has stick number \(\geq 9\).
Theorem [Kuiper, Jin, Adams et al., others]
The superbridge index is known for all torus knots, and the stick number is known for an infinite family of torus knots.
Mantra
Examples provide upper bounds!
Results
Theorem [with Eddy]
The stick number of each of the knots \(9_{35}\), \(9_{39}\), \(9_{43}\), \(9_{45}\), and \(9_{48}\) is exactly 9.
Corollary
Each of the knots \(9_{35}\), \(9_{39}\), \(9_{43}\), \(9_{45}\), and \(9_{48}\) has superbridge index equal to 4.





\(9_{35}\)
\(9_{39}\)
\(9_{43}\)
\(9_{45}\)
\(9_{48}\)
Proof.
\(\operatorname{b}(K) < \operatorname{sb}(K) \leq \frac{1}{2} \operatorname{stick}(K)\) and each of these knots has bridge index 3.
Proof.
The stick number is bounded below by 9, and we found 9-stick examples.
Theorem [with Eddy]
The equilateral stick number of each of the knots \(9_2\), \(9_3\), \(9_{11}\), \(9_{15}\), \(9_{21}\), \(9_{25}\), \(9_{27}\), \(10_8\), \(10_{16}\), \(10_{17}\), \(10_{56}\), \(10_{83}\), \(10_{85}\), \(10_{90}\), \(10_{91}\), \(10_{94}\), \(10_{103}\), \(10_{105}\), \(10_{106}\), \(10_{107}\), \(10_{110}\), \(10_{111}\), \(10_{112}\), \(10_{115}\), \(10_{117}\), \(10_{118}\), \(10_{119}\), \(10_{126}\), \(10_{131}\), \(10_{133}\), \(10_{137}\), \(10_{138}\), \(10_{142}\), \(10_{143}\), \(10_{147}\), \(10_{148}\), \(10_{149}\), \(10_{153}\), and \(10_{164}\) is less than or equal to 10.
The equilateral stick number of each of the knots \(10_3\), \(10_6\), \(10_7\), \(10_{10}\), \(10_{15}\), \(10_{18}\), \(10_{20}\), \(10_{21}\), \(10_{22}\), \(10_{23}\), \(10_{24}\), \(10_{26}\), \(10_{28}\), \(10_{30}\), \(10_{31}\), \(10_{34}\), \(10_{35}\), \(10_{38}\), \(10_{39}\), \(10_{43}\), \(10_{44}\), \(10_{46}\), \(10_{47}\), \(10_{50}\), \(10_{51}\), \(10_{53}\), \(10_{54}\), \(10_{55}\), \(10_{57}\), \(10_{62}\), \(10_{64}\), \(10_{65}\), \(10_{68}\), \(10_{70}\), \(10_{71}\), \(10_{72}\), \(10_{73}\), \(10_{74}\), \(10_{75}\), \(10_{77}\), \(10_{78}\), \(10_{82}\), \(10_{84}\), \(10_{95}\), \(10_{97}\), \(10_{100}\), and \(10_{101}\) is less than or equal to 11.
The equilateral stick number of each of the knots \(10_{76}\) and \(10_{80}\) is less than or equal to 12.
In particular, all knots up to 10 crossings have equilateral stick number \(\leq 12\).
Results
Theorem [with Eddy]
The equilateral stick number of each of the knots \(9_2\), \(9_3\), \(9_{11}\), \(9_{15}\), \(9_{21}\), \(9_{25}\), \(9_{27}\), \(10_8\), \(10_{16}\), \(10_{17}\), \(10_{18}\), \(10_{56}\), \(10_{68}\), \(10_{82}\), \(10_{83}\), \(10_{85}\), \(10_{90}\), \(10_{91}\), \(10_{94}\), \(10_{100}\), \(10_{103}\), \(10_{105}\), \(10_{106}\), \(10_{107}\), \(10_{110}\), \(10_{111}\), \(10_{112}\), \(10_{115}\), \(10_{117}\), \(10_{118}\), \(10_{119}\), \(10_{126}\), \(10_{131}\), \(10_{133}\), \(10_{137}\), \(10_{138}\), \(10_{142}\), \(10_{143}\), \(10_{147}\), \(10_{148}\), \(10_{149}\), \(10_{153}\), and \(10_{164}\) is less than or equal to 10.
The equilateral stick number of each of the knots \(10_3\), \(10_6\), \(10_7\), \(10_{10}\), \(10_{15}\), \(\sout{10_{18}}\), \(10_{20}\), \(10_{21}\), \(10_{22}\), \(10_{23}\), \(10_{24}\), \(10_{26}\), \(10_{28}\), \(10_{30}\), \(10_{31}\), \(10_{34}\), \(10_{35}\), \(10_{38}\), \(10_{39}\), \(10_{43}\), \(10_{44}\), \(10_{46}\), \(10_{47}\), \(10_{50}\), \(10_{51}\), \(10_{53}\), \(10_{54}\), \(10_{55}\), \(10_{57}\), \(10_{62}\), \(10_{64}\), \(10_{65}\), \(\sout{10_{68}}\), \(10_{70}\), \(10_{71}\), \(10_{72}\), \(10_{73}\), \(10_{74}\), \(10_{75}\), \(10_{77}\), \(10_{78}\), \(\sout{10_{82}}\), \(10_{84}\), \(10_{95}\), \(10_{97}\), \(\sout{10_{100}}\), and \(10_{101}\) is less than or equal to 11.
The equilateral stick number of each of the knots \(10_{76}\) and \(10_{80}\) is less than or equal to 12.
In particular, all knots up to 10 crossings have equilateral stick number \(\leq 12\).
Results


\(10_{16}\)
\(10_{84}\)
Results
Theorem [with Blair, Eddy, and Morrison]
The knots \(13n_{592}\) and \(15n_{41,127}\) have bridge index 4, superbridge index 5, and stick number 10.


\(13n_{592}\)
\(15n_{41,127}\)
Proof.
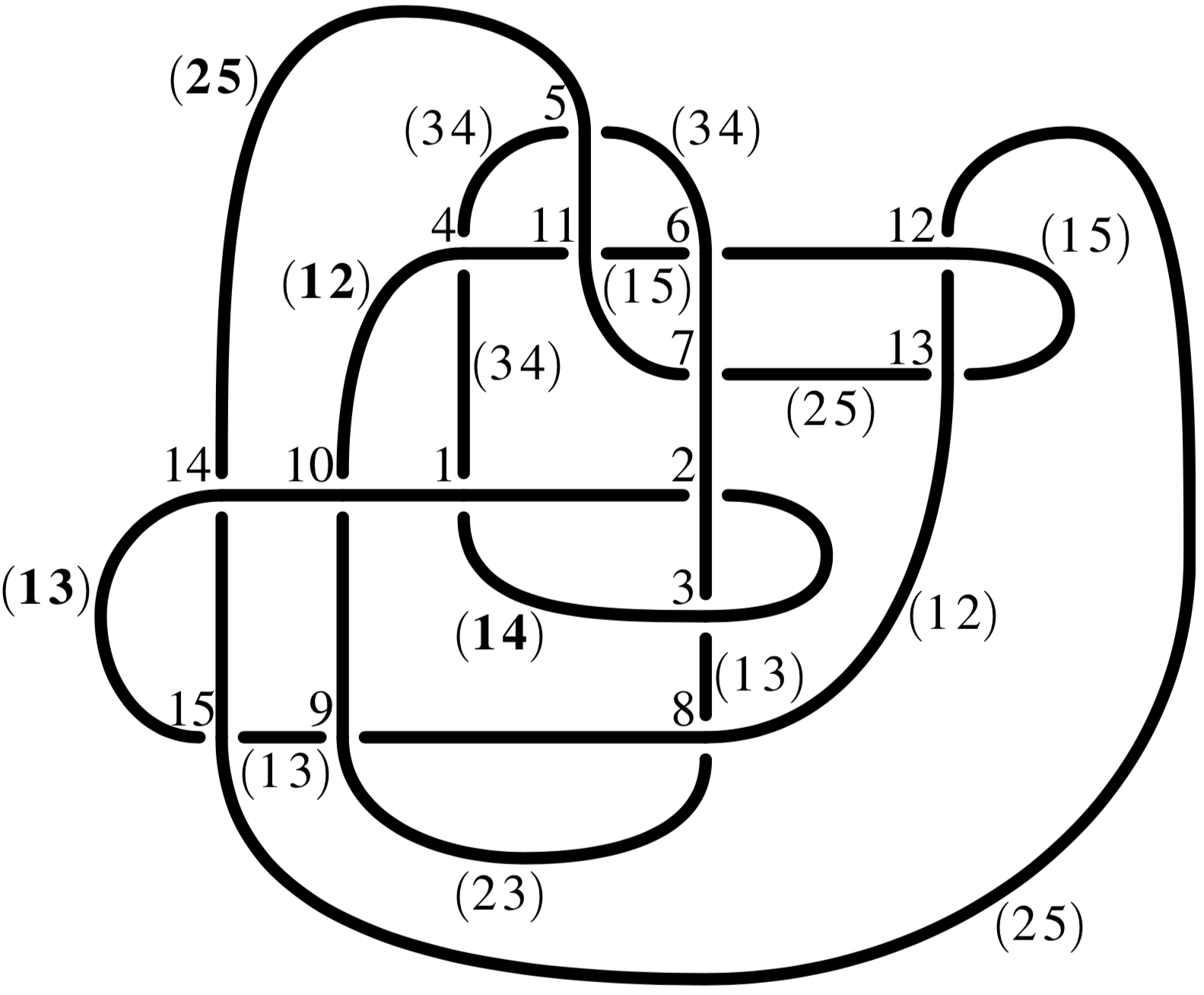


Surjective homomorphism \(\pi_1(S^3 \backslash 15n_{41,127}) \to S_5\), so
\(4 \leq \operatorname{b} < \operatorname{sb} \leq \frac{1}{2}\operatorname{stick} \leq 5\).
\(15n_{41,127}\)
\(\overline{13n_{592}}\)
Results
Theorem [—]
The knots \(8_1\), \(8_2\), \(8_3\), \(8_5\), \(8_6\), \(8_7\), \(8_8\), \(8_{10}\), \(8_{11}\), \(8_{12}\), \(8_{13}\), \(8_{14}\), \(8_{15}\), \(9_7\), \(9_{16}\), \(9_{20}\), \(9_{26}\), \(9_{28}\), \(9_{32}\), and \(9_{33}\) all have superbridge index equal to 4.
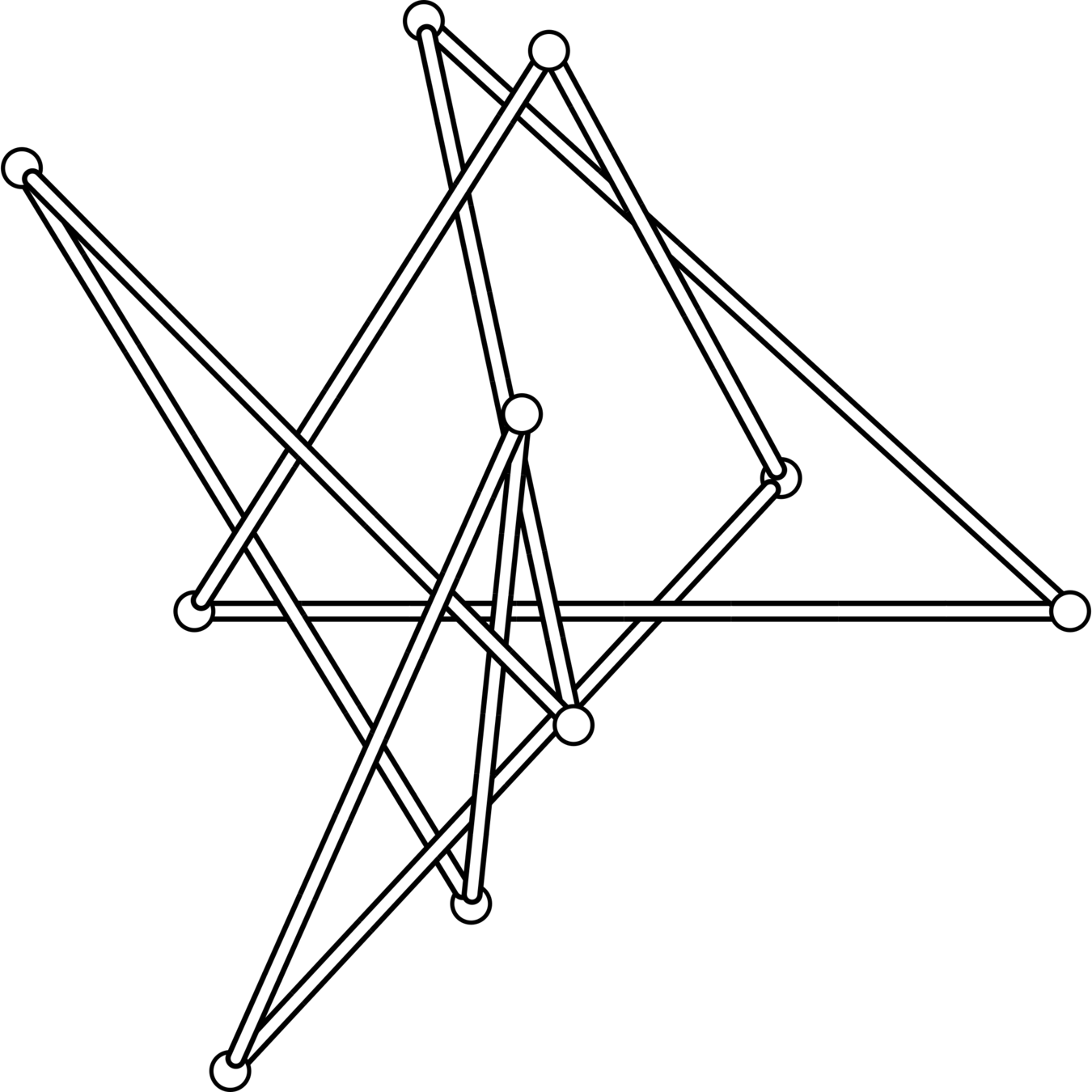
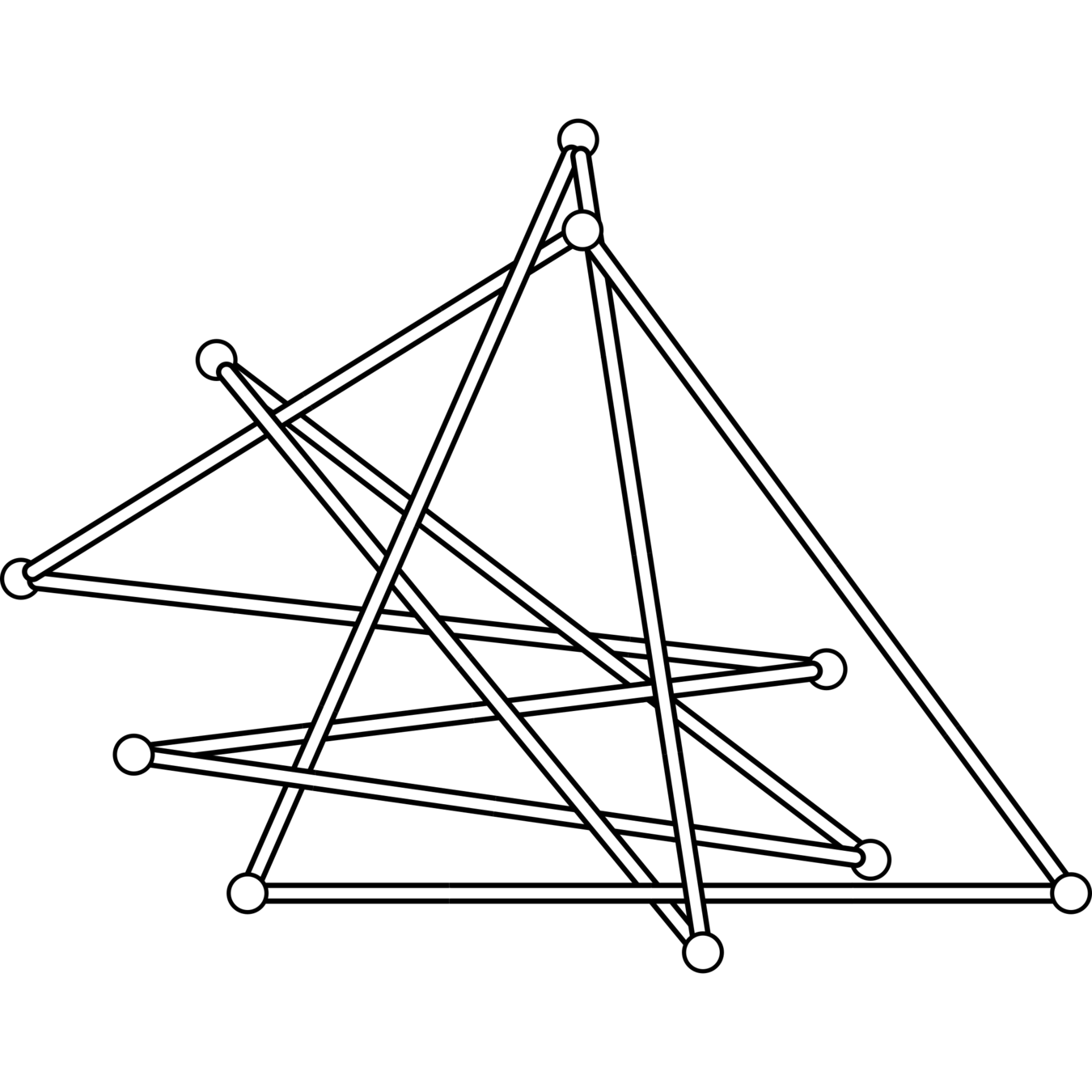
\(8_{10}\)
\(9_7\)
Proof.
For each knot, \(4 \leq \mathrm{sb}[K]\leq \frac{1}{2}\mathrm{stick}[K] \leq 5\).
If \(\mathrm{sb} = 5\) for a 10-stick realization, then there exists \(v\in S^2\) so that
\(v^T [e_1 | -e_2 | \cdots | -e_{10} ] \)
has all positive entries. By Gordan’s theorem, this system of linear inequalities is feasible if and only if
\([e_1 | -e_2 | \cdots | -e_{10}] u = 0\)
cannot be solved for a nonzero vector u with nonnegative entries.
Results
…or on Github, along with source code!
Results have also been added to KnotInfo
Strategy
Generate hundreds of billions of random polygons in tight confinement and look for new examples.
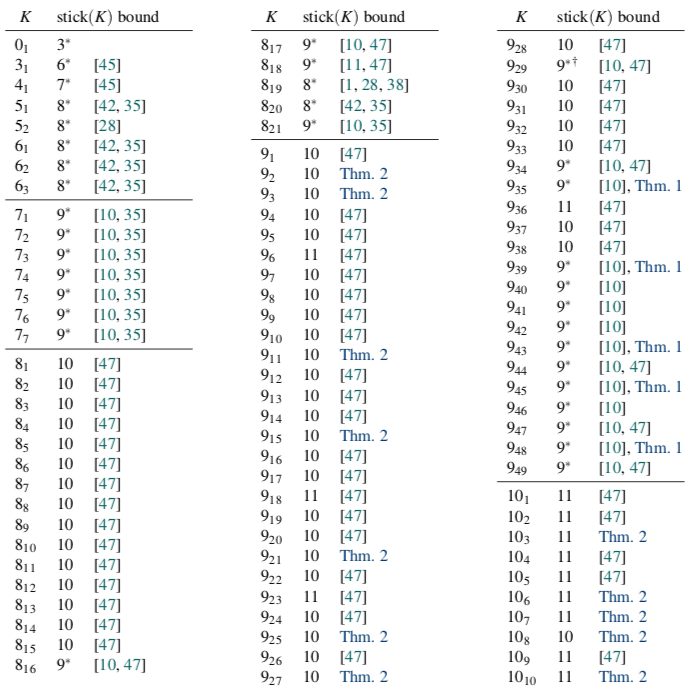
Some Numbers
- 390+ billion polygons generated
- Identified knot types of all but 59(!)
- 93.3% unknots
- 2484 distinct knot types, 2449 prime, including 11 different 16-crossing knots
- \(\approx\)100,000 core-hours of CPU time (or 11.4 core-years)
Data for 10-gons
Random Walks
The freely jointed chain/random walk model for polymers dates back to Kuhn in the 1930s.
Modern polymer physics is based on the analogy between a polymer chain and a random walk.
Simulating random walks in \(\mathbb{R}^3\) is easy
Generate \(n\) independent uniform random points in \(\mathbb{R}^3\) according to your favorite probability distribution and treat them as an ordered list of edge vectors.

Viewpoint
Topologically constrained random walk \(\Leftrightarrow\) point in some (nice!) configuration space
A random polygonal knot is a random walk subject to a topological constraint.
Equilateral Polygons
The space of equilateral \(n\)-gons can be constructed as a symplectic reduction (see Kapovich–Millson and Hausmann–Knutson):
Continuous symmetry \(\Rightarrow\) conserved quantity
\(n-3\) commuting symmetries
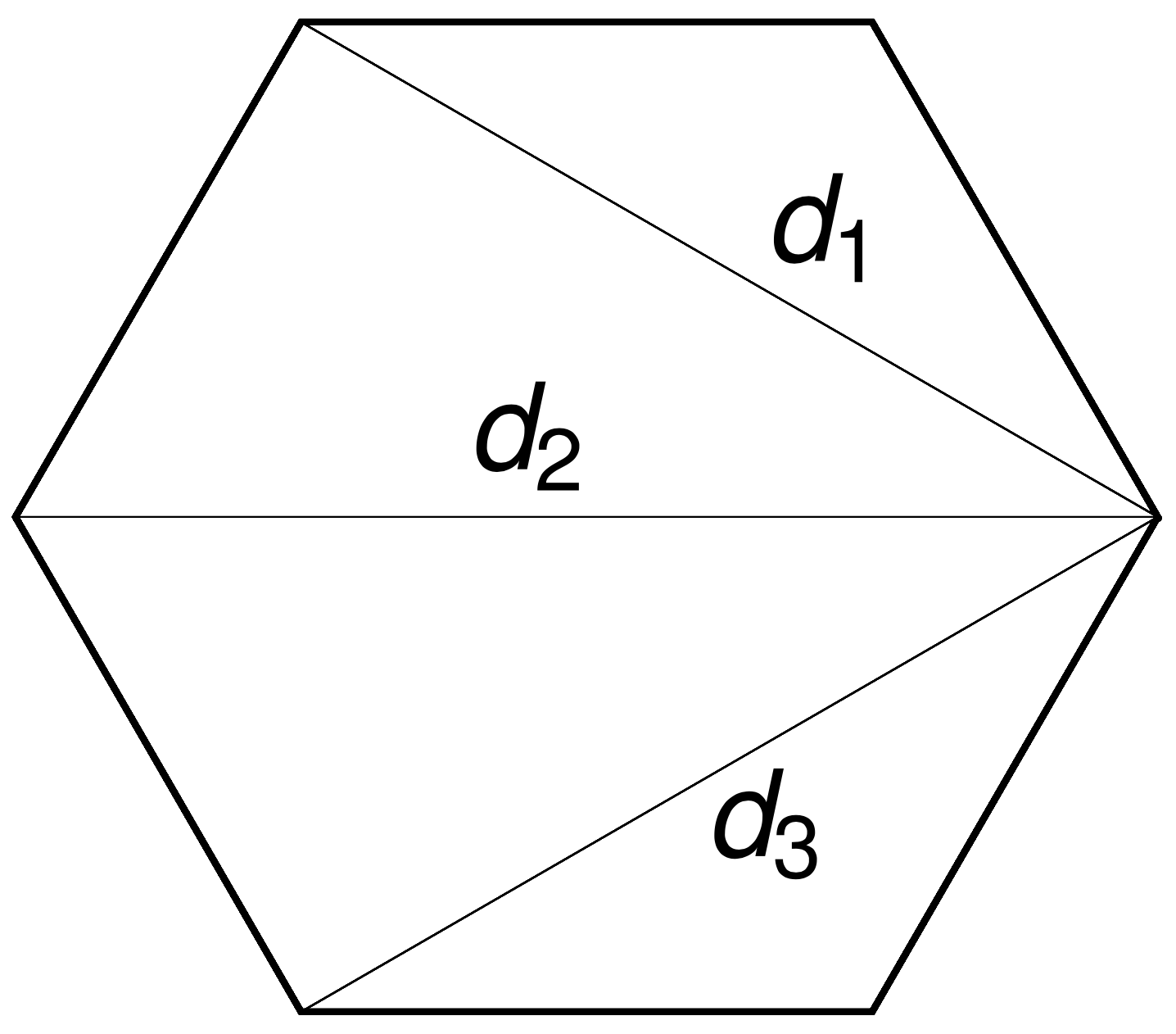
Rotations around \(n-3\) chords \(d_i\) by \(n-3\) angles \(\theta_i\) commute.


More precisely, \(\operatorname{ePol}(n)\) is (almost) toric, and the \(d_i\) and \(\theta_i\) are action-angle coordinates.
Chord distributions
Theorem [with Cantarella]
The joint distribution of \(d_1,\ldots , d_{n-3}\) and \(\theta_1, \ldots , \theta_{n-3}\) are all uniform on their domains.
Therefore, sampling equilateral \(n\)-gons is equivalent to sampling random points in the convex polytope of \(d_i\)’s and random angles \(\theta_i\).
A polytope
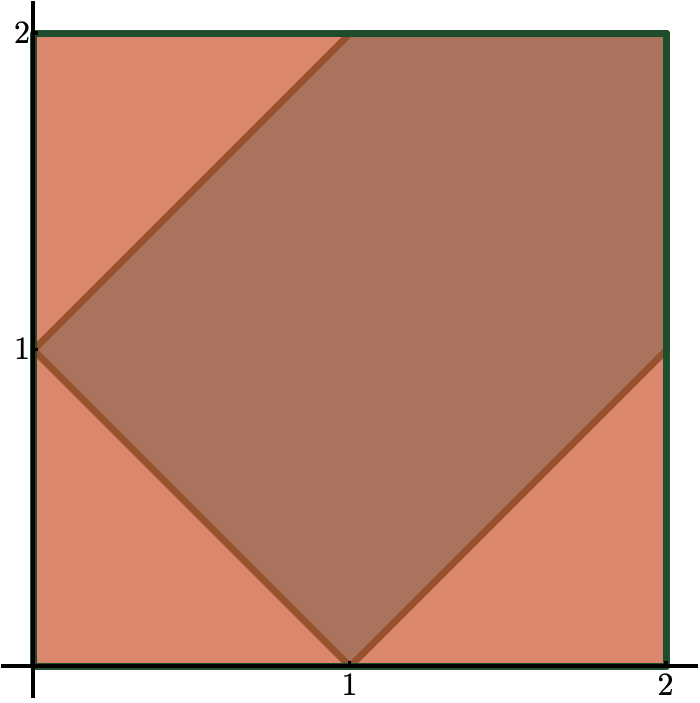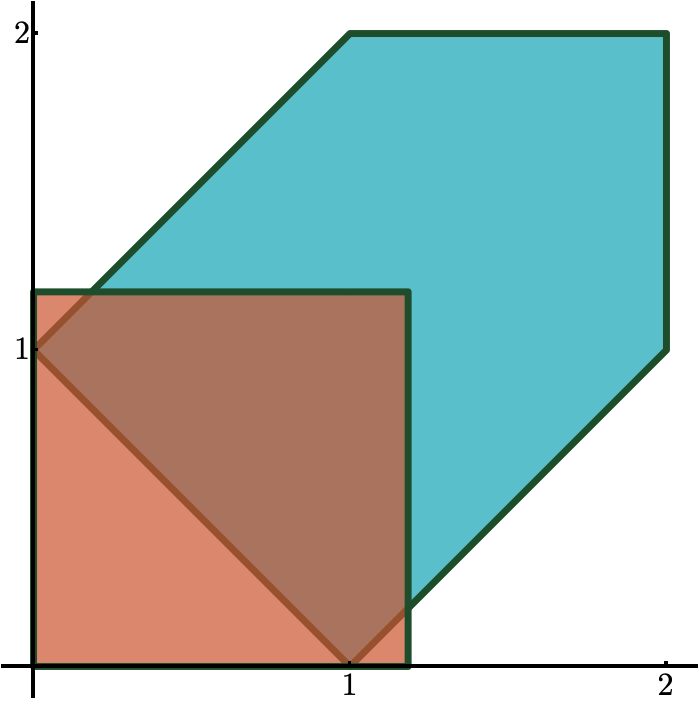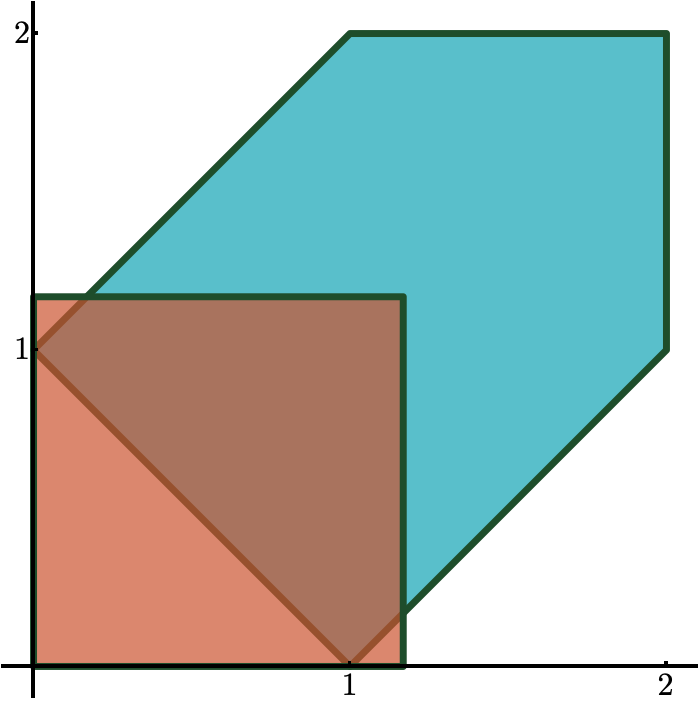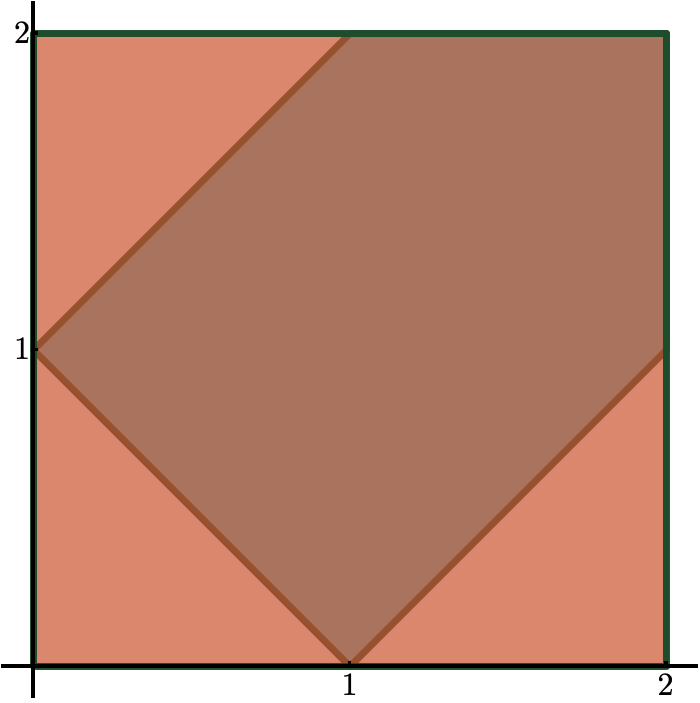
The \((n-3)\)-dimensional moment polytope \(\mathcal{P}_n \subset \mathbb{R}^{n-3}\) is defined by the triangle inequalities
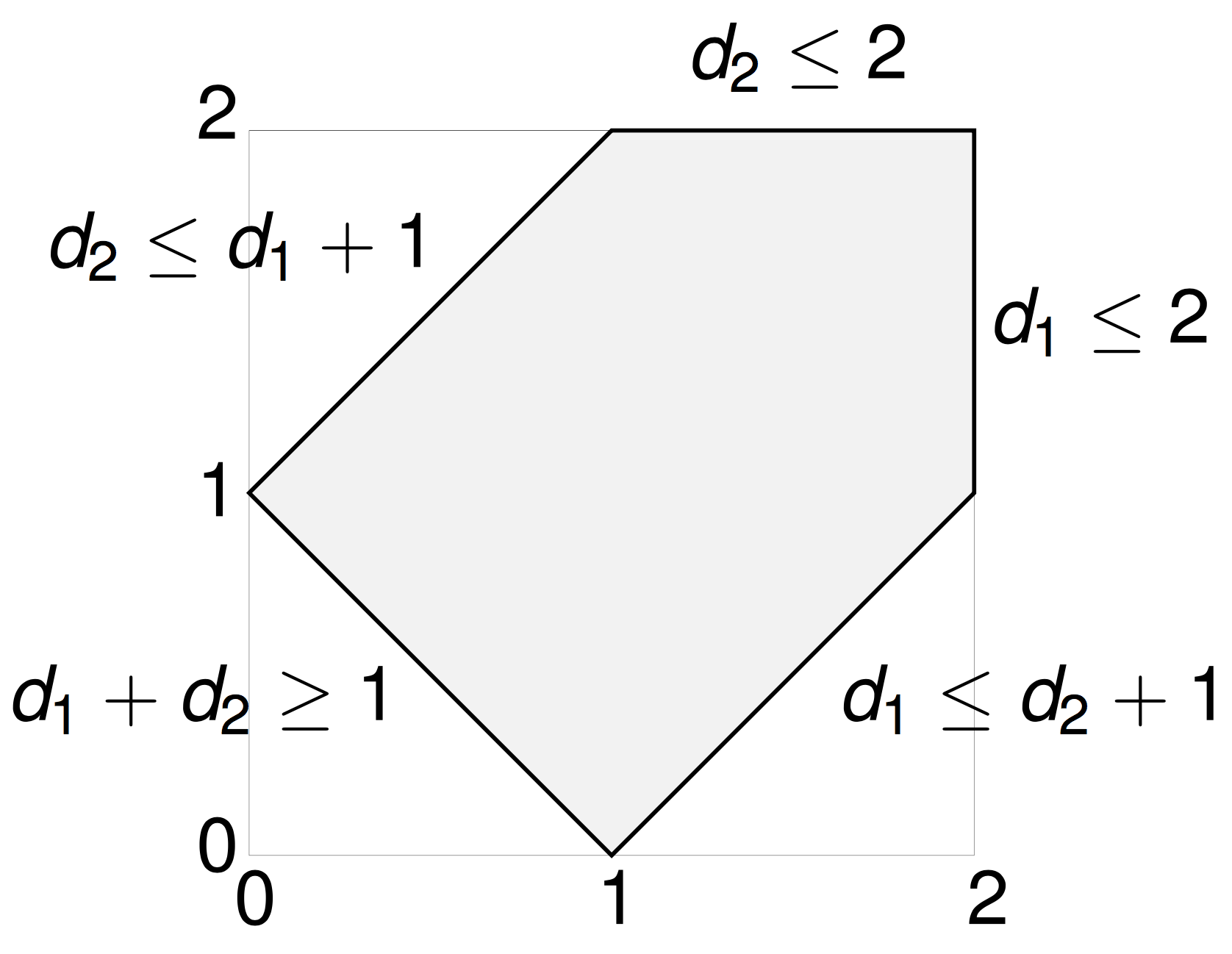
Reconstruction
Sampling
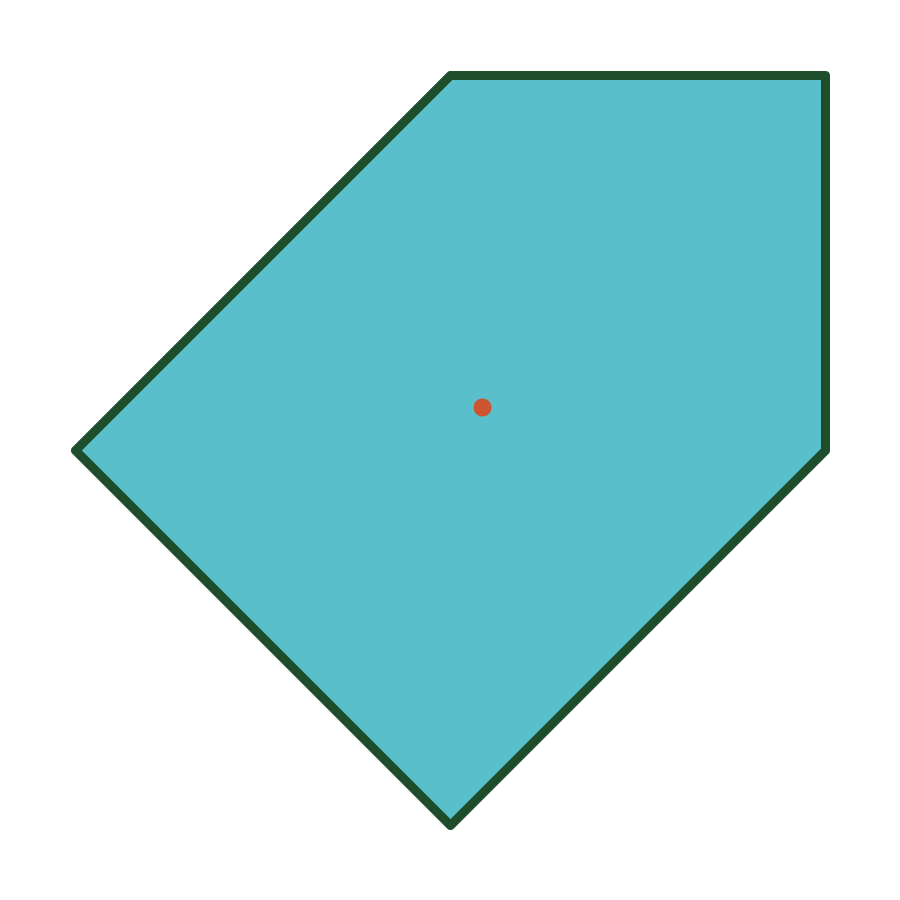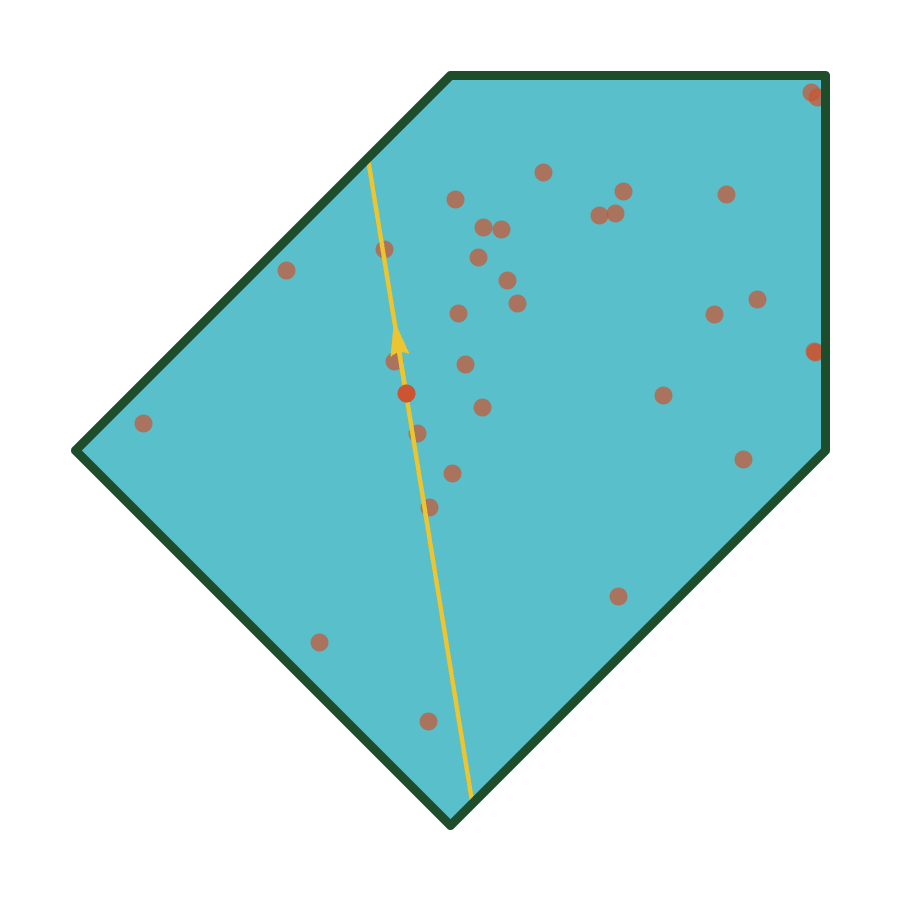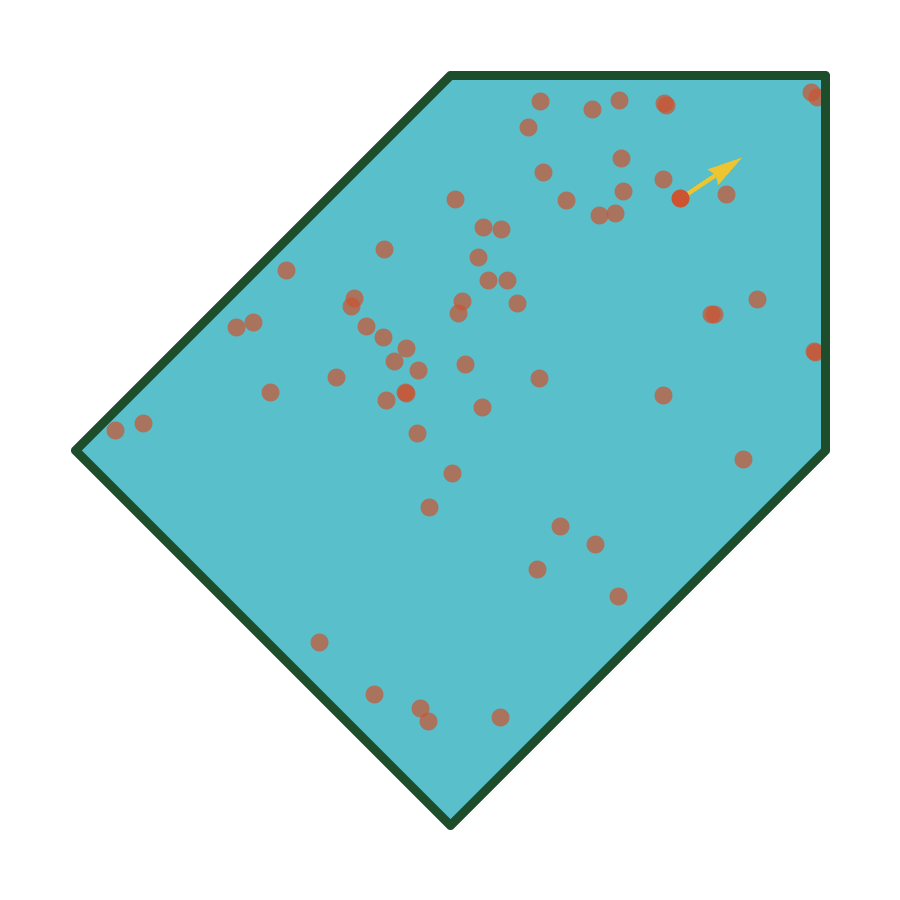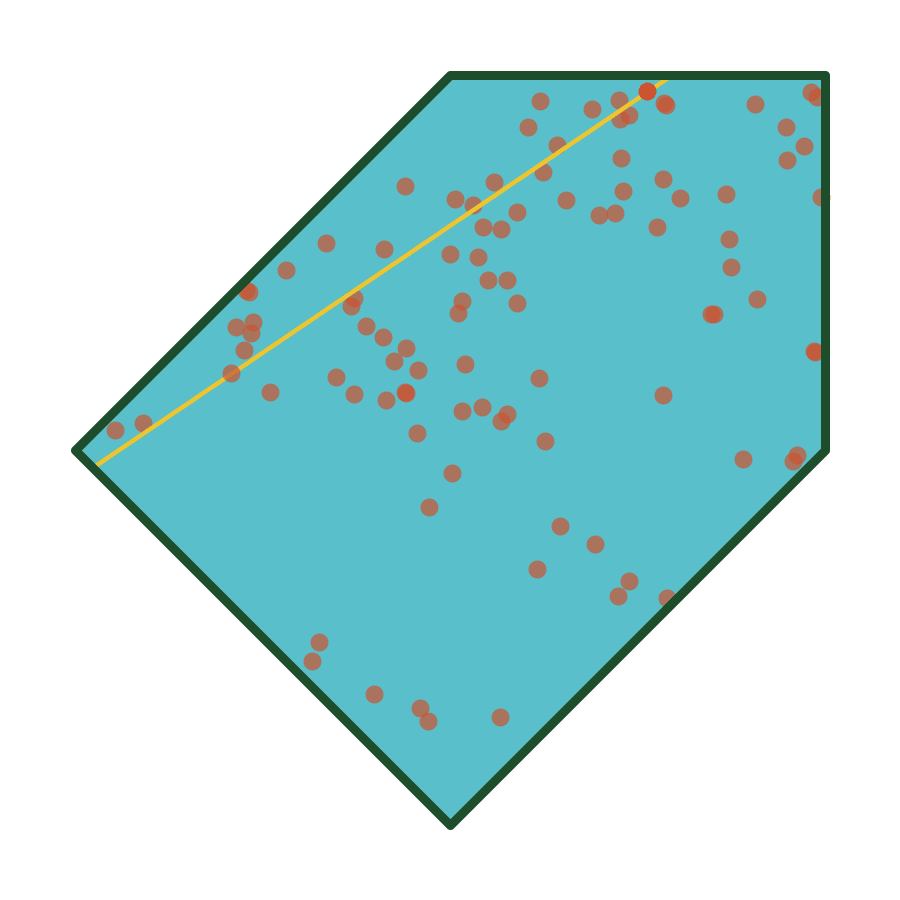
Theorem [Smith, 1984]
For any convex polytope \(\mathcal{P}\), the hit-and-run Markov chain is uniformly ergodic with respect to Lebesgue measure on \(\mathcal{P}\).
Simulations
Algorithm (w/ Cantarella)
A uniformly ergodic Markov chain for simulating random equilateral \(n\)-gons (implemented in plCurve).
More generally, a uniformly ergodic Markov chain for simulating random points from any toric symplectic manifold.

Confined Polygons
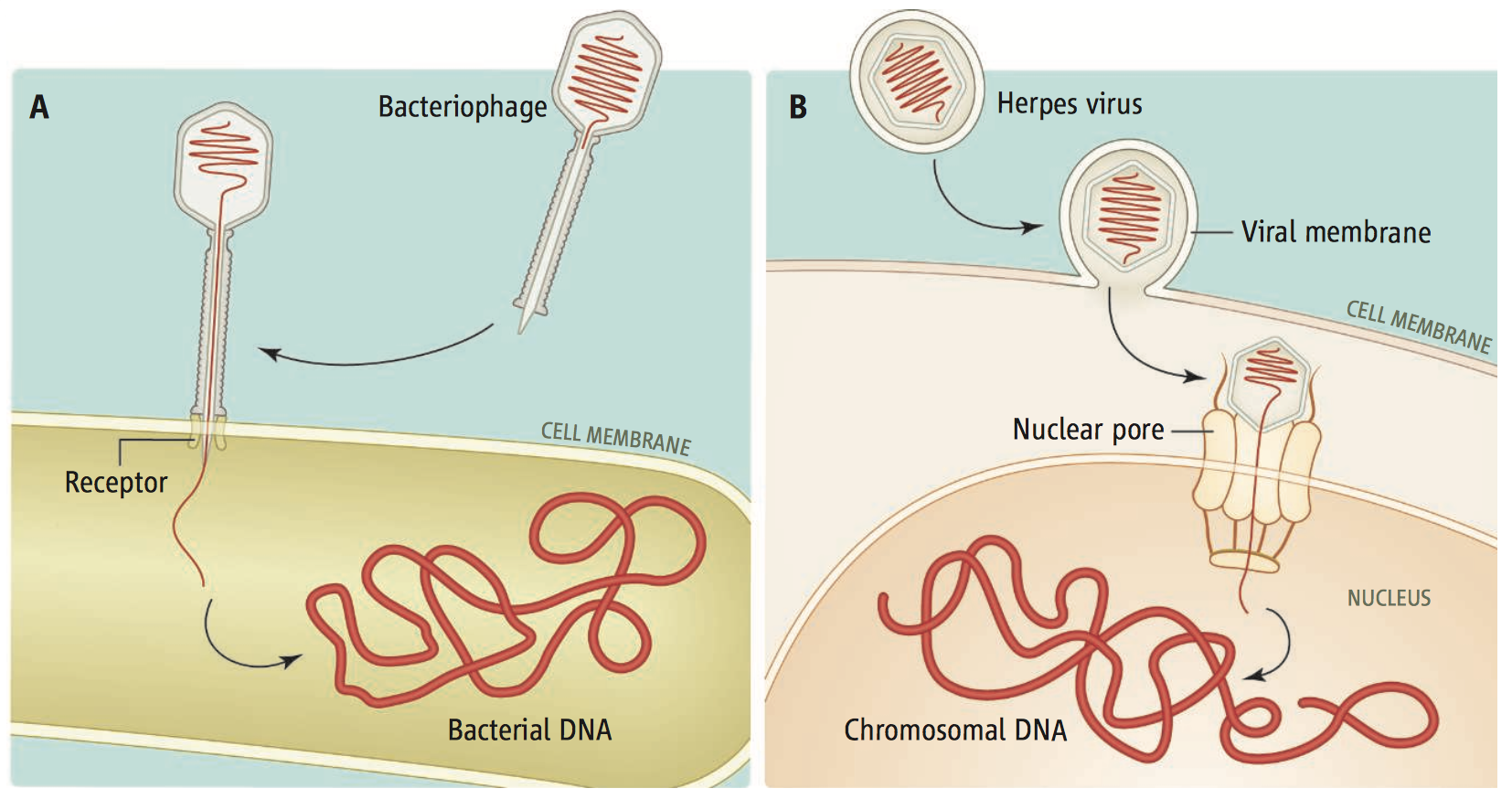
The same algorithm works even better for tightly confined polygons: let \(d_i \leq R\) for all \(i\).



Pipeline
Hyperbolic volume
check for uniqueness
(Knot ID, vertices)
Verification for New Bounds
DT code
KnotInfo’s
Knot ID
vertices
Questions
Our examples are all equilateral; are stick number and equilateral stick number distinct invariants?
Other strategies for generating large ensembles of random polygons in tight confinement?
Other lower bounds on stick number or superbridge index?
Questions
Is there any connection to hyperbolic knot theory?
Most common 11-crossing knots among 10-gons:
| DT name | SnapPea Census Name |
|---|---|
| K11n38 | K5_13 |
| K11n92 | [10 tetrahedra] |
| K11n12 | K9_684 |
| K11n19 | K6_22 |
Also, K13n592 and K15n41127 from the theorem with Blair, Eddy, and Morrison are K8_301 and K6_37, respectively.
| DT name | SnapPea Census Name |
|---|---|
| K12n591 | K8_154 |
| K12n242 | K3_1 |
| K12n749 | K8_121 |
| K12n121 | K6_10 |
Most common 12-crossing knots among 11-gons:
Thank you!
References
New stick number bounds from random sampling of confined polygons
Thomas D. Eddy and Clayton Shonkwiler
Experimental Mathematics, to appear, arXiv:1909.00917
Ryan Blair, Thomas D. Eddy, Nathaniel Morrison, and Clayton Shonkwiler
Journal of Knot Theory and Its Ramifications 29 (2020), no. 3, 2050011
New computations of the superbridge index
Clayton Shonkwiler
Journal of Knot Theory and Its Ramifications doi:10.1142/S0218216520500960
The symplectic geometry of closed equilateral random walks in 3-space
Jason Cantarella and Clayton Shonkwiler
Annals of Applied Probability 26 (2016), no. 1, 549–596