Optimization and Normal Matrices
/fsu24
this talk!
AMS Special Session on Geometry and Symmetry in Data Science
March 23, 2024
Joint Work With:
Florida State University
Funding
National Science Foundation (DMS–2107700)

Normal Matrices
Definition.
\(A \in \mathbb{C}^{d \times d}\) is normal if \(AA^\ast = A^\ast A\).
Equivalently,
\(0 = AA^\ast - A^\ast A = [A,A^\ast]\).
Define the non-normal energy \(\operatorname{E}:\mathbb{C}^{d \times d} \to \mathbb{R}\) by
\(\operatorname{E}(A) := \|[A,A^\ast]\|^2.\)
Obvious Fact.
The normal matrices are the global minima of \(\operatorname{E}\).
\(\operatorname{E}\) is not quasiconvex!
Critical Points
\(\operatorname{E}(A) = \|[A,A^\ast]\|^2\)
\(\nabla \operatorname{E}(A) = [A,[A,A^\ast]]\)
\(A\) is a critical point of \(\operatorname{E} \Leftrightarrow 0=[A,[A,A^\ast]]\).
Lemma [Jacobson, 1935]
If \(A\) and \(B\) are \(d \times d\) matrices over a field of characteristic 0 and \(A\) commutes with \([A,B]\), then \([A,B]\) is nilpotent.
Theorem [with Needham]
The only critical points of \(\operatorname{E}\) are the global minima; i.e., the normal matrices.
Gradient Descent
Let \(\mathcal{F}: \mathbb{C}^{d \times d} \times \mathbb{R} \to \mathbb{C}^{d \times d}\) be negative gradient descent of \(\operatorname{E}\); i.e.,
\(\mathcal{F}(A_0,0) = A_0 \qquad \frac{d}{dt}\mathcal{F}(A_0,t) = -\nabla \operatorname{E}(\mathcal{F}(A_0,t))\)
Theorem (with Needham)
For any \(A_0 \in \mathbb{C}^{d \times d}\), the matrix \(A_\infty := \lim_{t \to \infty} \mathcal{F}(A_0,t)\) exists, is normal, has the same eigenvalues as \(A_0\), and is real if \(A_0\) is.
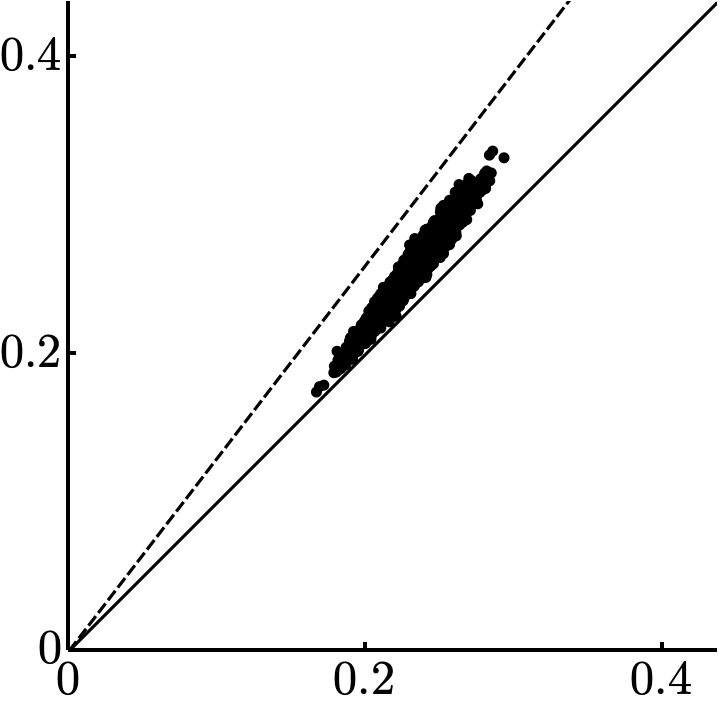
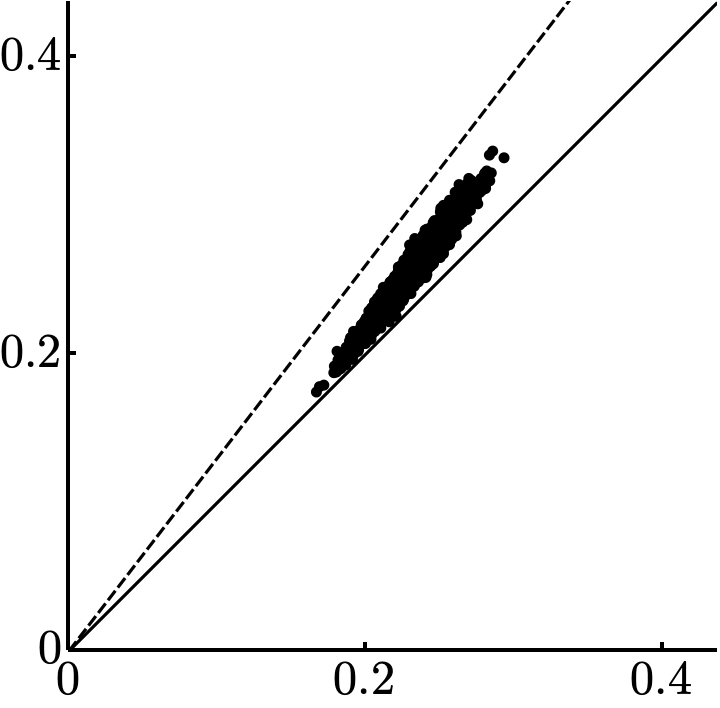
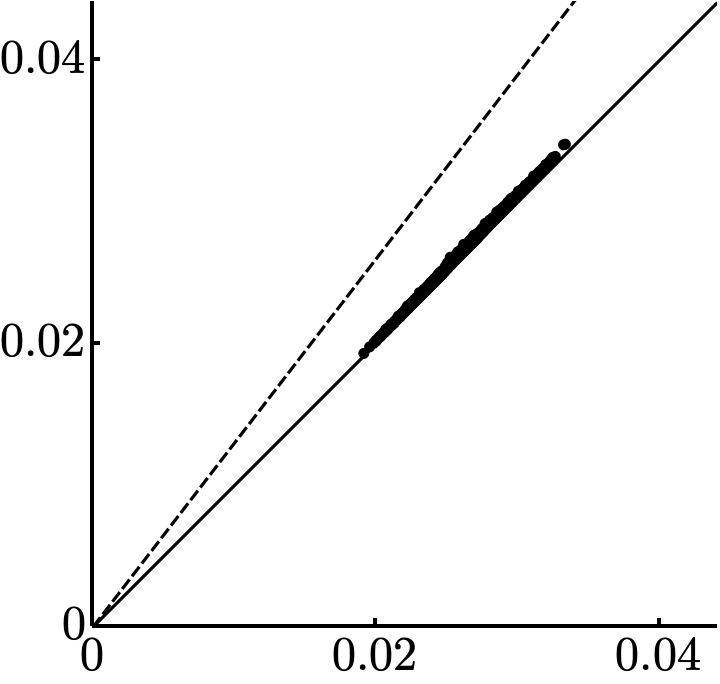
There is an equivalent result in which \(A_0\) is required to be non-nilpotent and Frobenius norm is preserved rather than spectrum.
Moreover, there exist \(c, \epsilon > 0\) so that, if \(\operatorname{E}(A_0)< \epsilon\), then \(\|A_0 - A_\infty\|^2 \leq c \sqrt{\operatorname{E}(A_0)}\).
Why?
\(\mathbb{C}^{d \times d}\) is symplectic, with symplectic form \(\omega_A(X,Y) = -\mathrm{Im}\langle X,Y \rangle = -\mathrm{Im}\mathrm{Tr}(Y^\ast X)\).
A symplectic manifold is a smooth manifold \(M\) together with a closed, non-degenerate 2-form \(\omega \in \Omega^2(M)\).
Example: \((\mathbb{R}^2,dx \wedge dy) = (\mathbb{C},\frac{i}{2}dz \wedge d\bar{z})\)
Why?
\(\mathbb{C}^{d \times d}\) is symplectic, with symplectic form \(\omega_A(X,Y) = -\mathrm{Im}\langle X,Y \rangle = -\mathrm{Im}\mathrm{Tr}(Y^\ast X)\).
Consider the conjugation action of \(\operatorname{SU}(d)\) on \(\mathbb{C}^{d \times d}\): \(U \cdot A = U A U^\ast\).
This action is Hamiltonian with associated momentum map \(\mu: \mathbb{C}^{d \times d} \to \mathscr{H}_0(d)\) given by
\(\mu(A) := [A,A^\ast]\).
So \(\operatorname{E}(A) = \|\mu(A)\|^2\).

Frances Kirwan
Gert-Martin Greuel [CC BY-SA 2.0 DE], from Oberwolfach Photo Collection
Image by rawpixel.com on Freepik

This kind of function is really nice!
Theorem (with Needham)
The space of normal matrices with Frobenius norm 1 is connected.
Geometric Invariant Theory (GIT)
The GIT quotient consists of group orbits which can be distinguished by \(G\)-invariant (homogeneous) polynomials.
\(\mathbb{C}^* \curvearrowright \mathbb{CP}^2\)
\(t \cdot [z_0:z_1:z_2] = [z_0: tz_1:\frac{1}{t}z_2]\)

Roughly: identify orbits whose closures intersect, throw away orbits on which all \(G\)-invariant polynomials vanish.
\( \mathbb{CP}^2/\!/\,\mathbb{C}^* \cong\mathbb{CP}^1\)
Abelian Version
Let \(T \simeq \operatorname{U}(1)^{d-1}\) be the diagonal subgroup of \(\operatorname{SU}(d)\). The conjugation action of \(T\) on \(\mathbb{C}^{d \times d}\) is also Hamiltonian, with momentum map
\(A \mapsto \mathrm{diag}([A,A^\ast])\).
\([A,A^\ast]_{ii} = \|A_i\|^2 - \|A^i\|^2\), where \(A_i\) is the \(i\)th row of \(A\) and \(A^i\) is the \(i\)th column.
If \(A = \left(a_{ij}\right)_{i,j} \in \mathbb{R}^{d \times d}\) such that \(\mathrm{diag}([A,A^\ast]) = 0\), then \(\widehat{A} = \left(a_{ij}^2\right)_{i,j}\) is the adjacency matrix of a balanced multigraph.
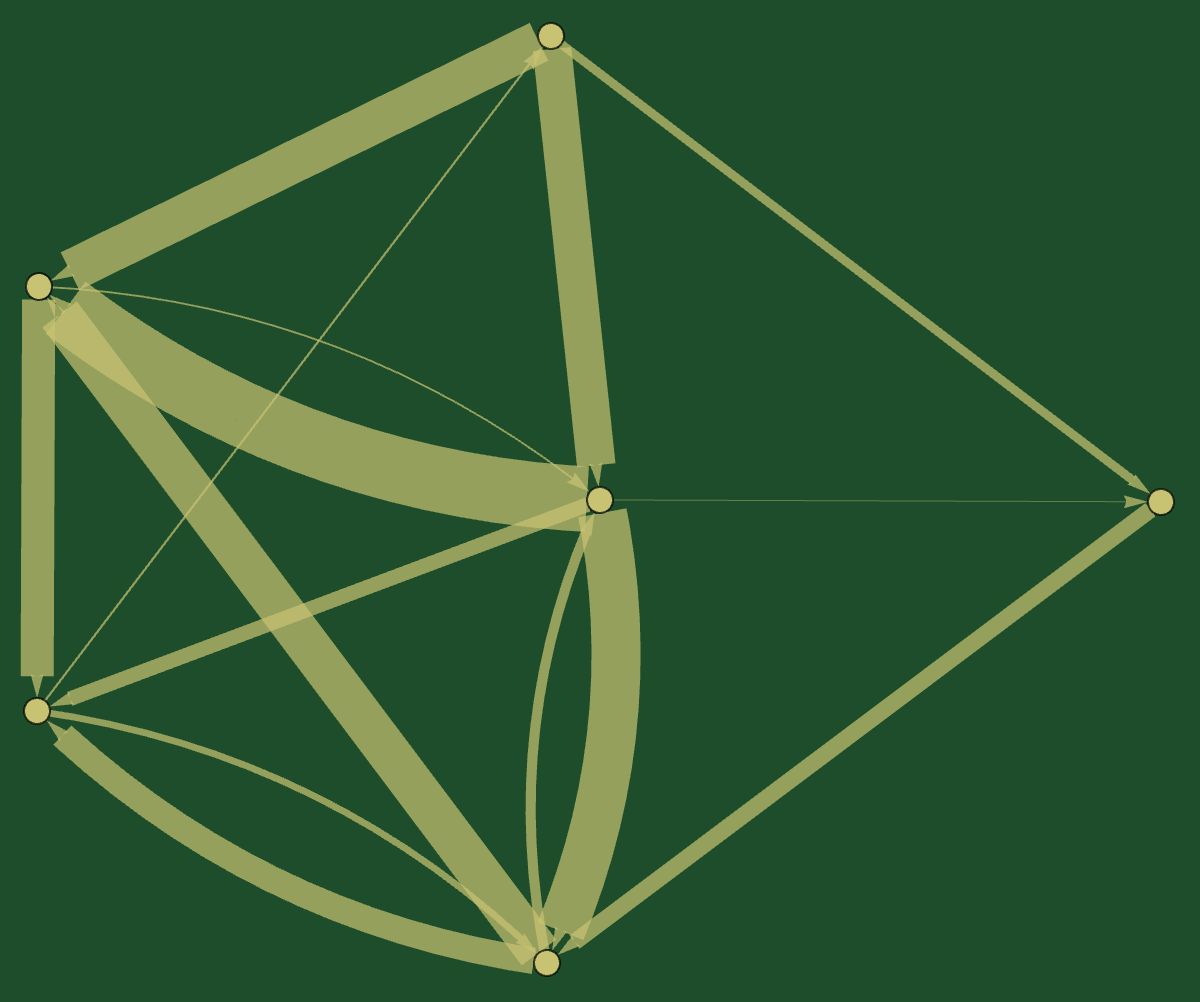
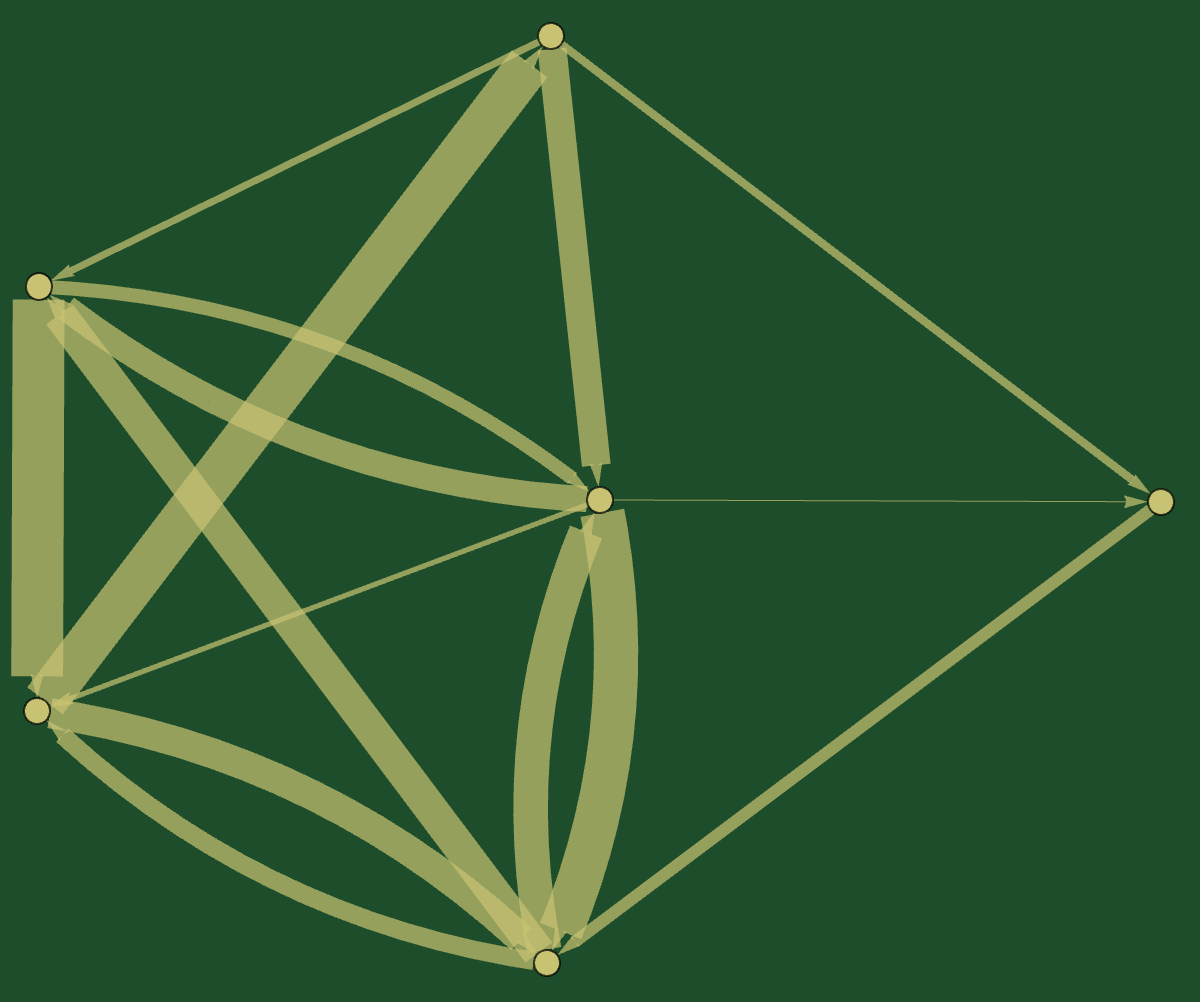
Balancing Graphs
Define the unbalanced energy \(\operatorname{B}(A) := \|\mathrm{diag}([A,A^\ast])\|^2 = \sum \left(\|A_i\|^2 - \|A^i\|^2\right)^2\).
Let \(\mathscr{F}(A_0,0) = A_0, \frac{d}{dt}\mathscr{F}(A_0,t) = - \nabla \operatorname{B}(\mathscr{F}(A_0,t))\) be negative gradient flow of \(\operatorname{B}\).
Theorem (with Needham)
For any \(A_0 \in \mathbb{C}^{d \times d}\), the matrix \(A_\infty := \lim_{t \to \infty} \mathscr{F}(A_0,t)\) exists, is balanced, has the same eigenvalues and principal minors as \(A_0\), and has zero entries whenever \(A_0\) does.
If \(A_0\) is real, so is \(A_\infty\), and if \(A_0\) has all non-negative entries, then so does \(A_\infty\).
This is “local”: \(a_{ij}\) is updated by a multiple of \((\|A_j\|^2-\|A^j\|^2)-(\|A_i\|^2-\|A^i\|^2)\).
Balancing Graphs
Theorem (with Needham)
For any \(A_0 \in \mathbb{C}^{d \times d}\), the matrix \(A_\infty := \lim_{t \to \infty} \mathscr{F}(A_0,t)\) exists, is balanced, has the same eigenvalues and principal minors as \(A_0\), and has zero entries whenever \(A_0\) does.
If \(A_0\) is real, so is \(A_\infty\), and if \(A_0\) has all non-negative entries, then so does \(A_\infty\).

Balancing Graphs
Theorem (with Needham)
For any \(A_0 \in \mathbb{C}^{d \times d}\), the matrix \(A_\infty := \lim_{t \to \infty} \mathscr{F}(A_0,t)\) exists, is balanced, has the same eigenvalues and principal minors as \(A_0\), and has zero entries whenever \(A_0\) does.
If \(A_0\) is real, so is \(A_\infty\), and if \(A_0\) has all non-negative entries, then so does \(A_\infty\).
Balancing Graphs
Theorem (with Needham)
For any \(A_0 \in \mathbb{C}^{d \times d}\), the matrix \(A_\infty := \lim_{t \to \infty} \mathscr{F}(A_0,t)\) exists, is balanced, has the same eigenvalues and principal minors as \(A_0\), and has zero entries whenever \(A_0\) does.
If \(A_0\) is real, so is \(A_\infty\), and if \(A_0\) has all non-negative entries, then so does \(A_\infty\).


\(\|A\|^2=1\)
\(\|A\|^2=0.569\)
Balancing Graphs
Theorem (with Needham)
For any \(A_0 \in \mathbb{C}^{d \times d}\), the matrix \(A_\infty := \lim_{t \to \infty} \mathscr{F}(A_0,t)\) exists, is balanced, has the same eigenvalues and principal minors as \(A_0\), and has zero entries whenever \(A_0\) does.
If \(A_0\) is real, so is \(A_\infty\), and if \(A_0\) has all non-negative entries, then so does \(A_\infty\).
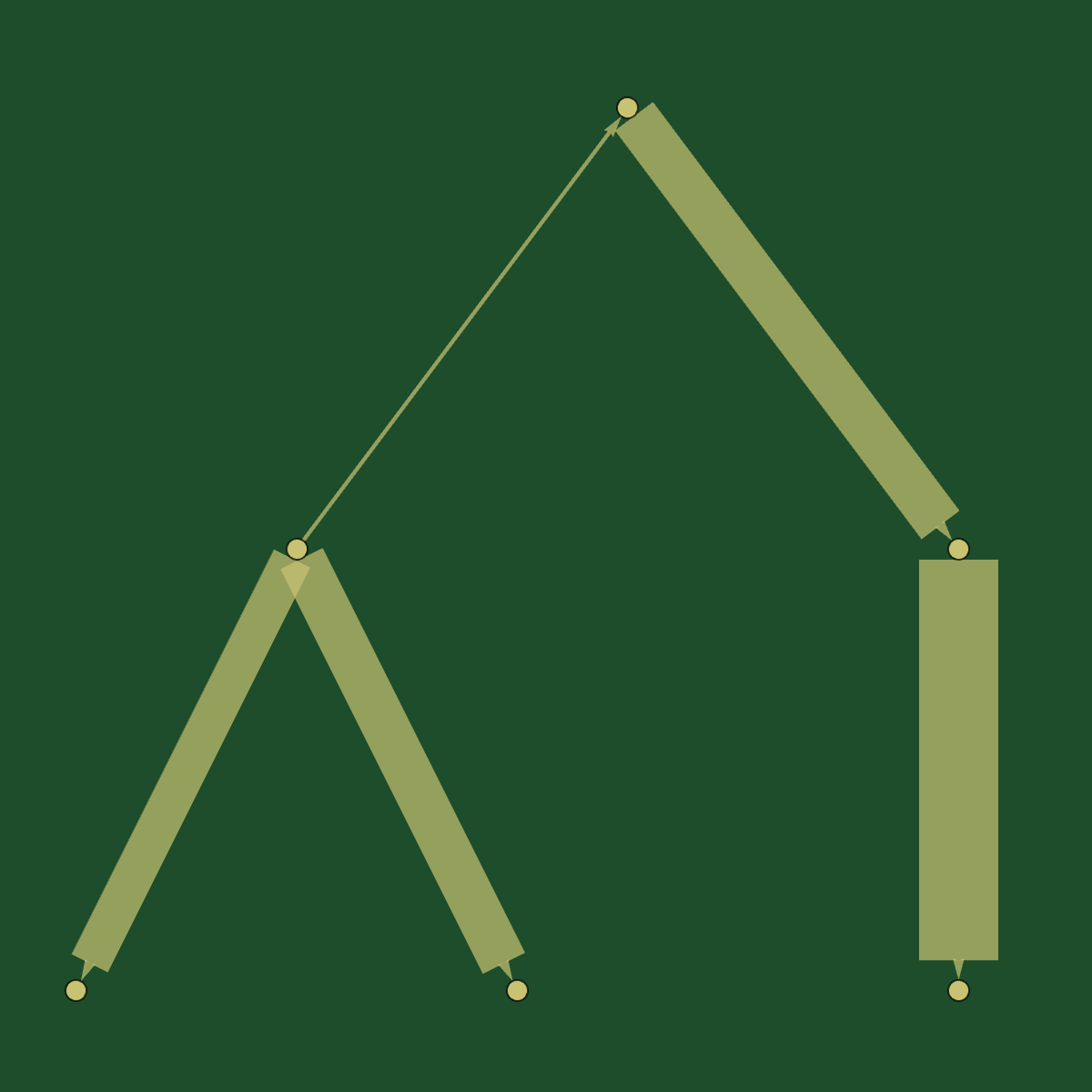
Balancing Graphs
Theorem (with Needham)
For any \(A_0 \in \mathbb{C}^{d \times d}\), the matrix \(A_\infty := \lim_{t \to \infty} \mathscr{F}(A_0,t)\) exists, is balanced, has the same eigenvalues and principal minors as \(A_0\), and has zero entries whenever \(A_0\) does.
If \(A_0\) is real, so is \(A_\infty\), and if \(A_0\) has all non-negative entries, then so does \(A_\infty\).
Preserving Weights
By doing gradient flow \(\overline{\mathscr{F}}\) on the unit sphere, we can preserve weights:
Theorem (with Needham)
For any non-nilpotent \(A_0 \in \mathbb{C}^{d \times d}\) with \(\|A\|^2=1\), the matrix \(A_\infty := \lim_{t \to \infty} \overline{\mathscr{F}}(A_0,t)\) exists, is balanced, has Frobenius norm 1, and has zero entries whenever \(A_0\) does.
If \(A_0\) is real, so is \(A_\infty\), and if \(A_0\) has all non-negative entries, then so does \(A_\infty\).

Preserving Weights
By doing gradient flow \(\overline{\mathscr{F}}\) on the unit sphere, we can preserve weights:
Theorem (with Needham)
For any non-nilpotent \(A_0 \in \mathbb{C}^{d \times d}\) with \(\|A\|^2=1\), the matrix \(A_\infty := \lim_{t \to \infty} \overline{\mathscr{F}}(A_0,t)\) exists, is balanced, has Frobenius norm 1, and has zero entries whenever \(A_0\) does.
If \(A_0\) is real, so is \(A_\infty\), and if \(A_0\) has all non-negative entries, then so does \(A_\infty\).
Preserving Weights
By doing gradient flow \(\overline{\mathscr{F}}\) on the unit sphere, we can preserve weights:
Theorem (with Needham)
For any non-nilpotent \(A_0 \in \mathbb{C}^{d \times d}\) with \(\|A\|^2=1\), the matrix \(A_\infty := \lim_{t \to \infty} \overline{\mathscr{F}}(A_0,t)\) exists, is balanced, has Frobenius norm 1, and has zero entries whenever \(A_0\) does.
If \(A_0\) is real, so is \(A_\infty\), and if \(A_0\) has all non-negative entries, then so does \(A_\infty\).

Preserving Weights
By doing gradient flow \(\overline{\mathscr{F}}\) on the unit sphere, we can preserve weights:
Theorem (with Needham)
For any non-nilpotent \(A_0 \in \mathbb{C}^{d \times d}\) with \(\|A\|^2=1\), the matrix \(A_\infty := \lim_{t \to \infty} \overline{\mathscr{F}}(A_0,t)\) exists, is balanced, has Frobenius norm 1, and has zero entries whenever \(A_0\) does.
If \(A_0\) is real, so is \(A_\infty\), and if \(A_0\) has all non-negative entries, then so does \(A_\infty\).
Applications?
Thank you!
Related Background
Fusion frame homotopy and tightening fusion frames by gradient descent
Tom Needham and Clayton Shonkwiler
Journal of Fourier Analysis and Applications 29 (2023), no. 4, 51
Three proofs of the Benedetto–Fickus theorem
Dustin Mixon, Tom Needham, Clayton Shonkwiler, and Soledad Villar
Sampling, Approximation, and Signal Analysis (Harmonic Analysis in the Spirit of J. Rowland Higgins), Stephen D. Casey, M. Maurice Dodson, Paulo J. S. G. Ferreira and Ahmed Zayed, eds., Birkhäuser, Cham, 2023, 371–391