Geometric Approaches to Frame Theory
/isu22
this talk!
Geometric Analysis Seminar, Feb. 28, 2022
Collaborator

Florida State University
Funding
National Science Foundation (DMS–2107700)
Simons Foundation (#709150)
Finite Frames
\(\mathfrak{H} = \mathbb{R}^d\) or \(\mathbb{C}^d\). A (finite) frame in \(\mathfrak{H}\) is a spanning set \(f_1, \dots, f_N \in \mathfrak{H}\).

The Model Problem
Signal: \(v \in \mathfrak{H}\)
Design: \(f_1, \dots , f_N \in \mathfrak{H}\)
Measurements: \(\langle f_1, v \rangle, \dots , \langle f_N, v \rangle \).
Parseval’s Theorem
If \(f_1, \dots , f_d \in \mathfrak{H}\) is an orthonormal basis,
\(\|v\|^2 = \sum |\langle f_i, v \rangle |^2 = \|F^* v\|^2\)
for any \(v \in \mathfrak{H}\).
Even better,
\(v = \sum \langle f_i, v \rangle f_i = FF^* v \).
If \(F = [f_1 \, f_2 \dots f_N]\), the measurement vector is \(F^*v\).
\(\Leftrightarrow FF^* = \mathrm{Id}_{d \times d}\)
Parseval frame
Fact: For any \(n \geq d\), there exist Parseval frames \(f_1, \dots , f_N \in \mathfrak{H}\) so that \(\|f_i\|=\|f_j\|\) for all \( i,j\); these are the equal-norm Parseval frames (ENPs).
This is fragile! What if a measurement gets lost?
Questions
We are often interested in specifying \(\operatorname{spec}(FF^\ast) = (\lambda_1, \dots , \lambda_d)\) and/or \((\|f_1\|^2,\dots , \|f_N\|^2) = (r_1, \dots, r_N)\).
- [Admissibility] Is the space of frames with this data non-empty? Is it smooth?
- [Frame homotopy] Is it connected?
- [Sampling] Can we randomly sample it?
- [Robustness] Is a typical frame with this data well-suited to the reconstruction problem?
Gram Matrices
Both \(\operatorname{spec}(FF^\ast) = (\lambda_1, \dots , \lambda_d)\) and \((\|f_1\|^2,\dots , \|f_N\|^2) = (r_1, \dots, r_N)\) are present in the Gram matrix
\(F^\ast F = \left[\langle f_i, f_j\rangle \right]_{i,j} \in \mathscr{H}(N)\)
since \(F^\ast F\) and \(F F^\ast\) have the same rank and nonzero eigenvalues.
Unitary equivalence classes of frames have the same Gram matrix: if \(U \in O(d)\) or \(U(d)\), then
\((UF)^\ast(UF) = F^\ast U^\ast U F = F^\ast F\).
For \(\boldsymbol{\lambda} = (\lambda_1, \dots , \lambda_d, 0, \dots 0)\),
\(\mathcal{O}_{\boldsymbol{\lambda}} := \{U \operatorname{diag}(\boldsymbol{\lambda}) U^\ast | U \in U(N) \text{ or } O(N)\}\subset \mathscr{H}(N)\)
is a flag manifold.
Lie Groups
Informal Definition. A Lie group is a group that is also a manifold (a “continuous group of symmetries”).
Examples.
- \(\mathbb{R}^n\), \(\mathbb{C}^n\)
- \(GL_n(\mathbb{R})\), \(GL_n(\mathbb{C})\)
- \(SL_n(\mathbb{R})\), \(SL_n(\mathbb{C})\)
- \(O(n)\), \(SO(n)\), \(U(n)\), \(SU(n)\) (e.g., \(SO(3)\simeq \mathbb{RP}^3\), \(SU(2) \simeq S^3\))
- Products (e.g. the compact torus \(U(1)^n\))


Lie Algebras
Informal Definition. A Lie algebra \(\mathfrak{g}\) (or \(\operatorname{Lie}(G)\)) associated to a Lie group \(G\) is the tangent space at the identity (the “infinitesimal symmetries”).

Examples.
- \(\operatorname{Lie}(\mathbb{R}^n) \simeq \mathbb{R}^n\)
- \(\mathfrak{gl}_n(\mathbb{R}) \simeq \mathbb{R}^{n \times n}\), \(\mathfrak{gl}_n(\mathbb{C}) \simeq \mathbb{C}^{n \times n}\)
- \(\mathfrak{sl}_n(\mathbb{R}) \simeq \{\text{traceless matrices}\}\), \(\mathfrak{sl}_n(\mathbb{C}) \simeq \{\text{traceless matrices}\}\)
- \(\mathfrak{o}(n) = \mathfrak{so}(n) \simeq \{\text{skew-symmetric matrices}\}\), \(\mathfrak{u}(n) \simeq \{\text{skew-Hermitian matrices}\}\), \(\mathfrak{su}(n) \simeq \{\text{traceless skew-Hermitian}\}\)
Suppose \(\gamma(t) \in U(n)\) with \(\gamma(0)=I\). Since \(I = \gamma(t)\gamma(t)^\ast\),
\(0 = \left. \frac{d}{dt}\right|_{t=0} \gamma(t)\gamma(t)^\ast = \gamma'(0)\gamma(0)^\ast + \gamma(0)\gamma'(t)^\ast = \gamma'(0) + \gamma'(0)^\ast\)
The Lie bracket \([\cdot , \cdot ]\) is the matrix commutator on matrix groups: \([A,B] = AB-BA\).
Adjoint Actions
A Lie group \(G\) acts on itself by conjugation: \(g \cdot h := g h g^{-1}\).
This fixes the identity, so linearizing gives an action of \(G\) on \(\mathfrak{g}\), called the adjoint action.
For matrix groups, the adjoint action is the conjugation action.
Example. \(\mathfrak{so}(3) \simeq \left\{\begin{pmatrix} 0 & -z & y \\ z & 0 & -x \\ -y & x & 0\end{pmatrix}:x,y,z \in \mathbb{R}\right\}\simeq (\mathbb{R}^3, \times)\)
Adjoint Orbits
If \(G\) is a Lie group, each orbit of the adjoint action is a symplectic manifold.\(^1\)
1. Strictly speaking, coadjoint orbits in \(\mathfrak{g}^\ast\) are symplectic.

\(i\mathscr{H}(N) = \mathfrak{u}(N)\), so conjugation orbits of Hermitian matrices can be interpreted as adjoint orbits.
Symplectic Geometry
A symplectic manifold is a smooth manifold \(M\) together with a closed, non-degenerate 2-form \(\omega \in \Omega^2(M)\).
Example: \((\mathbb{R}^2,dx \wedge dy) = (\mathbb{C},\frac{i}{2}dz \wedge d\bar{z})\)
Non-Example: \((\mathbb{R}^3, dx \wedge dy)\)
For any vector \(v\), \(dx \wedge dy\left(\frac{\partial}{\partial z}, v\right) = 0\), so \(dx \wedge dy\) is degenerate.
Non-Example: \((\mathbb{R}^4, dx_1 \wedge dy_1 + y_1 dx_2 \wedge dy_2)\)
Because of the coefficient \(y_1\), this is not closed (“not divergence-free”).
Examples
\((S^2,d\theta\wedge dz)\)
\((\mathbb{R}^2,dx \wedge dy) = (\mathbb{C},\frac{i}{2}dz \wedge d\bar{z})\)
\((S^2,\omega)\), where \(\omega_p(u,v) = (u \times v) \cdot p\)
\((\mathbb{R}^2,\omega)\) where \(\omega(u,v) = \langle i u, v \rangle \)
\((\mathbb{C}^n, \frac{i}{2} \sum dz_k \wedge d\overline{z}_k)\)
\((\mathbb{C}^{m \times n}, \omega)\) with \(\omega(X_1,X_2) = -\operatorname{Im} \operatorname{trace}(X_1^* X_2)\).
\((T^* \mathbb{R}^n,\sum dq_i \wedge dp_i)\)
phase space
position
momentum
Symplectic Geometry and Frame Theory
\(\mathcal{O}_{\boldsymbol{\lambda}} = \{U \operatorname{diag}(\boldsymbol{\lambda})U^\ast | U \in U(N)\} \simeq \{F \in \mathbb{C}^{d \times N} | \operatorname{spec}(FF^\ast) = (\lambda_1, \dots , \lambda_d)\}/U(d)\) is symplectic.
Proposition. The map recording diagonal entries is the momentum map of a Hamiltonian torus action.
Theorem [Atiyah and Guillemin–Sternberg]
Momentum maps of Hamiltonian torus actions have convex image and connected level sets.
Theorem [with Needham, 2021]
The space \(\mathscr{F}_{\boldsymbol{\lambda}}^{\mathbb{C}^d,N}(\boldsymbol{r})\subset \mathbb{C}^{d \times N}\) of frames with \(\operatorname{spec}(FF^\ast) = (\lambda_1, \dots , \lambda_d)\) and \(\|f_i\|^2 = r_i\) for \(i=1, \dots , N\) is path-connected.

This solves the general frame homotopy problem for complex frames.
Robustness
For compressed sensing, it is desirable to require every minor of the \(d \times N\) matrix \(F\) to be invertible. Such an \(F\) is said to have full spark.
Theorem [with Needham]
Fix the spectrum of \(FF^\ast\) and fix \(\|f_1\|,\dots,\|f_N\|\). There are three possibilities:
- It is impossible for a frame to have these data
- It is impossible for a frame with these data to have full spark
- A random frame with these data will have full spark with probability 1.
How Could This Generalize?
\(\dim(\mathfrak{o}(N)) = \frac{N(N-1)}{2}\)
\(\dim(\{\text{symmetric } N \times N \text{ matrices}\})=\frac{N(N+1)}{2}\)
The analog of the unitary group for symplectic matrices is the (compact) symplectic group \(\operatorname{Sp}(N)\); its Lie algebra \(\mathfrak{sp}(N)\) consists of quaternionic skew-Hermitian matrices.
\(\dim(\mathfrak{sp}(N)) = 2N^2+N\)
\(\dim(\{\text{Hermitian quaternionic } N \times N \text{ matrices}\}) = 2N^2-N\)
Can’t identify these!
Isoparametric Submanifolds
Definition. A submanifold \(M\) of a Riemannian manifold \(N\) is isoparametric if its normal bundle \(\nu(M)\) is flat and the principal curvatures along any parallel normal field are constant.
Proposition/Example. If \(\boldsymbol{\lambda}\) is generic (i.e., \(\lambda_i \neq \lambda_j\) for \(i \neq j\)), then \(\mathcal{O}_{\boldsymbol{\lambda}}\subset \mathscr{H}(N)\) is isoparametric.
If \(\boldsymbol{\lambda}\) is not generic, then \(\mathcal{O}_{\boldsymbol{\lambda}}\) is parallel to an isoparametric submanifold.
If \(\xi\) is a parallel section of \(\nu(M)\), then \(M_\xi :=\{p+\xi(p):p \in M\}\) is parallel to \(M\)
Nice Features
Theorem [Terng]
Let \(M_\xi\subset \mathbb{R}^n\) be parallel to an isoparametric submanifold \(M\). Let \(p \in M\) so that \(p+\xi(p) \in M_\xi\), let \(\nu_p(M)\) be the normal space to \(M\) at \(p\), and let \(P:M_\xi \to \nu_p(M)\) be orthogonal projection. Then \(P(M_\xi)\) is a convex polytope.
Theorem [Mare]
Let \(M\subset \mathbb{R}^n\) be isoparametric with all multiplicities \(\geq 2\) and let \(M_\xi\) be parallel to \(M\). If \(p \in M\) and \(b \in \nu_p(M)\) is in the image of the projection \(P: M_\xi \to \nu_p(M)\), then \(P^{-1}(b)\) is connected.
Theorem [Atiyah and Guillemin–Sternberg]
Momentum maps of Hamiltonian torus actions have convex image and connected level sets.
For adjoint orbits, this is the difference in dimension between principal and sub-principal orbits.
Cartan Decomposition
An involution \(\theta: \mathfrak{g} \to \mathfrak{g}\) is a Cartan involution if \(-B(\cdot , \theta \cdot)\) is positive-definite, where \(B(\cdot , \cdot)\) is the Killing form.
Example. \(\theta: \mathfrak{sl}_n(\mathbb{R}) \to \mathfrak{sl}_n(\mathbb{R})\) defined by \(\theta(X) = -X^T\). This is the derivative of the involution on \(SL_n(\mathbb{R})\) given by \(U \mapsto (U^{-1})^T\).
\(E_{+1} =: \mathfrak{k}\) consists of skew-symmetric matrices
\(E_{-1} =: \mathfrak{p}\) consists of (traceless) symmetric matrices
\(\mathfrak{sl}_n(\mathbb{R}) = \mathfrak{k} \oplus \mathfrak{p}\) is an orthogonal decomposition — the Cartan decomposition
\([\mathfrak{k},\mathfrak{p}]\subseteq \mathfrak{p}\), so the adjoint action of \(SO(n) = \exp(\mathfrak{k})\) restricts to an action on \(\mathfrak{p}\)
\([\mathfrak{p},\mathfrak{p}]\subseteq\mathfrak{k}\), so any Lie subalgebra of \(\mathfrak{p}\) is abelian.
Theorem. \(G\) non-compact, semisimple, and \(\mathfrak{g} = \mathfrak{k} \oplus \mathfrak{p}\) a Cartan decomposition with \(K = \exp(\mathfrak{k})\) and \(P = \exp(\mathfrak{p})\), then \(G = KP\) and \(T_{[I]} G/K \simeq \mathfrak{p}\).
The adjoint action of \(K\) on \(\mathfrak{p}\) is often called the isotropy representation.
Kostant’s Convexity Theorem
Proposition [see, e.g., Palais–Terng Example 6.5.6]
Let \(G\) be a semisimple Lie group with Cartan decomposition \(\mathfrak{g} = \mathfrak{k} \oplus \mathfrak{p}\).
The isotropy orbits are (parallel to) isoparametric submanifolds of \(\mathfrak{p}\), and, if \(\mathfrak{a} \subset \mathfrak{p}\) is a maximal abelian subspace and \(a \in \mathfrak{a}\), then \(\nu_a(\mathcal{O}_a) = \mathfrak{a}\).
Example.
\(G = SL_n(\mathbb{C})\), \(K=SU(N)\), \(\mathfrak{k} = \mathfrak{su}(N)\), \(\mathfrak{p} = \mathscr{H}_0(N)\), \(a = \operatorname{diag}(a_1, \dots , a_N)\),
\(\mathcal{O}_a = \{UaU^\ast | U \in SU(N)\}\)
\(P(\mathcal{O}_a) = \operatorname{conv}(S_N \cdot a)\) is essentially Schur–Horn.
This gives a non-symplectic proof of frame homotopy for complex frame spaces!
In particular, Terng and Mare’s theorems imply the projection of \(\mathcal{O}_a\) onto \(\mathfrak{a}\) has convex image and connected level sets.
Quaternions
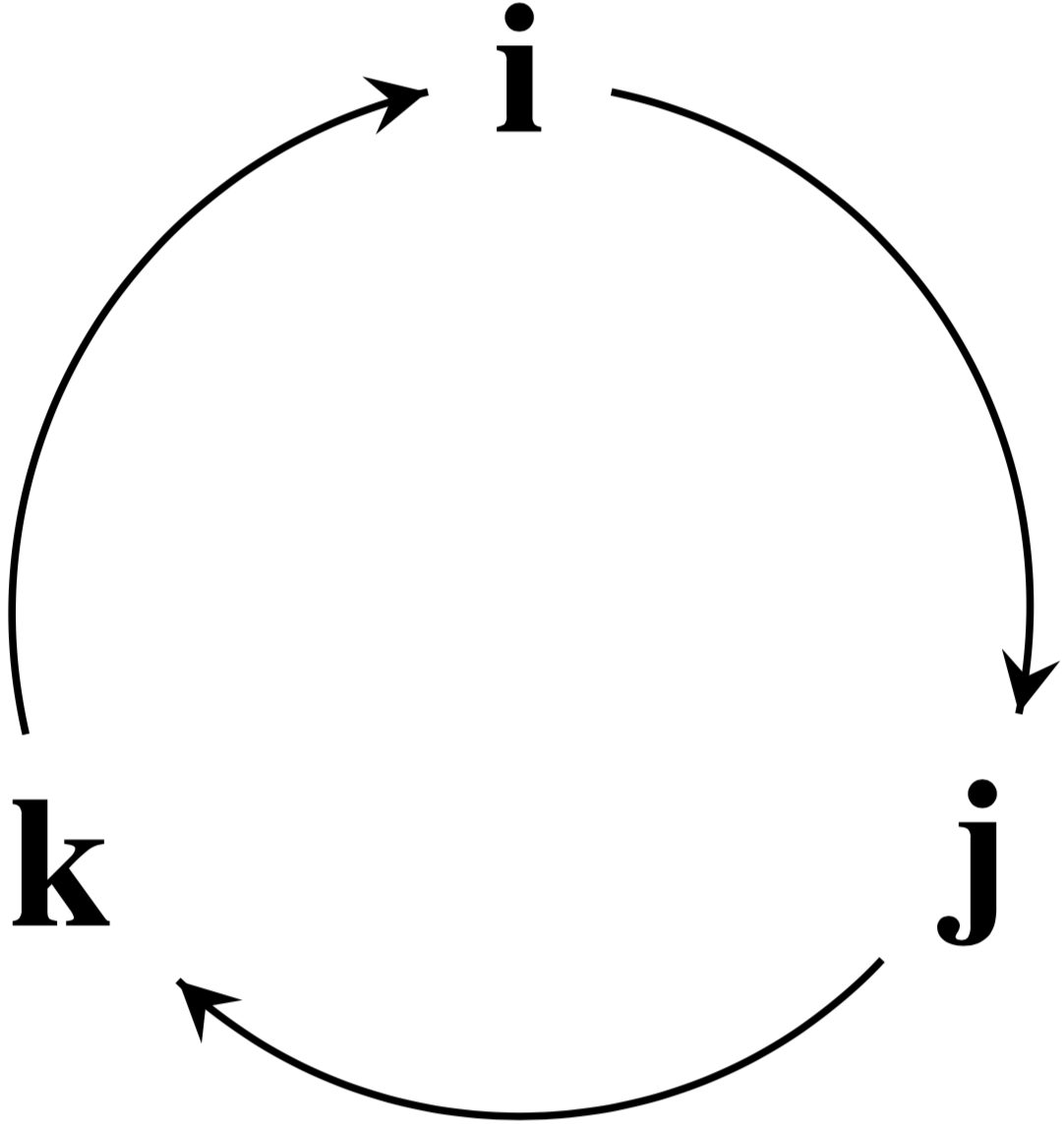
\(\mathbb{H} = \{a + b \boldsymbol{i} + c \boldsymbol{j} + d \boldsymbol{k}\}\)
\(\boldsymbol{i}^2 = \boldsymbol{j}^2 = \boldsymbol{k}^2 = -1\)
\(\boldsymbol{i}\boldsymbol{j}\boldsymbol{k} = -1\)
\(z+w \boldsymbol{j} \mapsto \begin{pmatrix} z & w \\ -\overline{w} & \overline{z}\end{pmatrix}\)
\(\mathbb{H}^d\) is a right vector space over the skew-field \(\mathbb{H}\).
Quaternionic Frames
A spanning set \(\{f_1, \dots , f_N\} \subset \mathbb{H}^d\) is a (finite) frame for \(\mathbb{H}^d\).
Much of standard frame theory goes through for quaternionic frames (see, e.g., Waldron).
In particular, the frame operator \(FF^\ast\) and the Gram matrix \(F^\ast F\) are well-defined, and \(\operatorname{Sp}(d)\) equivalence classes of frames in \(\mathbb{H}^{d \times N}\) are uniquely determined by their Gram matrices.
Realizing Quaternion Matrices as Complex Matrices
\(\Psi:\mathbb{H}^{N \times N} \to \mathbb{C}^{2N \times 2N}\) given by
\(\Psi(Z + W\boldsymbol{j}) = \begin{pmatrix} Z & W \\ -\overline{W} & \overline{Z} \end{pmatrix}\).
\(\Psi(\operatorname{Sp}(N)) \subset SU(2N)\) is the fixed point set of the involution
\(U \mapsto \Omega^\ast \overline{U} \Omega\),
where \(\Omega = \begin{pmatrix} 0 & I \\ -I & 0 \end{pmatrix}\).
Corresponding Cartan decomposition of the Lie algebra:
\(\mathfrak{su}(2N) = \mathfrak{k} \oplus \mathfrak{p} \simeq \Psi(\mathfrak{sp}(N)) \oplus \Psi(\mathscr{H}_0(N))\).
Results
Admissibility for Quaternionic Frames [with Needham]
\(\mathscr{F}_{\boldsymbol{\lambda}}^{\mathbb{H}^d,N}(\boldsymbol{r})\neq \emptyset\) if and only if \(\boldsymbol{r} \in \operatorname{conv}(S_N \cdot (\lambda_1, \dots , \lambda_d, 0, \dots , 0))\) (cf. Casazza–Leon).
\(\mathscr{F}_{\boldsymbol{\lambda}}^{\mathbb{H}^d,N}(\boldsymbol{r}):= \{F \in \mathbb{H}^{d \times N} | \operatorname{spec}(FF^\ast)=\boldsymbol{\lambda}, \|f_i\|^2 = r_i \text{ for all } i=1,\dots, N\}\)
\(\mathcal{O}_{\boldsymbol{\lambda}} = \{U \operatorname{diag}(\lambda_1, \dots , \lambda_d, 0, \dots , 0)U^\ast | U \in \operatorname{Sp}(N)\}\)
Key Idea. Terng/Kostant convexity.
Generalized Frame Homotopy for Quaternionic Frames [with Needham]
\(\mathscr{F}_{\boldsymbol{\lambda}}^{\mathbb{H}^d,N}(\boldsymbol{r})\) is always path-connected.
Key Idea. Mare’s connectedness theorem.
Questions
Isotropy orbits of real symmetric matrices do not satisfy the technical hypothesis in Mare’s theorem; indeed, some \(\mathscr{F}_{\boldsymbol{\lambda}}^{\mathbb{R}^d,N}(\boldsymbol{r})\) spaces are disconnected. Can we characterize the \((\boldsymbol{\lambda},\boldsymbol{r})\) which lead to connectedness?
Does the Riemannian geomery of isoparametric submanifolds give any insight into the measure on real or quaternionic frame spaces? Does this lead to a sampling algorithm?
Thank you!
References
Symplectic geometry and connectivity of spaces of frames
Tom Needham and Clayton Shonkwiler
Advances in Computational Mathematics 47 (2021), no. 1, 5
Admissibility and frame homotopy for quaternionic frames
Tom Needham and Clayton Shonkwiler
Preprint, 2021