Introduction to Knot Theory
Clayton Shonkwiler
MATH 192
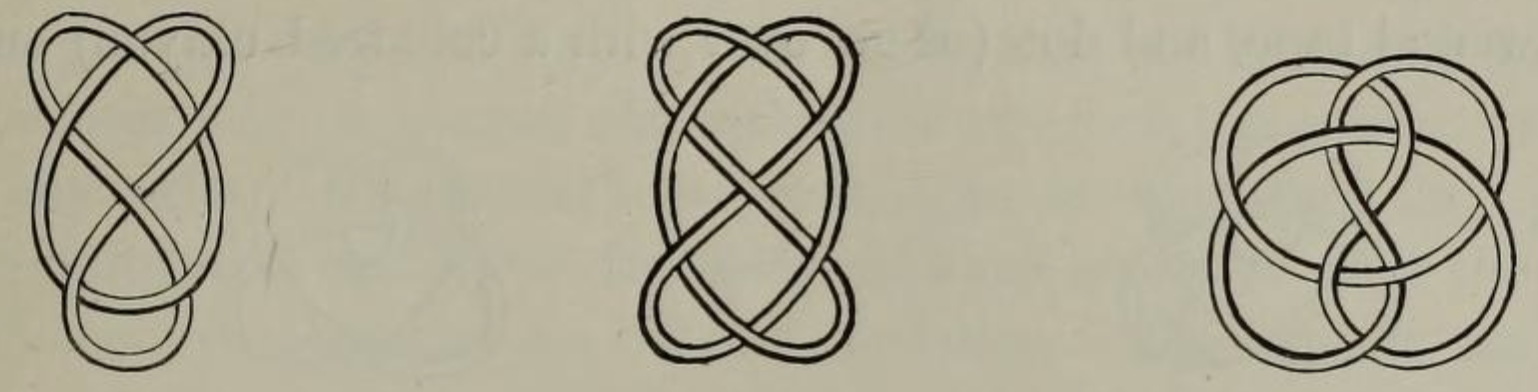
A knot is a closed loop in space




Peter Guthrie Tait
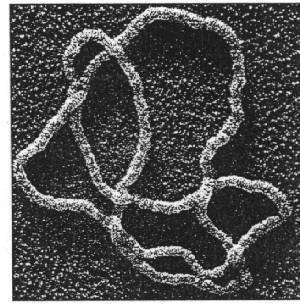

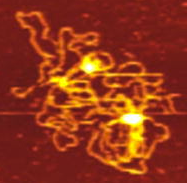
Plasmid DNA
Alonso–Sarduy, Dietler Lab
EPF Lausanne
Which of these are knots? (1 piece)
Which are links? (More than 1 piece)
Which are equivalent?

Is there a way to assign crossings to this projection to make it the unknot?
The Unknotting–Knotting Game

Two players: the Knotter and the Unknotter.
K and U take turns assigning crossings; K’s goal is to make the diagram knotted and U’s goal is to make it unknotted.
In pairs, decide who is K and who is U.
Then decide who goes first.
Play the game.
Who won? Did the winner have an advantage?
Play again, switching who goes first. Who won? Did they have an advantage?
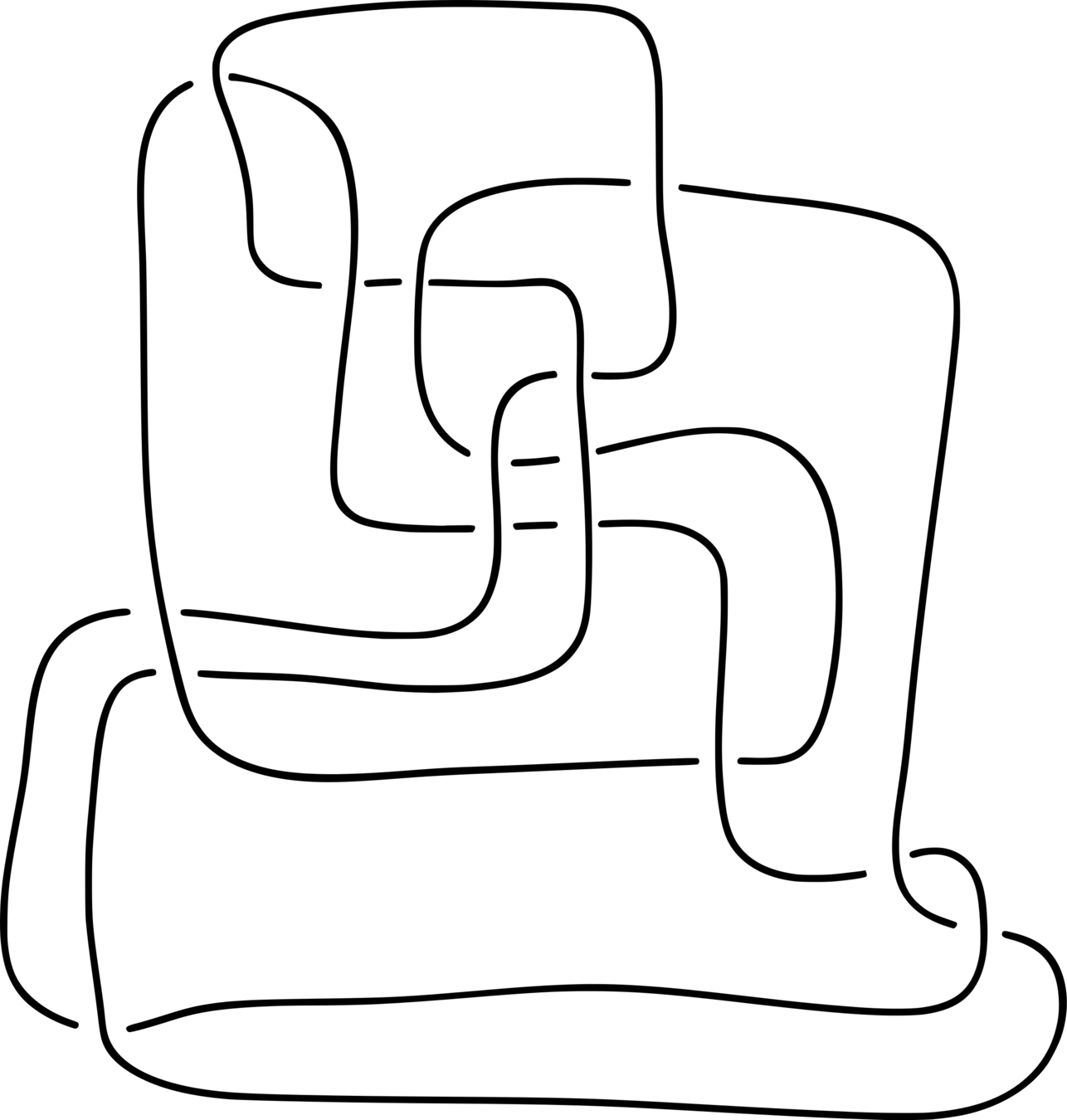
Thistlethwaite unknot
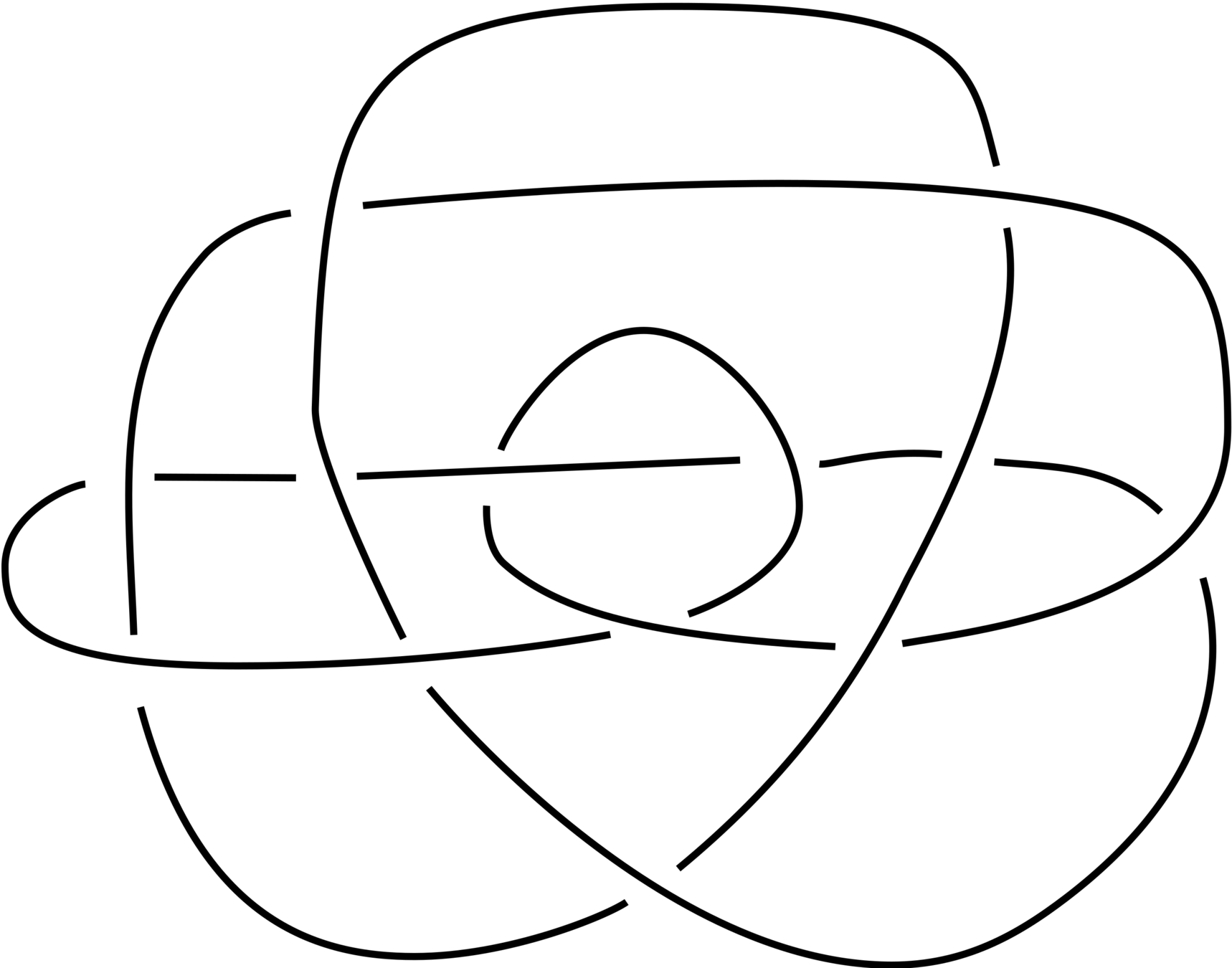
Ochiai unknot
How hard is it to recognize unknots?
Theorem [Hass–Lagarias–Pippenger]
Unknottedness is in NP.
Theorem [Lackenby]
Unknottedness is in co-NP.
An Unsolved Problem in Mathematics
Can unknots be recognized in polynomial time?

Knots in Nature
Formal Definitions
A knot is a simple, closed, polygonal curve in space.
A link is a collection of pairwise non-intersecting knots.
A two-dimensional picture of a knot is a diagram.
We often allow the segments to become very short, so the curve appears to be smooth.


- Build a knot, then draw a good diagram of it.
- Now draw a bad diagram of the same knot. For example, can you make a diagram from which the knot cannot be reconstructed from crossing information? Other diagram weirdness?
- Make a list of Properties to Avoid in diagrams.

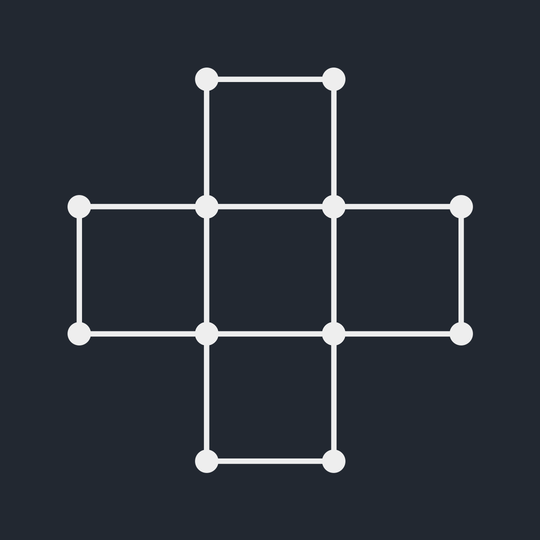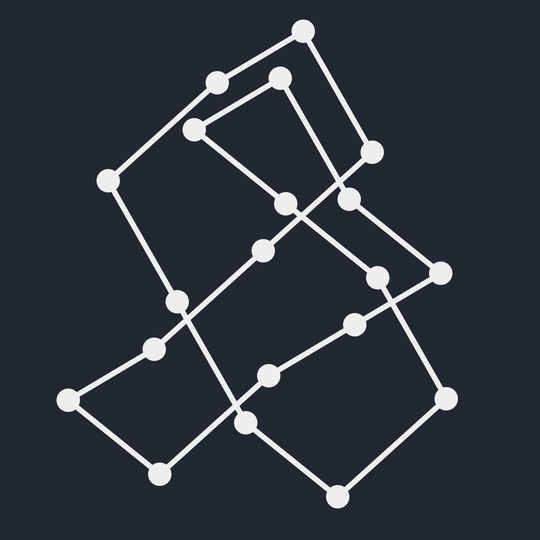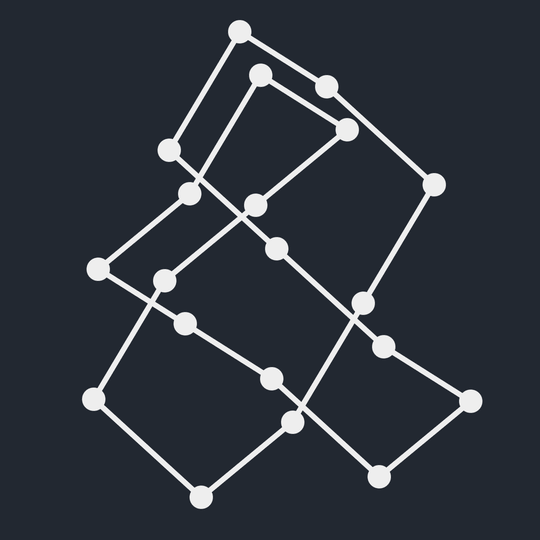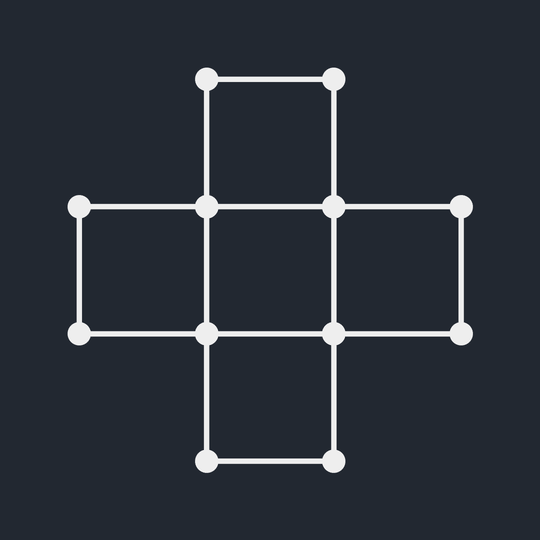
Reidemeister moves
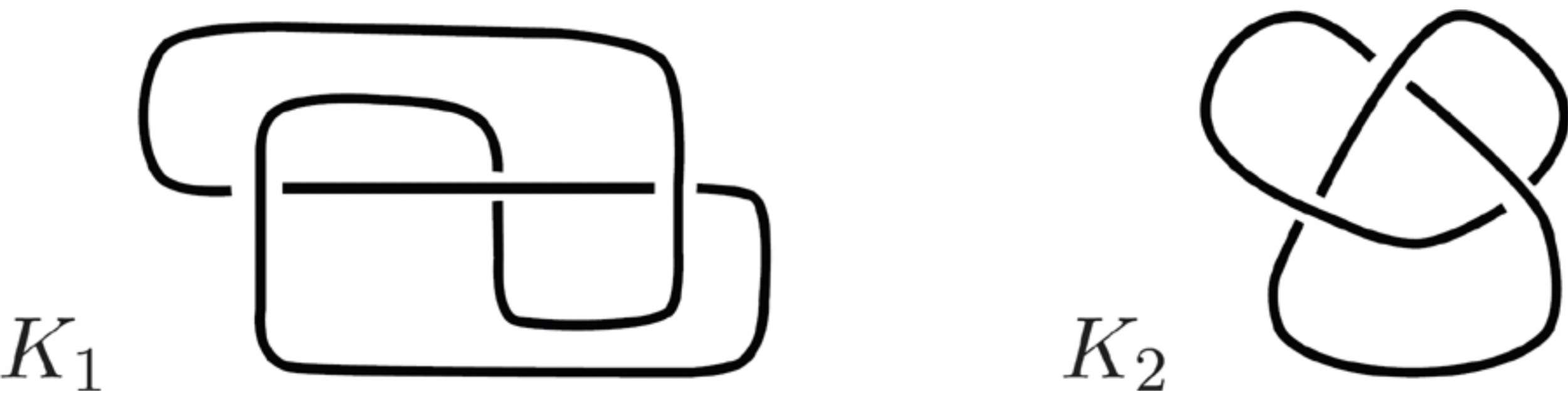
Find a sequence of Reidemeister moves from \(K_1\) to \(K_2\).
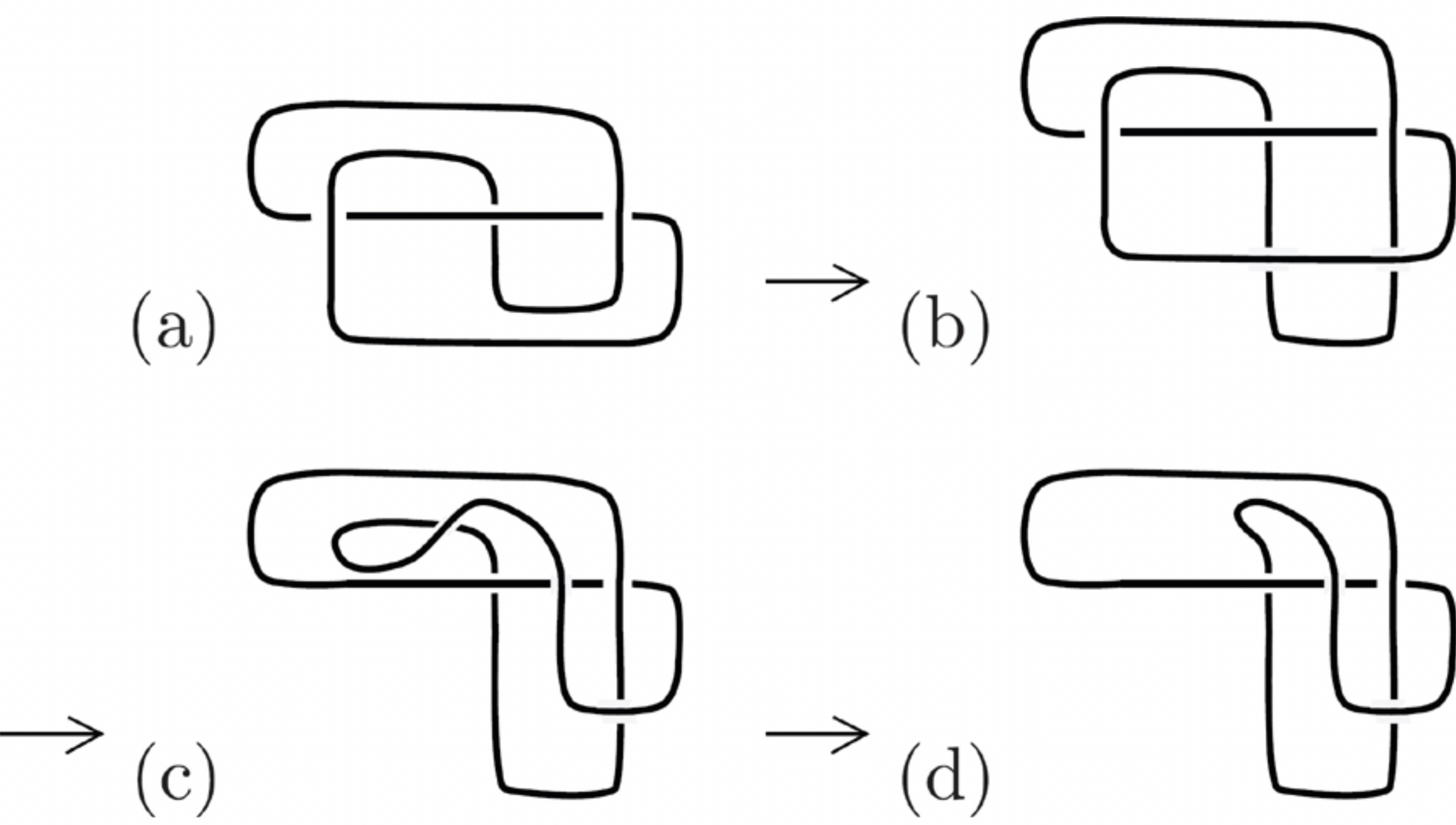
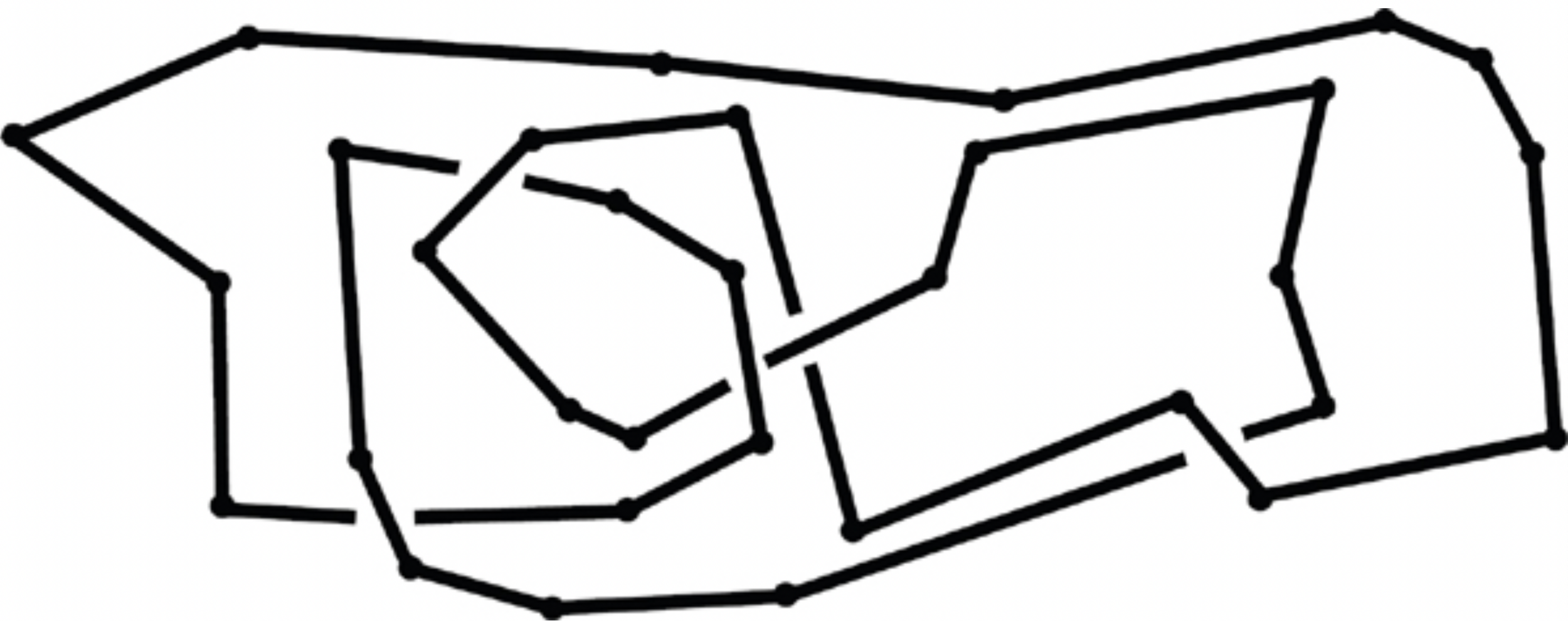
Hint:
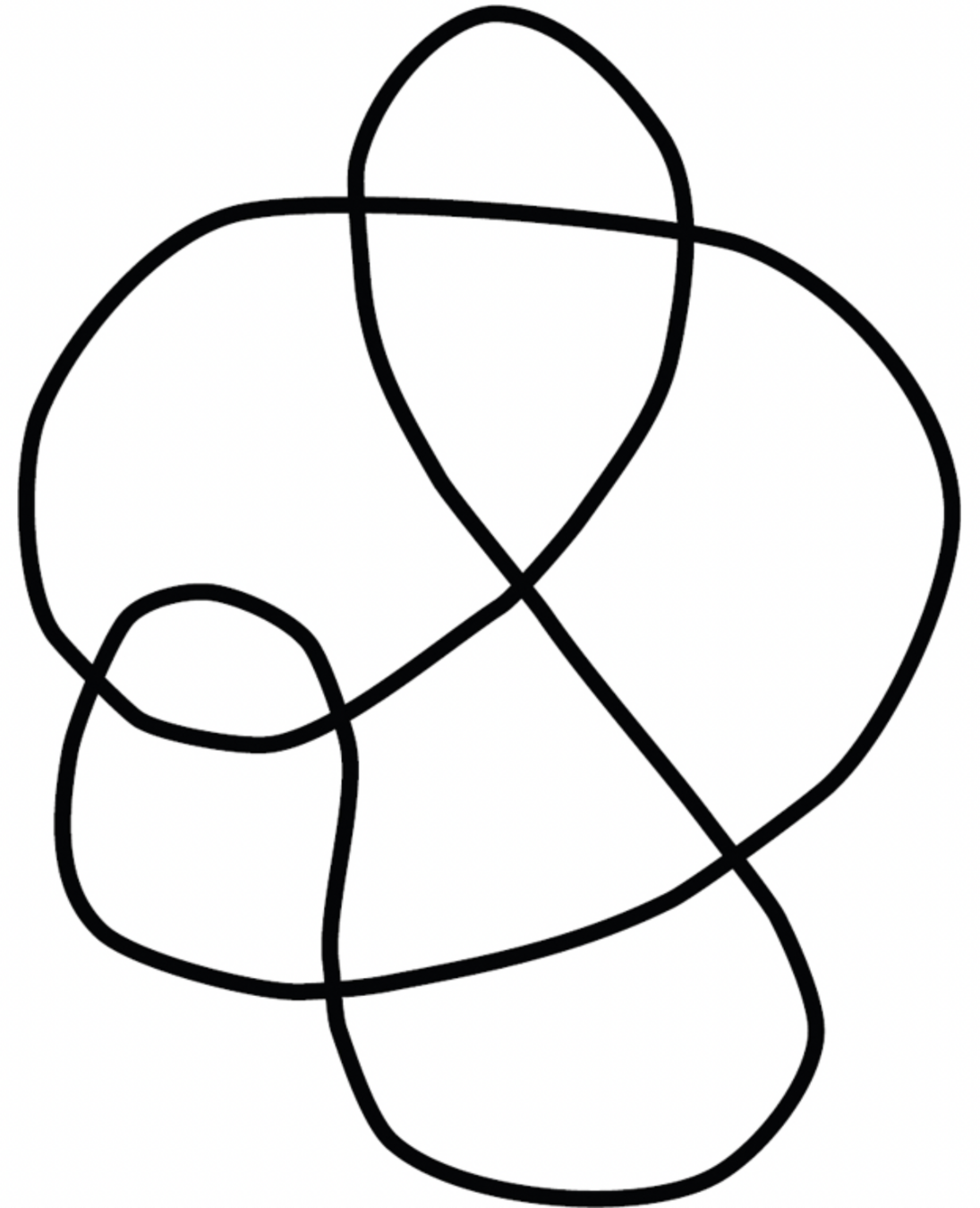
For each knot \(K\) shown below, some assignment of crossings in the projection to the left is equivalent to \(K\). Can you find this crossing assignment? And can you show that a sequence of Reidemeister moves connects the two diagrams?
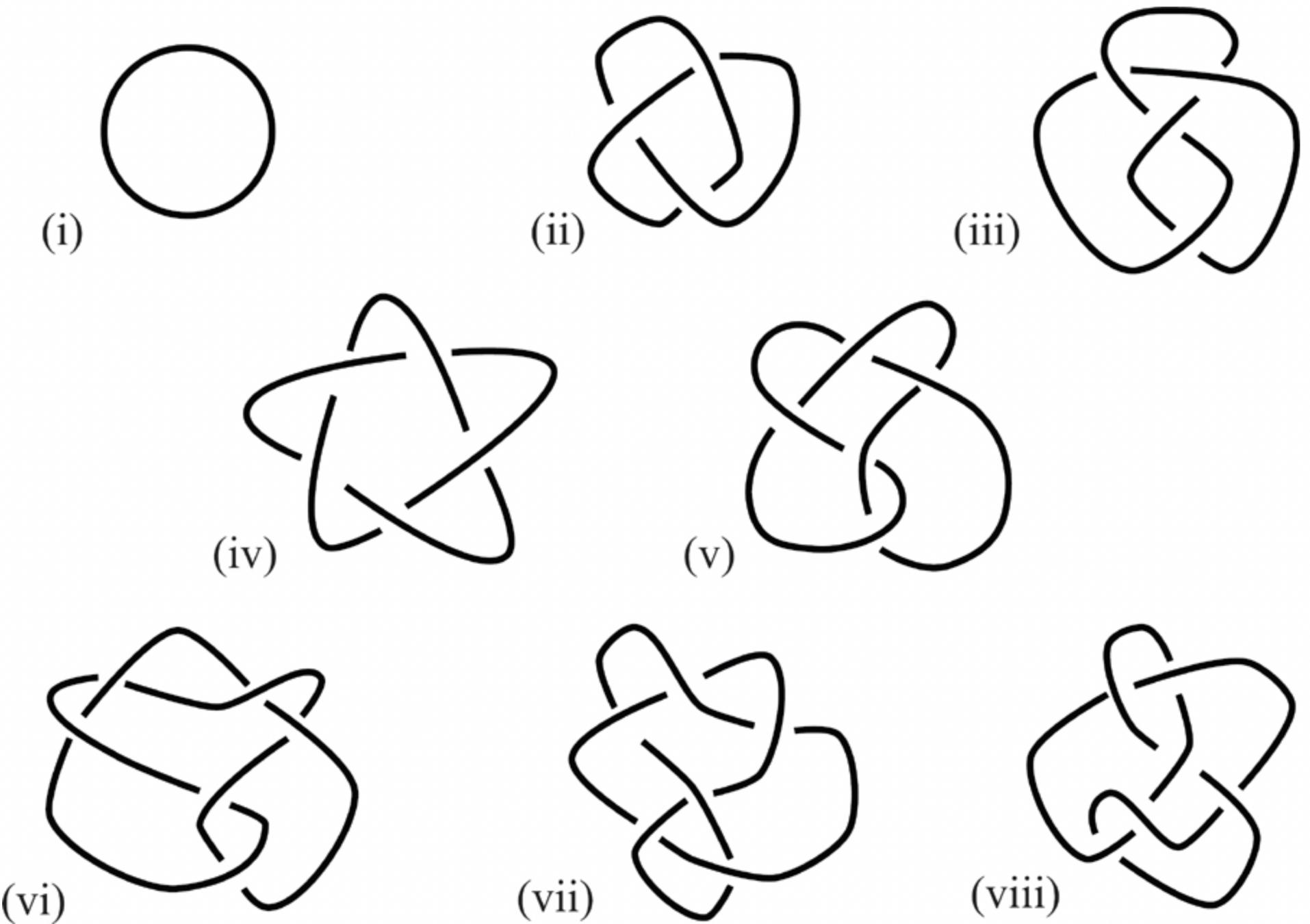
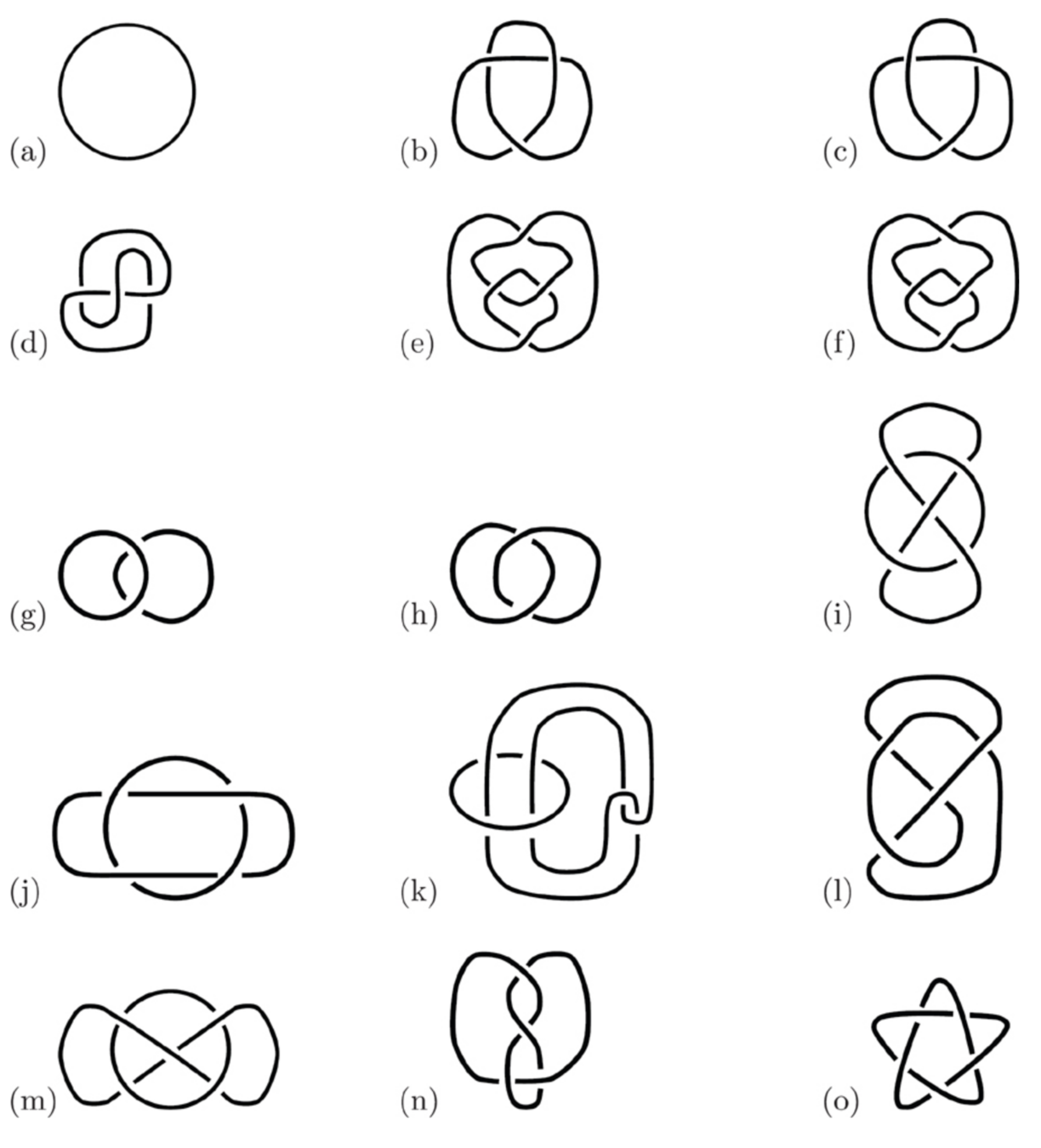
All (prime) knots with 6 crossings
Theorem [Reidemeister]
Two knots \(K_1\) and \(K_2\) are equivalent if and only if any diagram for \(K_1\) and any diagram for \(K_2\) can be related by a sequence of Reidemeister moves.
Equivalence and non-equivalence
The Fundamental Problem of Knot Theory
How can you tell when two knots are not equivalent?
- \(>1.8\) trillion random knots generated
- 92.8% unknots
- 13,020 distinct knot types, including 20 different 19-crossing knots
- \(\approx\)300,000 core-hours of CPU time (or 34.2 core-years)
Some data from a large experiment
The Basic Problems
How can we tell when two knots are not equivalent? How to prove it?
How can we tell when two knots are equivalent? How to prove it?

equivalent?
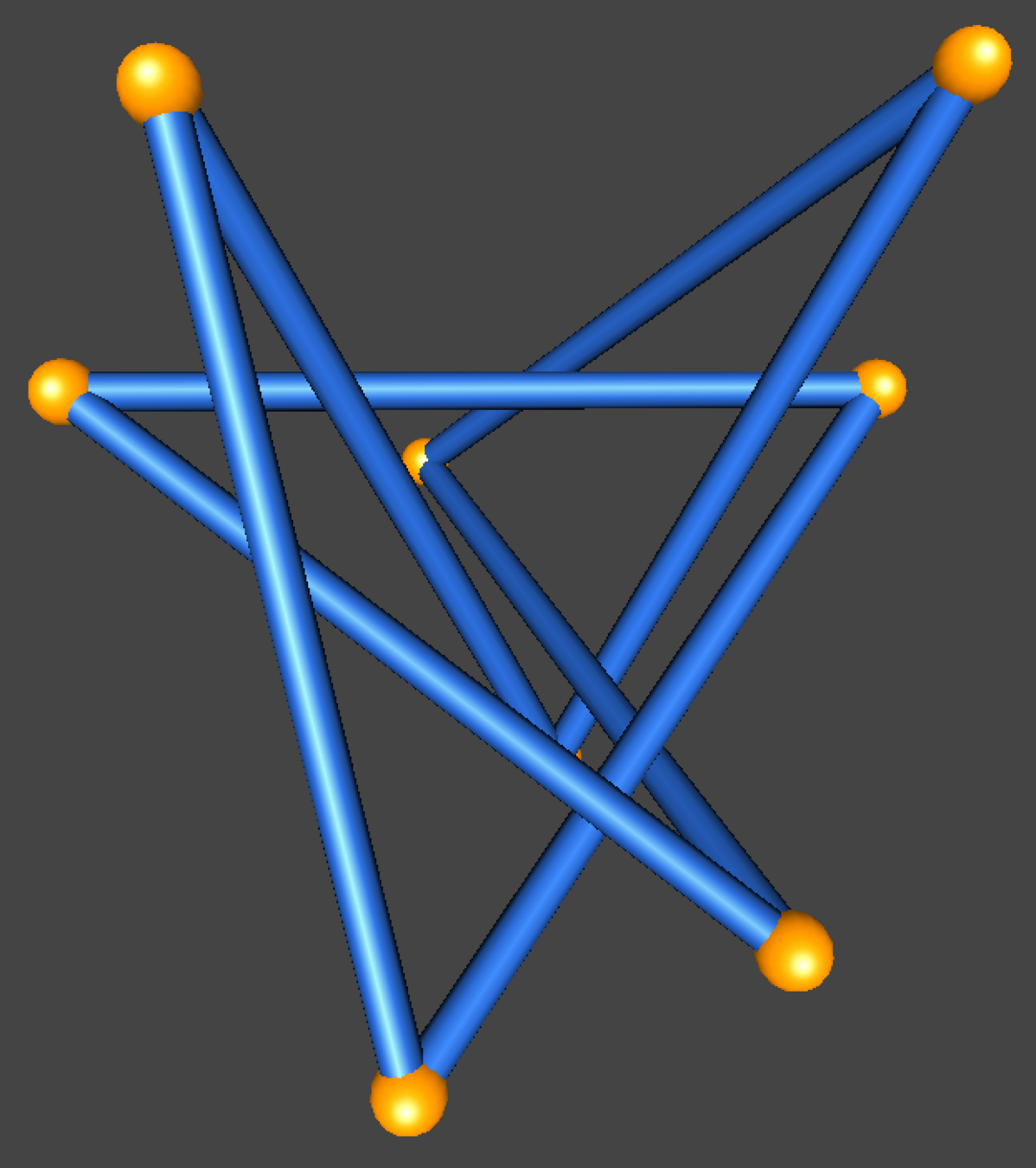
Knot Invariants
Definition
A knot invariant is a function whose domain is the set of equivalence classes of knots.
| Invariant | Value |
|---|---|
| Bridge index | 2 |
| Alternating | T |
| Hyperbolic volume | 2.029883213 |
| Alexander polynomial | |
| HOMFLY polynomial | |
| Knot Floer homology |

Ansatz
If you suspect two knots are not equivalent, find an example of an invariant you can compute, then show that the two knots produce different values.


equivalent?
No!
HOMFLY polynomial
Tricolorability
Definition
A knot diagram is called tricolorable if each arc in the diagram can be drawn using one of three colors, say blue, green, and pink, in such a way that the following two conditions hold:
- At least two colors are used in the diagram.
- At each crossing, either all arcs are colored the same or all arcs are colored differently.



Tricoloring
Finish assigning colors to the black arcs in this diagram to give a valid tricoloring.

Which of the diagrams in this table are tricolorable?

Tricolorability is an Invariant
Theorem [Fox]
If any diagram of a knot \(K\) is tricolorable, then every diagram of \(K\) is tricolorable.
Definition
A knot is called tricolorable if any (and hence every) diagram for the knot is tricolorable.
Is the figure-eight knot tricolorable?
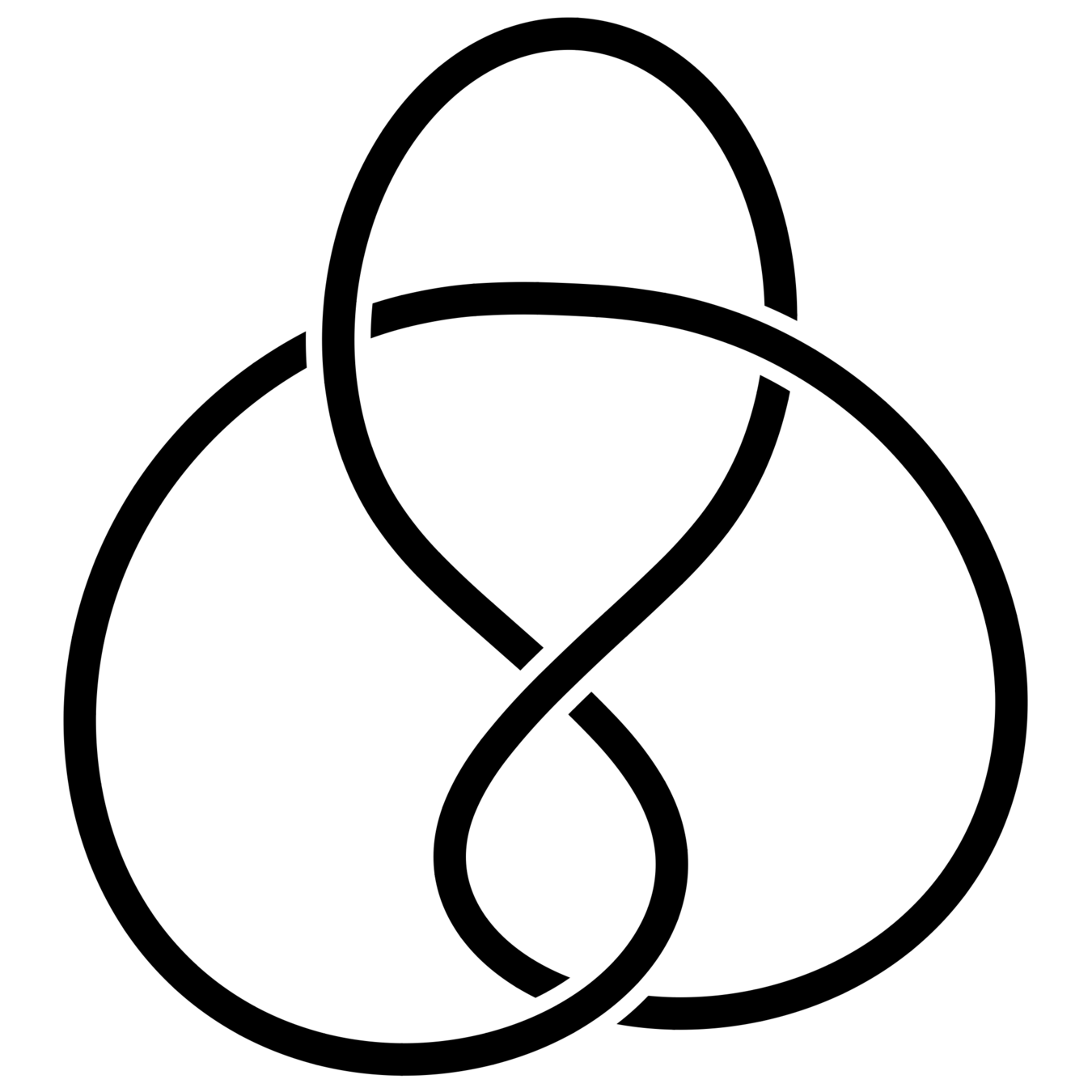
The trefoil is nontrivial
Prove that the trefoil and the unknot are not equivalent.

