Knot Theory

Clayton Shonkwiler

shonkwiler.org

MATH 192

A knot is a closed loop in space

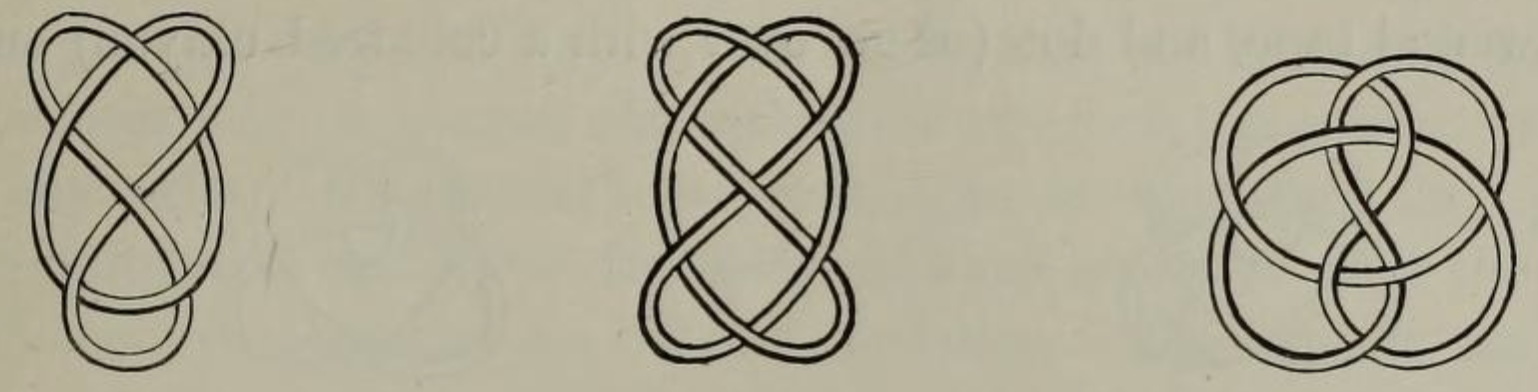
Peter Guthrie Tait

P.G. Tait, Trans. Royal Soc. Edinburgh 32 (1884), 327–342

Wassermann et al. Science 229 (1985), 171–174

Lyubchenko, Micron 42 (2011), 196--206

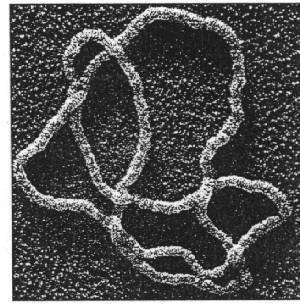
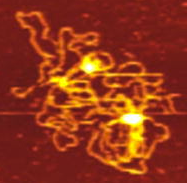
Plasmid DNA

Alonso–Sarduy, Dietler Lab

EPF Lausanne

Vortex Knots

Irvine Lab, U. Chicago

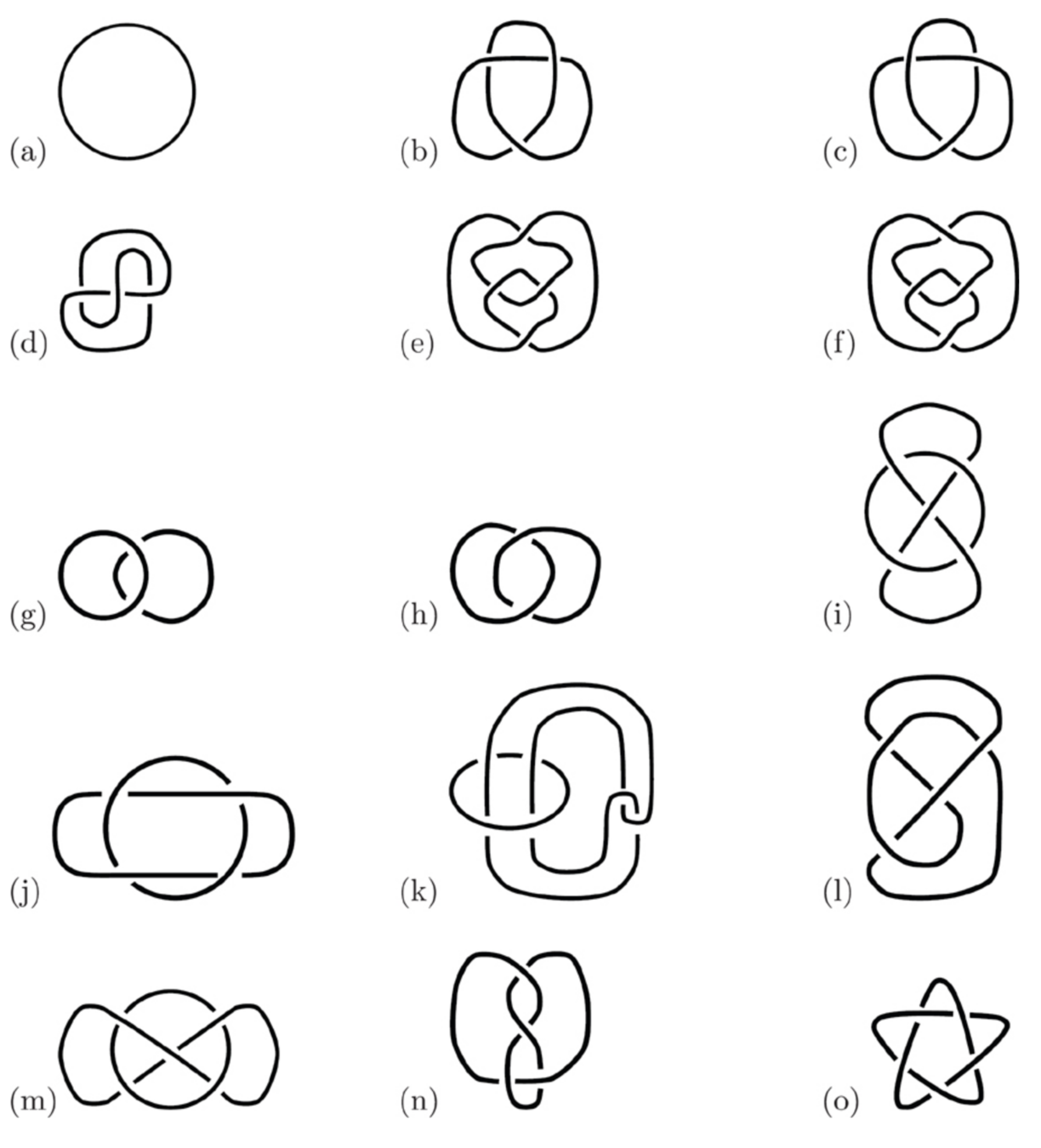
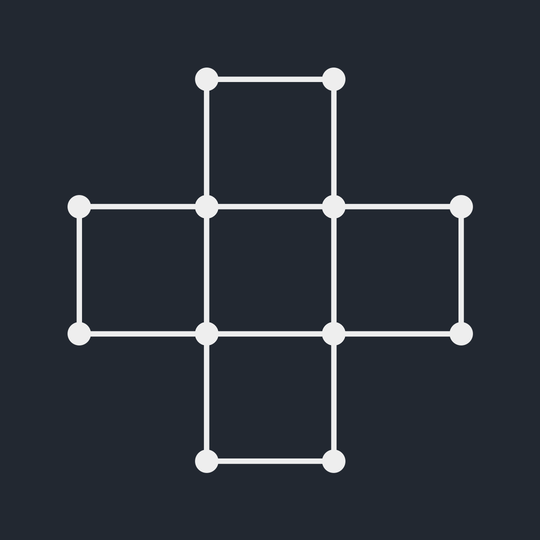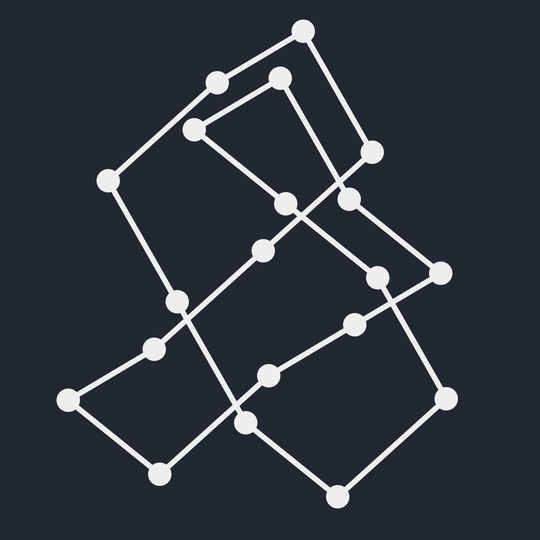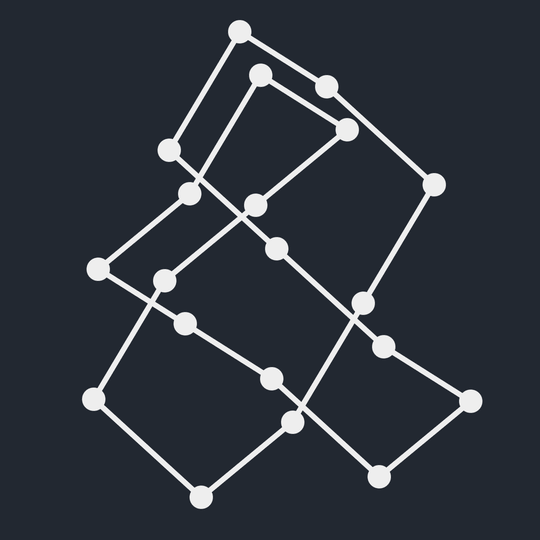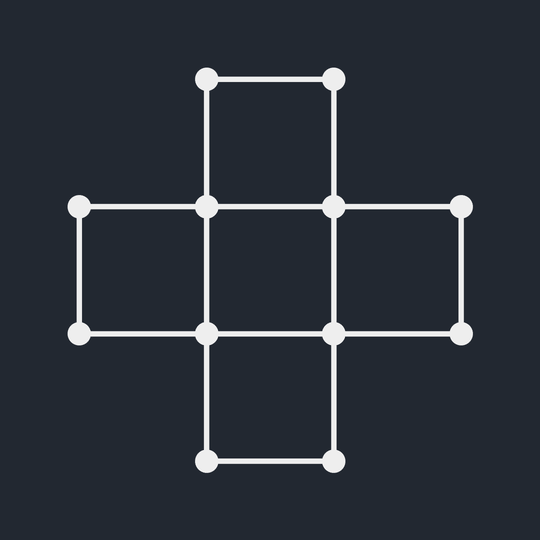
Which of these are knots? (1 piece)

Which are links? (More than 1 piece)

Which are equivalent?

Is there a way to assign crossings to this projection to make it the unknot?

The Basic Problems

How can we tell when two knots are not equivalent? How to prove it?

How can we tell when two knots are equivalent? How to prove it?

equivalent?

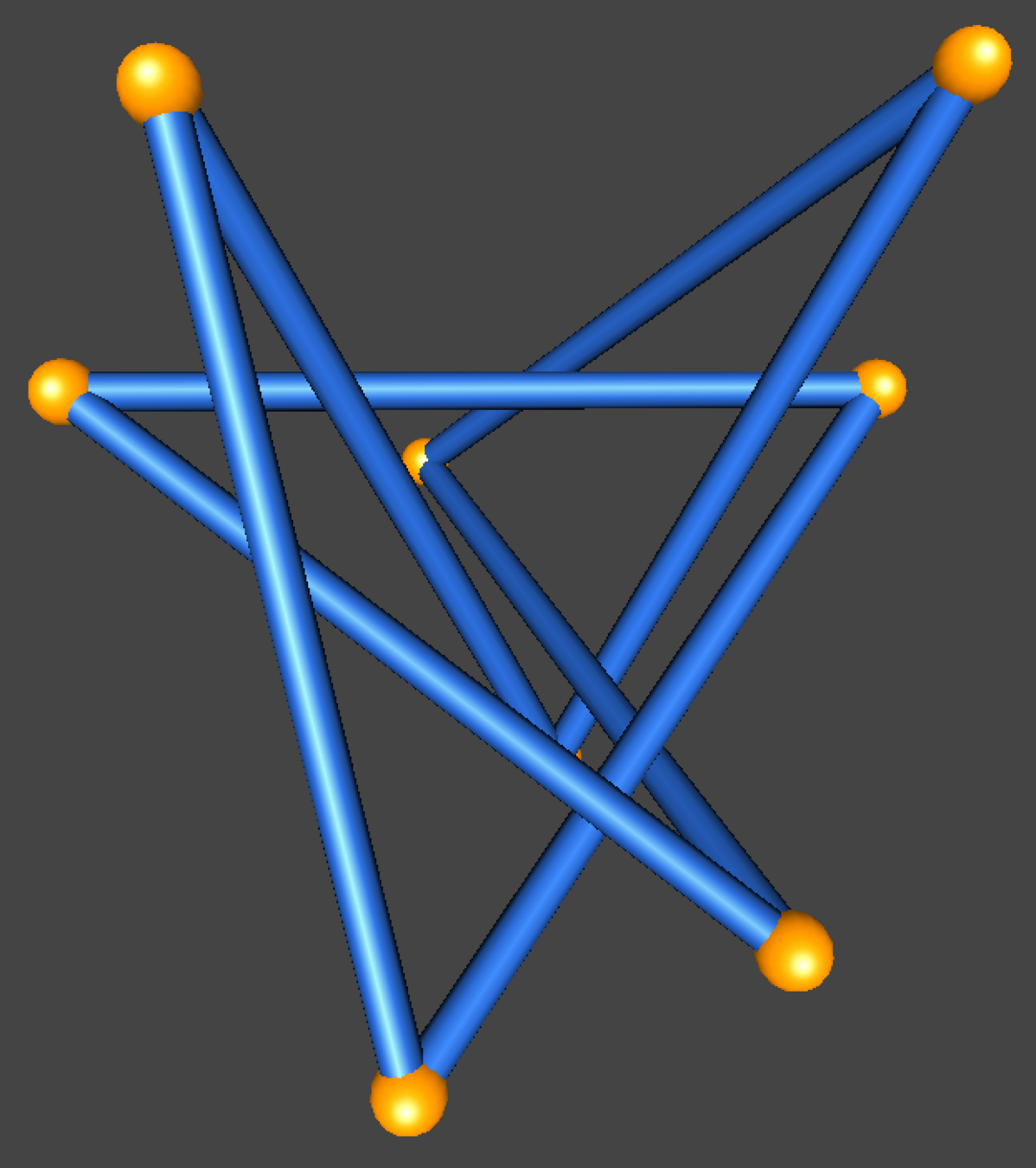
Knot Invariants

Definition

A knot invariant is a function whose domain is the set of equivalence classes of knots.

Invariant	Value
Bridge index	2
Alternating	T
Hyperbolic volume	2.029883213
Alexander polynomial
HOMFLY polynomial
Knot Floer homology

1-3t+t^2

\frac{1}{v^2} - 1 + v^2 - z^2

Ansatz

If you suspect two knots are not equivalent, find an example of an invariant you can compute, then show that the two knots produce different values.

(2-2v^2+v^4)+(1-3v^2+v^4)z^2-\frac{1}{v^2}z^4

\left(\frac{-1}{v^2}+3-v^2\right)+\left(\frac{-1}{v^2}+3-v^2\right)z^2+z^4

equivalent?

No!

HOMFLY polynomial

How hard is it to recognize unknots?

Theorem [Hass–Lagarias–Pippenger]

Unknottedness is in NP.

Theorem [Lackenby]

Unknottedness is in co-NP.

An Unsolved Problem in Mathematics

Can unknots be recognized in polynomial time?

Thank you!

The Unknotting–Knotting Game

Two players: the Knotter and the Unknotter.

K and U take turns assigning crossings; K’s goal is to make the diagram knotted and U’s goal is to make it unknotted.

In pairs, decide who is K and who is U.

Then decide who goes first.

Play the game.

Who won? Did the winner have an advantage?

Play again, switching who goes first. Who won? Did they have an advantage?