Lewis Carroll’s Pillow Problem #58


Earlier versions
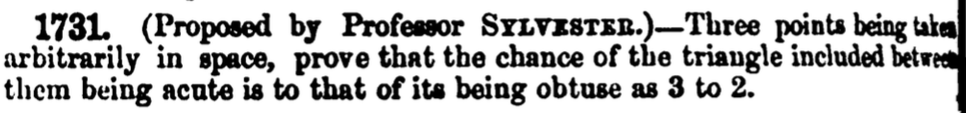

W. S. B. Woolhouse, Educational Times 18 (1865), p. 189
J. J. Sylvester, Educational Times 18 (1865), p. 68

W. S. B. Woolhouse, The Lady's and Gentleman's Diary 158 (1861), p. 76
Carroll’s answer
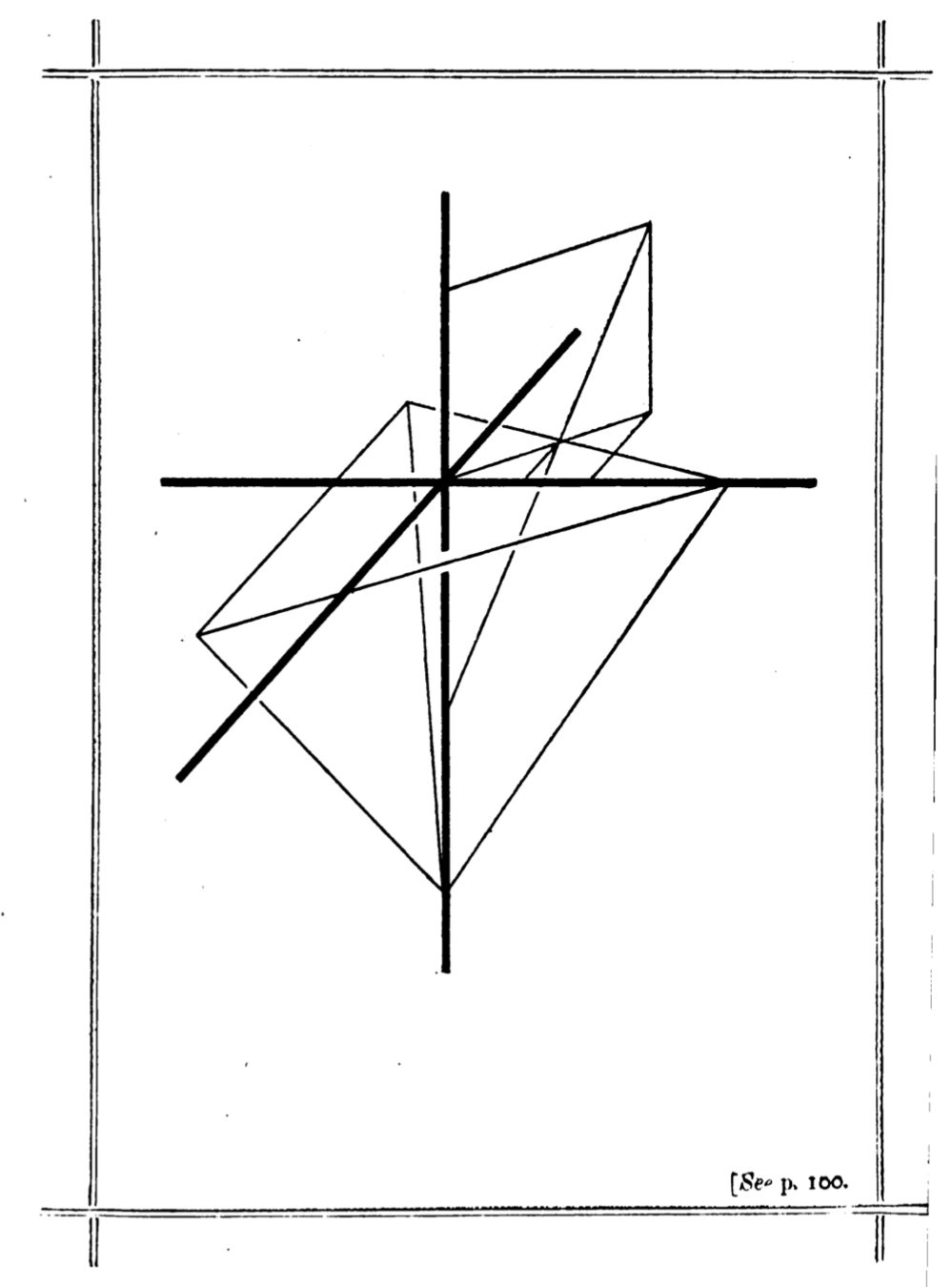
Suppose \(AB\) is the longest side. Then
\(\mathbb{P}(\text{obtuse})=\frac{\pi/8}{\pi/3-\sqrt{3}/4} \approx 0.64\)
But if \(AB\) is the second longest side,
\(\mathbb{P}(\text{obtuse}) = \frac{\pi/2}{\pi/3+\sqrt{3}/2} \approx 0.82\)
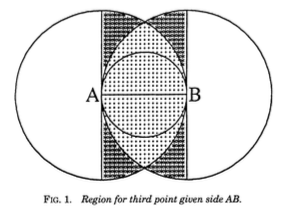
Random Points on an Infinite Plane
Probability \(p\)
\(p\)
\(p\)
\(p\)
\(p\)
Uh oh!
In Fact...
There is no way to choose points randomly in the plane so that the probability that a point lies in a region depends only on the size of the region.
Fancier Version
The uniform measure on the plane is not a probability measure.
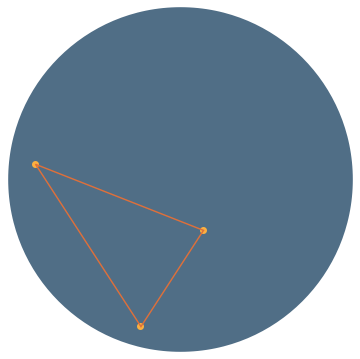
Choose three vertices uniformly in the disk:
\(\mathbb{P}(\text{obtuse})=\frac{9}{8}-\frac{4}{\pi^2}\approx 0.7197\)
Restricted domain?

Choose three vertices uniformly in the square:
\(\mathbb{P}(\text{obtuse})=\frac{97}{150}-\frac{\pi}{40}\approx 0.7252\)
J.J. Sylvester, Educational Times, April 1864
Sylvester’s four point problem
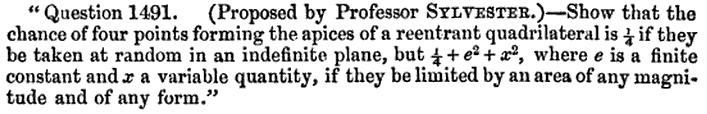
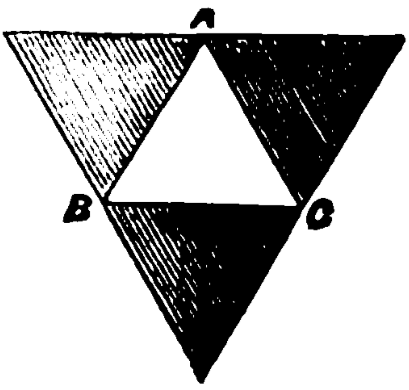
Sylvester and Cayley’s solution

J.J. Sylvester, Phil. Trans. R. Soc. London 154 (1864), p. 654, footnote 64(b)
W.S.B. Woolhouse, Mathematical Questions with Their Solutions VII (1867), p. 81
A. De Morgan’s solution

A. De Morgan, Trans. Cambridge Phil. Soc. XI (1871), pp. 147–148
W.S.B. Woolhouse, Mathematical Questions with Their Solutions VI (1866), p. 52

C.M. Ingleby, Mathematical Questions with Their Solutions V (1865), p. 82
C.M. Ingleby’s solution
G. C. De Morgan’s solution

G.C. De Morgan, Mathematical Questions with Their Solutions V (1865), p. 109

W.S.B. Woolhouse’s solution

W.S.B. Woolhouse, Mathematical Questions with Their Solutions VI (1866), p. 52
W.S.B. Woolhouse’s solutions
W.S.B. Woolhouse, Mathematical Questions with Their Solutions VIII (1868), p. 105
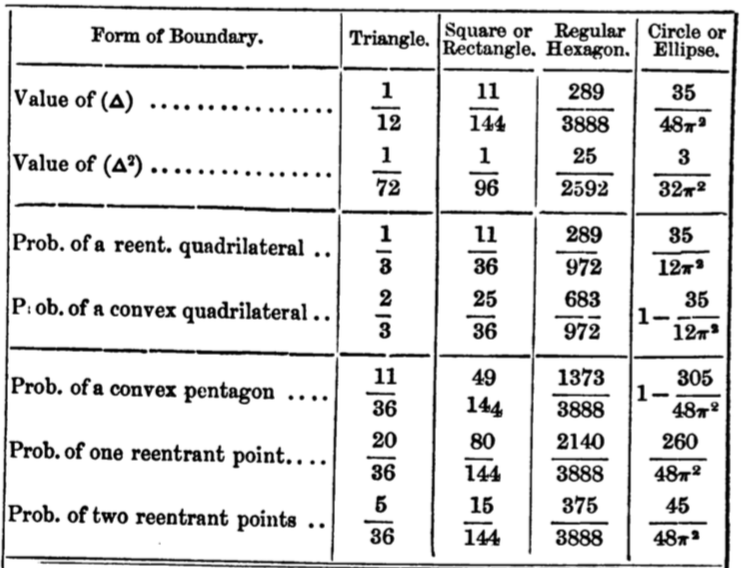
Quadrilaterals in convex bodies
\(\mathbb{P}(\text{reflex})=\frac{1}{3}\)
\(\mathbb{P}(\text{reflex})=\frac{35}{12\pi^2}\approx 0.296\)
Theorem [Blaschke, 1917]
\(\frac{35}{12\pi^2}\leq\mathbb{P}(\text{reflex})\leq\frac{1}{3}\)
J.M. Wilson’s solution

J.M. Wilson, Mathematical Questions with Their Solutions V (1866), p. 81





We need measure theory!
W.A. Whitworth, Mathematical Questions with Their Solutions VIII (1868), p. 36

Report on J.J. Sylvester’s presentation of his paper “On a Special Class of Questions on the Theory of Probabilities” to the British Association for the Advancement of Science, 1865
We need geometry!
Random polygons?
Are these questions really about choosing random points, or are they actually about choosing random polygons?
How would you choose a polygon “at random”?

— Stephen Portnoy, Statistical Science 9 (1994), 279–284
Geometric idea
The space of all \(n\)-gons should be a nice space \(P_n\) with a transitive symmetry group. We should use the invariant probability measure on \(P_n\). Then we should compute the measure of the subset of \(n\)-gons satisfying our favorite condition.
Polygons and Stiefel manifolds
Let \(e_1, \ldots , e_n\) be the edges of a planar \(n\)-gon with total perimeter 2. Choose \(z_1, \ldots , z_n\) so that \(z_k^2 = e_k\). Let \(z_k = u_k + i v_k\).
The polygon is closed \(\Leftrightarrow e_1 + \ldots + e_n = 0\)
\(\sum e_k =\sum z_k^2 = \left(\sum u_k^2 - \sum v_k^2\right) + 2i \sum u_k v_k\)
The polygon is closed \(\Leftrightarrow \|\vec{u}\|=\|\vec{v}\|\) and \(\vec{u} \bot \vec{v}\)
Since \(\sum |e_k| = \sum u_k^2 + \sum v_k^2 = \|\vec{u}\|^2 + \|\vec{v}\|^2\), we see that \((\vec{u},\vec{v})\) is an orthonormal pair of vectors in \(n\)-dimensional space; the collection of such things is called a Stiefel manifold.
Polygons and Grassmannians
Proposition: Rotating \((\vec{u},\vec{v})\) in the plane it spans rotates the corresponding \(n\)-gon twice as fast.
Corollary [Hausmann–Knutson]
The \(n\)-gons of perimeter 2 correspond to the collection of planes in \(n\)-dimensional space. This collection is called a Grassmann manifold.
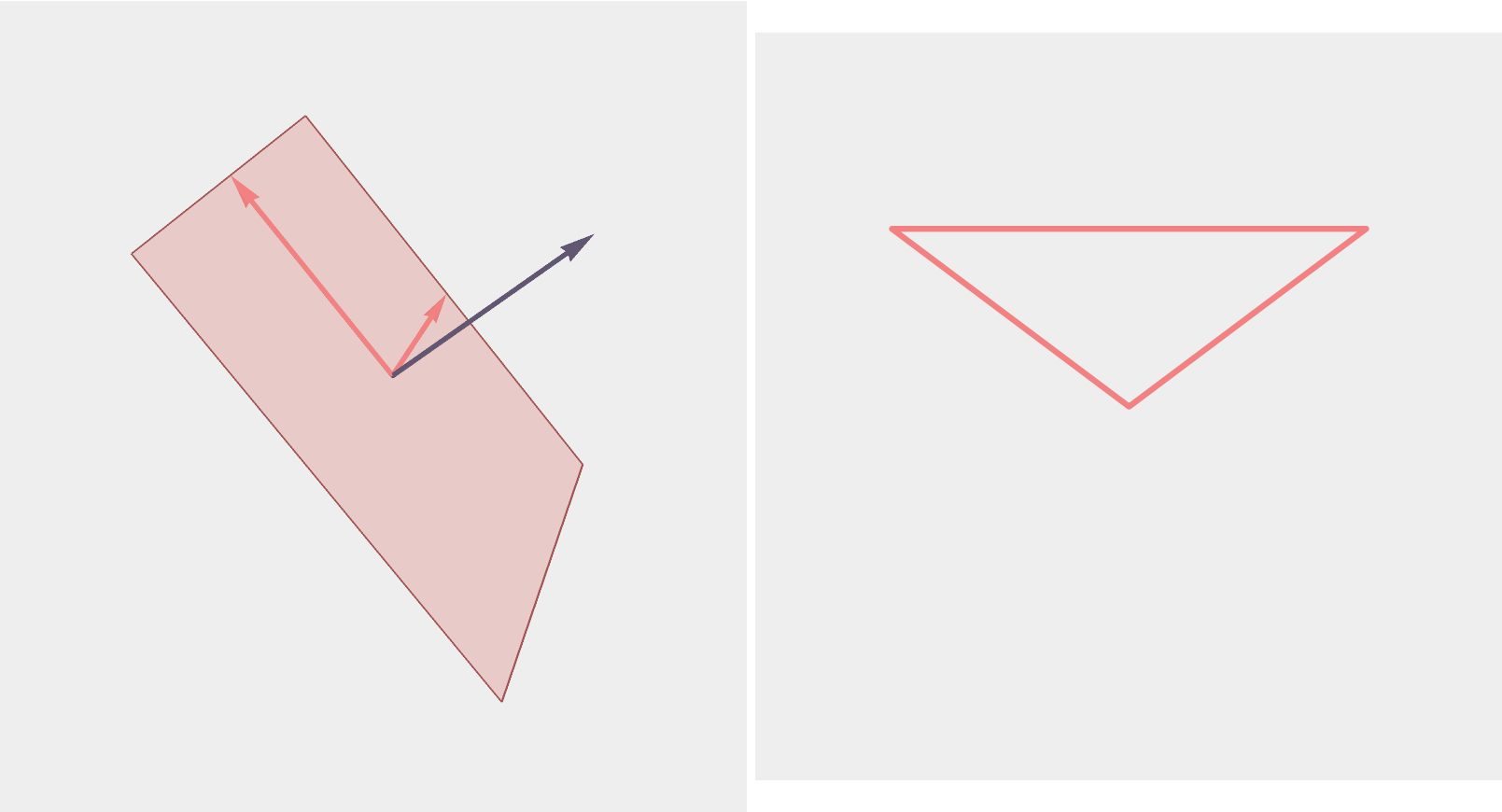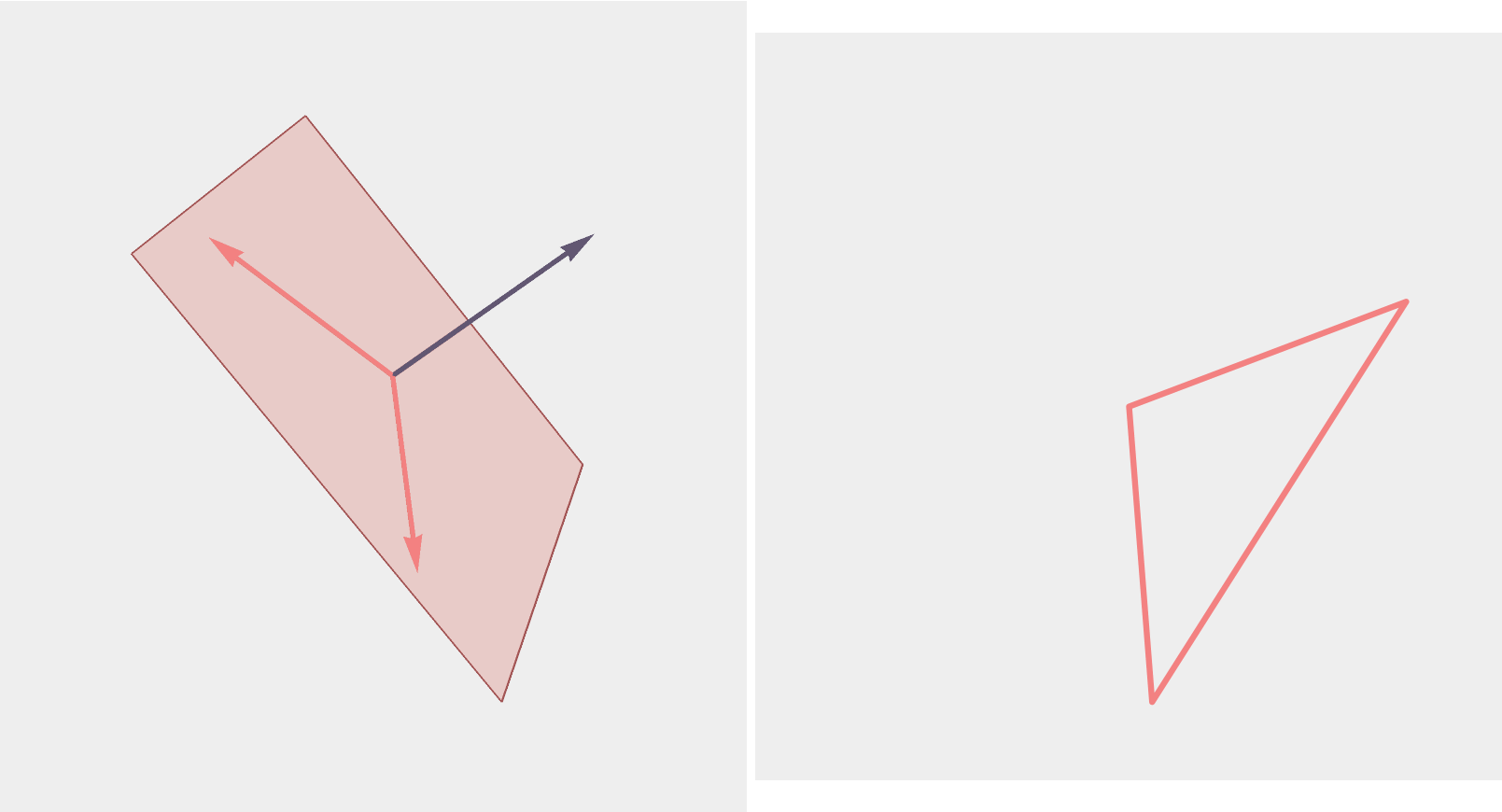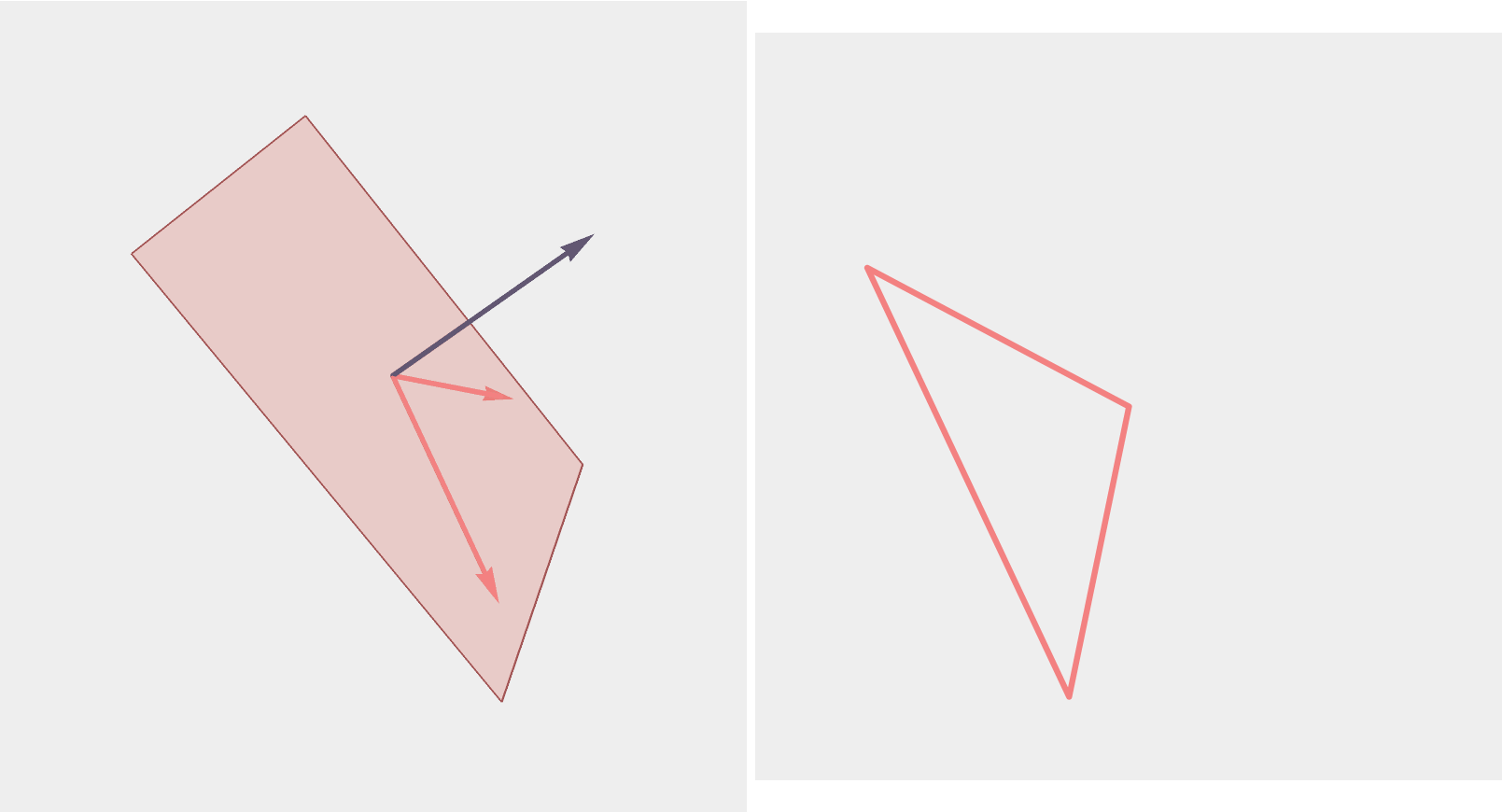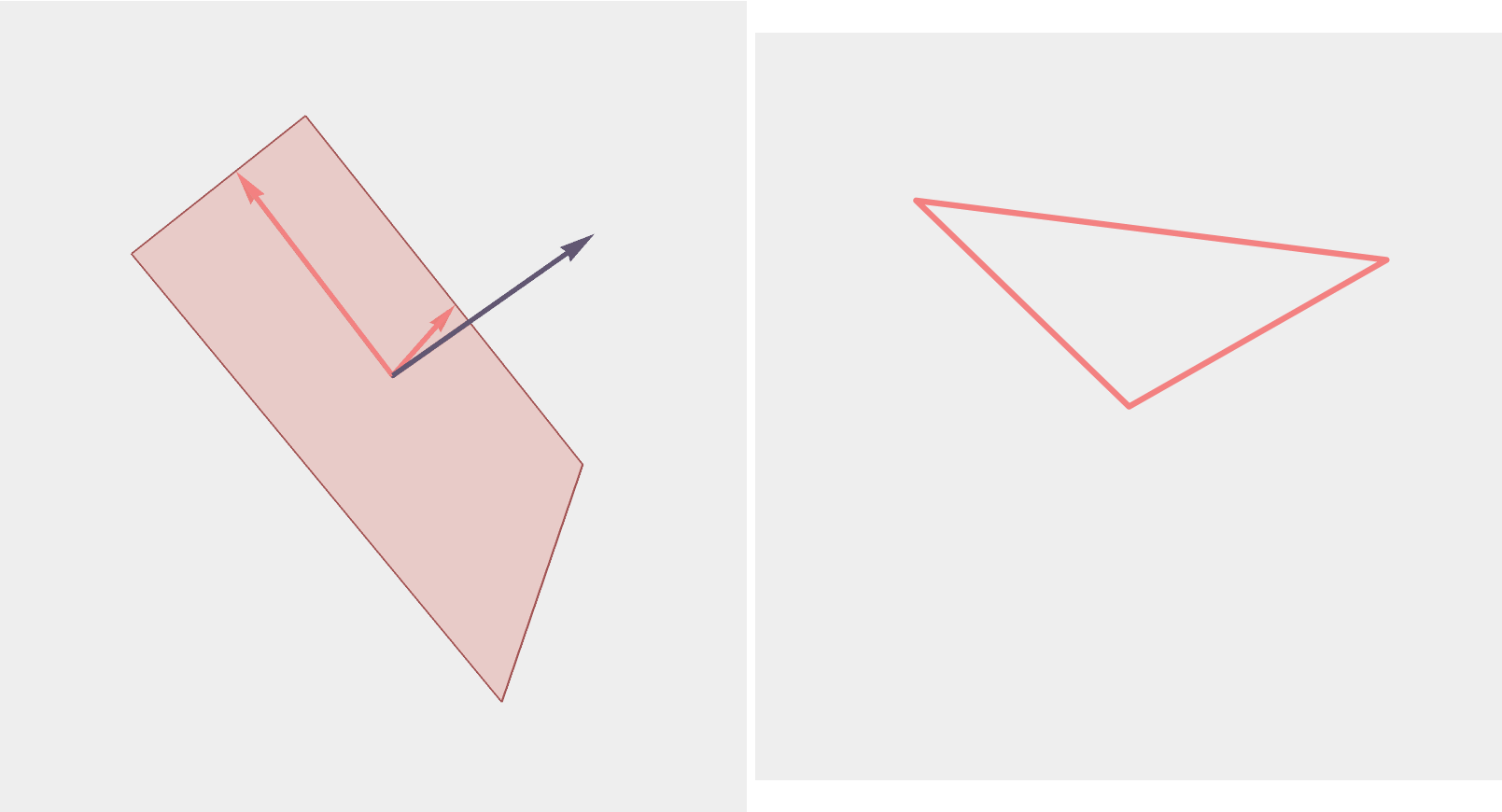
Triangles
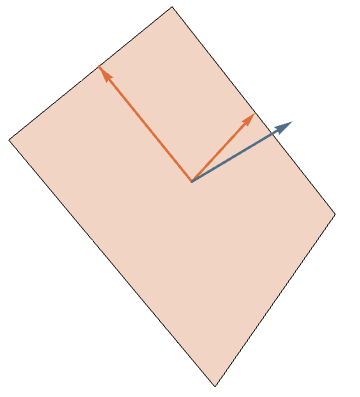
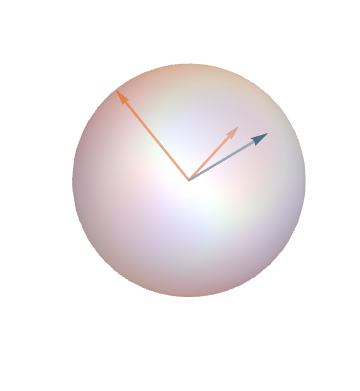
A triangle corresponds to a plane in \(\mathbb{R}^3\) with orthonormal basis \((\vec{u},\vec{v})\)...
or, equivalently, the line through
\(\vec{p}=\vec{u}\times \vec{v}\)
so
Translating to side lengths
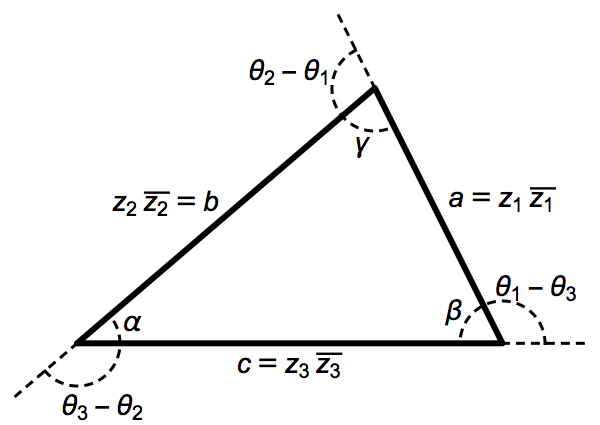
The transitive group
The rotations are natural transformations of the sphere, and the corresponding action on triangles is natural.
\(c=1-z^2\) fixed
\(z\) fixed
\(C(\theta) = (\frac{z^2+1}{2}\cos 2\theta, z \sin 2\theta)\)
The equal-area-in-equal-time parametrization of the ellipse
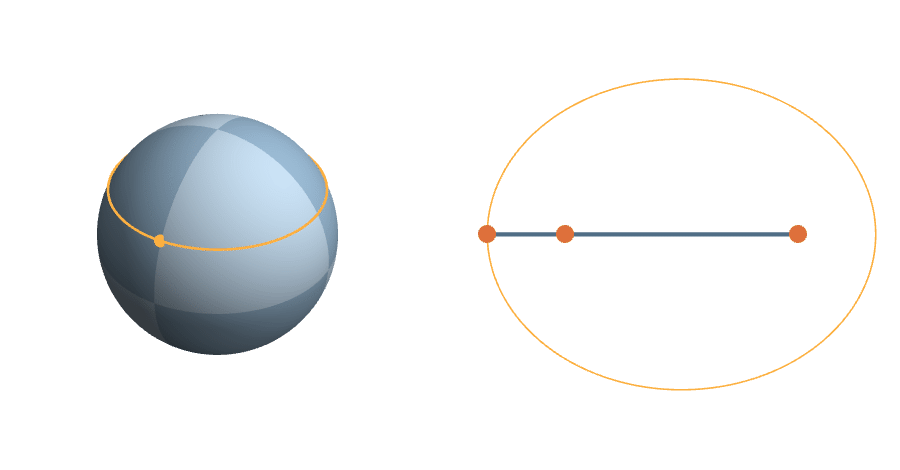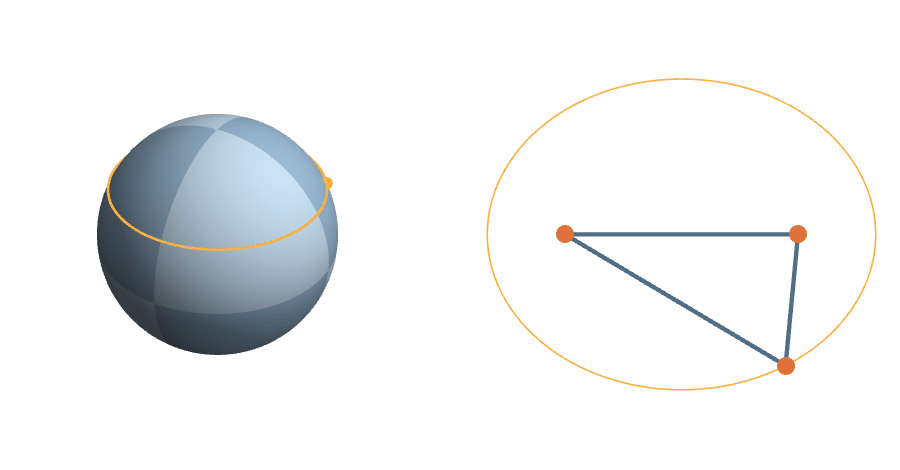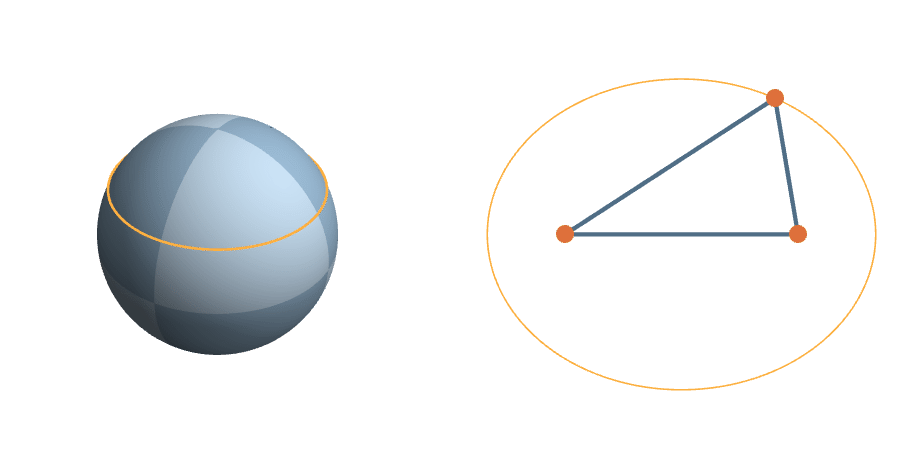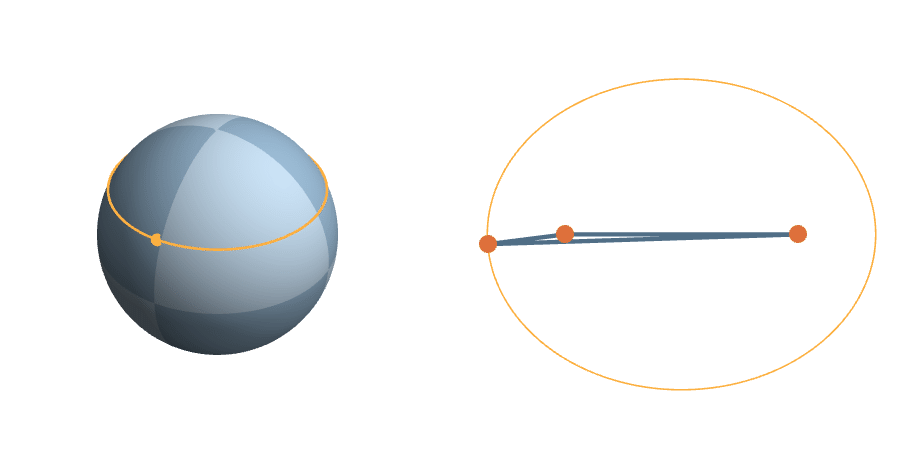
A more complicated rotation
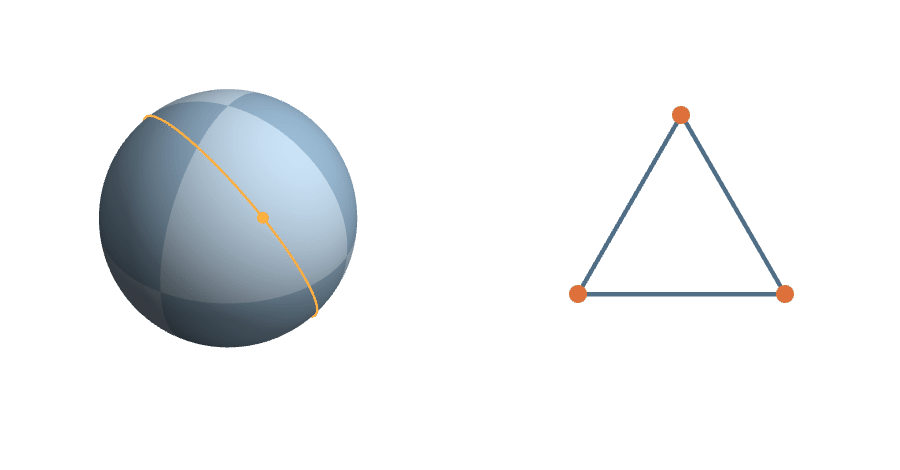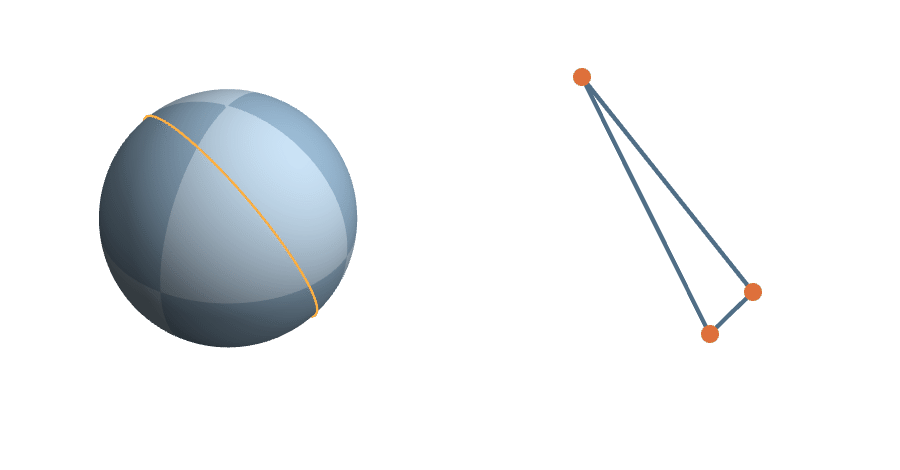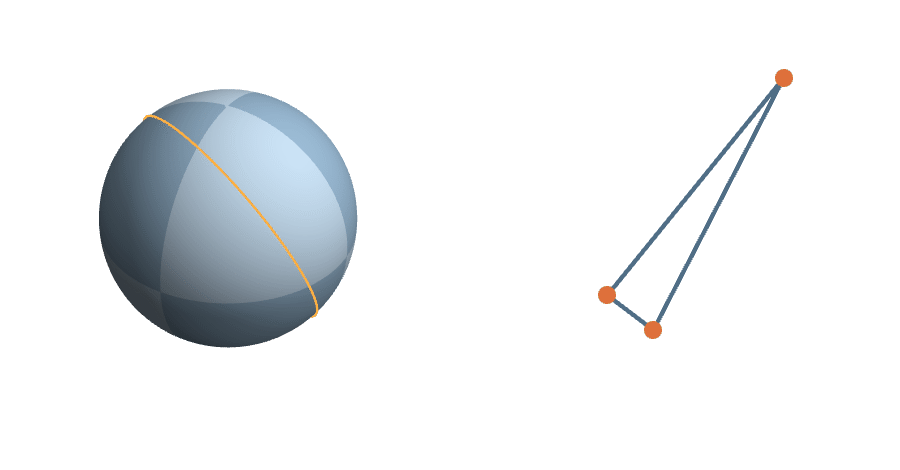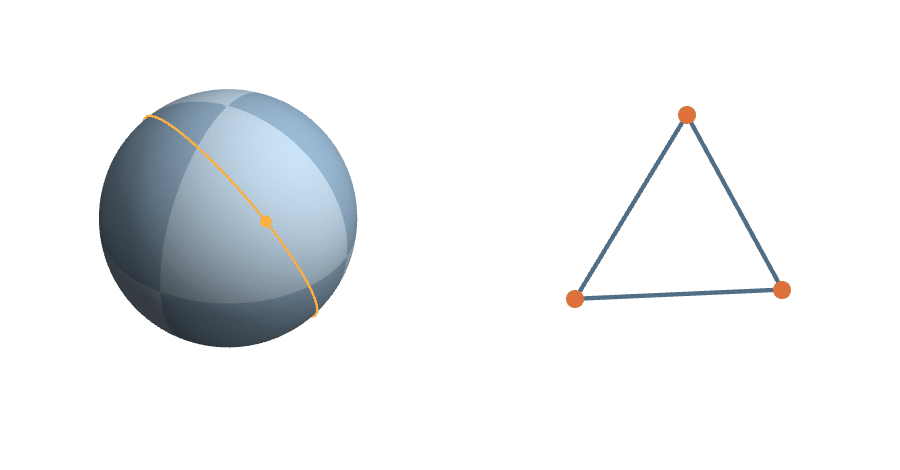
Right triangles
The right triangles are exactly those satisfying
\(a^2+b^2=c^2\) & permutations
Since \(a=1-x^2\), etc., the right triangles are determined by the quartic
\((1-x^2)^2+(1-y^2)^2=(1-z^2)^2\) & permutations
\(x^2 + x^2y^2 + y^2 = 1\), etc.

Obtuse triangles
\(\mathbb{P}(\text{obtuse})=\frac{1}{4\pi}\text{Area} = \frac{24}{4\pi} \int_R d\theta dz\)


But now \(C\) has the parametrization
And the integral reduces to
Solution to the pillow problem
By Stokes’ Theorem

\(\frac{6}{\pi} \int_R d\theta dz=\frac{6}{\pi}\int_{\partial R}z d\theta = \frac{6}{\pi}\left(\int_{z=0} zd\theta + \int_C zd\theta \right)\)
\(\left(\sqrt{\frac{1-y^2}{1+y^2}},y,y\sqrt{\frac{1-y^2}{1+y^2}}\right)\)
\(\frac{6}{\pi} \int_0^1 \left(\frac{2y}{1+y^4}-\frac{y}{1+y^2}\right)dy\)
Our Answer
Theorem [with Cantarella, Needham, Stewart]
With respect to the symmetric measure on triangles, the probability that a random triangle is obtuse is
\(\frac{3}{2}-\frac{3\ln 2}{\pi}\approx0.838\)
Sylvester’s Four Point Problem
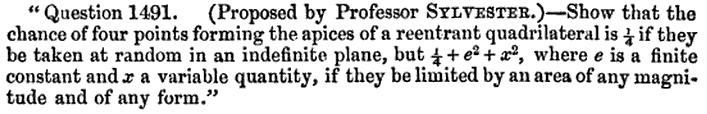

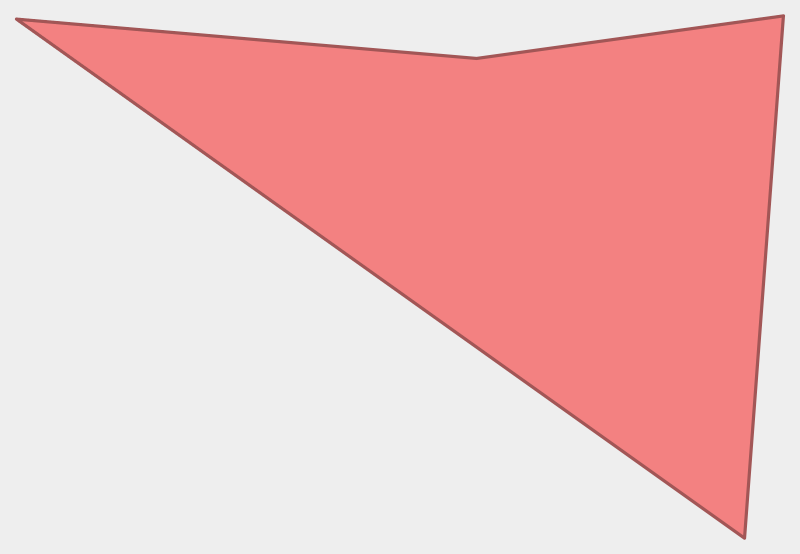
convex
reflex/reentrant
self-intersecting
Modern Reformulation: What is the probability that all vertices of a random quadrilateral lie on its convex hull?
The symmetric group orbit
Theorem [with Cantarella, Needham, Stewart]
Convex, reflex, and self-intersecting quadrilaterals are all equiprobable.

What is the least symmetric triangle?

Symmetric triangles
Isosceles
triangles
Degenerate
triangles

The least symmetric triangle
Theorem [with Bowden, Haynes, Shukert]
The least symmetric triangle has side length ratio
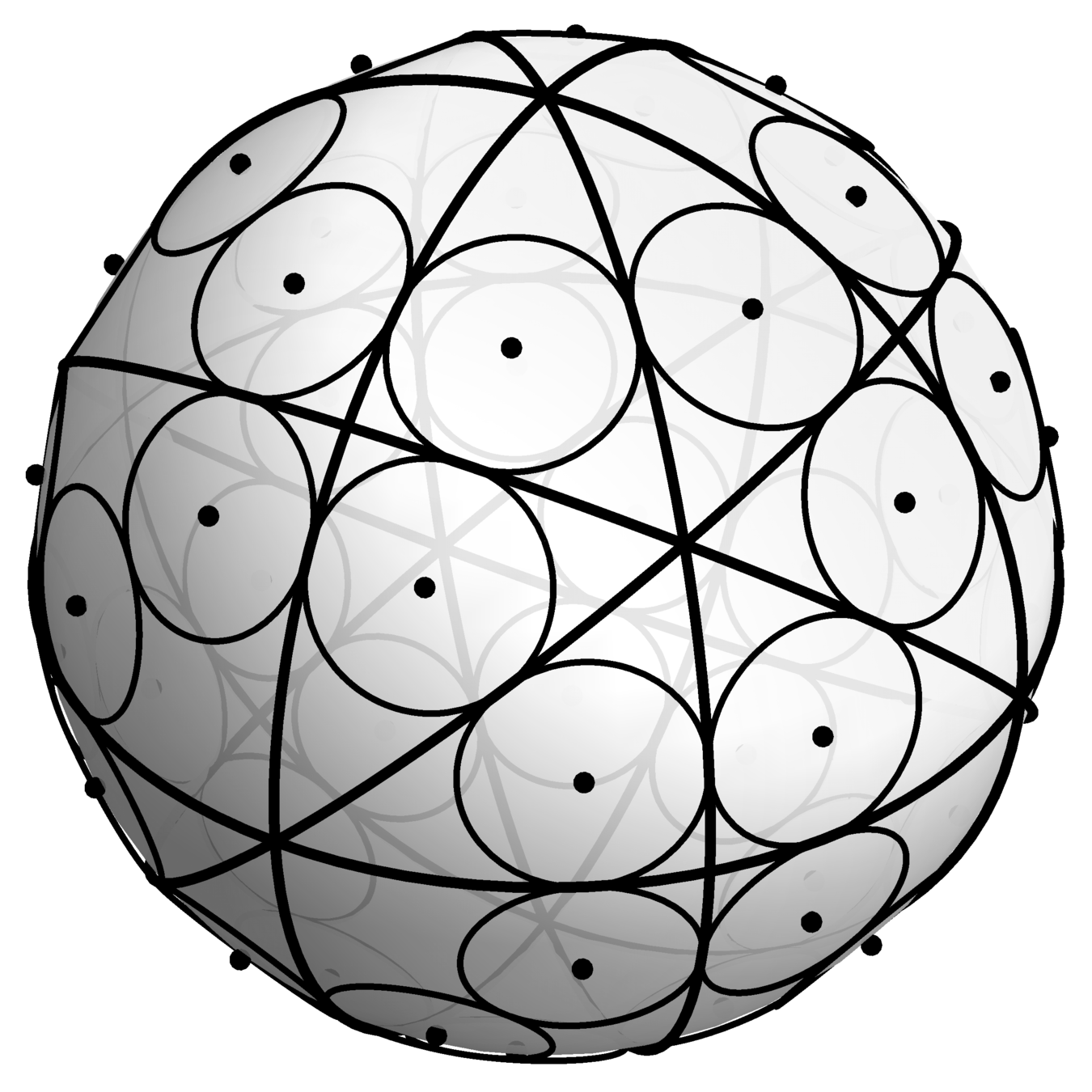
Polygons in Space
There is a version of this story for \(n\)-gons in space as well.
Polygons in space provide a foundational theoretical and computational model for ring polymers like bacterial DNA.
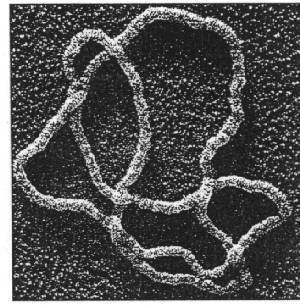

Wassermann et al., Science 229, 171--174

Lyubchenko, Micron 42, 196--206

Polygons in space
Polygons in \(\mathbb{R}^3\) correspond to points in \(G_2(\mathbb{C}^n)\) and the analog of the squaring map is the Hopf map.