The Geometry of Polygon Space
Acute Triangles, Convex Quadrilaterals, Flag Means, and More
/tokyo17
this talk!

Collaborators


Jason Cantarella
U. of Georgia
Tom Needham
Ohio State
Gavin Stewart
NYU
Laney Bowden
CSU
Andrea Haynes
CSU
Aaron Shukert
CSU



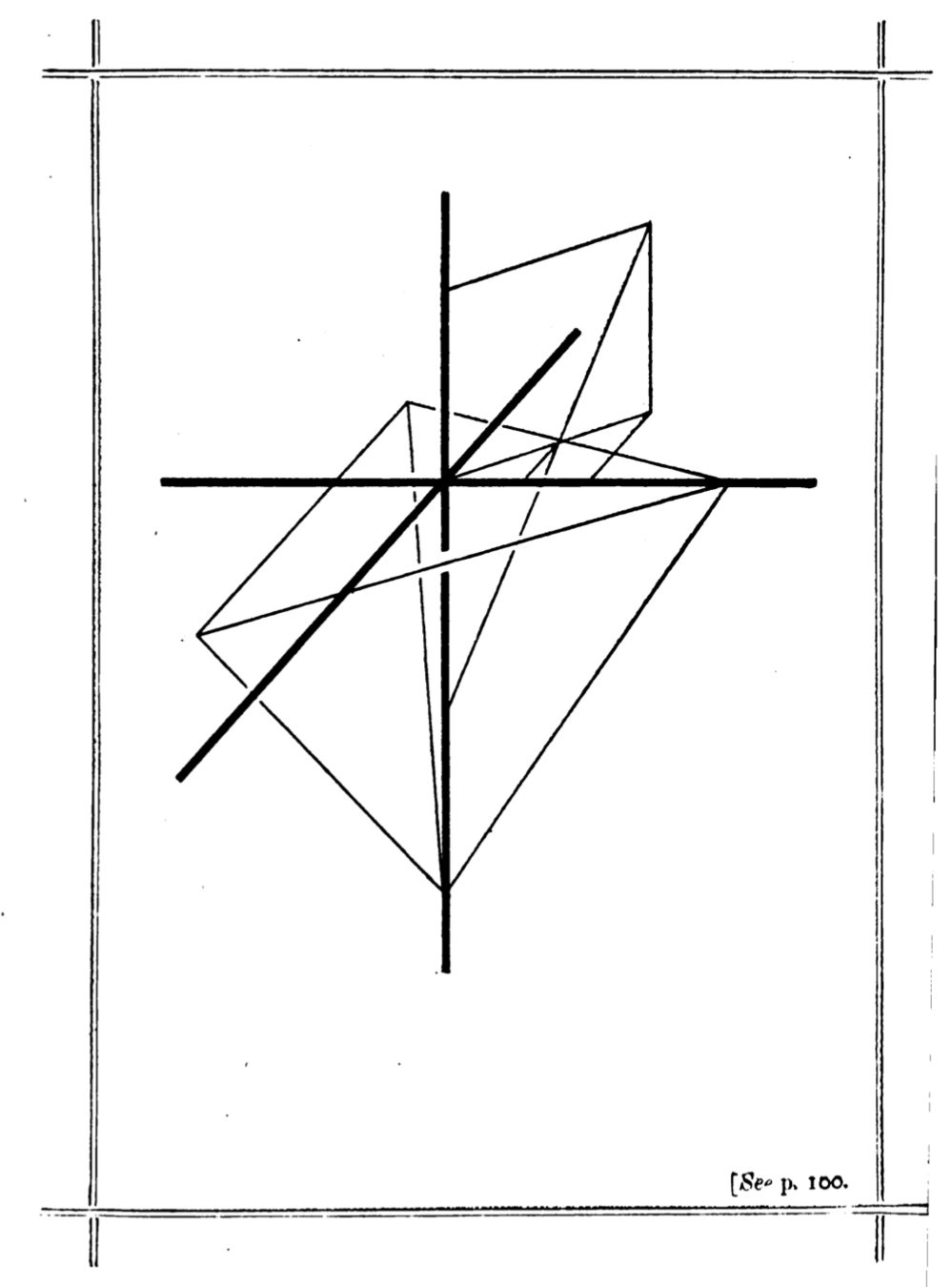
Lewis Carroll’s Pillow Problem #58


Earlier versions

W. S. B. Woolhouse, Educational Times 18 (1865), p. 189
J. J. Sylvester, Educational Times 18 (1865), p. 68

W. S. B. Woolhouse, The Lady's and Gentleman's Diary 158 (1861), p. 76
Carroll’s answer
Suppose \(AB\) is the longest side. Then
\(\mathbb{P}(\text{obtuse})=\frac{\pi/8}{\pi/3-\sqrt{3}/4} \approx 0.64\)
But if \(AB\) is the second longest side,
\(\mathbb{P}(\text{obtuse}) = \frac{\pi/2}{\pi/3+\sqrt{3}/2} \approx 0.82\)
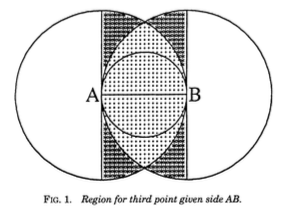
A probabilist’s answer
Proposition [Portnoy]: If the distribution of \((x_1,y_1,x_2,y_2,x_3,y_3)\in\mathbb{R}^6\) is spherically symmetric (for example, a standard Gaussian), then
\(\mathbb{P}(\text{obtuse}) = \frac{3}{4}\)
Consider the vertices \((x_1,y_1),(x_2,y_2),(x_3,y_3)\) as determining a single point in \(\mathbb{R}^6\).
For example, when the vertices of the triangle are chosen from independent, identically-distributed Gaussians on \(\mathbb{R}^2\).
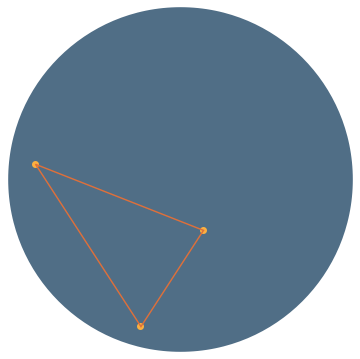
Choose three vertices uniformly in the disk:
\(\mathbb{P}(\text{obtuse})=\frac{9}{8}-\frac{4}{\pi^2}\approx 0.7197\)
Restricted domain?

Choose three vertices uniformly in the square:
\(\mathbb{P}(\text{obtuse})=\frac{97}{150}-\frac{\pi}{40}\approx 0.7252\)

reentrant
J.J. Sylvester, Educational Times, April 1864
Sylvester’s four point problem
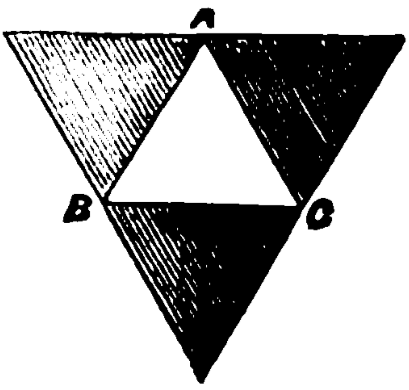
Sylvester and Cayley’s solution

J.J. Sylvester, Phil. Trans. R. Soc. London 154 (1864), p. 654, footnote 64(b)
W.S.B. Woolhouse, Mathematical Questions with Their Solutions VII (1867), p. 81
A. De Morgan’s solution

A. De Morgan, Trans. Cambridge Phil. Soc. XI (1871), pp. 147–148
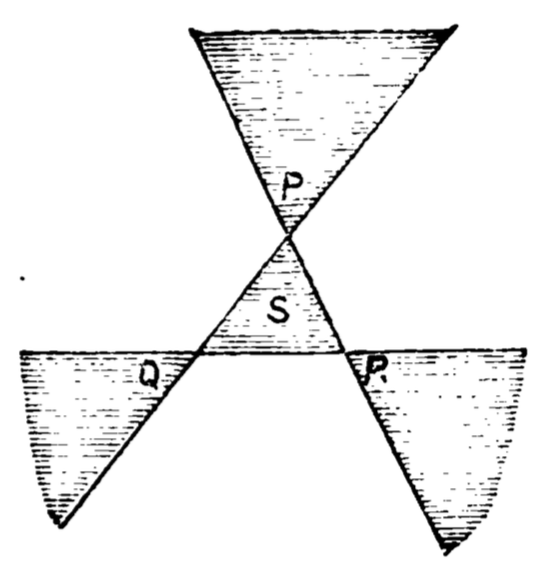
W.S.B. Woolhouse, Mathematical Questions with Their Solutions VI (1866), p. 52

C.M. Ingleby, Mathematical Questions with Their Solutions V (1865), p. 82
C.M. Ingleby’s solution
G. C. De Morgan’s solution

G.C. De Morgan, Mathematical Questions with Their Solutions V (1865), p. 109

W.S.B. Woolhouse’s solution

W.S.B. Woolhouse, Mathematical Questions with Their Solutions VI (1866), p. 52
W.S.B. Woolhouse’s solutions
W.S.B. Woolhouse, Mathematical Questions with Their Solutions VIII (1868), p. 105
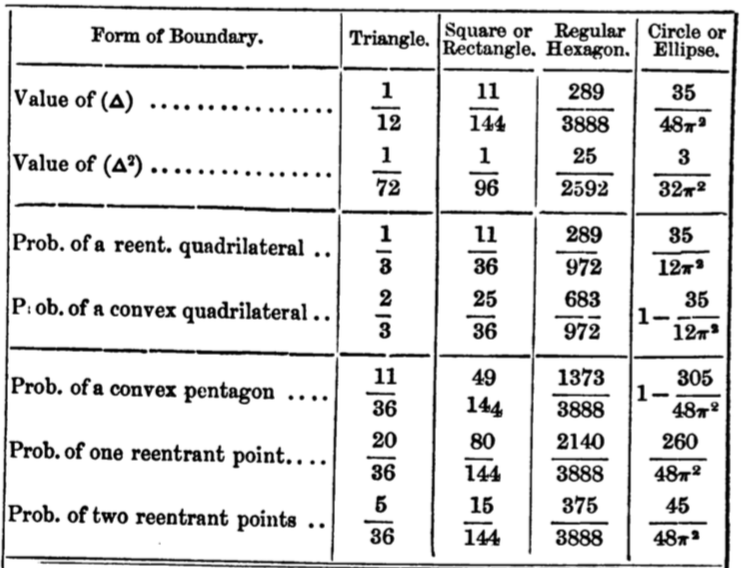
Quadrilaterals in convex bodies
\(\mathbb{P}(\text{reflex})=\frac{1}{3}\)
\(\mathbb{P}(\text{reflex})=\frac{35}{12\pi^2}\approx 0.296\)
Theorem [Blaschke, 1917]
\(\frac{35}{12\pi^2}\leq\mathbb{P}(\text{reflex})\leq\frac{1}{3}\)
J.M. Wilson’s solution

J.M. Wilson, Mathematical Questions with Their Solutions V (1866), p. 81





We need measure theory!
W.A. Whitworth, Mathematical Questions with Their Solutions VIII (1868), p. 36

Report on J.J. Sylvester’s presentation of his paper “On a Special Class of Questions on the Theory of Probabilities” to the British Association for the Advancement of Science, 1865
We need geometry!
Random polygons?
Are these questions really about choosing random points, or are they actually about choosing random polygons?
How would you choose a polygon “at random”?

— Stephen Portnoy, Statistical Science 9 (1994), 279–284
Geometric idea
The space of all \(n\)-gons should be a (preferably compact) manifold \(P_n\) with a transitive isometry group. We should use the left-invariant metric on \(P_n\), scaled so vol\((P_n)=1\). Then the Riemannian volume form induced by this metric is a natural probability measure on \(P_n\), and we should compute the volume of the subset of \(n\)-gons satisfying our favorite condition.
Spoiler: \(P_n \simeq G_2\mathbb{R}^n\)
Polygons and Stiefel manifolds
Let \(e_1, \ldots , e_n\) be the edges of a planar \(n\)-gon with total perimeter 2. Choose \(z_1, \ldots , z_n\) so that \(z_k^2 = e_k\). Let \(z_k = a_k + i b_k\).
The polygon is closed \(\Leftrightarrow e_1 + \ldots + e_n = 0\)
\(\sum e_k =\sum z_k^2 = \left(\sum a_k^2 - \sum b_k^2\right) + 2i \sum a_k b_k\)
The polygon is closed \(\Leftrightarrow \|a\|=\|b\|\) and \(a \bot b\)
Since \(\sum |e_k| = \sum a_k^2 + \sum b_k^2 = \|a\|^2 + \|b\|^2\), we see that \((a,b) \in V_2(\mathbb{R}^n)\), the Stiefel manifold of 2-frames in \(\mathbb{R}^n\).
Polygons and Grassmannians
Proposition: Rotating \((a,b)\) in the plane it spans rotates the corresponding \(n\)-gon twice as fast.
Corollary [Hausmann–Knutson]
The Grassmannian \(G_2(\mathbb{R}^n)\) is (almost) a \(2^n\)-fold covering of the space of planar \(n\)-gons of perimeter 2.
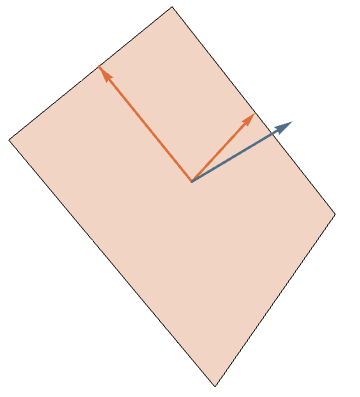
The symmetric measure
Definition [w/ Cantarella & Deguchi]
The symmetric measure on \(n\)-gons of perimeter 2 up to translation and rotation is the pushforward of Haar measure on \(G_2(\mathbb{R}^n)\).
Therefore, \(SO(n)\) acts transitively on \(n\)-gons and preserves the symmetric measure.
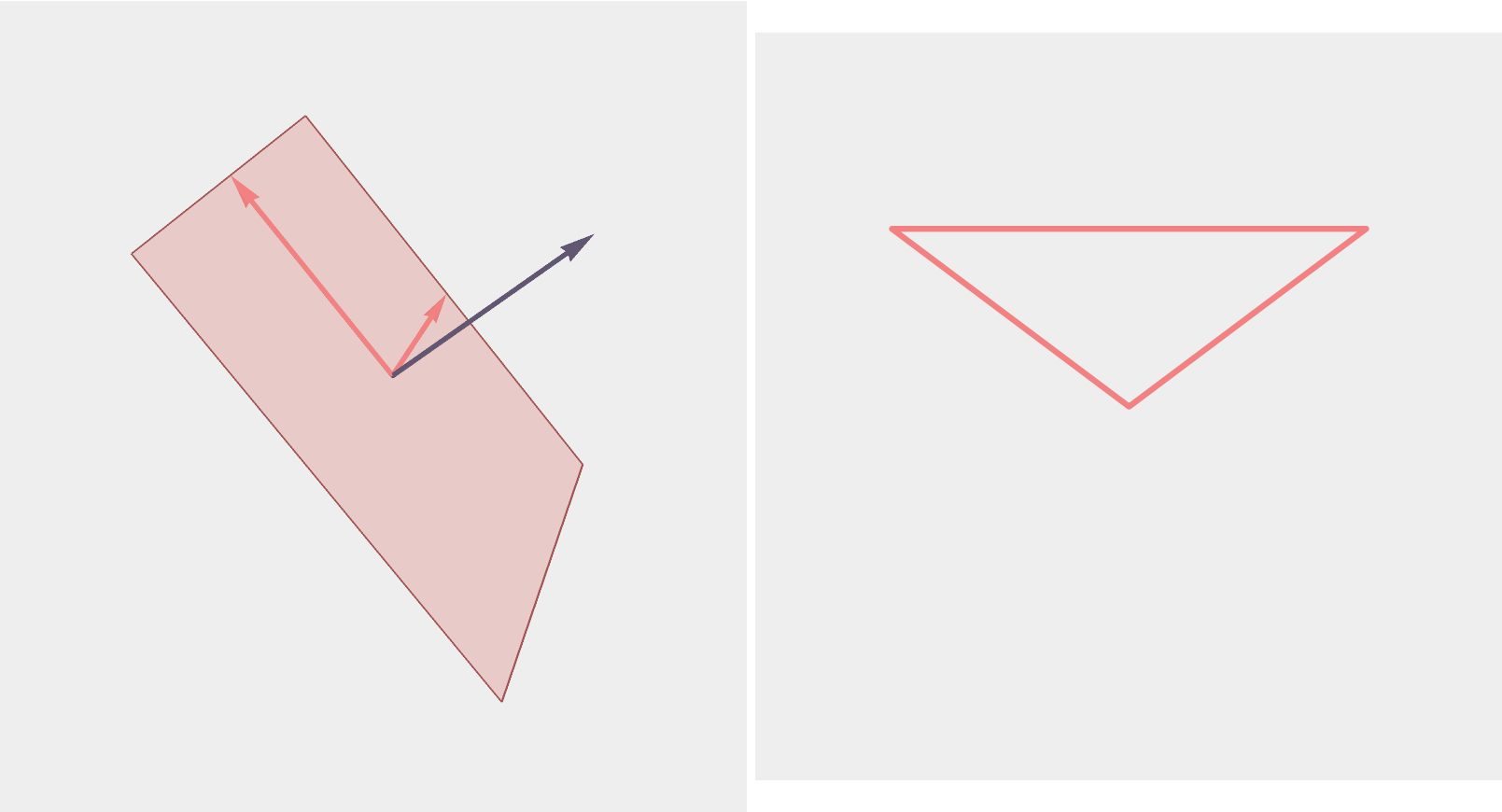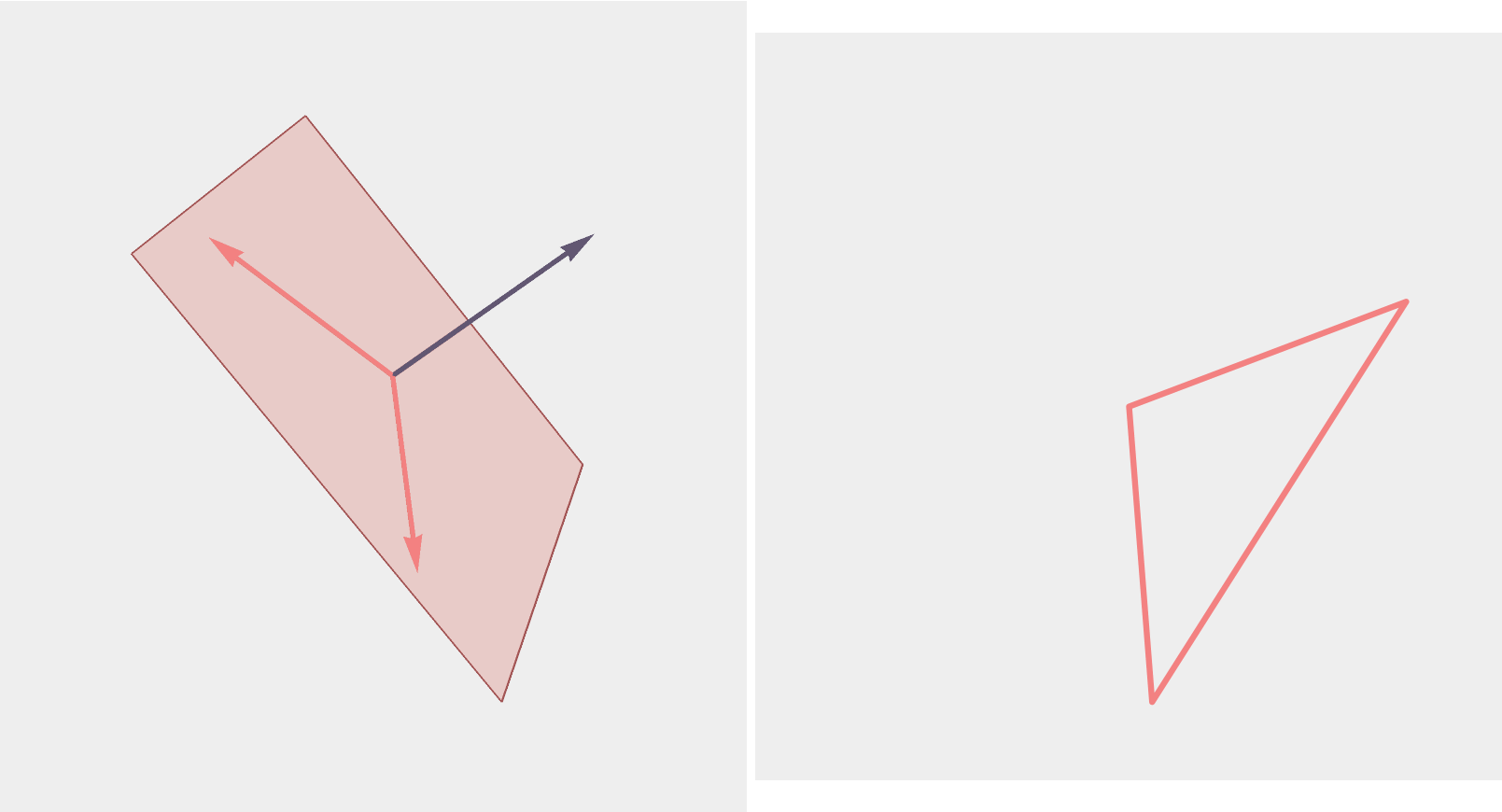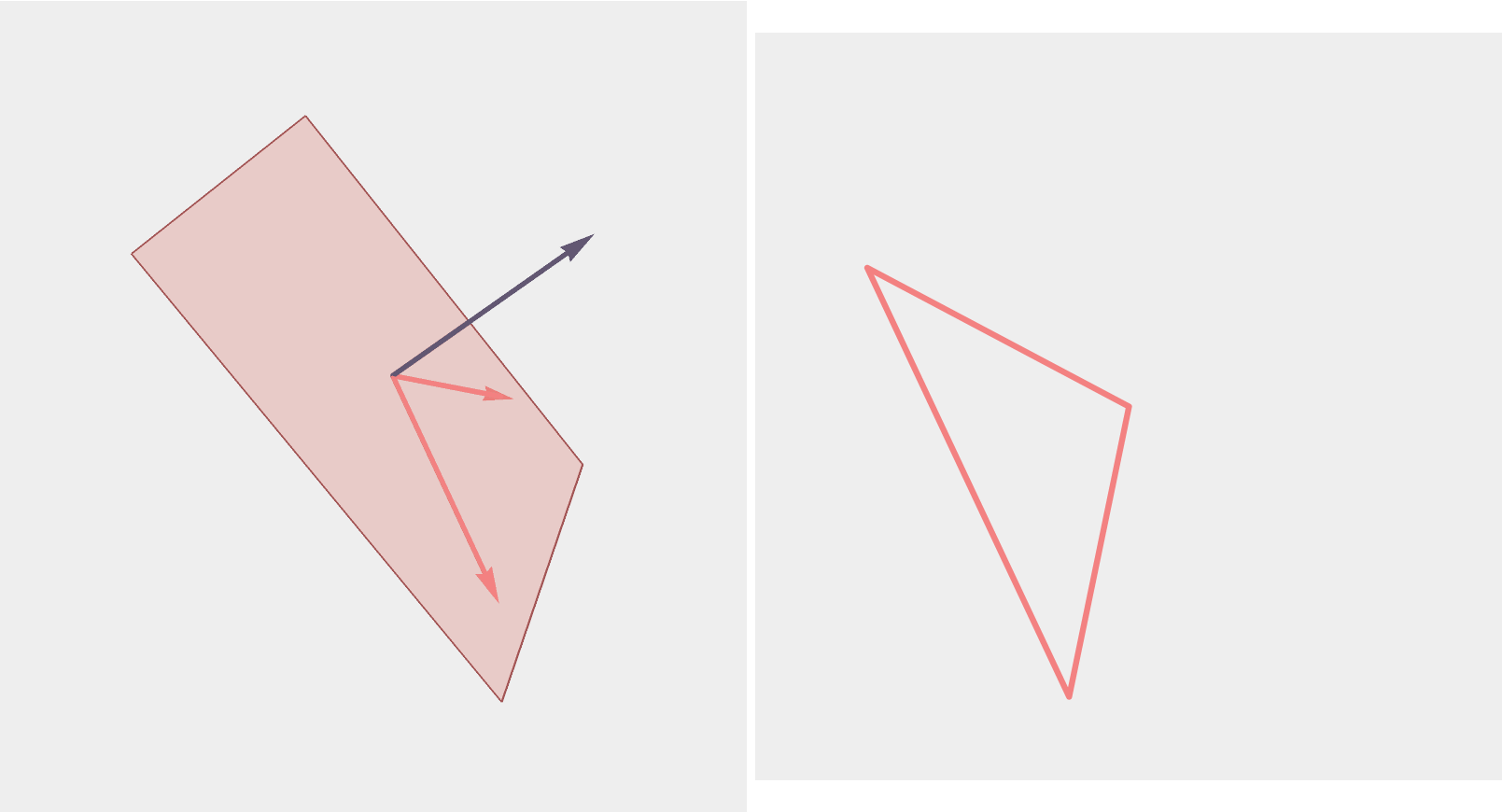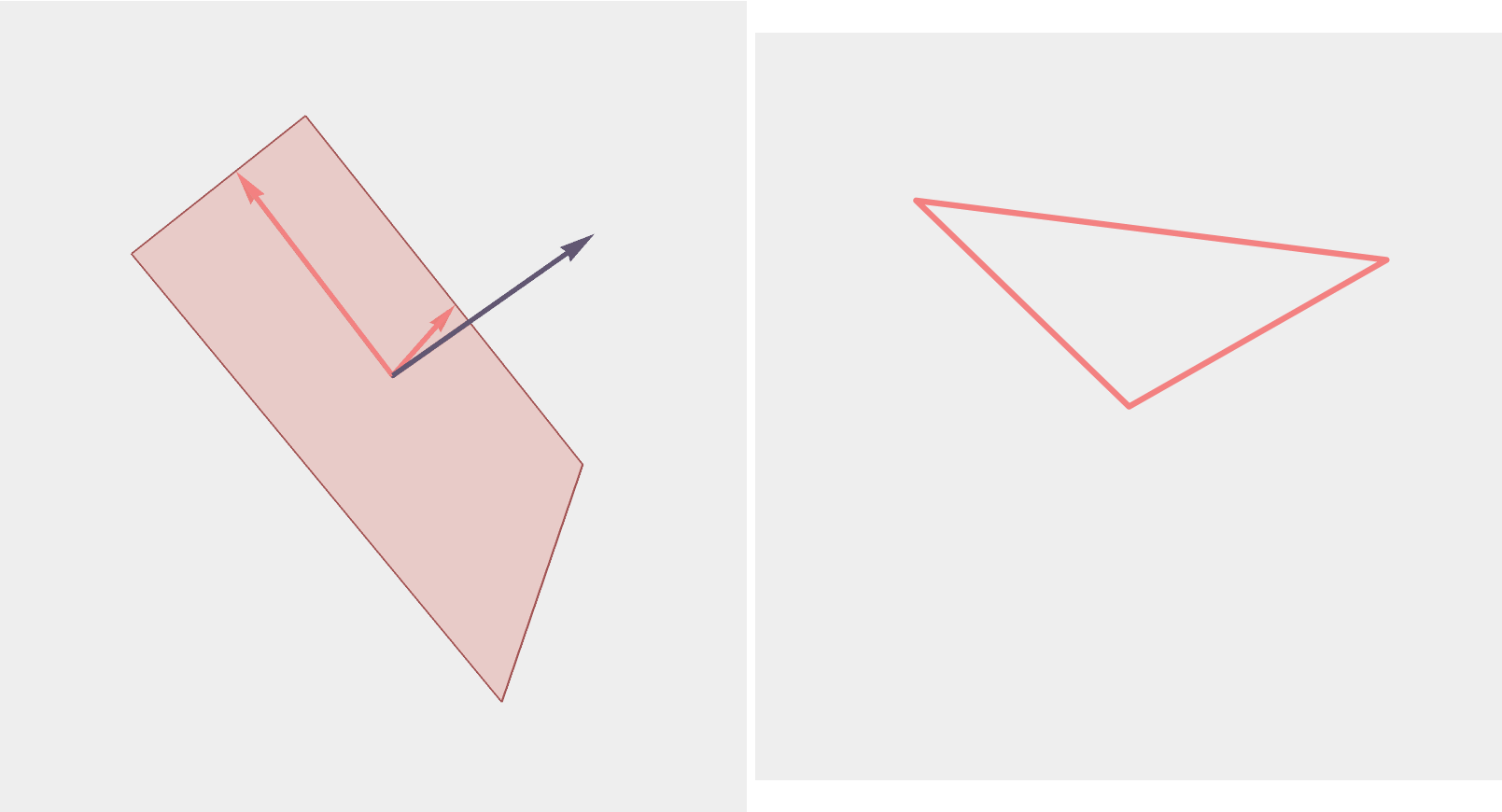
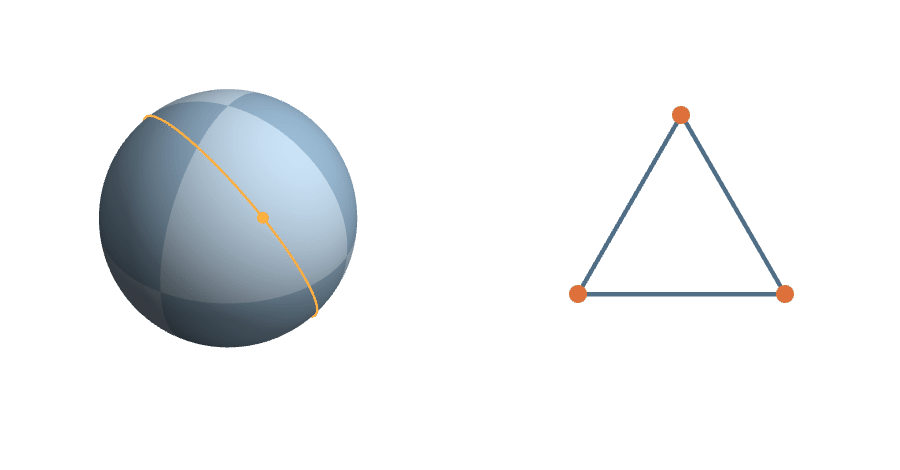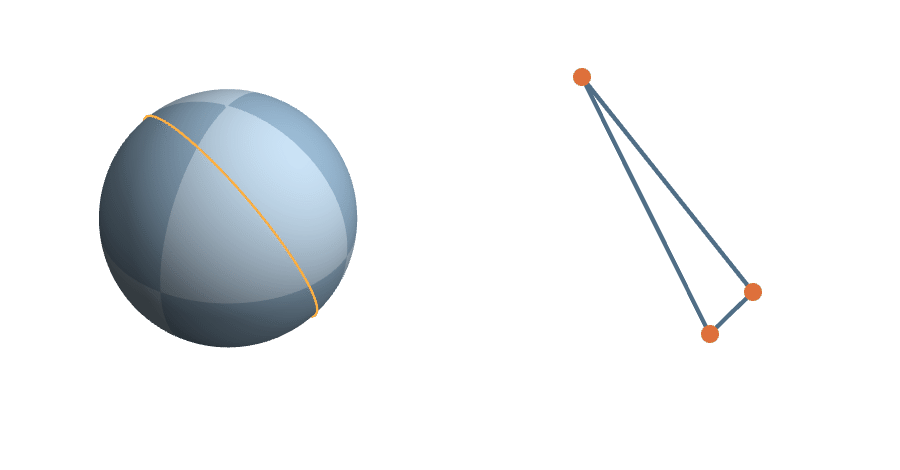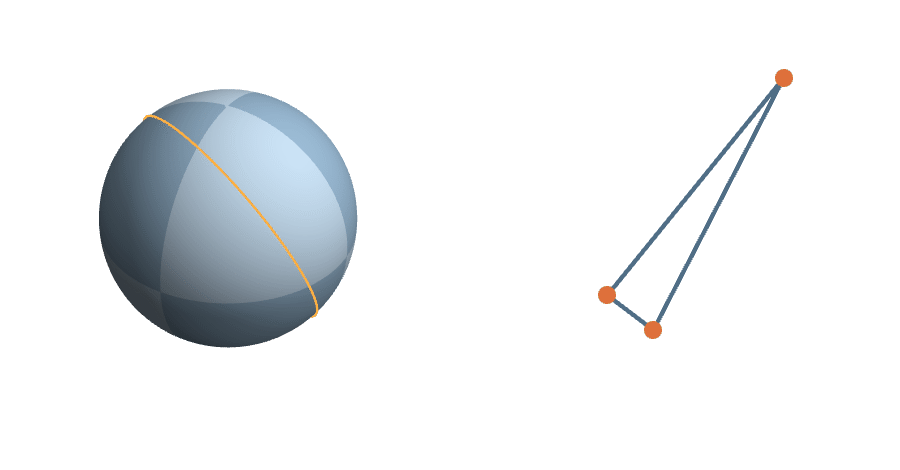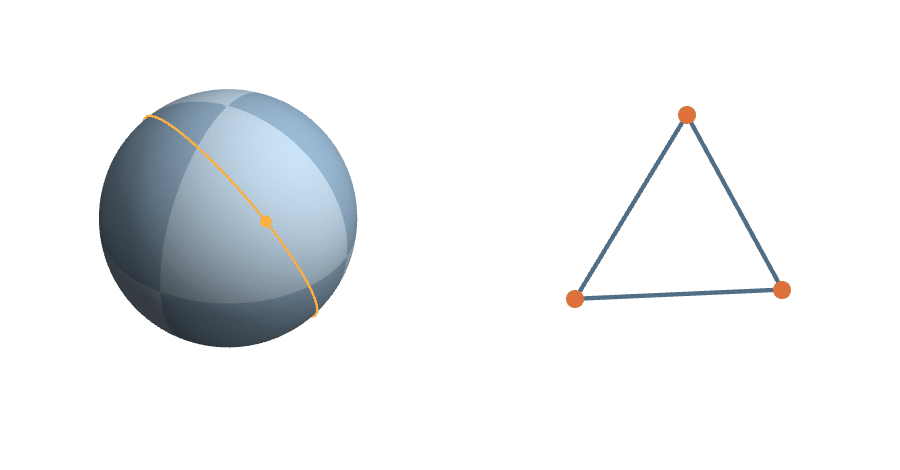
Triangles
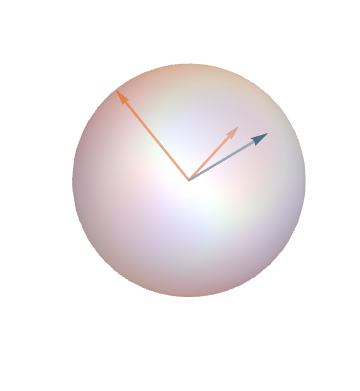
A triangle corresponds to an element of \(G_2(\mathbb{R}^3)\), which is a plane in \(\mathbb{R}^3\) with ON basis \((a,b)\)...
or, equivalently, the line through
\(p=a\times b\)
so
Translating to side lengths
Law of Cosines
Perimeter \(2\)
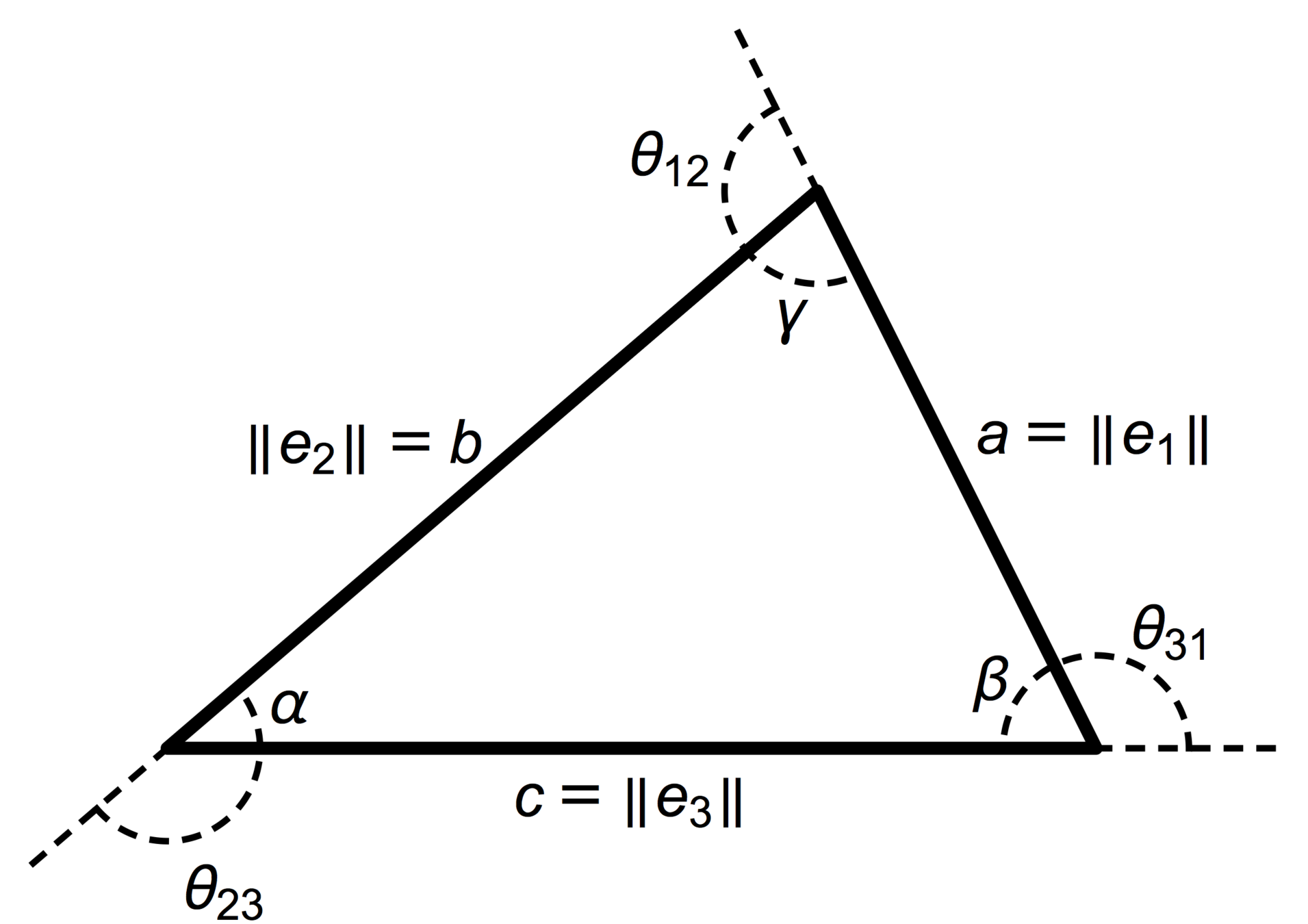
Translating to side lengths

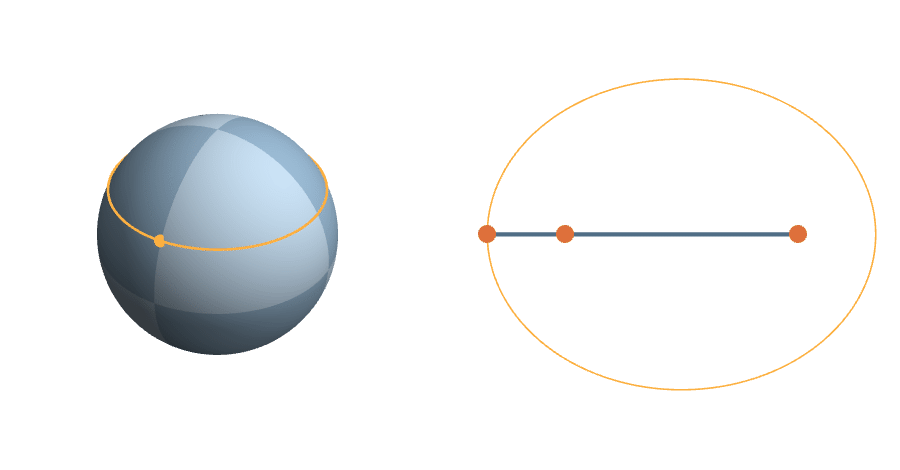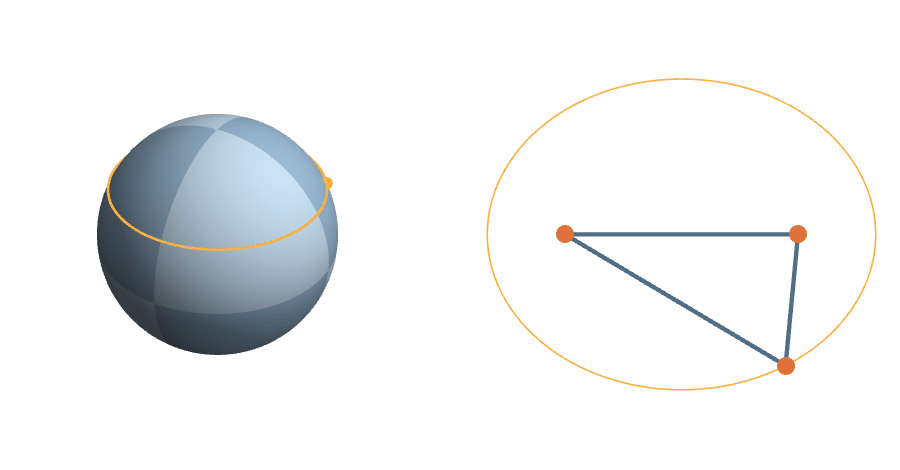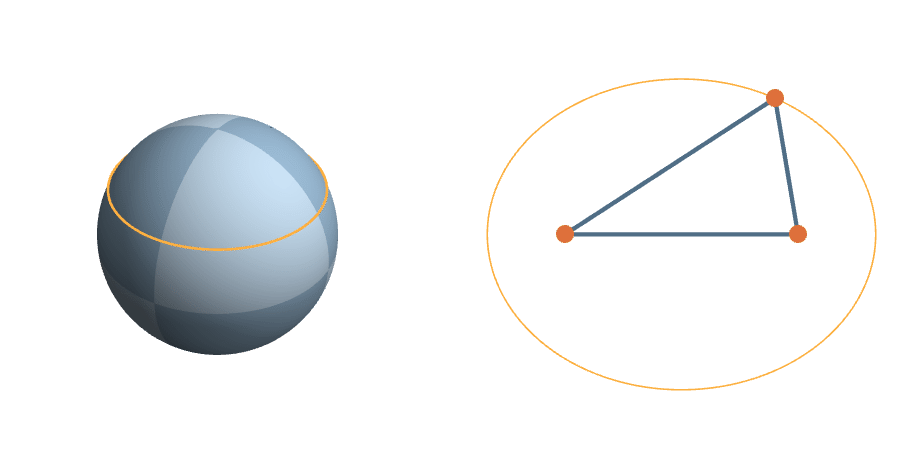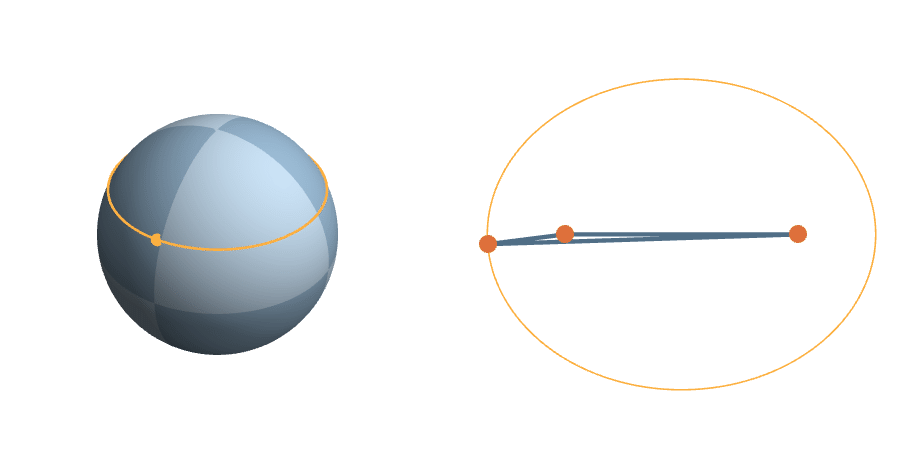
The transitive group
The rotations are natural transformations of the sphere, and the corresponding action on triangles is natural.
\(c=1-z^2\) fixed
\(z\) fixed
\(C(\theta) = (\frac{z^2+1}{2}\cos 2\theta, z \sin 2\theta)\)
The equal-area-in-equal-time parametrization of the ellipse
A more complicated rotation
Right triangles
The right triangles are exactly those satisfying
\(a^2+b^2=c^2\) & permutations
Since \(a=1-x^2\), etc., the right triangles are determined by the quartic
\((1-x^2)^2+(1-y^2)^2=(1-z^2)^2\) & permutations
\(x^2 + x^2y^2 + y^2 = 1\), etc.

Obtuse triangles
\(\mathbb{P}(\text{obtuse})=\frac{1}{4\pi}\text{Area} = \frac{24}{4\pi} \int_R d\theta dz\)


But now \(C\) has the parametrization
And the integral reduces to
Solution to the pillow problem
By Stokes’ Theorem

\(\frac{6}{\pi} \int_R d\theta dz=\frac{6}{\pi}\int_{\partial R}z d\theta = \frac{6}{\pi}\left(\int_{z=0} zd\theta + \int_C zd\theta \right)\)
\(\left(\sqrt{\frac{1-y^2}{1+y^2}},y,y\sqrt{\frac{1-y^2}{1+y^2}}\right)\)
\(\frac{6}{\pi} \int_0^1 \left(\frac{2y}{1+y^4}-\frac{y}{1+y^2}\right)dy\)
Our Answer
Theorem [with Cantarella, Needham, Stewart]
With respect to the symmetric measure on triangles, the probability that a random triangle is obtuse is
\(\frac{3}{2}-\frac{3\ln 2}{\pi}\approx0.838\)
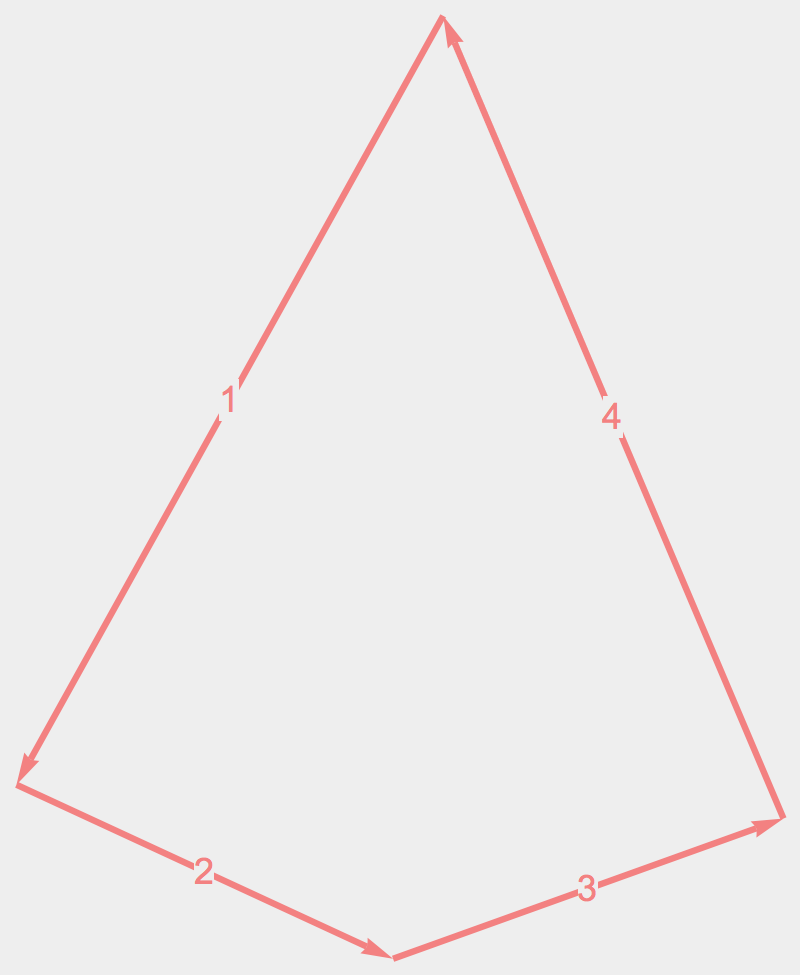
Sylvester’s Four Point Problem
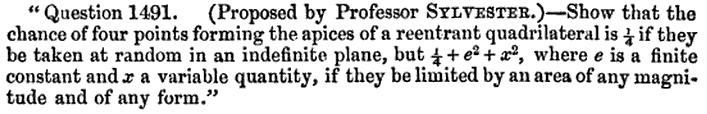

convex
reflex/reentrant
self-intersecting
Modern Reformulation: What is the probability that all vertices of a random quadrilateral lie on its convex hull?
A discrete group action
A polygon corresponds to \(\begin{bmatrix} a_1 & b_1 \\ a_2 & b_2 \\ \vdots & \vdots \\ a_n & v_n \end{bmatrix}\), where \((a_k + i b_k)^2 = e_k\).
\((a_k,b_k)\mapsto(-a_k,-b_k)\) doesn’t change the polygon, so \((\mathbb{Z}/2\mathbb{Z})^n\) acts trivially on polygons.
\(S_n \le SO(n)\) permutes rows and hence edges.
The hyperoctahedral group \(B_n = (\mathbb{Z}/2\mathbb{Z})^n \rtimes S_n = S_2 \wr S_n\) acts by isometries on \(G_2(\mathbb{R}^n)\) and permutes edges.
\(|B_n| = 2^n n!\); e.g., \(|B_3| = 2^3 3! = 48\).
\(S_n \le SO(n)\) permutes rows and hence edges.
\(S_n \le SO(n)\) permutes rows and hence edges.

Proposition [with Cantarella, Needham, Stewart]
- The fundamental domain \(\mathcal{D}_n\) of the \(B_n\) action on \(G_2(\mathbb{R}^n)\) consists of (certain lifts of) the convex \(n\)-gons in which all pairs of adjacent or opposite sides form oriented bases in the same class.
- The stabilizer of \(\mathcal{D}_4\) has order 4, so \(G_2(\mathbb{R}^4)\) is built from 96 isometric copies of \(\mathcal{D}_4\).
- Each of these 96 cells consists of all convex, all reflex, or all self-intersecting quadrilaterals.
- \(\mathcal{D}_4\) is path-connected.
Upshot: We can count how many elements of the permutation orbit of a single element of \(\mathcal{D}_4\) are convex, reflex, and self-intersecting.
Volumes via algebra
The average convex quadrilateral
The (empirical) flag mean of \(\mathcal{D}_4\).
The flag mean of
is (the plane spanned by) the first two left singular vectors of the matrix
The symmetric group orbit
Theorem [with Cantarella, Needham, Stewart]
Convex, reflex, and self-intersecting quadrilaterals are all equiprobable.

A partial generalization
Theorem [with Cantarella, Needham, Stewart]
With respect to any measure on \(n\)-gon space which is invariant under permuting edges, the fraction of convex \(n\)-gons is exactly \(\frac{2}{(n-1)!}\).

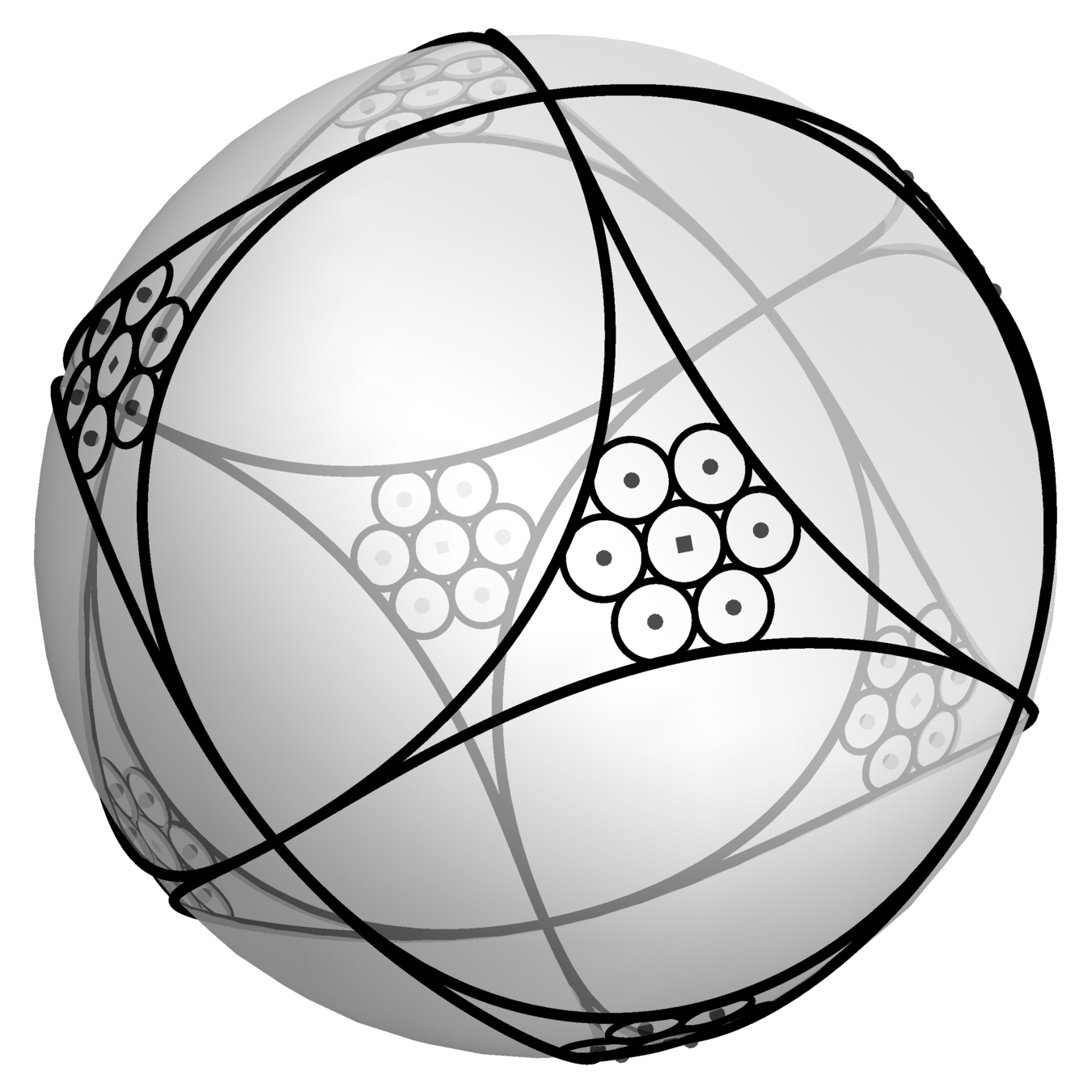
What is the least symmetric triangle?

Symmetric triangles
Isosceles
triangles
Degenerate
triangles

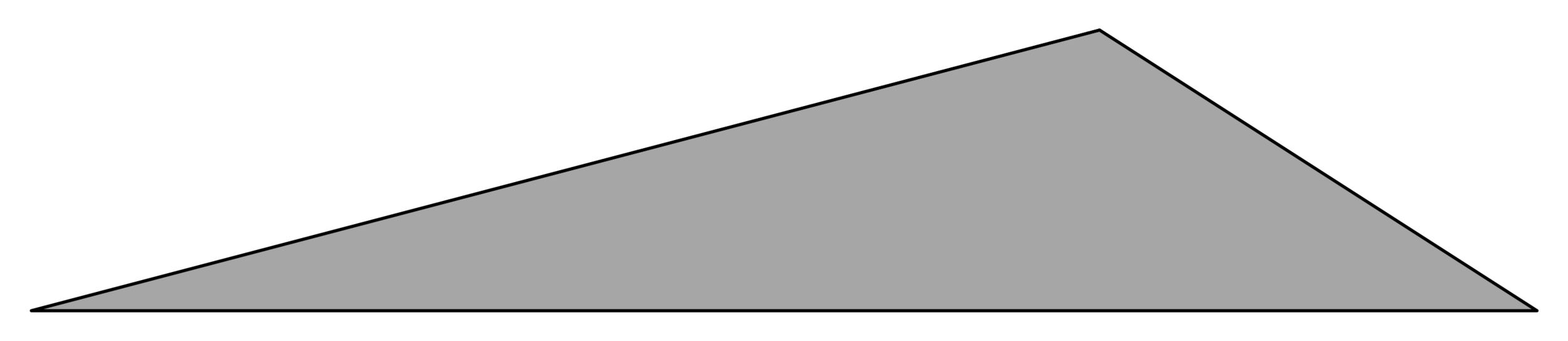
The least symmetric triangle
Theorem [with Bowden, Haynes, Shukert]
The least symmetric triangle has side length ratio
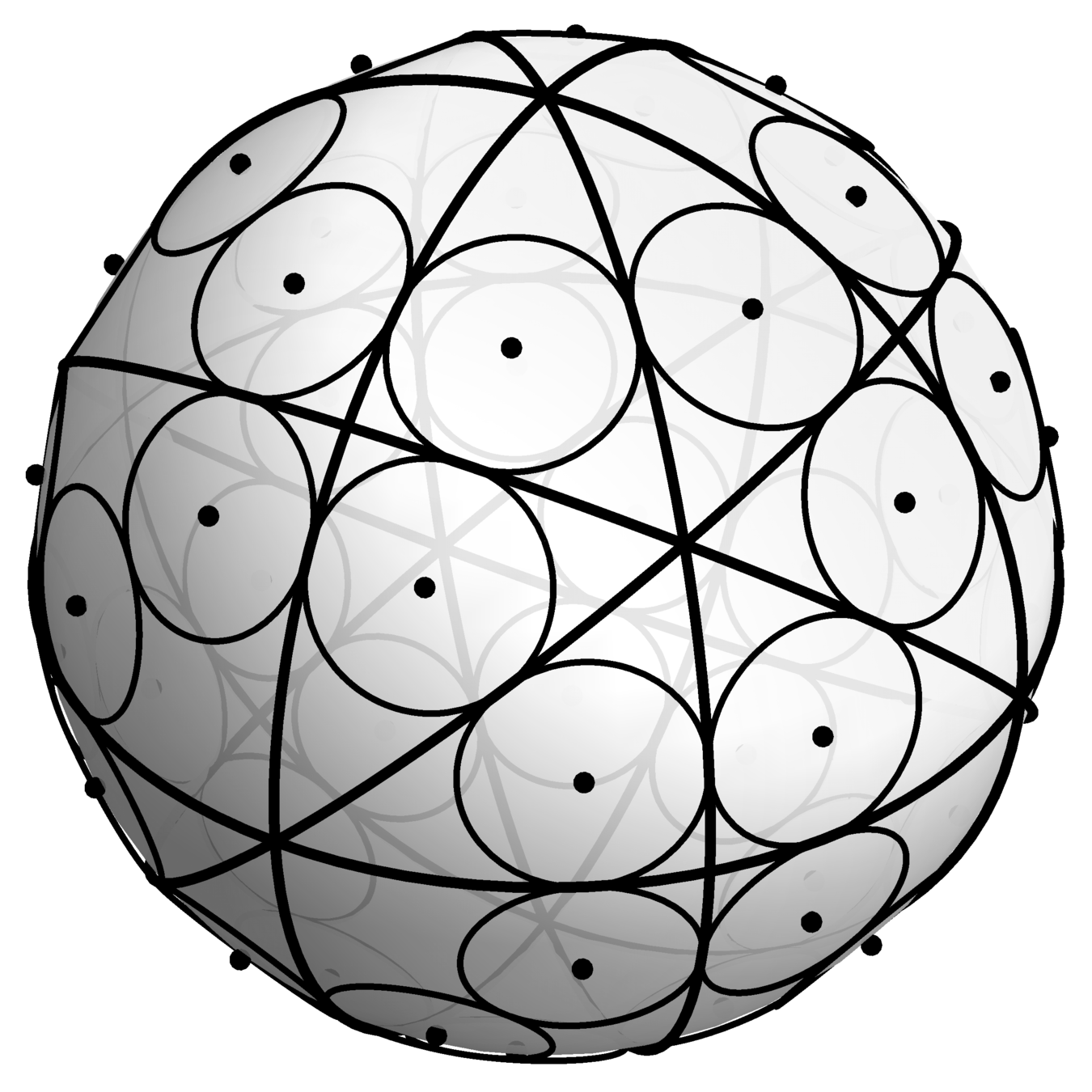
The least symmetric obtuse triangle
Theorem [with Bowden, Haynes, Shukert]
The least symmetric obtuse triangle has side length ratio
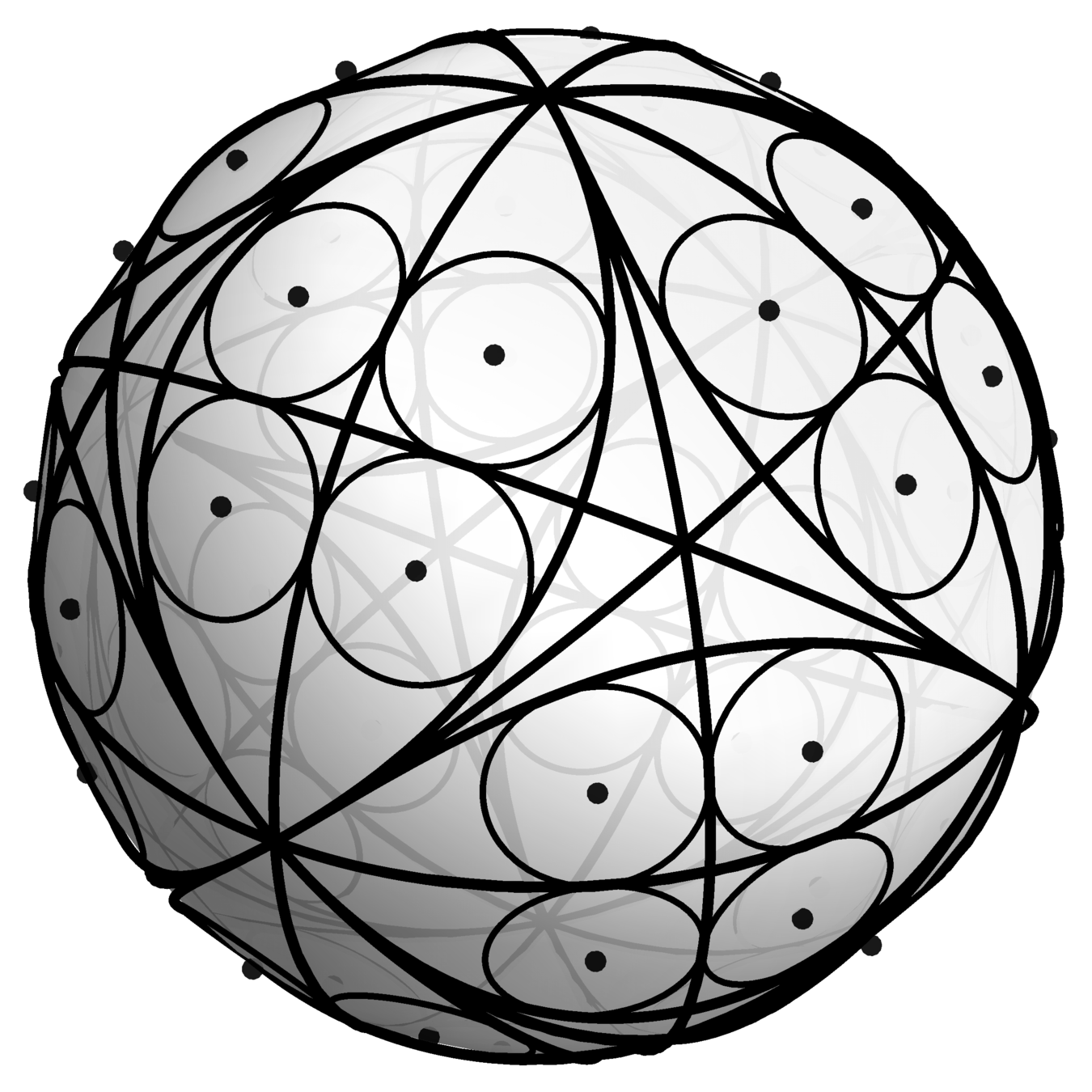
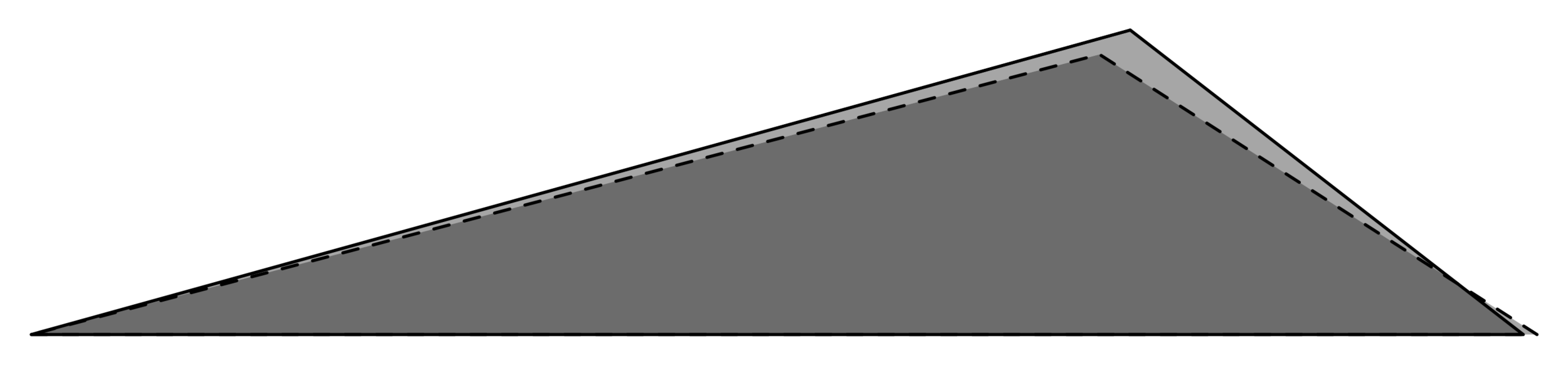
The least symmetric acute triangle
Theorem [with Bowden, Haynes, Shukert]
The least symmetric acute triangle has side length ratio
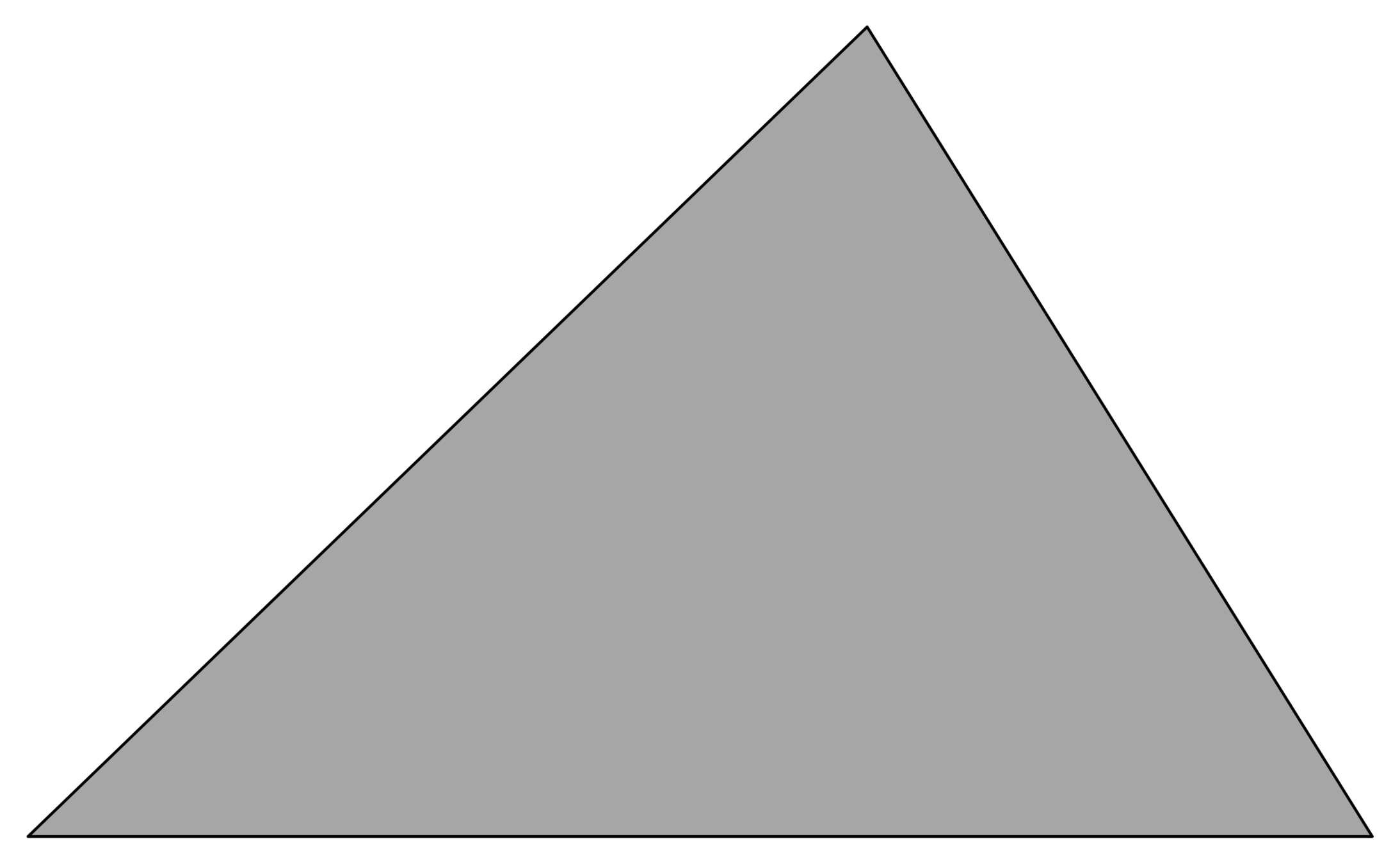
Polygons in space
Example Theorem [w/ Cantarella, Grosberg, Kusner]
The expected total curvature of a random space \(n\)-gon is exactly
\(\frac{\pi}{2}n + \frac{\pi}{4} \frac{2n}{2n-3}\)
Polygons in \(\mathbb{R}^3\) correspond to points in \(G_2(\mathbb{C}^n)\) and the analog of the squaring map is the Hopf map.

Questions
- What is the average \(n\)-edge trefoil?
Observation [Needham]: The flag mean of the equilateral six-edge trefoils is
Theorem*: The flag mean of the positive Grassmannian is the regular \(n\)-gon.
- What is the most knotted \(n\)-gon?
- What is the flag mean good for in a polygons context?

Observation [Needham]: The flag mean of the equilateral six-edge positive trefoils is

Theorem [Baxter]
The expected number of vertices on the convex hull of a random planar \(n\)-gon is
A Conjecture on Convex Hulls
Conjecture
The expected perimeter of the convex hull of a random planar \(n\)-gon is
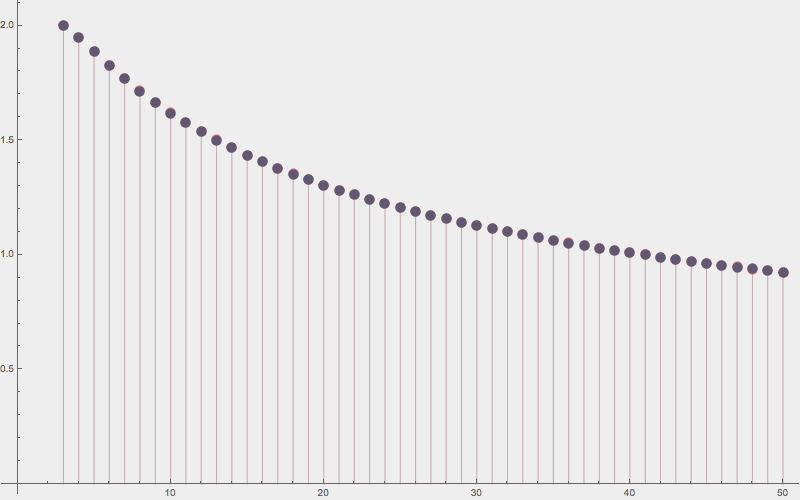
Conjecture vs. sample average (100,000 samples)
Conjecture
The expected perimeter of the convex hull of a random planar \(n\)-gon is





Thank you!
Funding: Simons Foundation
References
Probability Theory of Random Polygons from the Quaternionic Perspective
J. Cantarella, T. Deguchi, and C. Shonkwiler
Communications on Pure and Applied Mathematics 67
(2014), 1658–1699
Random Triangles and Polygons in the Plane
J. Cantarella, T. Needham, C. Shonkwiler, and G. Stewart
arXiv: 1702.01027
Spherical Geometry and the Least Symmetric Triangle
L. Bowden, A. Haynes, C. Shonkwiler, and A. Shukert
arXiv:1708.01559
The Expected Total Curvature of Random Polygons
J. Cantarella, A. Grosberg, R. Kusner, and C. Shonkwiler
American Journal of Mathematics 137 (2015), 411–438