Polyhedra, Sampling Algorithms for Random Polygons, and Applications to Ring Polymer Models

Clayton Shonkwiler

Colorado State University

http://shonkwiler.org

08.01.17

/ag17

This talk!

Statistical physics Viewpoint

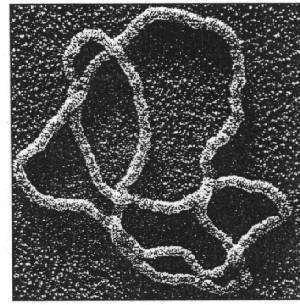
A ring polymer in solution takes on an ensemble of random shapes, with topology (knot type!) as the unique conserved quantity.

Knotted DNA

Wassermann et al.

Science 229, 171–174

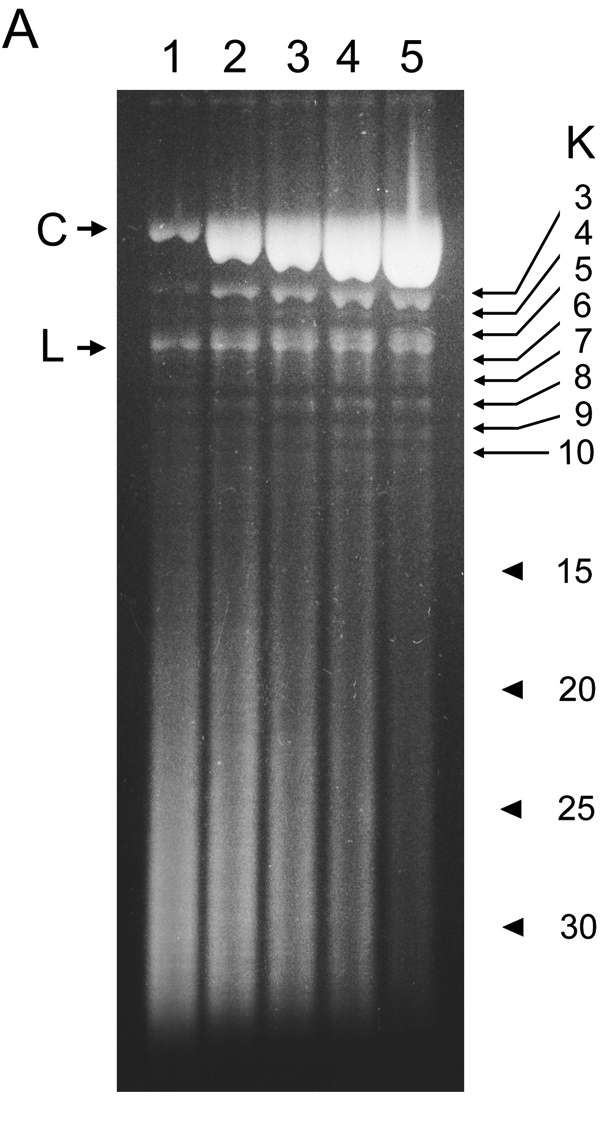
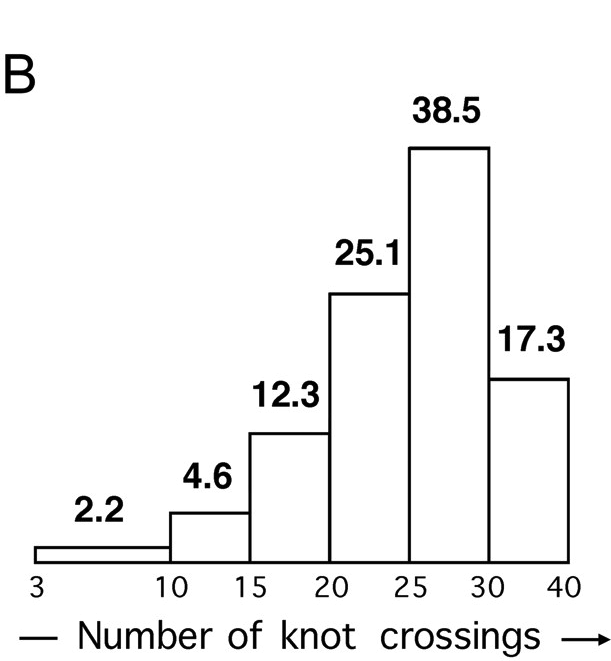
Knot complexity in DNA from P4 tailless mutants

Arsuaga et al., PNAS 99 (2002), 5373–5377

Is this surprising?

Statistical physics viewpoint

A polymer in solution takes on an ensemble of random shapes, with topology as the unique conserved quantity.

Modern polymer physics is based on the analogy between a polymer chain and a random walk.

– Alexander Grosberg

Protonated P2VP

Roiter/Minko

Clarkson University

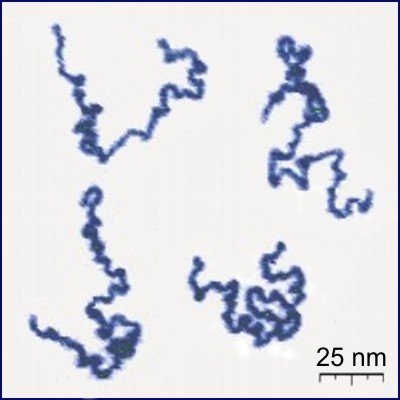
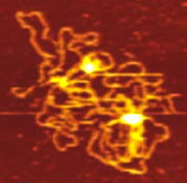
Plasmid DNA

Alonso–Sarduy, Dietler Lab

EPF Lausanne

Sampling random walks is easy

Generate \(n\) independent uniform random points on \(S^2\) and treat them as an ordered list of edge vectors.

...but sampling random polygons is hard

Alvarado, Calvo, Millett, J. Stat. Phys. 143 (2011), 102–138

Ansatz

Random Polygon \(\Leftrightarrow\) point in some (nice!) configuration space

Knowledge of the (differential, symplectic, algebraic) geometry of these conformation spaces leads to both

theorems and fast numerical algorithms for studying and comparing polygons in \(\mathbb{R}^3\).

A random closed \(n\)-edge polygon is a \(k\)-edge random walk and an \((n-k)\)-edge random walk, conditioned on having the same end-to-end distance.

Key Idea

Density of the end-to-end distance

Classical Fact: The density of the end-to-end vector of an \(n\)-step random walk is

\phi_n(\ell) = \frac{2\ell}{\pi} \int_0^\infty x \sin \ell x \,\mathrm{sinc}^n x \,\mathrm{d}x
= \frac{2^{-n-1}}{\pi \ell(n-2)!} \sum_{k=0}^{n-1} (-1)^k \binom{n-1}{k} \left([-2k+\ell +n-2]_+^ {n-2}\right.
\left.- [-2 k+\ell +n]_+^{n-2}\right)

Proof: Fourier transform (since \(\mathrm{sinc}\) is the transform of the boxcar function).

This is piecewise-polynomial in \(\ell\) of degree \(n-3\)

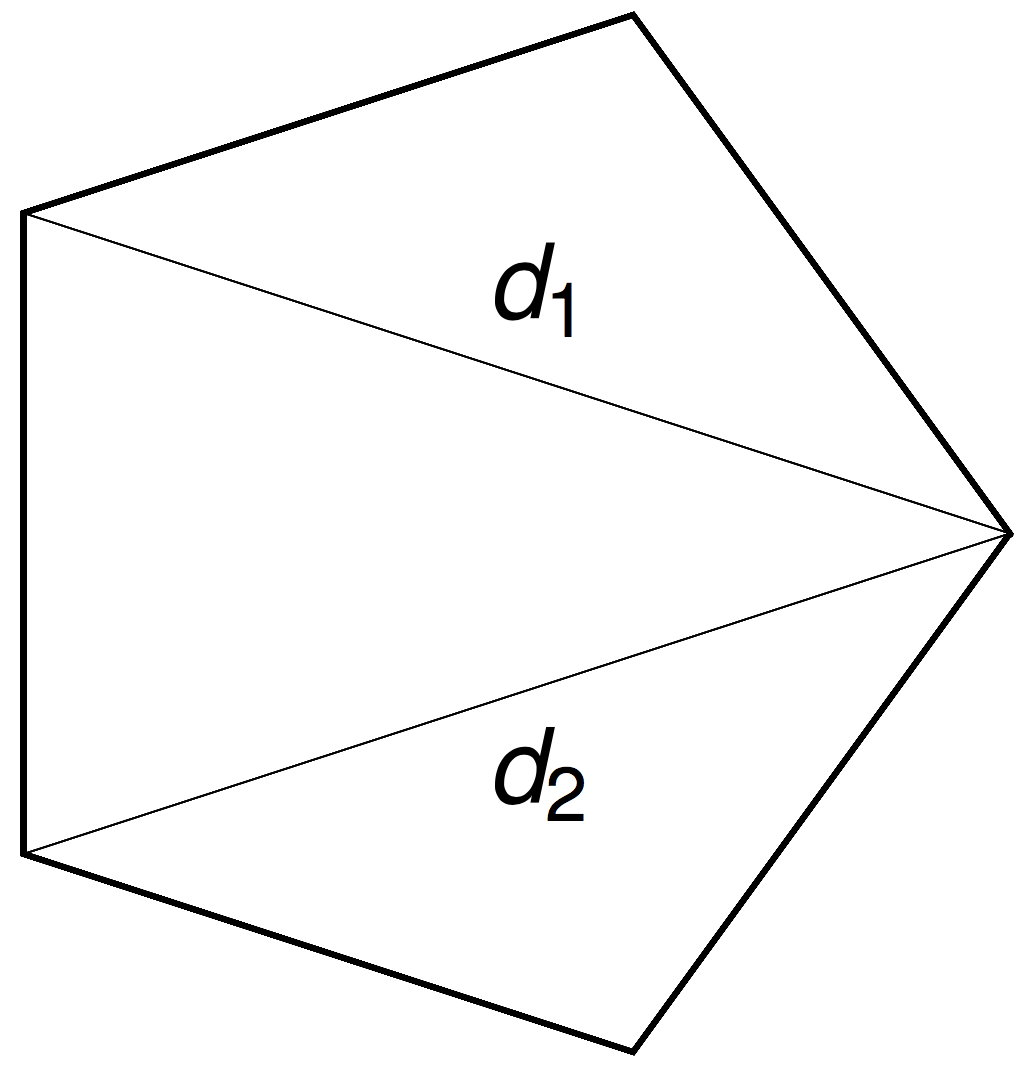
Density of a polygon chord

Proposition (with Cantarella): The pdf of the chord connecting \(v_1\) with \(v_{k+1}\) in an \(n\)-gon is

\frac{4 \pi \ell^2}{C_n} \phi_k(\ell) \phi_{n-k}(\ell)

where \(C_n = 2^{n-5}\pi^{n-4} \int_{-\infty}^{\infty} x^2 \,\mathrm{sinc}^n x \,\mathrm{d}x\).

Fact: This is piecewise-polynomial in \(\ell\) of degree \(n-4\).

Expected values of chordlengths

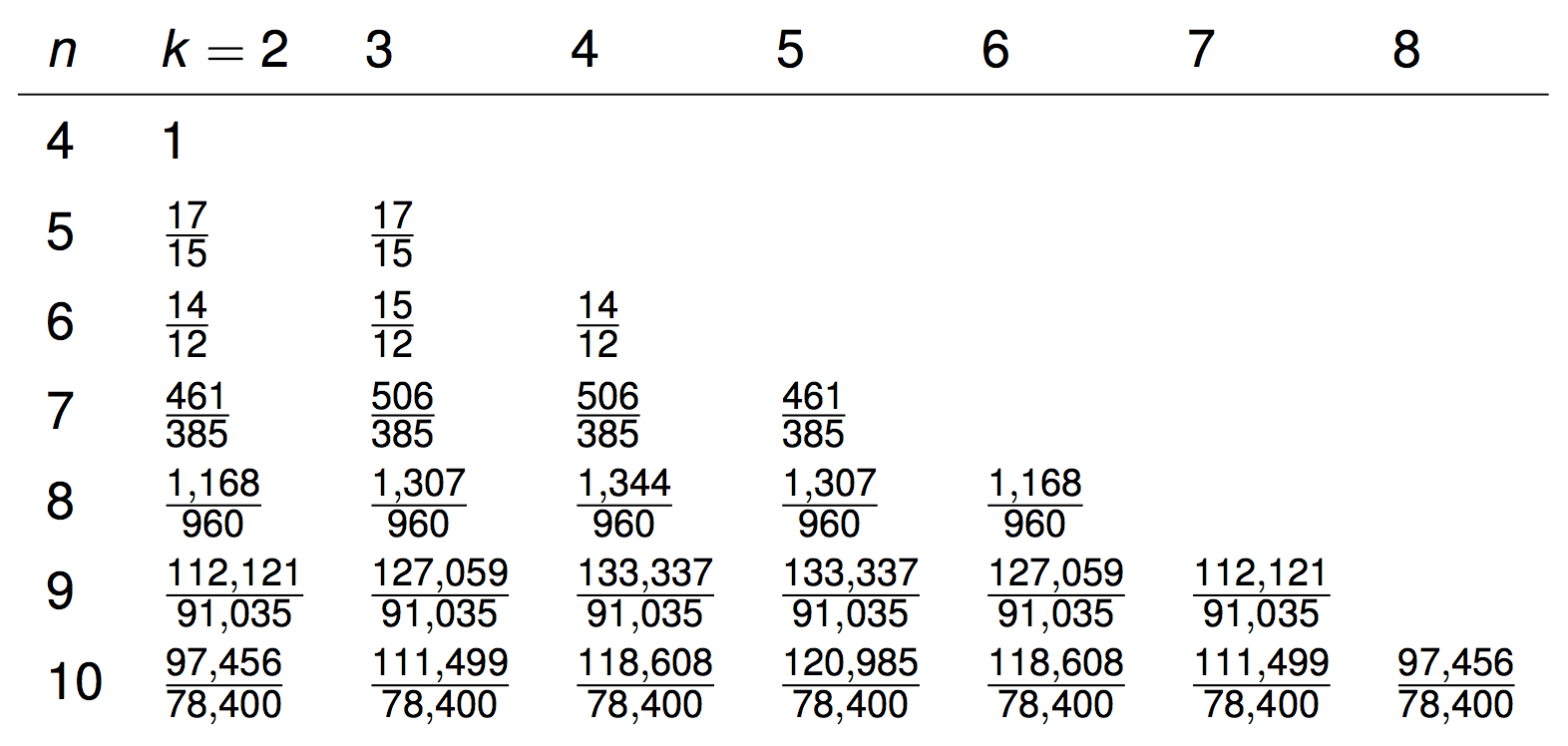
Questions

Why are the expectations rational?

Why degree \(n-4\)?

Where the heck are the polyhedra?

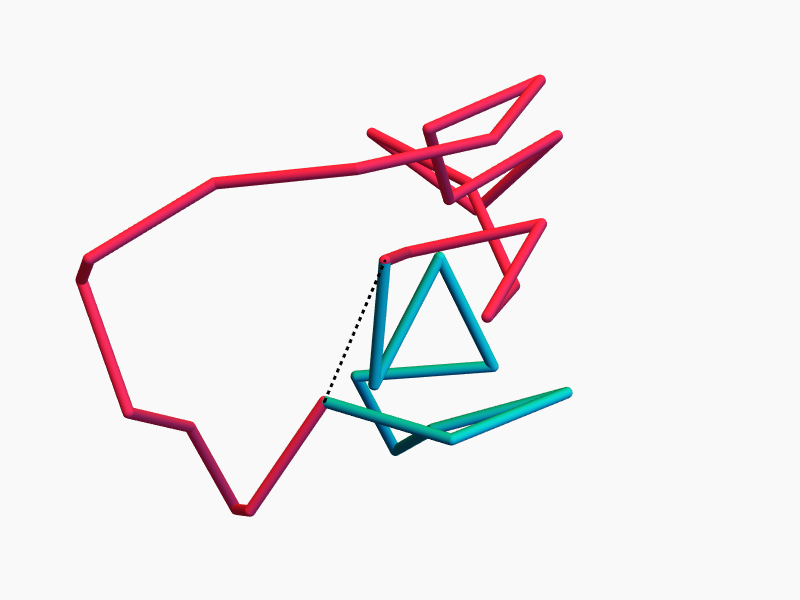
Continuous symmetry \(\Rightarrow\) conserved quantity

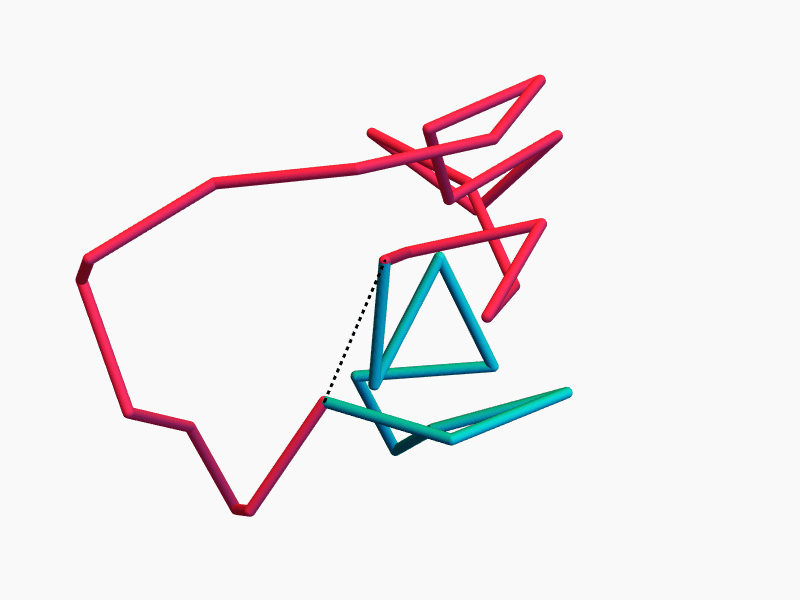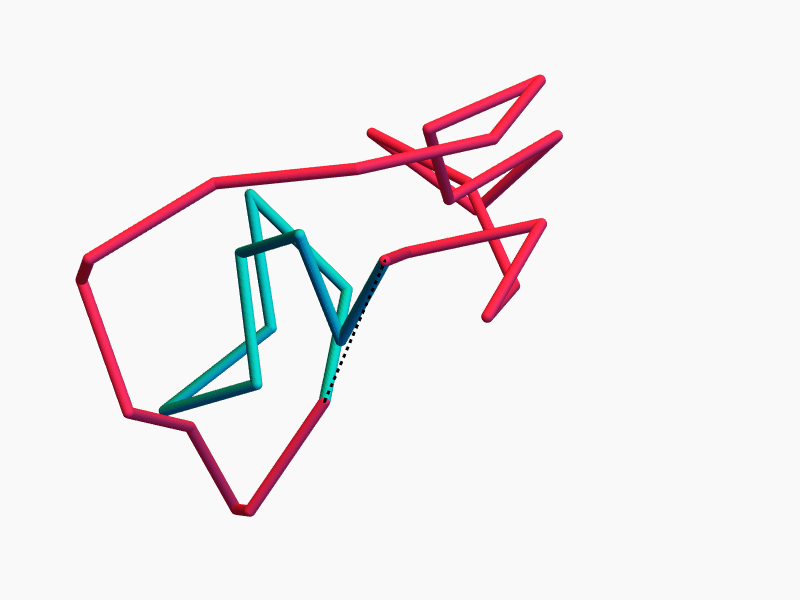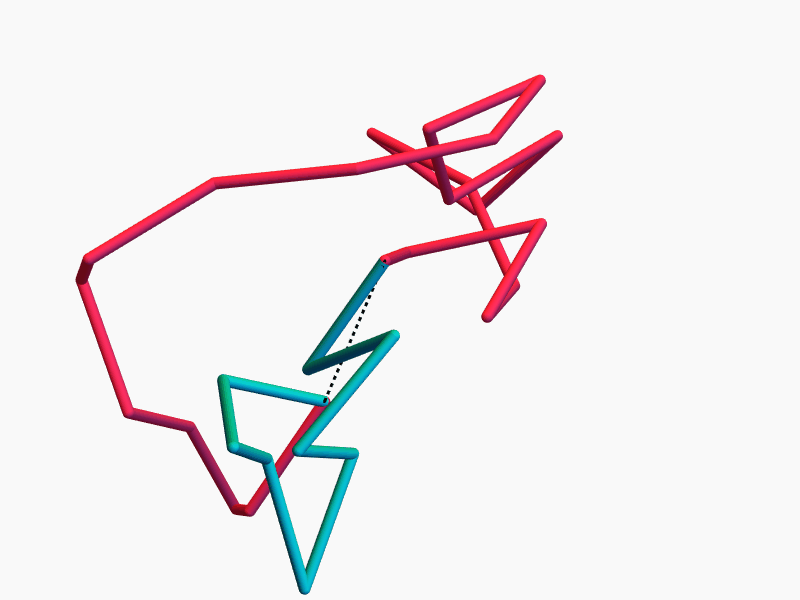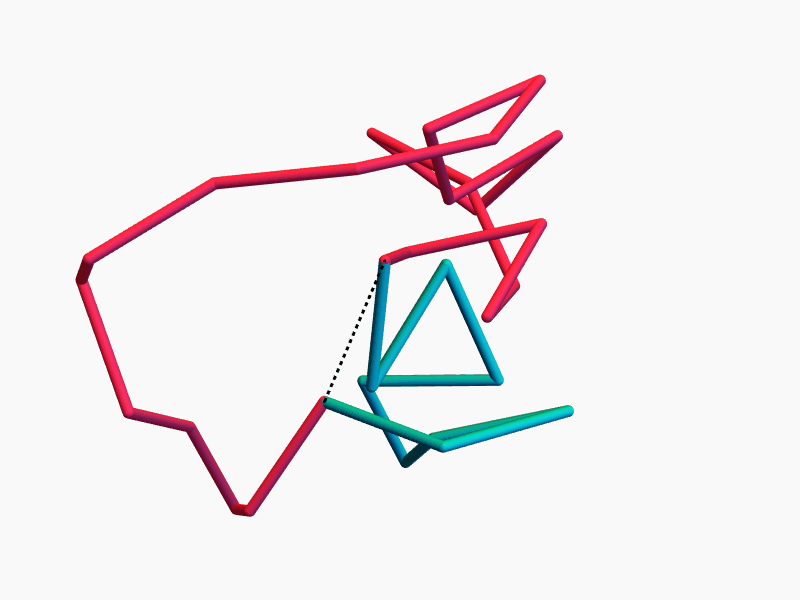
Some classical mechanics

Duistermaat–Heckman Theorem (stated informally): On a \(2m\)-dimensional symplectic manifold, \(d\) commuting Hamiltonian symmetries (a Hamiltonian \(T^d\)-action) induce \(d\) conserved quantities (momenta).

The joint distribution of the momenta is continuous, piecewise polynomial, degree \(\leq m-d\).

\(n\)-gons up to rotation are \(2m=(2n-6)\)-dimensional, so chord length is piecewise polynomial of degree \(\leq\)

\(m-1=(n-3)-1=n-4\)

We actually have more symmetries!

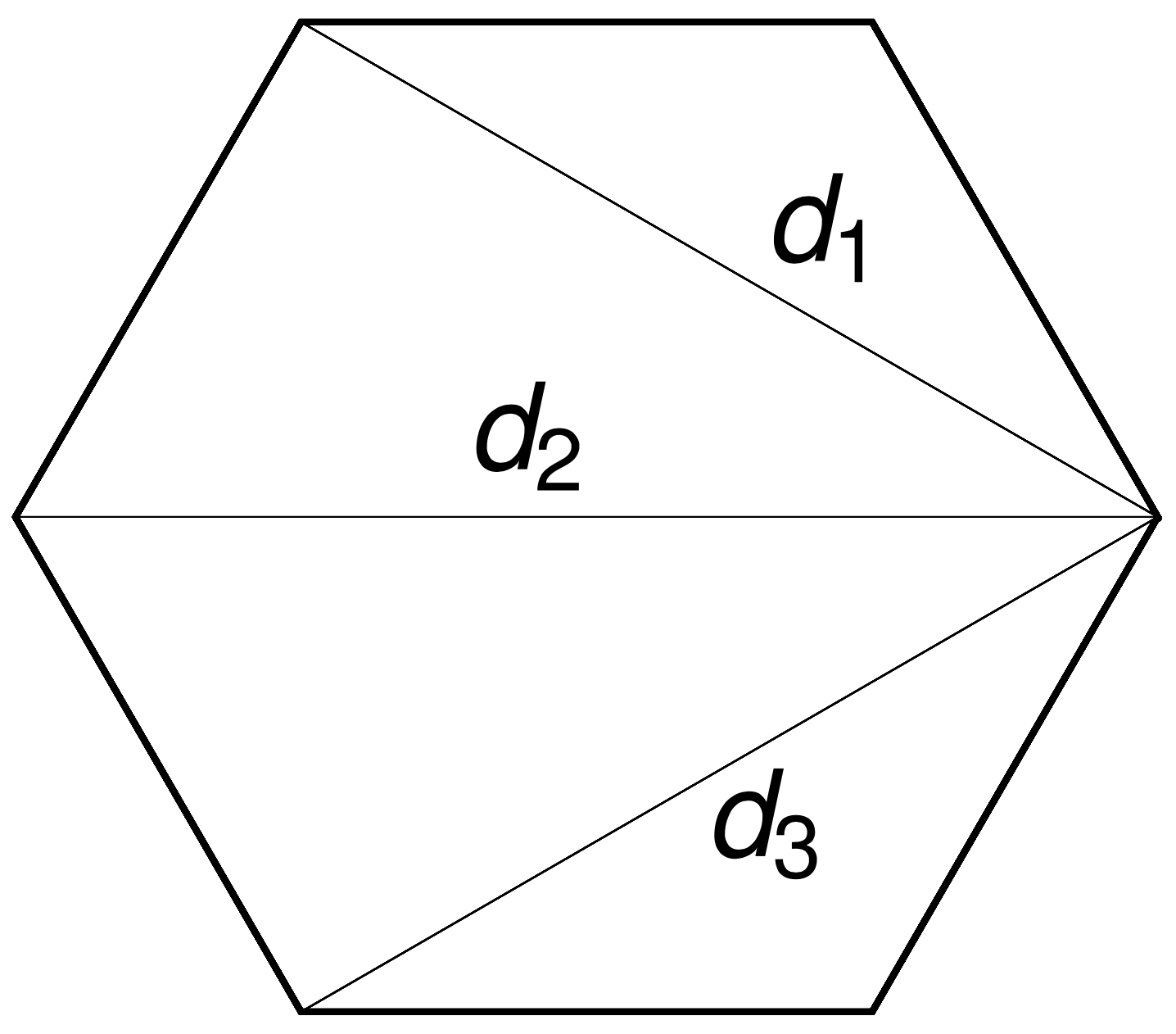
\(n-3\) commuting symmetries

Rotations around \(n-3\) chords \(d_i\) by \(n-3\) angles \(\theta_i\) commute.

Main Theorem

Theorem (with Cantarella, ’16): The joint distribution of \(d_1,\ldots , d_{n-3}\) and \(\theta_1, \ldots , \theta_{n-3}\) are all uniform on their domains.

Proof: Check that D–H applies (this is the hard part, since the torus action is not defined everywhere).

Then count: \(m=n-3\) and we have \(d=n-3\) symmetries, so the pdf of the \(d_i\) is piecewise polynomial of degree \(\leq\)

\(m-d = (n-3)-(n-3)=0\).

Since the pdf is continuous and the domain is connected, it must be constant.

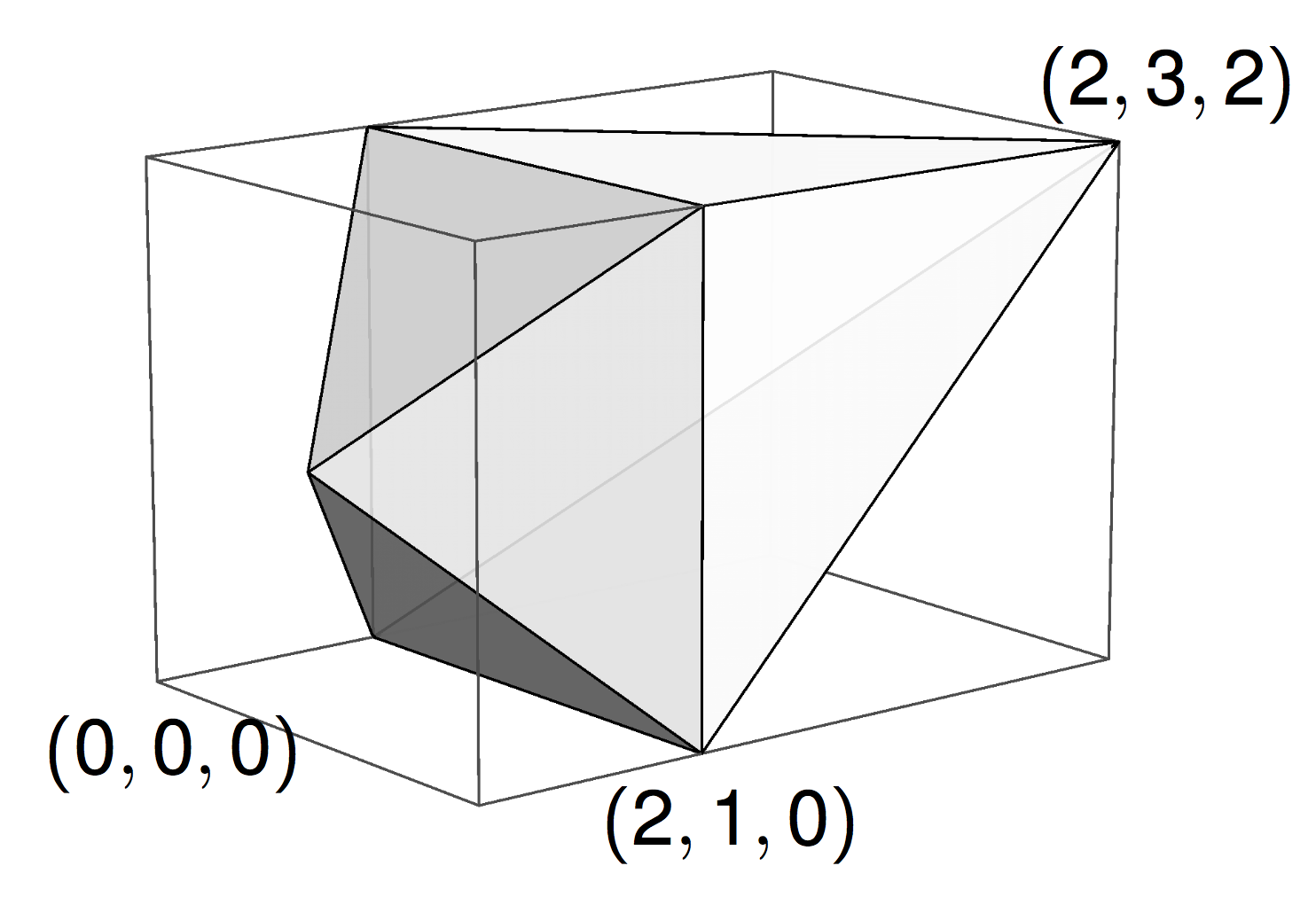
A polytope (finally!)

The \((n-3)\)-dimensional moment polytope \(\mathcal{P}_n \subset \mathbb{R}^{n-3}\) is defined by the triangle inequalities

0 \leq d_i \leq 2
1 \leq d_i + d_{i-1}
|d_i - d_{i-1}| \leq 1
0 \leq d_{n-3} \leq 2

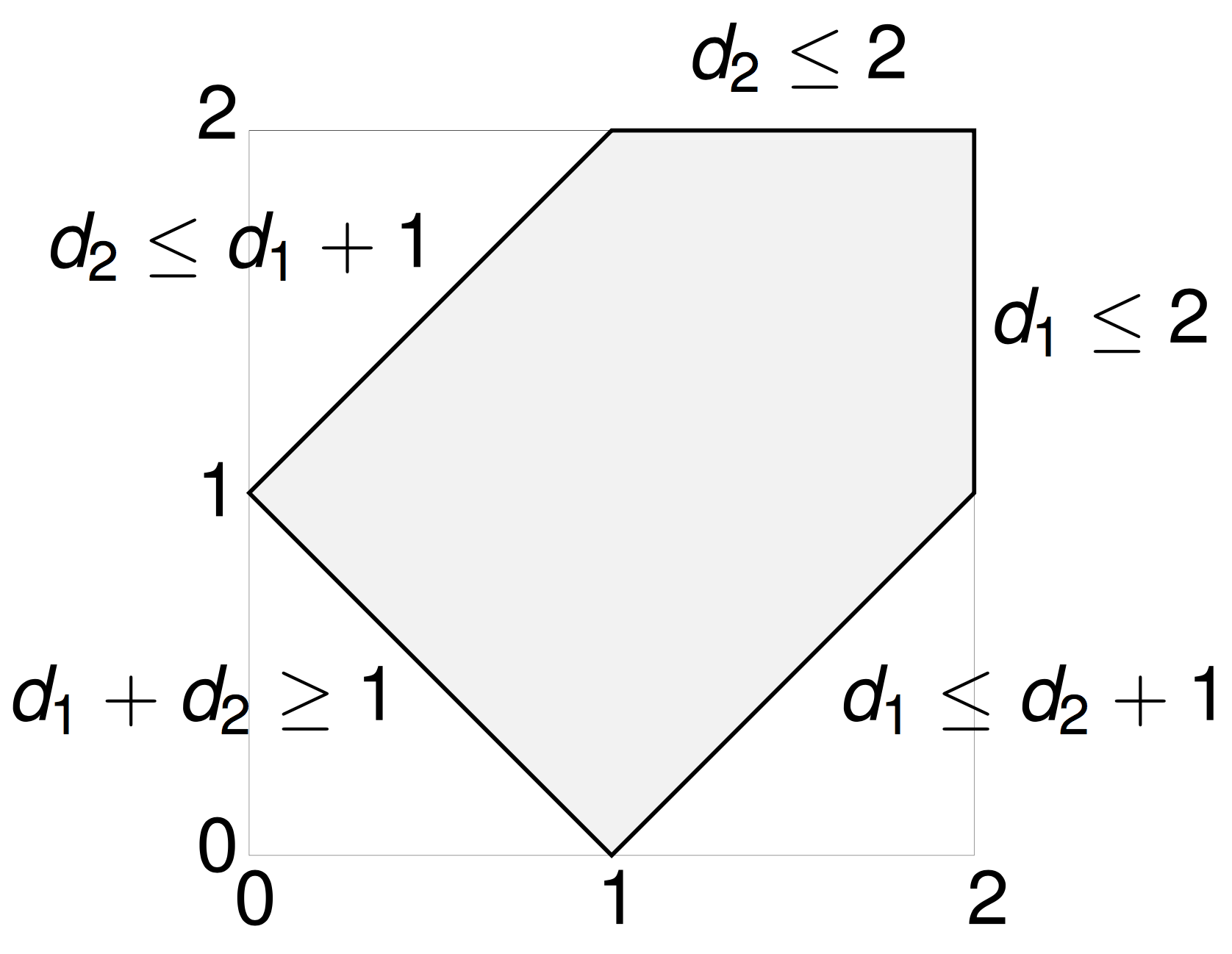
A sampling algorithm

Theorem (with Cantarella, Duplantier, Uehara, ’16):  A direct sampling algorithm for equilateral \(n\)-gons with expected performance \(O(n^{5/2})\).

If we let \(s_i = d_i - d_{i-1}\) for \(i=1,\ldots , n-2\) and \(s_i \in [-1,1]\), then we have \(|d_i - d_{i-1}|\leq 1\). 

Proposition (with Cantarella, Duplantier, Uehara): If we build \(d_i\) from \(s_i\) sampled uniformly from the hypercube \([-1,1]^{n-3}\), the \(d_i\) obey the triangle inequalities with probability asymptotic to

6 \sqrt{\frac{6}{\pi}} n^{-3/2}.
RandomDiagonals[n_] := 
  Accumulate[
   Join[{1}, RandomVariate[UniformDistribution[{-1, 1}], n]]];

InMomentPolytopeQ[d_] := 
  And[Last[d] >= 0, Last[d] <= 2, 
   And @@ (Total[#] >= 1 & /@ Partition[d, 2, 1])];

DiagonalSample[n_] := Module[{d},
   For[d = RandomDiagonals[n], ! InMomentPolytopeQ[d], , 
    d = RandomDiagonals[n]];
   d[[2 ;;]]
   ];

Diagonal sampling in 3 lines of code

Not the first direct sampler (Grosberg–Moore, Diao–Ernst–Montemayor–Ziegler), but simple and fast.

An explicit grid on the moment polytope

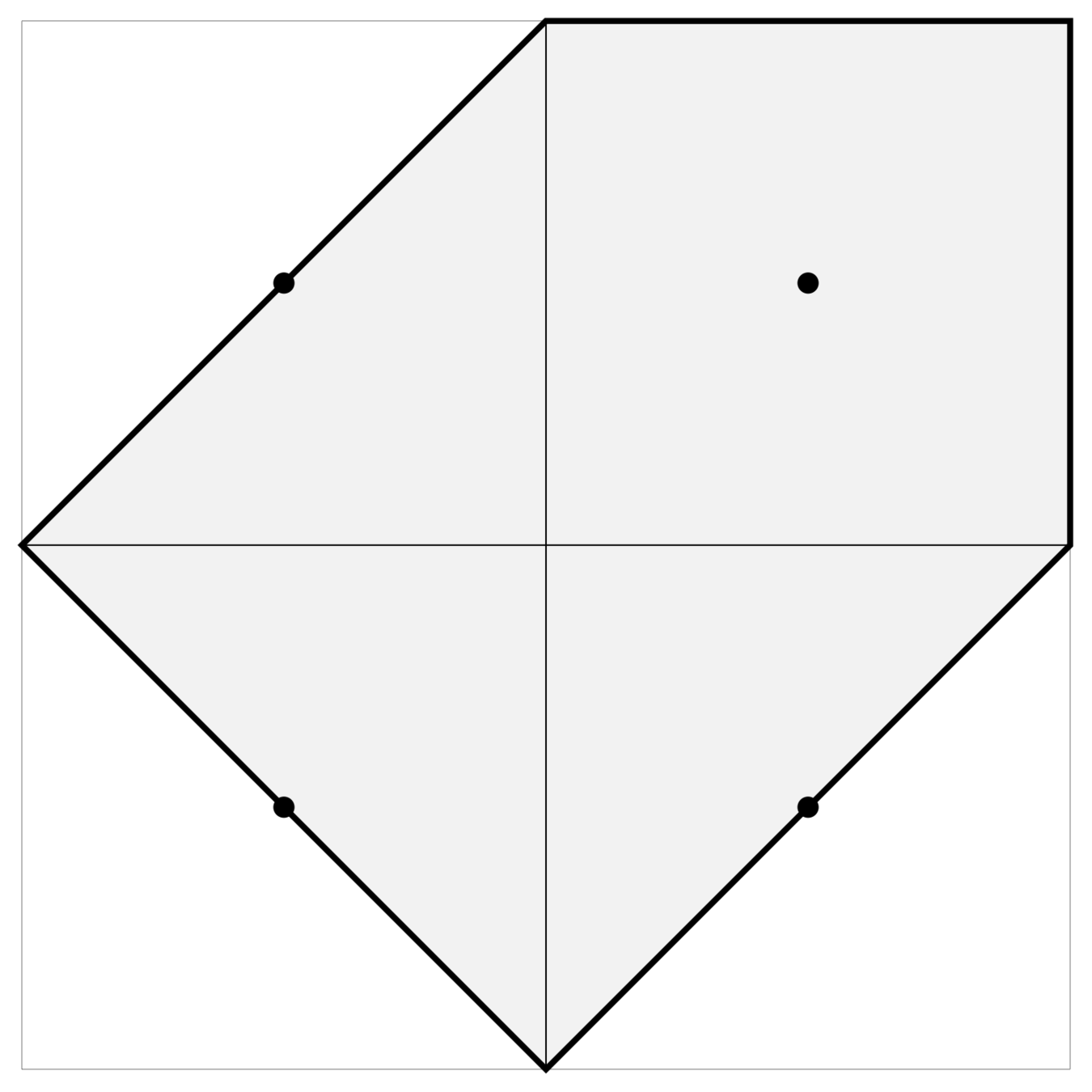
If we round every point \((d_1),\ldots , d_{n-3})\) in the moment polytope to the nearest point with half-integer coordinates \(\frac{1}{2}(x_1, \ldots , x_{n-3})\) …

Orthoscheme decomposition

… and subdivide the regions of attraction by

ordering and sign of \(d_i - \frac{1}{2} x_i\), we get a collection of identical, orthogonal simplices of equal area (this works for any \(n\)):

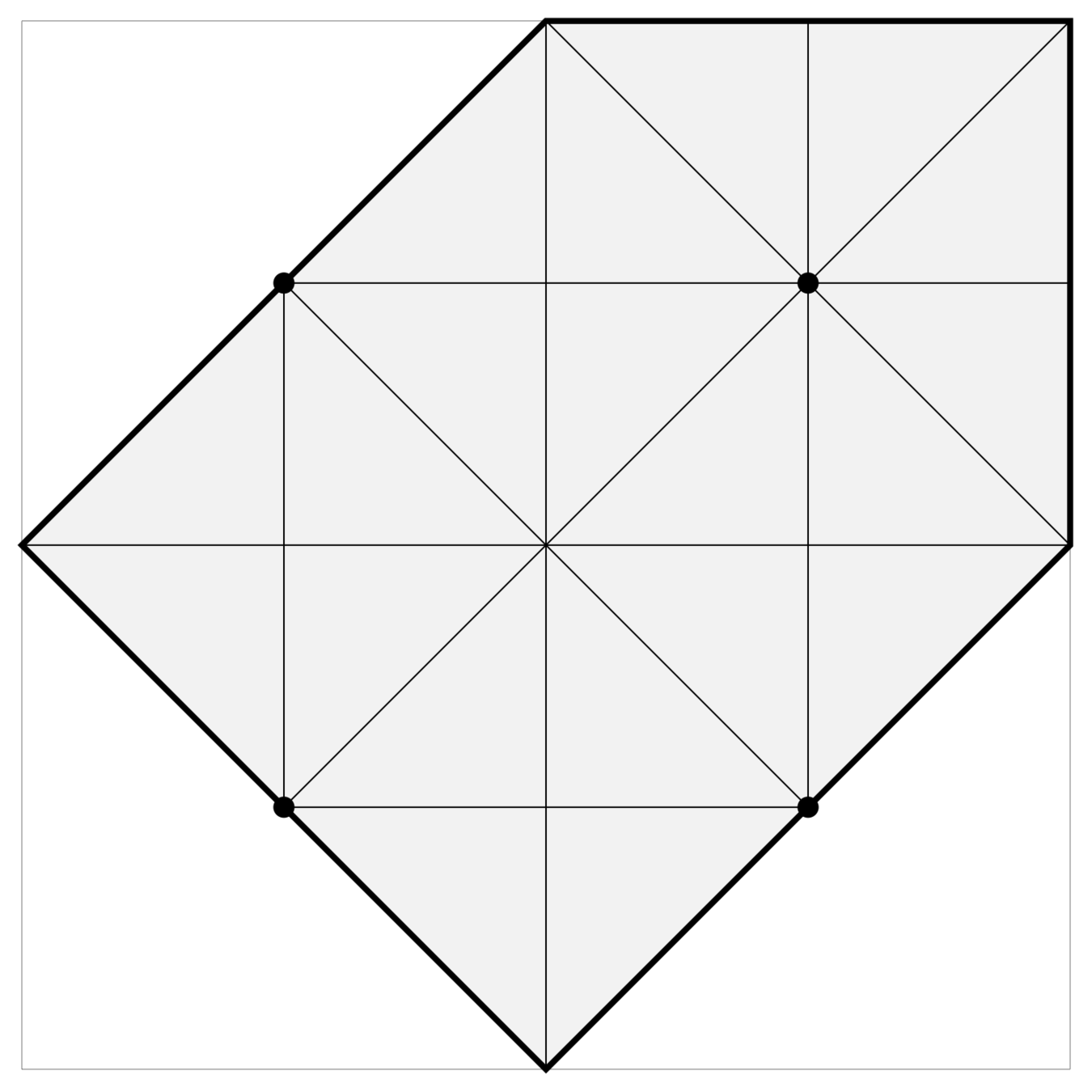
There are lots of simplices…

Proposition*: The number of half-integer points in \(\mathcal{P}_n\) is the Motzkin number

M_{n-3} = \sum_{k=0}^{\lfloor \frac{n-2}{2}\rfloor} \binom{n-2}{2k} C_k
\sim \sqrt{3} \frac{1 + \frac{1}{16(n-3)}}{(2n-3)\sqrt{(n-1)\pi}} 3^{n-2}

Therefore, there are exponentially many simplices in this decomposition. ☹️

… clever data structures to the rescue

Theorem (K. Chapman, in progress): With \(O(n^3)\) preprocessing of the transition probabilities, a direct sampling algorithm for equilateral \(n\)-gons in \(O(n^2 (\log n)^2)\) time.

The simplices are indexed by certain permutations.

We can recursively construct Lehmer codes of valid permutations using a Markov chain.

Questions

  • What’s the corresponding story for planar \(n\)-gons?
  • Polygons form a Kähler manifold, so there’s a well-defined distance between \(n\)-gons. How should we optimally register polygons? Can we find explicit geodesics?
  • What about more complicated polymer topologies?

Thank you!

References

The symplectic geometry of closed equilateral random walks in 3-space

J. Cantarella & C. Shonkwiler

Annals of Applied Probability 26 (2016), no. 1, 549–596

A fast direct sampling algorithm for equilateral closed polygons

J. Cantarella, B. Duplantier, C. Shonkwiler, & E. Uehara

Journal of Physics A 49 (2016), no. 27, 275202

J. Phys. A Highlight of 2016

Sampling knots using orthoschemes

K. Chapman

In preparation