Visualizing Higher Dimensions
Clayton Shonkwiler
What do we mean, “higher dimensions”?
“Visualizing higher dimensions is an exercise in creative lying.”
—Herman Gluck
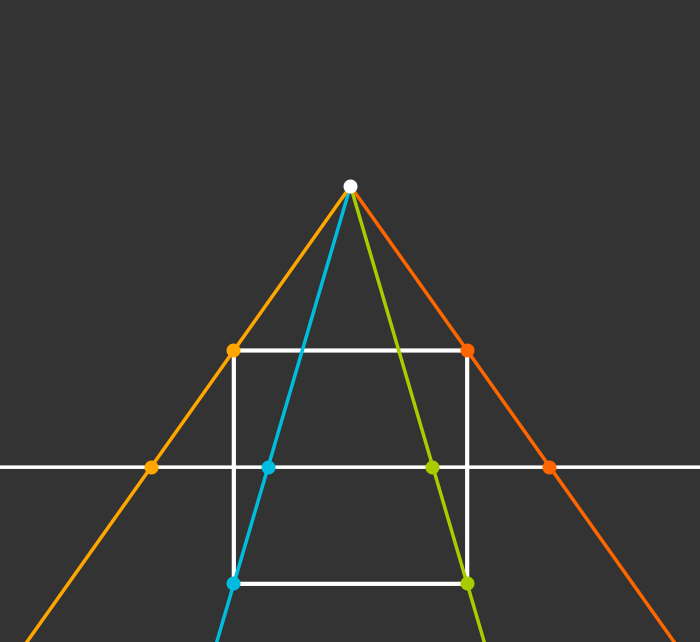
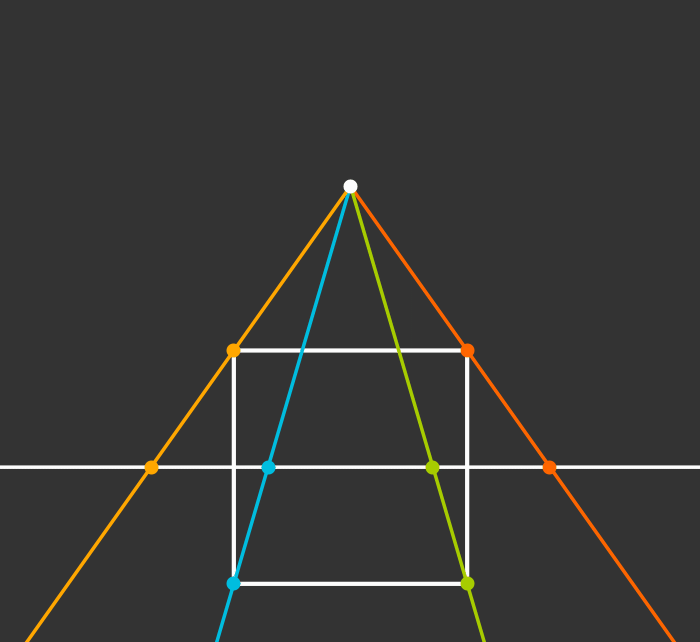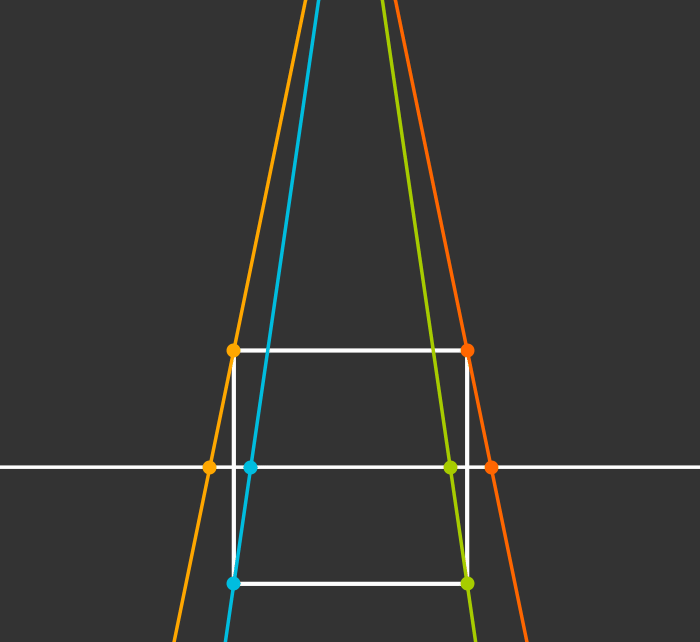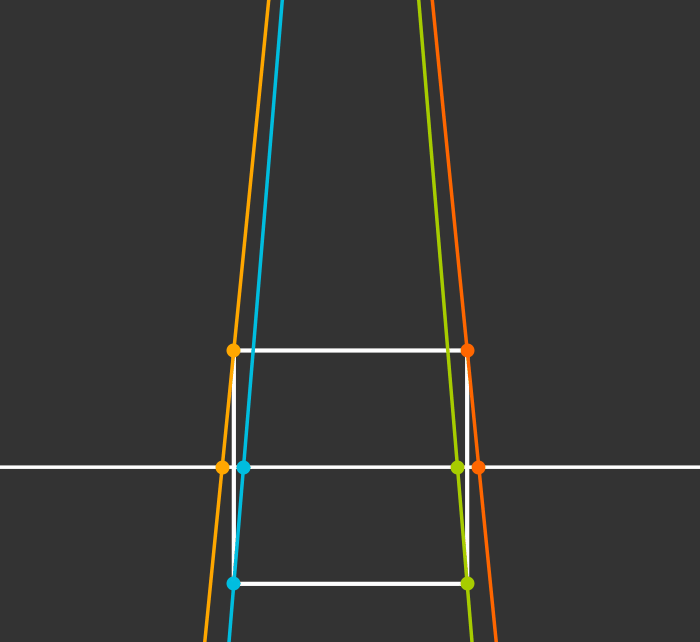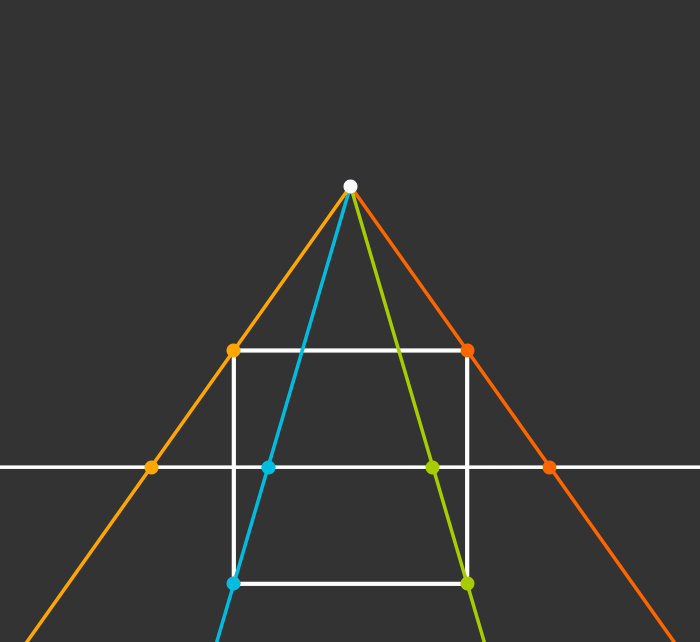

Projection to 1D
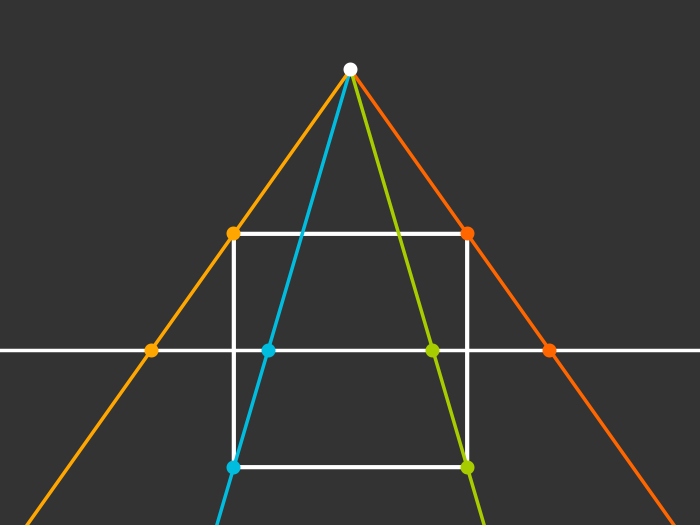
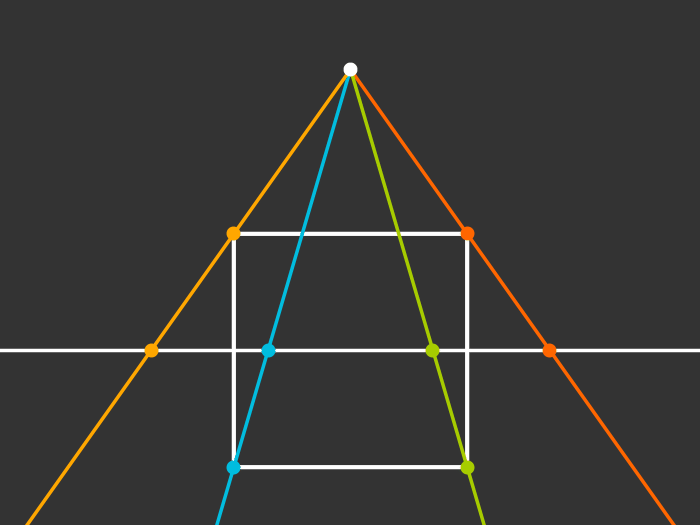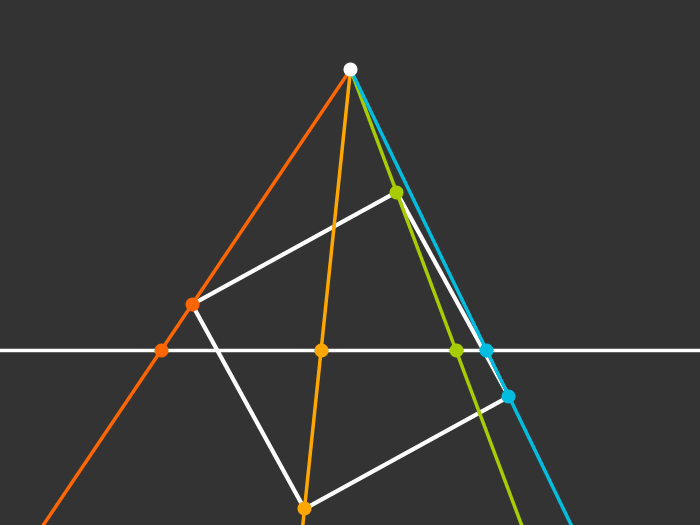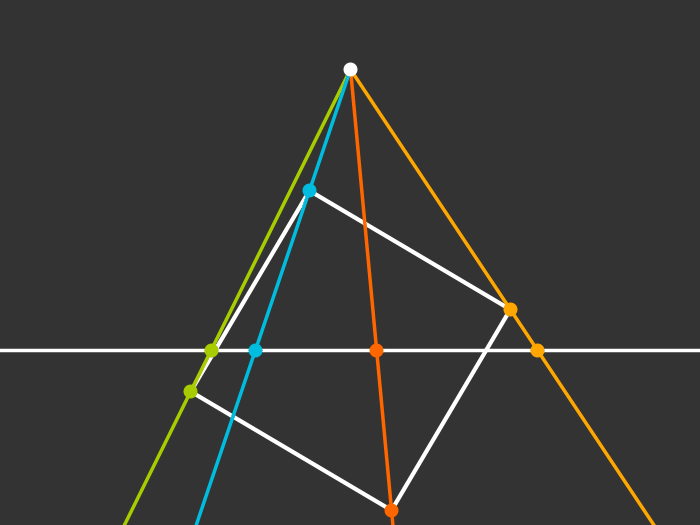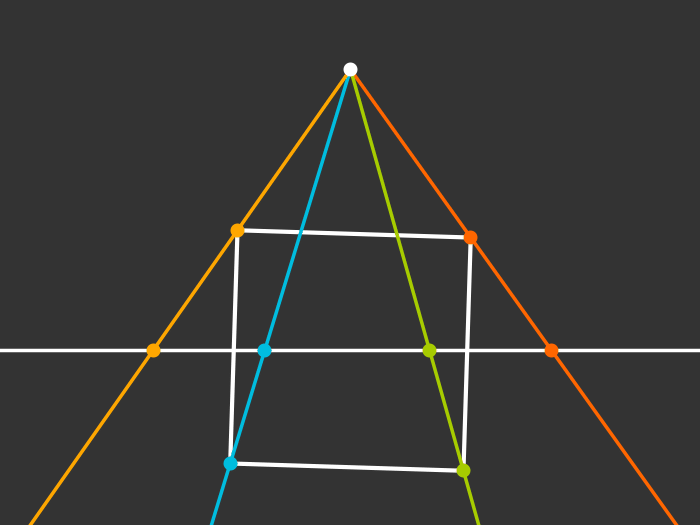

Rotating
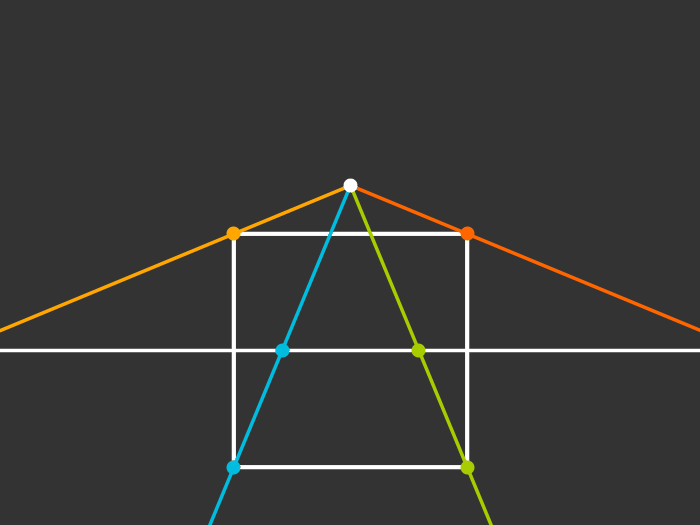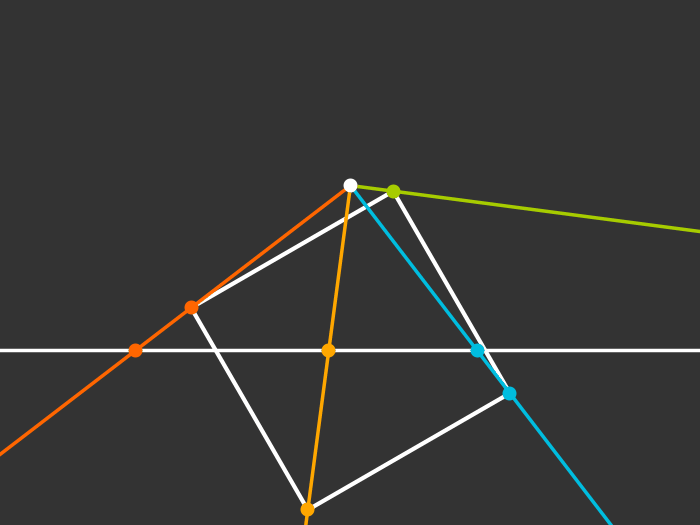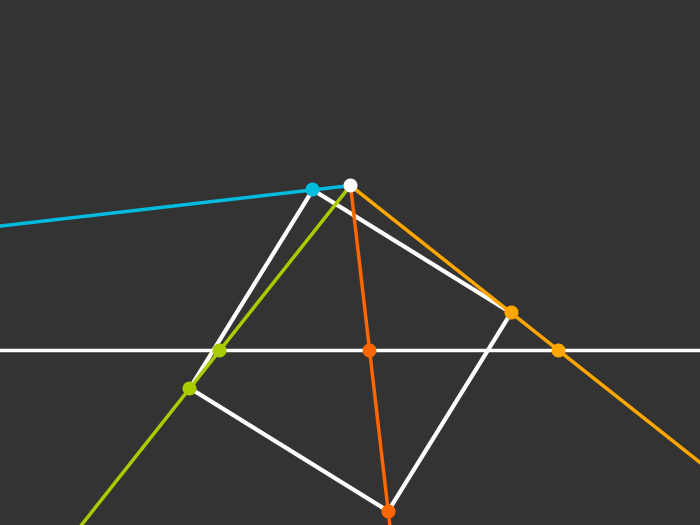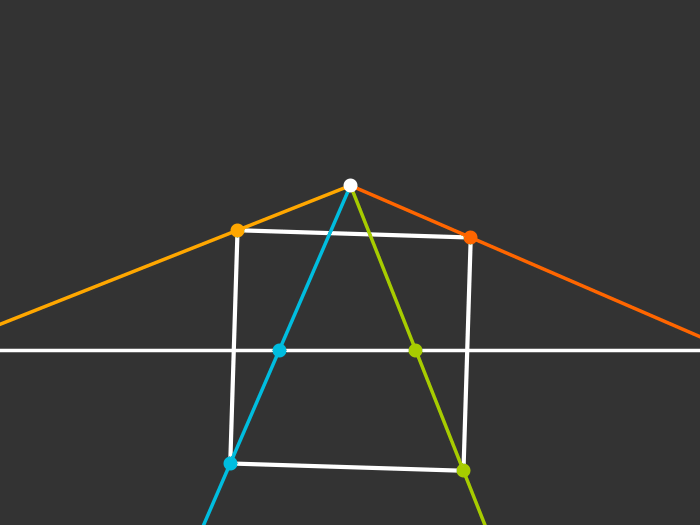

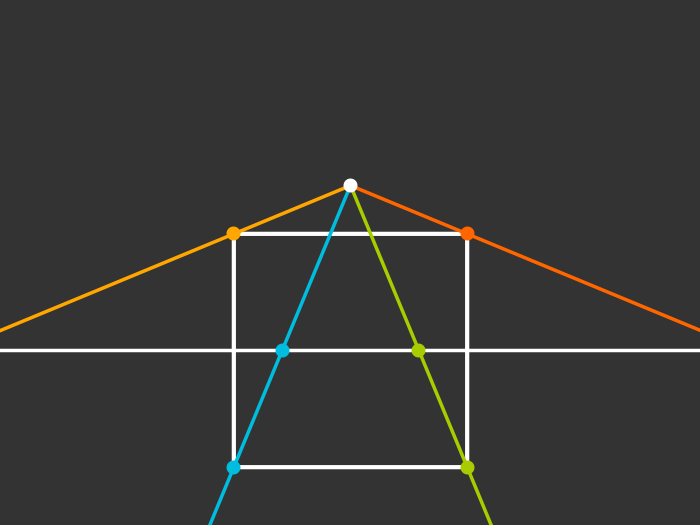
Singularity
Projection to 2D
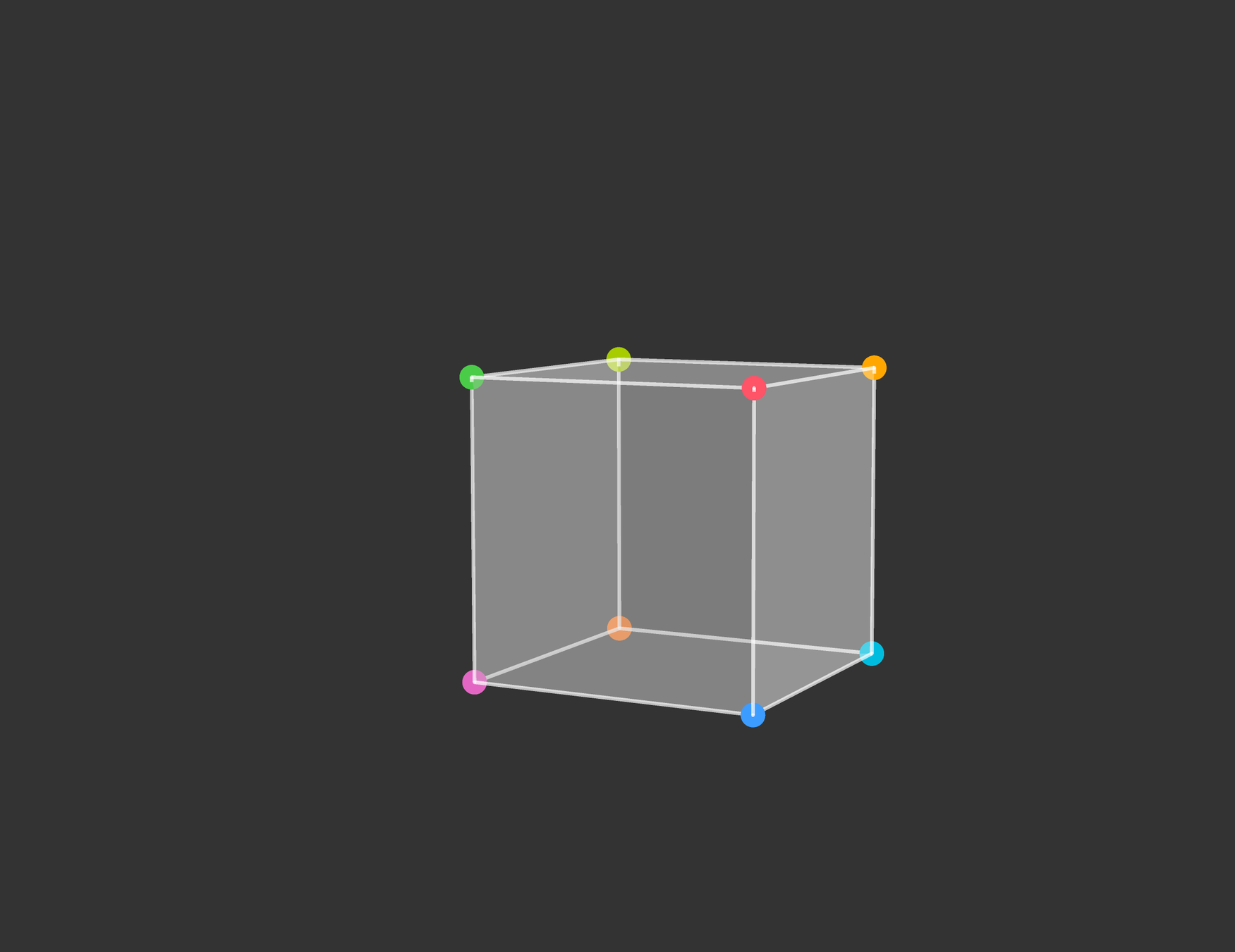
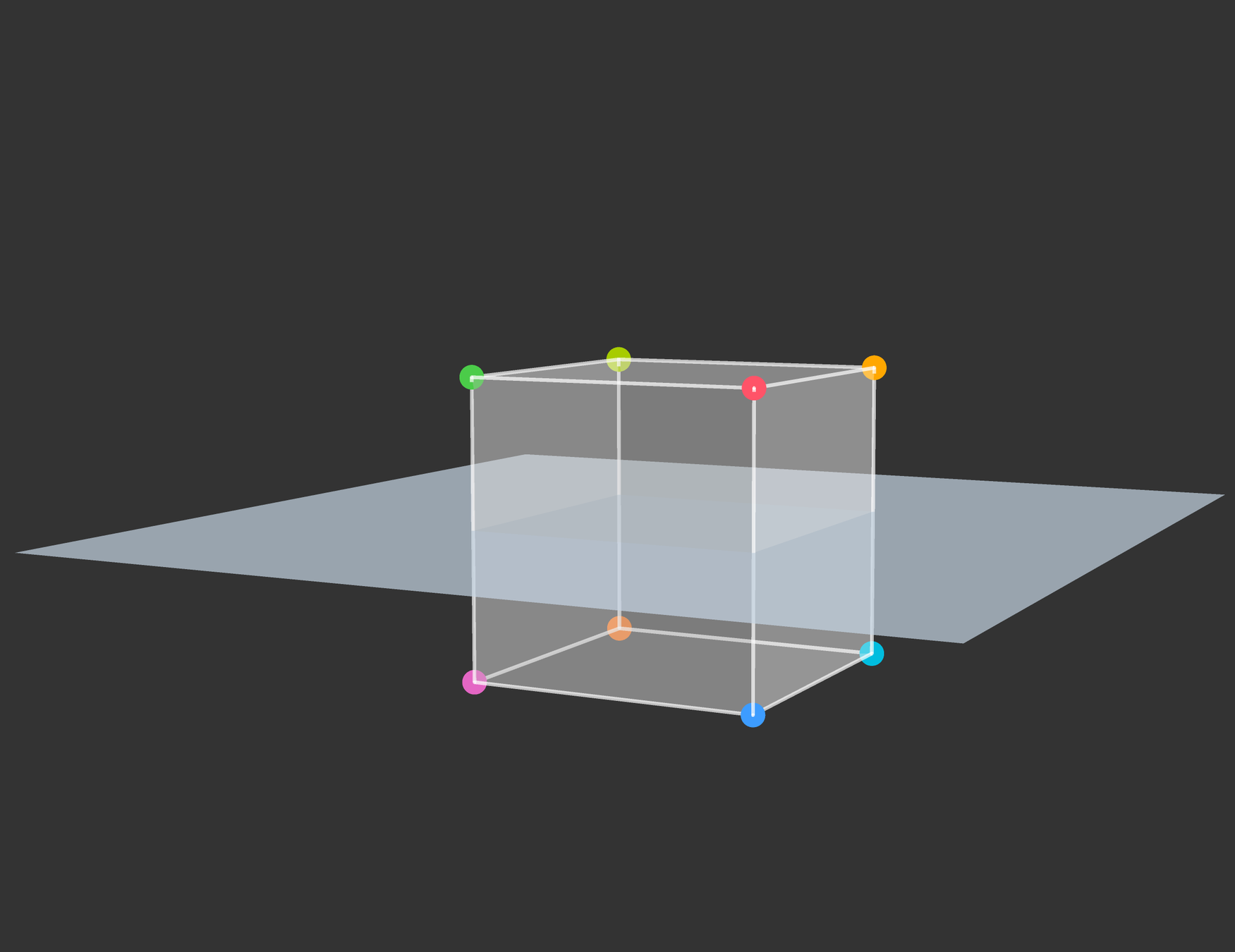




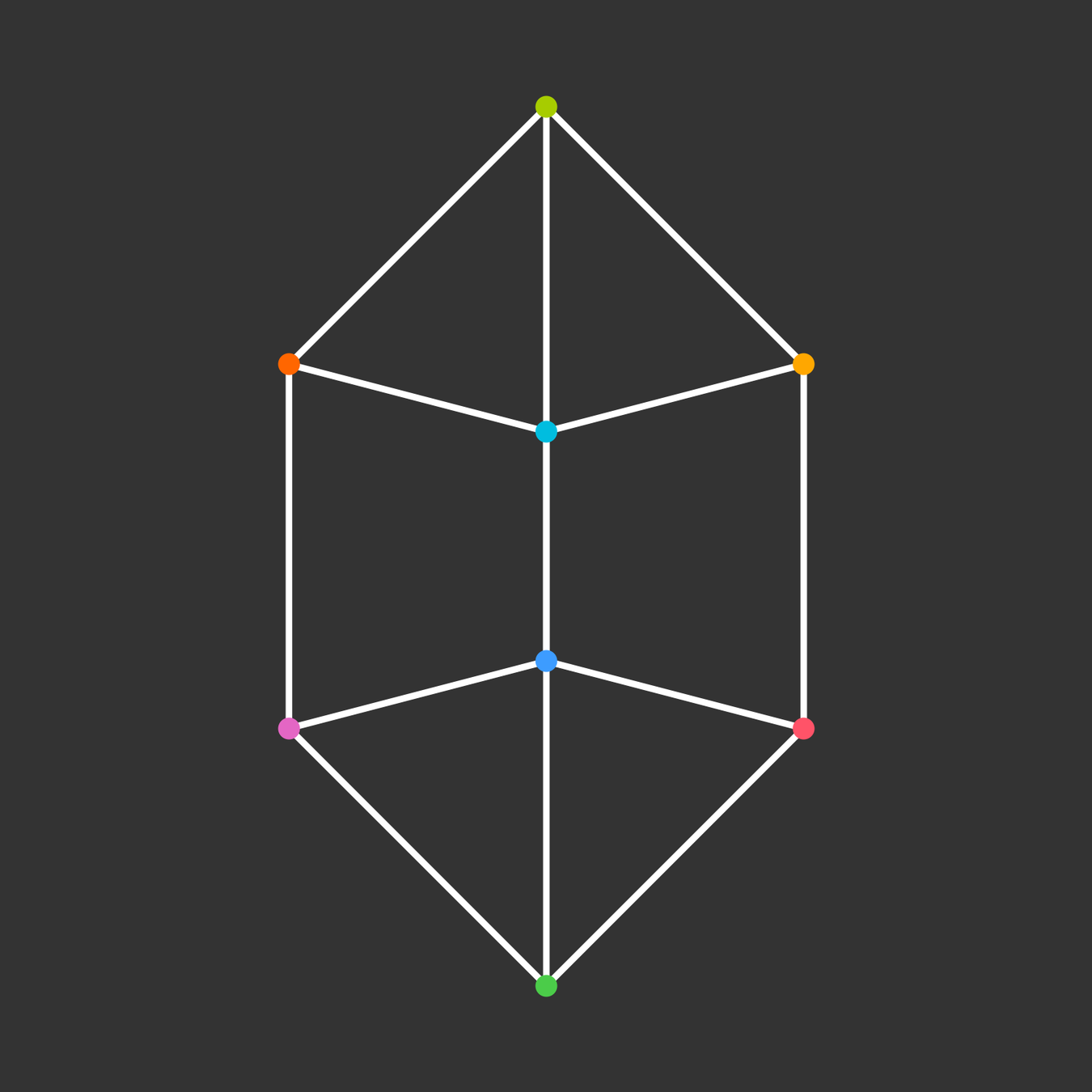



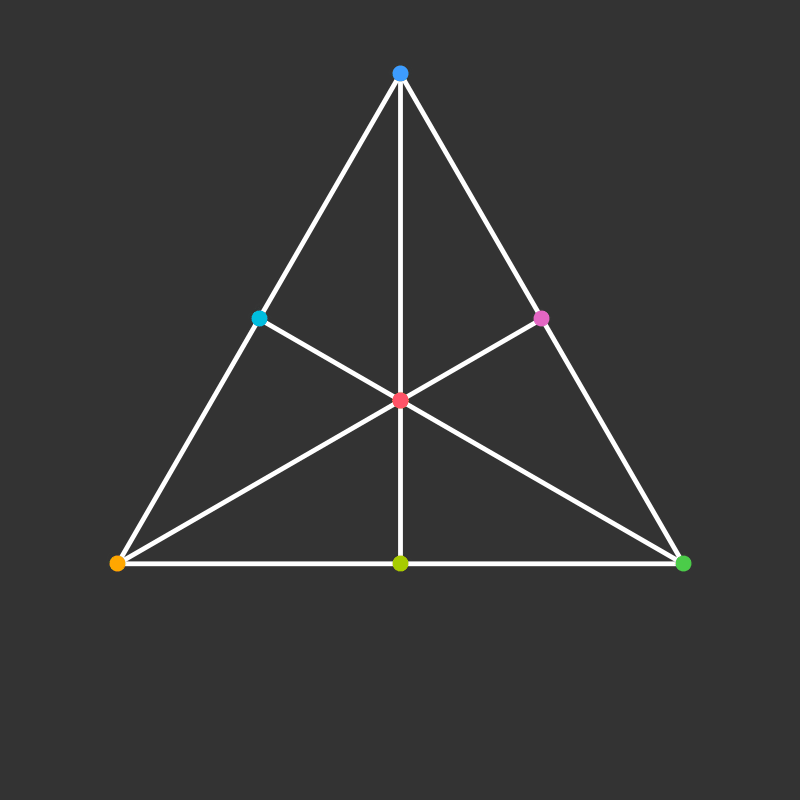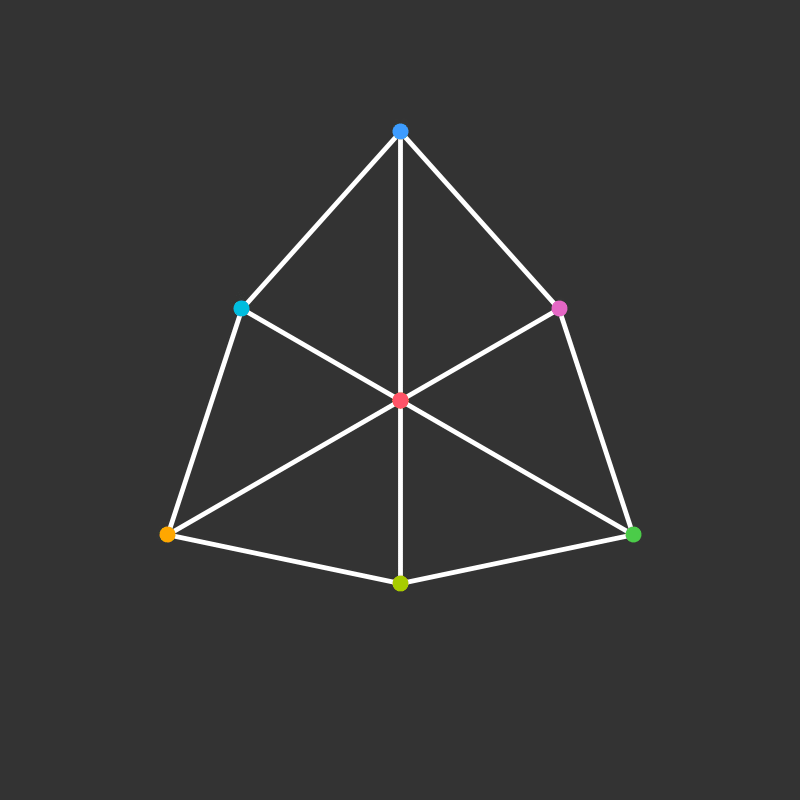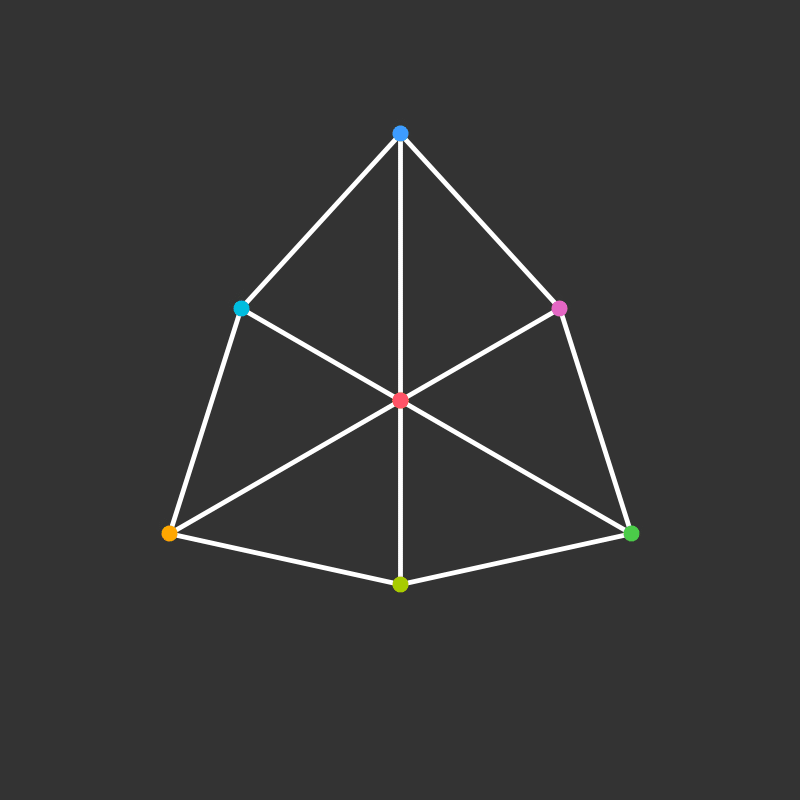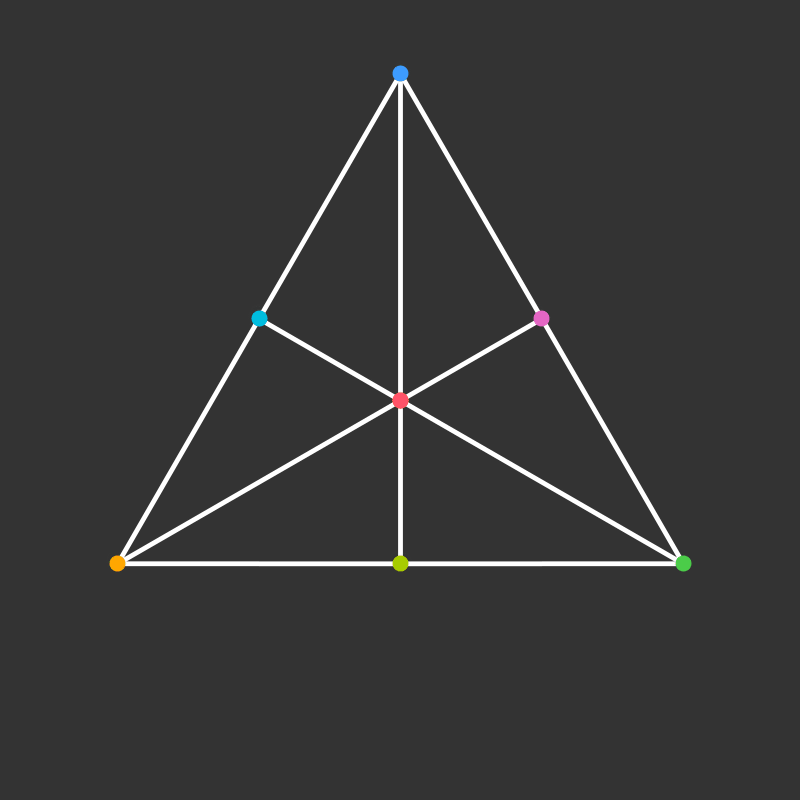
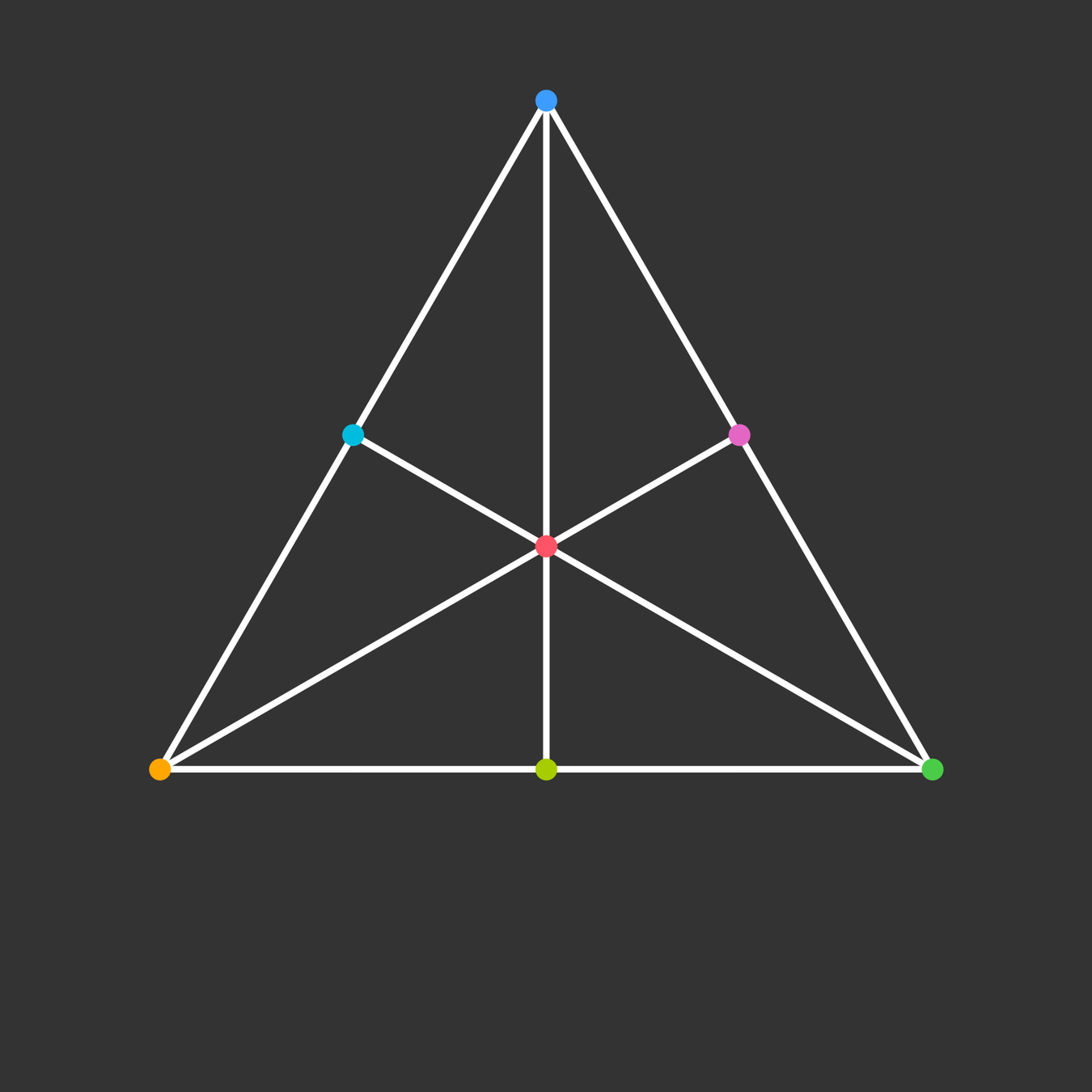
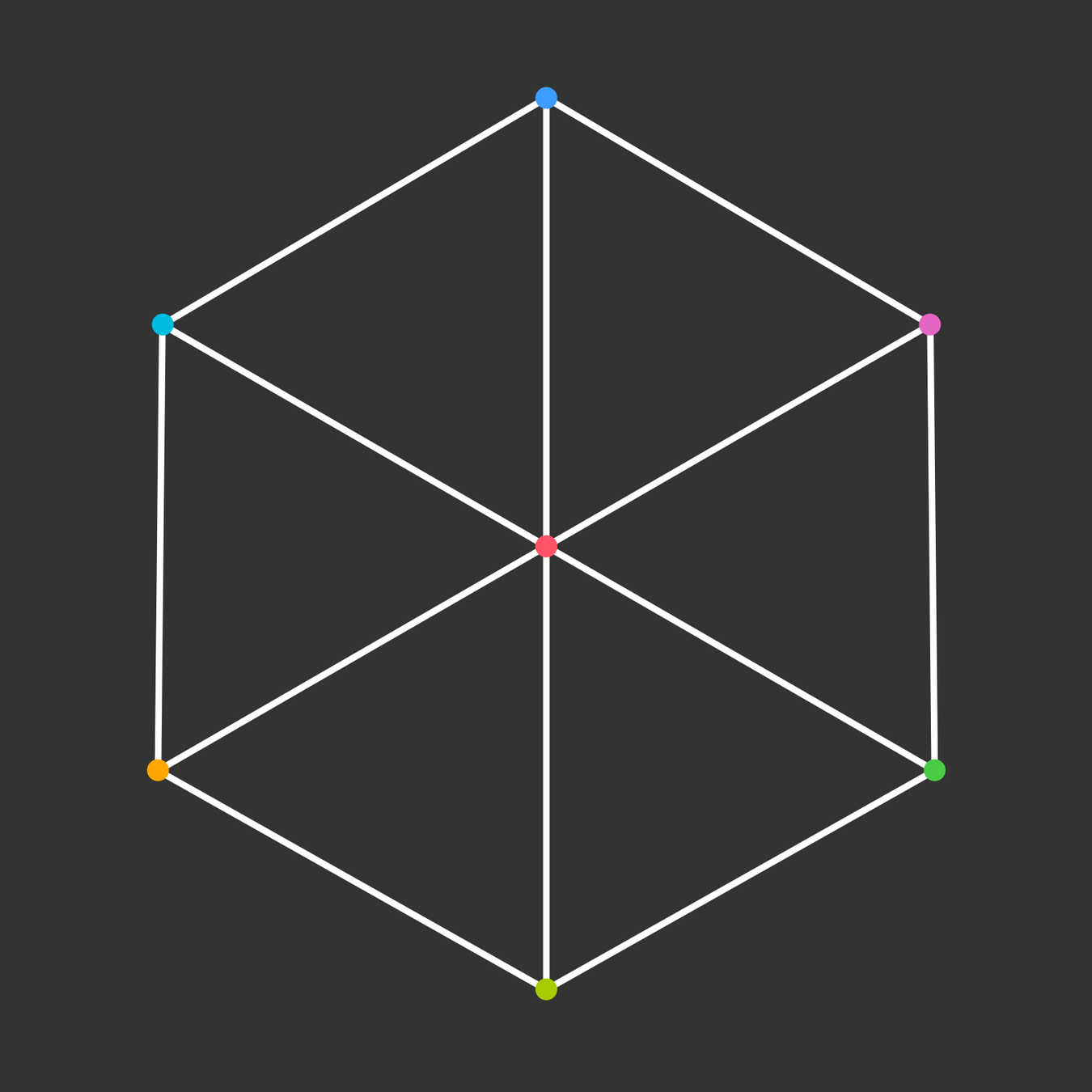
Rotation




The Sphere
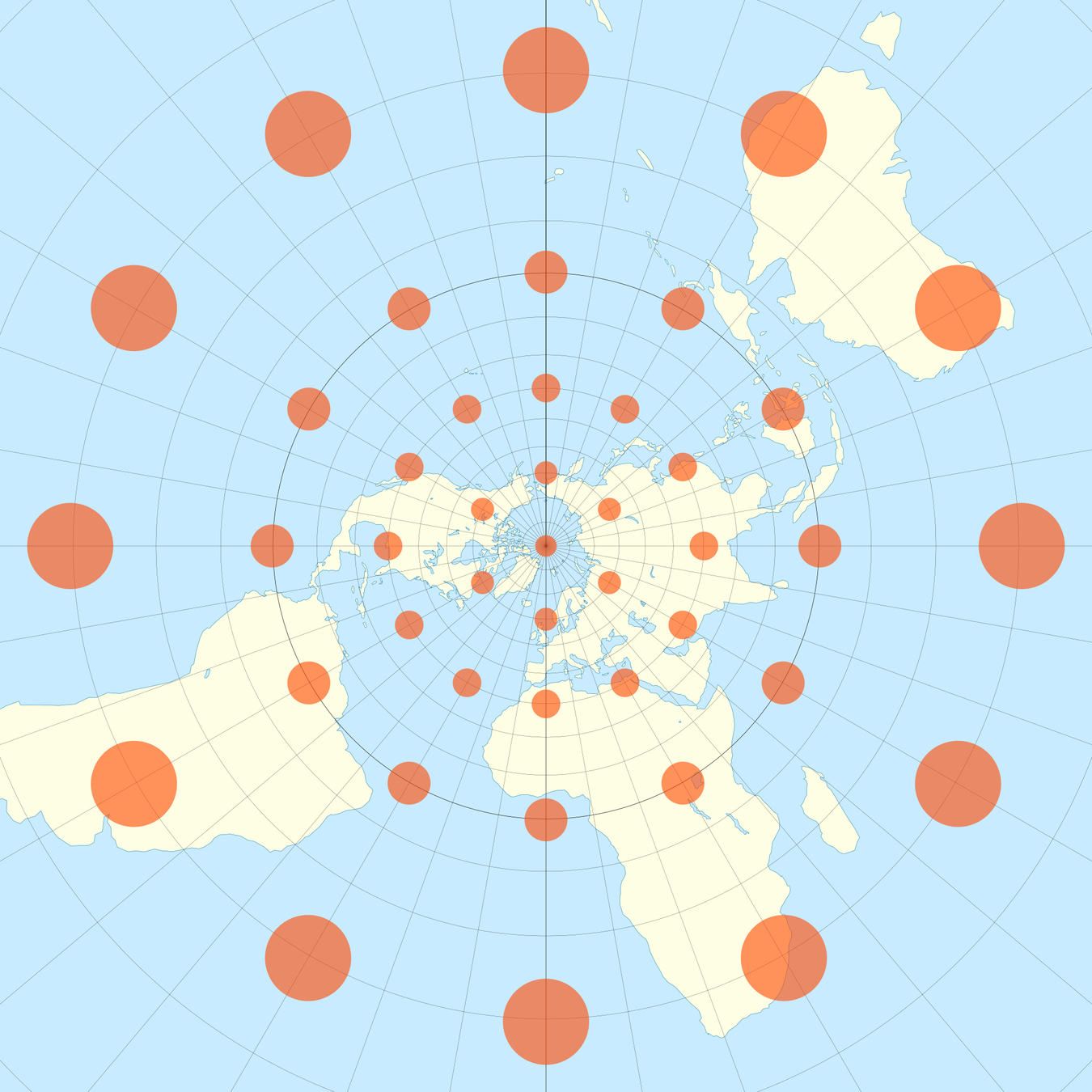
Slicing






What are the coordinates of a cube?
How about a hypercube?
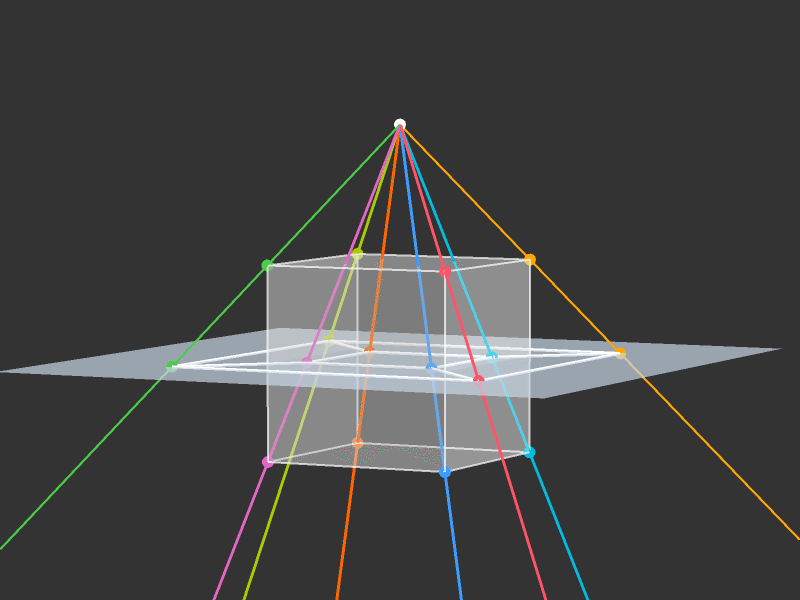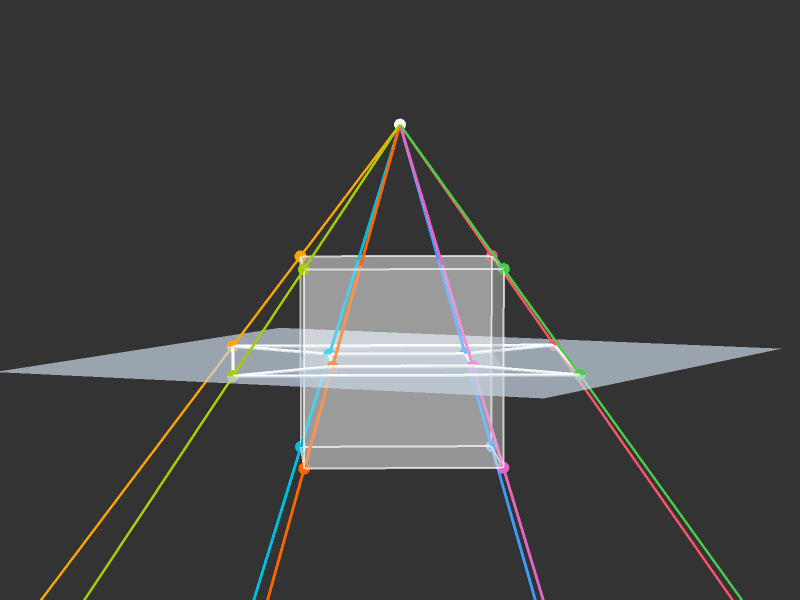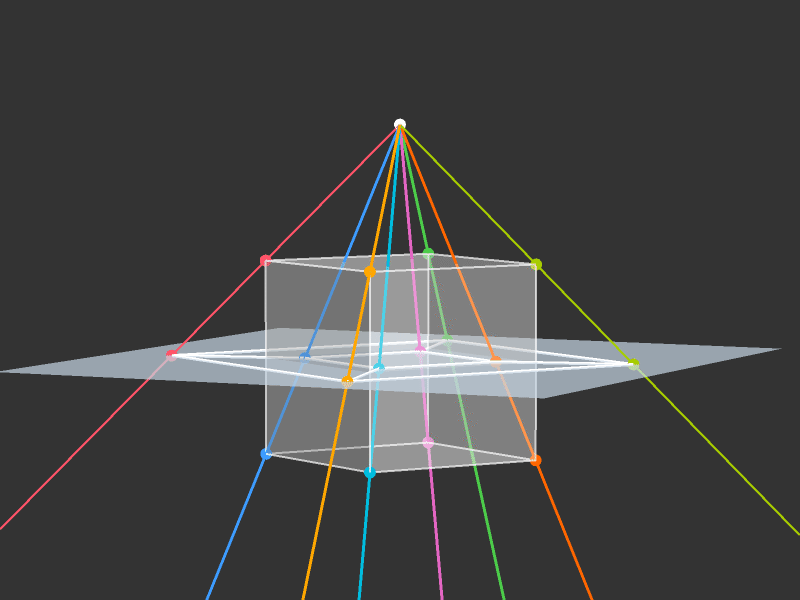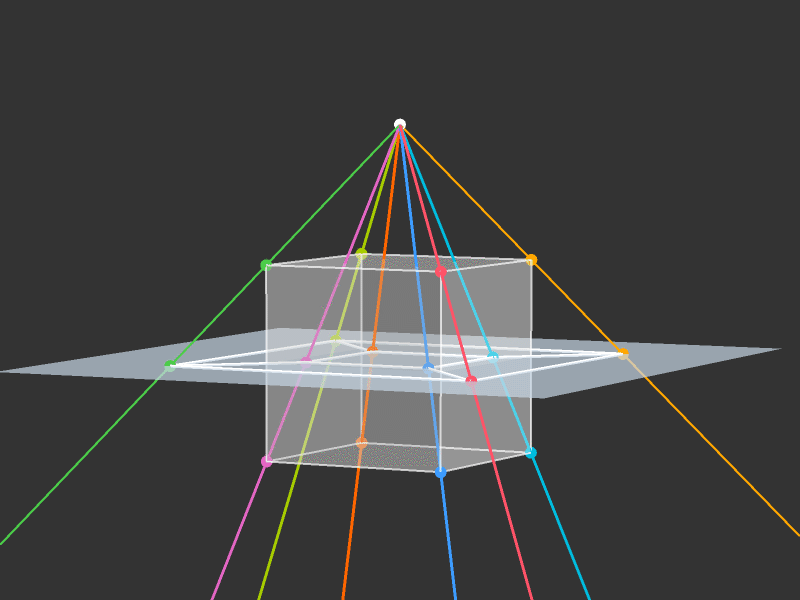
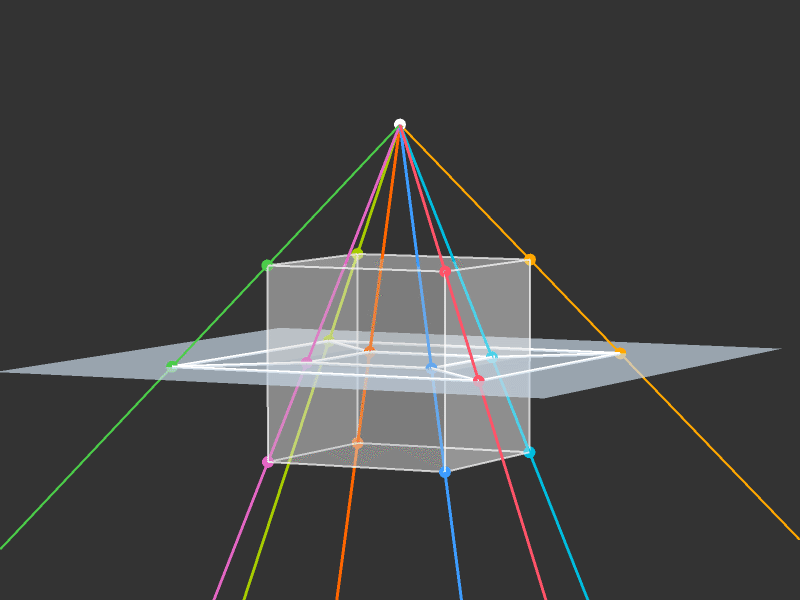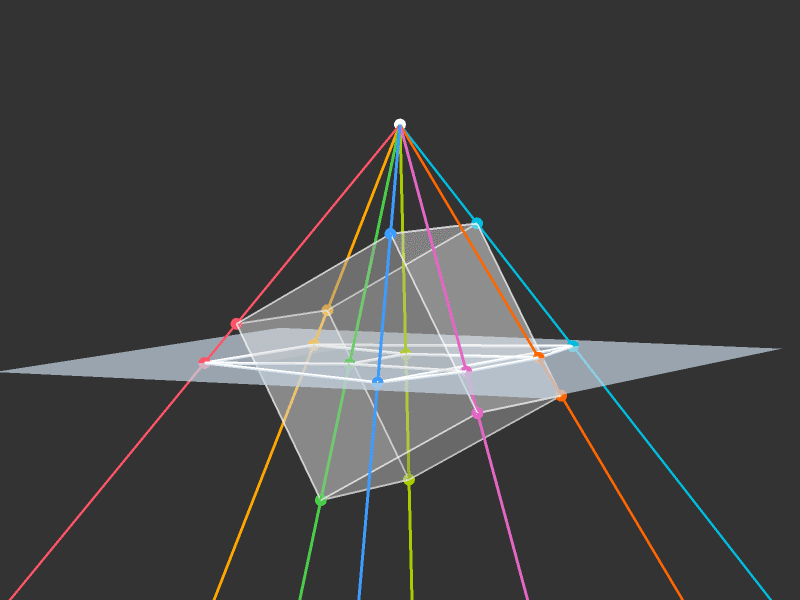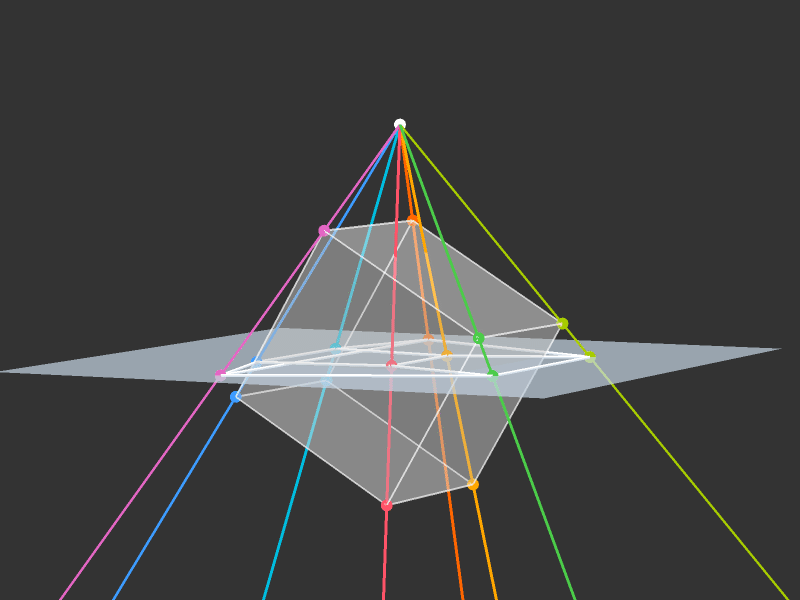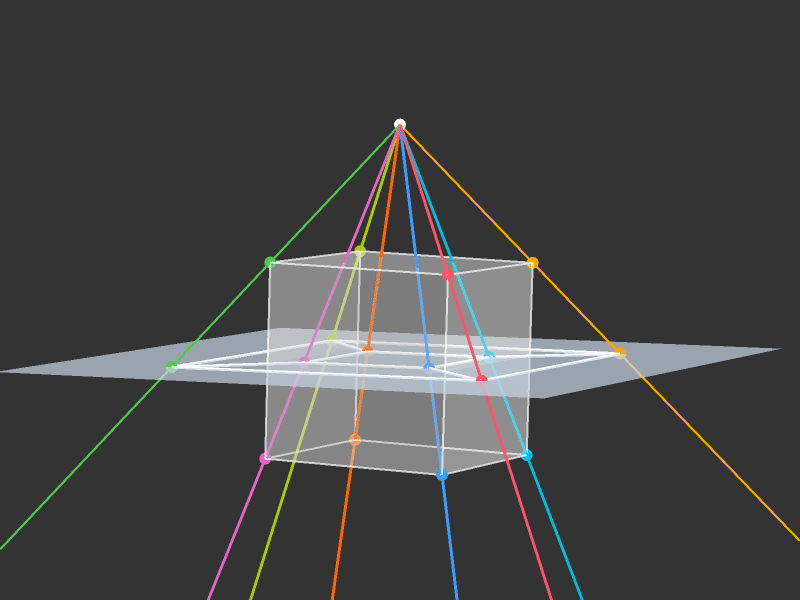
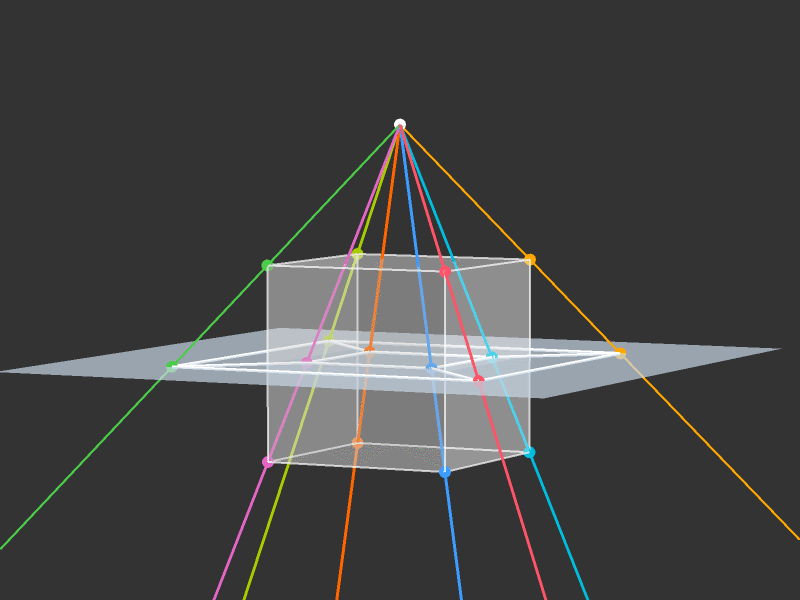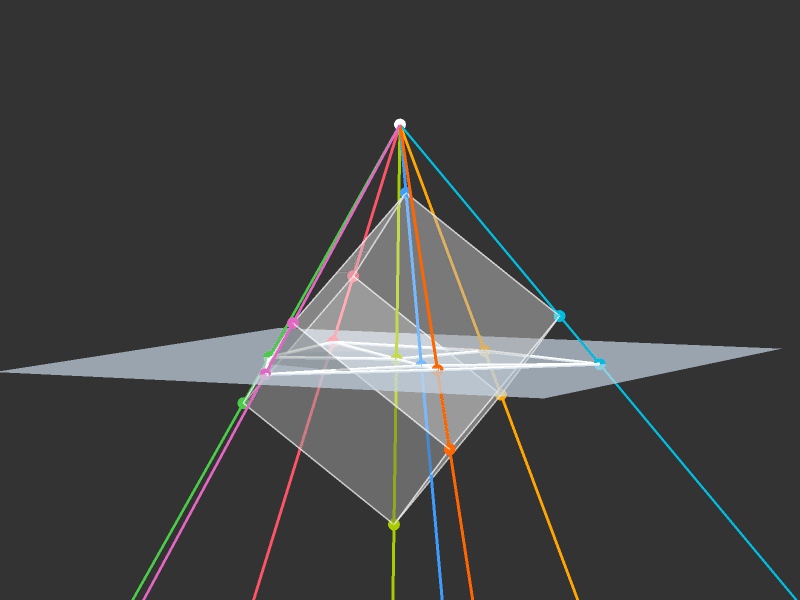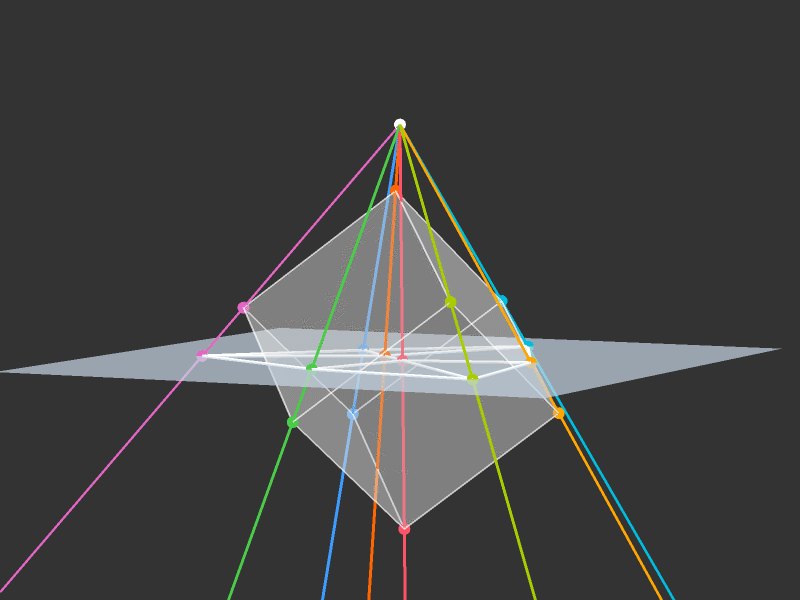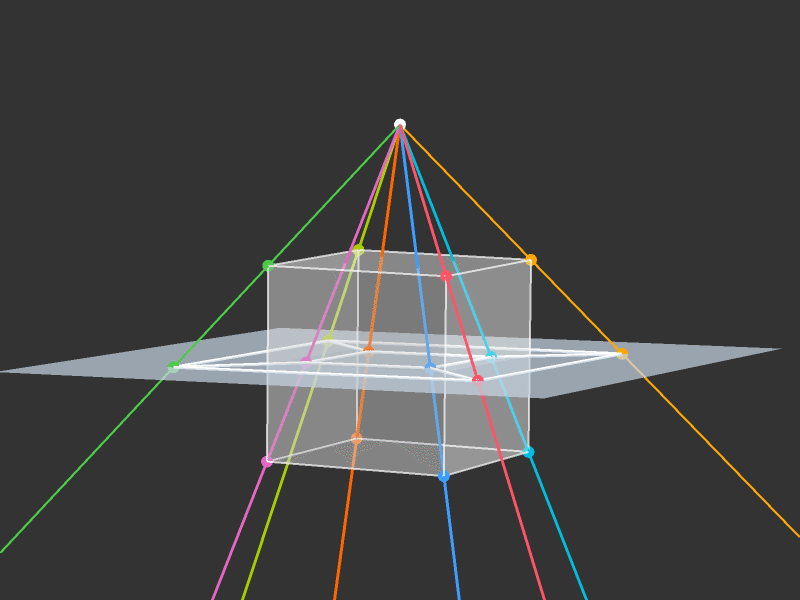
Projection to 3D










Rotations



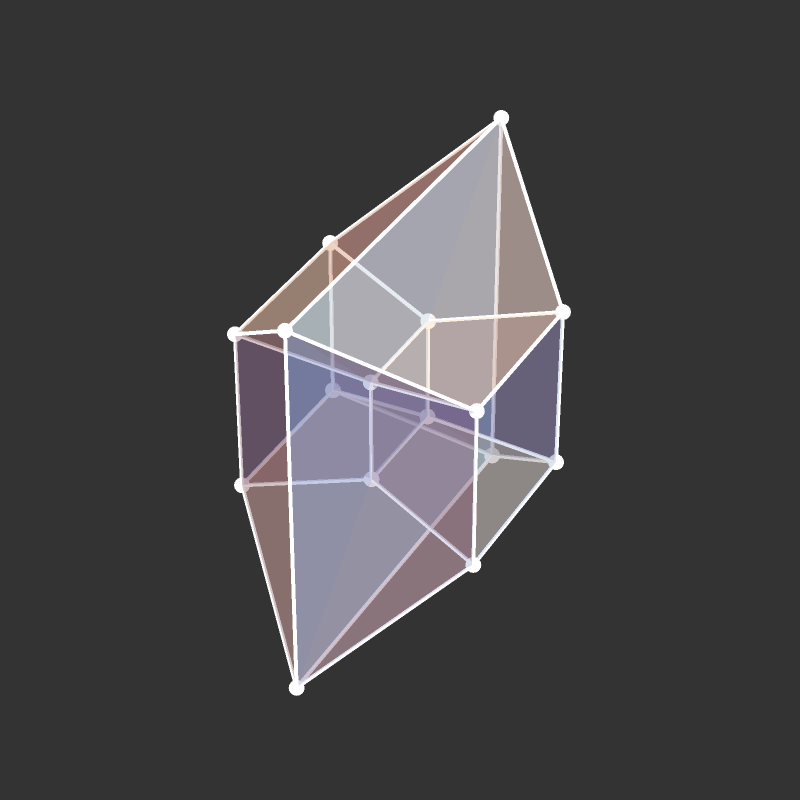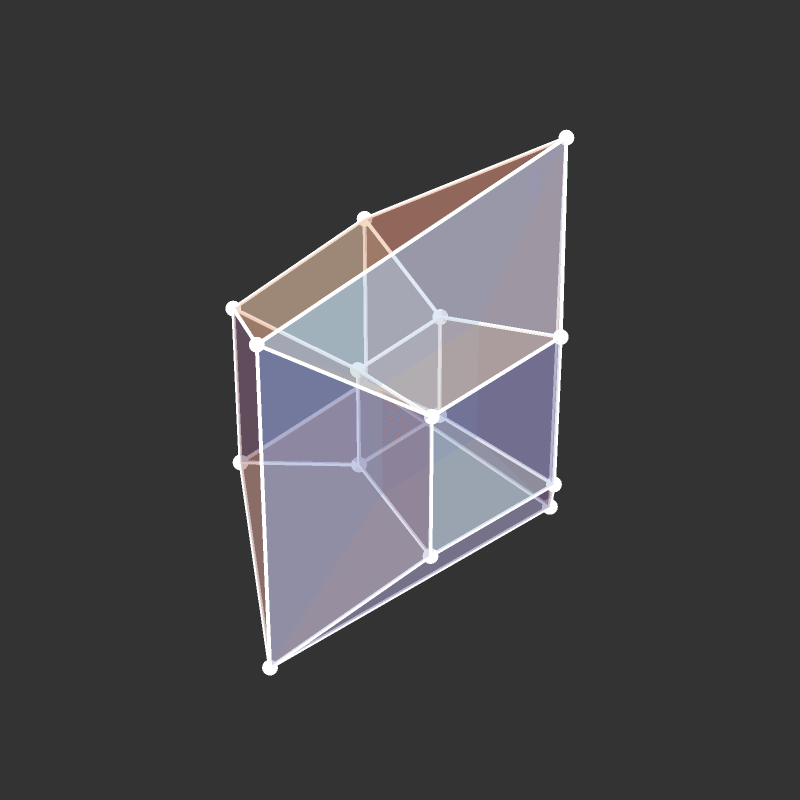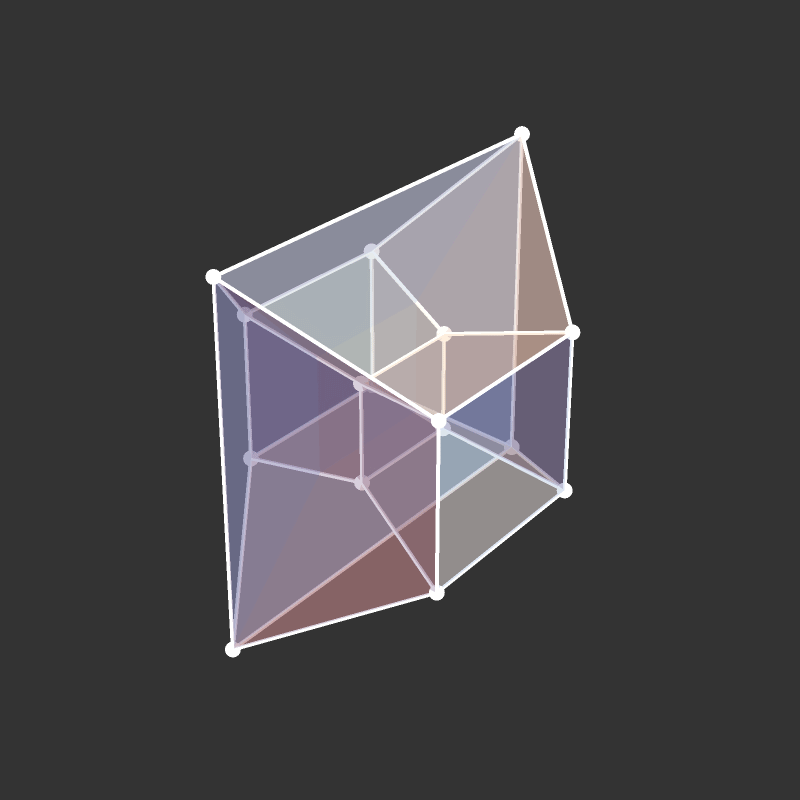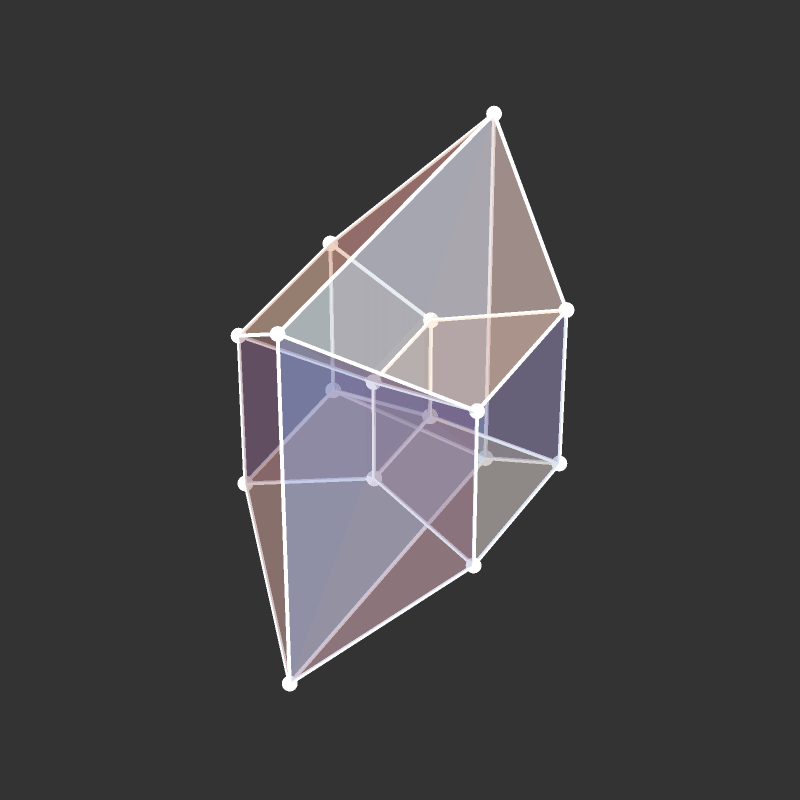
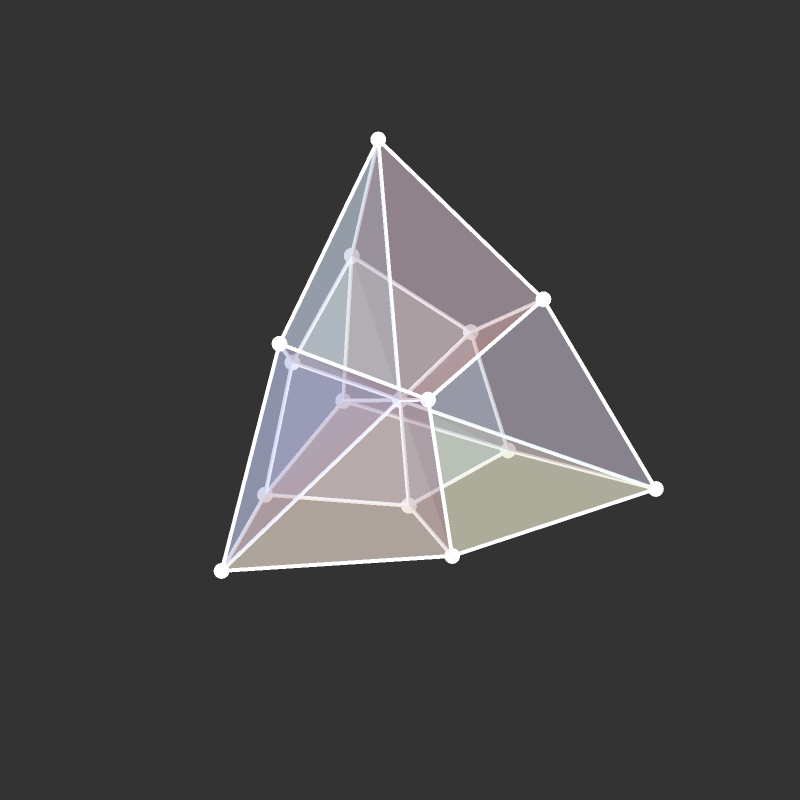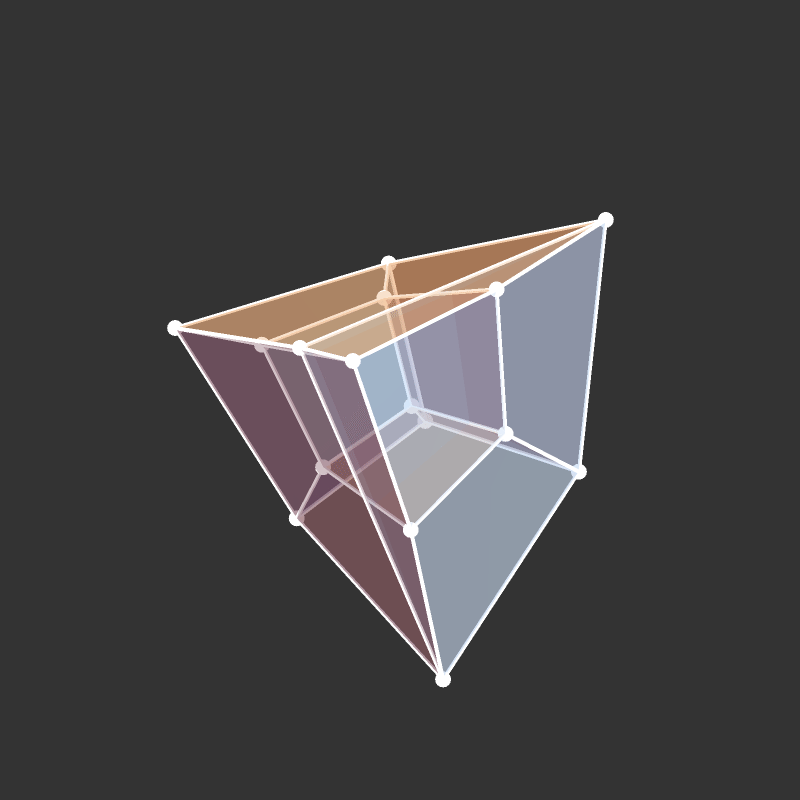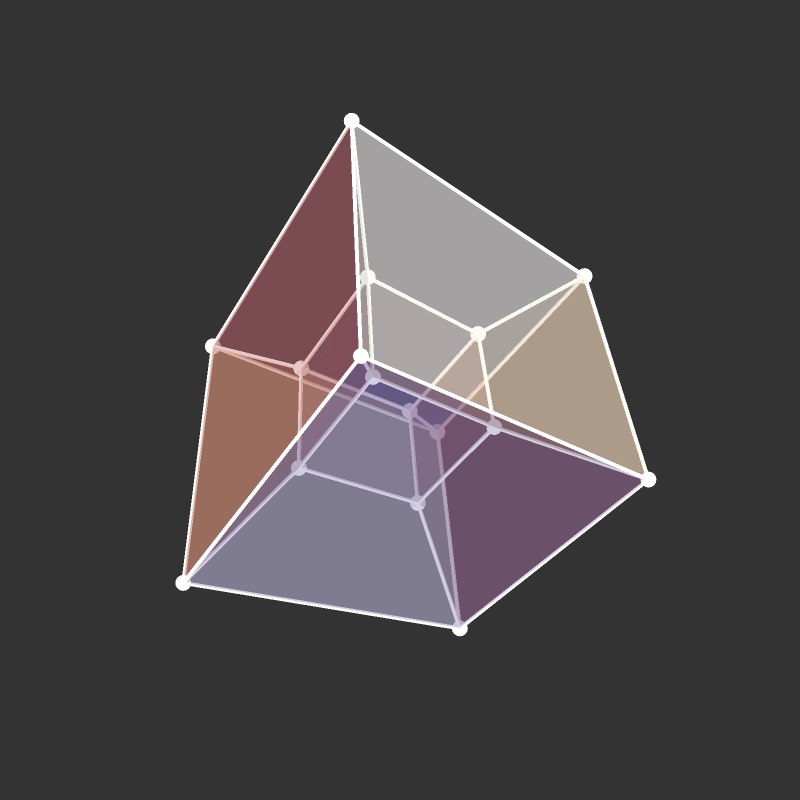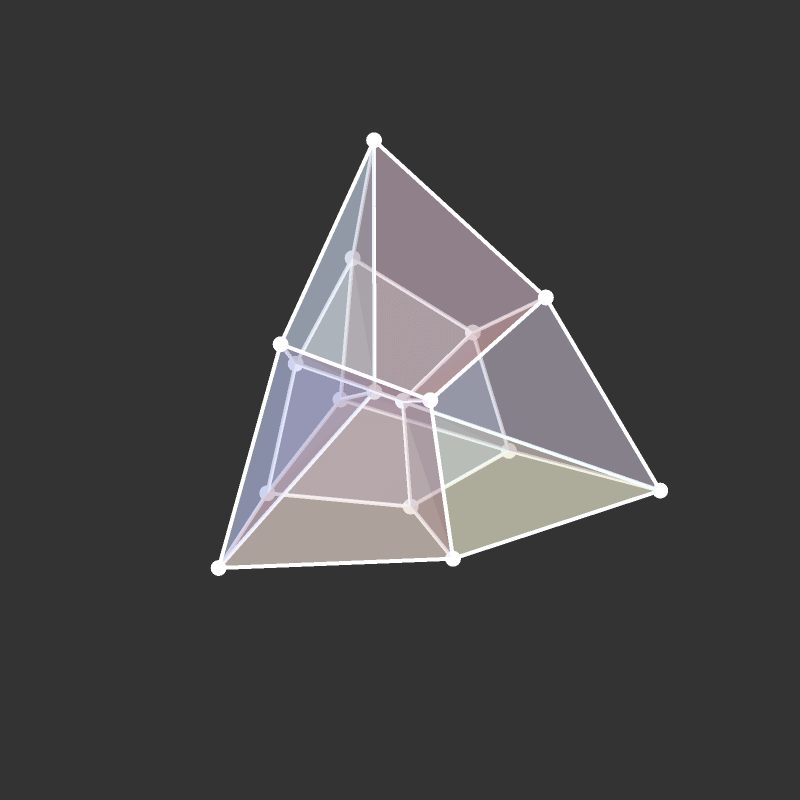

Slicing








Unfolding
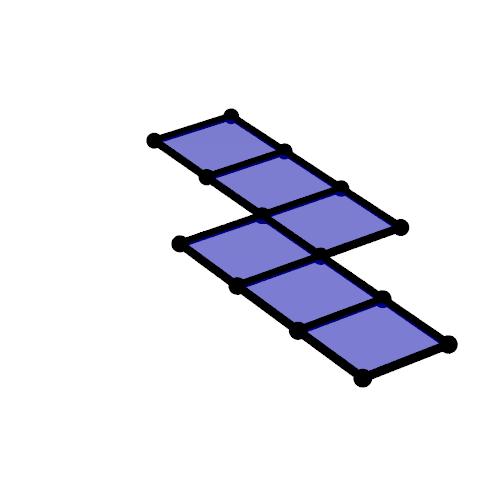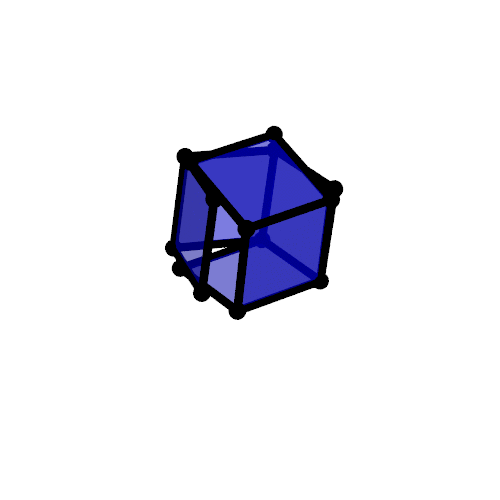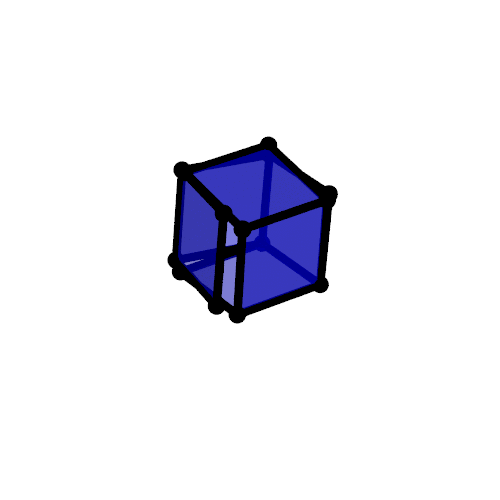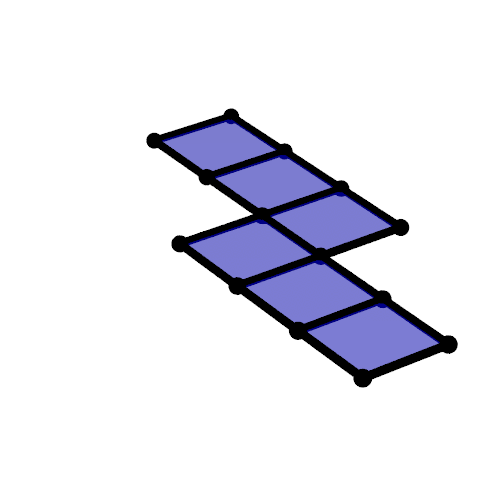
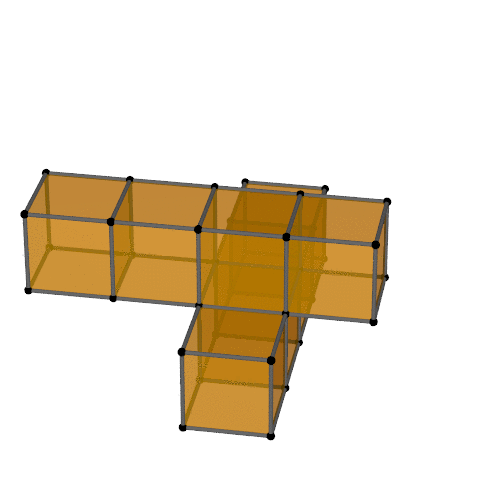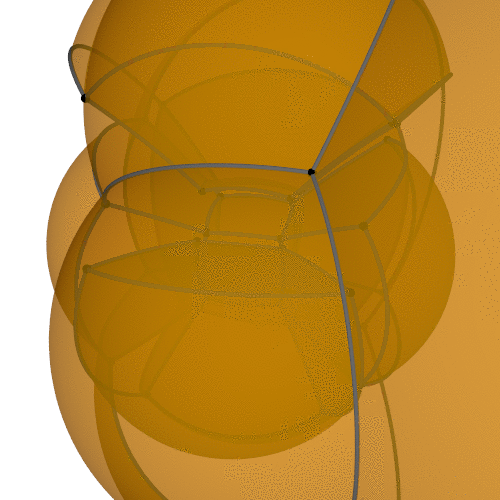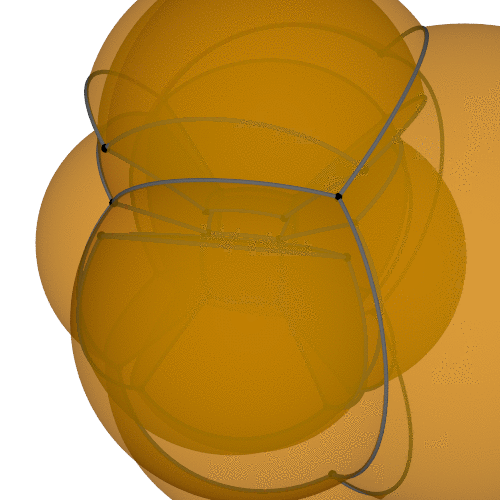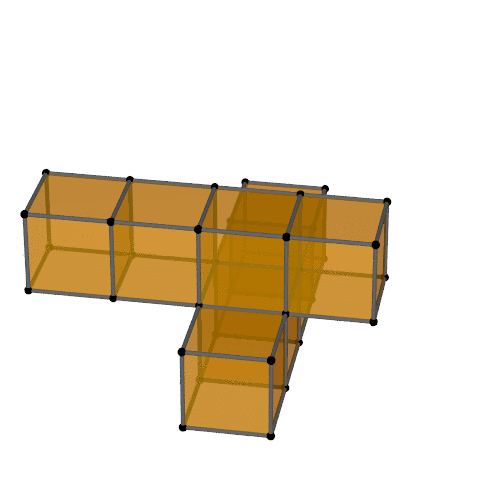

Can you build it?
Practice: 5-Cell
-
Build a tetrahedron.
-
How does it project to the plane?
-
What if it’s rotating?
-
Visualize the 4-dimensional version of the tetrahedron (called the 5-cell).
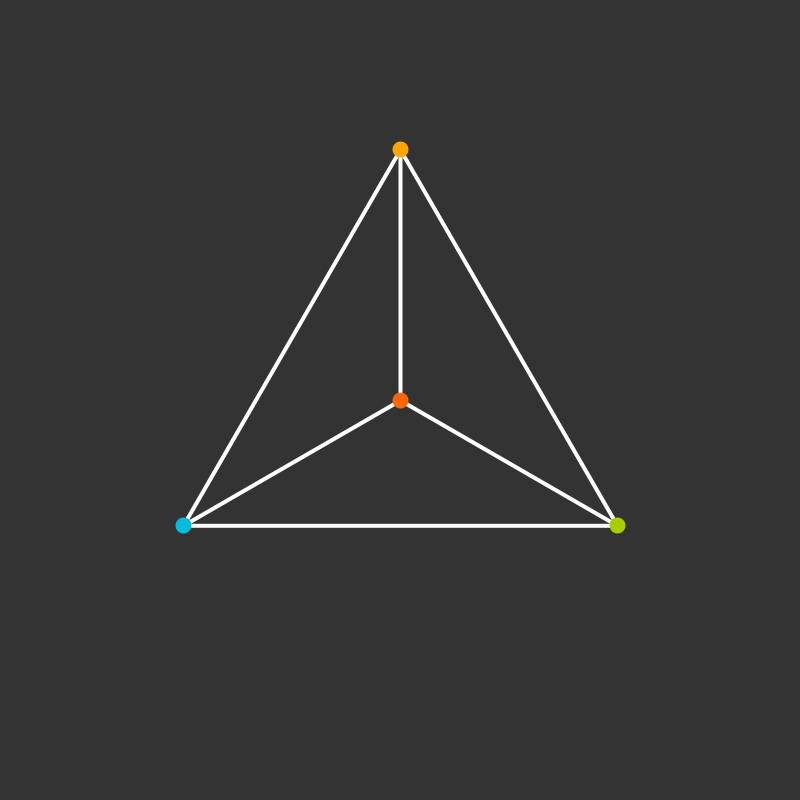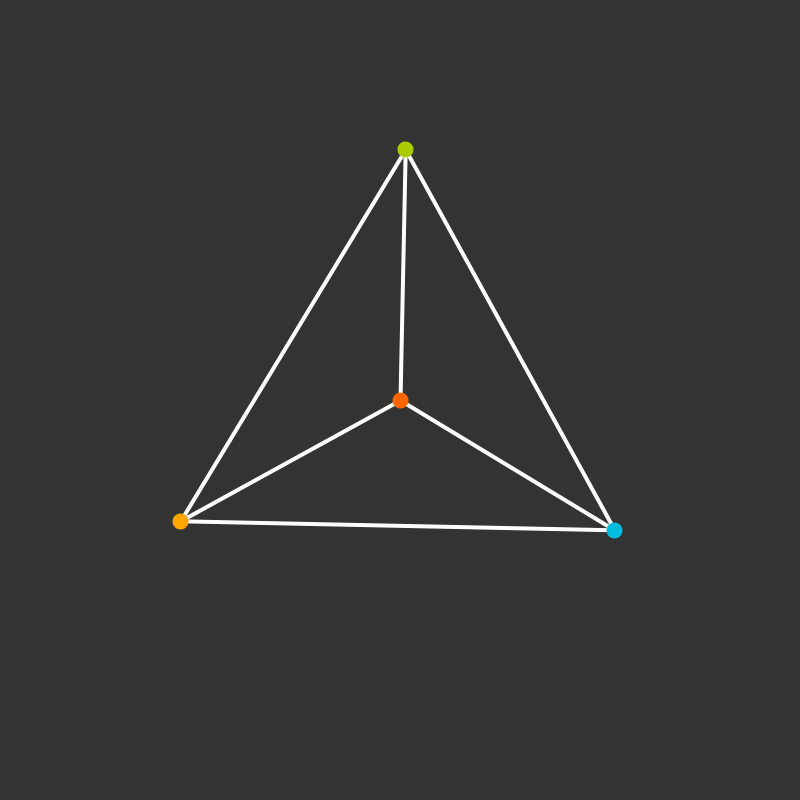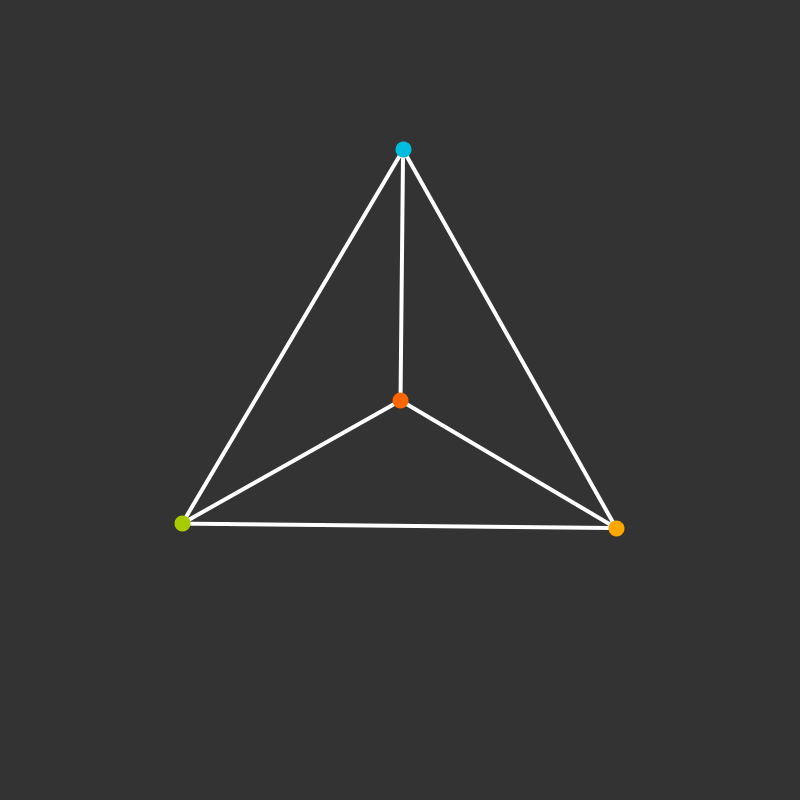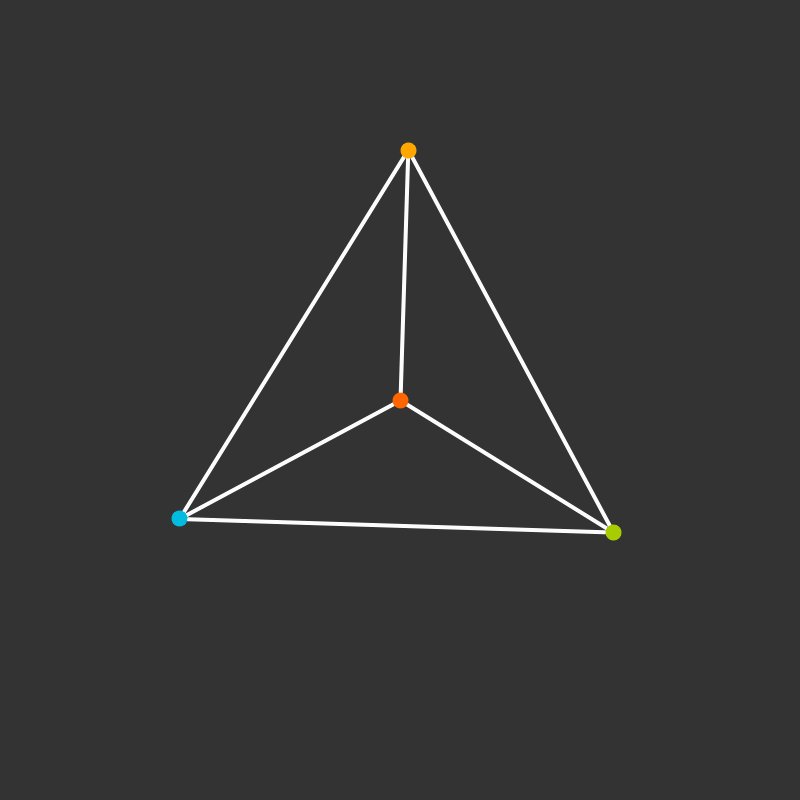
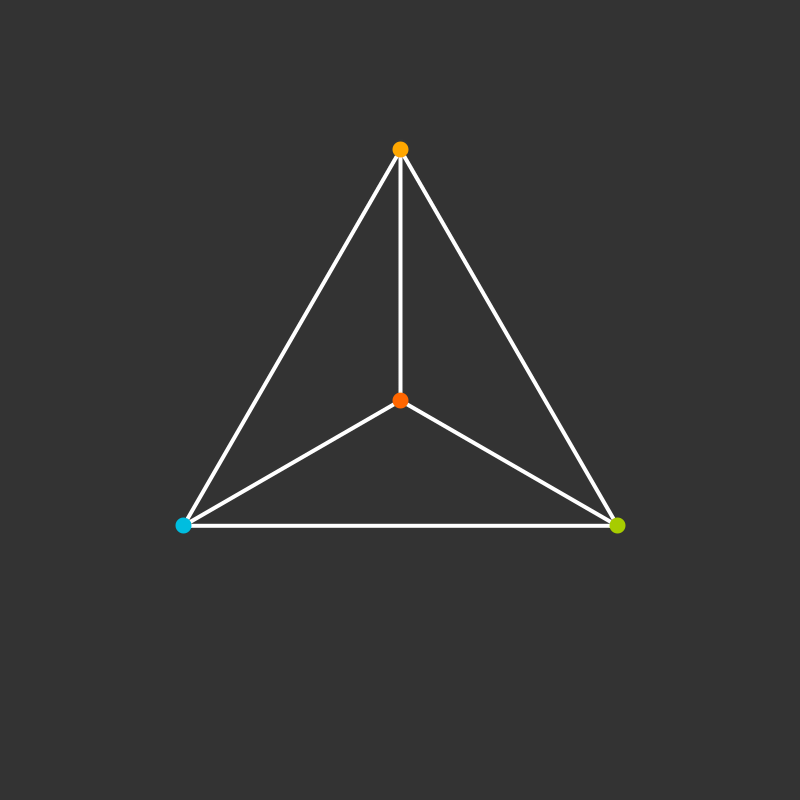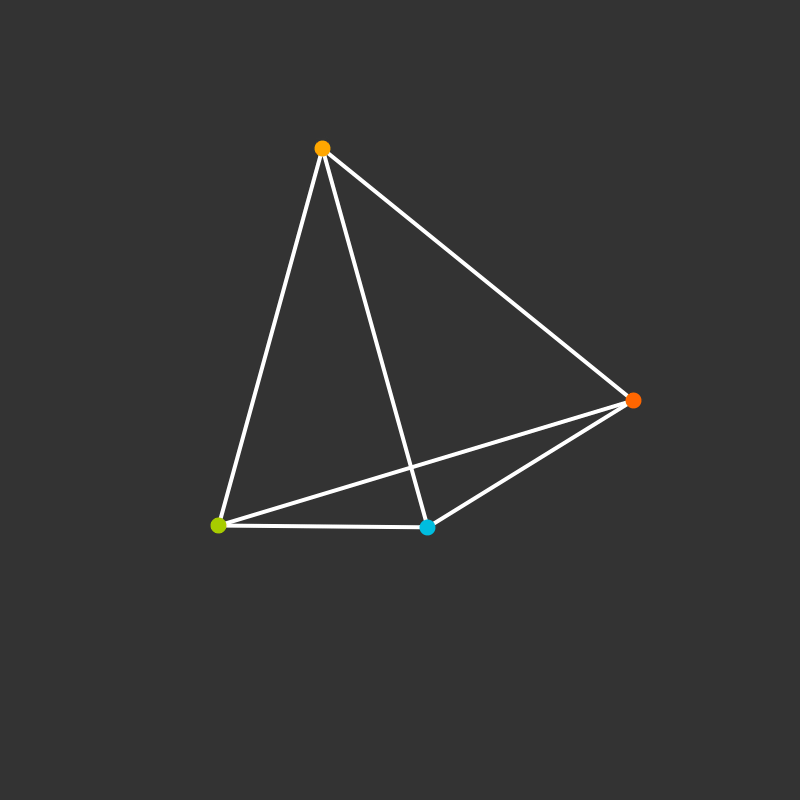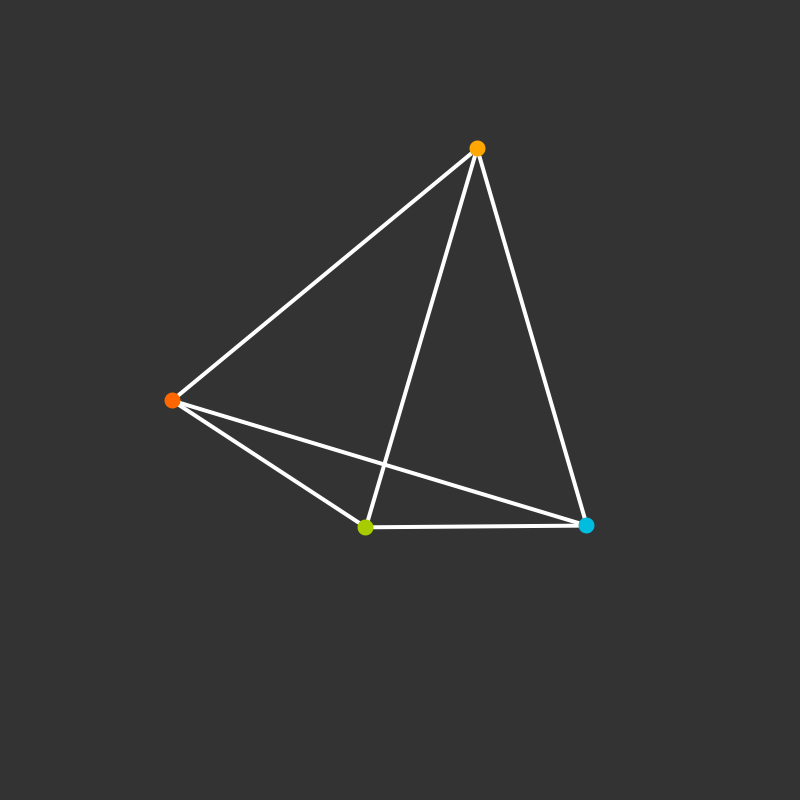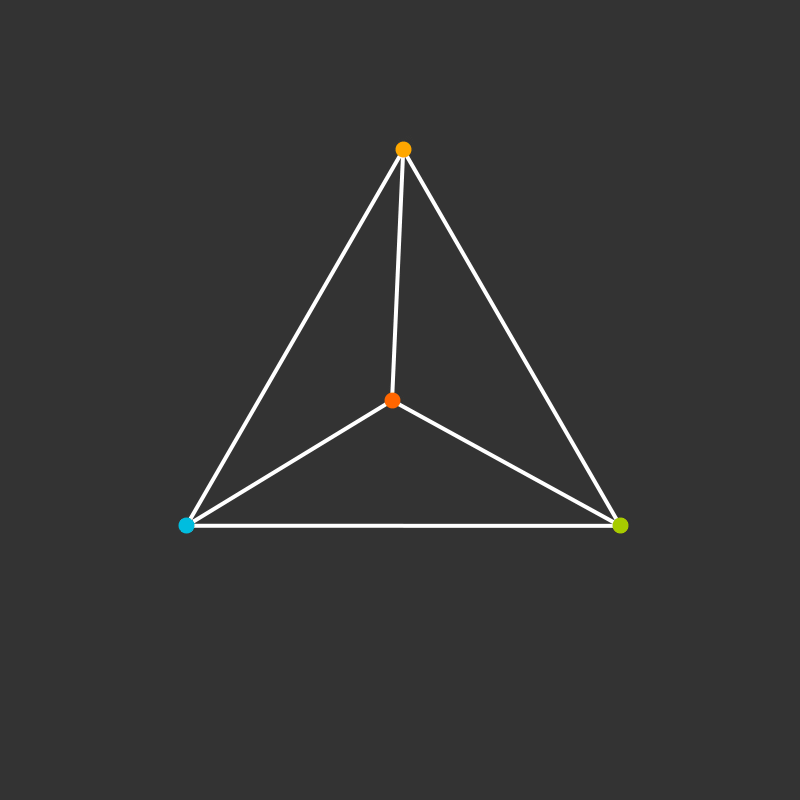
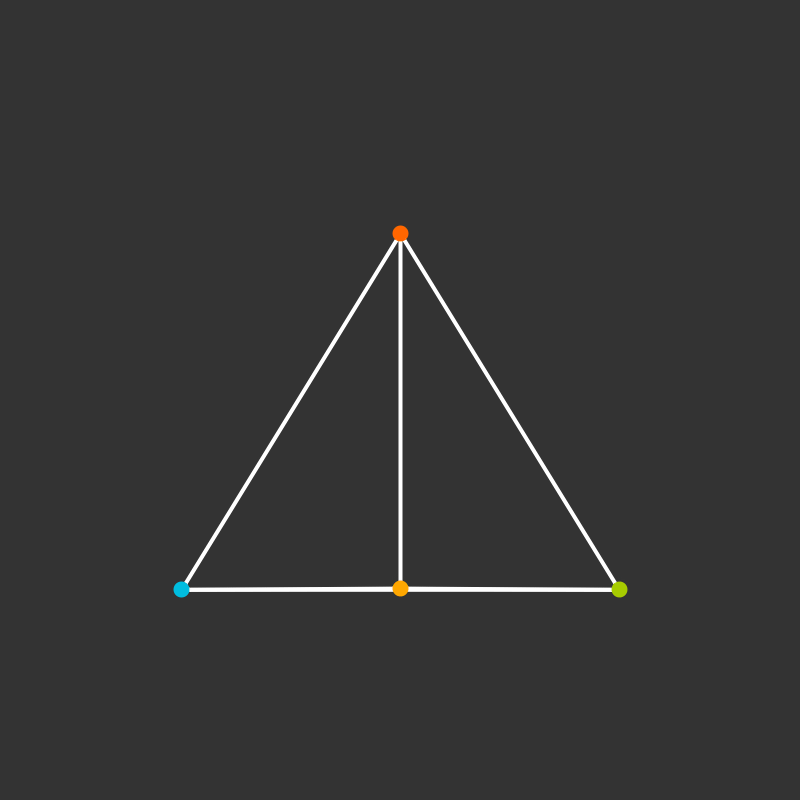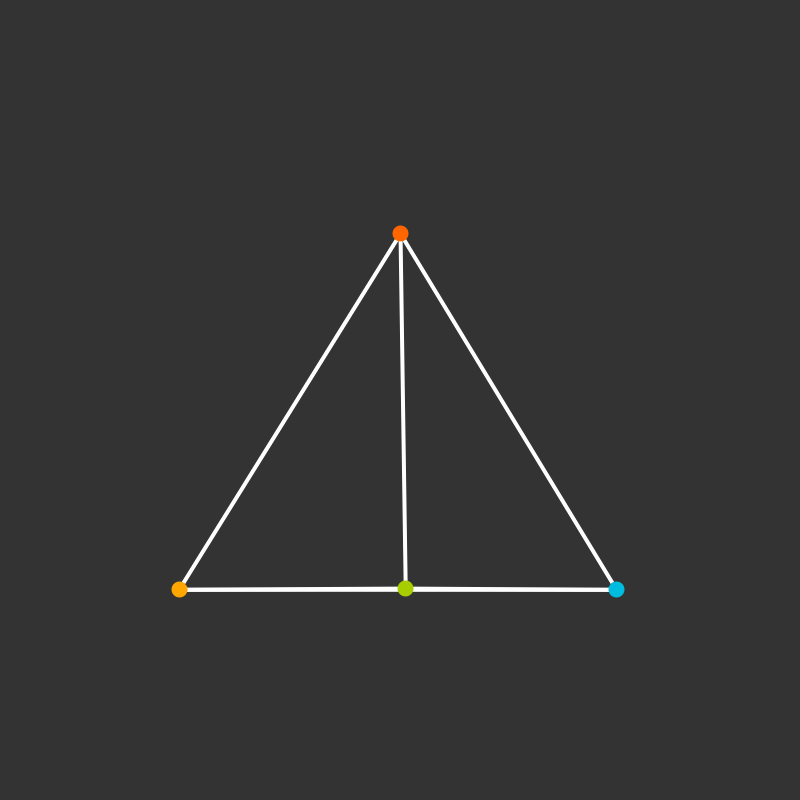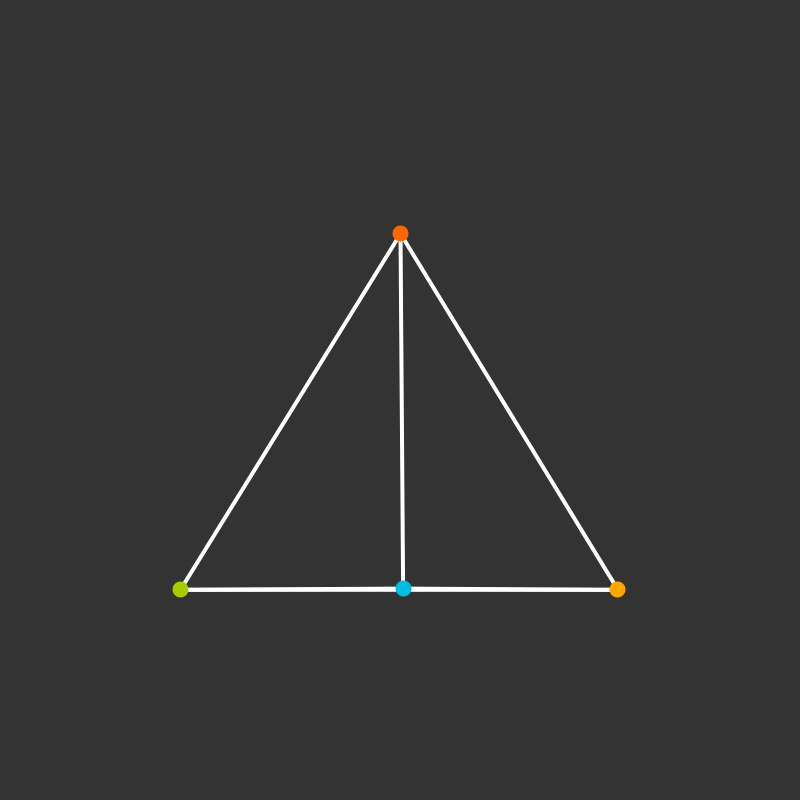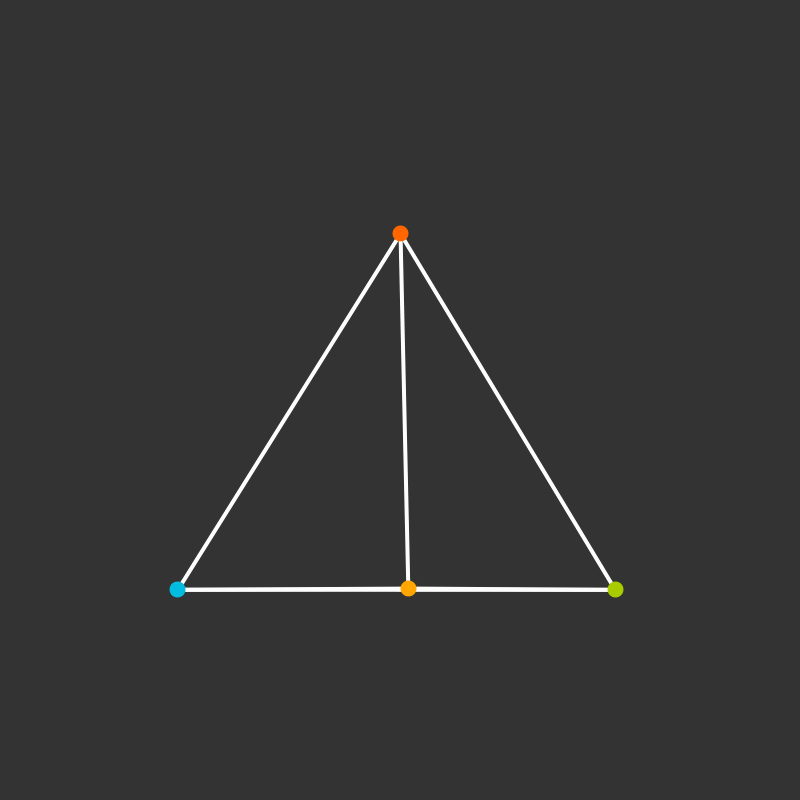
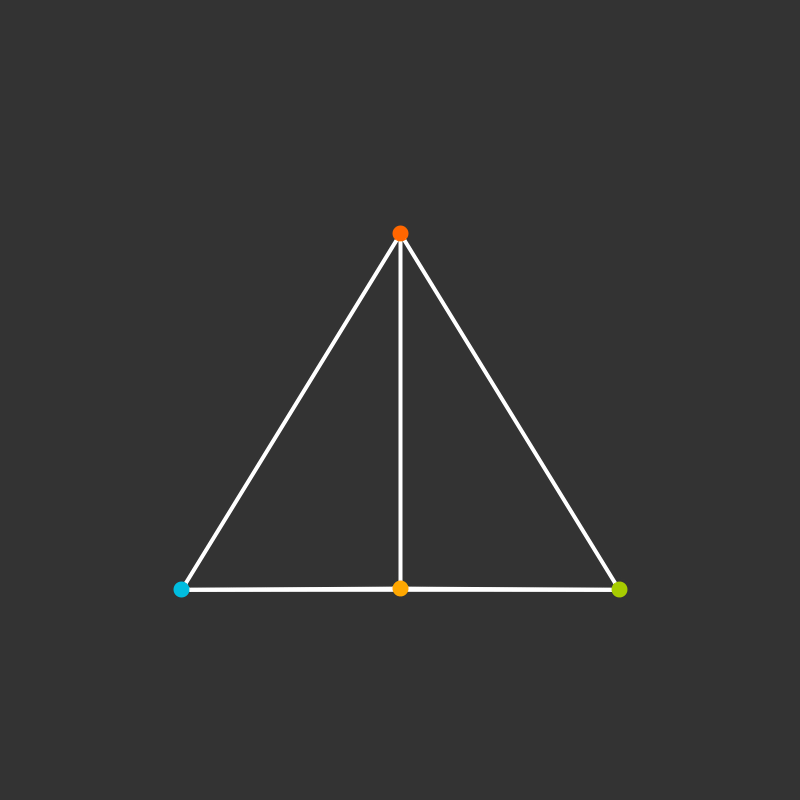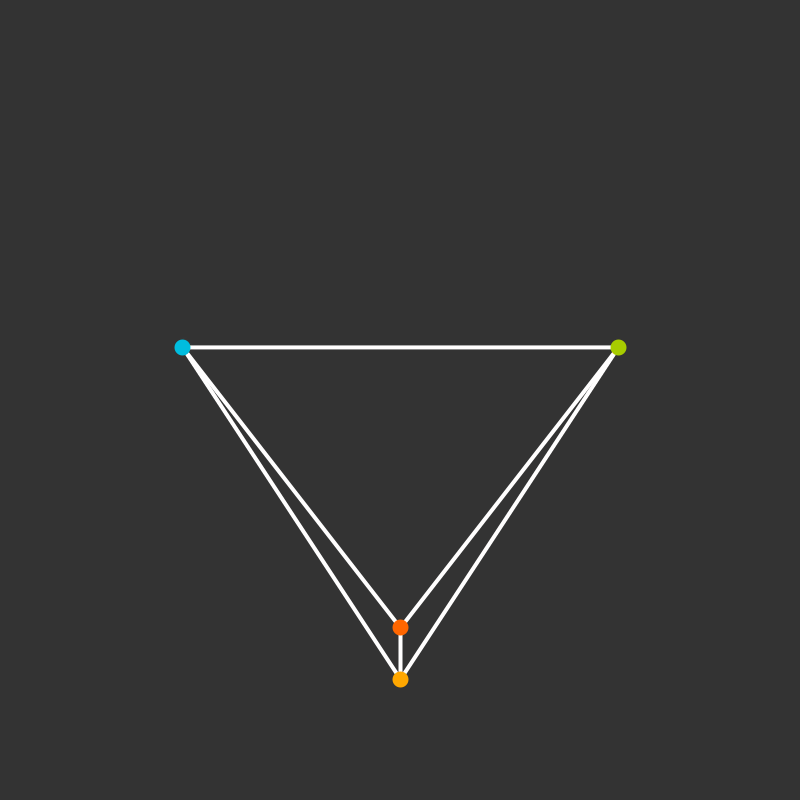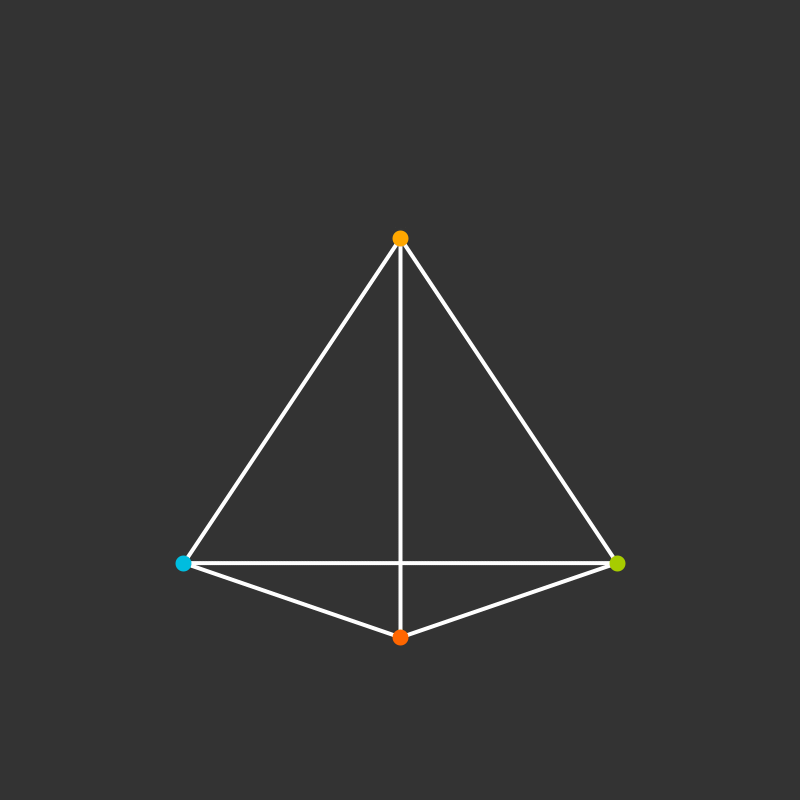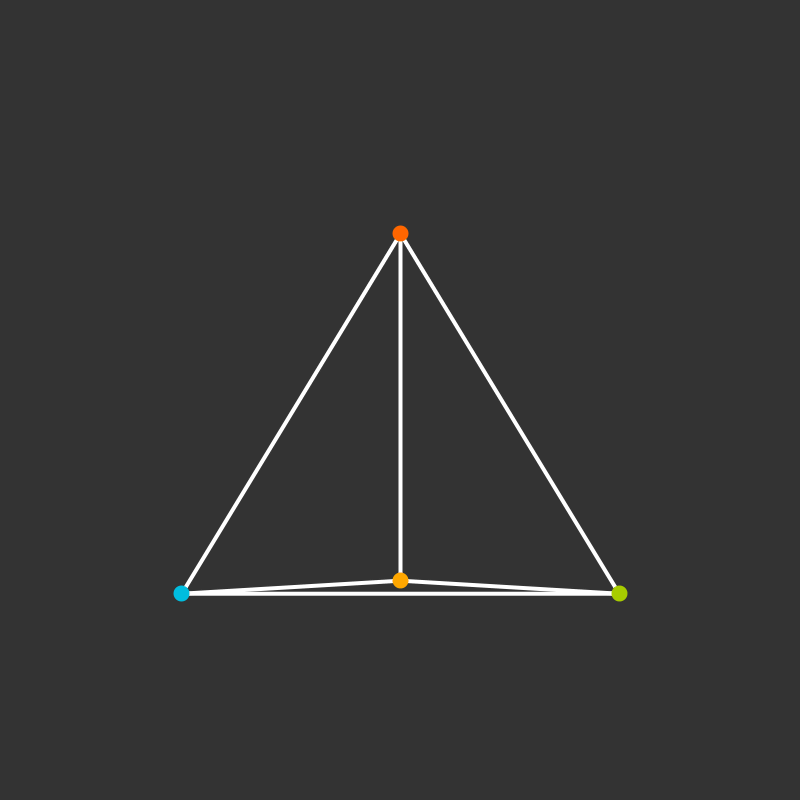
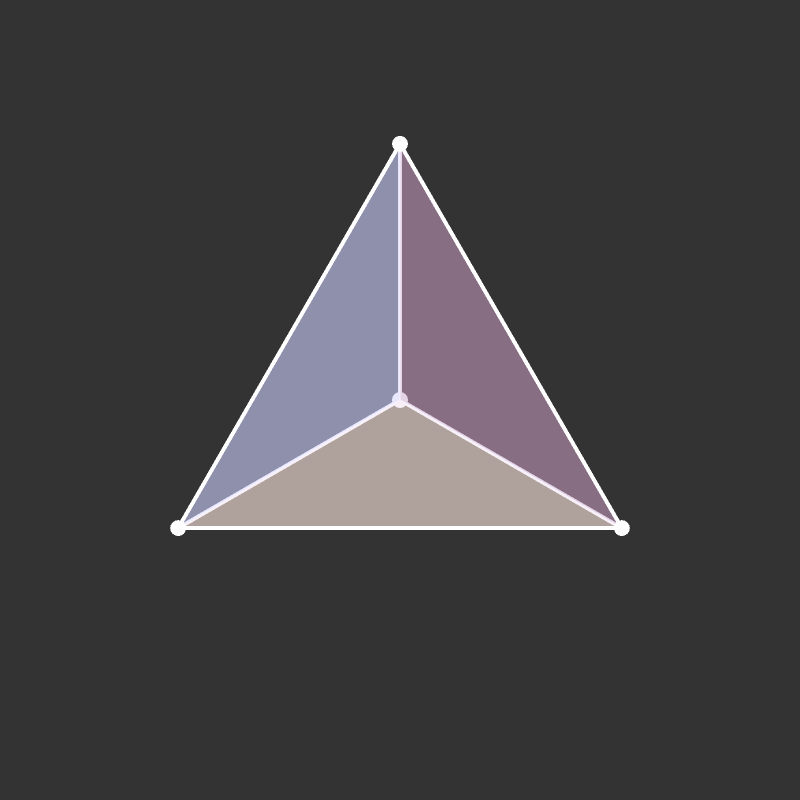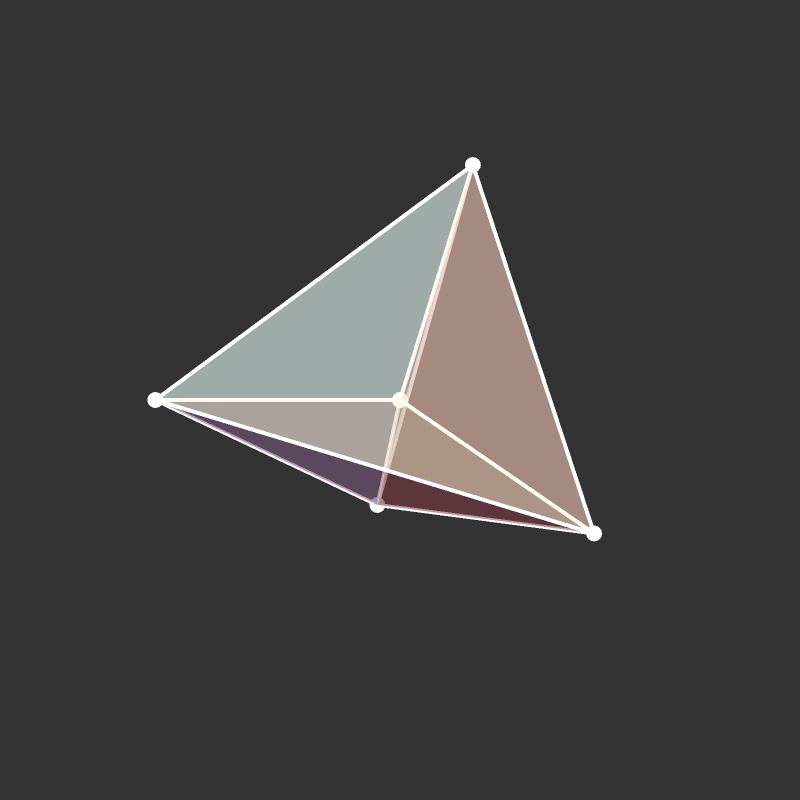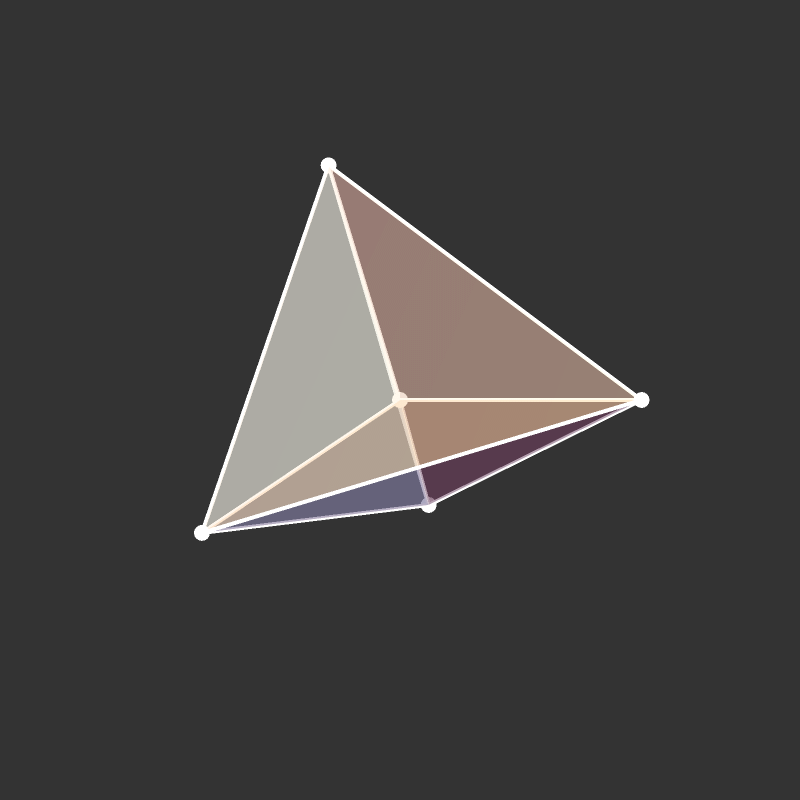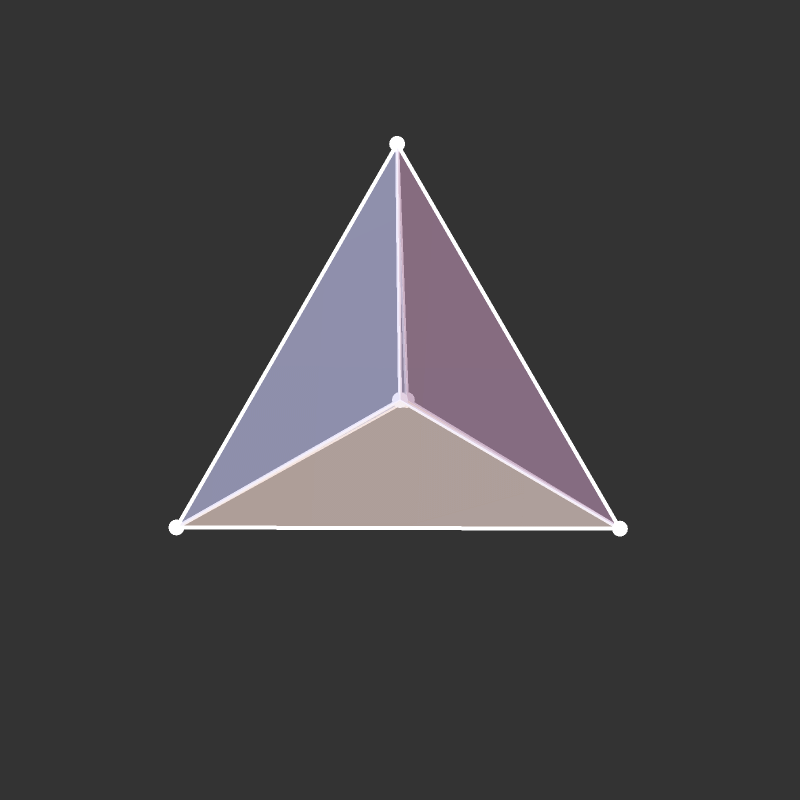

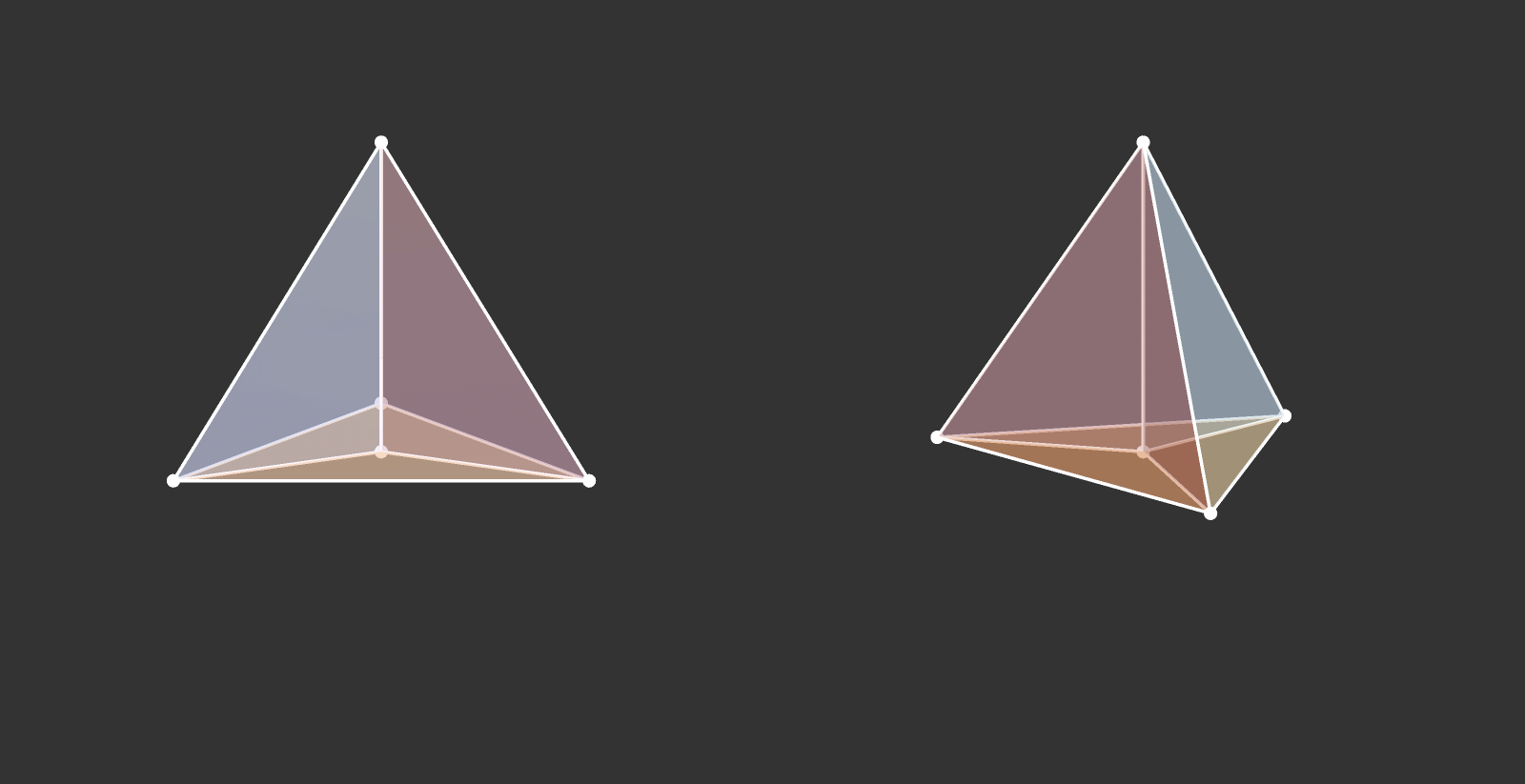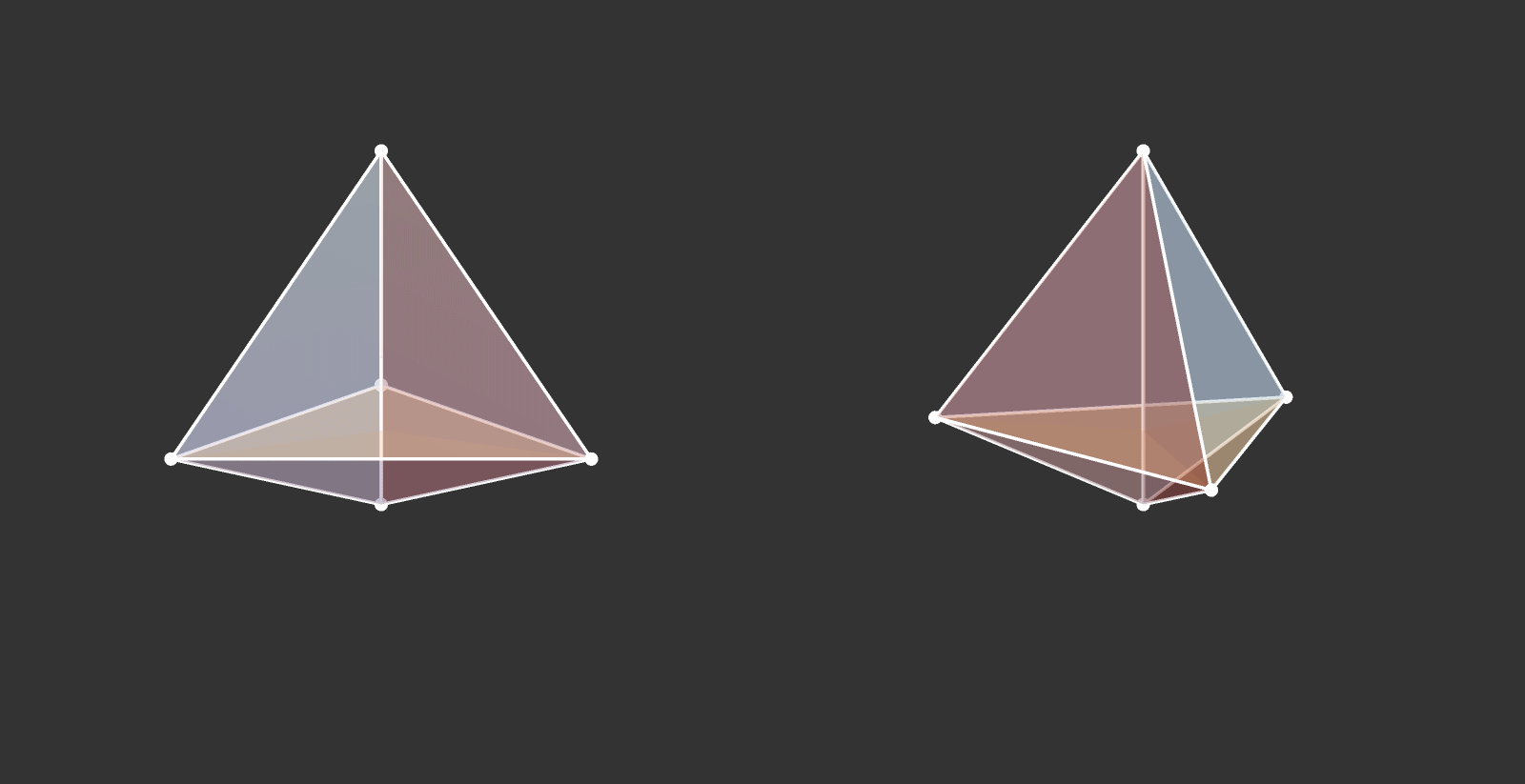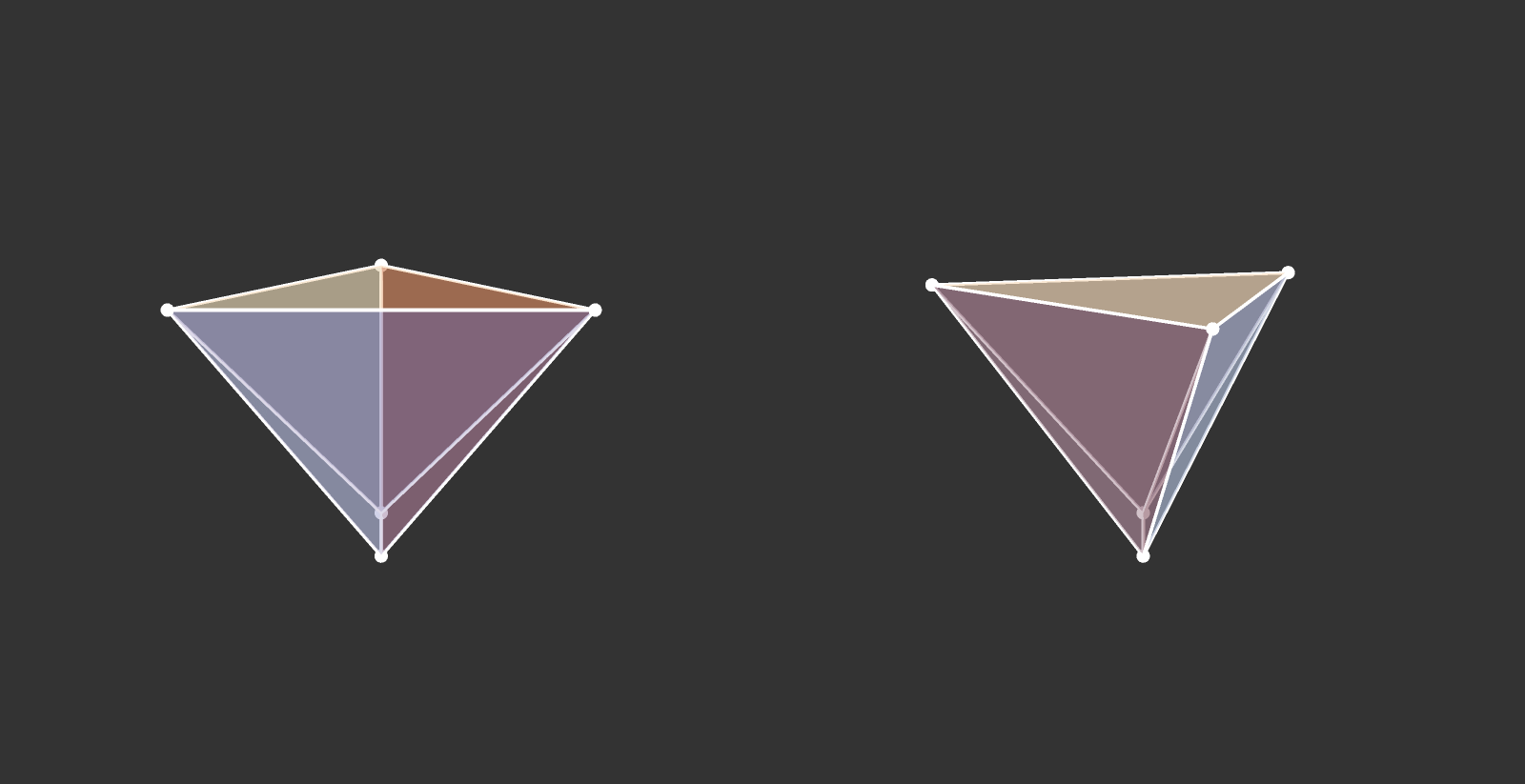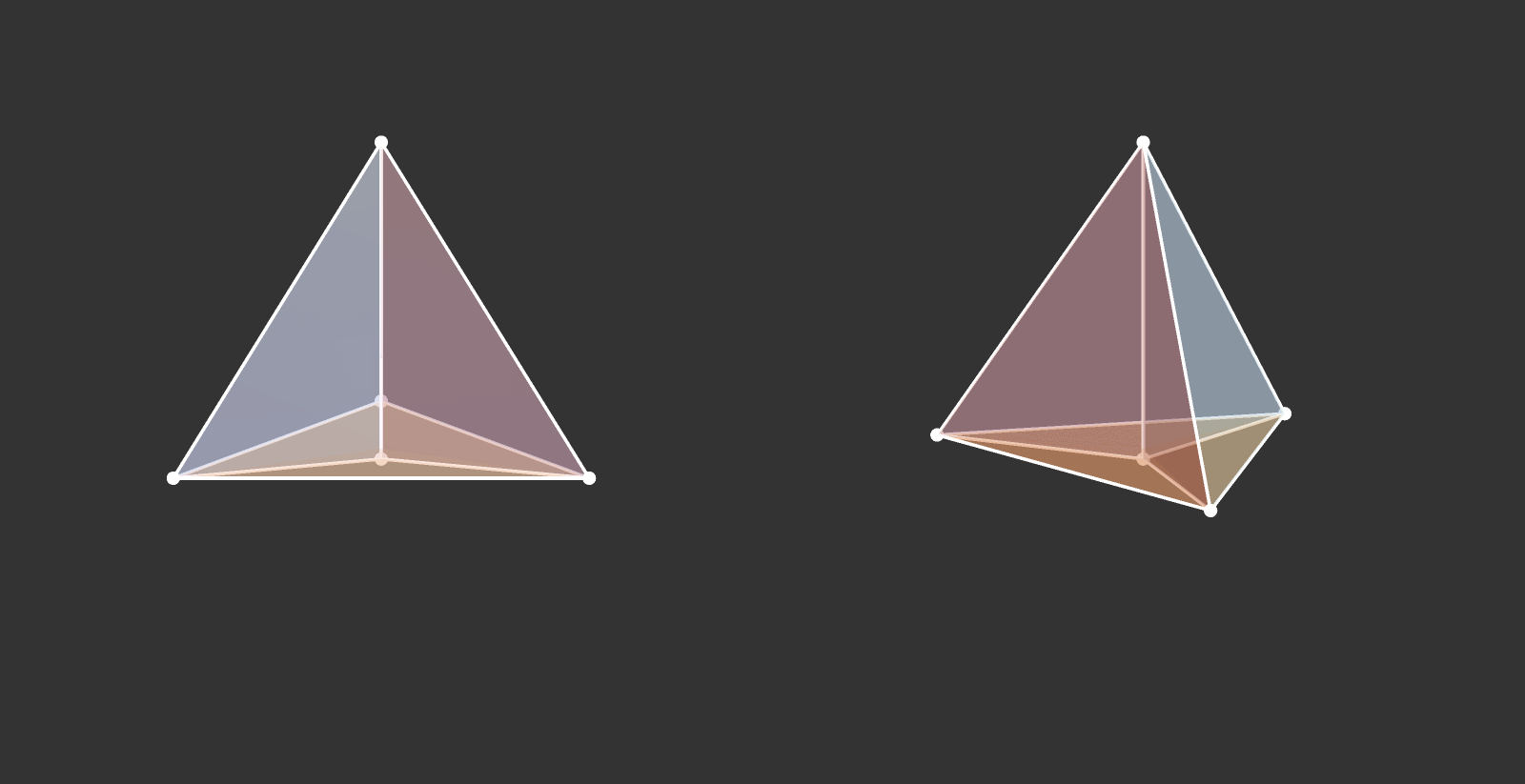
Some more visualizations of higher dimensions





Stereo[p_] := p[[;; -2]]/(1 + p[[-1]]);
vertices =
Normalize /@
DeleteDuplicates[
Flatten[
Permutations /@ ({-1, -1, 0, 0}^Join[#, {1, 1}] & /@
Tuples[{0, 1}, 2]), 1]];
edges = Select[Subsets[vertices, {2}],
#[[1]] != -#[[2]] && HammingDistance[#[[1]], #[[2]]] == 2 &];
smootheststep[t_] := -20 t^7 + 70 t^6 - 84 t^5 + 35 t^4;
With[{viewpoint = 100 Normalize[{1, 1 - Sqrt[2], 0}],
cols = RGBColor /@ {"#0CCA98", "#5E366A", "#201940"}},
Manipulate[
Graphics3D[{Thickness[.004],
Tube[#, .05] & /@
(Stereo[
RotationTransform[π/2 smootheststep[t], {{1, 1, 0,
0}, {0, 0, 1, 1}}][#]]
& /@ # & /@ edges)},
PlotRange -> 3.1, ImageSize -> {800, 600}, ViewPoint -> viewpoint,
ViewVertical -> {0, 0, 1}, Boxed -> False, ViewAngle -> π/300,
Lighting -> {{"Point", cols[[1]], {0, -3, 0}}, {"Point",
cols[[2]], {3, 0, 0}}, {"Ambient", cols[[-1]], viewpoint}},
Background -> cols[[-1]]],
{t, 0, 1}]]