Concavity, a question of Sylvester, and how to generate random quadrilaterals
/charleston2017
This talk!

Collaborators


Jason Cantarella
U. of Georgia
Tom Needham
Ohio State
Gavin Stewart
NYU

reentrant
J.J. Sylvester, Educational Times, April 1864
Sylvester’s Four Point Problem
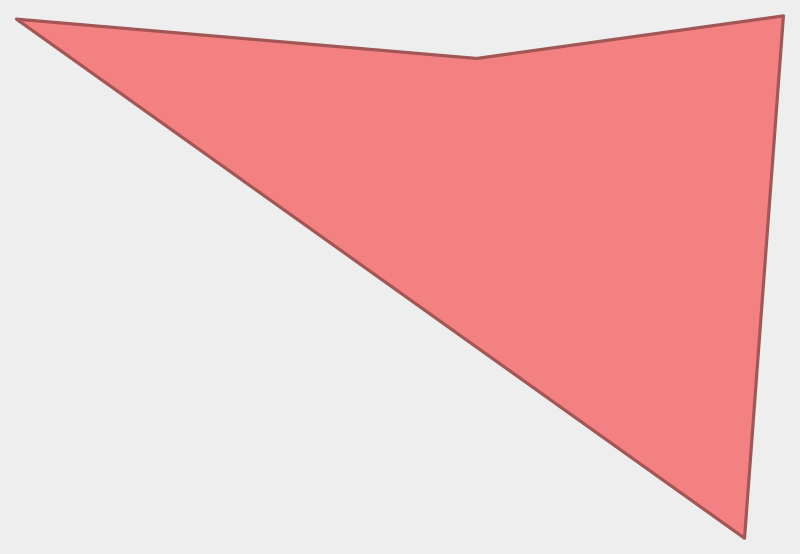
Sylvester and Cayley’s Solution

J.J. Sylvester, Phil. Trans. R. Soc. London 154 (1864), p. 654, footnote 64(b)
W.S.B. Woolhouse, Mathematical Questions with Their Solutions VII (1867), p. 81
A. De Morgan’s Solution

A. De Morgan, Trans. Cambridge Phil. Soc. XI (1871), pp. 147–148
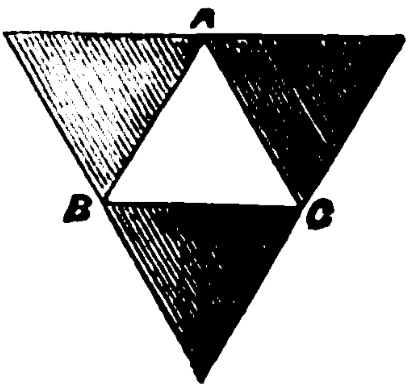
W.S.B. Woolhouse, Mathematical Questions with Their Solutions VI (1866), p. 52

C.M. Ingleby, Mathematical Questions with Their Solutions V (1865), p. 82
C.M. Ingleby’s Solution
G. C. De Morgan’s Solution

G.C. De Morgan, Mathematical Questions with Their Solutions V (1865), p. 109

W.S.B. Woolhouse’s Solution

W.S.B. Woolhouse, Mathematical Questions with Their Solutions VI (1866), p. 52
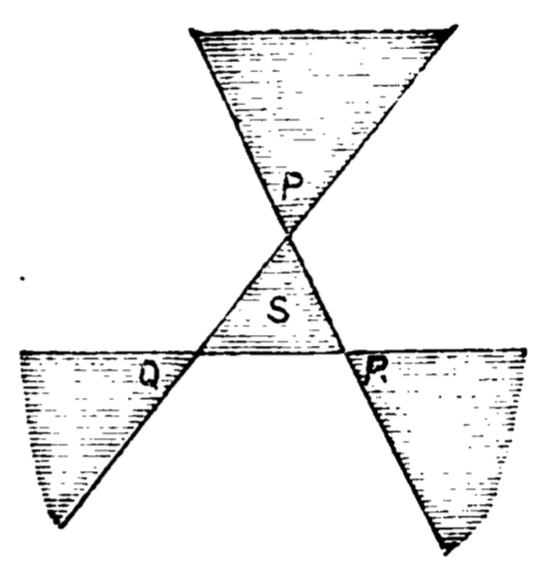
W.S.B. Woolhouse’s Solutions
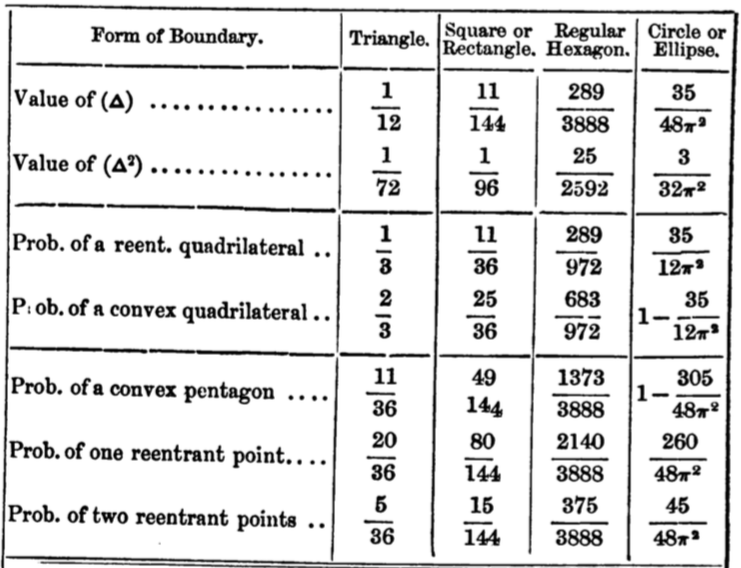
W.S.B. Woolhouse, Mathematical Questions with Their Solutions VIII (1868), p. 105
Quadrilaterals in Convex Bodies
\(\mathbb{P}(\text{reflex})=\frac{1}{3}\)
\(\mathbb{P}(\text{reflex})=\frac{35}{12\pi^2}\approx 0.296\)
Theorem [Blaschke, 1917]
\(\frac{35}{12\pi^2}\leq\mathbb{P}(\text{reflex})\leq\frac{1}{3}\)
J.M. Wilson’s Solution

J.M. Wilson, Mathematical Questions with Their Solutions V (1866), p. 81





We Need Measure Theory!
W.A. Whitworth, Mathematical Questions with Their Solutions VIII (1868), p. 36

Report on J.J. Sylvester’s presentation of his paper “On a Special Class of Questions on the Theory of Probabilities” to the British Association for the Advancement of Science, 1865
We Need Geometry!
Geometric Idea
The space of all quadrilaterals should be a (preferably compact) manifold \(Q\) with a transitive isometry group. We should use the left-invariant metric on \(Q\), scaled so vol\((Q)=1\). Then the Riemannian volume form induced by this metric is a natural probability measure on \(Q\), and we should compute the volume of the subset of reflex quadrilaterals.
Ideally, this construction should generalize to \(n\)-gons.
Spoiler: \(Q \simeq G_2\mathbb{R}^4\)
Polygons and Stiefel Manifolds
Let \(e_1, \ldots , e_n\) be the edges of a planar \(n\)-gon with total perimeter 2. Choose \(z_1, \ldots , z_n\) so that \(z_k^2 = e_k\). Let \(z_k = a_k + i b_k\).
The polygon is closed \(\Leftrightarrow e_1 + \ldots + e_n = 0\)
\(\sum e_k =\sum z_k^2 = \left(\sum a_k^2 - \sum b_k^2\right) + 2i \sum a_k b_k\)
The polygon is closed \(\Leftrightarrow \|a\|=\|b\|\) and \(a \bot b\)
Since \(\sum |e_k| = \sum a_k^2 + \sum b_k^2 = \|a\|^2 + \|b\|^2\), we see that \((a,b) \in V_2(\mathbb{R}^n)\), the Stiefel manifold of 2-frames in \(\mathbb{R}^n\).
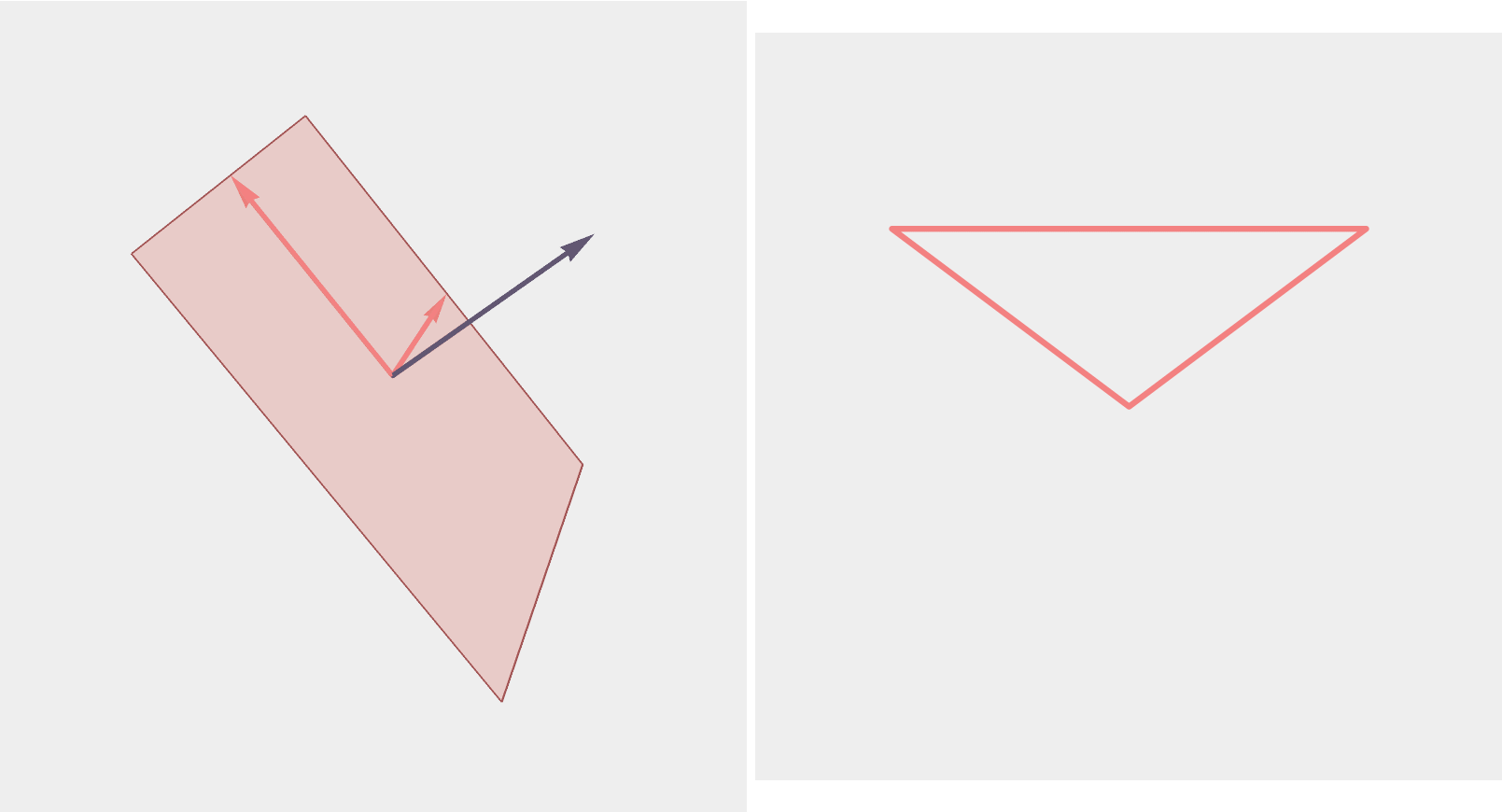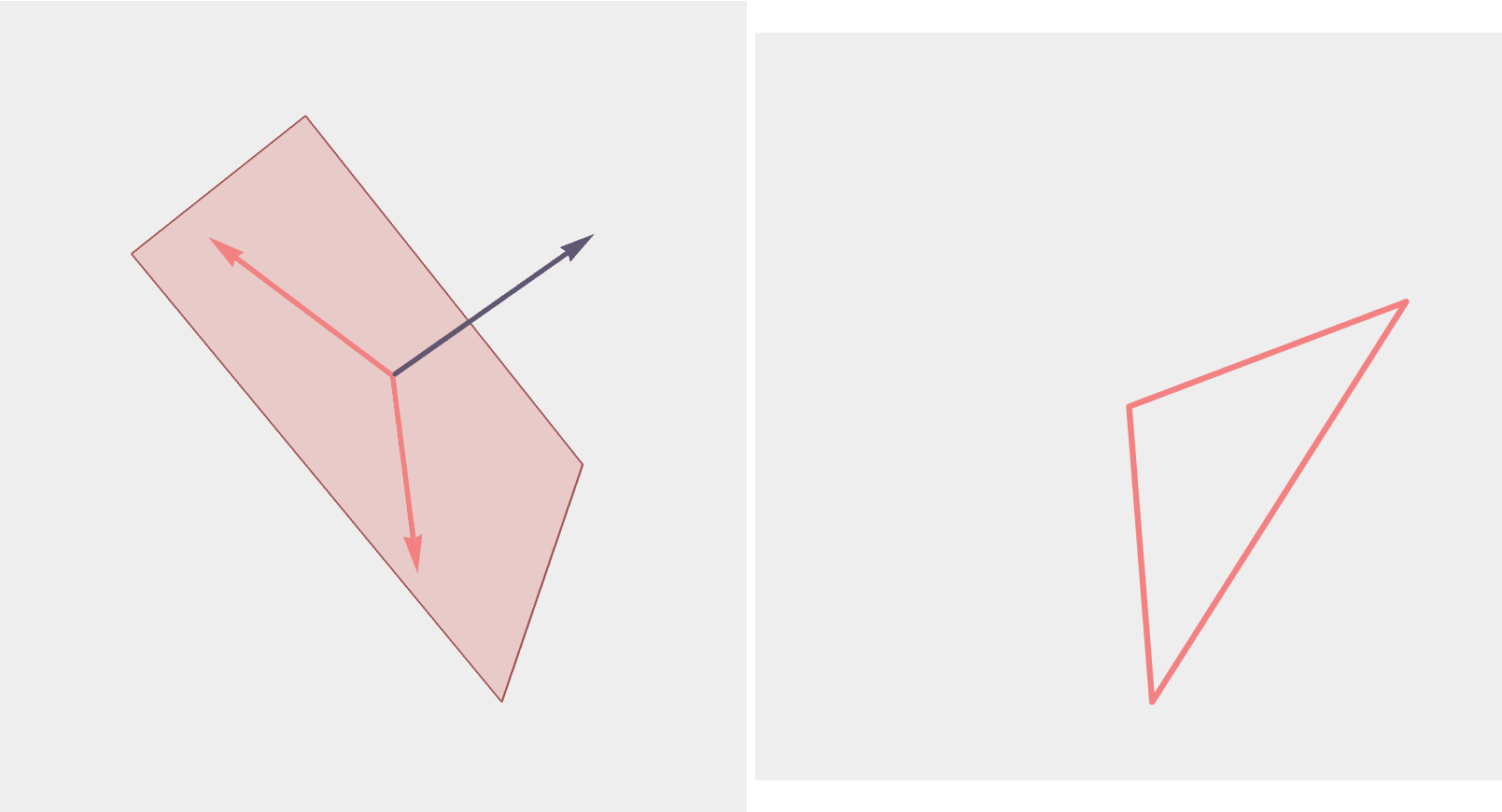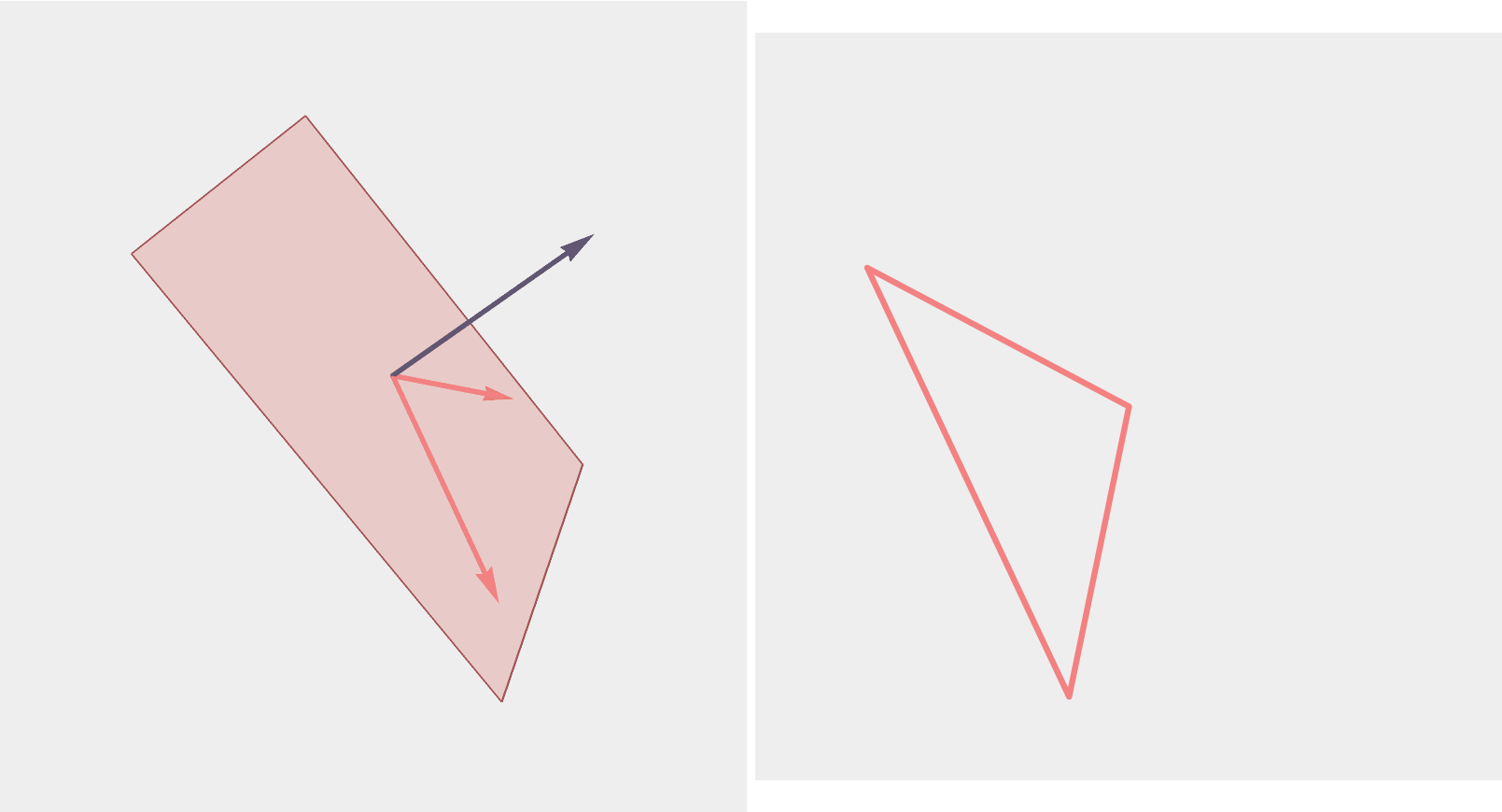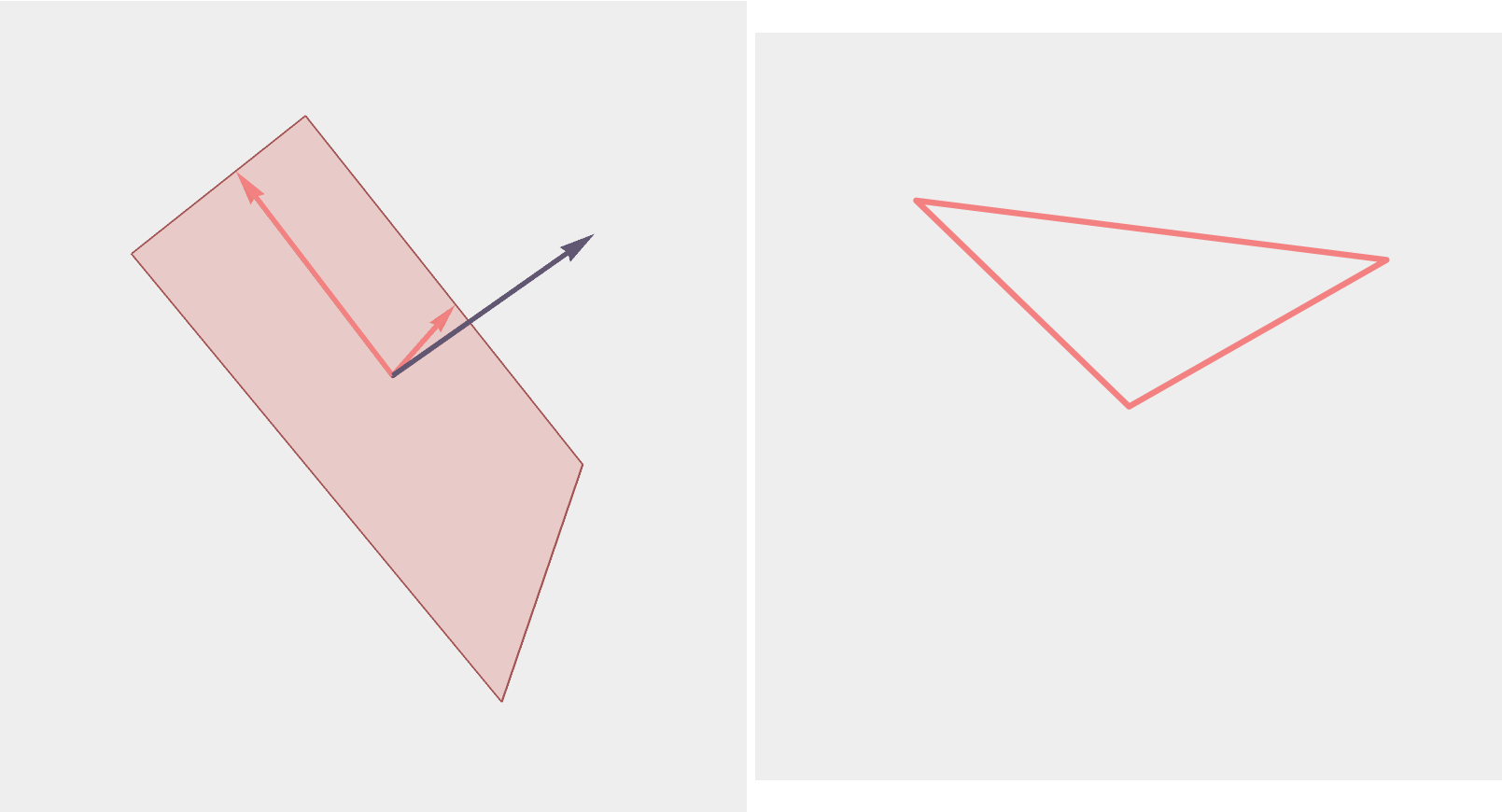
Polygons and Grassmannians
Proposition: Rotating \((a,b)\) in the plane it spans rotates the corresponding \(n\)-gon twice as fast.
Corollary [Hausmann–Knutson]
The Grassmannian \(G_2(\mathbb{R}^n)\) is (almost) a \(2^n\)-fold covering of the space of planar \(n\)-gons of perimeter 2.
The Symmetric Measure
Definition [w/ Cantarella & Deguchi]
The symmetric measure on \(n\)-gons of perimeter 2 up to translation and rotation is the pushforward of Haar measure on \(G_2(\mathbb{R}^n)\).
Therefore, \(SO(n)\) acts transitively on \(n\)-gons and preserves the symmetric measure.
A Hyperoctahedral Group Action
A polygon corresponds to \(\begin{bmatrix} a_1 & b_1 \\ a_2 & b_2 \\ \vdots & \vdots \\ a_n & v_n \end{bmatrix}\), where \((a_k + i b_k)^2 = e_k\).
\((a_k,b_k)\mapsto(-a_k,-b_k)\) doesn’t change the polygon, so \((\mathbb{Z}/2\mathbb{Z})^n\) acts trivially on polygons.
\(S_n \le SO(n)\) permutes rows and hence edges.
The hyperoctahedral group \(B_n = (\mathbb{Z}/2\mathbb{Z})^n \rtimes S_n\) acts by isometries on \(G_2(\mathbb{R}^n)\) and permutes edges.
\(|B_n| = 2^n n!\); e.g., \(|B_4| = 2^4 4! = 384\).
Proposition [with Cantarella, Needham, Stewart]
- The fundamental domain \(\mathcal{D}_n\) of the \(B_n\) action on \(G_2(\mathbb{R}^n)\) consists of (certain lifts of) the convex \(n\)-gons in which all pairs of adjacent or opposite sides form oriented bases in the same class.
- The stabilizer of \(\mathcal{D}_4\) has order 4, so \(G_2(\mathbb{R}^4)\) is built from 96 isometric copies of \(\mathcal{D}_4\).
- Each of these 96 cells consists of all convex, all reflex, or all self-intersecting quadrilaterals.
- \(\mathcal{D}_4\) is path-connected.
Upshot: We can count how many elements of the permutation orbit of a single element of \(\mathcal{D}_4\) are convex, reflex, and self-intersecting.
Volumes via Algebra
The Average Convex Quadrilateral
The flag mean of \(\mathcal{D}_4\).
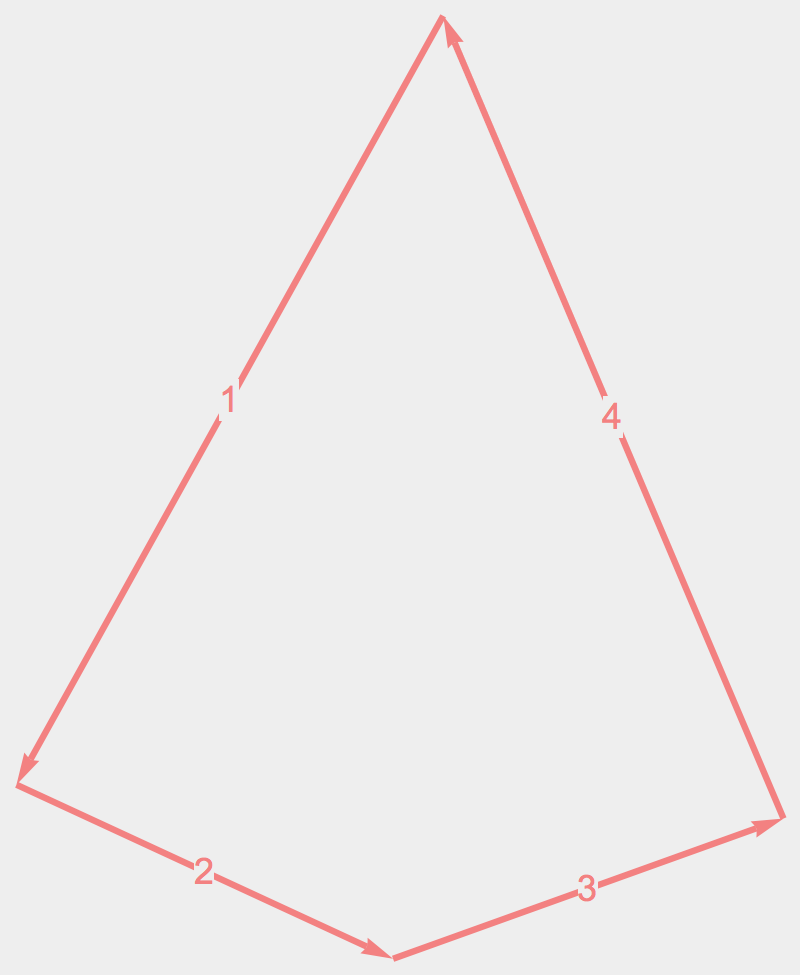
The Symmetric Group Orbit
Theorem [with Cantarella, Needham, Stewart]
Convex, reflex, and self-intersecting quadrilaterals are all equiprobable.

A Partial Generalization
Theorem [with Cantarella, Needham, Stewart]
With respect to any measure on \(n\)-gon space which is invariant under permuting edges, the fraction of convex \(n\)-gons is exactly \(\frac{2}{(n-1)!}\).

Quadrilaterals are Special
\(G_2(\mathbb{R}^n)\) has more symmetry than expected:
If \(P \in G_2(\mathbb{R}^4)\), then \(P^\bot \in G_2(\mathbb{R}^4)\) as well.
The map \(P \mapsto P^\bot\) is an isometry of \(G_2(\mathbb{R}^4)\) which is a fixed-point free involution.
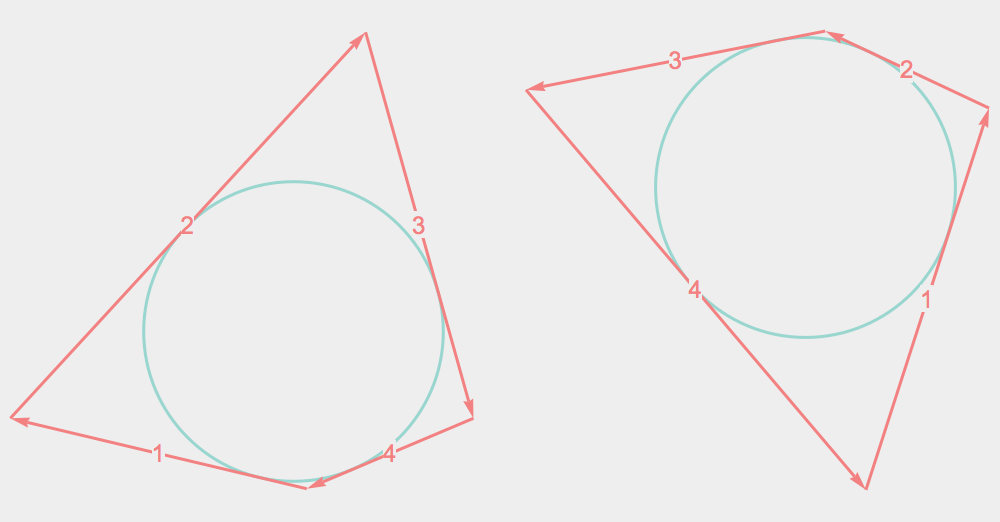
This induces a duality map on quadrilaterals...
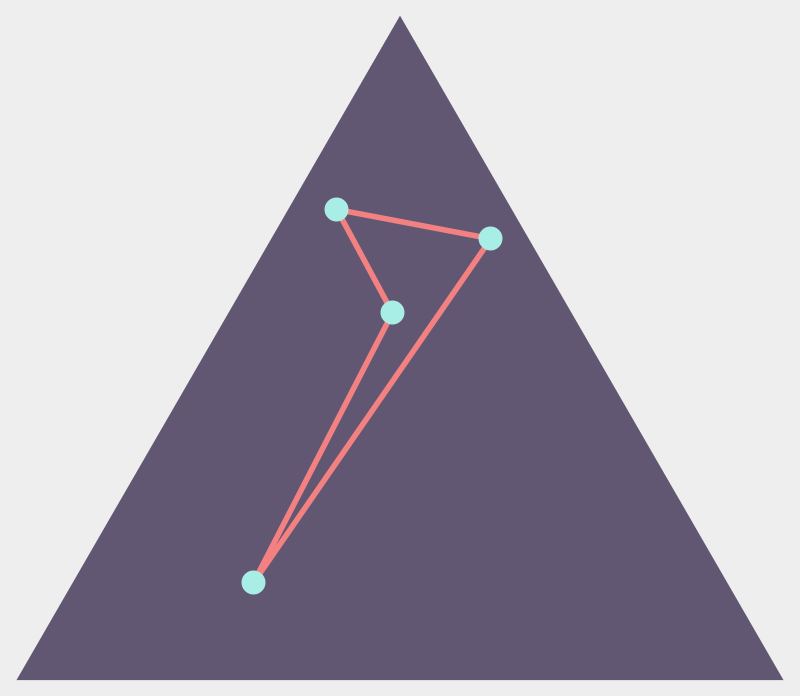
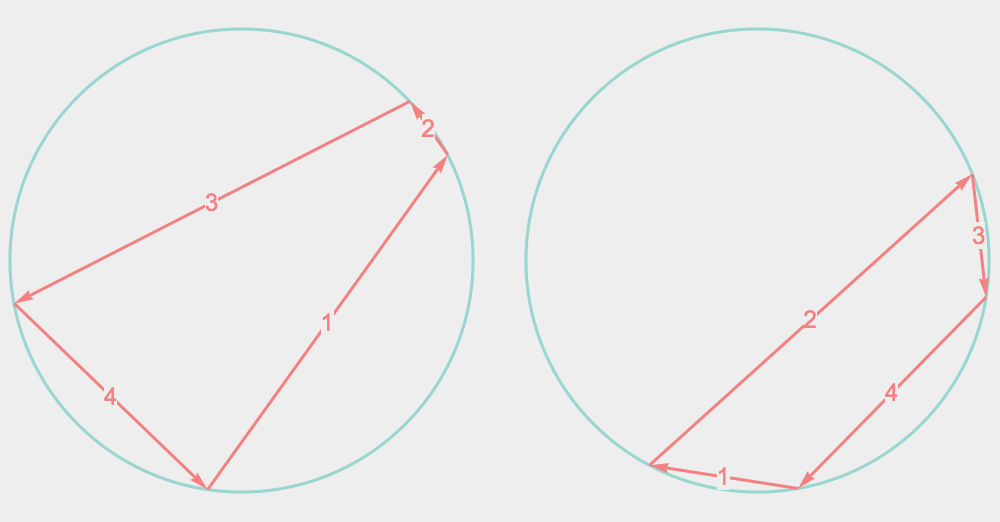
Some Random Quadrilaterals and Their Duals

Proposition
Duality preserves the three classes of quadrilaterals: convex, reflex, and self-intersecting.
Neat Fact I
Proposition
For any permutation \(\{i,j,k,\ell\}\) of \(\{1,2,3,4\}\), taking duals conserves the equation
\(|e_i|+|e_j| = |e_k| + |e_\ell|\).
Corollary
Duals of tangential quadrilaterals are tangential.
Neat Fact II
Corollary
Duals of cyclic quadrilaterals are cyclic.
Proposition
For any permutation \(\{i,j,k,\ell\}\) of \(\{1,2,3,4\}\), taking duals conserves the equation
\(\theta_i + \theta_j = \theta_k + \theta_\ell\).
Neat Fact III
Proposition
Let \(e_1,e_2,e_3,e_4\) be the edge vectors of a quadrilateral and let \(\psi_{ij}\) be the (exterior) angle between \(e_i\) and \(e_j\).
Let \(f_1,f_2,f_3,f_4\) be the edge vectors of the dual quadrilateral and let \(\varphi_{ij}\) be the angle between \(f_i\) and \(f_j\).
Then \(|f_i| = 1- |e_i|\) for each \(i\) and
\(\cos(\varphi_{ij}) = 1-(1-\cos(\psi_{k\ell})) \frac{|e_k||e_\ell|}{|f_i||f_j|}\)
for any permutation \(\{i,j,k,\ell\}\) of \(\{1,2,3,4\}\).
Open Questions
- Is there an elementary quadrilateral-based description of duality?
- What do geodesics on \(G_2(\mathbb{R}^4) \simeq S^2 \times S^2\) look like at the level of quadrilaterals?
- What is the geometric description and interpretation of the hyperoctahedral group action on \(n\)-gons?
- What is the corresponding theory of equilateral planar polygons?
Theorem [Baxter]
The expected number of vertices on the convex hull of a random \(n\)-gon is
A Conjecture on Convex Hulls
Conjecture
The expected perimeter of the convex hull of a random \(n\)-gon is
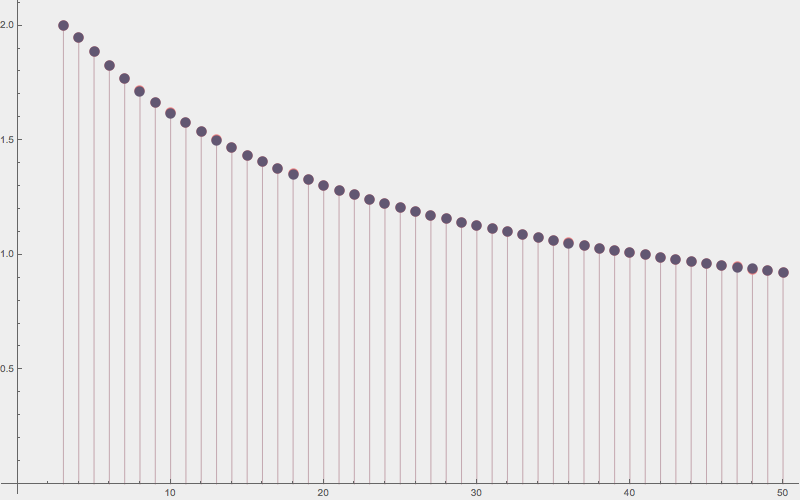
Conjecture vs. sample average (100,000 samples)
Conjecture
The expected perimeter of the convex hull of a random \(n\)-gon is




Thank you!
References
Probability Theory of Random Polygons from the Quaternionic Perspective
J. Cantarella, T. Deguchi, and C. Shonkwiler
Communications on Pure and Applied Mathematics 67
(2014), no. 10, 1658–1699
Random Triangles and Polygons in the Plane
J. Cantarella, T. Needham, C. Shonkwiler, and G. Stewart
arXiv: 1702.01027