What’s the probability that a random triangle is obtuse?
or:
What the heck is a random triangle, anyway?
Clayton Shonkwiler
Colorado State University
09.15.16

Collaborators


Jason Cantarella
U. of Georgia
Thomas Needham
Ohio State
Gavin Stewart
NYU

Lewis Carroll's Pillow Problem #58
Carroll’s Answer
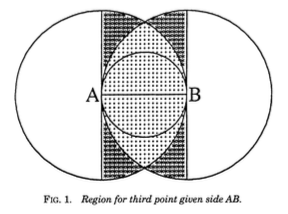
Suppose \(AB\) is the longest side. Then
\(\mathbb{P}(\text{obtuse})=\frac{\pi/8}{\pi/3-\sqrt{3}/4} \approx 0.64\)
But if \(AB\) is the second longest side,
\(\mathbb{P}(\text{obtuse}) = \frac{\pi/2}{\pi/3+\sqrt{3}/2} \approx 0.82\)
Text
A Probabilist’s Answer
Proposition [Portnoy]: If the distribution of \((x_1,y_1,x_2,y_2,x_3,y_3)\in\mathbb{R}^6\) is spherically symmetric (for example, a standard Gaussian), then
\(\mathbb{P}(\text{obtuse}) = \frac{3}{4}\)
Consider the vertices \((x_1,y_1),(x_2,y_2),(x_3,y_3)\) as determining a single point in \(\mathbb{R}^6\).
For example, when the vertices of the triangle are chosen from independent, identically-distributed Gaussians on \(\mathbb{R}^2\).
And more...
Three vertices uniformly in the disk:
\(\mathbb{P}(\text{obtuse})=\frac{9}{8}-\frac{4}{\pi^2}\approx 0.72\)
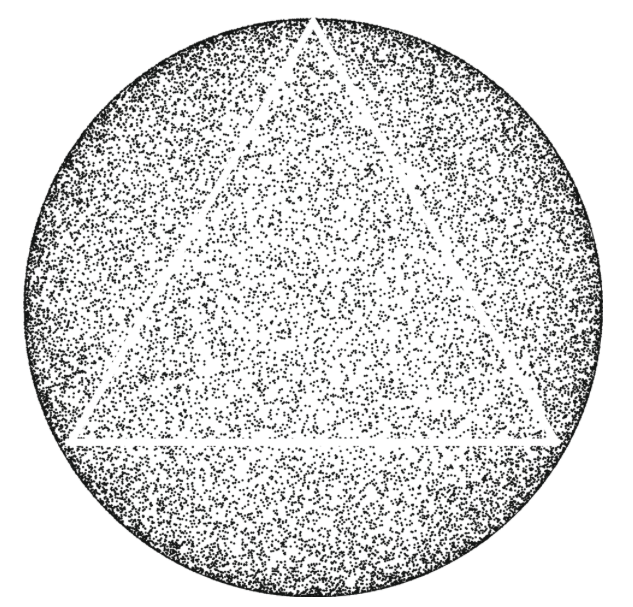
[Edelman–Strang]: Normalize sides so \(a^2+b^2+c^2=1\):
\(\mathbb{P}(\text{obtuse})=\frac{3}{4}\)

— Stephen Portnoy, Statistical Science 9 (1994), 279–284
Random Triangles...?
Translation for Geometers
The space of all triangles should be a (preferably compact) manifold \(T\) with a transitive isometry group. We should use the left-invariant metric on \(T\), scaled so vol\((M)=1\). Then the Riemannian volume form induced by this metric is a natural probability measure on \(T\), and we should compute the volume of the subset of obtuse triangles.
Ideally, this should generalize to \(n\)-gons.
Spoiler: \(T\simeq\mathbb{RP}^2=G_2\mathbb{R}^3\)
Observations
- The sidelengths \((a,b,c)\) uniquely determine a triangle (remember SSS from high school)
- Obtuseness is scale-invariant
Idea
Rescale so that \(a+b+c=2\); then a triangle shape is uniquely specified by a point in the simplex.
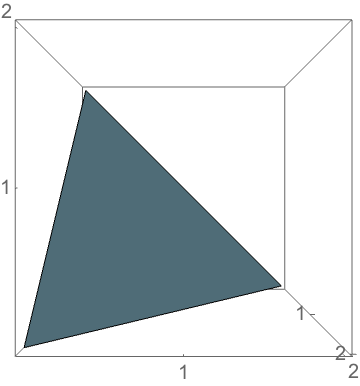
Problem
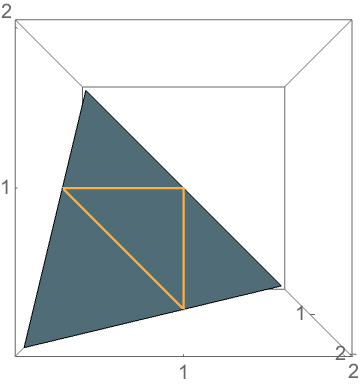
Not all points in the simplex correspond to triangles
\(b+c<a\)
\(a+b<c\)
\(a+c<b\)
Yet Another Pillow Problem Answer
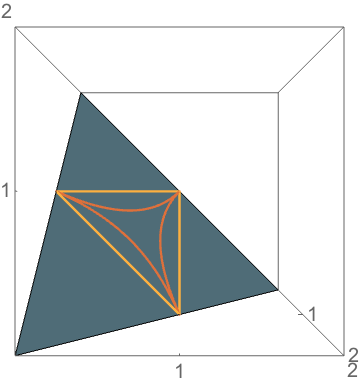
\(\mathbb{P}(\text{obtuse})=9-12\ln 2 \approx 0.68\)
\(b^2+c^2=a^2\)
\(a^2+b^2=c^2\)
\(a^2+c^2=b^2\)
A Change of Coordinates
Let \(s=\frac{1}{2}(a+b+c)\) and define

Note: This is why we chose the normalization \(a+b+c=2\)
\(s_a=s-a, \quad s_b = s-b, \quad s_c = s-c\)
Then
\(s_a+s_b+s_c=3s-(a+b+c)=3s-2s=s\)
and the triangle inequalities become
\(s_a>0, \quad s_b > 0, \quad s_c > 0\)
Text
The Same Answer Again
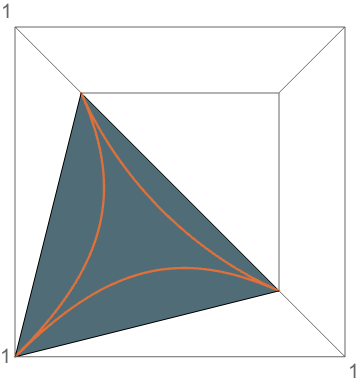
\((1-s_a)^2+(1-s_b)^2=(1-s_c)^2\)
\(\mathbb{P}(\text{obtuse})=9-12\ln 2 \approx 0.68\)
But there’s no transitive group...
Take Square Roots!
Consider \((x,y,z)\) so that
\(x^2=s_a, \quad y^2 = s_b, \quad z^2 = s_c\)
The unit sphere is a \(2^3\)-fold cover of triangle space

The Transitive Group
\(SO(3)\) obviously acts transitively on the sphere, and the corresponding action on triangles is natural.
\(c=1-z^2\) fixed
\(z\) fixed
\(C(\theta) = (\frac{z^2+1}{2}\cos 2\theta, z \sin 2\theta)\)

A Measure on Triangle Space
Since the uniform measure is the unique (up to scale) measure on \(S^2\) invariant under the action of \(SO(3)\)...
Definition
The symmetric measure on triangle space is the probability measure proportional to the uniform measure on the sphere.
Right Triangles
The right triangles are exactly those satisfying
\(a^2+b^2=c^2\) & permutations
Since \(a=1-s_a=1-x^2\), etc., the right triangles are determined by the quartic
\((1-x^2)^2+(1-y^2)^2=(1-z^2)^2\) & permutations
\(x^2 + x^2y^2 + y^2 = 1\), etc.

Obtuse Triangles
\(\mathbb{P}(\text{obtuse})=\frac{1}{4\pi}\text{Area} = \frac{24}{4\pi} \int_R d\theta dz\)


But now \(C\) has the parametrization
And the integral reduces to
Solution to the Pillow Problem
By Stokes’ Theorem

\(\frac{6}{\pi} \int_R d\theta dz=\frac{6}{\pi}\int_{\partial R}z d\theta = \frac{6}{\pi}\left(\int_{z=0} zd\theta + \int_C zd\theta \right)\)
\(\left(\sqrt{\frac{1-y^2}{1+y^2}},y,y\sqrt{\frac{1-y^2}{1+y^2}}\right)\)
\(\frac{6}{\pi} \int_0^1 \left(\frac{2y}{1+y^4}-\frac{y}{1+y^2}\right)dy\)
Our Answer
Theorem [w/ Cantarella, Needham, Stewart]
With respect to the symmetric measure on triangles, the probability that a random triangle is obtuse is
\(\frac{3}{2}-\frac{3\ln 2}{\pi}\approx0.838\)
Naturality
The pushforward of the uniform measure on the sphere to the simplex \(s_a+s_b+s_c=1\) has density
\(\frac{1}{2\pi \sqrt{s s_a s_b s_c}}\)
This is the Dirichlet(1/2,1/2,1/2) distribution.
By Heron's formula, the density is proportional to \(\frac{1}{\text{Area}}\).
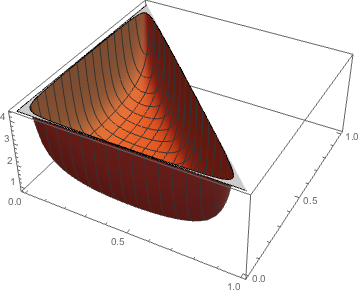
Expectations
Corollary [w/ Cantarella, Needham, Stewart]
The expected area of a random triangle is \(\frac{1}{4\pi}\).
Corollary [w/ Cantarella, Needham, Stewart]
The expected curvature of the circumscribed circle to a random triangle is \(\frac{2}{\pi}\).
Generalization
For \(n>3\), the sidelengths do not uniquely determine an \(n\)-gon, so the simplex approach doesn‘t obviously generalize.
Key Observation: The coordinates \((x,y,z)\) of a point on the sphere are the Plücker coordinates of the perpendicular 2-plane.
\(\vec{p}=\vec{a} \times \vec{b}\)
Plücker coordinates
\(\vec{p}=\vec{a} \times \vec{b} = \begin{pmatrix} \begin{vmatrix} a_2 & b_2 \\ a_3 & b_3 \end{vmatrix} \\ \begin{vmatrix} a_3 & b_3 \\ a_1 & b_1 \end{vmatrix} \\ \begin{vmatrix} a_1 & b_1 \\ a_2 & b_2 \end{vmatrix}\end{pmatrix}\)

Plücker coordinates
In general, \(G_k(\mathbb{R}^n)\) is the Grassmannian of \(k\)-dimensional linear subspace of \(\mathbb{R}^n\).
If \(P \in G_k(\mathbb{R}^n)\) and \(\{a_1,\ldots , a_n\}\) is a basis for \(P\), then the map \(G_k(\mathbb{R}^n) \to \mathbb{RP}^{\binom{n}{k}-1}\) recording all \(k \times k\) minors of the matrix \([a_1 \cdots a_k]\) is called the Plücker embedding of \(G_k(\mathbb{R}^n)\).
Equivalently, \(P \mapsto a_1 \wedge \ldots \wedge a_k \in \mathbb{P}(\bigwedge^k \mathbb{R}^n) \simeq \mathbb{RP}^{\binom{n}{k}-1}\).
The Plücker coordinates satisfy certain relations; in the case of \(G_2(\mathbb{R}^4)\), these reduce to
\(\Delta_{12}\Delta_{34}-\Delta_{13}\Delta_{24}+\Delta_{14}\Delta_{23}=0\)
Triangles and the Grassmannian
Suppose \(T\) is a triangle with edge vectors \(e_1, e_2, e_3\). Let \(p \in S^2\) be any lift of \(T\), and let \((a,b)\) be any orthonormal basis of \(p^\bot\).
\((a, b) = \begin{pmatrix} a_1 & b_1 \\ a_2 & b_2 \\ a_3 & b_3 \end{pmatrix}\)
Let \(z_k = a_k + i b_k\) for each \(k\).
Up to rotation,
\(e_k = z_k^2\) as complex numbers
Polygons and Stiefel Manifolds
Let \(e_1, \ldots , e_n\) be the edges of a planar \(n\)-gon with total perimeter 2. Choose \(z_1, \ldots , z_n\) so that \(z_k^2 = e_k\). Let \(z_k = a_k + i b_k\).
The polygon is closed \(\Leftrightarrow e_1 + \ldots e_n = 0\)
\(\sum e_k =\sum z_k^2 = \left(\sum a_k^2 - \sum b_k^2\right) + 2i \sum a_k b_k\)
The polygon is closed \(\Leftrightarrow |a|=|b|\) and \(a \bot b\)
Since \(\sum |e_k| = \sum a_k^2 + \sum b_k^2 = |a|^2 + |b|^2\), we see that \((a,b) \in V_2(\mathbb{R}^n)\), the Stiefel manifold of 2-frames in \(\mathbb{R}^n\).
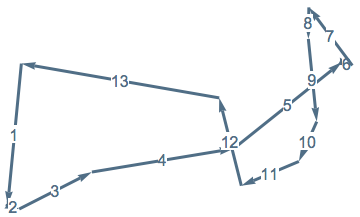
Polygons and Grassmannians
Proposition: Rotating \((a,b)\) in the plane it spans rotates the corresponding \(n\)-gon twice as fast.
Corollary [Hausmann–Knutson]
The Grassmannian \(G_2(\mathbb{R}^n)\) is (almost) a \(2^n\)-fold covering of the space of planar \(n\)-gons of perimeter 2.
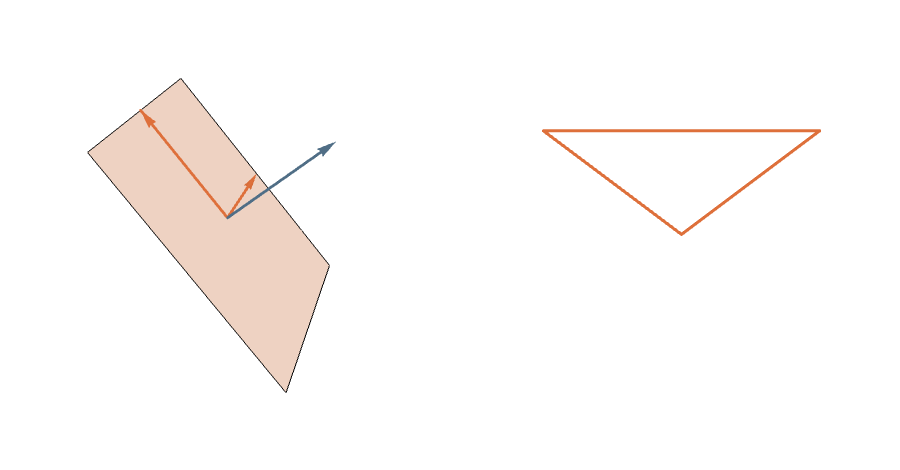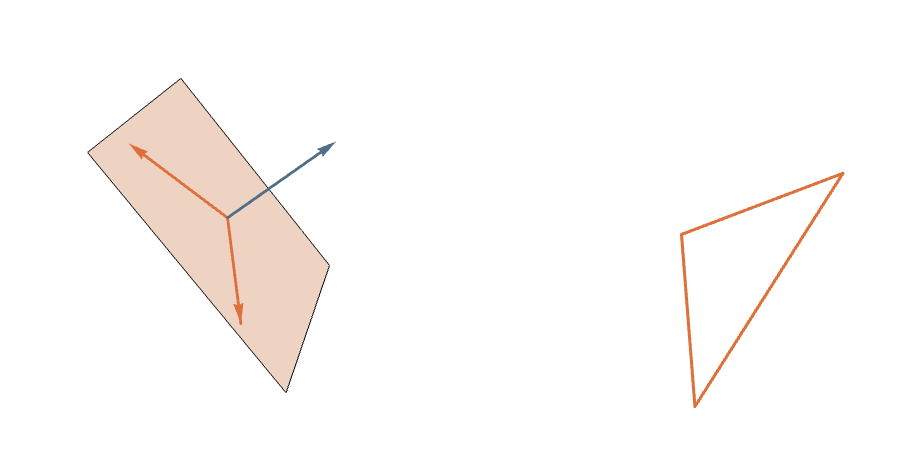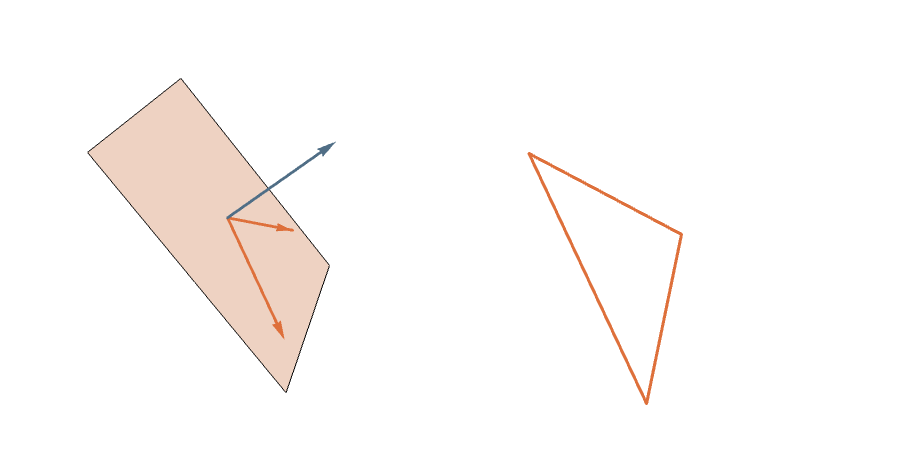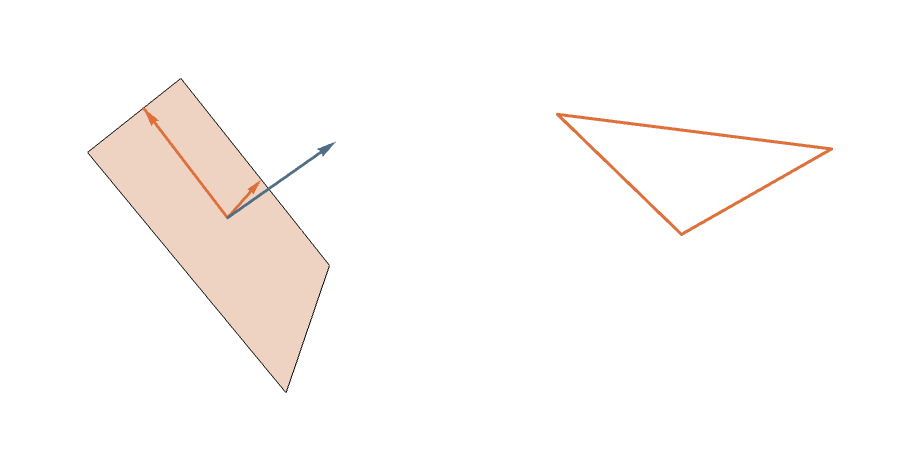
The Symmetric Measure
Definition [w/ Cantarella & Deguchi]
The symmetric measure on \(n\)-gons of perimeter 2 up to translation and rotation is the pushforward of Haar measure on \(G_2(\mathbb{R}^n)\).
Therefore, \(SO(n)\) acts transitively on \(n\)-gons and preserves the symmetric measure.
In particular, notice that the symmetric measure is invariant under permutations of the edges.
Plücker Matrices
We can package the Plücker coordinates \(\Delta_{ij} = \begin{vmatrix} a_i & b_i \\ a_j & b_j \end{vmatrix}\) of a point in \(G_2(\mathbb{R}^n)\) as a skew-symmetric matrix
\(\Delta = (\Delta_{ij})_{i,j}\)
In other words, this is the matrix of cross products of the \((a_k,b_k)\).
Semi-Miraculous Fact: \(-\Delta^2\) is the Gram matrix (i.e., matrix of dot products) of the \((a_k,b_k)\).
Sign Matrices
Definition: Given \(P \in G_2(\mathbb{R}^n)\), the Plücker sign matrix of \(P\) is \(\operatorname{sgn} \Delta(P)\) and the projection sign matrix of \(P\) is \(\operatorname{sgn}( -\Delta(P)^2)\).
Since \((a_k + i b_k)^2=e_k\), the Plücker sign matrix and projection sign matrix notice when two edges in a polygon become parallel or anti-parallel.
The sign matrices notice, among other things, when a polygon becomes non-convex or non-embedded.

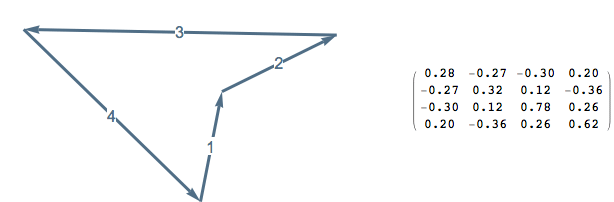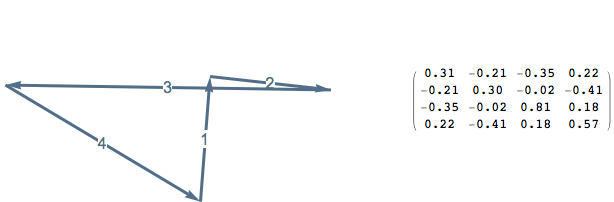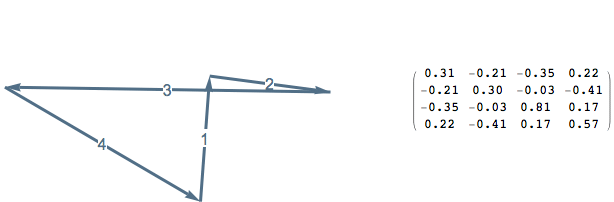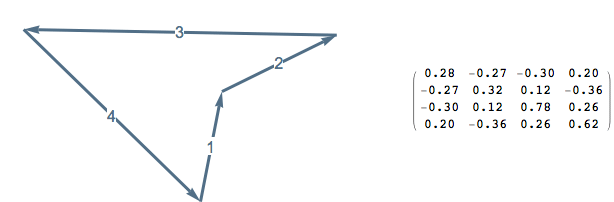
Sylvester’s Four Point Problem
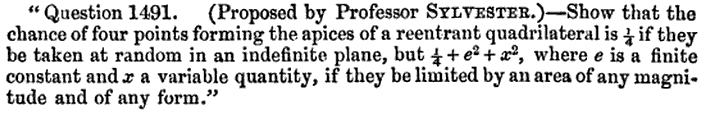

convex
reflex/reentrant
self-intersecting
Modern Reformulation: What is the probability that all vertices of a random quadrilateral lie on its convex hull?
Some Answers
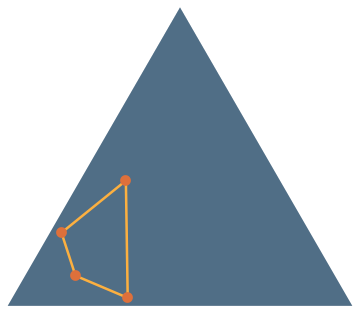
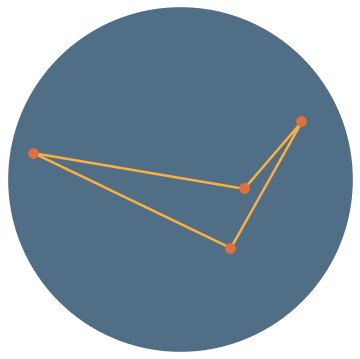
\(\mathbb{P}(\text{reflex})=\frac{1}{3}\)
\(\mathbb{P}(\text{reflex})=\frac{35}{12\pi^2}\approx 0.296\)
Theorem [Blaschke]

\(\frac{35}{12\pi^2}\leq\mathbb{P}(\text{reflex})\leq\frac{1}{3}\)
Our Answer
Theorem [w/ Cantarella, Needham, Stewart]
With respect to the symmetric measure, each of the three classes of quadrilaterals occurs with equal probability. In particular, \(\mathbb{P}(\text{reflex})=\frac{1}{3}\).
More generally...
Theorem [w/ Cantarella, Needham, Stewart]
With respect to any permutation-invariant measure on \(n\)-gon space, the probability that a random \(n\)-gon is convex is \(\frac{2}{(n-1)!}\).
Polygons in Space
There is a version of this story for polygons in \(\mathbb{R}^3\) as well.
Example Theorem [w/ Cantarella, Grosberg, Kusner]
The expected total curvature of a random space \(n\)-gon is exactly
\(\frac{\pi}{2}n + \frac{\pi}{4} \frac{2n}{2n-3}\)
The polygon space is \(G_2(\mathbb{C}^n)\) and the analog of the squaring map is the Hopf map.

Open Problem
What is the manifold of equilateral planar \(n\)-gons up to translation and rotation?
Is there a good parametrization of this manifold?
Thank you!
References
- J. Cantarella, T. Deguchi, and C. Shonkwiler. Probability theory of random polygons from the quaternionic perspective. Communications on Pure and Applied Mathematics 67 (2014), 1658–1699
- J. Cantarella, A. Y. Grosberg, R. Kusner, and C. Shonkwiler. Expected total curvature of random polygons. American Journal of Mathematics 137 (2015), 411–438
- J. Cantarella, T. Needham, C. Shonkwiler, and G. Stewart. Random triangles and polygons in the plane. Coming soon!