An Introduction to Symplectic Geometry and Some Applications
/rtg20
this talk!
Take-Home Message
Symplectic geometry can sound scary, but it turns out to be useful in some surprising contexts.

Symplecti-wha?
—Dusa McDuff & Dietmar Salamon
Introduction to Symplectic Topology
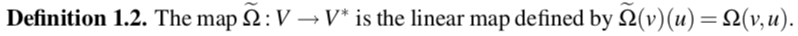


—Ana Cannas da Silva
A nice space, where multivariable calculus makes sense. Think spheres, tori, projective spaces, …

A rule for assigning a number to pairs of tangent vectors which transforms like (signed) area of the parallelogram they span.
Symplectic Manifold
Must be closed (think: divergence-free) and non-degenerate (doesn’t annihilate any vector).
Standard Example and Some Non-Examples
Example: \((\mathbb{R}^2,dx \wedge dy) = (\mathbb{C},\frac{i}{2}dz \wedge d\bar{z})\)
Non-Example: \((\mathbb{R}^3, dx \wedge dy)\)
For any vector \(v\), \(dx \wedge dy\left(\frac{\partial}{\partial z}, v\right) = 0\), so \(dx \wedge dy\) is degenerate.
Non-Example: \((\mathbb{R}^4, dx_1 \wedge dy_1 + y_1 dx_2 \wedge dy_2)\)
Because of the coefficient \(y_1\), this is not closed (“not divergence-free”).
Examples
\((S^2,d\theta\wedge dz)\)
\((\mathbb{R}^2,dx \wedge dy) = (\mathbb{C},\frac{i}{2}dz \wedge d\bar{z})\)
\((S^2,\omega)\), where \(\omega_p(u,v) = (u \times v) \cdot p\)
\((\mathbb{R}^2,\omega)\) where \(\omega(u,v) = \langle i u, v \rangle \)
\((\mathbb{C}^n, \frac{i}{2} \sum dz_k \wedge d\overline{z}_k)\)
\((\mathbb{C}^{m \times n}, \omega)\) with \(\omega(X_1,X_2) = -\operatorname{Im} \operatorname{trace}(X_1^* X_2)\).
\((T^* \mathbb{R}^n,\sum dq_i \wedge dp_i)\)
phase space
position
momentum
What does this get you?
Volume
\(\omega^{\wedge n} = \omega \wedge \dots \wedge \omega\) is a volume form on \(M\), and induces a measure
called Liouville measure on \(M\).
In particular, if \(M\) is compact, this can be normalized to give a probability measure.
Theorem [Archimedes]
\(\mathrm{d}\theta \wedge \mathrm{d}z\) is the standard area form on the unit sphere \(S^2\).
A (Very) Classical Example

KoenB [ ] from Wikimedia Commons

Hamiltonian Mechanics
“Evolution of a physical system follows the symplectic gradient”
Functions and Symplectic Gradients
If \(H: M \to \mathbb{R}\) is smooth, then there exists a unique vector field \(X_H\) so that \({dH = \iota_{X_H}\omega}\), i.e.,
(\(X_H\) is called the Hamiltonian vector field for \(H\), or sometimes the symplectic gradient of \(H\))
Example. \(H: (S^2, d\theta\wedge dz) \to \mathbb{R}\) given by \(H(\theta,z) = z\).
\(dH = dz = \iota_{\frac{\partial}{\partial \theta}}(d\theta\wedge dz)\), so \(X_H = \frac{\partial}{\partial \theta}\).


\(H\) is constant on orbits of \(X_H\):
\(\mathcal{L}_{X_H}(H) = dH(X_H)=\omega(X_H,X_H) = 0\)
Some Mechanics
Suppose we have a particle of mass \(m\) with position \(\vec{q} = (q_1,q_2,q_3)\).
Suppose the particle is subject to a potential \(V(\vec{q})\).
Newton’s Second Law: \(-\nabla V(\vec{q}) = m \frac{d^2 \vec{q}}{dt^2}\).
Momenta \(p_i := m \frac{dq_i}{dt}\).
\((\vec{q},\vec{p})\in T^*\mathbb{R}^3 \cong \mathbb{R}^6\); canonical symplectic form \(\omega = dq_1 \wedge dp_1 + dq_2 \wedge dp_2 + dq_3 \wedge dp_3\).
The Hamiltonian Formulation
Energy function (or Hamiltonian)
\(H(\vec{q},\vec{p}) := \frac{1}{2m}|\vec{p}|^2 + V(\vec{q})\).
\(dH = \sum\left(\frac{\partial H}{\partial p_i} dp_i + \frac{\partial H}{\partial q_i}dq_i\right)\),
\((\vec{q}(t),\vec{p}(t))\) is an integral curve for \(X_H\) if and only if
\(\frac{dq_i}{dt} = \frac{\partial H}{\partial p_i} = \frac{1}{m} p_i\)
\(\frac{dp_i}{dt} = -\frac{\partial H}{\partial q_i} = -\frac{\partial V}{\partial q_i}.\)
This is Newton’s Second Law written as a first-order system!
\(X_H = \sum\left(\frac{\partial H}{\partial p_i} \frac{\partial}{\partial q_i} - \frac{\partial H}{\partial q_i} \frac{\partial}{\partial p_i}\right)\).
Noether’s Theorem
“Every continuous symmetry has a corresponding conserved quantity”
Circle Actions
A circle action on \((M,\omega)\) determines a vector field \(X\) by

\(S^1=U(1)\) acts on \((S^2,d\theta \wedge dz)\) by
So \(X = \frac{\partial}{\partial \theta}\).
Symmetries and Conserved Quantities
Definition. A circle action on \((M,\omega)\) is Hamiltonian if there exists a map
so that \(d\mu = \iota_{X}\omega = \omega(X,\cdot)\), where \(X\) is the vector field generated by the circle action. In other words, \(X = X_\mu\).

\(X = \frac{\partial}{\partial \theta}\)
\(\mu(\theta,z) = z\)
\(\iota_X\omega = \iota_{\frac{\partial}{\partial \theta}} d\theta \wedge dz = dz \)
Extremely Deep Fact
Archimedes’ Theorem can be suitably generalized to any symplectic manifold with a Hamiltonian circle action (or, better yet, many commuting Hamiltonian circle actions).
See: Atiyah, Guillemin–Sternberg, Duistermaat–Heckman, and toric symplectic manifolds (and toric varieties)
Application to Polymers
In solution, linear polymers become crumpled:
Protonated P2VP
Roiter–Minko, J. Am. Chem. Soc. 127 (2005), 15688-15689
[CC BY-SA 3.0], from Wikimedia Commons

Modern polymer physics is based on the analogy between a polymer chain and a random walk.
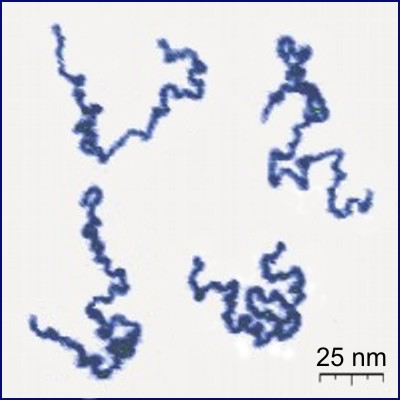
Ring Polymers
Lots of Symmetries!
Continuous symmetry \(\Rightarrow\) conserved quantity
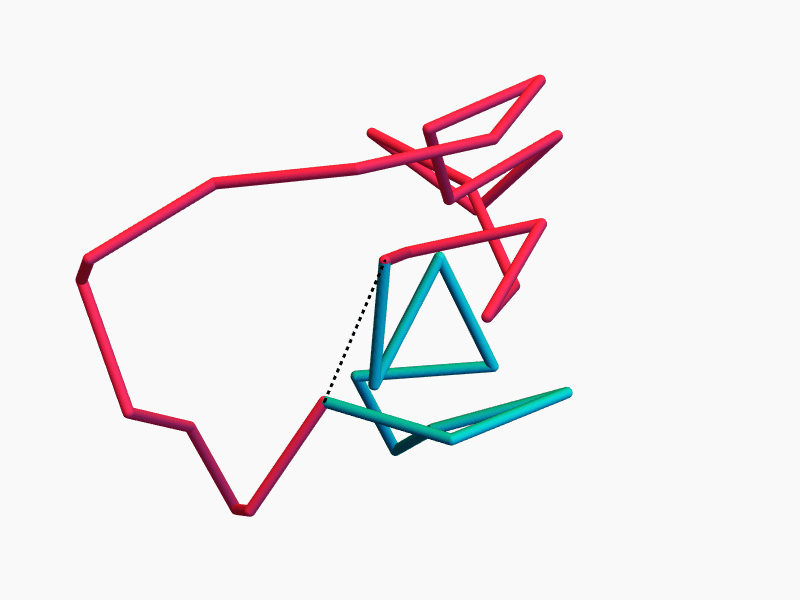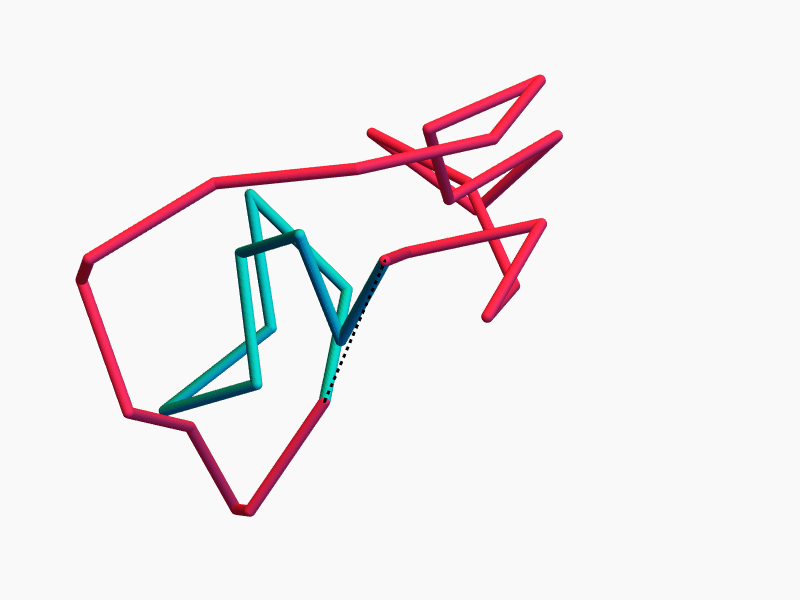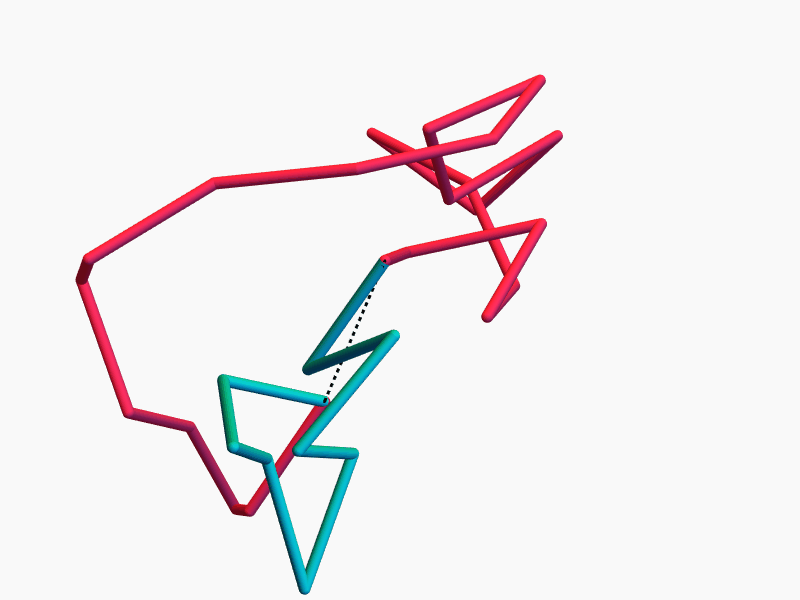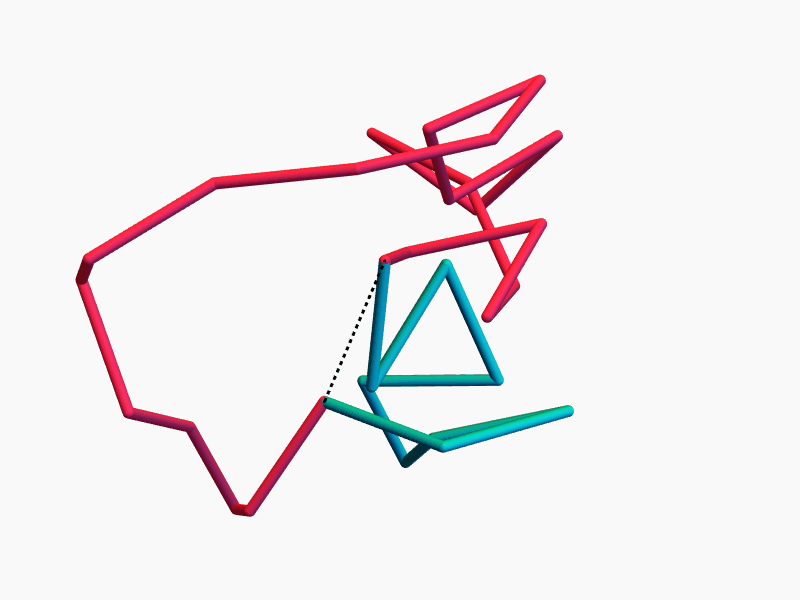
The space of equilateral \(n\)-gons has lots of symmetries...
A Generalized Archimedes Theorem
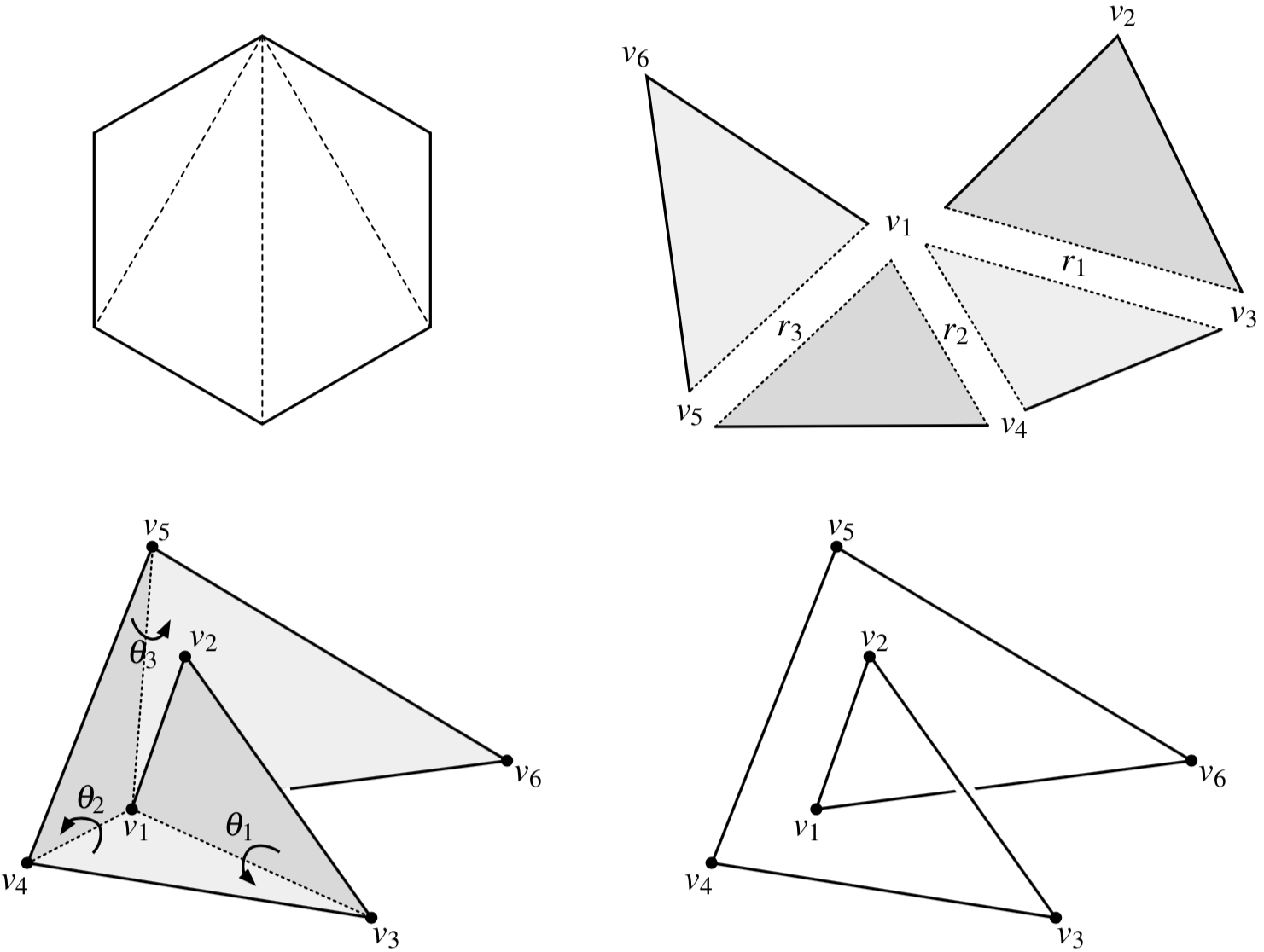
Theorem [with Cantarella]
The standard volume form on polygon space is
\(\mathrm{d}\theta_1 \wedge \dots \wedge \mathrm{d}\theta_{n-3} \wedge \mathrm{d} r_1 \wedge \dots \wedge \mathrm{d}r_{n-3}\)
Corollary [with Cantarella, Duplantier, Uehara]
The first efficient, provably correct algorithm for sampling equilateral random polygons in \(\mathbb{R}^3\).
Application to Frame Theory
Signal: \(v \in \mathbb{C}^d\)
Design: \(f_1, \dots , f_n \in \mathbb{C}^d\)
Measurements: \(\langle f_1, v \rangle, \dots , \langle f_n, v \rangle \).
Parseval’s Theorem
If \(f_1, \dots , f_d \in \mathbb{C}^d\) is an orthonormal basis,
\(\|v\|^2 = \sum |\langle f_i, v \rangle |^2 = \|F^* v\|^2\)
for any \(v \in \mathbb{C}^d\).
Even better,
\(v = \sum \langle f_i, v \rangle f_i = FF^* v \).
If \(F = [f_1 \, f_2 \dots f_n]\), the measurement vector is \(F^*v\).
\(\Leftrightarrow FF^* = \mathrm{Id}_{d \times d}\)
Parseval frame
Fact: For any \(n \geq d\), there exist Parseval frames \(f_1, \dots , f_n \in \mathbb{C}^d\) so that \(\|f_i\|=\|f_j\|\) for all \( i,j\); these are the equal-norm Parseval frames (ENPs).
This is fragile! What if a measurement gets lost?
Group Actions on Frames
Some nice group actions on \(\mathbb{C}^{d \times n}\):
- \(U(d)\) acts on the left
- \(U(n)\) acts on the right
- \(U(1)^d\) acts on the left
- \(U(1)^n\) acts on the right
Parseval frames
\(\mu_{U(d)}^{-1}(I_{d\times d})\)
equal-norm frames
\(\mu_{U(1)^N}^{-1}\left(-\frac{1}{2}r,\dots , -\frac{1}{2}r\right)\)
ENPs: \(\mu_{U(d)}^{-1}(I_{d \times d}) \cap \mu_{U(1)^n}^{-1}\left(-\frac{d}{2n}, \dots , -\frac{d}{2n}\right)\)
A Generalization of the Frame Homotopy Conjecture
Theorem [with Needham]
There is a continuous interpolation between any two frames \(f_1, \dots , f_n\) and \(g_1, \dots , g_n\) with \(FF^* = GG^*\) and \(\|f_i\| = \|g_i\|\) preserving these conditions.

Thank you!
Funding: Simons Foundation
References
Symplectic geometry and connectivity of space of frames
Tom Needham and Clayton Shonkwiler
The geometry of constrained random walks and an application to frame theory
Clayton Shonkwiler
2018 IEEE Statistical Signal Processing Workshop (SSP), 343–347
The symplectic geometry of closed equilateral random walks in 3-space
Jason Cantarella and Clayton Shonkwiler
Annals of Applied Probability 26 (2016), no. 1, 549–596
A fast direct sampling algorithm for equilateral closed polygons
Jason Cantarella, Bernard Duplantier, Clayton Shonkwiler, and Erica Uehara
Journal of Physics A: Mathematical and Theoretical 49 (2016), no. 27, 275202