Using Differential Geometry to Model Complex Biopolymers
/scmb
this talk!
Linear polymers
A linear polymer is a chain of molecular units with free ends.
Polyethylene


Nicole Gordine [CC BY 3.0] from Wikimedia Commons
Shape of linear polymers
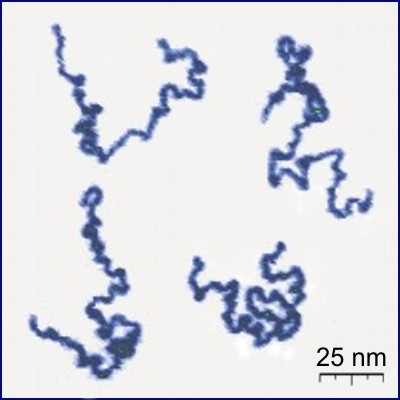
In solution, linear polymers become crumpled:
Protonated P2VP
Roiter–Minko, J. Am. Chem. Soc. 127 (2005), 15688-15689
[CC BY-SA 3.0], from Wikimedia Commons
Random Walks
Simple model: The freely jointed chain/random walk model dates back to Kuhn in the 1930s.
Rayleigh (1919): The probability density function of the end-to-end vector \(\vec{\ell}\) of a 3D equilateral random walk is
Corollary (see e.g. de Gennes or Khokhlov–Grosberg–Pande): The expected end-to-end distance and radius of gyration of a random walk of \(N\) segments scale like \(\sqrt{N}\).
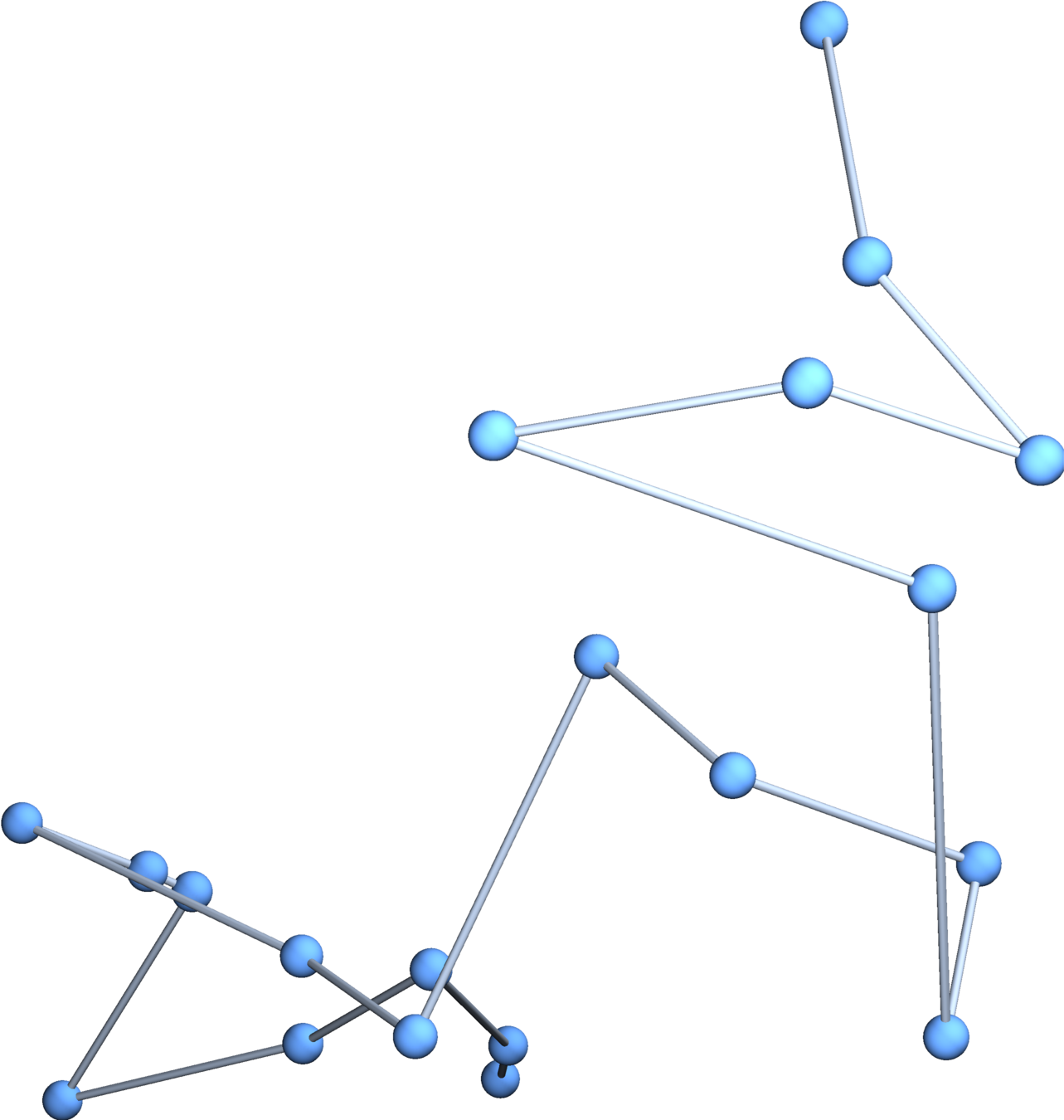
Modern polymer physics is based on the analogy between a polymer chain and a random walk.
Simulating random walks in \(\mathbb{R}^3\) is easy
Generate \(N\) independent uniform random points in \(\mathbb{R}^3\) according to your favorite probability distribution and treat them as an ordered list of edge vectors.

Alternatives & Refinements
Self-avoiding walks on the lattice (see, Madras–Slade): Scaling exponent agrees with polymers in dilute solution with good solvent.
Thick off-lattice random walks (see Plunkett–Chapman): Markov chain simulation algorithm and experimental evidence of the same scaling exponent as lattice SAWs.

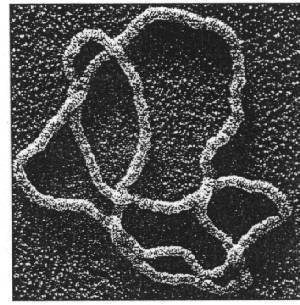
Ring Polymers
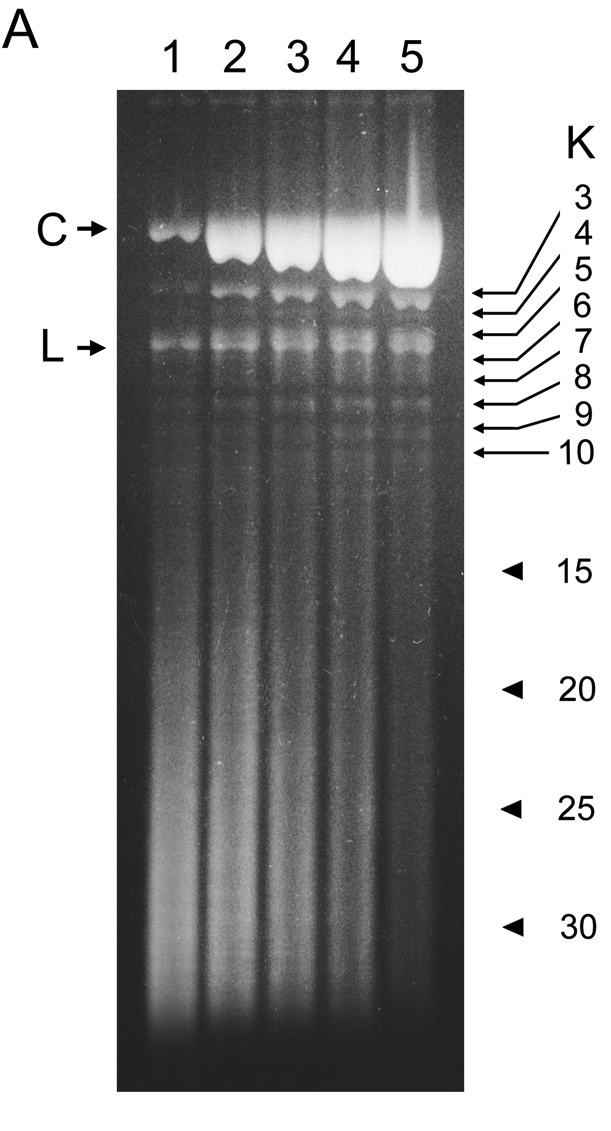
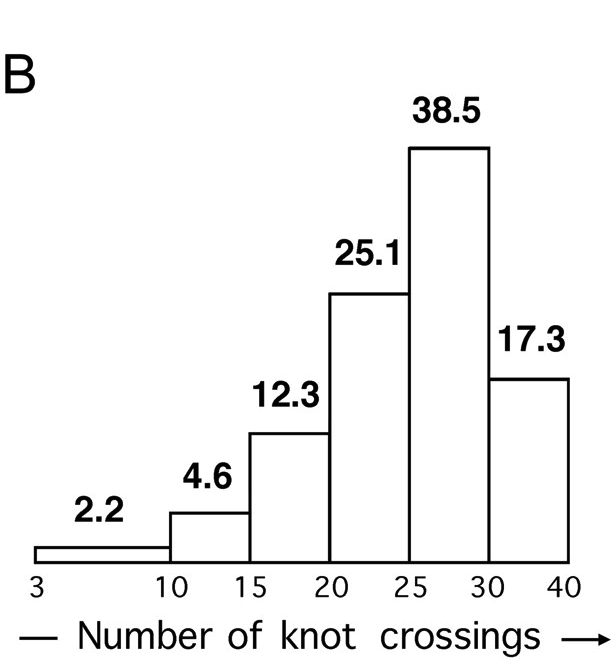
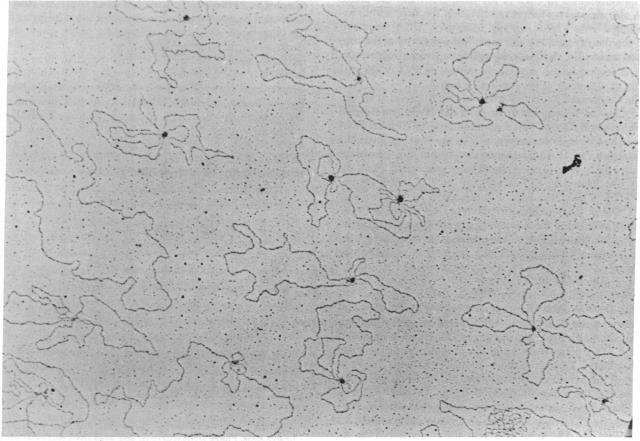
Knot complexity in DNA from P4 tailless mutants
Is this surprising?
Sampling random rings is hard

Two Standard Strategies
Lattice Polygons: Reduces the problem to combinatorics
(see, e.g., Sumners–Whittington or many works from the Arsuaga–Vazquez Lab)
cf. Diao
Off-Lattice Markov Chains: Randomized simulation
(see, e.g., Alvarado–Calvo–Millett)
Ansatz
Topologically constrained random walk \(\Leftrightarrow\) point in some (nice!) configuration space
Knowledge of the (differential, symplectic, algebraic) geometry of these conformation spaces leads to both
theorems and fast numerical algorithms for studying and TCRWs in \(\mathbb{R}^3\).
Grassmannians and framed polygons
The space of framed polygons of fixed total length but variable edge lengths lifts to the complex Grassmannian \(\operatorname{Gr}_2(\mathbb{C}^N)\) (see Hausmann–Knutson, Howard–Manon–Millson, and Cantarella–Deguchi–Shonkwiler).

Algorithm (w/ Cantarella & Deguchi)
Simulation of framed \(N\)-gons in \(\Theta(n)\) time.
Theorem (w/ Cantarella, Grosberg, & Kusner)
The expected total curvature of framed \(N\)-gons is \(\frac{\pi}{2}N + \frac{\pi}{4}\frac{2N}{2N-3}\).

Corollary
At least \(\frac{1}{3}\) of hexagons and \(\frac{1}{11}\) of heptagons are knotted.
Planar polygons
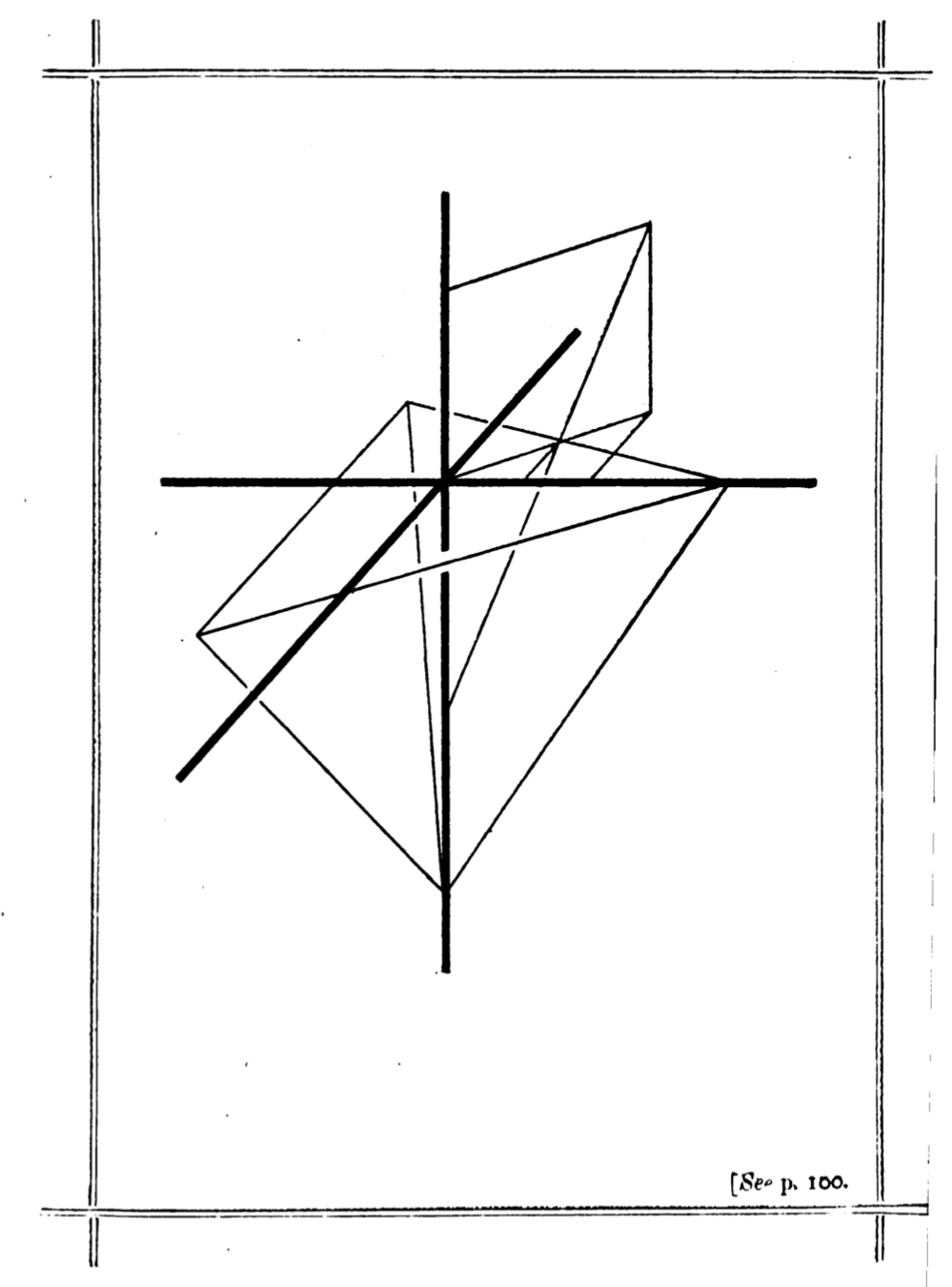


Theorem (w/ Cantarella, Needham, Stewart)
The probability that a random triangle is obtuse is
\(\frac{3}{2}-\frac{3\ln 2}{\pi}\approx0.838\)
Equilateral Polygons
The space of equilateral \(N\)-gons can be constructed as a symplectic reduction of the Grassmannian (see Kapovich–Millson and Hausmann–Knutson):
Continuous symmetry \(\Rightarrow\) conserved quantity
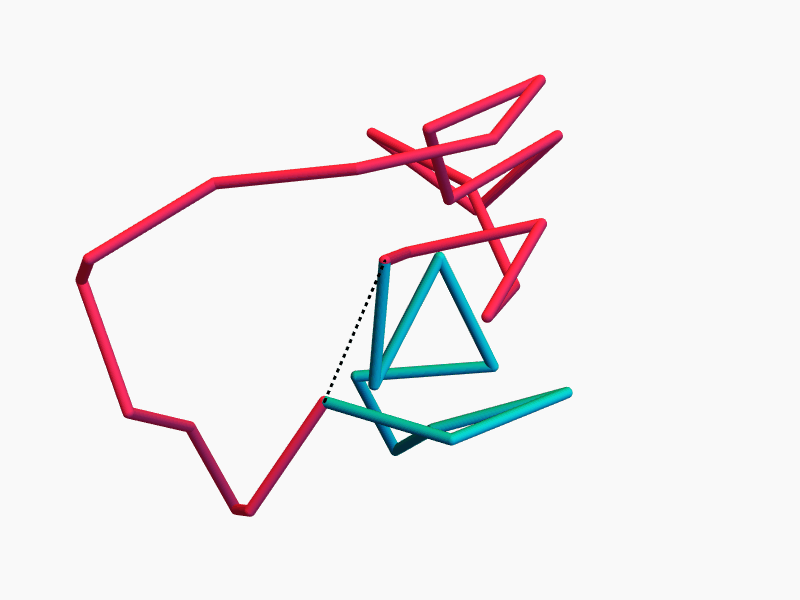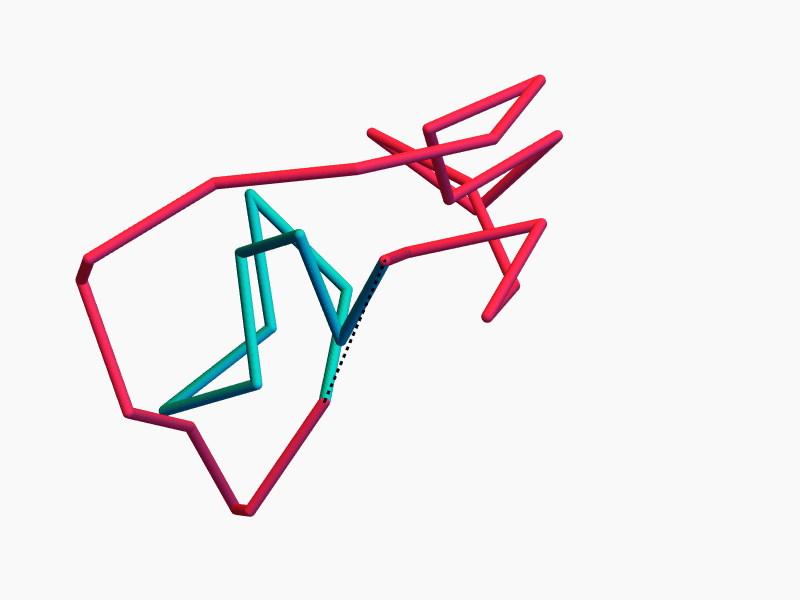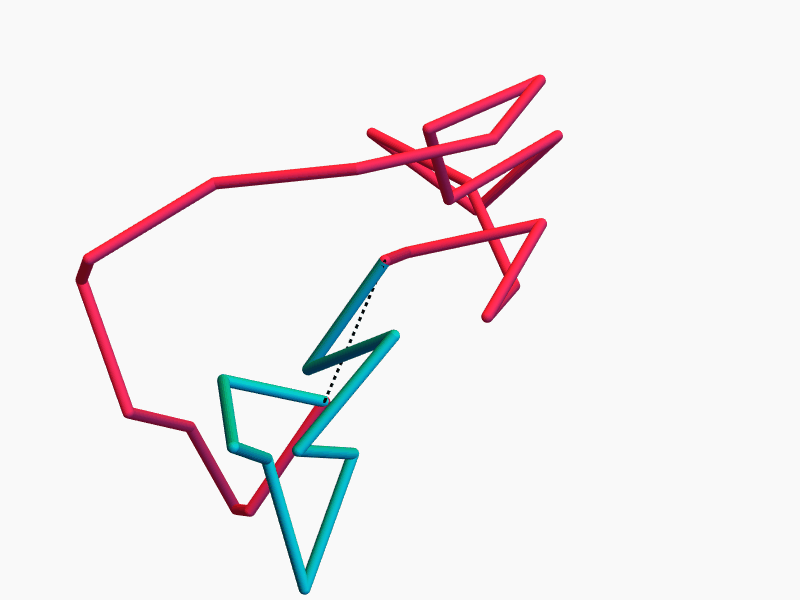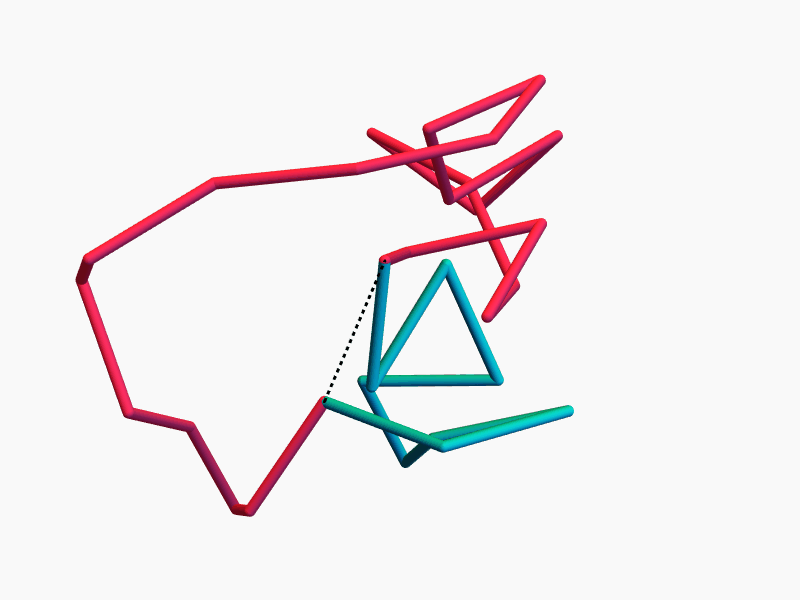
\(N-3\) commuting symmetries
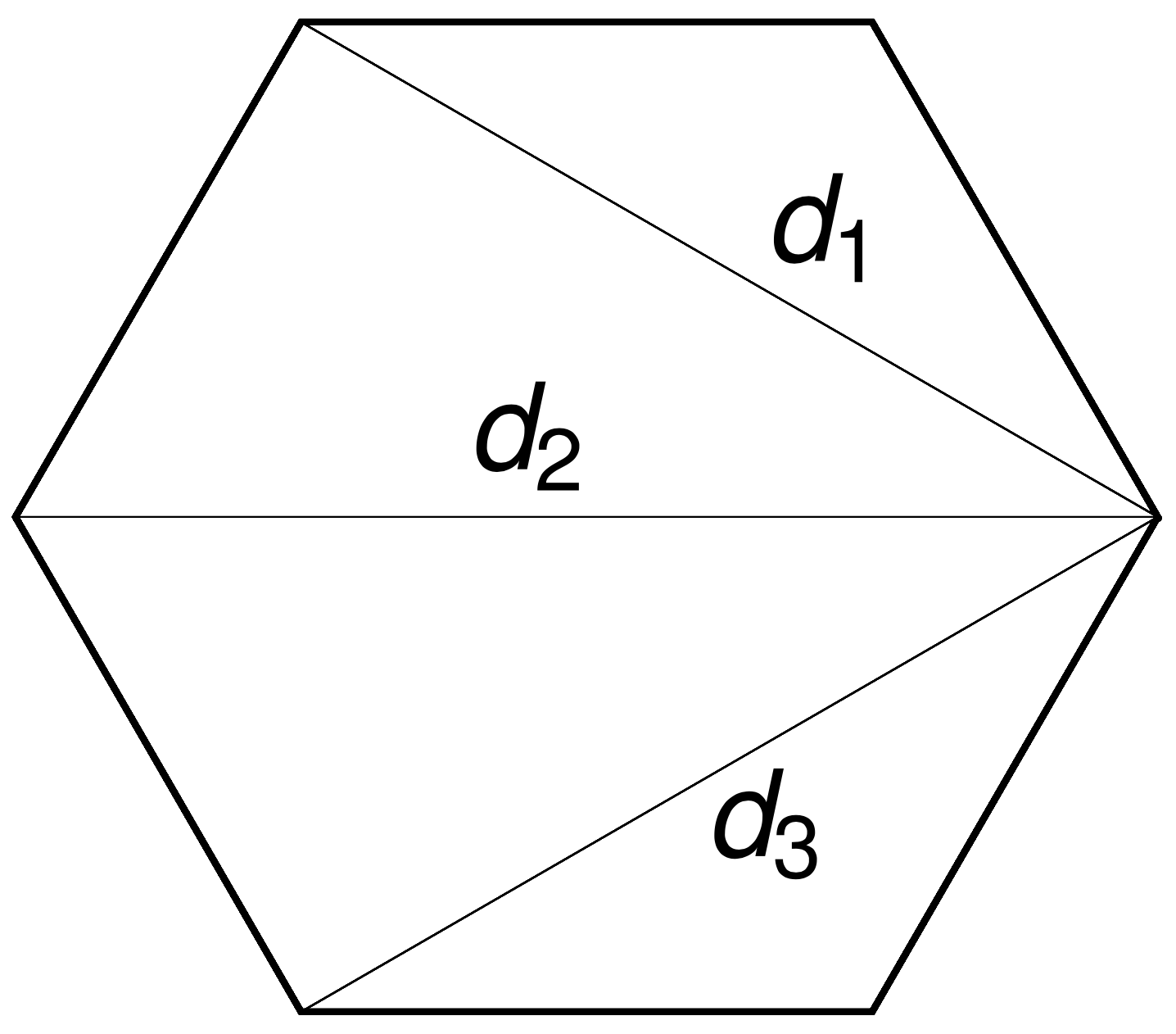
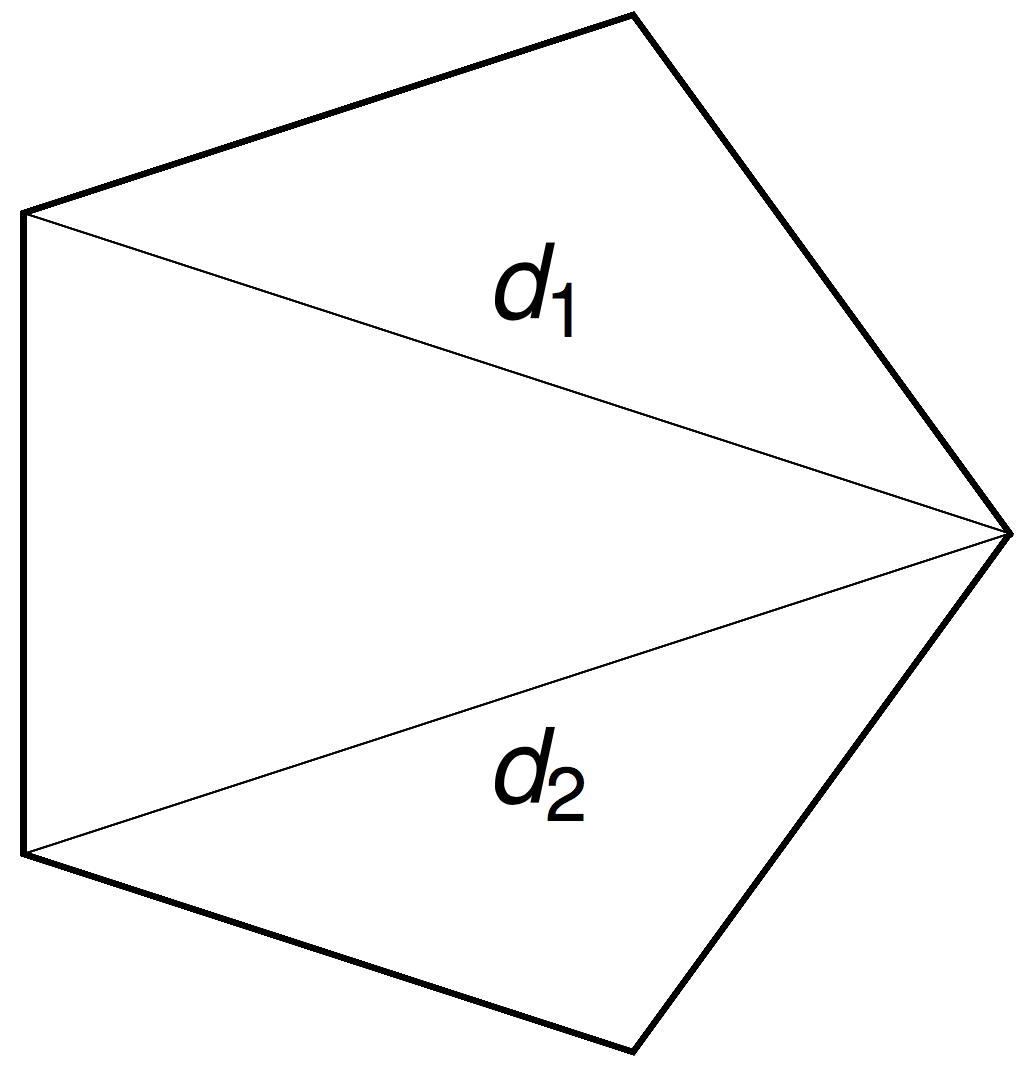
Rotations around \(N-3\) chords \(d_i\) by \(N-3\) angles \(\theta_i\) commute.


Chord distributions
Theorem (w/ Cantarella)
The joint distribution of \(d_1,\ldots , d_{N-3}\) and \(\theta_1, \ldots , \theta_{N-3}\) are all uniform on their domains.
Therefore, simulating equilateral \(N\)-gons is equivalent to sampling random points in the convex polytope of \(d_i\)’s and random angles \(\theta_i\).
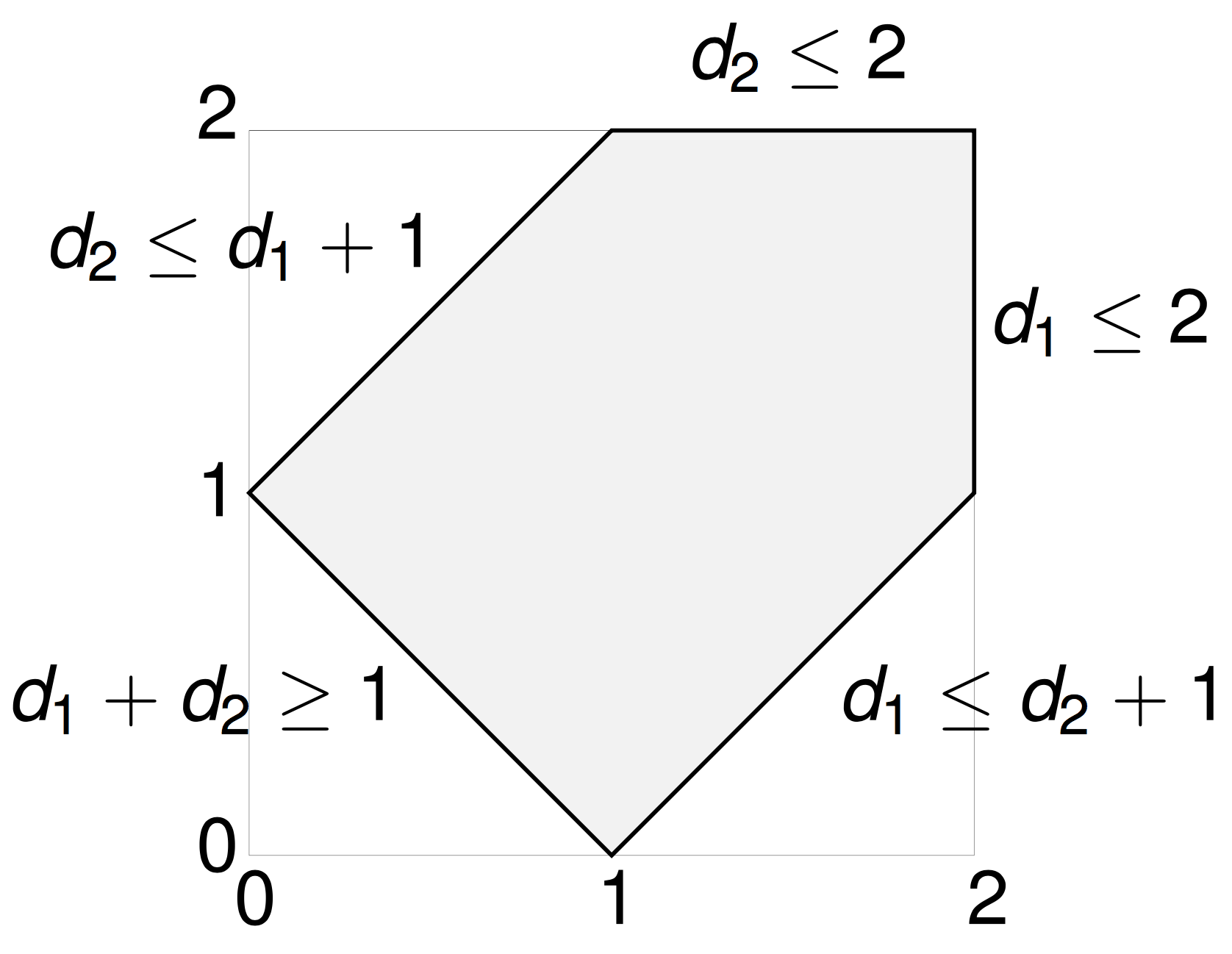
A polytope
The \((N-3)\)-dimensional moment polytope \(\mathcal{P}_N \subset \mathbb{R}^{N-3}\) is defined by the triangle inequalities
Simulations
Algorithm (w/ Cantarella)
A uniformly ergodic Markov chain for simulating random equilateral \(n\)-gons.
More generally, a uniformly ergodic Markov chain for simulating random points from any toric symplectic manifold.

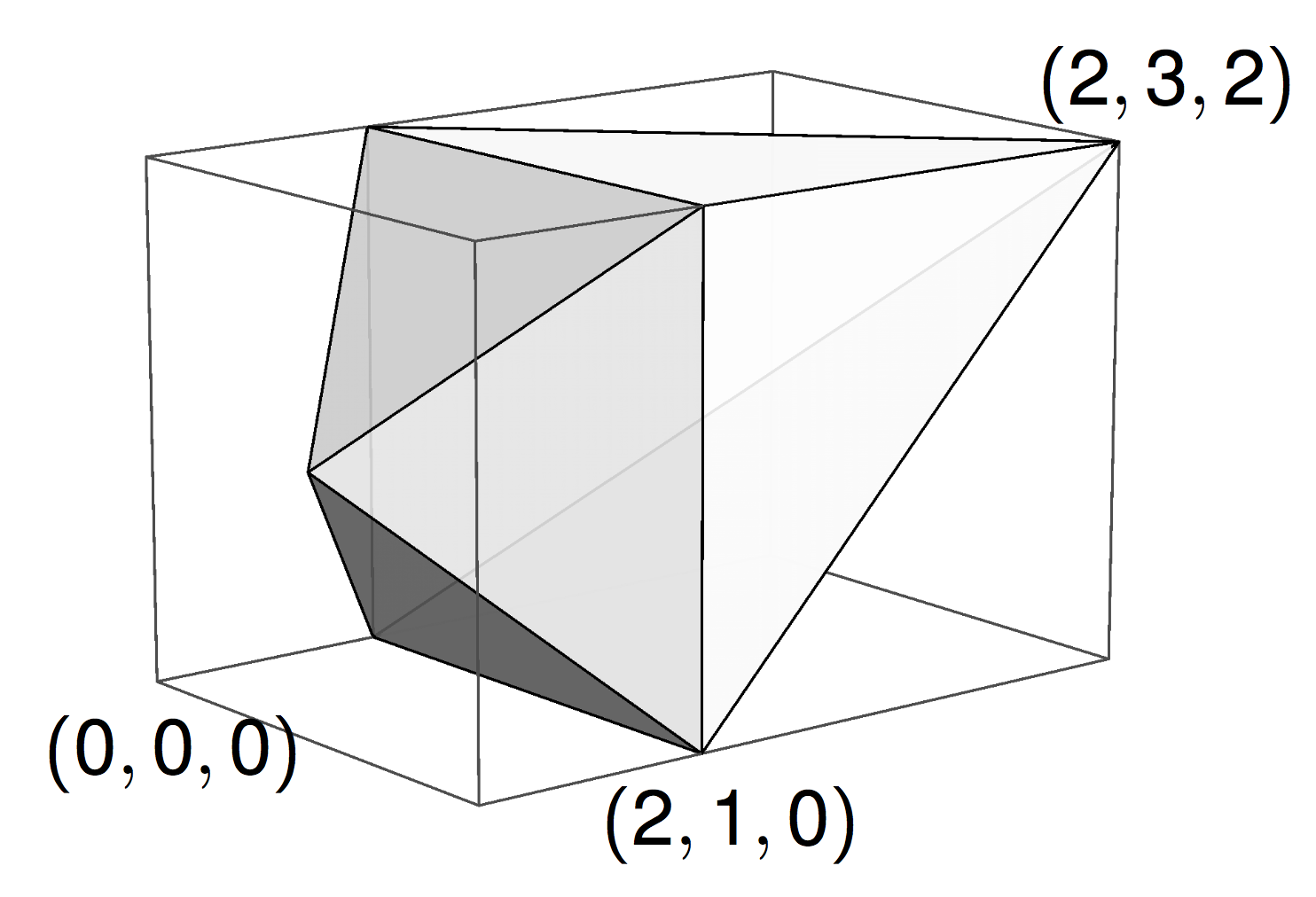
Viral DNA and Confined Polygons
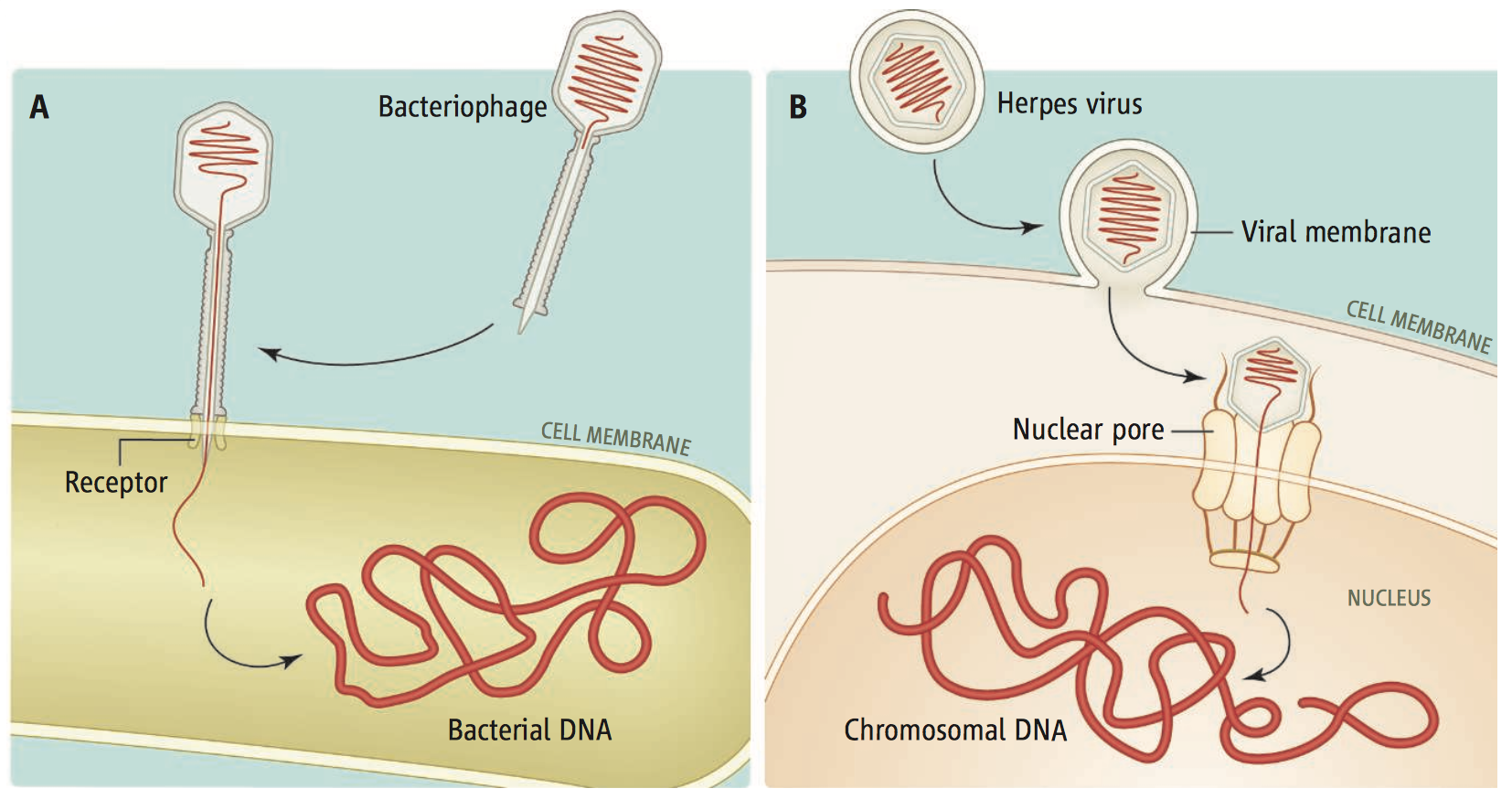
The same algorithm works even better for tightly confined polygons.


Consequences & Refinements
Theorem (Hake)
The fraction of random equilateral 6-gons which are knotted is no bigger than \(\frac{14-3\pi}{192} < \frac{1}{42}\).
Algorithm (w/ Cantarella, Duplantier, & Uehara)
Direct sampling of equilateral \(N\)-gons in \(\Theta(N^{5/2})\) time.
Theorem (Eddy; see poster session)
The stick number of the \(9_{43}\) and \(9_{48}\) knots is 9.
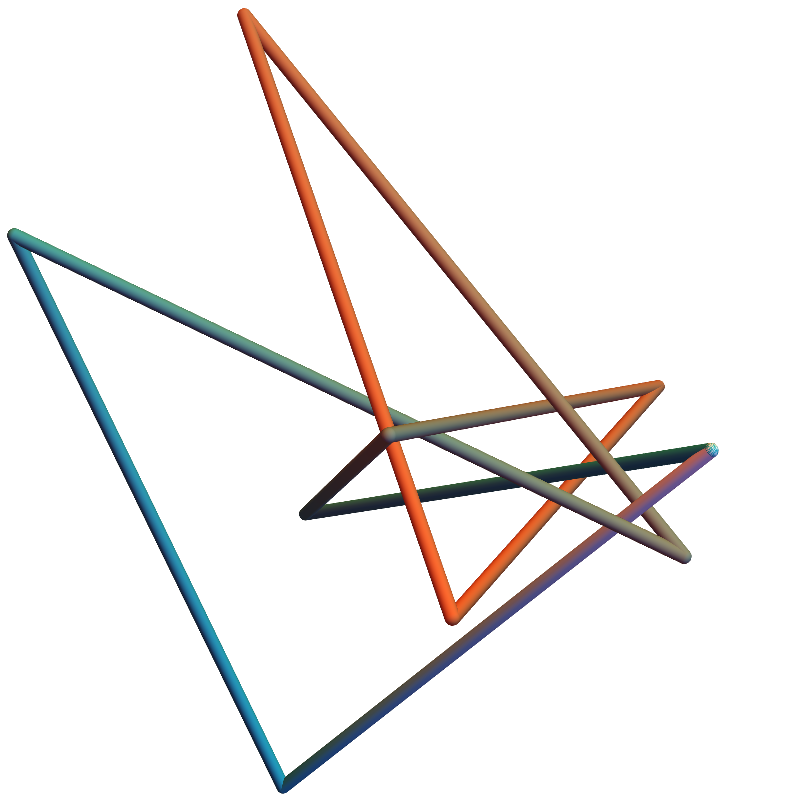
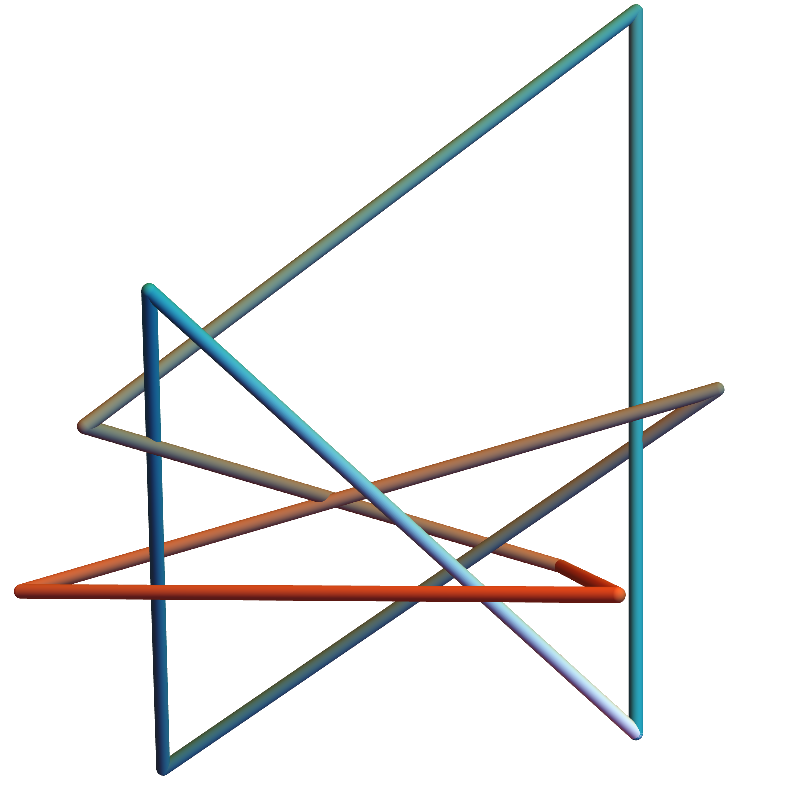
Open Knots

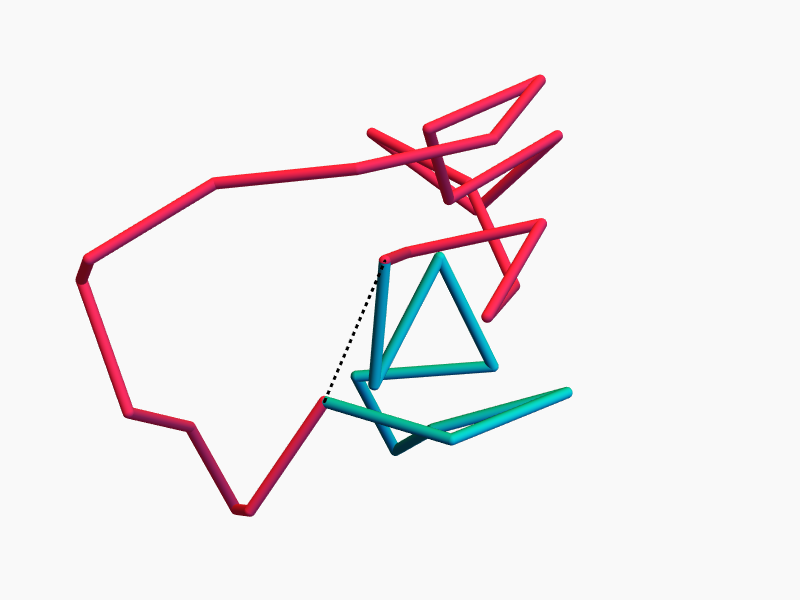
Theorem (w/ Cantarella, Chapman, and Reiter)
The closest equilateral polygon to an open chain is given by geometric median closure.
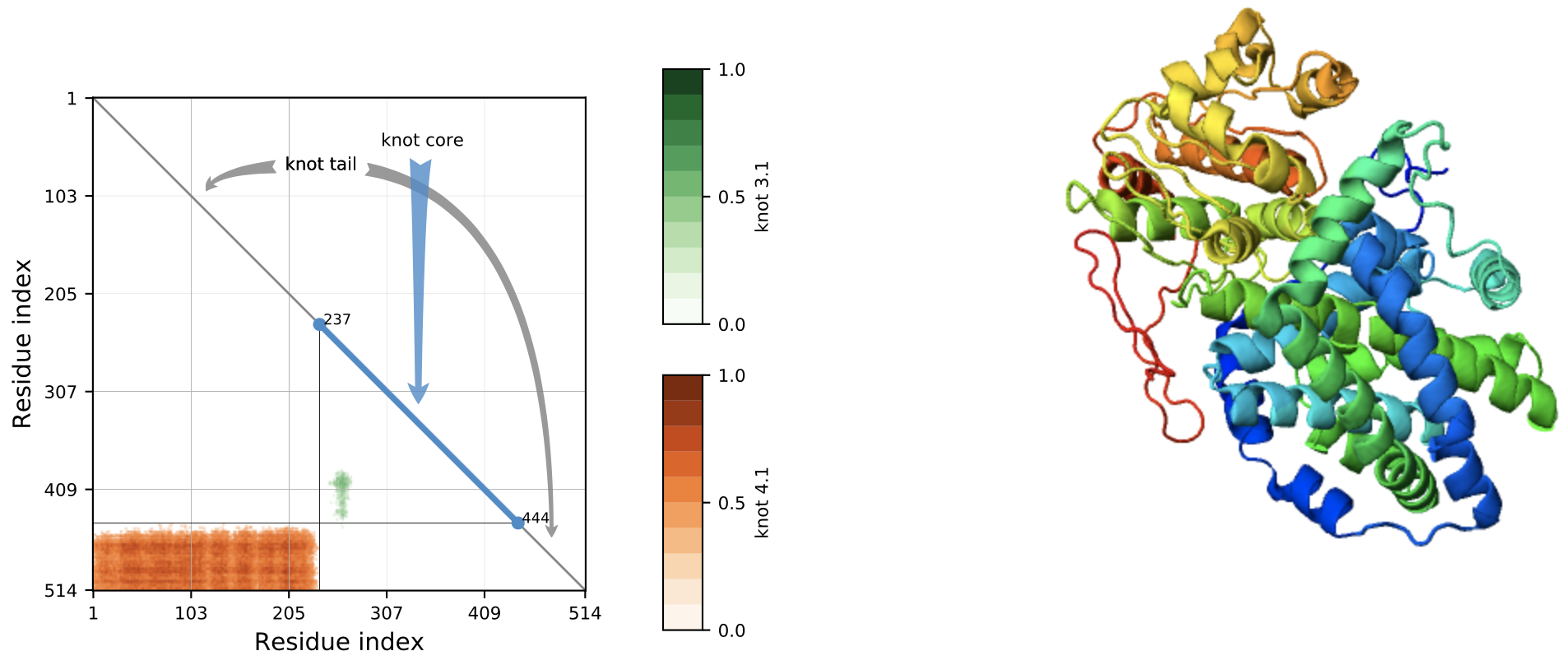
1QMG – From KnotProt
Small knots in proteins persist
3L05
More Complicated Topological Biopolymers
Wood-based nanofibrillated cellulose
Qspheroid4 [CC BY-SA 4.0], from Wikimedia Commons
Synthetic topological polymers
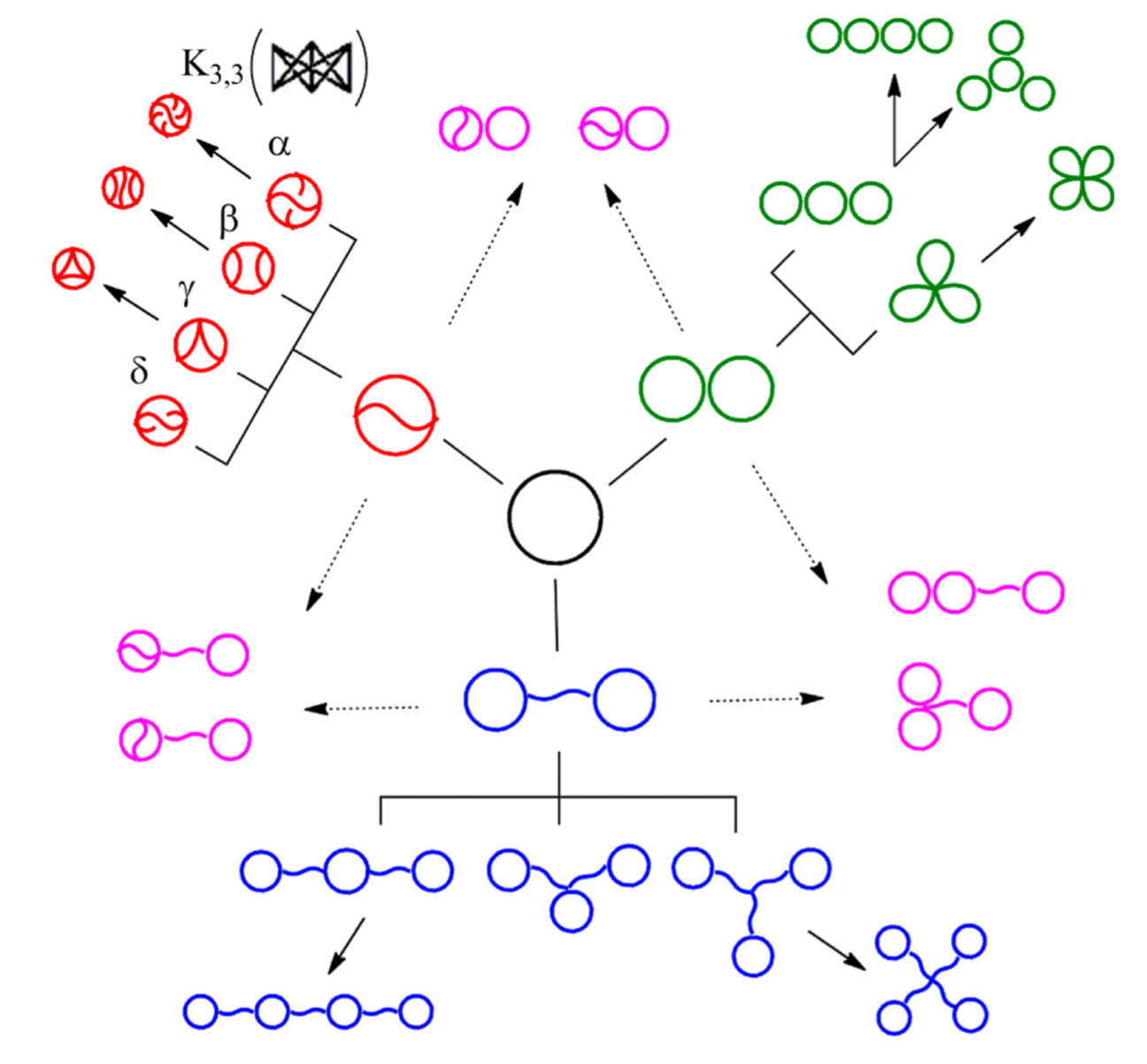
The Tezuka lab in Tokyo can now synthesize many topological polymers in usable quantities
Expected radius of gyration
Theorem (w/ Cantarella, Deguchi, & Uehara; also Estrada–Hatano)
If \(\lambda_i\) are the eigenvalues of \(L\), the expected squared radius of gyration of a Gaussian random embedding of \(\mathfrak{G}\) in \(\mathbb{R}^3\) is
This quantity is called the Kirchhoff index of \(\mathfrak{G}\).
Suppose \(\mathfrak{G}\) is a graph with \(\mathfrak{V}\) vertices. Let \(L\) be the graph Laplacian of \(\mathfrak{G}\).
Two Synthetic Topological Polymers
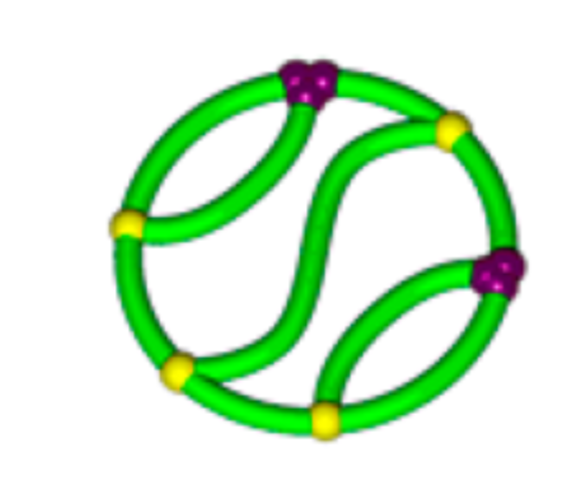
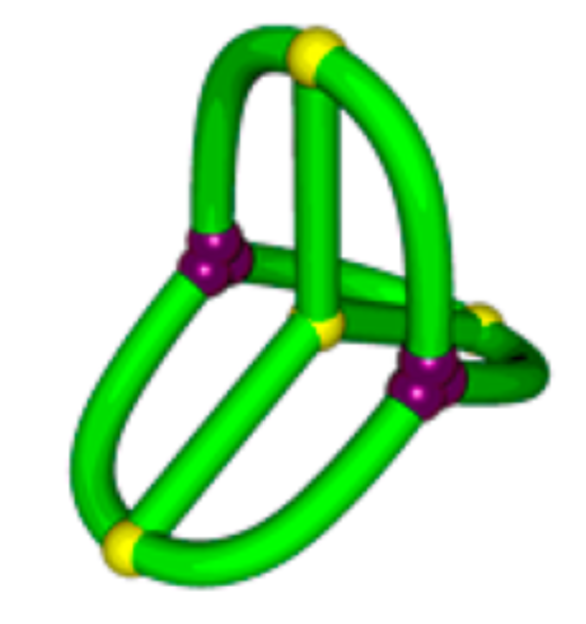
\(K_{3,3}\) (subdivided)
ladder graph (subdivided)


Topological polymers
Size exclusion chromatograph
Distinguishing graph types in the lab
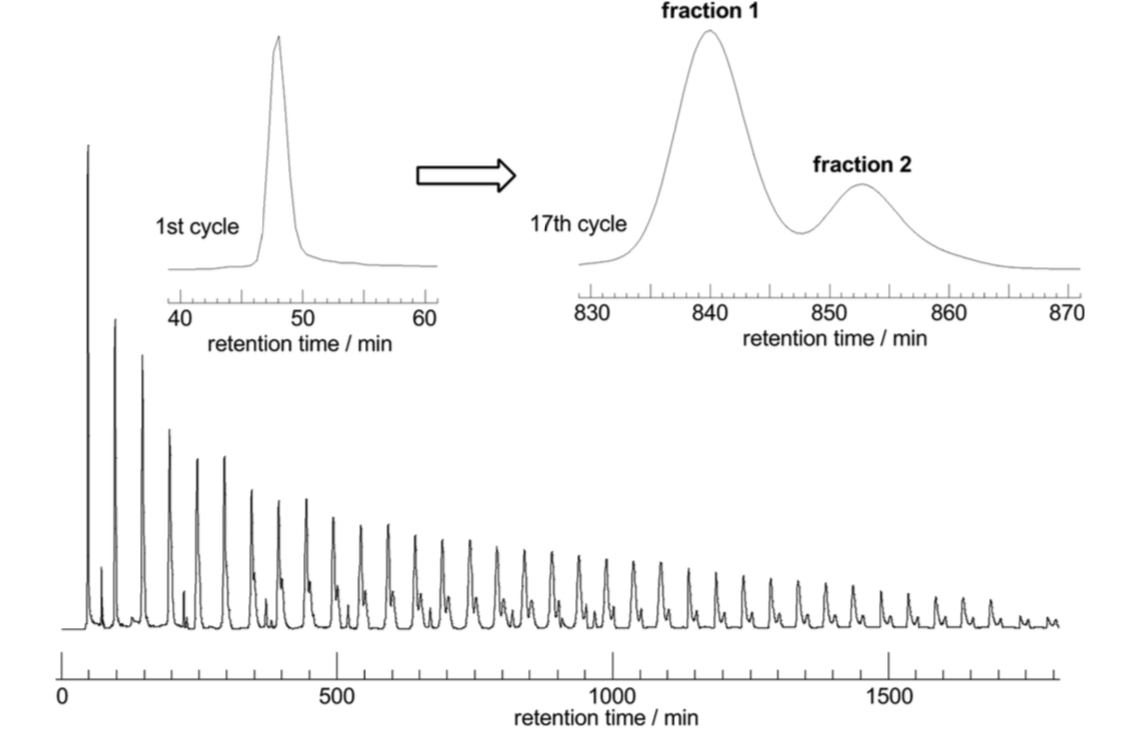
larger molecule
smaller molecule
Different sizes
Proposition (with Cantarella, Deguchi, & Uehara)
If each edge is subdivided equally to make \(\mathfrak{V}\) vertices total:
So the smaller molecule is predicted to be \(K_{3,3}\)!

Thank you!
References
The symplectic geometry of closed equilateral random walks in 3-space
J. Cantarella & C. Shonkwiler
Annals of Applied Probability 26 (2016), no. 1, 549–596
A fast direct sampling algorithm for equilateral closed polygons
J. Cantarella, B. Duplantier, C. Shonkwiler, & E. Uehara
Journal of Physics A 49 (2016), no. 27, 275202
Funding: Simons Foundation
Probability theory of random polygons from the quaternionic viewpoint
J. Cantarella, T. Deguchi, & C. Shonkwiler
Communications on Pure and Applied Mathematics 67 (2014), no. 10, 1658–1699
The expected total curvature of random polygons
J. Cantarella, A.Y. Grosberg, R. Kusner, & C. Shonkwiler
American Journal of Mathematics 137 (2015), no. 2, 411–438
Spherical geometry and the least symmetric triangle
L. Bowden, A. Haynes, C. Shonkwiler, & A. Shukert
Geometriae Dedicata (2018), https://doi.org/10.1007/s10711-018-0327-4
Random triangles and polygons in the plane
J. Cantarella, T. Needham, C. Shonkwiler, & G. Stewart
The American Mathematical Monthly, to appear, arXiv:1702.01027 [math.MG]