The (Symplectic) Geometry of Spaces of Frames
/sissa21
this talk!
Signal Analysis
Signal: \(v \in \mathbb{C}^d\)
Design: Choose \(f_1, \dots , f_n \in \mathbb{C}^d\)
Measurements: \(\langle f_1, v \rangle, \dots , \langle f_n, v \rangle \).
Goal: Reconstruct the signal \(v\) from \(F^* v\)
If \(F = \begin{bmatrix} f_1 & \cdots & f_n\end{bmatrix}\), the measurement vector is \(F^*v\).
Orthonormal Bases
If \(f_1,\dots , f_d\in \mathbb{C}^d\) form an orthonormal basis, then
\(v=\sum \langle f_k,v\rangle f_k = FF^* v\).
\(\Leftrightarrow FF^* = \mathrm{Id}_{d \times d}\)
This is fragile! What if a measurement gets lost?
Definition.
\(\{f_1,\dots, f_n\}\subset \mathbb{C}^d\) is a Parseval frame if \(\operatorname{Id}_{d\times d}=FF^*=f_1f_1^*+\dots+f_nf_n^*\).
The rows of \(F\) form an orthonormal set in \(\mathbb{C}^n\), so the space of all length-\(n\) Parseval frames in \(\mathbb{C}^d\) is the Stiefel manifold \(\operatorname{St}_d(\mathbb{C}^n)\).
real subvariety of \(\mathbb{C}^{d \times n}\)
Dealing with Erasures
Lost measurements are still a problem:
\(F=\begin{bmatrix} 1/\sqrt{2} & 1/\sqrt{2} & 0 \\ 0 & 0 & 1 \end{bmatrix}\)
An equal-norm Parseval frame (ENP frame) is a Parseval frame \(f_1,\dots , f_n\) with \(\|f_i\|^2=\|f_j\|^2\) for all \(i\) and \(j\).

Theorem [Casazza–Kovačevic, Goyal–Kovačevic–Kelner, Holmes–Paulsen]
ENP frames are optimal for signal reconstruction in the presence of additive white Gaussian noise and erasures.
real condition
\(\sum \|f_i\|^2=\operatorname{tr}F^*F=\operatorname{tr}FF^*=\operatorname{tr}\operatorname{Id}_{d \times d} = d\), so each \(\|f_i\|^2=\frac{d}{n}\).
Generalizations
More generally, we may want to consider
- frames with fixed frame vector norms: \(\|f_i\|^2=r_i\) for specified \(r_i>0\)
- frames with \(FF^*=S\) for specified positive-definite, Hermitian \(S\)
real conditions
The spaces of frames satisfying 1, 2, or both are only real subvarieties of \(\mathbb{C}^{d \times n}\).
Some Questions
The Frame Homotopy Conjecture [Larsen, 2002]
The space of ENP frames is path-connected.
Proved by Cahill–Mixon–Strawn in 2017.
Generalized Frame Homotopy Conjecture
For given positive-definite, Hermitian \(S\) and \(r_1,\dots , r_n>0\), the space of frames with \(FF^*=S\) and \(\|f_i\|^2=r_i\) is path-connected.
Genericity of Full Spark Frames
With probability 1, a random ENP frame has full spark—meaning every size-\(d\) subset of the \(f_i\) spans \(\mathbb{C}^d\).
frame with fixed \(FF^*\) and fixed \(\|f_1\|^2,\dots, \|f_n\|^2\)
Objects of Interest
We are interested in \(F=\begin{bmatrix}f_1 & f_2 & \cdots & f_n\end{bmatrix}\in \mathbb{C}^{d \times n}\) with
\(FF^* = S\)
and/or
\(\|f_1\|^2=r_1, \dots , \|f_n\|^2=r_n\).
Symplectic Geometry
Definition. A symplectic manifold is a smooth manifold \(M\) together with a closed, non-degenerate 2-form \({\omega \in \Omega^2(M)}\).
\((S^2,d\theta\wedge dz)\)
\((\mathbb{R}^2,dx \wedge dy) = (\mathbb{C},\frac{i}{2}dz \wedge d\bar{z})\)
\((S^2,\omega)\), where \(\omega_p(u,v) = (u \times v) \cdot p\)
\((\mathbb{R}^2,\omega)\) where \(\omega(u,v) = \langle i u, v \rangle \)
\((\mathbb{C}^n, \frac{i}{2} \sum dz_k \wedge d\overline{z}_k)\)
\((\mathbb{C}^{d \times N}, \omega)\) with \(\omega(X_1,X_2) = -\operatorname{Im} \operatorname{trace}(X_1^* X_2)\).
The name ‘complex group’ formerly proposed by me…has become more and more embarrassing through collision with the word ‘complex’ in the connotation of complex number. I therefore propose to replace it by the corresponding Greek adjective ‘symplectic’.
— Hermann Weyl
Volume
\(\omega^{\wedge n} = \omega \wedge \dots \wedge \omega\) is a volume form on \(M\), and induces a measure
called Liouville measure on \(M\).
If \(M\) is compact, this can be normalized to give a probability measure.
Functions and Symplectic Gradients
If \(H: M \to \mathbb{R}\) is smooth, then there exists a unique vector field \(X_H\) so that \({dH = \iota_{X_H}\omega}\), i.e.,
(\(X_H\) is the Hamiltonian vector field for \(H\) or the symplectic gradient of \(H\))
Example. \(H: (S^2, d\theta\wedge dz) \to \mathbb{R}\) given by \(H(\theta,z) = z\).
\(dH = dz = \iota_{\frac{\partial}{\partial \theta}}(d\theta\wedge dz)\), so \(X_H = \frac{\partial}{\partial \theta}\).


\(H\) is constant on orbits of \(X_H\):
\(\mathcal{L}_{X_H}(H) = dH(X_H)=\omega(X_H,X_H) = 0\)
Lie Group Actions

\(S^1=U(1)\) acts on \((S^2,d\theta \wedge dz)\) by
For \(r \in \mathbb{R} \simeq \mathfrak{u}(1)\), \(X_r = r\frac{\partial}{\partial \theta}\).
Let \(G\) be a Lie group, and let \(\mathfrak{g}\) be its Lie algebra. If \(G\) acts on \((M,\omega)\), then each \(V \in \mathfrak{g}\) determines a vector field \(X_V\) on \(M\) by
Lie Group Actions
Let \(G\) be a Lie group, and let \(\mathfrak{g}\) be its Lie algebra. If \(G\) acts on \((M,\omega)\), then each \(V \in \mathfrak{g}\) determines a vector field \(X_V\) on \(M\) by

\(SO(3)\) acts on \(S^2\) by rotations.
\(= (a,b,c) \times (x,y,z)\)
For \(V_{(a,b,c)} = \begin{bmatrix} 0 & -c & b \\ c & 0 & -a \\ -b & a & 0 \end{bmatrix} \in \mathfrak{so}(3)\),
\(X_{V_{(a,b,c)}}((x,y,z))\)
\(= (bz-cy)\frac{\partial}{\partial x} + (cx - az) \frac{\partial}{\partial y} +(ay - bx) \frac{\partial}{\partial z}\)
Symmetries and Conserved Quantities
Definition. A \(U(1)\) action on \((M,\omega)\) is Hamiltonian if there exists a map
so that \(d\mu = \iota_{X}\omega = \omega(X,\cdot)\), where \(X\) is the vector field generated by the action.
\(X = \frac{\partial}{\partial \theta}\)
\(\mu(\theta,z) = z\)
\(\iota_X\omega = \iota_{\frac{\partial}{\partial \theta}} d\theta \wedge dz = dz \)

Moment Maps
Definition. An action of \(G\) on \((M,\omega)\) is Hamiltonian if each one-parameter subgroup action is Hamiltonian. Equivalently, there exists a map
so that \(\omega_p(X_V, X) = D_p \mu(X)(V)\) for each \(p \in M\), \(X \in T_pM\), and \(V \in \mathfrak{g}\).

\(X_{V_{(a,b,c)}}(x,y,z) = (a,b,c) \times (x,y,z)\)
\((\iota_{X_{V_{(a,b,c)}}}\omega)_{(x,y,z)} = a dx + b dy + c dz \)
\(\mu(x,y,z)(V_{(a,b,c)}) = (x,y,z)\cdot(a,b,c)\)
Key Tools
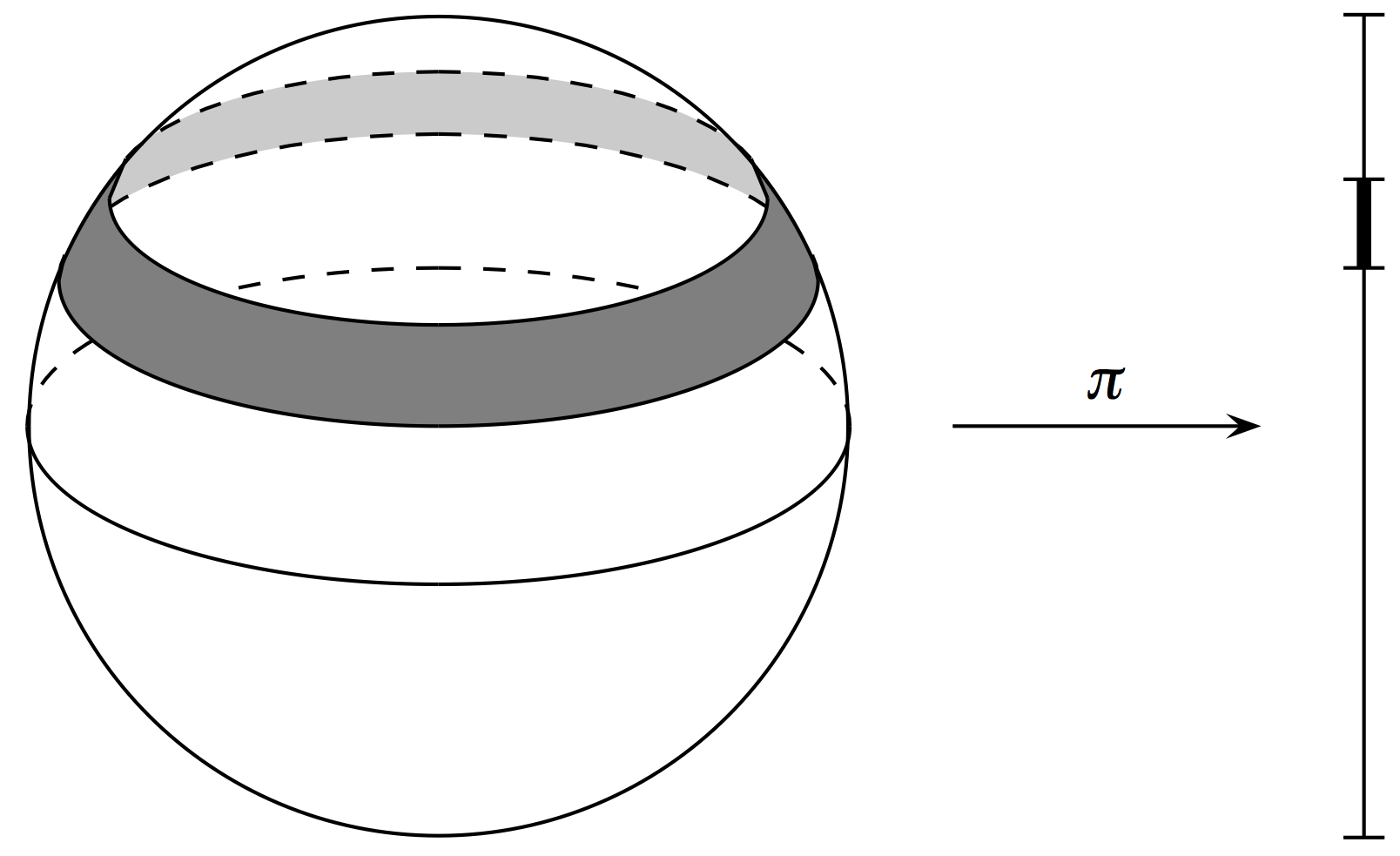
Theorem [Atiyah, Guillemin–Sternberg]
Let \((M^{2n},\omega)\) be a compact connected symplectic manifold with a Hamiltonian \(k\)-torus action with momentum map \(\mu: M \to \mathbb{R}^k\). Then
- the nonempty level sets of \(\mu\) are connected;
- the image of \(\mu\) is convex (called the moment polytope);
- the image of \(\mu\) is the convex hull of the images of fixed points of the action.
Key Tools
Theorem [Atiyah, Guillemin–Sternberg]
Let \((M^{2n},\omega)\) be a compact connected symplectic manifold with a Hamiltonian \(k\)-torus action with momentum map \(\mu: M \to \mathbb{R}^k\). Then
- the nonempty level sets of \(\mu\) are connected;
- the image of \(\mu\) is convex (called the moment polytope);
- the image of \(\mu\) is the convex hull of the images of fixed points of the action.

\(U(1)^2\) acts on \(\mathbb{CP}^2\) by
\((e^{i\theta_1},e^{i\theta_2})\cdot [z_0:z_1:z_1]:=[z_1:e^{i\theta_1}z_1:e^{i\theta_2}z_2]\)
Moment map:
\(\mu([z_0:z_1:z_2]=-\frac{1}{2(|z_0|^2+|z_1|^2+|z_2|^2)}(|z_1|^2,|z_2|^2)\)
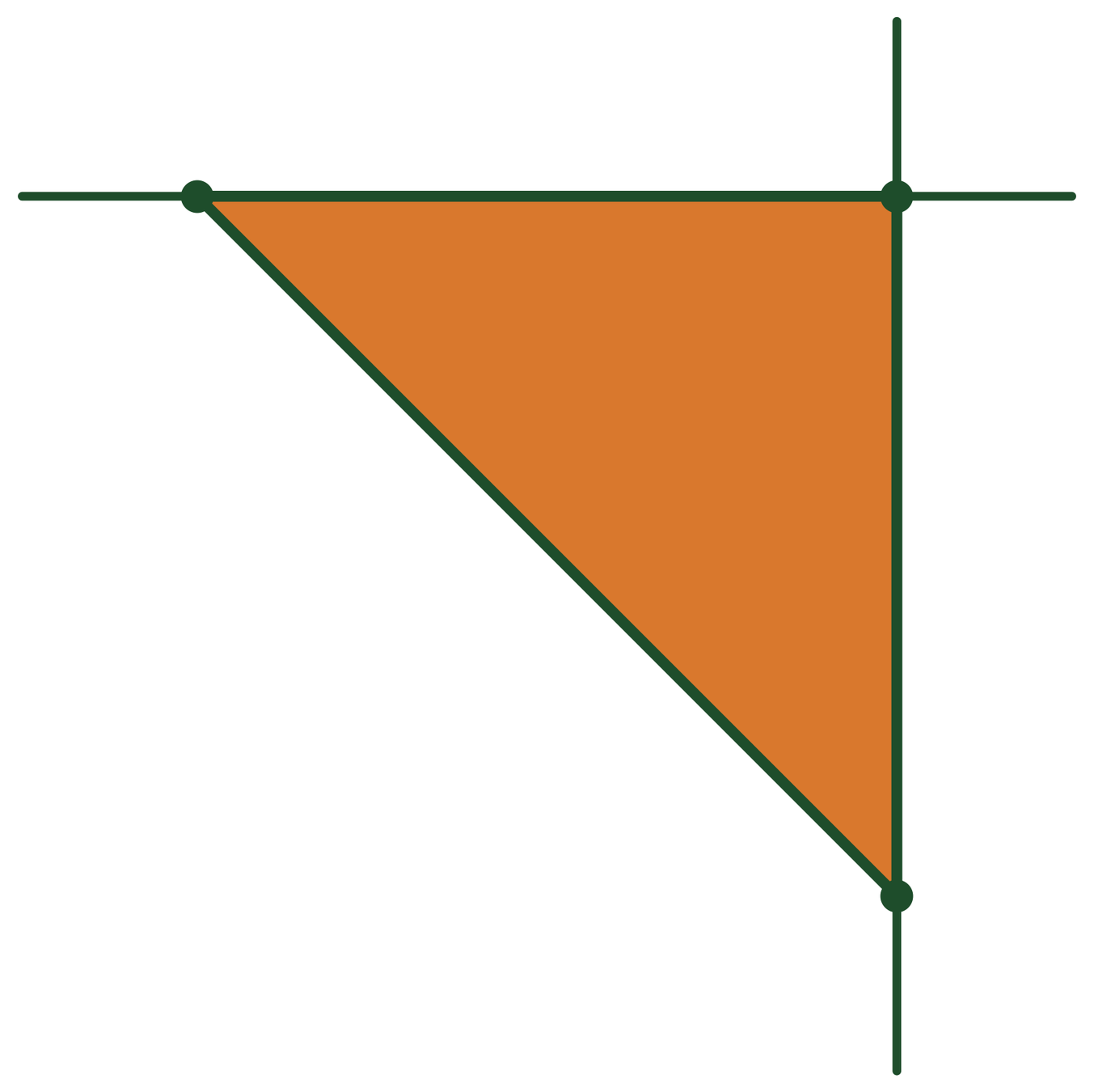
\((0,0)=\mu([1:0:0])\)
\((-\frac{1}{2},0)=\mu([0:1:0])\)
\((0,-\frac{1}{2})=\mu([0:0:1])\)
Theorem [Duistermaat–Heckman]
If \(k=n\), then the pushforward of Liouville measure to the moment polytope is a constant multiple of Lebesgue measure.
Symplectic Reduction
Theorem [Meyer, Marsden–Weinstein]
Let \(\mu: M \to \mathfrak{g}^*\) be the moment map for a Hamiltonian action of \(G\) on \((M,\omega)\). If \(\xi \in \mathfrak{g}^*\) is a regular value of \(\mu\) and \(\mathcal{O}_\xi\) is its coadjoint orbit, then
is a symplectic manifold with symplectic form \(\omega_{\text{red}}\) such that
\(\mu^{-1}(\mathcal{O}_\xi)\)
\(M //_\xi\, G = \mu^{-1}(\mathcal{O}_\xi)/G\)
\(M\)
\(\pi\)
\(\iota\)
A Circle Action on \(\mathbb{C}^d\)
Let \(U(1)\) act on \((\mathbb{C}^d,\omega_{\text{std}})\) by \(e^{it}\cdot \vec{v} = e^{it} \vec{v} \). The associated vector field is
so \((\iota_X\omega_{\text{std}})_{\vec{v}}(Y) = (\omega_{\text{std}})_{\vec{v}}(X,Y) = \langle iX,Y\rangle_{\vec{v}} = \langle -\vec{v},Y\rangle\).
The moment map is
since \(d\mu_{\vec{v}}(Y) = \left.\frac{d}{dt}\right|_{t=0} \left(-\frac{1}{2} \langle \vec{v} + tY, \vec{v} + tY\rangle\right) = \langle -\vec{v},Y\rangle\).
The symplectic reduction over \(-\frac{1}{2} \in \mathbb{R}\) is
\(\mathbb{C}^d//_{-\frac{1}{2}} U(1) = \mu^{-1}\left(-\frac{1}{2}\right)\!/U(1) \simeq \mathbb{CP}^{d-1}\).
Group Actions on Frames
What compact Lie groups act nicely on \(\mathbb{C}^{d \times n}\)?
- \(U(d)\) acts on the left
- \(U(n)\) acts on the right
- \(U(1)^d\) acts on the left
- \(U(1)^n\) acts on the right
Parseval frames
\(\mu_{U(d)}^{-1}(\operatorname{Id}_{d \times d})\)
fixed-norm frames
\(\mu_{U(1)^N}^{-1}\left(-\frac{r_1}{2},\dots , -\frac{r_n}{2}\right)\)
Parseval Frames and a Grassmannian
\(\mu_{U(d)}(F)=FF^*\), so
\(\mathbb{C}^{d \times n}//_{\operatorname{Id}_{d \times d}} U(d)\)
\(= \operatorname{St}_d(\mathbb{C}^n)/U(d)\)
\(= \mu_{U(d)}^{-1}(\operatorname{Id}_{d \times d})/U(d)\)
\(=\operatorname{Gr}_d(\mathbb{C}^n)\)
Theorem [Atiyah, Guillemin–Sternberg]
Let \((M^{2n},\omega)\) be a compact connected symplectic manifold with a Hamiltonian \(k\)-torus action with momentum map \(\mu: M \to \mathbb{R}^k\). Then
- the nonempty level sets of \(\mu\) are connected;
The Generalized Frame Homotopy Conjecture
Theorem [with Needham, ’21]
Let \(S\) be Hermitian and positive-definite and \(r_1,\dots , r_n > 0\). The space of frames with \(FF^*=S\) and \(\|f_1\|^2=r_1,\dots , \|f_n\|^2=r_n\) is either empty or path-connected.

(the non-emptiness condition is explicit and known)
Eigensteps
Example for ENP frames with \(N=6, d=3\):
The eigensteps of a frame \(F = \begin{bmatrix}f_1 & \cdots & f_n\end{bmatrix}\) are the eigenvalues \(\lambda_{kj}\) of the partial frame operators
Must satisfy \(\ldots \geq \lambda_{i,j} \geq \lambda_{i-1,j} \geq \lambda_{i,j+1} \geq \dots\)
Proposition [with Needham; cf. Flaschka–Millson]
The eigensteps of an ENP frame are coordinates of the moment map associated to a maximal torus action on (an open, dense subset of a quotient of) ENP frame space.
Corollary [using Duistermaat–Heckman]
The eigensteps of random ENP frames are distributed according to Lebesgue measure on the eigenstep polytope.
Some Results
Proposition [with Needham; cf. Flaschka–Millson]
The eigensteps of an ENP frame are coordinates of the moment map associated to a maximal torus action on ENP frame space.
\(\phi_1 \phi_1^* - \frac{1}{d}I_d\)
\(\phi_2 \phi_2^* - \frac{1}{d}I_d\)
\(\phi_3 \phi_3^* - \frac{1}{d}I_d\)
\(\phi_4 \phi_4^* - \frac{1}{d}I_d\)
\(\phi_5 \phi_5^* - \frac{1}{d}I_d\)
\(\phi_6 \phi_6^* - \frac{1}{d}I_d\)
\(\lambda_{2j}\)
\(\lambda_{3j}\)
\(\lambda_{4j}\)
Example
\(d=2,n=5\)
Genericity of Full Spark Frames
Proof sketch
The first \(d\) columns of \(F\) fail to be full spark only if
\(f_1f_1^*+\dots+f_df_d^*\)
has a zero eigenvalue; i.e., \(\lambda_{dd}=0\).
This is the fiber over a facet of the eigenstep polytope, and hence has measure zero.
By permutation invariance of the measure, the same is true for any \(d\) columns.
Theorem* [with Needham]
The spark-deficient frames have measure zero inside the space of ENP frames.
Similarly for any space with fixed \(FF^*\) and \(\|f_1\|^2,\dots,\|f_n\|^2\).
Questions
Real Frames. The symplectic machinery only seems to apply to complex frames; is there some analogous story for frames in \(\mathbb{R}^d\)?
Symplectic reductions correspond to GIT quotients; e.g.,
\(\mathbb{C}^{d \times n}/\!/\!_{\operatorname{Id}_{d \times d}} U(d) \simeq \mathbb{C}^{d \times n}/\!/\!_{\mathscr{L}}GL_n(\mathbb{C})\).
RIP Problem. What is the probability that a random ENP frame satisfies a Restricted Isometry Property?
\((1-\delta) \|v\|^2 \leq \|F^* v \|^2 \leq (1+\delta) \|v\|^2\) for all sufficiently sparse \(v\)
Thank you!
Funding: Simons Foundation
References
Symplectic geometry and connectivity of spaces of frames
Tom Needham and Clayton Shonkwiler
Advances in Computational Mathematics 47 (2021), no. 1, 5
The geometry of constrained random walks and an application to frame theory
Clayton Shonkwiler
2018 IEEE Statistical Signal Processing Workshop (SSP), 343–347