Frame Theory Basics

A frame in \(\mathbb{C}^d\) is a collection \(\{\phi_1,\dots ,\phi_N\}\subset \mathbb{C}^d\) so that

for some \(b\geq a > 0\) and for all \(v\in\mathbb{C}^d\).

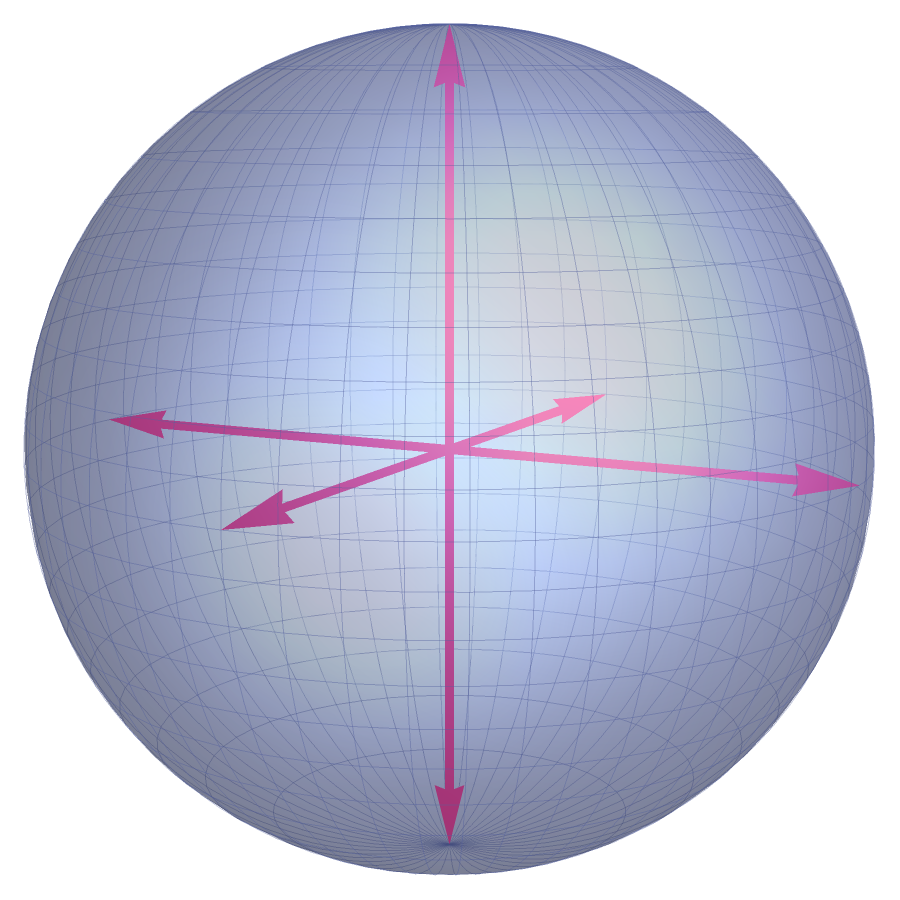
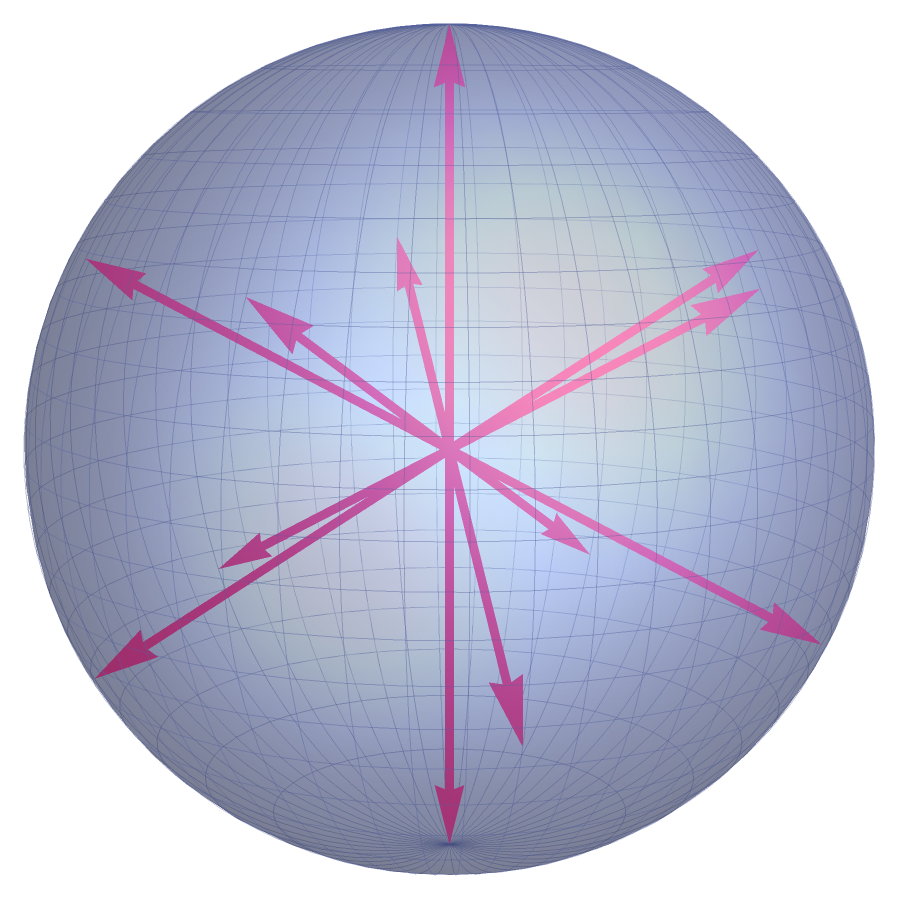
Why Care About FUNTFs?

• Tight frames are optimal for reconstructing signals in the presence of additive white noise.
• Using FUNTFs ensures each measurement has equal statistical power.
• FUNTFs are optimal for reconstructing signals in the presence of erasures.

Notation

\(\mathcal{F}^{N,d}_S\) is the collection of length-\(N\) frames in \(\mathbb{C}^d\) with frame operator \(S\); i.e., \(k \times N\) matrices \(\Phi\) with \(\Phi\Phi^*=S\).

Note that \(S\) is necessarily invertible and positive-definite.

\(\mathcal{F}^{N,d}_S(\vec{r})\) is the subset of \(\mathcal{F}^{N,d}_S\) of frames with \(\|\phi_i\| = r_i\).

In particular, the length-\(N\) FUNTFs in \(\mathbb{C}^d\) are precisely \(\mathcal{F}^{N,d}_{\frac{N}{d}I_d}(\vec{1})\) since

Symplecti-what?

Definition. A symplectic manifold is a smooth manifold \(M\) together with a closed, non-degenerate 2-form \({\omega \in \Omega^2(M)}\).

Complex Geometry

If \((M,\omega)\) is symplectic and \(g\) is a Riemannian metric on \(M\), then \(g(\cdot, \cdot) = \omega(\cdot , J \cdot)\) defines a compatible almost complex structure \(J\) on \(M\).

Consequences

A symplectic manifold must be even-dimensional (over \(\mathbb{R}\)).

Example

\(H: (S^2, d\theta\wedge dz) \to \mathbb{R}\) given by \(H(\theta,z) = z\).

\(dH = dz = \iota_{\frac{\partial}{\partial \theta}}\omega\), so \(X_H = \frac{\partial}{\partial \theta}\).

Lie Group Actions

Let \(G\) be a Lie group, and let \(\mathfrak{g}\) be its Lie algebra. If \(G\) acts on \((M,\omega)\), then each \(V \in \mathfrak{g}\) determines a vector field \(X_V\) on \(M\) by

Lie Group Actions

Let \(G\) be a Lie group, and let \(\mathfrak{g}\) be its Lie algebra. If \(G\) acts on \((M,\omega)\), then each \(V \in \mathfrak{g}\) determines a vector field \(X_V\) on \(M\) by

\(SO(3)\) acts on \(S^2\) by rotations. 

\(X_{V_{(a,b,c)}}((x,y,z)) = (bz-cy)\frac{\partial}{\partial x} + (cx - az) \frac{\partial}{\partial y} + (ay - bx) \frac{\partial}{\partial z}\)

For \(V_{(a,b,c)} = \begin{bmatrix} 0 & -c & b \\ c & 0 & -a \\ -b & a & 0 \end{bmatrix} \in \mathfrak{so}(3)\),

Moment(um) Maps

Definition. An action of \(U(1)\) on \((M,\omega)\) is Hamiltonian if there exists a map

so that \(d\mu = \iota_{X}\omega\), where \(X\) is the vector field generated by the circle action.

Moment(um) Maps

Definition. An action of \(G\) on \((M,\omega)\) is Hamiltonian if each one-parameter subgroup action is Hamiltonian. Equivalently, there exists a map

so that \(\omega_p(X_V, X) = D_p \mu(X)(V)\) for each \(p \in M\), \(X \in T_pM\), and \(V \in \mathfrak{g}\).

\(X_{V_{(a,b,c)}}(x,y,z) = (a,b,c) \times (x,y,z)\)

\((\iota_{X_{V_{(a,b,c)}}}\omega)_{(x,y,z)} = a dx + b dy + c dz \)

\(\mu(x,y,z)(V_{(a,b,c)}) = (x,y,z)\cdot(a,b,c)\)

A Circle Action on \(\mathbb{C}^d\)

Let \(U(1)\) act on \((\mathbb{C}^d,\omega_{\text{std}})\) by \(e^{it}\cdot \vec{v} = \vec{v} e^{-it}\).

The vector field generated by the circle action is

so \((\iota_X\omega_{\text{std}})_{\vec{v}}(Y) = (\omega_{\text{std}})_{\vec{v}}(X,Y) = \langle iX,Y\rangle_{\vec{v}} = \langle \vec{v},Y\rangle\).

Key Tool

Theorem (Atiyah, Guillemin–Sternberg). 

Let \((M^{2n},\omega)\) be a compact connected symplectic manifold with a Hamiltonian \(k\)-torus action with momentum map \(\mu: M \to \mathbb{R}^k\). Then

• the nonempty level sets of \(\mu\) are connected;
• the image of \(\mu\) is convex (called the moment polytope);
• the image of \(\mu\) is the convex hull of the images of fixed points of the action.

Symplectic Quotients

Theorem (Mayer, Marsden–Weinstein)

Let \(\mu: M \to \mathfrak{g}^*\) be the moment map for a Hamiltonian action of \(G\) on \((M,\omega)\). If \(\xi \in \mathfrak{g}^*\) is a regular value of \(\mu\) and \(\mathcal{O}_\xi\) is its coadjoint orbit, then

is a symplectic manifold with symplectic form \(\omega_{\text{red}}\) such that

\(\mu^{-1}(\mathcal{O}_\xi)\)

\(M /\!/\!_\xi\, G = \mu^{-1}(\mathcal{O}_\xi)/G\)

\(M\)

\(\pi\)

\(\iota\)

A Frame-Related Example

\(U(d)\) acts on \(\mathbb{C}^{d \times N}\) by left multiplication with moment map

given by

Grassmannians Enter the Story

Recall \(\mathcal{F}^{N,d}_{\frac{N}{d}I_d} =  \left\{\Phi : \Phi\Phi^* = \frac{N}{d}I_d\right\}\) is the space of tight frames which contains the FUNTFs.

is symplectic.

Observation.

...and Flag Manifolds

If \(S \in \mathcal{H}(d) \simeq \mathfrak{u}(d)^*\) is invertible and positive-definite, with eigenvalues \(\lambda_1 > \lambda_2 > \dots > \lambda_\ell > 0\) of multiplicities \(k_1, \dots , k_\ell\), then

where \(d_i = \sum_{j=1}^i k_j\).

is symplectic. \(\mu_{U(d)}^{-1}(\mathcal{O}_S)\) is the space of all frames whose frame operator is conjugate to \(S\); call it \(\widetilde{\mathcal{F}^{N,d}_S}\).

FUNTFs

Notice that FUNTF space \(\mathcal{F}^{N,d}_{\frac{N}{d}I_d}(\vec{1})\) is exactly

Since \(\mu:=\mu_{U(d)} \times \mu_{U(1)^N}\) is the moment map of the \(U(d) \times U(1)^N\) action on \(\mathbb{C}^{d \times N}\),

Reduction in Stages

By Atiyah’s connectedness theorem, this is connected!

The Frame Homotopy Conjecture

Theorem (Cahill–Mixon–Strawn ’17)

The space \(\mathcal{F}^{N,d}_{\frac{N}{d}I_d}(\vec{1})\) of length-\(N\) FUNTFs in \(\mathbb{C}^d\) is path-connected for all \(N \geq d\geq 1\).

Proof. By the foregoing, \(\mathcal{F}^{N,d}_{\frac{N}{d}I_d}(\vec{1})\) is connected.

Since this is a real algebraic set in \(\mathbb{C}^{d \times N} \simeq \mathbb{R}^{2dN}\), it is locally path-connected and therefore path-connected.