Frame Theory Basics

A frame in \(\mathbb{C}^k\) is a collection \(\{f_1,\dots ,f_N\}\subset \mathbb{C}^k\) so that

for some \(b\geq a > 0\) and for all \(v\in\mathbb{C}^k\).

Notation

\(\mathcal{F}^{N,k}_S\) is the collection of length-\(N\) frames in \(\mathbb{C}^k\) with frame operator \(S\); i.e., \(k \times N\) matrices \(F\) with \(FF^*=S\).

Note that \(S\) is necessarily invertible and positive-definite.

\(\mathcal{F}^{N,k}_S(\vec{r})\) is the subset of \(\mathcal{F}^{N,k}_S\) of frames with \(\|f_i\| = r_i\).

In particular, the length-\(N\) FUNTFs in \(\mathbb{C}^k\) are precisely \(\mathcal{F}^{N,k}_{\frac{N}{k}I_k}(\vec{1})\) since

Symplecti-what?

Definition. A symplectic manifold is a smooth manifold \(M\) together with a closed, non-degenerate 2-form \({\omega \in \Omega^2(M)}\).

Complex Geometry

If \((M,\omega)\) is symplectic and \(g\) is a Riemannian metric on \(M\), then \(g(\cdot, \cdot) = \omega(\cdot , J \cdot)\) defines a compatible almost complex structure \(J\) on \(M\).

Consequences

A symplectic manifold must be even-dimensional (over \(\mathbb{R}\)).

Example

\(H: (S^2, d\theta\wedge dz) \to \mathbb{R}\) given by \(H(\theta,z) = z\).

\(dH = dz = \iota_{\frac{\partial}{\partial \theta}}\omega\), so \(X_H = \frac{\partial}{\partial \theta}\).

Lie Group Actions

Let \(G\) be a Lie group, and let \(\mathfrak{g}\) be its Lie algebra. If \(G\) acts on \((M,\omega)\), then each \(V \in \mathfrak{g}\) determines a vector field \(X_V\) on \(M\) by

Lie Group Actions

Let \(G\) be a Lie group, and let \(\mathfrak{g}\) be its Lie algebra. If \(G\) acts on \((M,\omega)\), then each \(V \in \mathfrak{g}\) determines a vector field \(X_V\) on \(M\) by

\(SO(3)\) acts on \(S^2\) by rotations. 

\(X_{V_{(a,b,c)}}((x,y,z)) = (bz-cy)\frac{\partial}{\partial x} + (cx - az) \frac{\partial}{\partial y} + (ay - bx) \frac{\partial}{\partial z}\)

For \(V_{(a,b,c)} = \begin{bmatrix} 0 & -c & b \\ c & 0 & -a \\ -b & a & 0 \end{bmatrix} \in \mathfrak{so}(3)\),

Moment(um) Maps

Definition. An action of \(U(1)\) on \((M,\omega)\) is Hamiltonian if there exists a map

so that \(d\mu = \iota_{X}\omega\), where \(X\) is the vector field generated by the circle action.

Moment(um) Maps

Definition. An action of \(G\) on \((M,\omega)\) is Hamiltonian if each one-parameter subgroup action is Hamiltonian. Equivalently, there exists a map

so that \(\omega_p(X_V, X) = D_p \mu(X)(V)\) for each \(p \in M\), \(X \in T_pM\), and \(V \in \mathfrak{g}\).

\(X_{V_{(a,b,c)}}(x,y,z) = (a,b,c) \times (x,y,z)\)

\((\iota_{X_{V_{(a,b,c)}}}\omega)_{(x,y,z)} = a dx + b dy + c dz \)

\(\mu(x,y,z)(V_{(a,b,c)}) = (x,y,z)\cdot(a,b,c)\)

A Circle Action on \(\mathbb{C}^k\)

Let \(U(1)\) act on \((\mathbb{C}^k,\omega_{\text{std}})\) by scalar multiplication.

The vector field generated by the circle action is

so \((\iota_X\omega_{\text{std}})_{\vec{v}}(Y) = (\omega_{\text{std}})_{\vec{v}}(X,Y) = \langle iX,Y\rangle_{\vec{v}} = \langle -\vec{v},Y\rangle\).

The Big Guns

Theorem (Atiyah, Guillemin–Sternberg). 

Let \((M^{2n},\omega)\) be a compact connected symplectic manifold with a Hamiltonian \(d\)-torus action with momentum map \(\mu: M \to \mathbb{R}^d\). Then

• the nonempty level sets of \(\mu\) are connected;
• the image of \(\mu\) is convex (called the moment polytope);
• the image of \(\mu\) is the convex hull of the images of fixed points of the action.

Theorem (Duistermaat–Heckman)

The pushforward of Liouville measure on \((M^{2n},\omega)\) to the moment polytope is absolutely continuous w.r.t. Lebesgue measure, with continuous, piecewise-polynomial density of degree \(\leq n-d\).

Example

Theorem (Archimedes)

Let \(\mu: S^2 \to \mathbb{R}\) be given by \(\mu(x,y,z) = z\). Pushing forward the uniform measure on \(S^2\) to the image \([-1,1]\) gives Lebesgue measure.

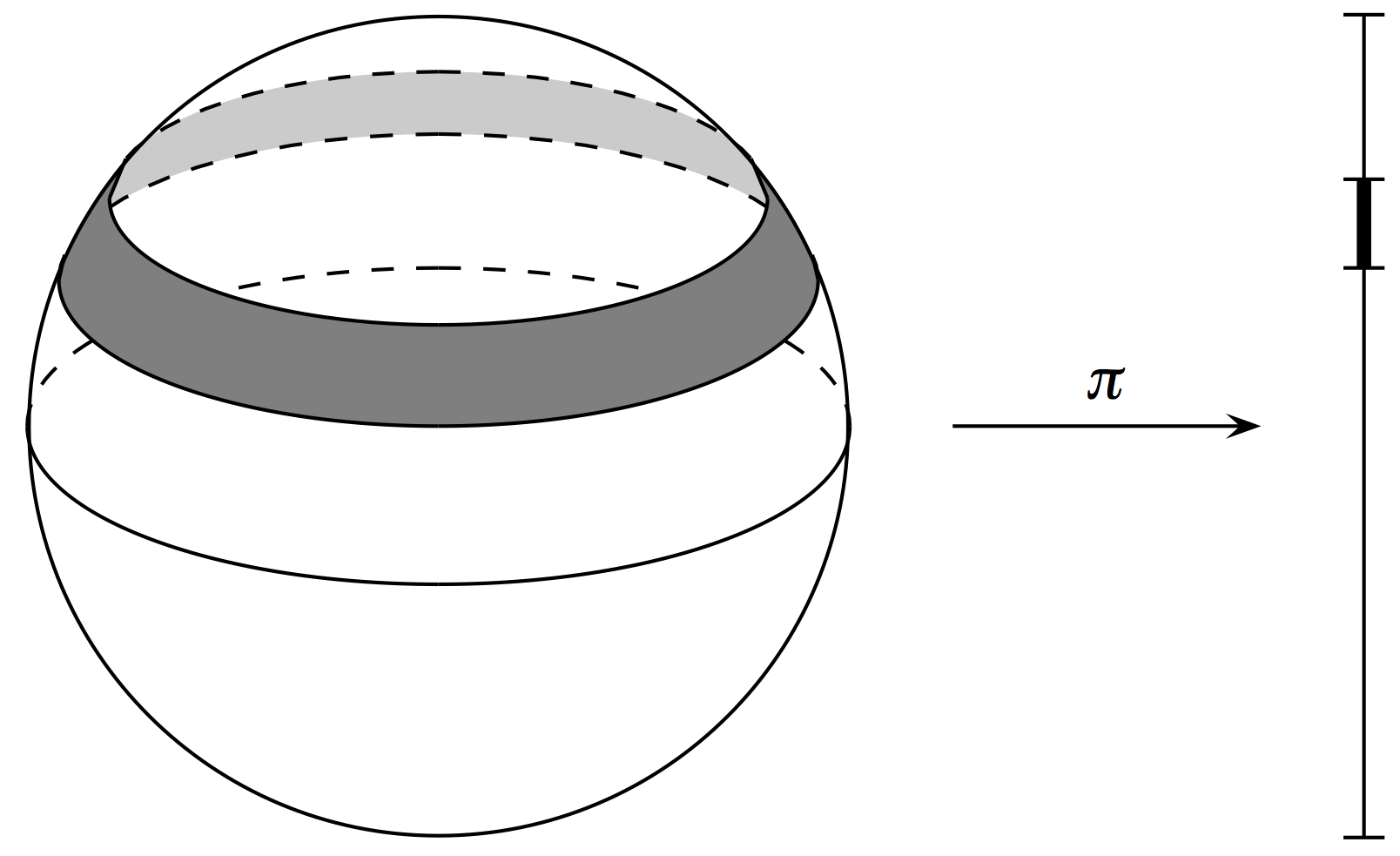
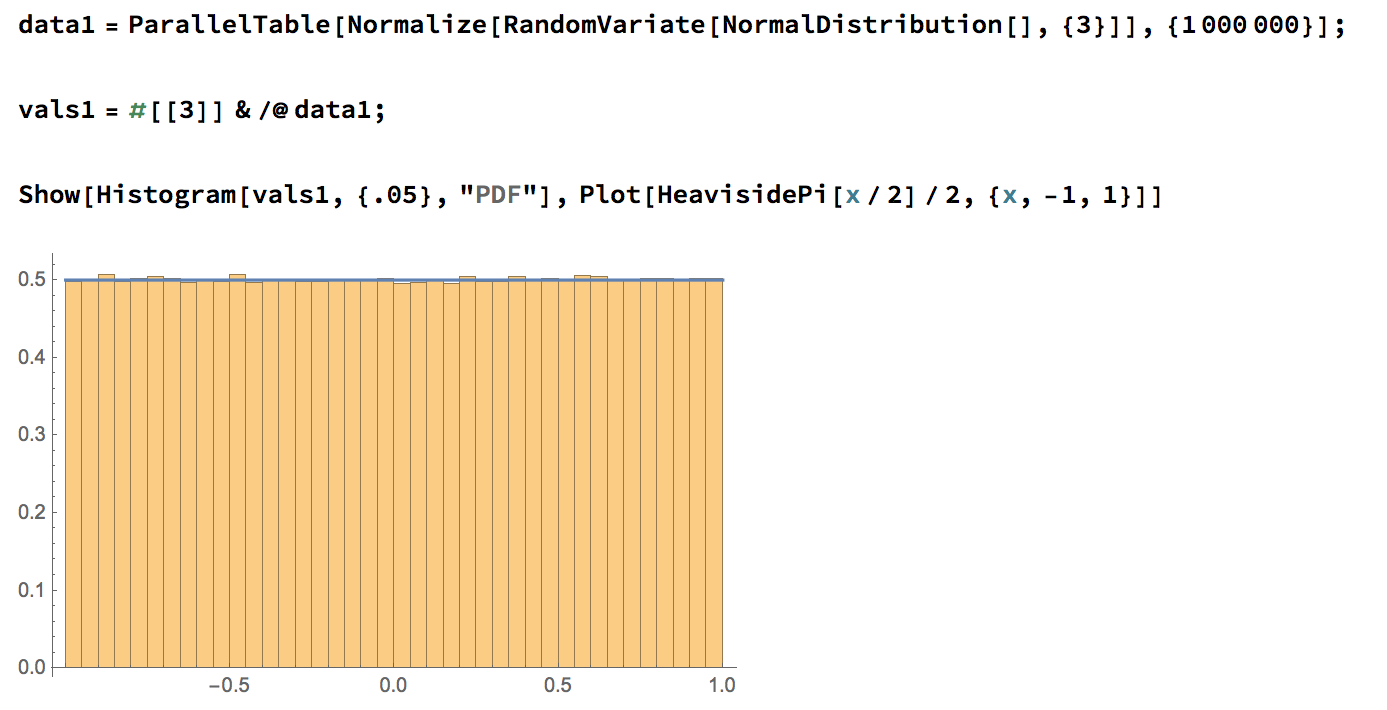
Example 2

Proposition. If we rotate both factors of \(S^2 \times S^2\) simultaneously around the \(z\)-axis, the moment map is \(((x_1,y_1,z_1),(x_2,y_2,z_2))\mapsto z_1 + z_2\), and the pushforward measure on \([-2,2]\) has density given by the triangle function.

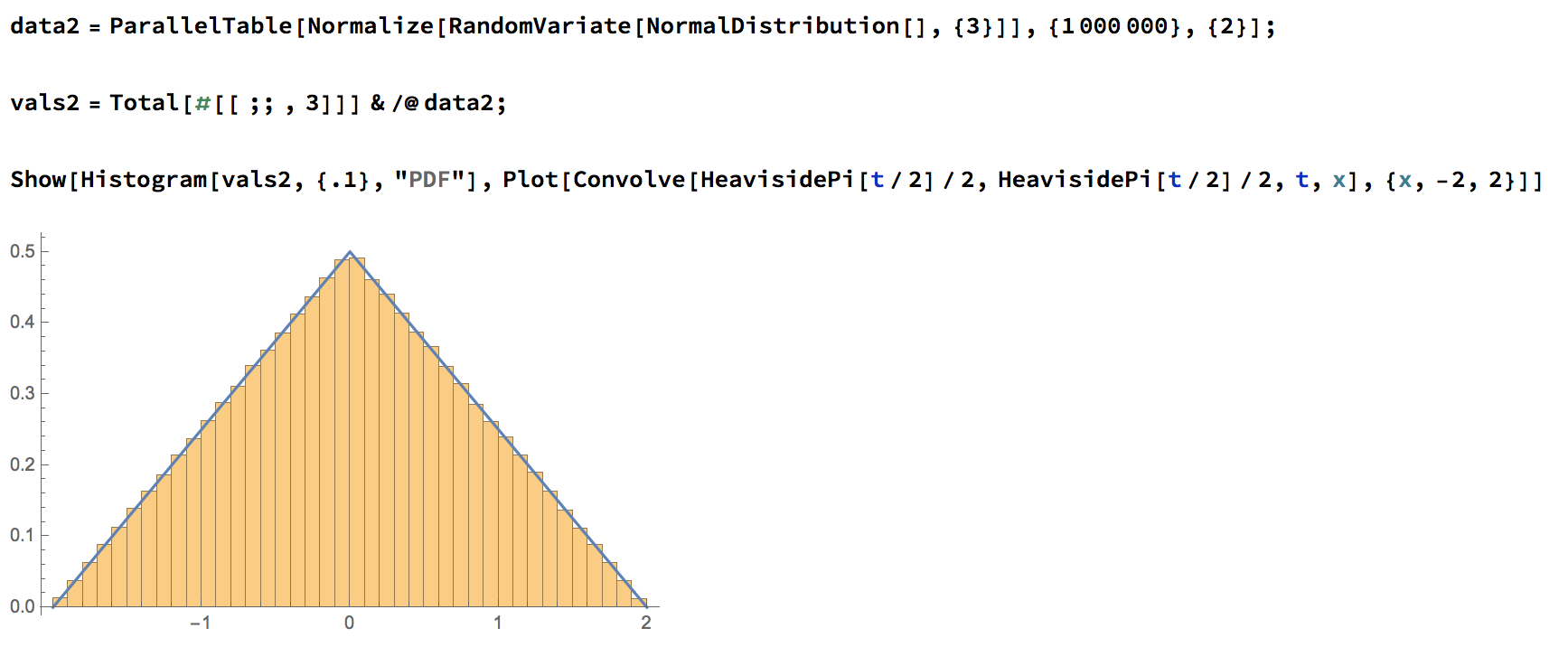
Complex Example

The \(\mathbb{T}^2 = U(1) \times U(1)\) action on \(\mathbb{CP}^2\) given by

has moment map

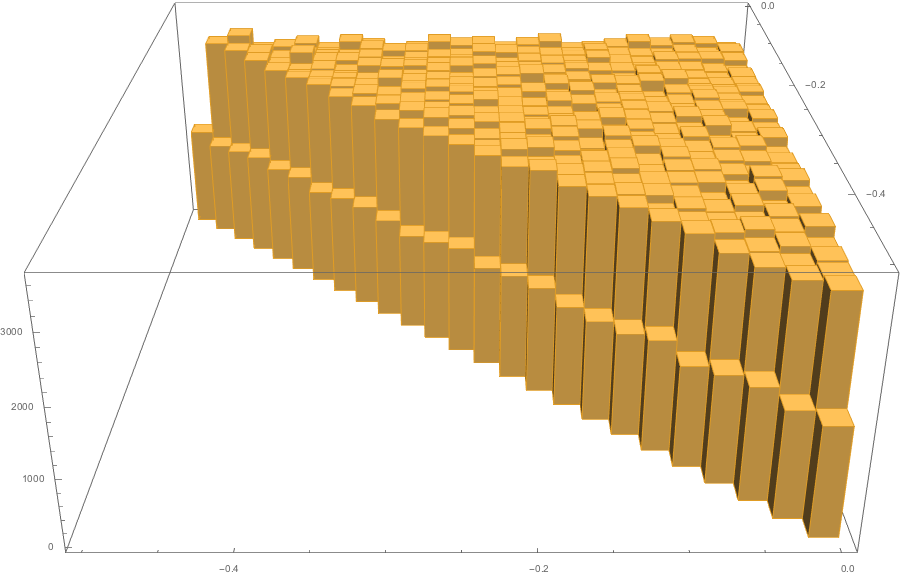
Symplectic Quotients

Theorem (Mayer, Marsden–Weinstein)

Let \(\mu: M \to \mathfrak{g}^*\) be the moment map for a Hamiltonian action of \(G\) on \((M,\omega)\). If \(\xi \in \mathfrak{g}^*\) is a regular value of \(\mu\) and \(\mathcal{O}_\xi\) is its coadjoint orbit, then

is a symplectic manifold with symplectic form \(\omega_{\text{red}}\) such that

\(\mu^{-1}(\mathcal{O}_\xi)\)

\(M /\!/\!_\xi\, G = \mu^{-1}(\mathcal{O}_\xi)/G\)

\(M\)

\(\pi\)

\(\iota\)

A Frame-Related Example

\(U(k)\) acts on \(\mathbb{C}^{k \times N}\) by left multiplication with moment map

given by

Grassmannians Enter the Story

Recall \(\mathcal{F}^{N,k}_{\frac{N}{k}I_k} =  \left\{F : FF^* = \frac{N}{k}I_k\right\}\) is the space of tight frames which contains the FUNTFs.

is symplectic.

Observation.

...and Flag Manifolds

If \(S \in \mathcal{H}(k) \simeq \mathfrak{u}(k)^*\) is invertible and positive-definite, with eigenvalues \(\lambda_1 > \lambda_2 > \dots > \lambda_\ell > 0\) of multiplicities \(k_1, \dots , k_\ell\), then

where \(d_i = \sum_{j=1}^i k_j\).

is symplectic. \(\mu^{-1}(\mathcal{O}_S)\) is the space of all frames whose frame operator is conjugate to \(S\); call it \(\widetilde{\mathcal{F}^{N,k}_S}\).

FUNTFs

Notice that FUNTF space \(\mathcal{F}_{\frac{N}{k}I_k}(\vec{1})\) is exactly

The Frame Homotopy Conjecture

Theorem (Cahill–Mixon–Strawn ’17)

The space \(\mathcal{F}^{N,k}_{\frac{N}{k}I_k}(\vec{1})\) of length-\(N\) FUNTFs in \(\mathbb{C}^k\) is path-connected for all \(N \geq k\geq 2\).