The Geometry of Topologically Constrained Random Walks
Statistical physics viewpoint
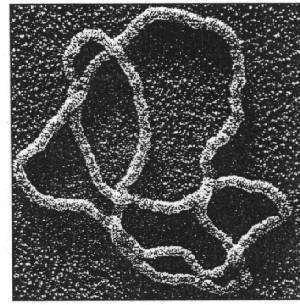
A ring polymer in solution takes on an ensemble of random shapes, with topology (knot type!) as the unique conserved quantity.
Knotted DNA
Wassermann et al.
Science 229, 171–174
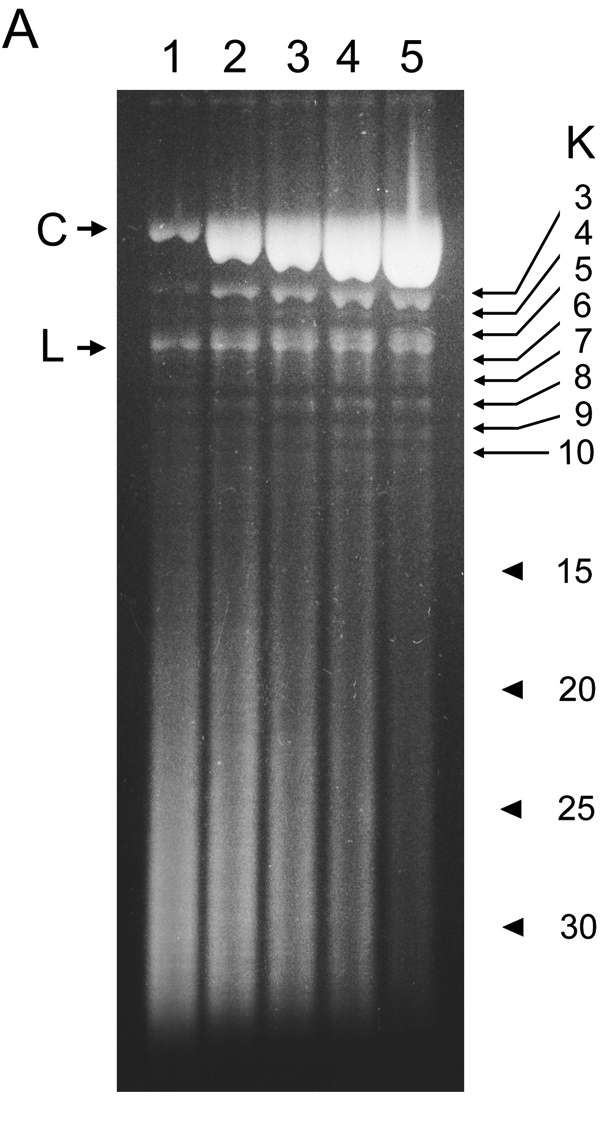
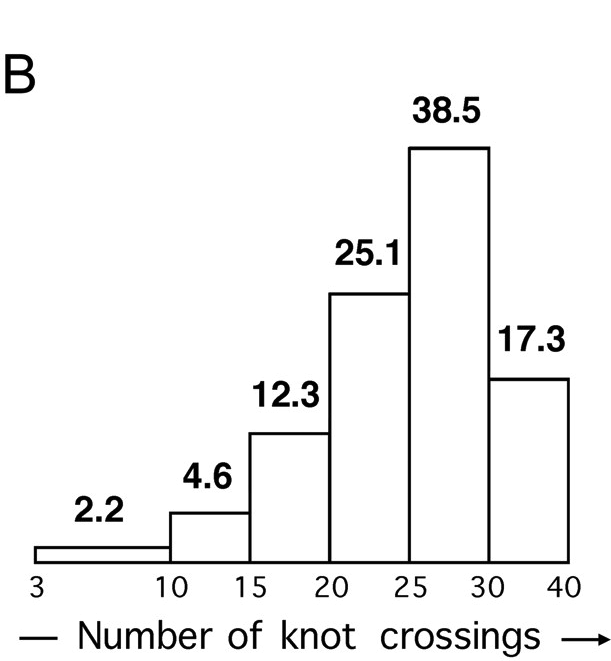
Knot complexity in DNA from P4 tailless mutants
Arsuaga et al., PNAS 99 (2002), 5373–5377
Is this surprising?
Synthetic Chemistry
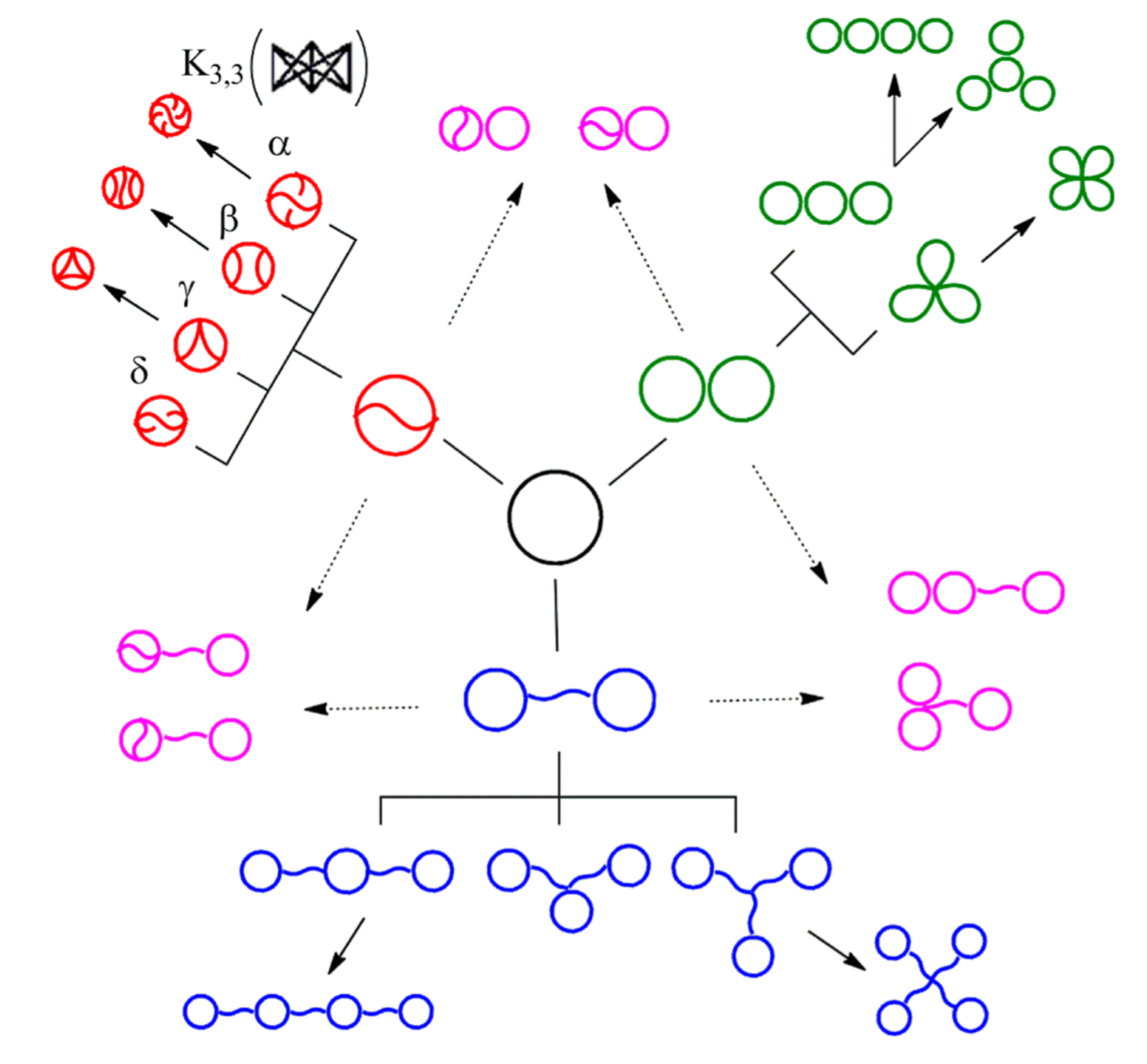
A Cambrian explosion of topological polymers
Tezuka Lab, Tokyo
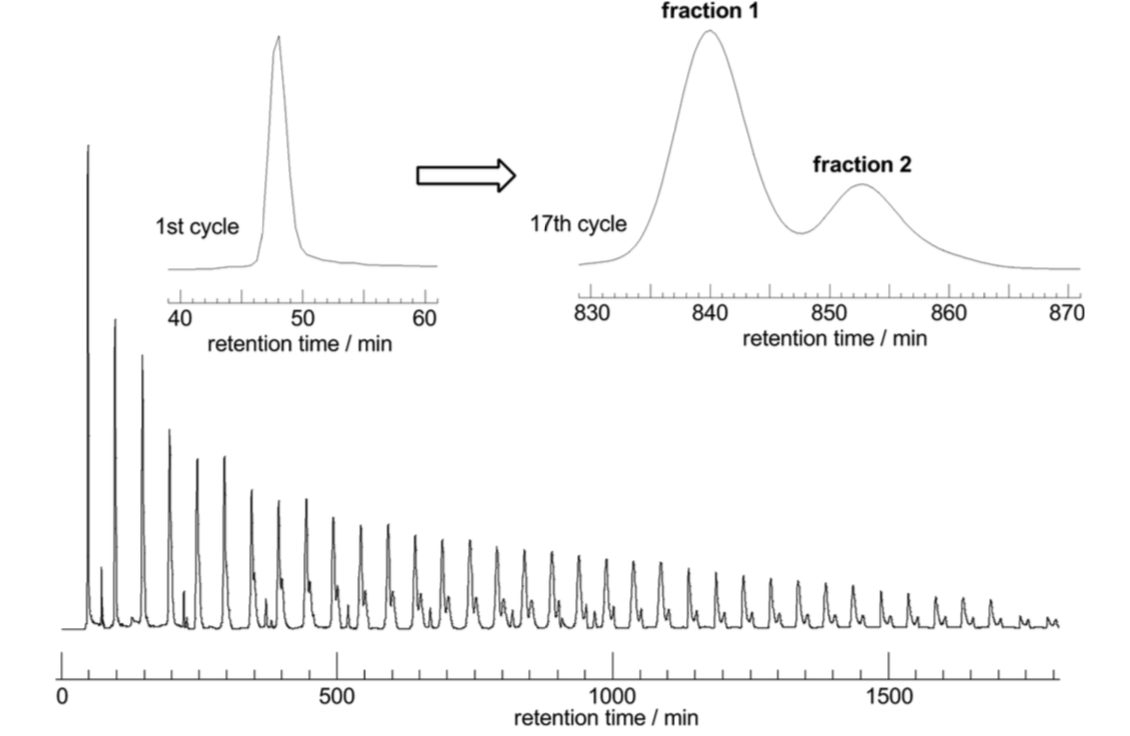
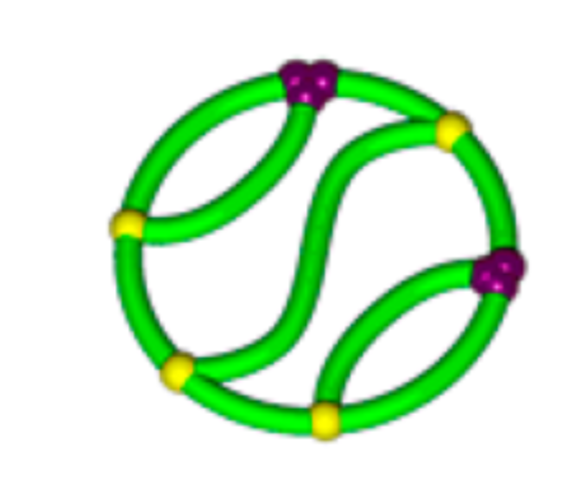
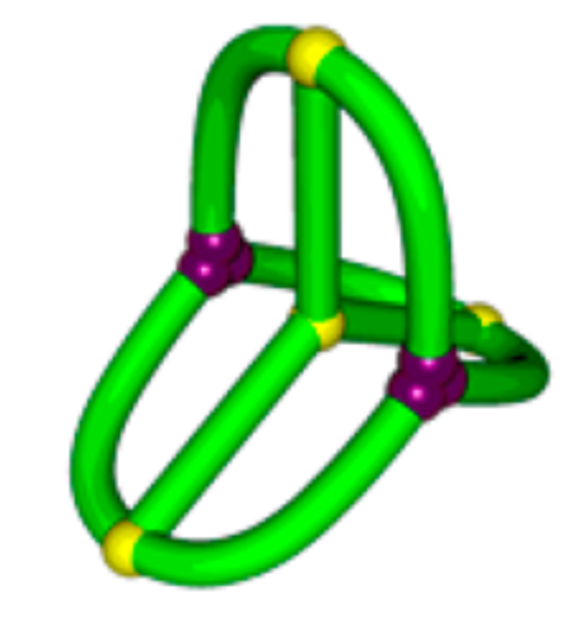
How do we know which is smaller?
The hunt for a polymer \(K_{3,3}\)
Statistical physics viewpoint
A polymer in solution takes on an ensemble of random shapes, with topology as the unique conserved quantity.
Modern polymer physics is based on the analogy between a polymer chain and a random walk.
– Alexander Grosberg
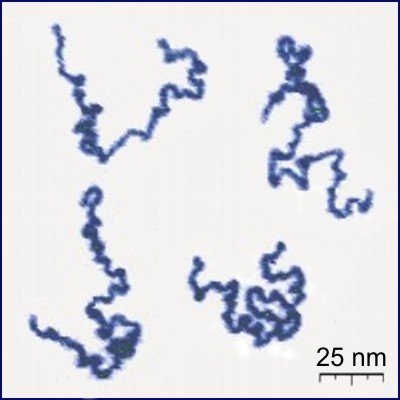
Protonated P2VP
Roiter/Minko
Clarkson University
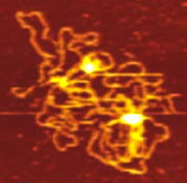
Plasmid DNA
Alonso–Sarduy, Dietler Lab
EPF Lausanne
Sampling random walks in \(\mathbb{R}^3\) is easy
Generate \(n\) independent uniform random points in \(\mathbb{R}^3\) according to your favorite probability distribution and treat them as an ordered list of edge vectors.

...but sampling random rings is hard

Alvarado, Calvo, Millett, J. Stat. Phys. 143 (2011), 102–138
Ansatz
Topologically constrained random walk \(\Leftrightarrow\) point in some (nice!) configuration space
Knowledge of the (differential, symplectic, algebraic) geometry of these conformation spaces leads to both
theorems and fast numerical algorithms for studying and TCRWs in \(\mathbb{R}^3\).
The (symplectic) geometry of random polygons
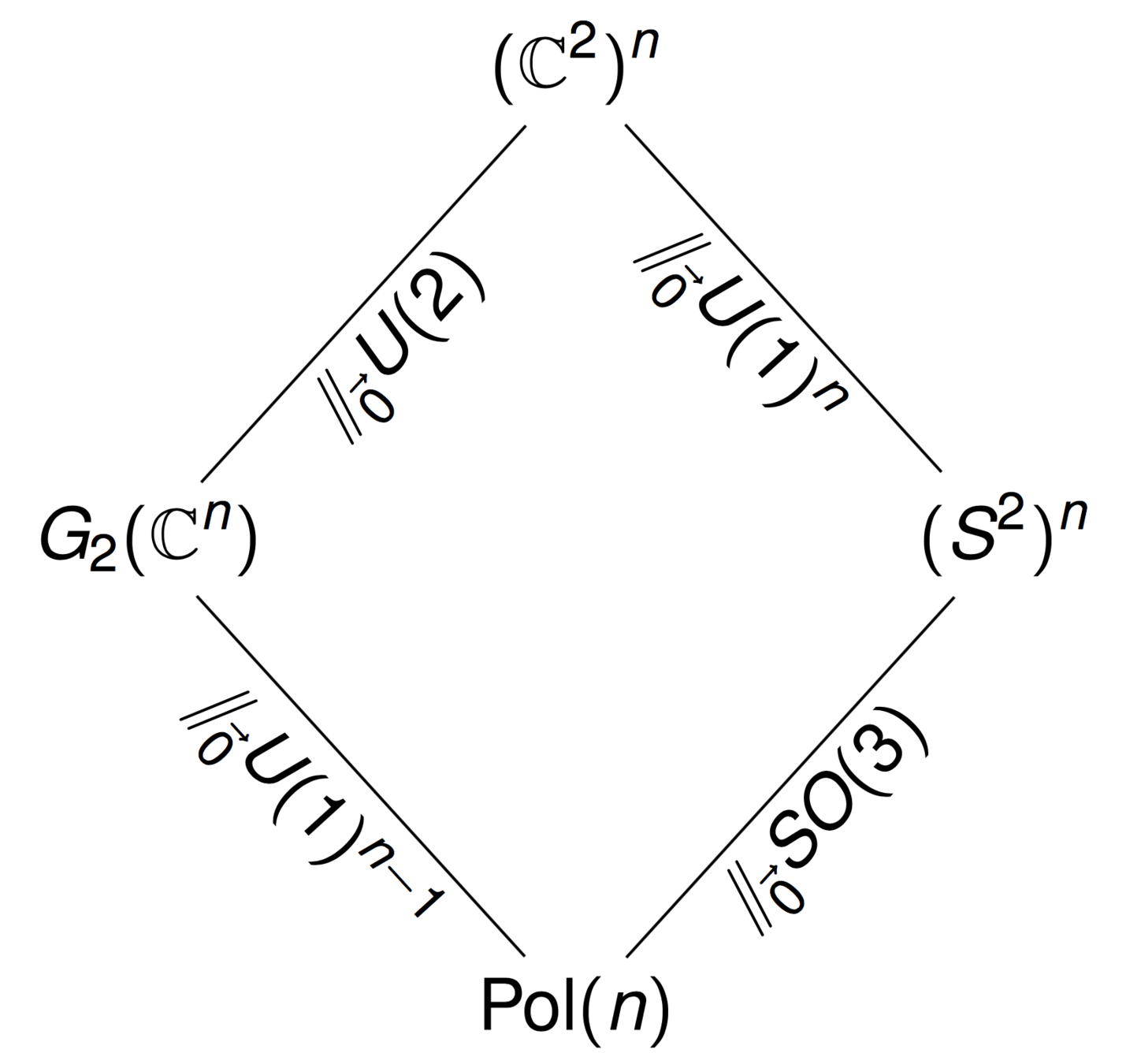
Kapovich–Millson, Hausmann–Knutson, Howard–Manon–Millson
Polygons and Grassmannians
Let \(P \in G_2(\mathbb{C}^n)\) and let \((\vec{u},\vec{v})\) be an orthonormal basis for \(P\).
\(q_\ell := u_\ell + v_\ell \mathbf{j} \in \mathbb{H}\)
\(\vec{e}_\ell := \overline{q}_\ell \mathbf{i} q_\ell\) is purely imaginary.
Proposition. \(\vec{e}_1, \dots , \vec{e}_n\) form the edges of a closed polygon in \(\mathbb{R}^3\) of perimeter 2.
\(\sum \vec{e}_\ell = \sum (\overline{u}_\ell - v_\ell \mathbf{j})\mathbf{i}(u_\ell + \mathbf{i}v_\ell) \mathbf{i}\)
\(\sum |\vec{e}_\ell| = \sum u_\ell \overline{u}_\ell + v_\ell \overline{v}_\ell = \|\vec{u}\|^2 + \|\vec{v}\|^2 = 2\)
\(=\sum \mathbf{i}(\overline{u}_\ell u_\ell - \overline{v}_\ell v_\ell+2 \overline{u}_\ell v_\ell \mathbf{j})\)
\( =\left(\|\vec{u}\|^2 - \|\vec{v}\|^2 + 2\langle \vec{u},\vec{v}\rangle\mathbf{j} \right)\)
\(=0\)
Grassmannians and framed polygons
This is really a story about framed polygons; the map \(q \mapsto [\overline{q}\mathbf{i}q \,|\, \overline{q}\mathbf{j}q \,|\, \overline{q}\mathbf{k}q]\) is just the standard double covering of \(SO(3)\) by \(SU(2) \simeq S^3\).
The symmetric measure
Definition [w/ Cantarella & Deguchi]
The symmetric measure on \(n\)-gons of perimeter 2 up to translation and rotation is the pushforward of Haar measure on \(G_2(\mathbb{C}^n)\).
Therefore, \(U(n)\) acts transitively on \(n\)-gons and preserves the symmetric measure.
Some consequences
Sampling is easy: generate 2 random Gaussians in \(\mathbb{C}^n\) and apply Gram–Schmidt. This is \(O(n)\) complexity!
Theorem [w/ Cantarella, Grosberg, Kusner]
The expected total curvature of a random space \(n\)-gon is exactly
\(\frac{\pi}{2}n + \frac{\pi}{4} \frac{2n}{2n-3}\).
Corollary
At least \(\frac{1}{3}\) of hexagons and \(\frac{1}{11}\) of heptagons are knotted.

A general result
Theorem [w/ Cantarella & Deguchi, also Zirbel–Millett]
For any probability distribution on \(n\)-gons which is invariant under permuting edges, the expected squared radius of gyration (mean squared distance to the center of mass) is
Corollary. For the symmetric measure, \(E[\text{Gyradius}]=\frac{1}{2n}\).
Corollary. For equilateral polygons with unit edges, \(E[\text{Gyradius}] = \frac{n+1}{12}\).
Corollary. For standard Gaussian polygons, \(E[\text{Gyradius}]=\frac{n^2-1}{4n}\).
Planar polygons and \(G_2(\mathbb{R}^n)\)
There’s a similar story for planar polygons using complex numbers rather than quaternions and \(z\mapsto z^2\) rather than \(q \mapsto \overline{q} \mathbf{i}q\)


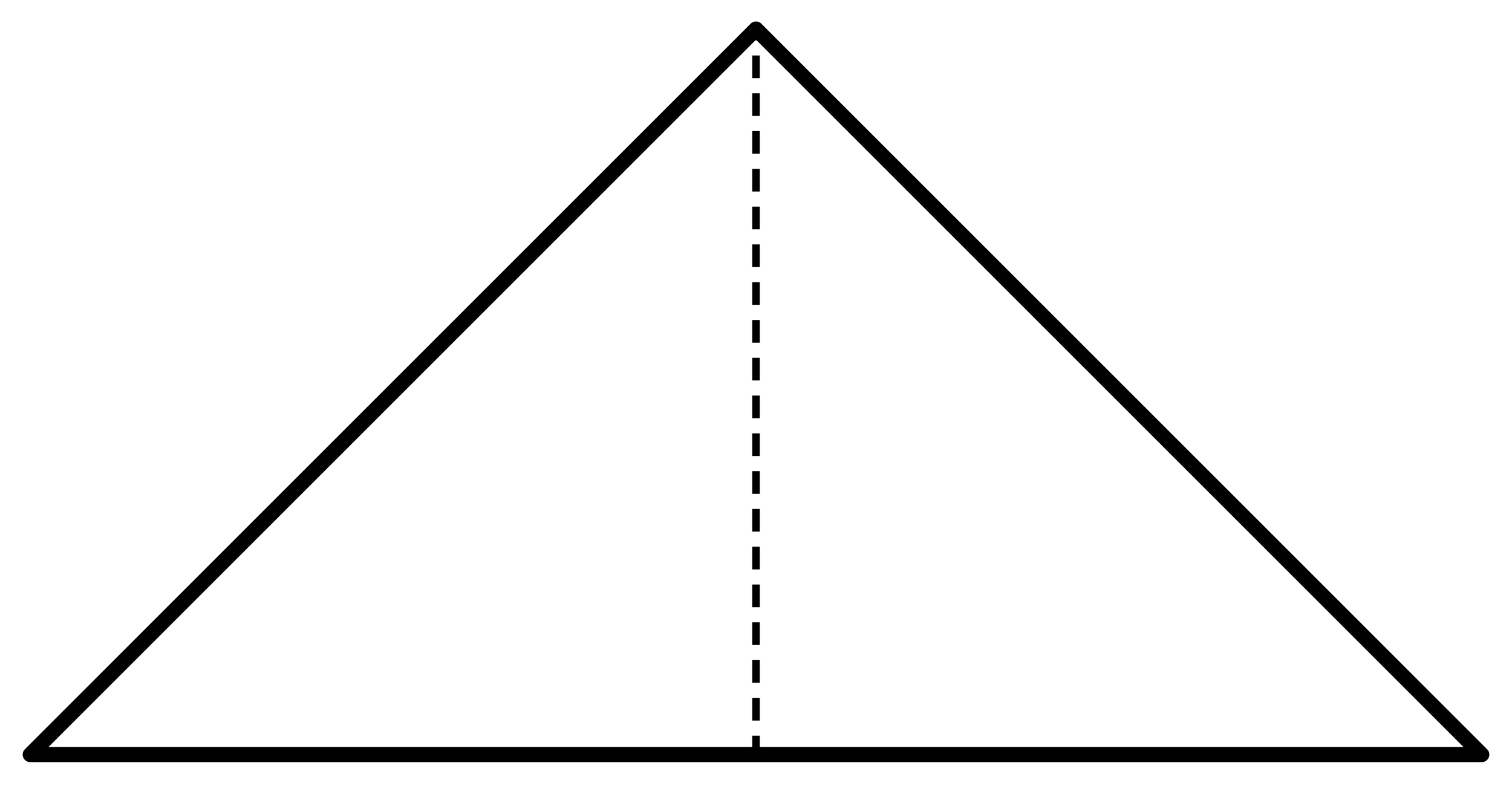
Obtuse triangles
\(\mathbb{P}(\text{obtuse})=\frac{1}{4\pi}\text{Area} = \frac{24}{4\pi} \int_R d\theta dz\)


Theorem [w/ Cantarella, Needham, Stewart]
The probability that a random triangle is obtuse is
\(\frac{3}{2}-\frac{3\ln 2}{\pi}\approx0.838\)
What is the least symmetric triangle?

Symmetric triangles
Isosceles
triangles
Degenerate
triangles

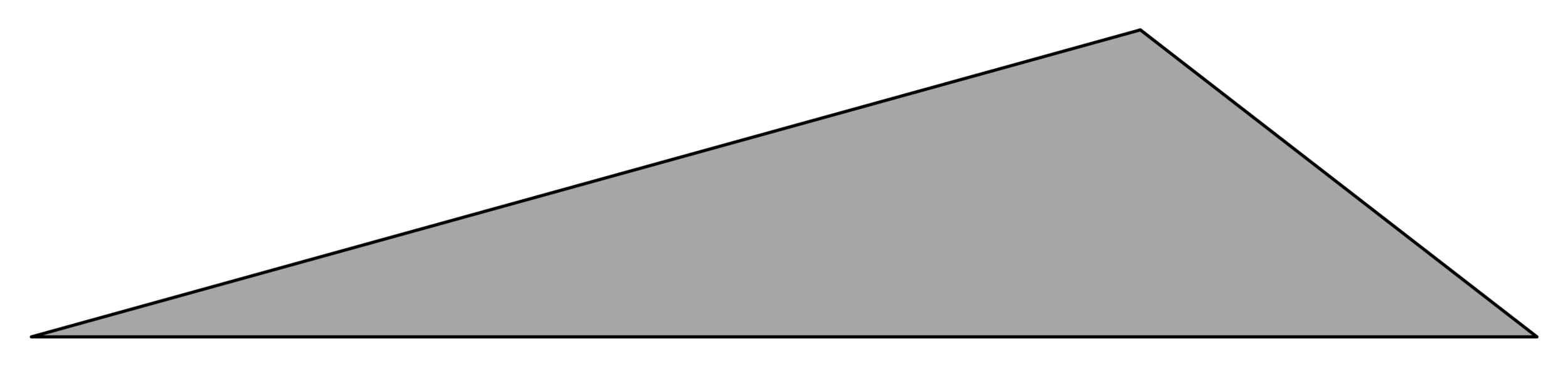
The least symmetric triangle
Theorem [with Bowden, Haynes, Shukert]
The least symmetric triangle has side length ratio
Sylvester’s Four Point Problem
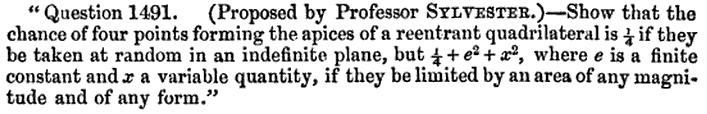

convex
reflex/reentrant
self-intersecting
Modern Reformulation: What is the probability that all vertices of a random quadrilateral lie on its convex hull?
The answer
Theorem [w/ Cantarella, Needham, Stewart]
Convex, reflex, and self-intersecting quadrilaterals are all equiprobable.

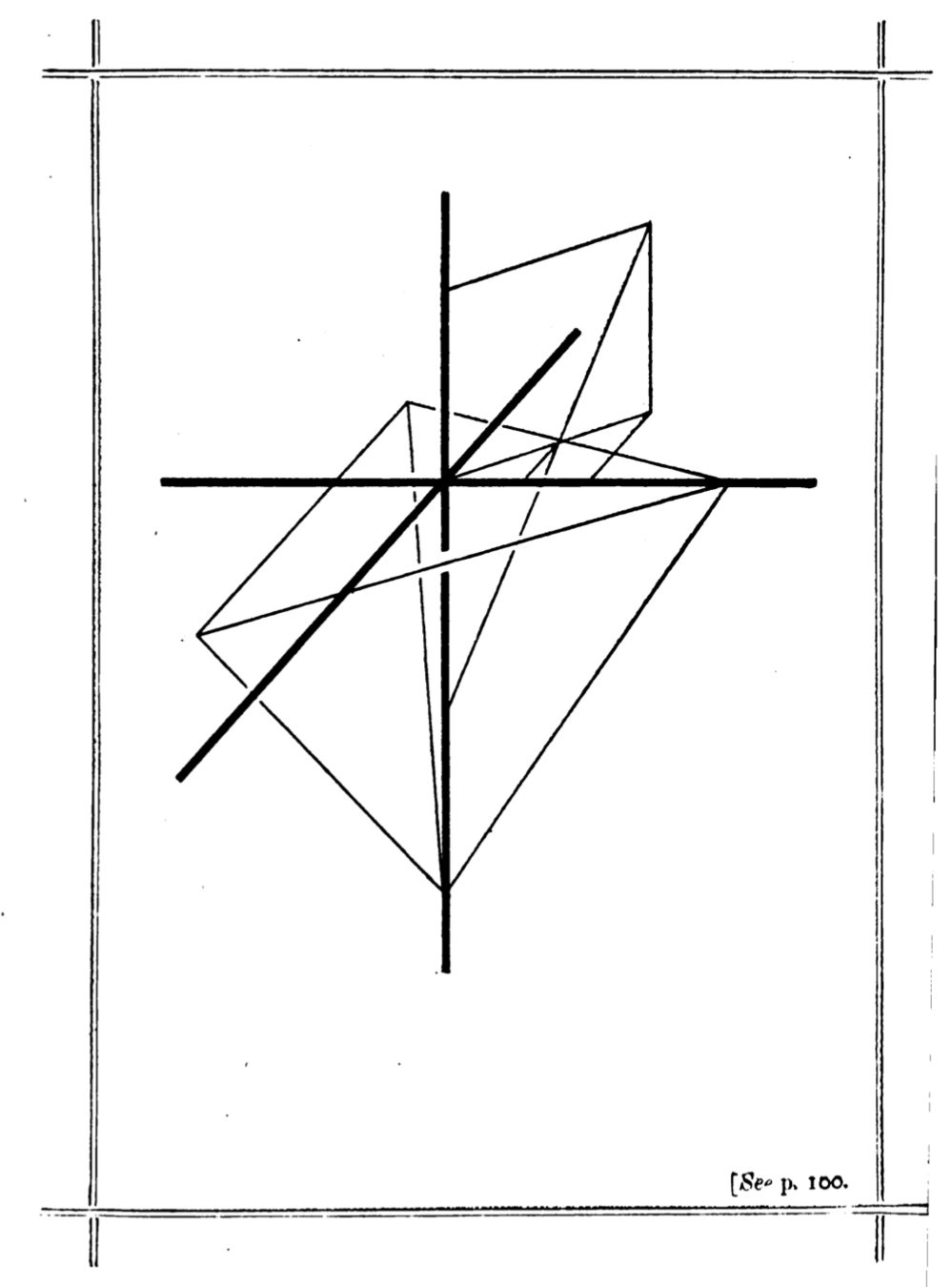
J.M. Wilson’s solution

J.M. Wilson, Mathematical Questions with Their Solutions V (1866), p. 81





Symplectic geometry review
Definition. A symplectic manifold is a smooth manifold \(M\) together with a closed, non-degenerate 2-form \({\omega \in \Omega^2(M)}\).
Example: \((S^2,d\theta\wedge dz)\)
Example. \((T^*\mathbb{R}^n, \sum_{i=1}^n dq_i \wedge dp_i)\)
Example. \((S^2,\omega)\), where \(\omega_p(u,v) = (u \times v) \cdot p\)
Example. \((\mathbb{C}^n, \frac{i}{2} \sum dz_k \wedge d\overline{z}_k)\)
\(\omega^{\wedge n} = \omega \wedge \dots \wedge \omega\) is a volume form on \(M\), and induces a measure
called Liouville measure on \(M\).
Lie group actions
Let \(G\) be a Lie group, and let \(\mathfrak{g}\) be its Lie algebra. If \(G\) acts on \((M,\omega)\), then each \(V \in \mathfrak{g}\) determines a vector field \(X_V\) on \(M\) by

\(SO(3)\) acts on \(S^2\) by rotations.
\(X_{V_{(a,b,c)}}((x,y,z)) = (bz-cy)\frac{\partial}{\partial x} + (cx - az) \frac{\partial}{\partial y} + (ay - bx) \frac{\partial}{\partial z}\)
For \(V_{(a,b,c)} = \begin{bmatrix} 0 & -c & b \\ c & 0 & -a \\ -b & a & 0 \end{bmatrix} \in \mathfrak{so}(3)\),
\(= (a,b,c) \times (x,y,z)\)
Moment(um) maps
Definition. An action of \(G\) on \((M,\omega)\) is Hamiltonian if each one-parameter subgroup action is Hamiltonian. Equivalently, there exists a map
so that \(\omega_p(X_V, X) = D_p \mu(X)(V)\) for each \(p \in M\), \(X \in T_pM\), and \(V \in \mathfrak{g}\).

\(X_{V_{(a,b,c)}}(x,y,z) = (a,b,c) \times (x,y,z)\)
\((\iota_{X_{V_{(a,b,c)}}}\omega)_{(x,y,z)} = a dx + b dy + c dz \)
\(\mu(x,y,z)(V_{(a,b,c)}) = (x,y,z)\cdot(a,b,c)\)
i.e., \(\mu(x,y,z)=(x,y,z)\).
Polygons, again
The diagonal \(SO(3)\) action on \(S^2 \times \dots \times S^2\) is Hamiltonian, with moment map
\(\mu:(\vec{e}_1, \dots , \vec{e}_n) \mapsto \vec{e}_1 + \dots + \vec{e}_n\)
Therefore, the space of equilateral polygons is \(\mu^{-1}(\vec{0})\), and the space of equilateral polygons modulo rotations is symplectic:
\(\operatorname{Pol}(n) := \mu^{-1}(\vec{0})/SO(3) = (S^2)^n /\!/\!_{\vec{0}} SO(3)\)
In fact, the same holds for polygons with any fixed edgelengths
Theorem [Khoi]
The space of equilateral polygons is larger than any other fixed edgelength polygon space.
Density of the end-to-end distance
Classical Fact: The density of the end-to-end vector of an \(n\)-step random walk in \(\mathbb{R}^3\) is
Proof: Fourier transform (since \(\mathrm{sinc}\) is the transform of the boxcar function).
This is piecewise-polynomial in \(\ell\) of degree \(n-3\)
Density of a polygon chord
Proposition [w/ Cantarella] The pdf of the chord connecting \(v_1\) with \(v_{k+1}\) in an \(n\)-gon is
where \(C_n = 2^{n-5}\pi^{n-4} \int_{-\infty}^{\infty} x^2 \,\mathrm{sinc}^n x \,\mathrm{d}x\).
Fact: This is piecewise-polynomial in \(\ell\) of degree \(n-4\).
Expected values of chordlengths

Questions
Why are the expectations rational?
Why degree \(n-4\)?
Where are these crazy polynomials coming from?
Continuous symmetry \(\Rightarrow\) conserved quantity
Duistermaat–Heckman Theorem (stated informally)
On a \(2m\)-dimensional symplectic manifold, \(d\) commuting Hamiltonian symmetries (a Hamiltonian \(T^d=(S^1)^d\)-action) induce \(d\) conserved quantities (momenta).
The joint distribution of the momenta on \(\mathbb{R}^d\) is continuous, piecewise polynomial, degree \(\leq m-d\).
Why degree \(n-4\)?
Example
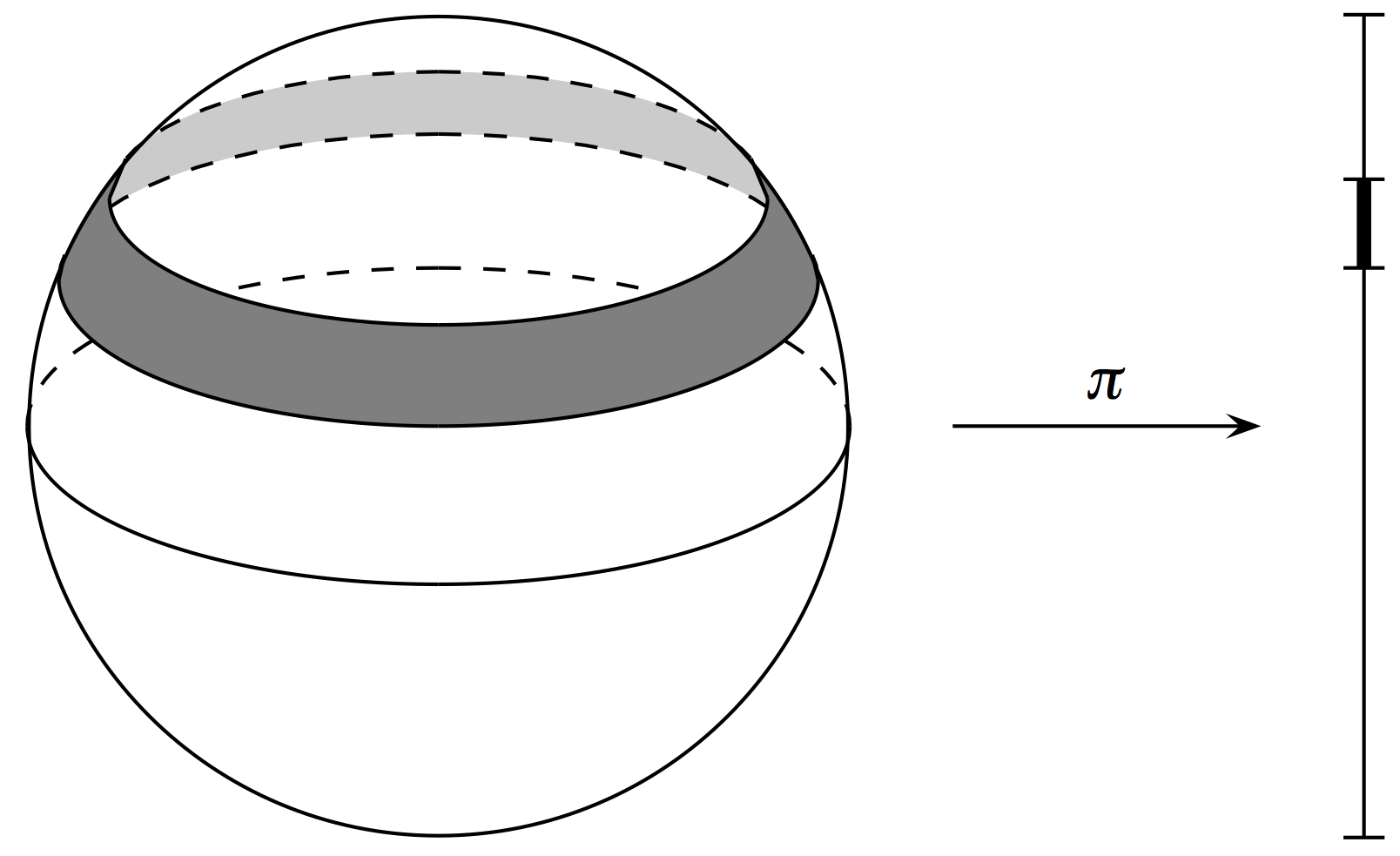
Theorem (Archimedes, Duistermaat–Heckman)
Let \(f: S^2 \to \mathbb{R}\) be given by \(f(x,y,z) = z\). Pushing forward the uniform measure on \(S^2\) to the image \([-1,1]\) gives Lebesgue measure.
Why degree \(n-4\)?
Duistermaat–Heckman Theorem (stated informally) On a \(2m\)-dimensional symplectic manifold, \(d\) commuting Hamiltonian symmetries (a Hamiltonian \(T^d\)-action) induce \(d\) conserved quantities (momenta).
The joint distribution of the momenta is continuous, piecewise polynomial, degree \(\leq m-d\).
\(n\)-gons up to rotation are \(2m=(2n-6)\)-dimensional, so chord length is piecewise polynomial of degree \(\leq\)
\(m-1=(n-3)-1=n-4\)
We actually have more symmetries!
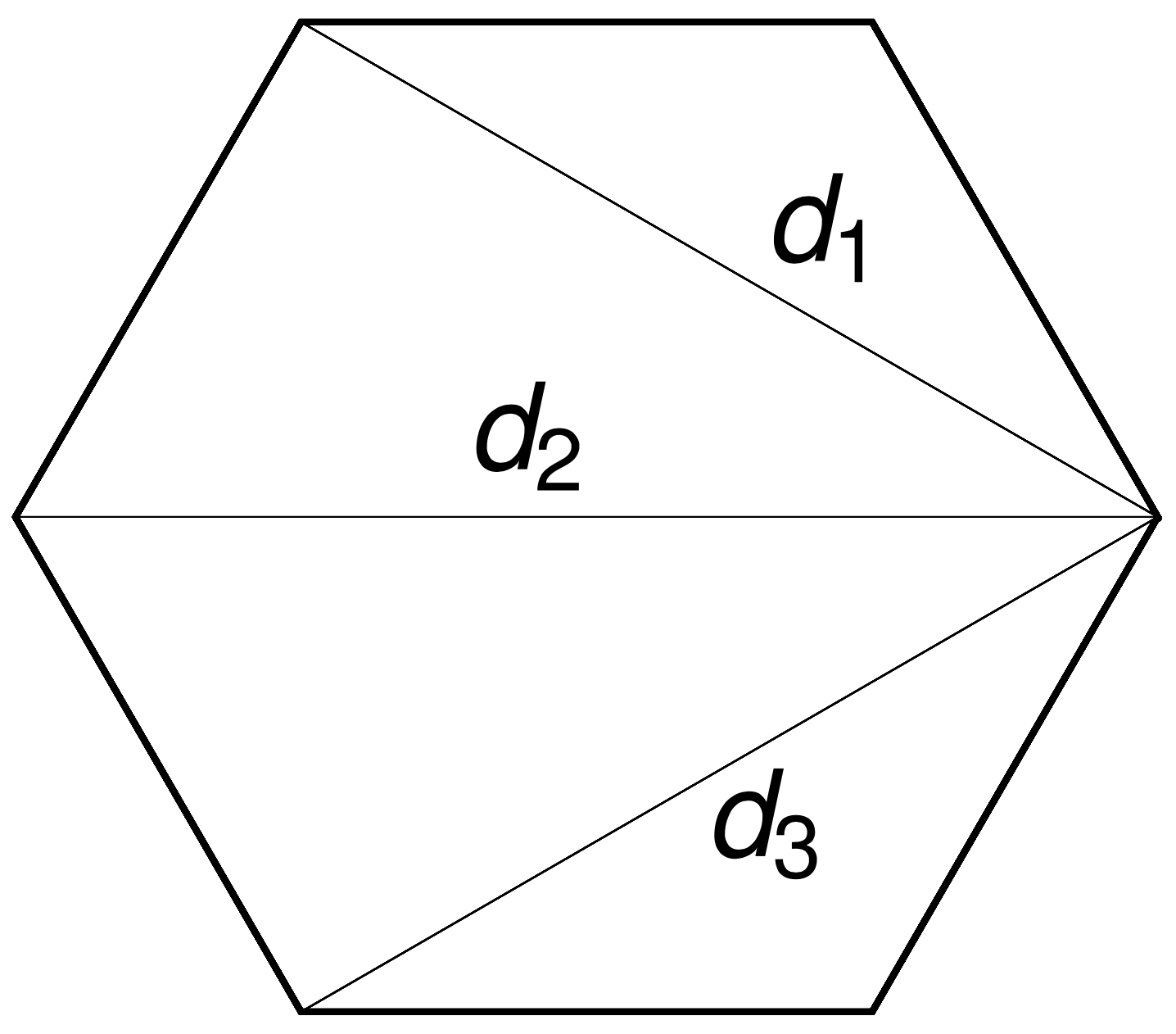
\(n-3\) commuting symmetries
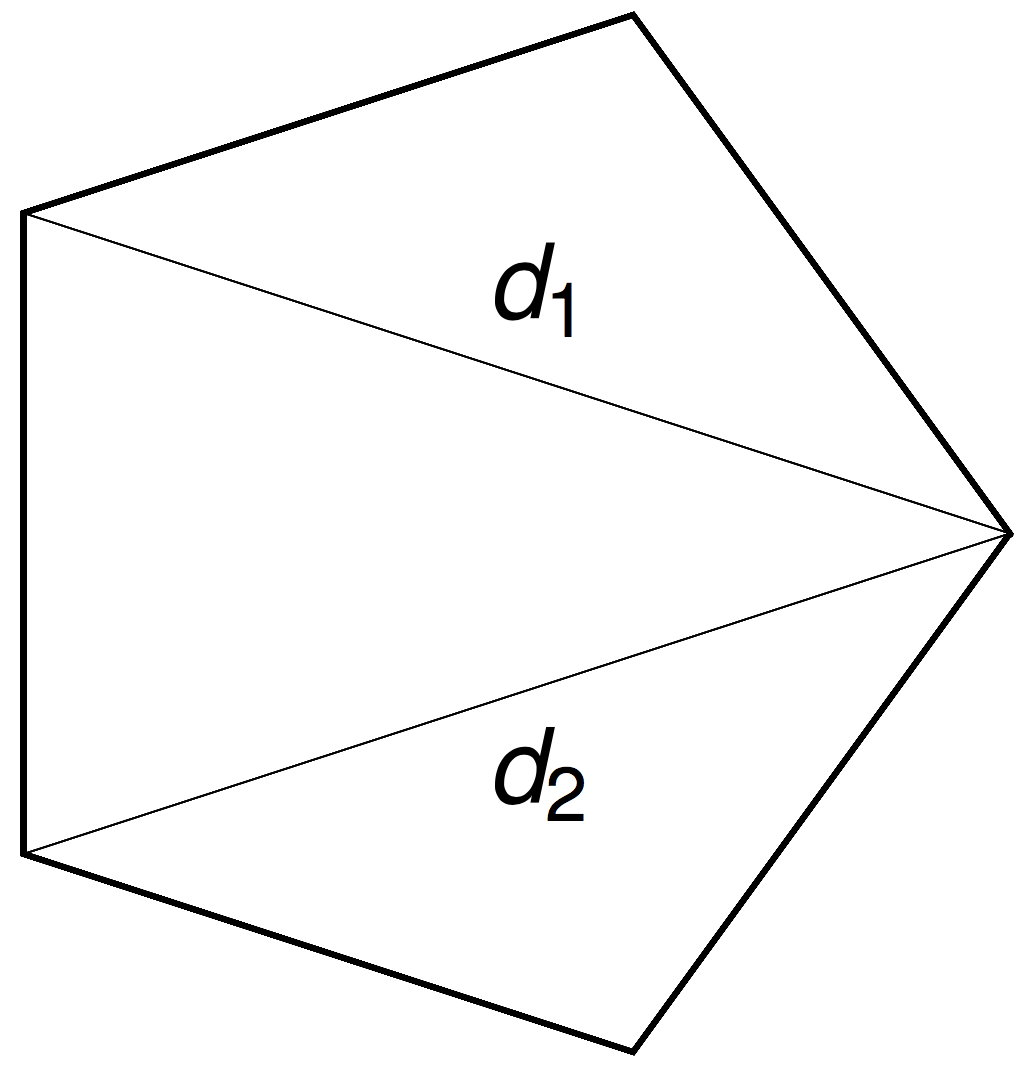
Rotations around \(n-3\) chords \(d_i\) by \(n-3\) angles \(\theta_i\) commute.


Chord distributions
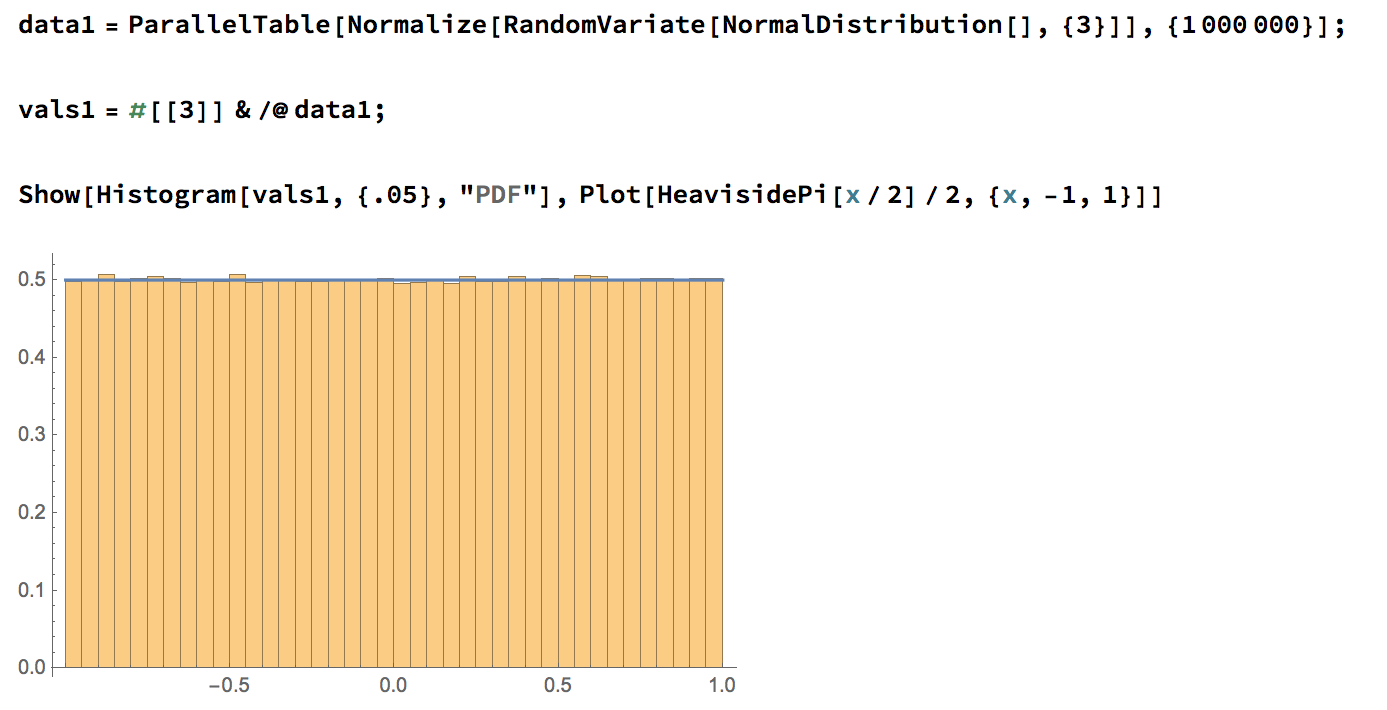
Theorem [w/ Cantarella]
The joint distribution of \(d_1,\ldots , d_{n-3}\) and \(\theta_1, \ldots , \theta_{n-3}\) are all uniform on their domains.
Proof: Check that D–H applies (this is the hard part, since the torus action is not defined everywhere).
Then count: \(m=n-3\) and we have \(d=n-3\) symmetries, so the pdf of the \(d_i\) is piecewise polynomial of degree \(\leq\)
\(m-d = (n-3)-(n-3)=0\).
Since the pdf is continuous and the domain is connected, it must be constant.
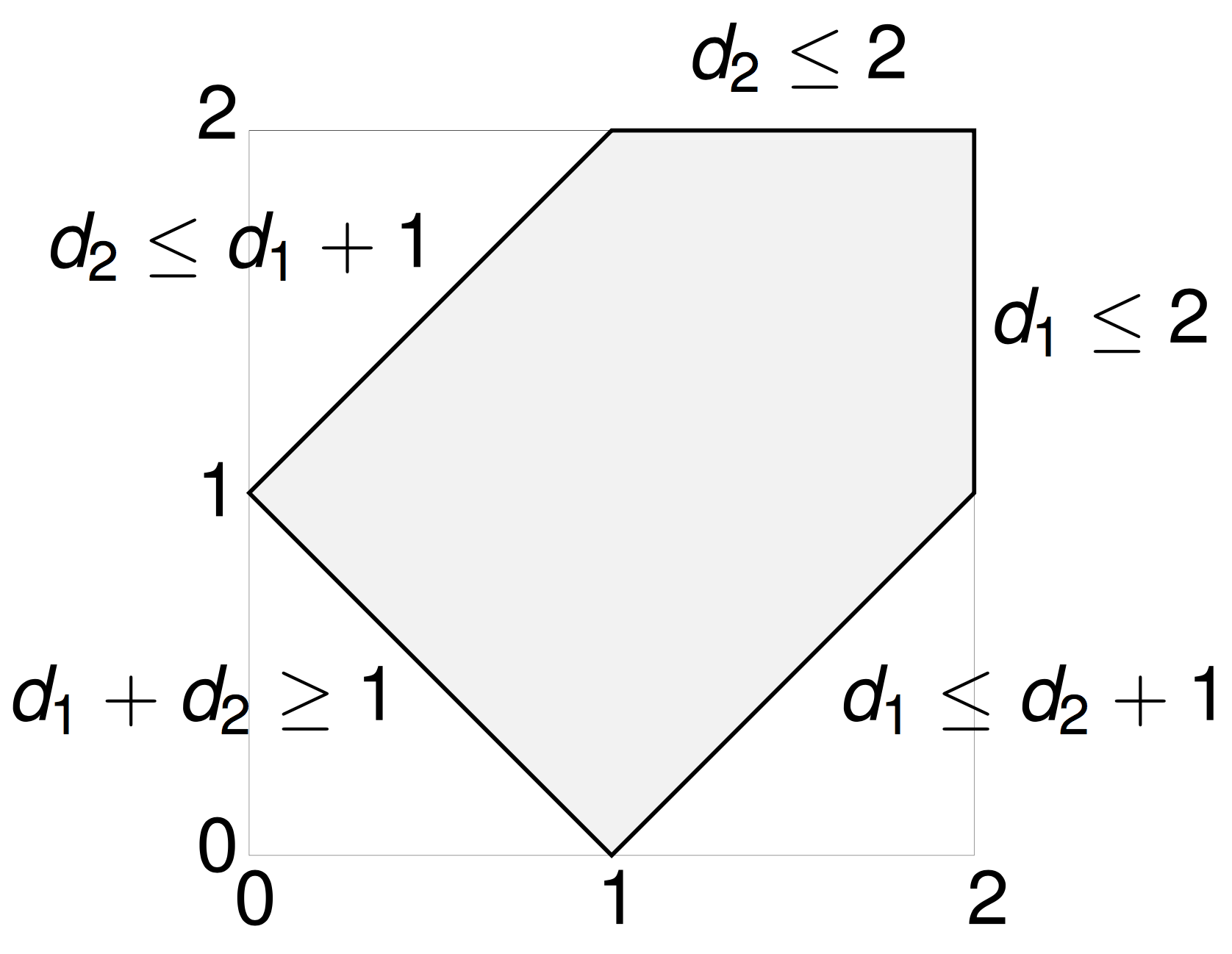
A polytope
The \((n-3)\)-dimensional moment polytope \(\mathcal{P}_n \subset \mathbb{R}^{n-3}\) is defined by the triangle inequalities
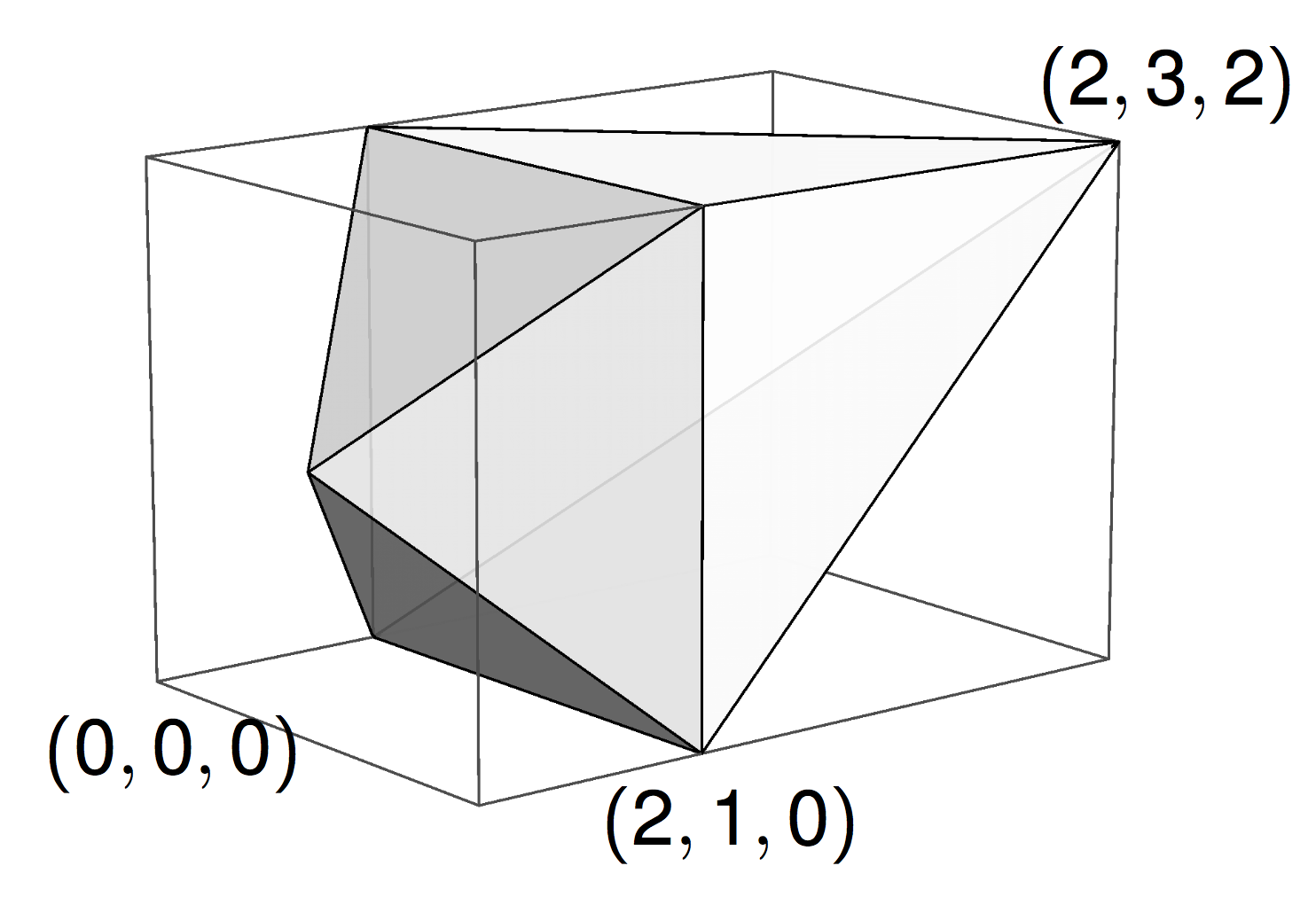
From action-angle coordinates to polygons
There exists an almost-everywhere defined map \(\alpha: \mathcal{P}_n \times (S^1)^{n-3} \to \{n\text{-gons}\}\) which is measure-preserving.
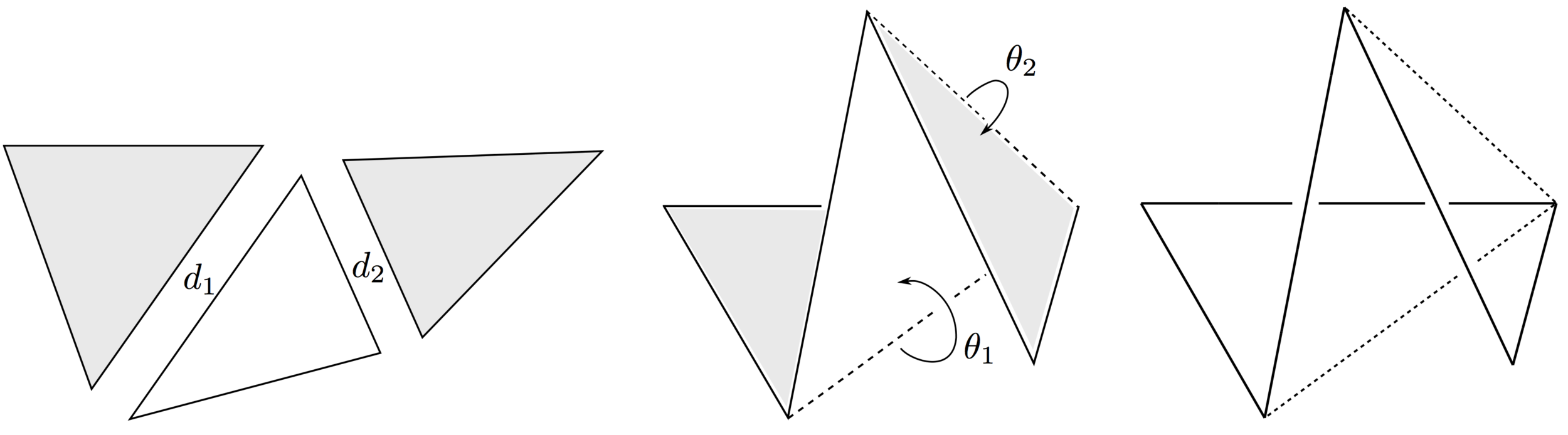
This is only sensible as a map to polygons modulo translation and rotation.
Direct Sampling
Introduce fake chordlengths \(d_0=1=d_{n-2}\) and make the linear change of variables
\(s_i = d_i - d_{i-1} \text{ for } 1 \leq i \leq n-2\).
Then \(\sum s_i = d_{n-2} - d_0 = 0\), so \(s_{n-2}\) is determined by \(s_1, \ldots , s_{n-3}\)
and the inequalities
become
\(-1 \leq s_i \leq 1, -1 \leq \sum_{i=1}^{n-3} s_i \leq 1\)
\(\sum_{j=1}^i s_j + \sum_{j=1}^{i+1}s_j \geq -1\)
The polytope is surprisingly large!
Let \(\mathcal{C}_n \subset \mathbb{R}^{n-3}\) be determined by
\(-1 \leq s_i \leq 1, -1 \leq \sum_{i=1}^{n-3} s_i \leq 1\)
\(\sum_{j=1}^i s_j + \sum_{j=1}^{i+1}s_j \geq -1\)
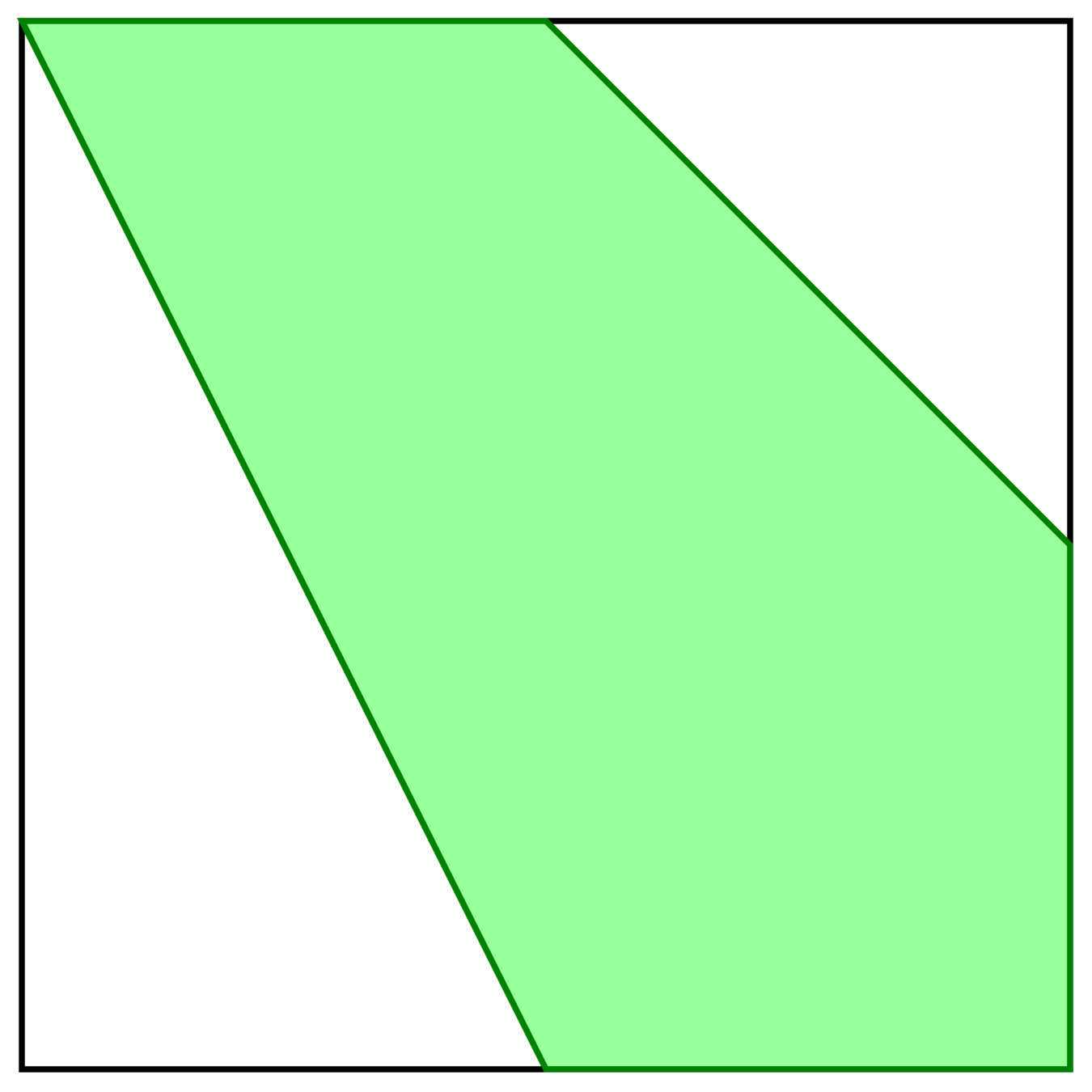
\(\mathcal{C}_5\)
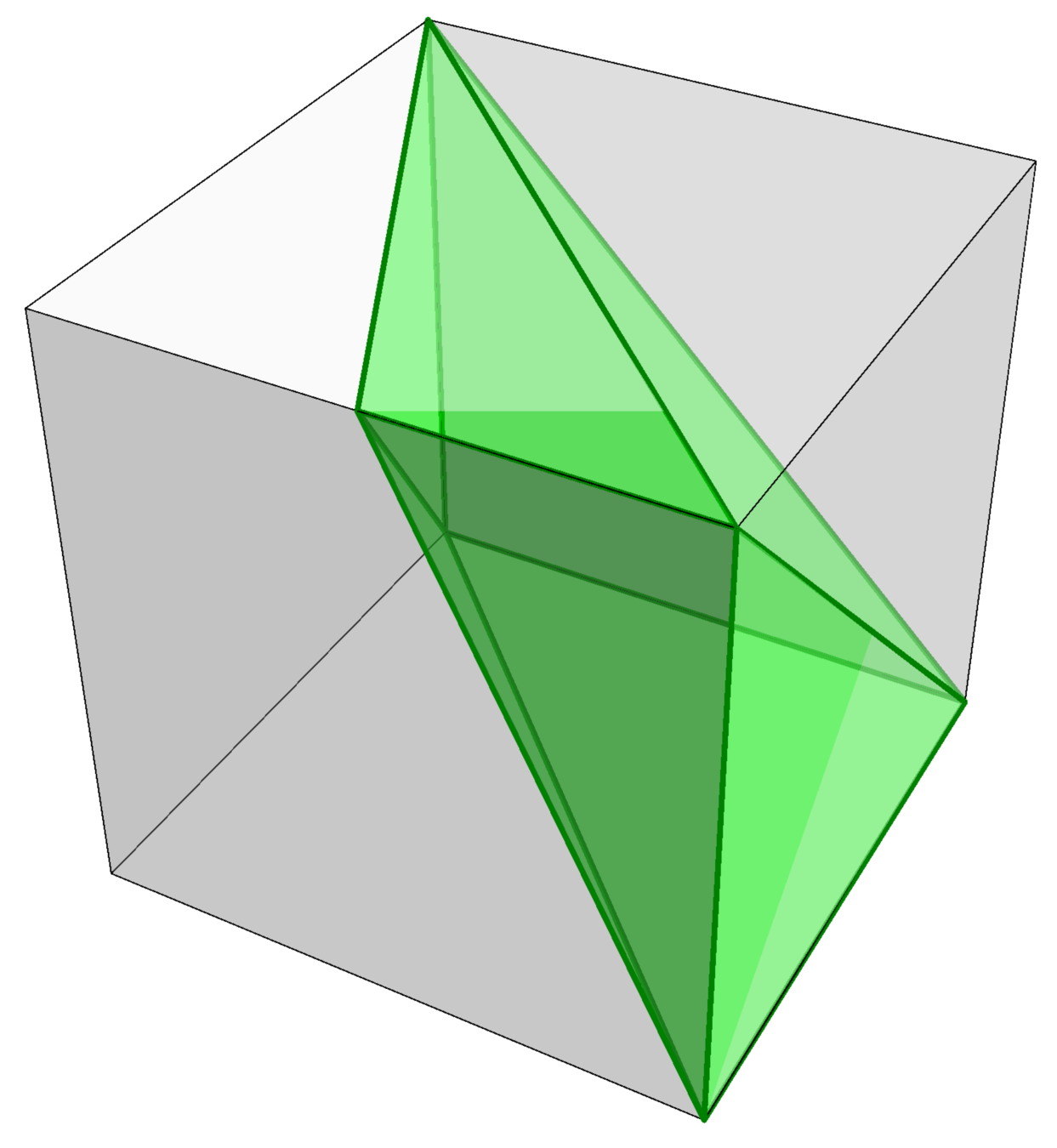
\(\mathcal{C}_6\)
Proposition [w/ Cantarella, Duplantier, Uehara]
The probability that a point in the hypercube lies in \(\mathcal{C}_n\) is asymptotic to
\(6 \sqrt{\frac{6}{\pi}}\frac{1}{n^{3/2}}\)
Direct sampling
Action-Angle Method
Theorem [w/ Cantarella, Duplantier, Uehara]
The action-angle method directly samples polygon space in expected time \(\Theta(n^{5/2})\).
- Generate \((s_1,\ldots , s_{n-3})\) uniformly on \([-1,1]^{n-3}\)
- Test whether \((s_1,\ldots , s_{n-3})\in \mathcal{C}_n\)
- Change to \((d_1, \ldots , d_{n-3})\) coordinates
- Generate dihedral angles from \(T^{n-3}\)
- Build corresponding polygon
\(O(n)\) time
acceptance probability \(\sim \frac{1}{n^{3/2}}\)
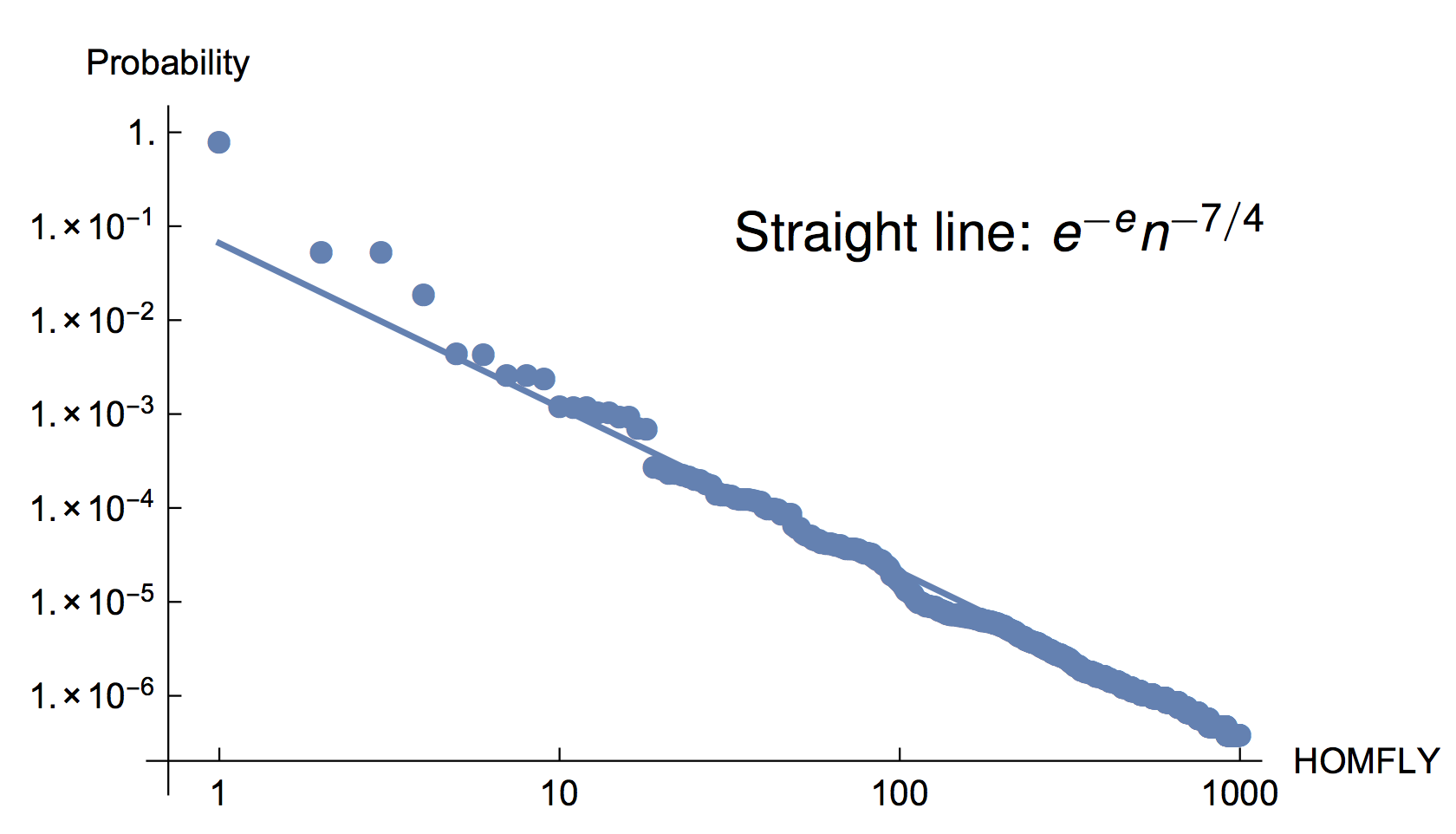
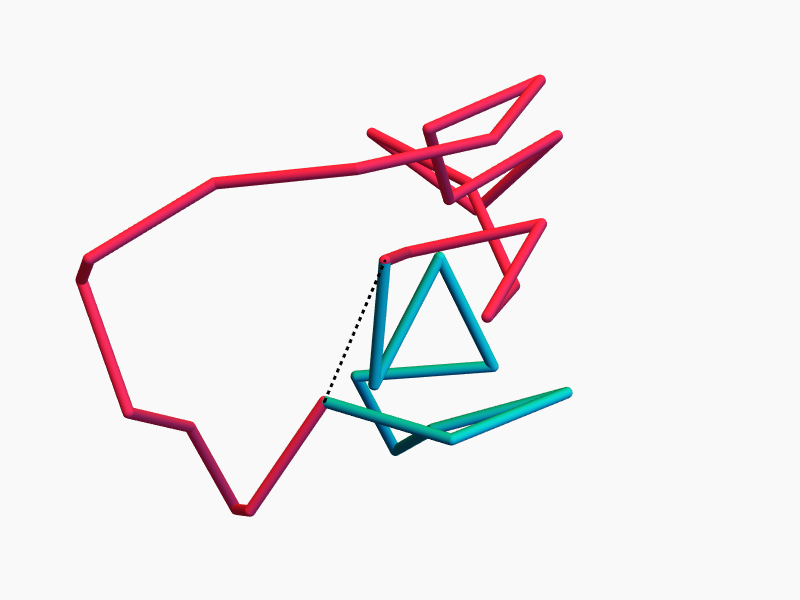
Knot types of 10 million 60-gons
Frequency plot of the HOMFLY polynomials produced by sampling 10 million random 60-gons (there were a total of 6371 distinct HOMFLYs).
cf. Baiesi–Orlandini–Stella
Very simple geometry
Theorem [w/ Cantarella, Deguchi, Uehara]
In a Gaussian random embedding of a graph \(G\), the vector of \(x\)-coordinates of the vertices is distributed as
where \(L\) is the graph Laplacian of \(G\) and \(L^+\) is its Moore–Penrose pseudoinverse.
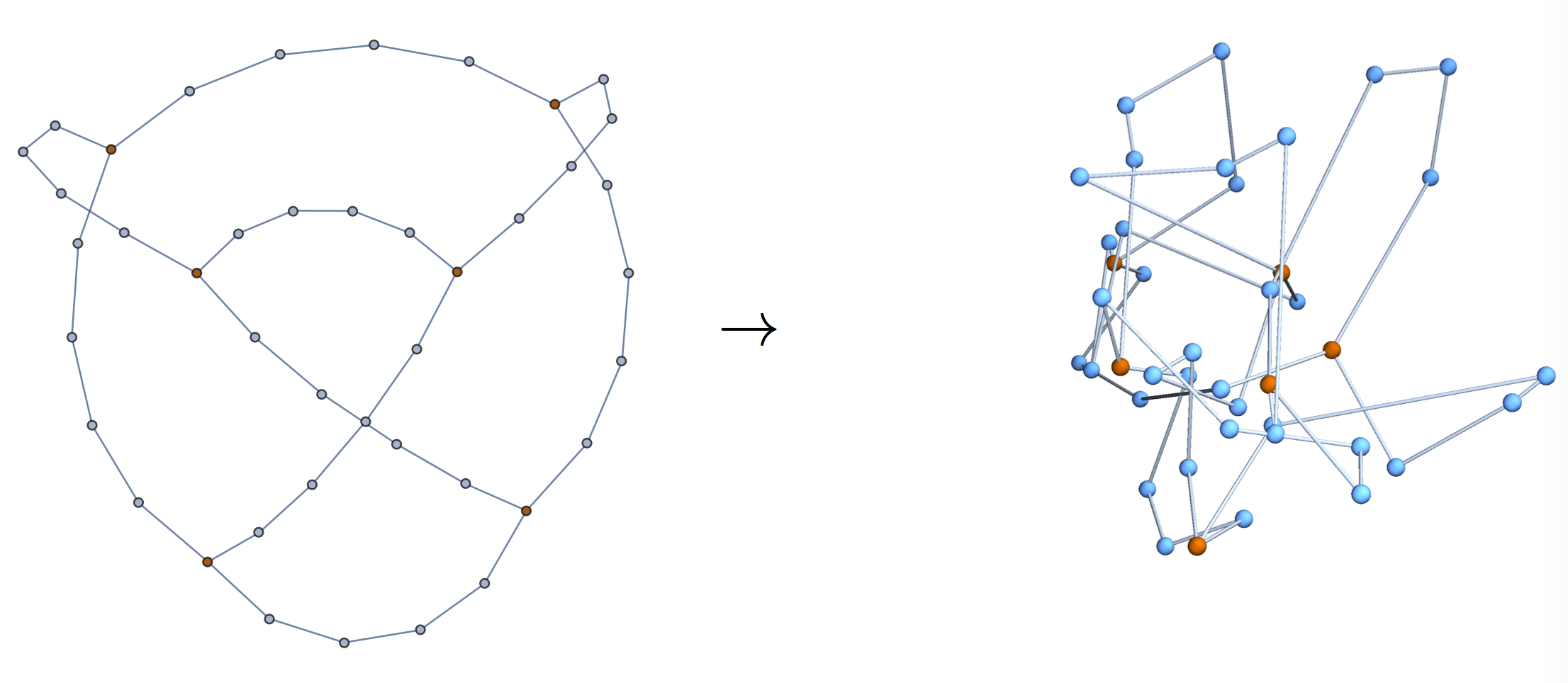
Theorem [w/ Cantarella, Deguchi, Uehara]
In a Gaussian random embedding of a graph \(G\), the vector of \(x\)-coordinates of the vertices is distributed as
where \(L\) is the graph Laplacian of \(G\) and \(L^+\) is its Moore–Penrose pseudoinverse.
Theorem [w/ Cantarella, Deguchi, Uehara]
If \(\lambda_i\) are the eigenvalues of \(L\), the expected radius of gyration of a Gaussian random embedding of \(G\) in \(\mathbb{R}^d\) is
This is the Kirchhoff index of the graph.
Thank you!
References
The symplectic geometry of closed equilateral random walks in 3-space
J. Cantarella & C. Shonkwiler
Annals of Applied Probability 26 (2016), no. 1, 549–596
A fast direct sampling algorithm for equilateral closed polygons
J. Cantarella, B. Duplantier, C. Shonkwiler, & E. Uehara
Journal of Physics A 49 (2016), no. 27, 275202
Funding: Simons Foundation
Probability theory of random polygons from the quaternionic viewpoint
J. Cantarella, T. Deguchi, & C. Shonkwiler
Communications on Pure and Applied Mathematics 67 (2014), no. 10, 1658–1699
The expected total curvature of random polygons
J. Cantarella, A.Y. Grosberg, R. Kusner, & C. Shonkwiler
American Journal of Mathematics 137 (2015), no. 2, 411–438
Spherical geometry and the least symmetric triangle
L. Bowden, A. Haynes, C. Shonkwiler, & A. Shukert
Geometriae Dedicata (2018), https://doi.org/10.1007/s10711-018-0327-4
Random triangles and polygons in the plane
J. Cantarella, T. Needham, C. Shonkwiler, & G. Stewart
The American Mathematical Monthly, to appear, arXiv:1702.01027 [math.MG]