Tensors in Differential Geometry

Clayton Shonkwiler

Colorado State University

shonkwiler.org

TACA 2019

/taca2019

This talk!

Funding: Simons Foundation

Colin Roberts

Colorado State

Harrison Chapman

Colorado State

Credits

The Basic Problem

\(M\)

\(T_x M\)

\(x\)

\(y\)

\(u\)

\(v\)

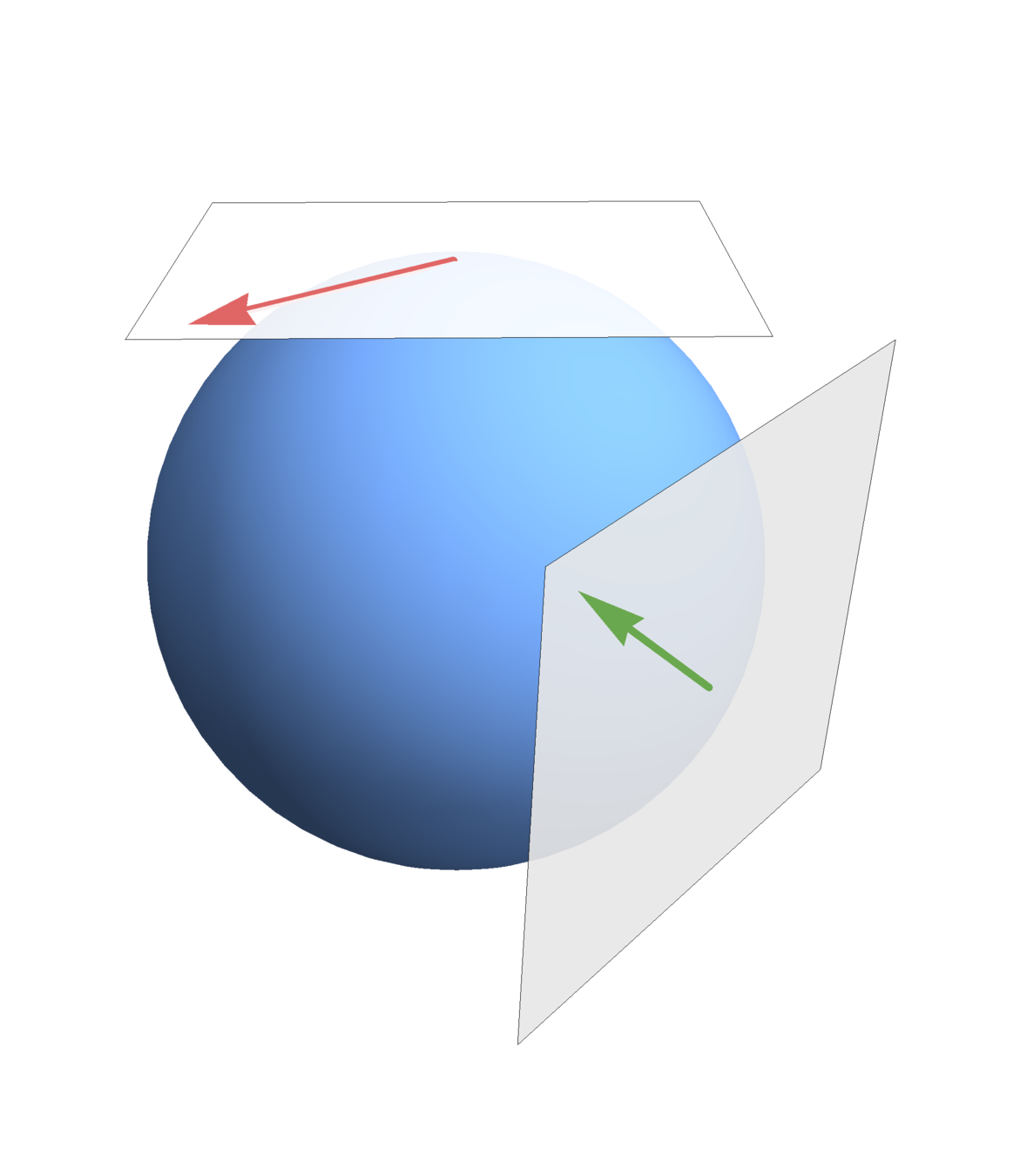
\(T_y M\)

\(u\) and \(v\) live in different vector spaces!

Vector Fields

The tangent bundle

\displaystyle TM := \bigsqcup_{x \in M} T_x M
M

A vector field on \(M\) is a (smooth) section of the tangent bundle; i.e., a smooth map \(X: M \to TM\) so that \(\pi \circ X= \operatorname{id}\).

\(\pi\)

  1. The collection \(\mathfrak{X}(M)\) of all vector fields on \(M\) forms a Lie algebra.
  2. \(\mathfrak{X}(M)\) is a \(C^\infty(M)\)-module.

Notes:

Vector Fields as Derivations

\(M\)

\(x=\gamma(0)\)

\(\gamma'(0)=X(x)\)

\(\gamma(t)\)

\(X \in \mathfrak{X}(M)\) is a differential operator: for \(f \in C^\infty(M)\), \(X(f) \in C^\infty(M)\) is defined by

X(f)(x) = (f \circ \gamma)'(0)

\(X(x)\)

\(x\)

The Lie bracket \([X,Y](f) := X(Y(f))-Y(X(f))\)

1-Forms

The cotangent bundle

\displaystyle T^*M := \bigsqcup_{x \in M} (T_x M)^*
M

A \(1\)-form on \(M\) is a (smooth) section of the cotangent bundle; i.e., a smooth map \(\omega: M \to T^*M\) so that \(\pi \circ \omega = \operatorname{id}\).

\(\pi\)

Example. If \(f: M \to \mathbb{R}\) is a smooth function, then the differential \(df\) is a 1-form.

The tensor space \(T^p_q(V)\) is the collection of multilinear maps \(\underbrace{V^* \times \dots \times V^*}_p \times \underbrace{V \times \dots \times V}_q \rightarrowtail \mathbb{R}\).

Tensor Bundles

The tensor bundle

\displaystyle \mathcal{T}^p_q(M):= \sqcup_{x \in M} T^p_q(T_x M)

\(\pi\)

M
  1.  \(\mathcal{T}^0_0(M)=C^\infty{M}\)
  2. \(\mathcal{T}^1_0(M)=TM\)
  3. \(\mathcal{T}^0_1(M) = T^*M\)

Implicitly using \(V^{**}\simeq V\): think of \(v \in V\) as a linear functional \(V^* \to \mathbb{R}\) by \(v(\varphi):=\varphi(v)\).

Examples.

(Can also think of \(\mathcal{T}^p_q(M)\) as a tensor product of \(TM\)’s and \(T^*M\)’s over \(C^\infty(M)\).)

Tensor Fields

The tensor bundle

\displaystyle \mathcal{T}^p_q(M):= \bigsqcup_{x \in M} T^p_q(T_x M)

\(\pi\)

M

A \((p,q)\)-tensor field (or just \((p,q)\)-tensor) on \(M\) is a (smooth) section of \(\mathcal{T}^p_q(M)\).

Examples. Functions, vector fields, 1-forms.

Example. A Riemannian metric (or metric tensor) is a positive-definite symmetric \((0,2)\)-tensor field \(g\); i.e., \(g(x)=:g_x\) is an inner product on \(T_xM\) for each \(x\).

Riemannian Metrics

A Riemannian metric \(g\) on \(M\) is often written as

g = \sum g_{ij} dx^i \otimes dx^j = g_{ij}dx^i \otimes dx^j

or just \(g_{ij}\). The notation \(ds^2 = \sum g_{ij}dx^i dx^j = g_{ij}dx^idx^j\) is also common.

Example. \(ds^2=dx^2 + dy^2\) on \(\mathbb{R}^2\) is just the standard dot product:

g\left(a \frac{\partial}{\partial x} + b \frac{\partial }{\partial y}, c \frac{\partial}{\partial x} + d \frac{\partial}{\partial y}\right) = ac+bd.

Example. \(ds^2 = \frac{1}{y^2}\left(dx^2 + dy^2\right)\) on \(\mathbb{H}^2:=\{(x,y) \in \mathbb{R}^2 | y>0\}\) gives the upper half-plane model of the hyperbolic plane.

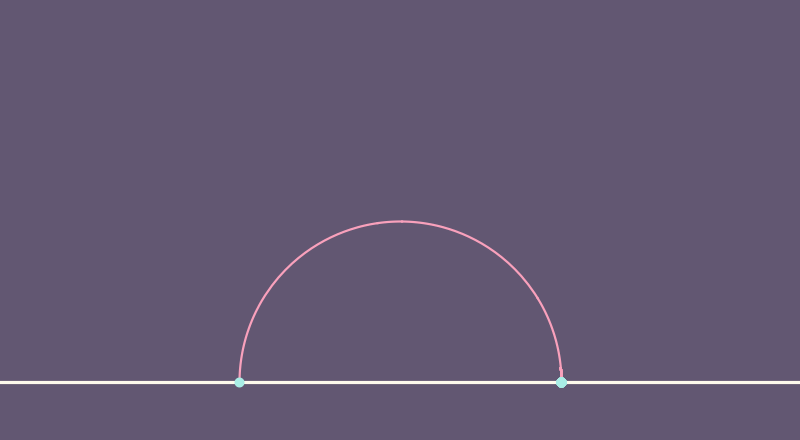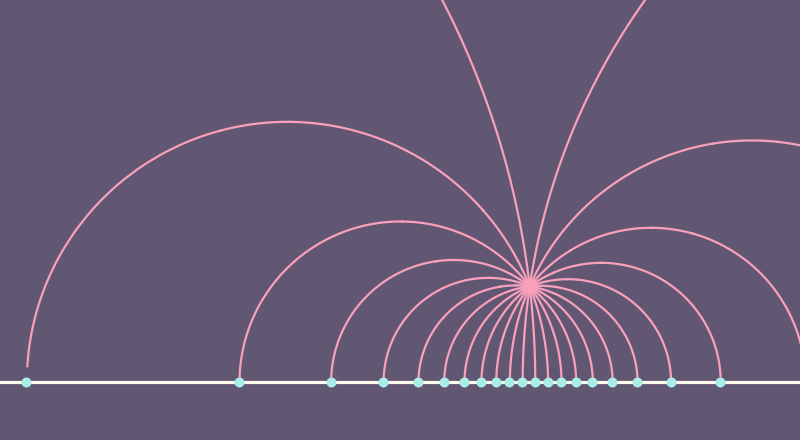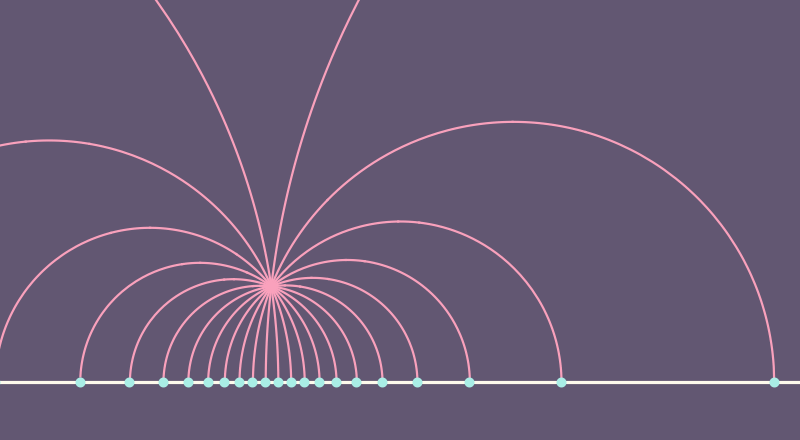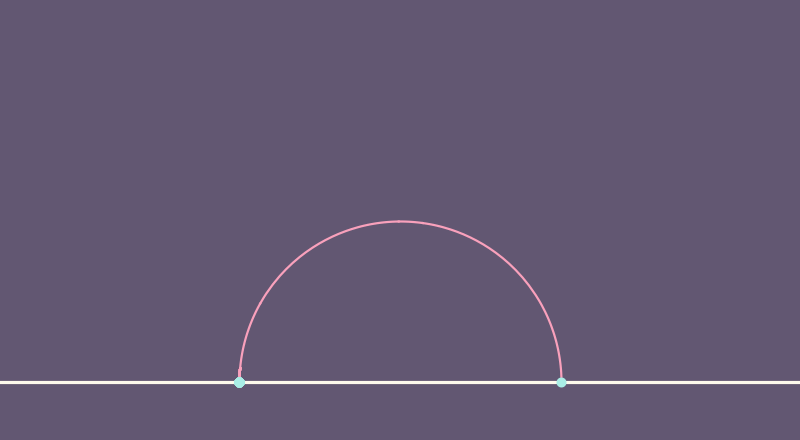
Riemannian Metrics and Lengths

Definition. Given a smooth curve \(\gamma: [a,b] \to M\), where \((M,g)\) is a Riemannian manifold, then length of \(\gamma\) is

\operatorname{Length}(\gamma) = \int_a^b \sqrt{g_{\gamma(t)}(\gamma'(t),\gamma'(t))} dt.

For \(x,y\in M\), the distance from \(x\) to \(y\) is

d_g(x,y) := \inf \{\operatorname{Length}(\gamma)| \gamma: [0,1]\to M, \gamma(0)=x, \gamma(1)=y\}

Differential Forms

A differential \(k\)-form on \(M\) is a section of the \(k\)th exterior bundle

\bigwedge^k(M):= {\displaystyle \bigsqcup_{x \in M}} \bigwedge^k((T_x M)^*)

\(\pi\)

M

The space of all \(k\)-forms is denoted \(\Omega^k(M)\).

If \(\omega \in \Omega^k(M)\), then at each \(x \in M\), \(\omega(x)\) is an alternating multilinear map \(T_xM \times \dots \times T_x M \rightarrowtail \mathbb{R}\).

Example. The standard area form on \(\mathbb{R}^2\) is \(dx \wedge dy\).

Example. The standard area form on \(S^2\) is

\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}
x dy \wedge dz + y dz \wedge dx + z dx \wedge dy = d\theta \wedge dz = \sin \theta d\theta \wedge d\phi.

Think: alternating \((0,k)\)-tensors

Exterior Derivative

The exterior derivative is an anti-derivation \(d\) of degree \(+1\) that makes this a (co)chain complex.

0 \stackrel{d}{\to} \Omega^0(M) \stackrel{d}{\to} \Omega^1(M) \stackrel{d}{\to} \dots \stackrel{d}{\to} \Omega^{n-1}(M) \stackrel{d}{\to} \Omega^n(M) \to 0

In local coordinates

\displaystyle d\left( \sum_{i_1 < \dots < i_k} f_{i_1\dots i_k} dx_{i_1} \wedge \dots \wedge dx_{i_k}\right)
\displaystyle = \sum_{i_1 < \dots < i_k} \sum_{j=1}^n \frac{\partial f_{i_1 \dots i_k}}{\partial x^j} dx_j \wedge dx_{i_1} \wedge \dots \wedge dx_{i_k}.

de Rham’s Theorem. The cohomology of the above cochain complex agrees with the singular cohomology of \(M\) with real coefficients.

Symplectic Geometry

Definition. A symplectic form on a manifold \(M\) is a closed, nondegenerate 2-form \(\omega\). The pair \((M,\omega)\) is called a symplectic manifold.

Example. Any area form on an oriented surface; e.g., \((\mathbb{R}^2,dx\wedge dy)\), \((S^2,d\theta\wedge dz)\), \((S^1 \times S^1, ds\wedge dt)\), ...

Example. The canonical form \(\sum dq_i \wedge dp_i\) on \(T^*\mathbb{R}^n\) (or more generally any cotangent bundle).

Darboux’s Theorem. Every symplectic form looks like this locally.

Consequences

A symplectic manifold must be even-dimensional (over \(\mathbb{R}\)).

\(\omega^{\wedge n} = \omega \wedge \dots \wedge \omega\) is a volume form on \(M\), and induces a measure

m(U) := \int_U \omega^{\wedge n}

called Liouville measure on \(M\).

If \(H: M \to \mathbb{R}\) is smooth, then there exists a unique vector field \(X_H\) (the Hamiltonian vector field for \(H\)) so that \({dH = \iota_{X_H}\omega}\), i.e.,

dH(\cdot) = \omega(X_H, \cdot)

(\(X_H\) is sometimes called the symplectic gradient of \(H\))

Example

\(H: (S^2, d\theta\wedge dz) \to \mathbb{R}\) given by \(H(\theta,z) = z\).

\(dH = dz = \iota_{\frac{\partial}{\partial \theta}}(d\theta\wedge dz)\), so \(X_H = \frac{\partial}{\partial \theta}\).

Integrating \(X_H\) produces the one-parameter family of diffeomorphisms \(\psi_t(\theta, z) = (\theta+t,z)\).

Some Useful Non-Tensors

A (semi-)Riemannian metric \(g\) on \(M\) induces a unique connection called the Levi-Civita connection so that

Christoffel symbols \(\Gamma_{ij}^k\) defined by \(\nabla_{X_i} X_j = \sum_k \Gamma_{ij}^k X_k\)

  1. \(\nabla_U V - \nabla_V U = [U,V]\) (symmetric)
  2. \(U g(V,W) = g(\nabla_U V,W) + g(V, \nabla_U W)\) (compatible)

Definition. An affine connection \(\nabla: \mathfrak{X}(M) \times \mathfrak{X}(M) \to \mathfrak{X}(M)\) satisfies

  1. \(\nabla_{f_1 V_1 + f_2V_2} W = f_1 \nabla_{V_1}W + f_2 \nabla_{V_2}W\).
  2. \(\nabla_V(W_1 + W_2) = \nabla_V W_1 + \nabla_V W_2\).
  3. \(\nabla_V f W = V(f) W + f \nabla_V W\).

Riemann Curvature Tensor

The Riemann curvature tensor is a \((1,3)\)-tensor field

\(R: \mathfrak{X}(M) \times \mathfrak{X}(M) \to (\mathfrak{X}(M) \to\mathfrak{X}(M))\) defined by

R(X,Y)Z=\nabla_Y \nabla_X Z -\nabla_X \nabla_Y Z + \nabla_{[X,Y]} Z

The sectional curvature of a 2-plane \(\sigma \subset T_x M\) is

K(\sigma):=\frac{g(R(u,v)u,v)}{g(u,u)g(v,v)-g(u,v)^2},

where \(\{u,v\}\) is any basis for \(\sigma\).

At a point \(x \in M\), the Ricci tensor \(\operatorname{Ric}: T_x M \times T_x M \to \mathbb{R}\) is

\operatorname{Ric}(u,v) := \operatorname{tr}(w \mapsto R(w,v)u)

Or, in index notation, \(\operatorname{Ric}_{ij} = R_{ikj}^k = g^{k\ell}R_{ki\ell j}\).

Ricci Tensor

For unit \(u \in T_x M\), the Ricci curvature of \(u\) is the value of the corresponding quadratic form: \(\operatorname{Ric}(u,u)\).

Fact. \(\operatorname{Ric}(u,u)\) is \(n-1\) times the average of \(K(\sigma)\) for all 2-planes \(\sigma \subset T_x M\) containing \(u\).

The scalar curvature \(S = \operatorname{tr}_g \operatorname{Ric} = g^{ij}\operatorname{Ric}_{ij}\)

Maxwell’s Equations

dF = 0
d\star F = \mu_0 J

Faraday tensor

(a 2-form)

current 3-form

Einstein’s Field Equations

G=8\pi T

stress-energy tensor

Einstein tensor: \(G = \operatorname{Ric} - \frac{1}{2} S g\)

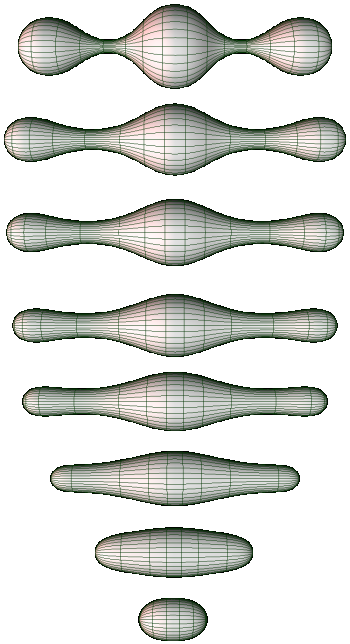
Ricci Flow

g_t = -2 \operatorname{Ric}

Grassmannians

Definition. The Grassmannian \(\operatorname{Gr}(d,V)\) is the space of \(d\)-dimensional linear subspaces of the vector space \(V\).

Example. \(\operatorname{Gr}(1,V) =\mathbb{P}(V)\).

Example. \(\operatorname{Gr}(2,\mathbb{R}^4) \simeq (S^2 \times S^2)/(p,q)\sim (-p,-q)\)

Plücker Embedding

\operatorname{Gr}(d,V) \to \mathbb{P}\left(\bigwedge^d V\right)
U \mapsto u_1 \wedge \dots \wedge u_d

\(\{u_1,\dots , u_d\}\) a basis for \(U \subset V\).

With respect to a preferred basis \(\{e_1, \dots , e_n\}\) for \(V\),

Theorem. The image is cut out by a system of quadratic equations (that say the wedge is decomposable).

Example. \(\operatorname{Gr}(2,\mathbb{K}^4)\mapsto\{\Delta_{12}\Delta_{34}-\Delta_{13}\Delta_{24}+\Delta_{14}\Delta_{23}=0\}\)

\(\Delta_U:=d!\, u_1 \wedge \dots \wedge u_d = \sum_{\sigma \in S_d} \operatorname{sgn}(\sigma) u_{\sigma(1)} \otimes \dots \otimes u_{\sigma(d)}\) is an alternating \(d\)-tensor.

\displaystyle u_1 \wedge \dots \wedge u_d = \sum_{i_1 < \dots < i_d} \Delta_{i_1\dots i_d} e_{i_1} \wedge \dots \wedge e_{i_d}

where the \(\Delta_{i_1\dots i_d}\) are the determinants of all the \(d \times d\) minors of \([u_1 \cdots u_d]\).

Projector Embedding

\operatorname{Gr}(d,\mathbb{R}^n) \to \operatorname{End}(\mathbb{R}^n)
\displaystyle U \mapsto \operatorname{Proj}_U

(See Conway–Hardin–Sloane)

Proposition (with Chapman). Let \(V = \mathbb{R}^n\). If \(\Delta_U\) is constructed from an orthonormal basis for \(U\), then

\Delta_U \cdot \Delta_U = (-1)^{d-1}(d-1)! \operatorname{Proj}_U.

\(\Delta_U(v)\)

\(\operatorname{Proj}_U(v)\)

\(v\)

\(\operatorname{Proj}_U\) is a symmetric \((1,1)\)-tensor.

{(\Delta_U)^k}_{i_1\dots i_{d-1}} {(\Delta_U)^{i_1\dots i_{d-1}}}_\ell = (-1)^{d-1}(d-1)! (\operatorname{Proj}_U)^k_\ell.

Questions I Have

The flag mean of \(\{U_1,\dots , U_k\} \subset \operatorname{Gr}(d,\mathbb{R}^n)\) is the span of the \(d\) leading (left) singular vectors of \(\operatorname{Proj}_{U_1}+\dots + \operatorname{Proj}_{U_k}\).

Question 1. Is there a notion of tensor SVD so that the flag mean of \(\{U_1,\dots , U_k\}\) is the \(d\) leading (left?) singular vectors of the \(\Delta_{U_1}+\dots+\Delta_{U_k}\)?

Question 2. What is the flag mean of the positive Grassmannian \(\operatorname{Gr}^+(d,\mathbb{R}^n)\), consisting of those \(U\) with all positive Plücker coordinates?

Question 3. Suppose \(U_1,U_2 \in \operatorname{Gr}(d,\mathbb{R}^n)\) and you are given \(a \Delta_{U_1}+b \Delta_{U_2}\) for unknown \(a,b \in \mathbb{R}\). Can you determine \(U_1\) and \(U_2\)?

Question 4. Is there a notion of Grassmannians of tensor subspaces? If so, what are good coordinates on this space?

Thank you!