New Stick Number Bounds from Random Sampling of Confined Polygons
/utc20
This talk!
Collaborators
Cal State Long Beach
Funding: Simons Foundation



Results
Theorem [with Eddy]
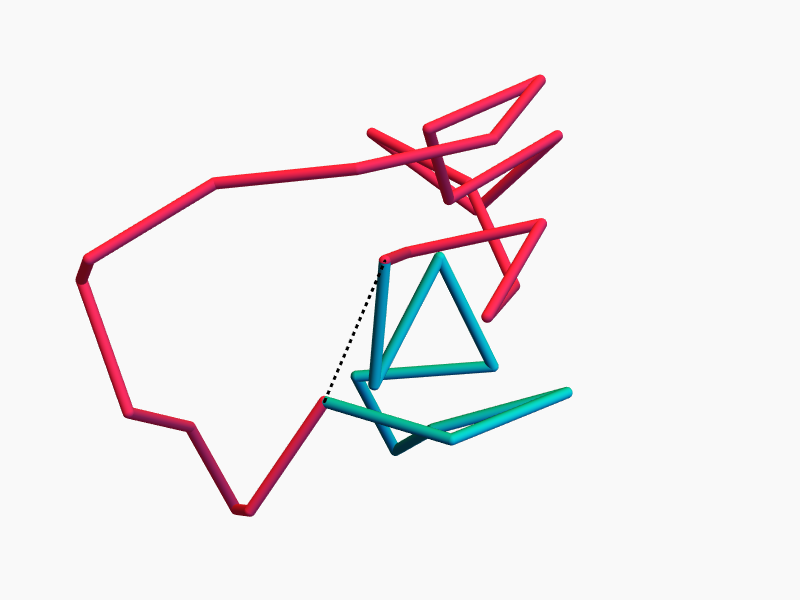
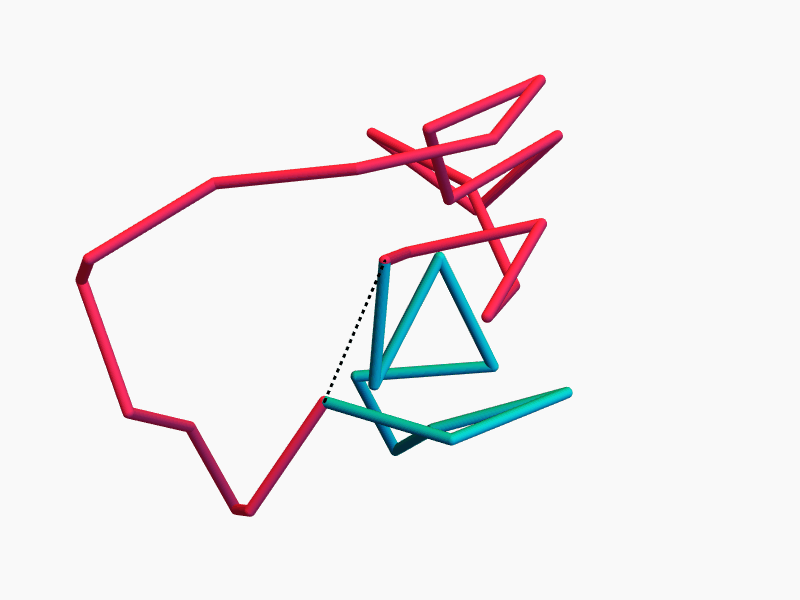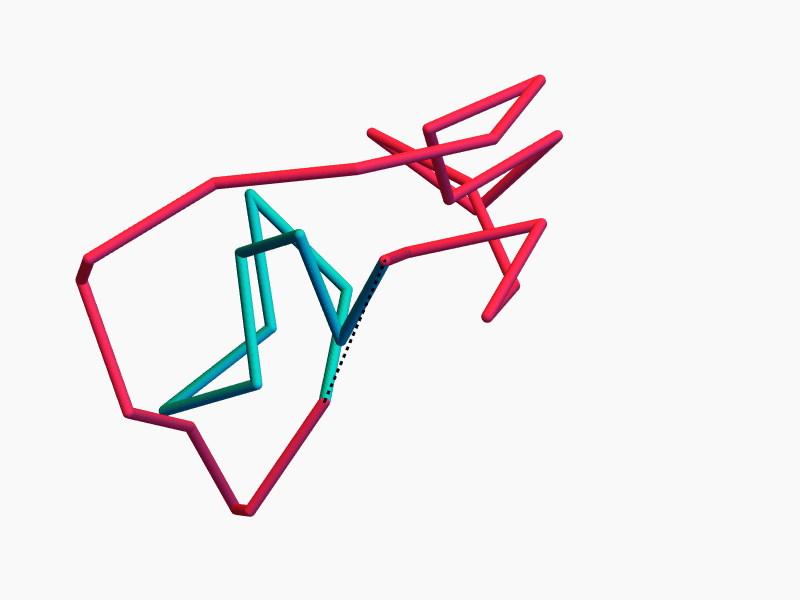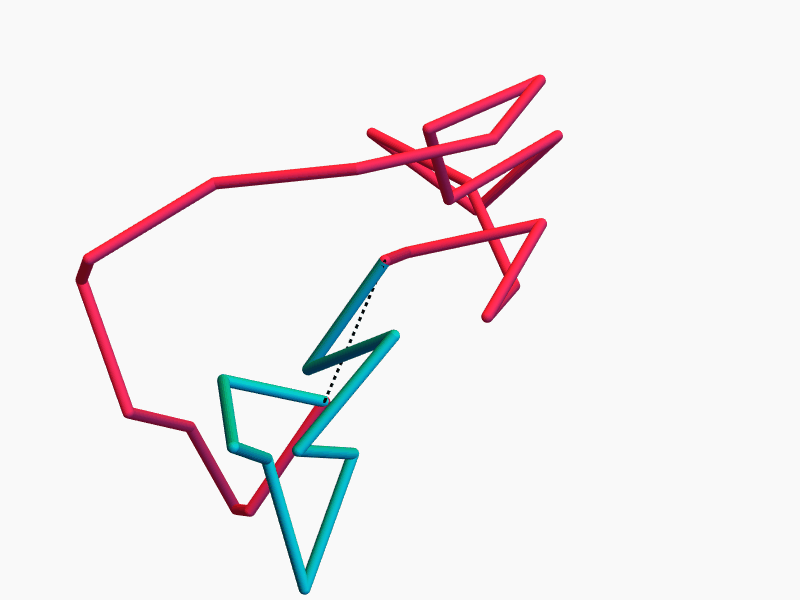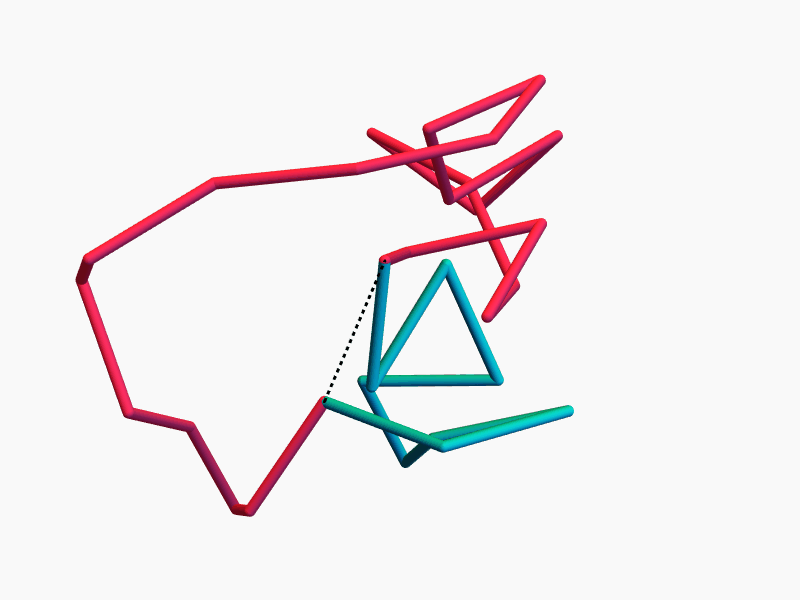
The stick number and equilateral stick number of each of the knots \(9_{35}\), \(9_{39}\), \(9_{43}\), \(9_{45}\), and \(9_{48}\) is exactly 9.
Corollary
Each of the knots \(9_{35}\), \(9_{39}\), \(9_{43}\), \(9_{45}\), and \(9_{48}\) has superbridge index equal to 4.





\(9_{35}\)
\(9_{39}\)
\(9_{43}\)
\(9_{45}\)
\(9_{48}\)
Proof.
\(\operatorname{b}(K) < \operatorname{sb}(K) \leq \frac{1}{2} \operatorname{stick}(K)\) and each of these knots has bridge index 3.
Proof.
By work of Calvo, the stick number is bounded below by 9, and we found 9-stick examples.
Theorem [with Eddy]
The equilateral stick number of each of the knots \(9_2\), \(9_3\), \(9_{11}\), \(9_{15}\), \(9_{21}\), \(9_{25}\), \(9_{27}\), \(10_8\), \(10_{16}\), \(10_{17}\), \(10_{56}\), \(10_{83}\), \(10_{85}\), \(10_{90}\), \(10_{91}\), \(10_{94}\), \(10_{103}\), \(10_{105}\), \(10_{106}\), \(10_{107}\), \(10_{110}\), \(10_{111}\), \(10_{112}\), \(10_{115}\), \(10_{117}\), \(10_{118}\), \(10_{119}\), \(10_{126}\), \(10_{131}\), \(10_{133}\), \(10_{137}\), \(10_{138}\), \(10_{142}\), \(10_{143}\), \(10_{147}\), \(10_{148}\), \(10_{149}\), \(10_{153}\), and \(10_{164}\) is less than or equal to 10.
The equilateral stick number of each of the knots \(10_3\), \(10_6\), \(10_7\), \(10_{10}\), \(10_{15}\), \(10_{18}\), \(10_{20}\), \(10_{21}\), \(10_{22}\), \(10_{23}\), \(10_{24}\), \(10_{26}\), \(10_{28}\), \(10_{30}\), \(10_{31}\), \(10_{34}\), \(10_{35}\), \(10_{38}\), \(10_{39}\), \(10_{43}\), \(10_{44}\), \(10_{46}\), \(10_{47}\), \(10_{50}\), \(10_{51}\), \(10_{53}\), \(10_{54}\), \(10_{55}\), \(10_{57}\), \(10_{62}\), \(10_{64}\), \(10_{65}\), \(10_{68}\), \(10_{70}\), \(10_{71}\), \(10_{72}\), \(10_{73}\), \(10_{74}\), \(10_{75}\), \(10_{77}\), \(10_{78}\), \(10_{82}\), \(10_{84}\), \(10_{95}\), \(10_{97}\), \(10_{100}\), and \(10_{101}\) is less than or equal to 11.
The equilateral stick number of each of the knots \(10_{76}\) and \(10_{80}\) is less than or equal to 12.
In particular, all knots up to 10 crossings have equilateral stick number \(\leq 12\).
Results
Theorem [with Eddy]
The equilateral stick number of each of the knots \(9_2\), \(9_3\), \(9_{11}\), \(9_{15}\), \(9_{21}\), \(9_{25}\), \(9_{27}\), \(10_8\), \(10_{16}\), \(10_{17}\), \(10_{18}\), \(10_{56}\), \(10_{82}\), \(10_{83}\), \(10_{85}\), \(10_{90}\), \(10_{91}\), \(10_{94}\), \(10_{100}\), \(10_{103}\), \(10_{105}\), \(10_{106}\), \(10_{107}\), \(10_{110}\), \(10_{111}\), \(10_{112}\), \(10_{115}\), \(10_{117}\), \(10_{118}\), \(10_{119}\), \(10_{126}\), \(10_{131}\), \(10_{133}\), \(10_{137}\), \(10_{138}\), \(10_{142}\), \(10_{143}\), \(10_{147}\), \(10_{148}\), \(10_{149}\), \(10_{153}\), and \(10_{164}\) is less than or equal to 10.
The equilateral stick number of each of the knots \(10_3\), \(10_6\), \(10_7\), \(10_{10}\), \(10_{15}\), \(\sout{10_{18}}\), \(10_{20}\), \(10_{21}\), \(10_{22}\), \(10_{23}\), \(10_{24}\), \(10_{26}\), \(10_{28}\), \(10_{30}\), \(10_{31}\), \(10_{34}\), \(10_{35}\), \(10_{38}\), \(10_{39}\), \(10_{43}\), \(10_{44}\), \(10_{46}\), \(10_{47}\), \(10_{50}\), \(10_{51}\), \(10_{53}\), \(10_{54}\), \(10_{55}\), \(10_{57}\), \(10_{62}\), \(10_{64}\), \(10_{65}\), \(10_{68}\), \(10_{70}\), \(10_{71}\), \(10_{72}\), \(10_{73}\), \(10_{74}\), \(10_{75}\), \(10_{77}\), \(10_{78}\), \(\sout{10_{82}}\), \(10_{84}\), \(10_{95}\), \(10_{97}\), \(\sout{10_{100}}\), and \(10_{101}\) is less than or equal to 11.
The equilateral stick number of each of the knots \(10_{76}\) and \(10_{80}\) is less than or equal to 12.
In particular, all knots up to 10 crossings have equilateral stick number \(\leq 12\).
Results


\(10_{16}\)
\(10_{84}\)
Results
Theorem [with Blair, Eddy, and Morrison]
The knots \(13n_{592}\) and \(15n_{41,127}\) have bridge index 4, superbridge index 5, and stick number 10.


\(13n_{592}\)
\(15n_{41,127}\)
Proof.
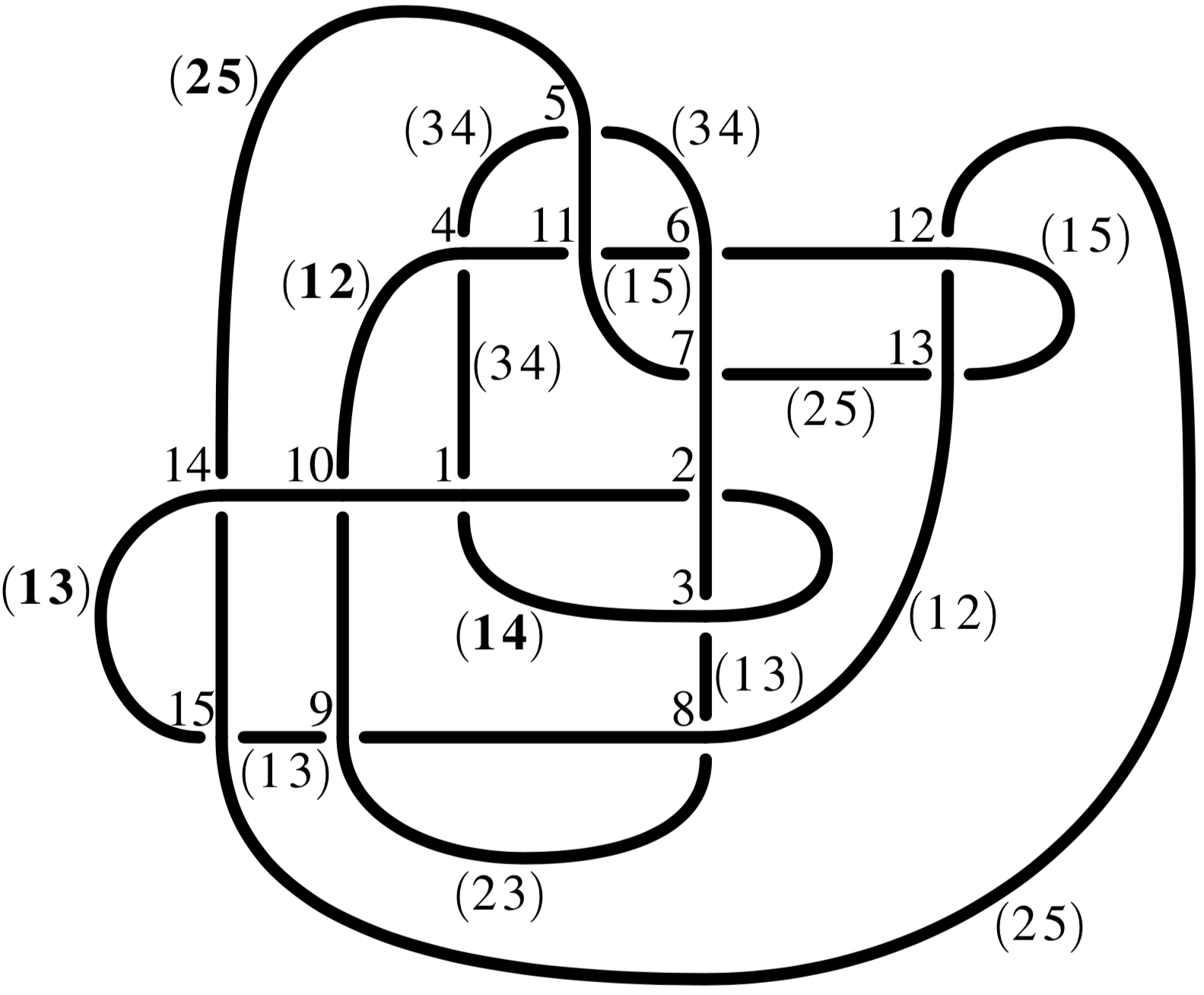


Surjective homomorphism \(\pi_1(S^3 \backslash 15n_{41,127}) \to S_5\), so
\(4 \leq \operatorname{b} < \operatorname{sb} \leq \frac{1}{2}\operatorname{stick} \leq 5\).
\(15n_{41,127}\)
\(\overline{13n_{592}}\)
Results
Theorem [—]
The knots \(8_1\), \(8_2\), \(8_3\), \(8_5\), \(8_6\), \(8_7\), \(8_8\), \(8_{10}\), \(8_{11}\), \(8_{12}\), \(8_{13}\), \(8_{14}\), \(8_{15}\), \(9_7\), \(9_{16}\), \(9_{20}\), \(9_{26}\), \(9_{28}\), \(9_{32}\), and \(9_{33}\) all have superbridge index equal to 4.
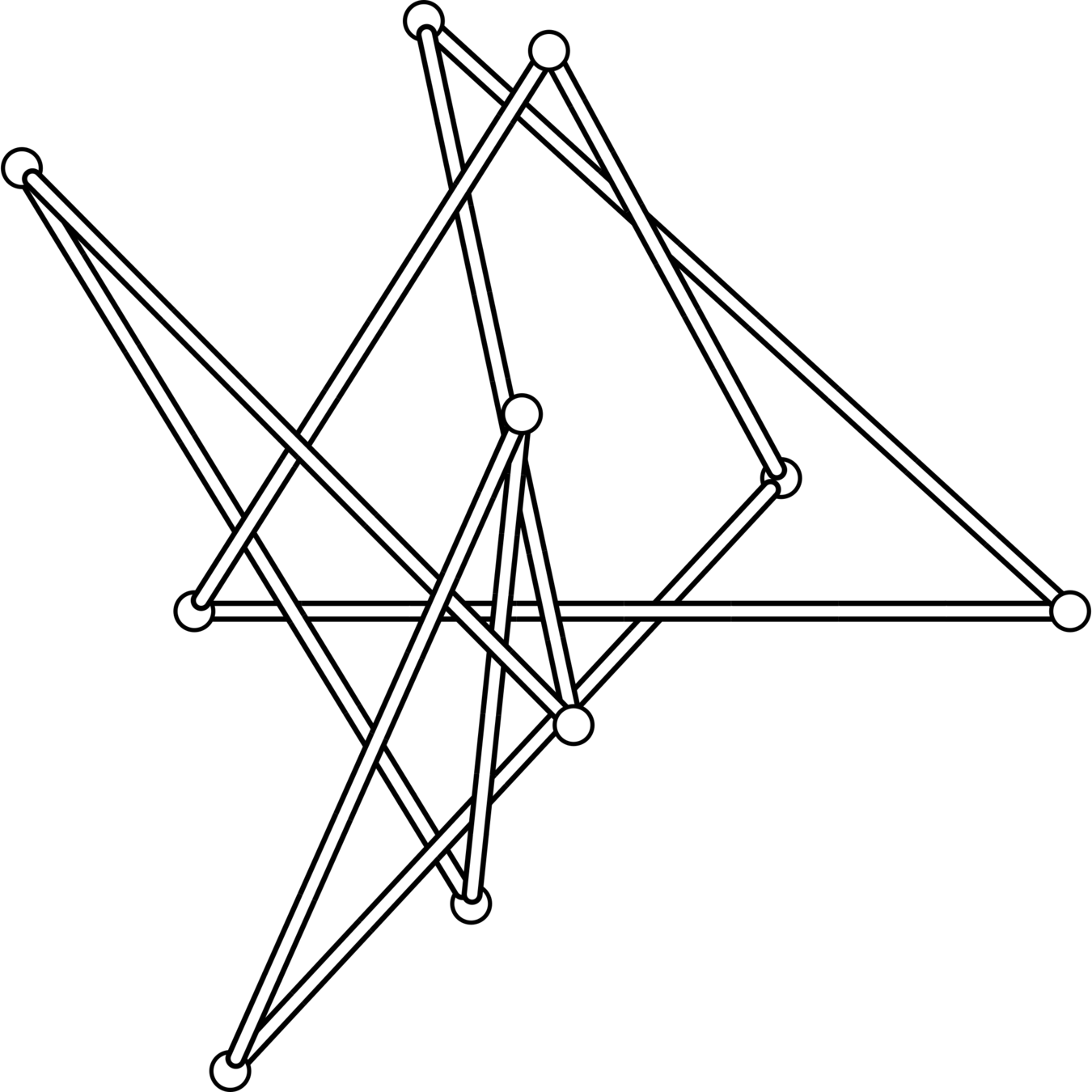
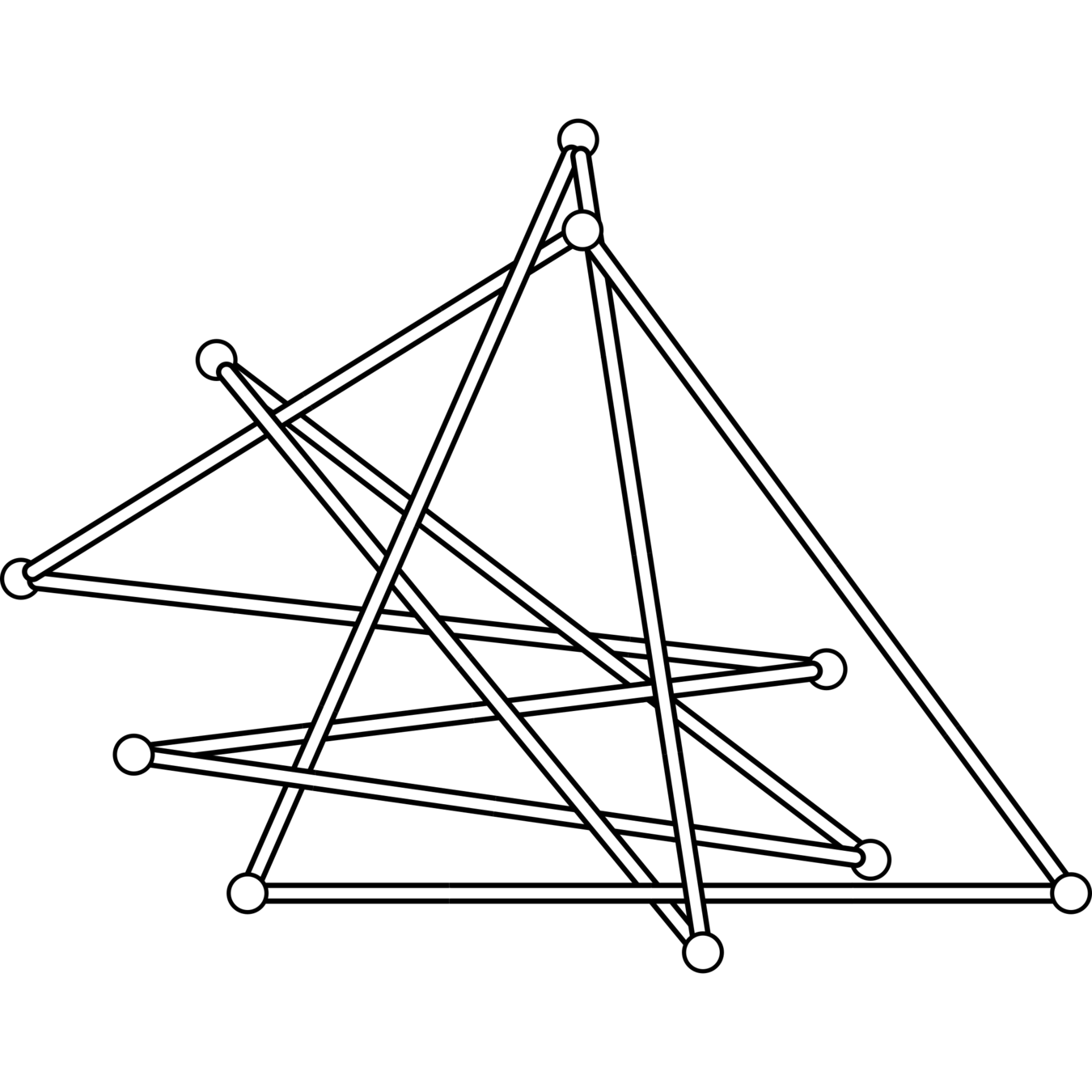
\(8_{10}\)
\(9_7\)
Proof.
For each knot, \(\mathrm{sb}(K)\leq \frac{1}{2}\mathrm{stick}(K) \leq 5\) and, using a result of Jeon and Jin, \(4 \leq \mathrm{sb}(K)\).
Can show that \(\mathrm{sb} = 5\) is equivalent to a linear system of inequalities with no solution.
Results
…or on Github, along with source code!
Results have also been added to KnotInfo
Strategy
Generate hundreds of billions of random polygons in tight confinement and look for new examples.
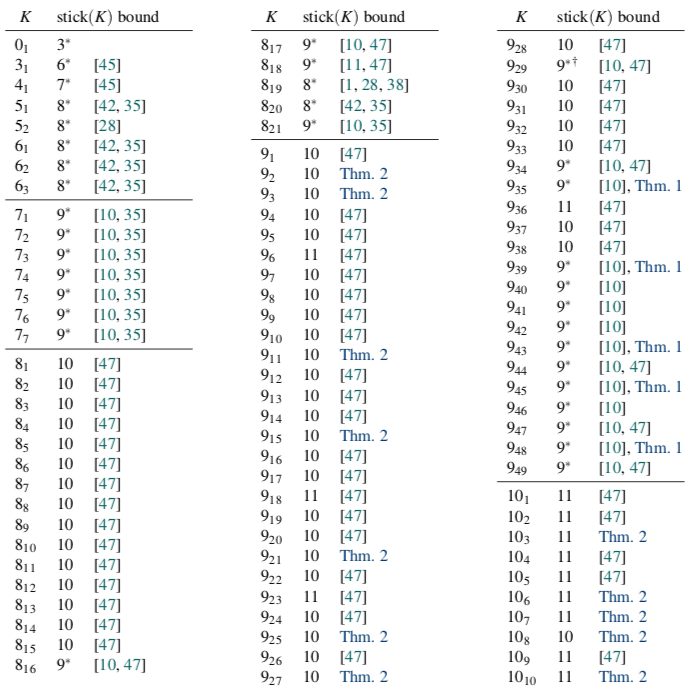
Some Numbers
- 220 billion polygons generated
- Identified knot types of all but 59(!)
- 93.3% unknots
- 2455 distinct knot types, 2420 prime, including 11 different 16-crossing knots
- 50,000 core-hours of CPU time (or 5.7 core-years)
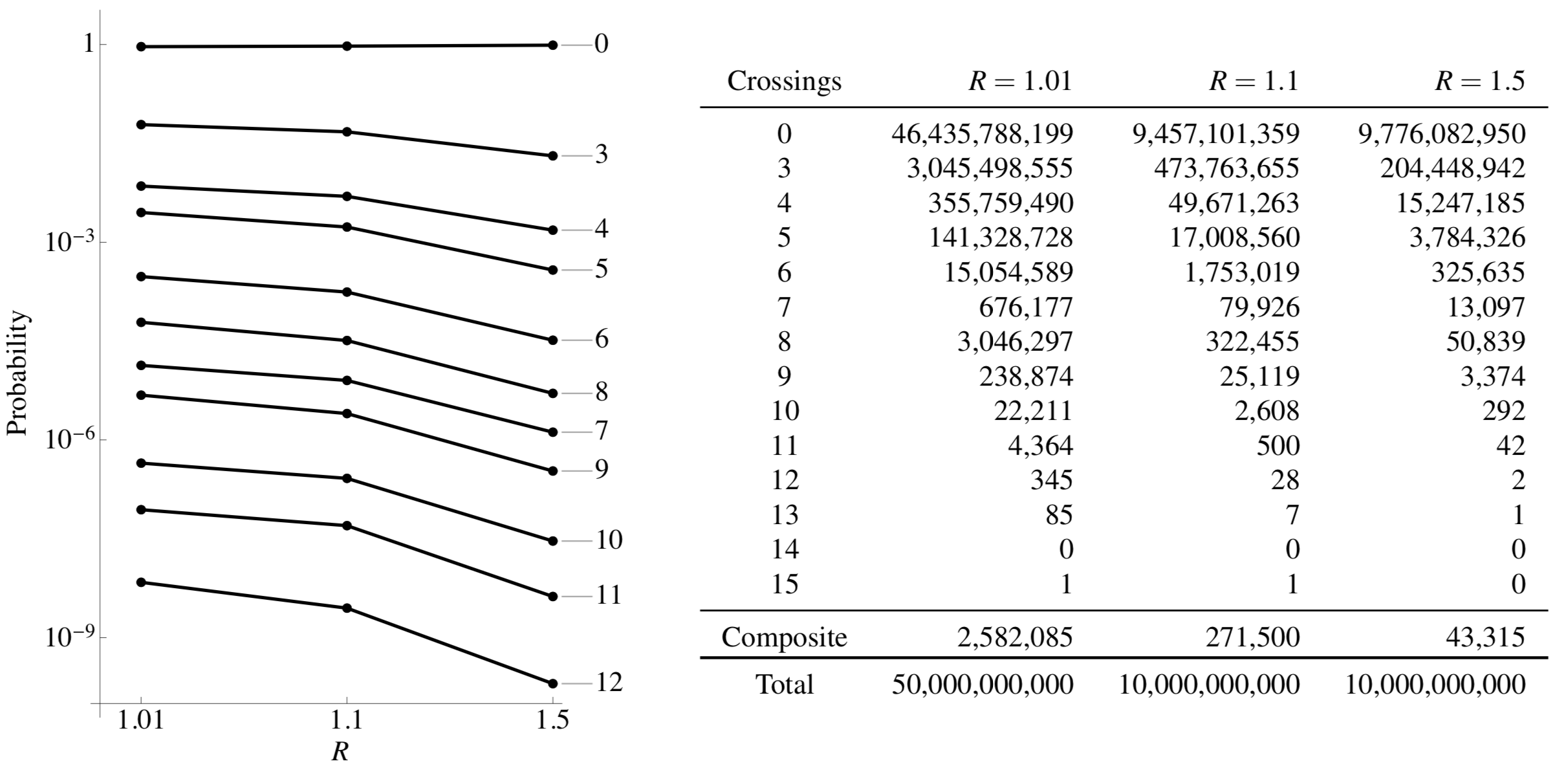
Data for 10-gons
Equilateral Polygons
Continuous symmetry \(\Rightarrow\) conserved quantity
The space of equilateral \(n\)-gons has lots of symmetries...
\(n-3\) commuting symmetries
Rotations around \(n-3\) chords \(d_i\) by \(n-3\) angles \(\theta_i\) commute.


Chord distributions
Theorem [with Cantarella]
The joint distribution of \(d_1,\ldots , d_{n-3}\) and \(\theta_1, \ldots , \theta_{n-3}\) are all uniform on their domains.
Therefore, sampling equilateral \(n\)-gons is equivalent to sampling random points in the convex polytope of \(d_i\)’s and random angles \(\theta_i\).
A polytope
The \((n-3)\)-dimensional moment polytope \(\mathcal{P}_n \subset \mathbb{R}^{n-3}\) is defined by the triangle inequalities
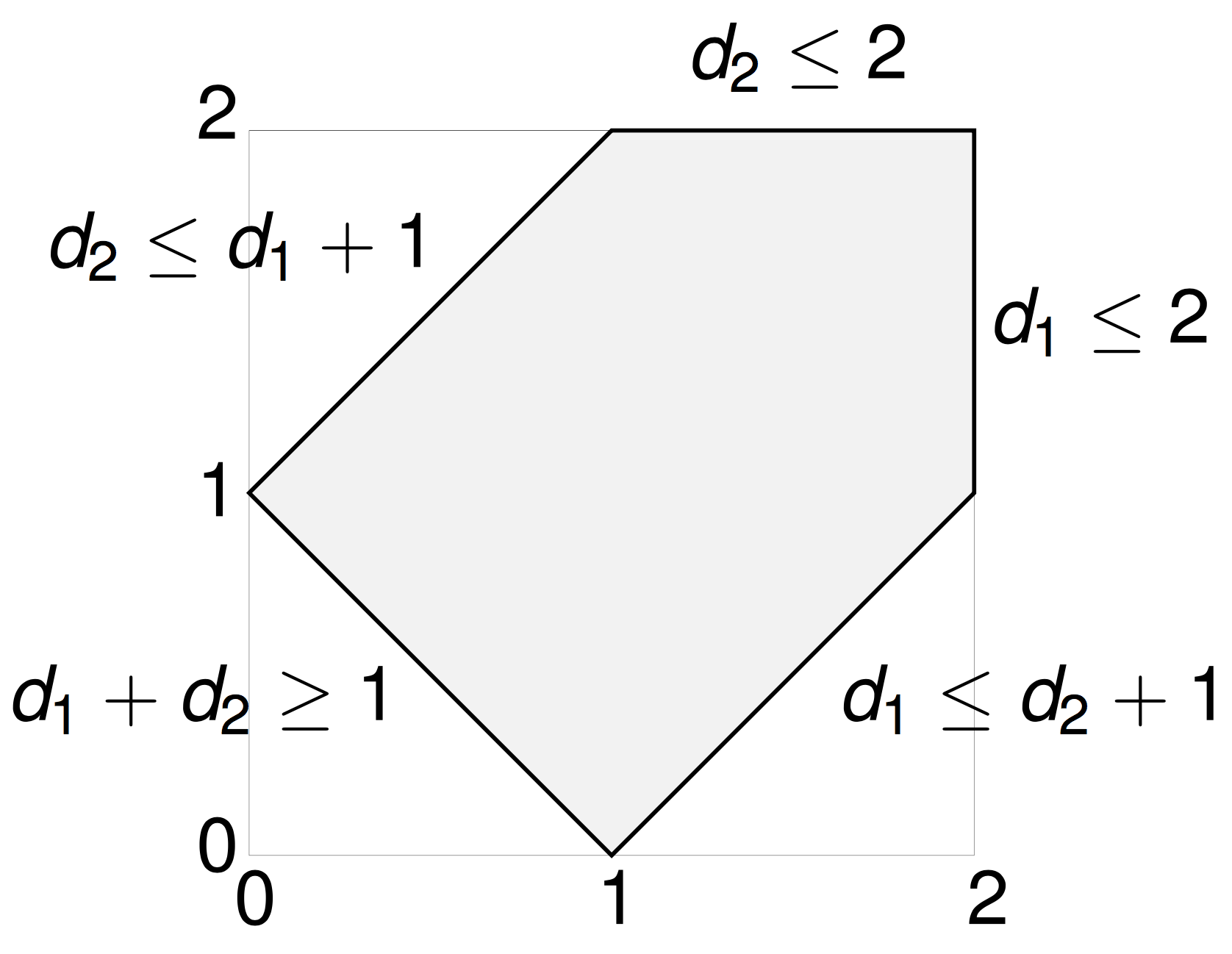
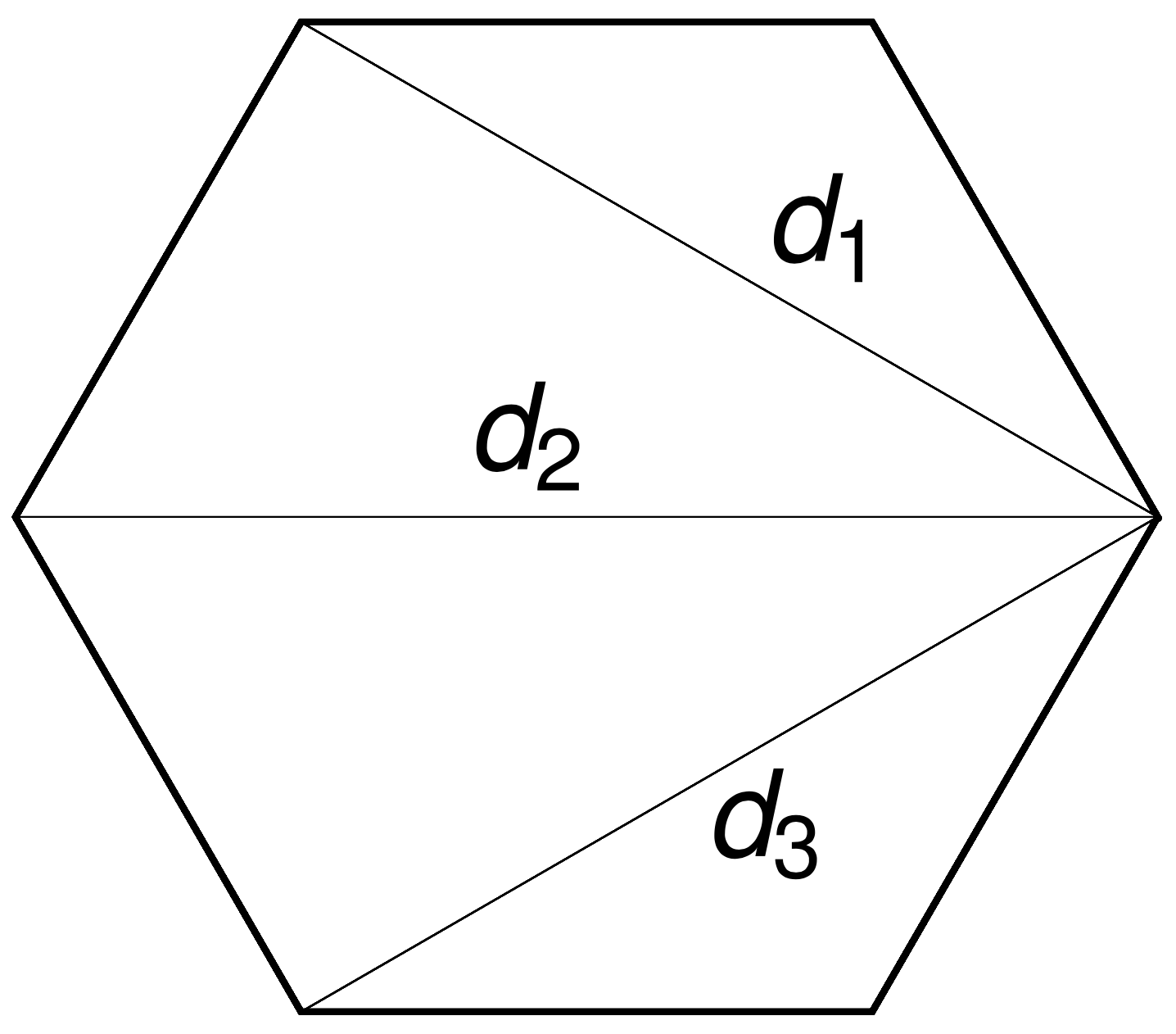
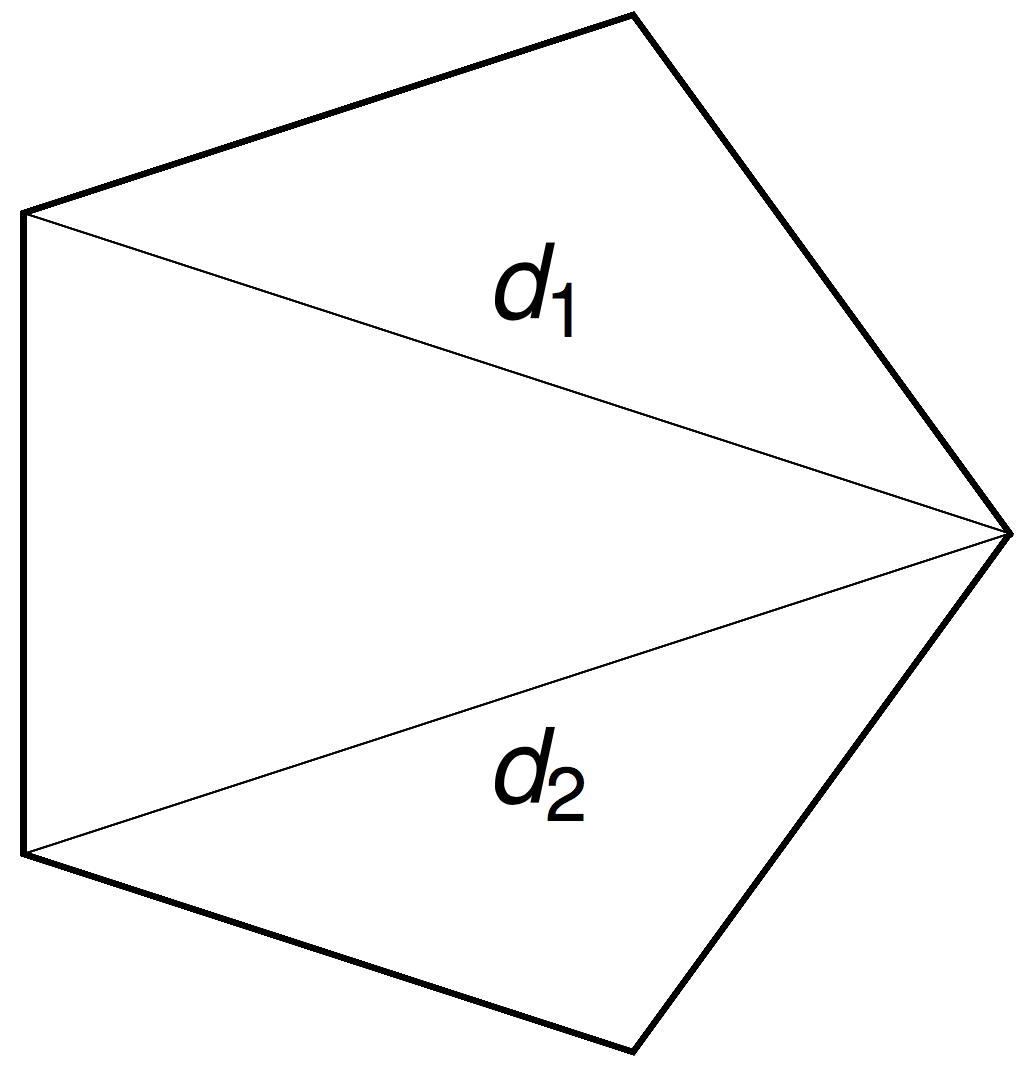
Reconstruction
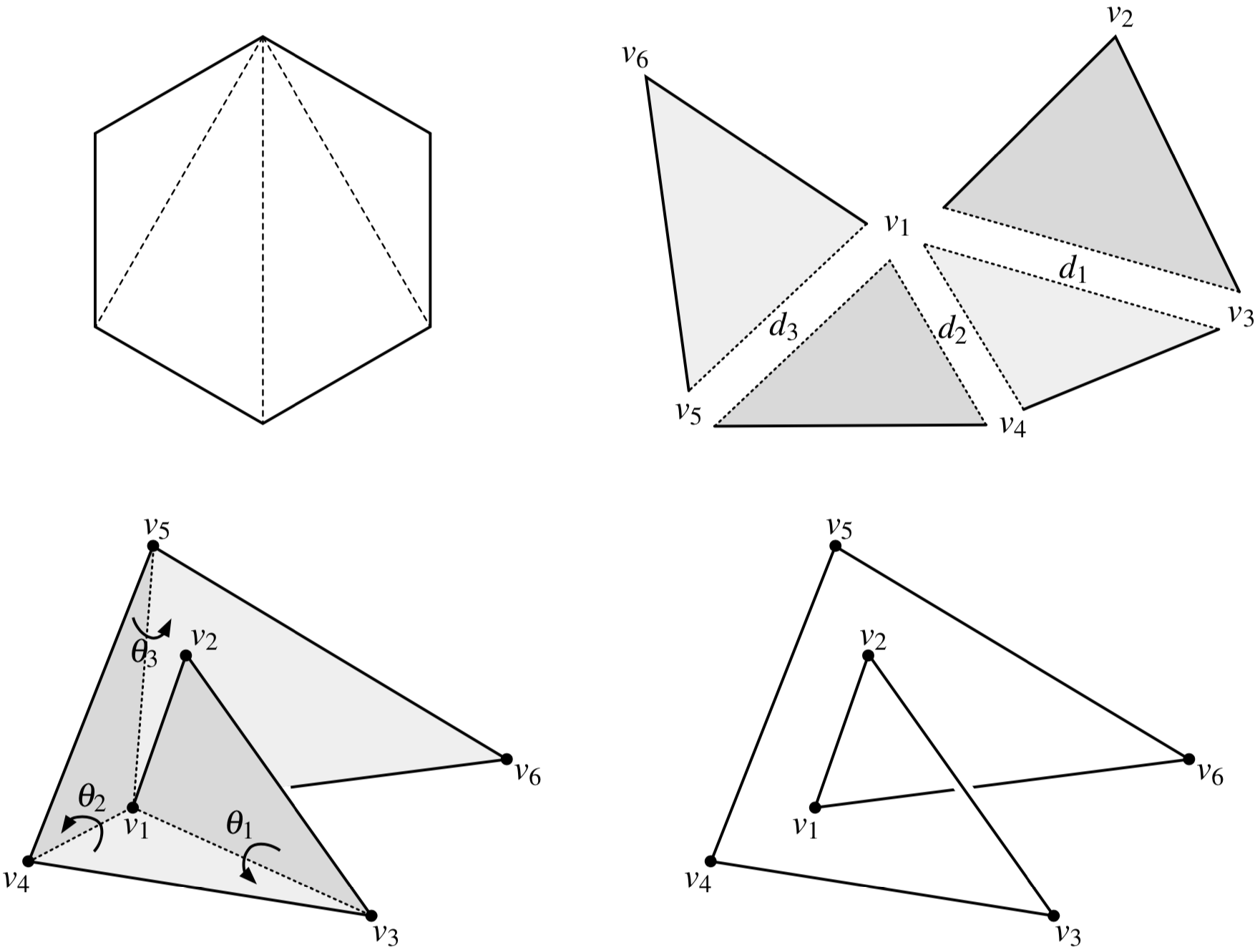
Sampling
Theorem [Smith, 1984]
For any convex polytope \(\mathcal{P}\), the hit-and-run Markov chain is uniformly ergodic with respect to Lebesgue measure on \(\mathcal{P}\).
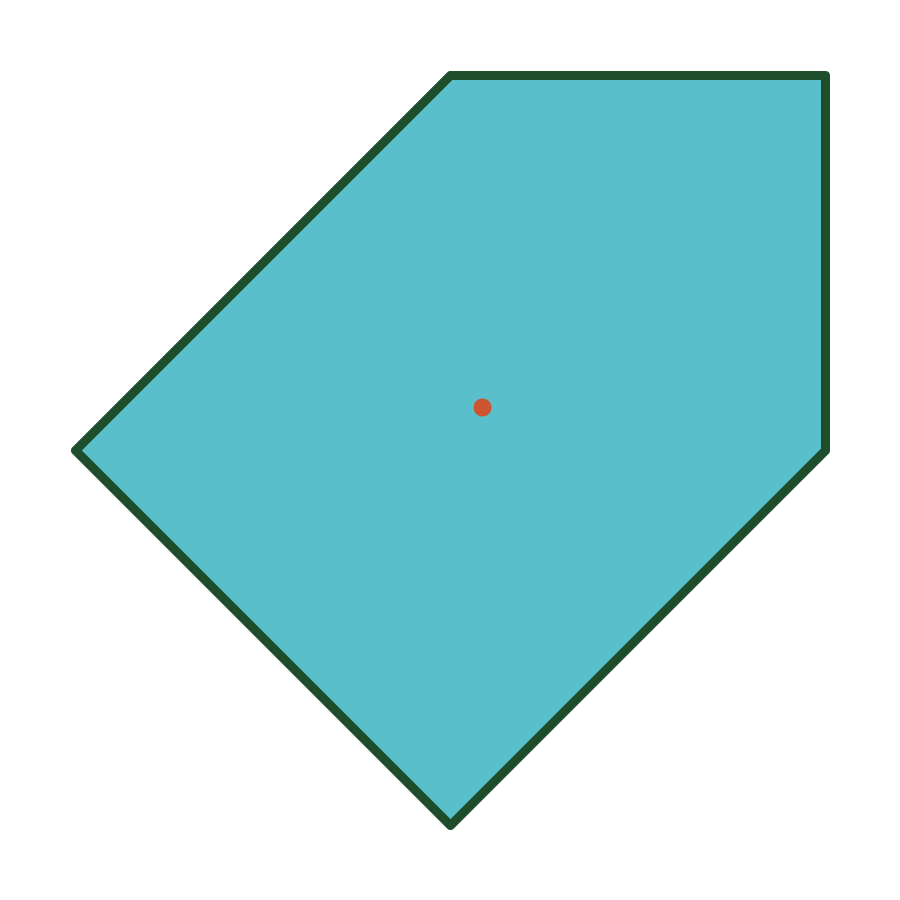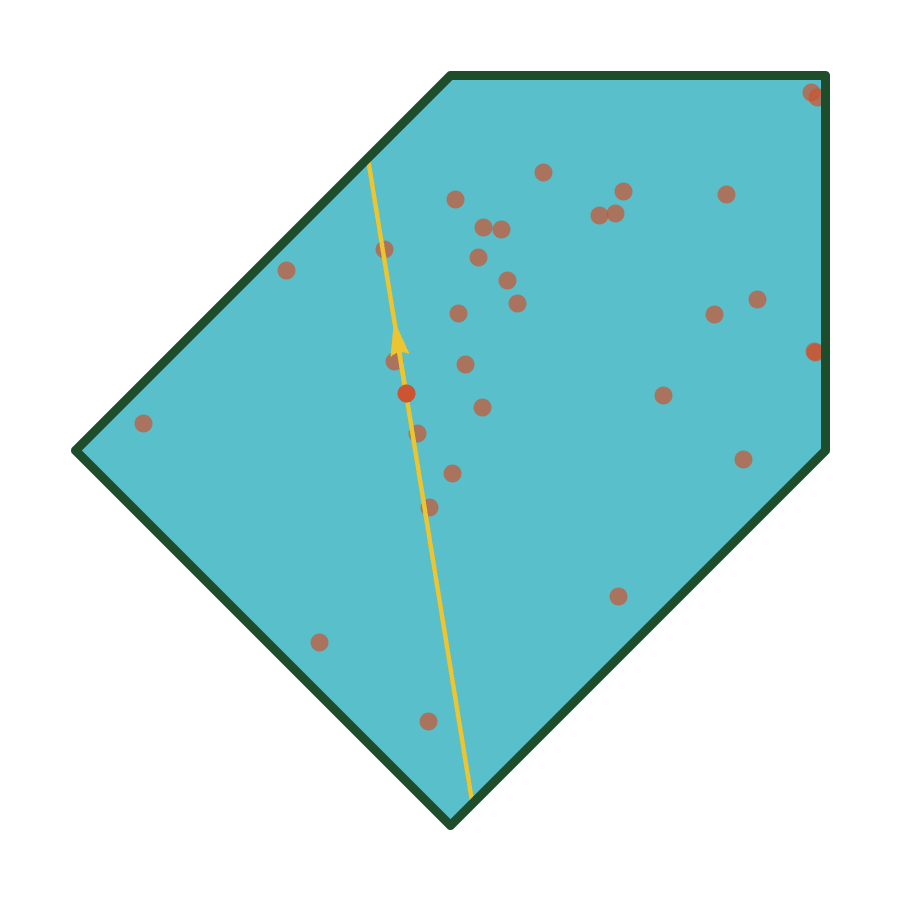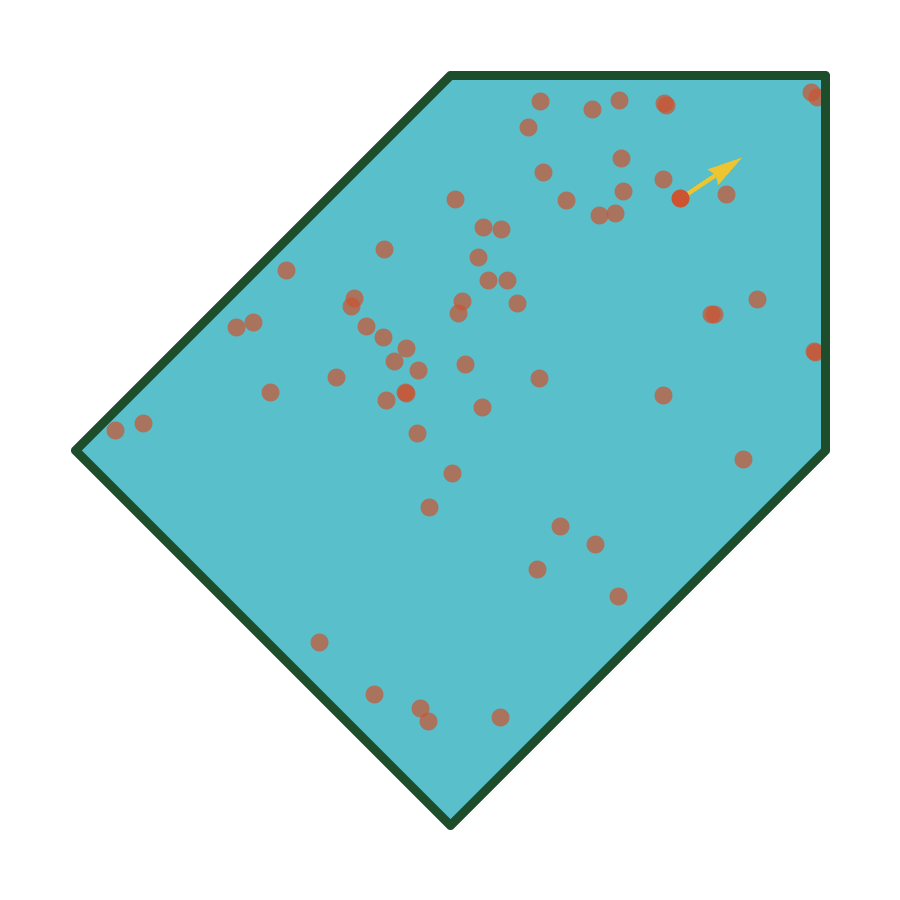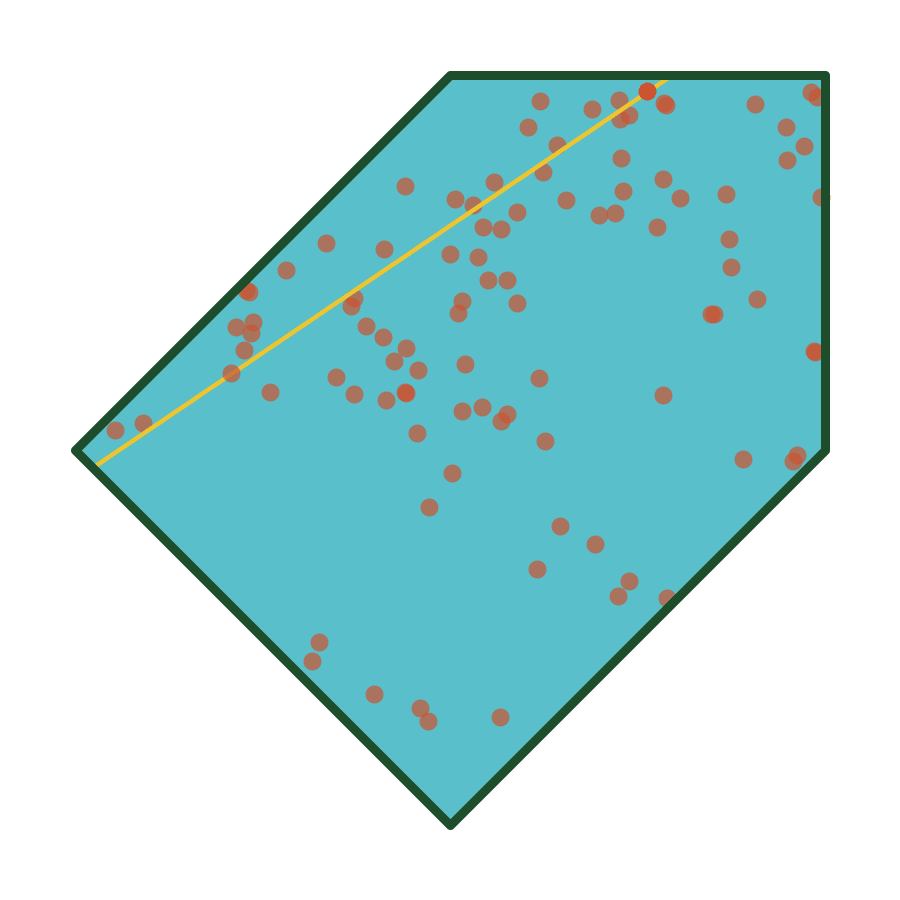
Confined Polygons
The same algorithm works even better for tightly confined polygons: let \(d_i \leq R\) for all \(i\).


Pipeline
Hyperbolic volume
check for uniqueness
(Knot ID, vertices)
Verification
DT code
KnotInfo’s
Knot ID
vertices
Questions
Only two examples where the best bound on stick number is different from the best bound on equilateral stick number:
Are there more (low-crossing) examples? Are these distinct invariants?
Other strategies for generating large ensembles of random polygons in tight confinement?
Other lower bounds on stick number or superbridge index?
Thank you!
References
New stick number bounds from random sampling of confined polygons
Thomas D. Eddy and Clayton Shonkwiler
Experimental Mathematics, to appear, arXiv:1909.00917
Ryan Blair, Thomas D. Eddy, Nathaniel Morrison, and Clayton Shonkwiler
Journal of Knot Theory and Its Ramifications 29 (2020), no. 3, 2050011