What is…
(Applied) Symplectic Geometry
?
Clay Shonkwiler
/sg
this talk!

Symplecti-wha?
—Dusa McDuff & Dietmar Salamon
Introduction to Symplectic Topology


—Ana Cannas da Silva
A nice space, where multivariable calculus makes sense. Think spheres, tori, projective spaces, …

A rule for assigning a number to pairs of tangent vectors which acts like (signed) area of the parallelogram they span.
Symplectic Manifold
Examples
\((S^2,d\theta\wedge dz)\)
\((\mathbb{R}^2,dx \wedge dy) = (\mathbb{C},\frac{i}{2}dz \wedge d\bar{z})\)
\((S^2,\omega)\), where \(\omega_p(u,v) = (u \times v) \cdot p\)
\((\mathbb{R}^2,\omega)\) where \(\omega(u,v) = \langle i u, v \rangle \)
\((\mathbb{C}^n, \frac{i}{2} \sum dz_k \wedge d\overline{z}_k)\)
\((\mathbb{C}^{m \times n}, \omega)\) with \(\omega(X_1,X_2) = -\operatorname{Im} \operatorname{trace}(X_1^* X_2)\).
\((T^* \mathbb{R}^n,\sum dq_i \wedge dp_i)\)
What does this get you?
Volume
\(\omega^{\wedge n} = \omega \wedge \dots \wedge \omega\) is a volume form on \(M\), and induces a measure
called Liouville measure on \(M\).
In particular, if \(M\) is compact, this can be normalized to give a probability measure.
Theorem [Archimedes]
\(d\theta \wedge dz\) is the standard area form on the unit sphere \(S^2\).
A (Very) Classical Example

KoenB [ ] from Wikimedia Commons

Noether’s Theorem
Every symmetry has a corresponding conserved quantity
Circle Actions
A circle action on \((M,\omega)\) determines a vector field \(X\) by

\(S^1=U(1)\) acts on \((S^2,d\theta \wedge dz)\) by
So \(X = \frac{\partial}{\partial \theta}\).
Symmetries and Conserved Quantities
Definition. A circle action on \((M,\omega)\) is Hamiltonian if there exists a map
so that \(d\mu = \iota_{X}\omega = \omega(X,\cdot)\), where \(X\) is the vector field generated by the circle action.

\(X = \frac{\partial}{\partial \theta}\)
\(\mu(\theta,z) = z\)
\(\iota_X\omega = \iota_{\frac{\partial}{\partial \theta}} d\theta \wedge dz = dz \)
Extremely Deep Fact
Archimedes’ Theorem can be suitably generalized to any symplectic manifold with a Hamiltonian circle action (or, better yet, many commuting Hamiltonian circle actions).
See: Atiyah, Guillemin–Sternberg, Duistermaat–Heckman, and toric symplectic manifolds (and toric varieties)
“(Applied)”…?
I am interested in mathematical models of topological polymers, especially ring-shaped biopolymers and synthetic materials…
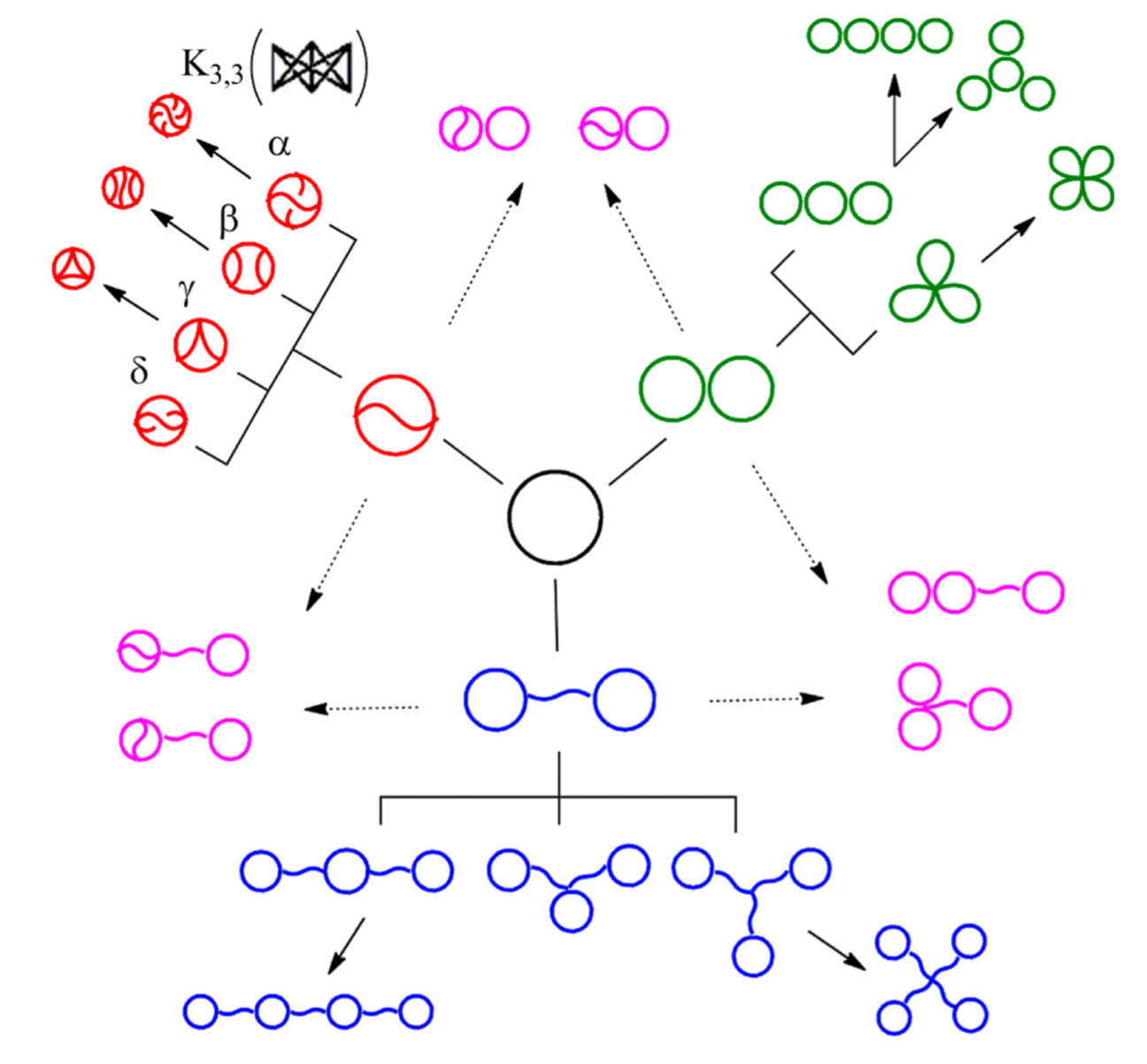
…and in frame theory and statistical signal processing.

Examples of Results
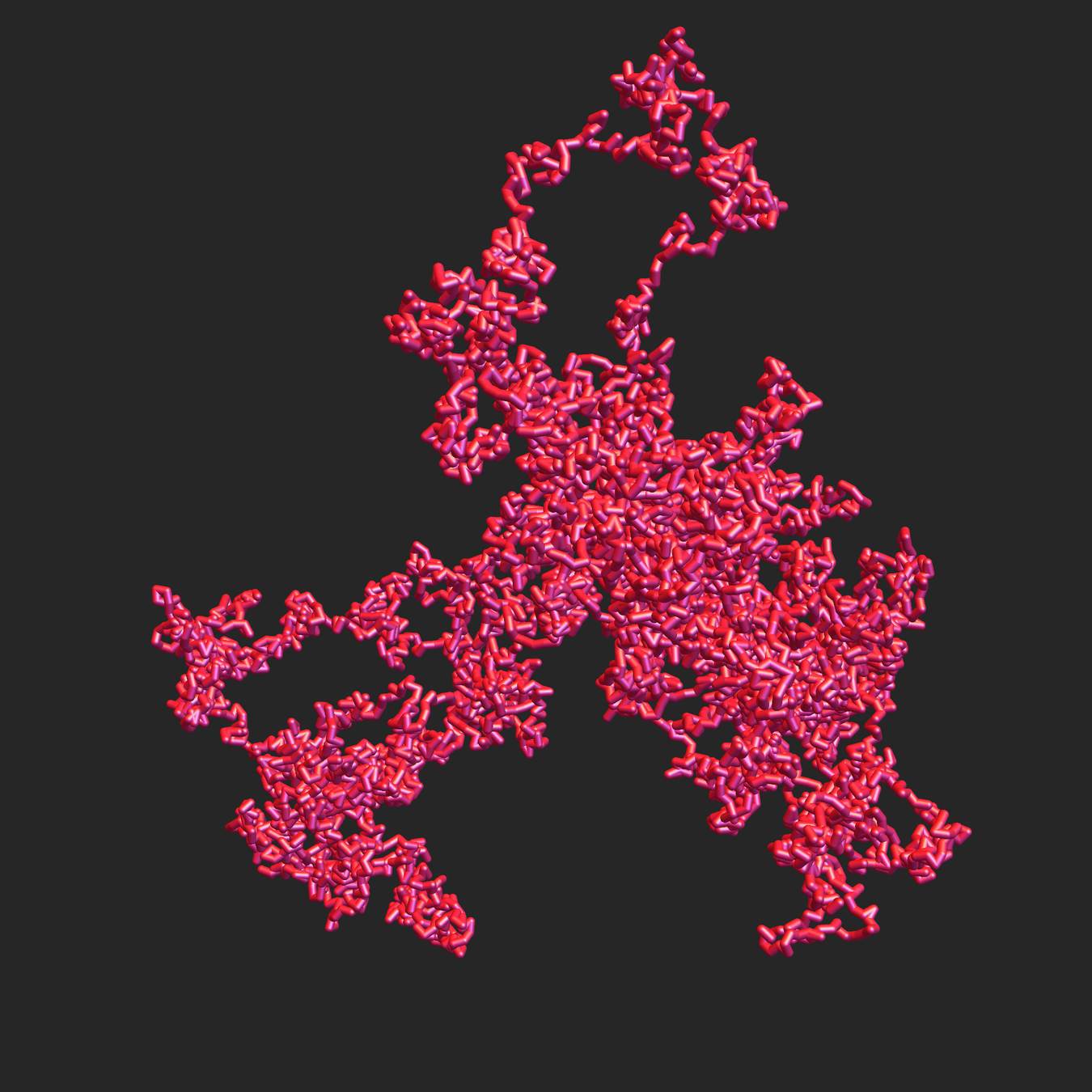
[with Cantarella, Duplantier, Uehara]
The first efficient, provably correct algorithm for sampling equilateral random polygons in \(\mathbb{R}^3\).
Examples of Results
Improved stick number bounds on ≈38% of the knots in the Rolfsen table.
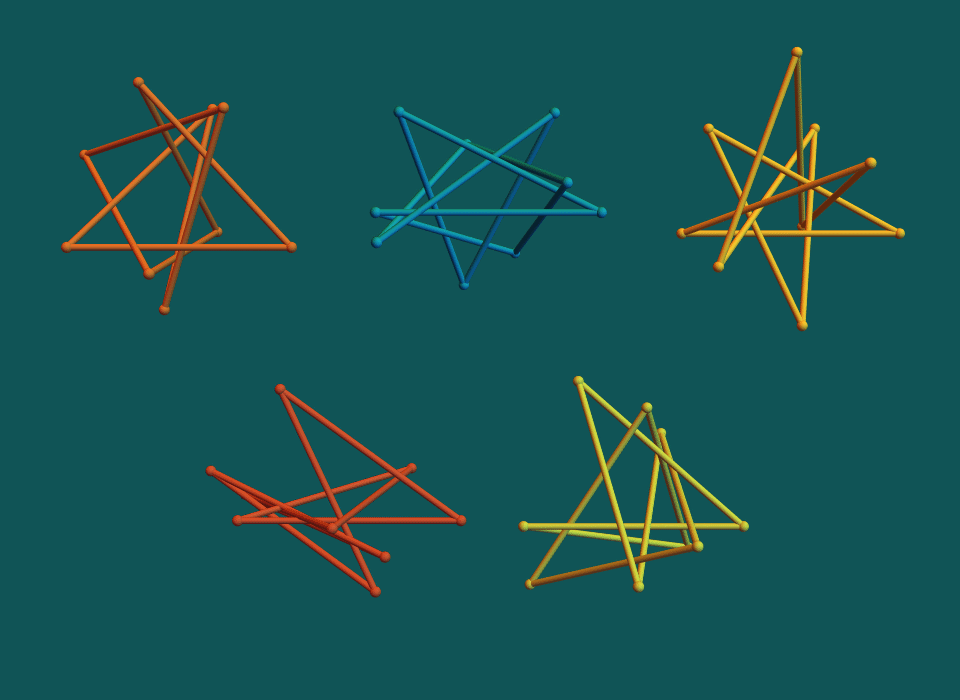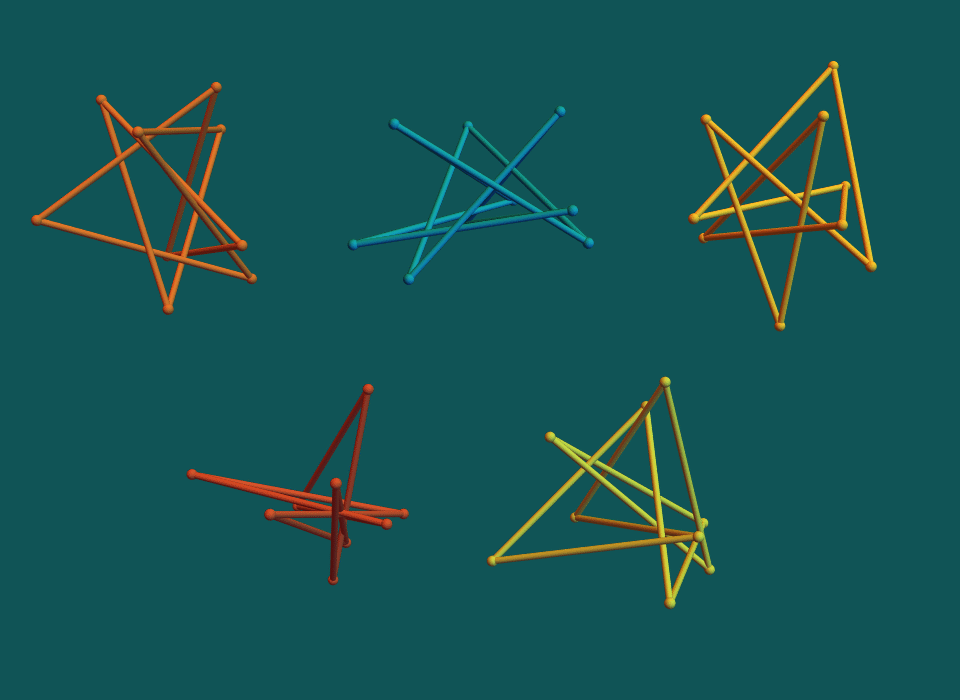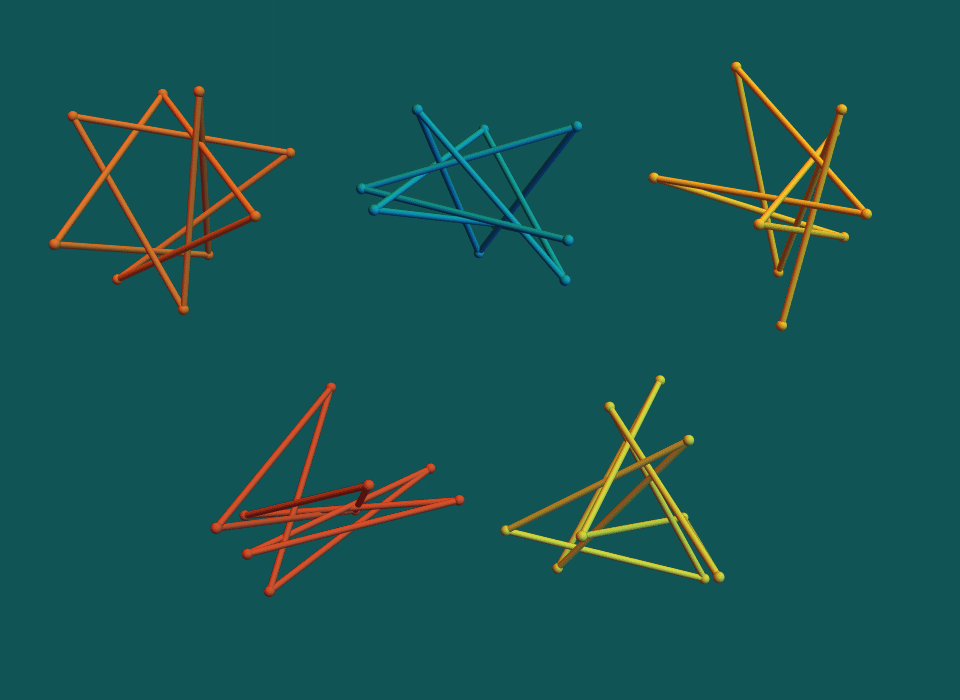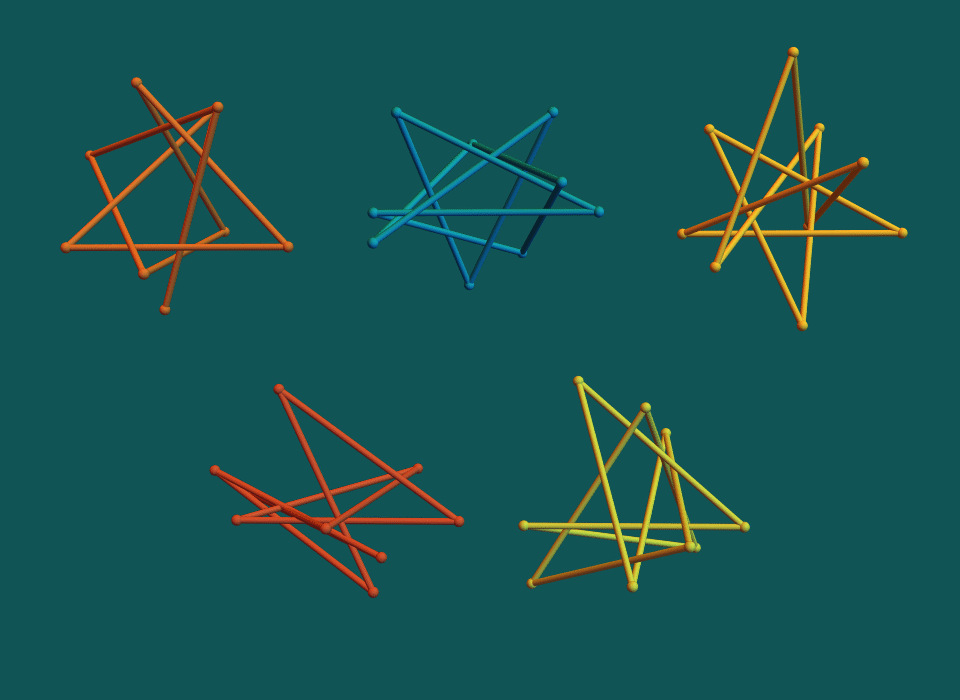
Examples of Results
A broad generalization of the Frame Homotopy Conjecture, which says the space of unit-norm tight frames is path-connected.