Demystifying:

wtf is a 'model'?

Sidney Bell, PhD

Last updated 2024

A model is a hypothesis, written down in math.

Text

Some things models are useful for:

  • Quantifying how well a given hypothesis explains
    the data we observe

  • Quantifying uncertainty

  • Interpolation of missing data

  • Extrapolation* / prediction

  • Generation of new data which shared properties of the input data

Modeling involves lots of choices
and is a bit of an art.
Some things to look for:

  • What is the hypothesis?
     
  • How well does the model formulation (equations) match what they say their hypothesis is? Are their equations unnecessarily complicated?
     
  • Do they have the right dataset to
    address that hypothesis?
     
  • How much error is there
    (i.e., how well does this hypothesis explain this data)?

Outline

  • Part 1: What is a "model?"
    • Case study: concrete, simple model of dengue virus evolution
       
  • Part 2: Ok, so what is "machine learning" and what makes it fancy?
    • Case study: popular flavors of ML models in single-cell biology right now

Expertise is deeply understanding a very small number of concepts

Loops

Conditionals

Variables

Functions

Data encoding

Model form

Training algo

Evaluation

Step by step

1. Curate input: Data
(counts, images, other)

2. Formulate: Based on your hypothesis, encode relationships between data “features” as mathematical function(s)

3. Train: “Learn” the value of variables in the model functions through iterative adjustment and evaluation

4. Test: the generalizability of these functions on held-out data

5. Interpret: this is the tricky part :)

Example / Case Study

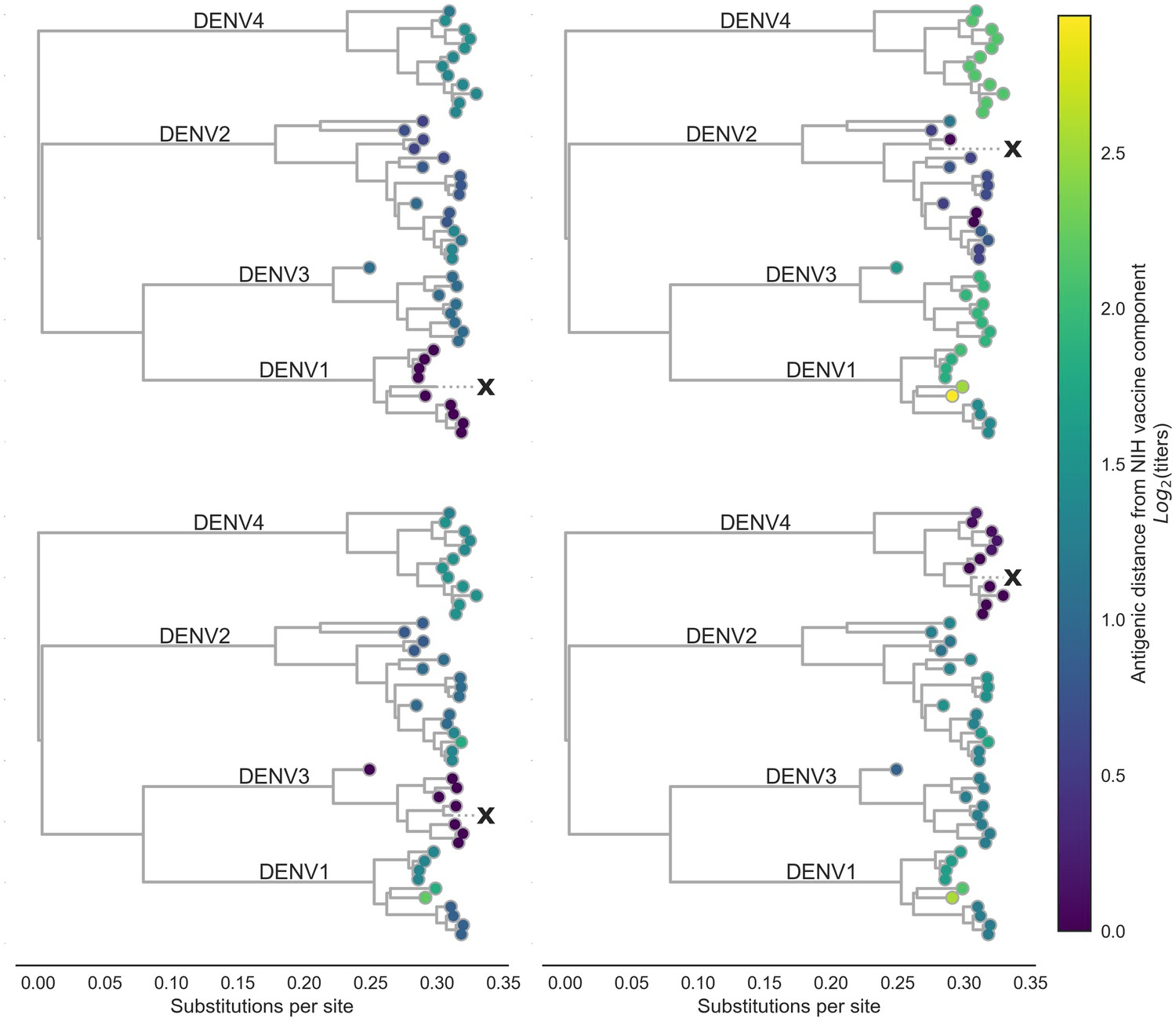
Vaccines are more effective against some variants than others. Why?

Bell et al, eLife 2019

1. Curate input data

Often a huge portion of the work is curating, annotating, normalizing and integrating data.

(Glossing over for now)

Example hypothesis:
dengue antigenic variation is driven by underlying genetic changes

Subtitle

Antigenic distance between viruses i, j

D_{ij} \propto \sum_{m}d_m

Mutations between i,j

2. Formulate

Effect of each mutation (unknown to "learn")

Experiment: how well does the hypothesis (model) explain reality (observed data)? 

Maximum likelihood

P(data | hypothesis is true)

Easier to estimate

Bayesian

P(hypothesis is true | data)

Harder to estimate

Sidebar: evaluation

Parameters are akin to experimental conditions

Maximum likelihood

P(data | hypothesis is true
under these conditions / parameters)

Running your experiment:

 

3. Train: Find the parameters that maximize the
"maximum likelihood"
(see what we did there?)


4. Test: Assess how well this hypothesis & best-fit parameters (experimental conditions) explain real-world data
 

5. Interpret: If it's a reasonably good model,
use the model to learn other things

Find the parameters which maximize
P(data | model, parameters)

"Training error": how different is the model's guess from the actual data?

"Regularization" is a corollary hypothesis:
Most antigenic change will be the result of a few large changes, not many small changes. So we expect most values of d to be 0, such that the distribution of d looks like an exponential distribution.

\propto

"Cost Function"

3. Train

3. Train

Try a value => assess training error => update value

 

Lots of algorithms + implementations readily available for how to pick the next value to try. 

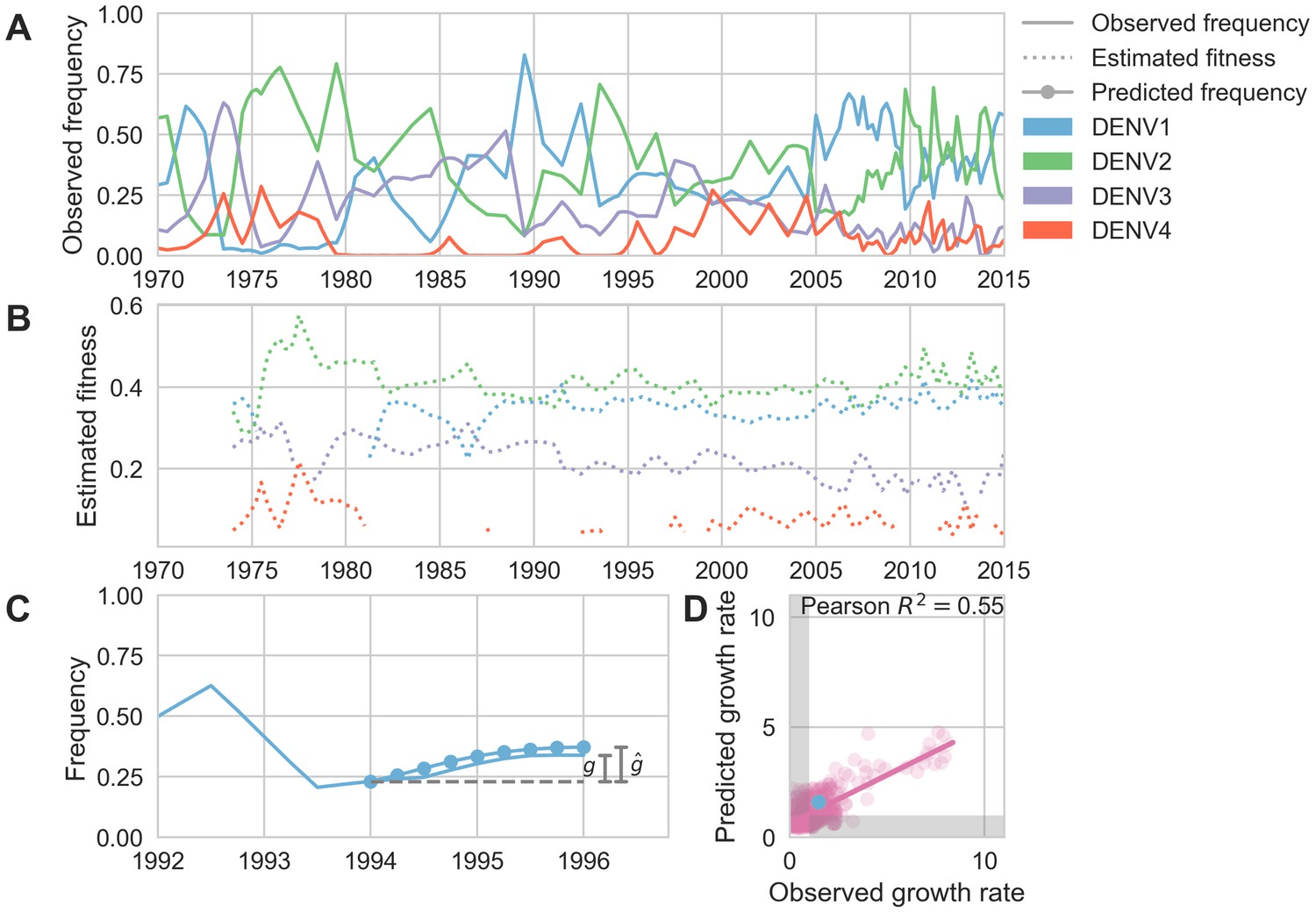
Assess how well this model & best-fit parameters explain real-world data

 "Root mean squared error" = 0.75 (95% CI 0.74–0.77)

(95% CI 0.77–0.79)

R^2=0.78

On average, the model's predictions of the antigenic distance between pairs of strains is within ~0.75 normalized log2 titer units

On average, this model (hypothesis) is able to explain about 78% of the variation in titer distances between strains

4. Test

Interpolation

Data

Interpolated data using model parameters

5. Interpret

Prediction

5. Interpret

Antigenic distance between viruses i, j

D_{ij} \propto \sum_{m}d_m

Effect of each mutation

We learned these and they reliably predict observed data

Predict antigenic distance between existing vaccine and the new circulating strain by adding up these values for each mutation in its genome

"Prompting"

Input to other models!

5. Interpret

Interpolated data using model parameters

1. Curate input

2. Formulate your hypothesis

3. Train to learn params

4. Test generalizability

5. Interpret

Additional model with another task

Input to other models!

5. Interpret

  • Models are just hypotheses, written down in math. They are not magic or scary. You use them every day.
     

  • There are a lot of decisions (art) involved in model design. Use this as a starting point for understanding and evaluation.
     

  • "Training" is just iteratively improving your estimates.
     

  • "Testing" is evaluating generalizability -- KEY!
     

  • Common interpretation pathways / tasks include interpolation, prediction, simulation, and input to other models.

Part 1 take-homes

Part 2:

Ok, but what is "machine learning" or "AI"?

"ML" and "AI" are fuzzy distinctions used to imply complexity

A common hypothesis among ML researchers is that biology is more complex that humans can conceptualize, and thus articulate as specific hypotheses.

Using models to represent these complex dynamics is often referred to as "learning 'emergent properties'
from the data."

You can think of neural networks as just many linear regressions, recursively chained together

The most popular flavors of ML models in single cell biology are neural network based

You can think of neural networks as just many linear regressions, recursively chained together

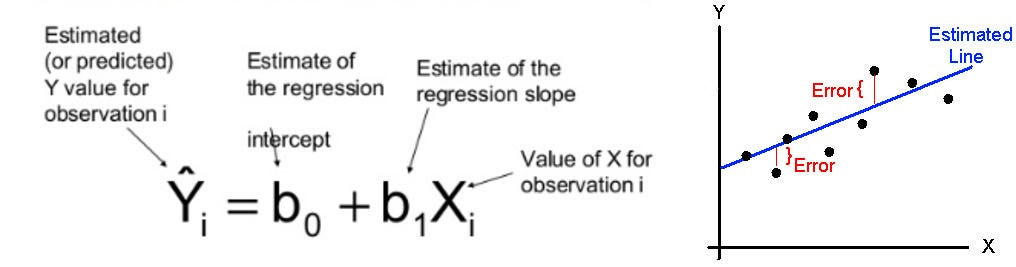
A "neuron" = one linear regression

 => some non-linear "activator function" (design decision) => output of this neuron, in the first layer

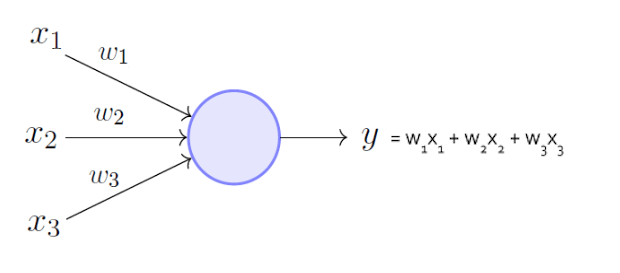
+ b0

Gene 1

Gene 2

Gene 3

You can think of neural networks as just many linear regressions, recursively chained together

1st "layer"

Linear model of Cell 1 as a f'n of its gene expression vector

Repeat for Cells 2, 3, ... N

2nd "layer"

Linear model of Cell N as a f'n of the outputs of layer 1, across all cells

You can think of neural networks as just many linear regressions, recursively chained together

Nth "layer"

Output values* of the last layer are used to calculate how well your model is performing (Evaluation)

Update weights and biases for every node in the network
(Training algorithm)

You can think of neural networks as just many linear regressions, recursively chained together

Nth "layer"

Outputs vary based on the activation function and number of nodes in the final layer

Most common flavors of ML models in single cell biology are neural network based

  • "Variational auto-encoders": representation learning. Useful for summarizing features, simulating realistic data, and anomaly detection.
     
  • "Transformers": predict the next thing in a sequence. Super efficient and powerful. Most appropriate for ordered data.

Variational auto-encoder overview

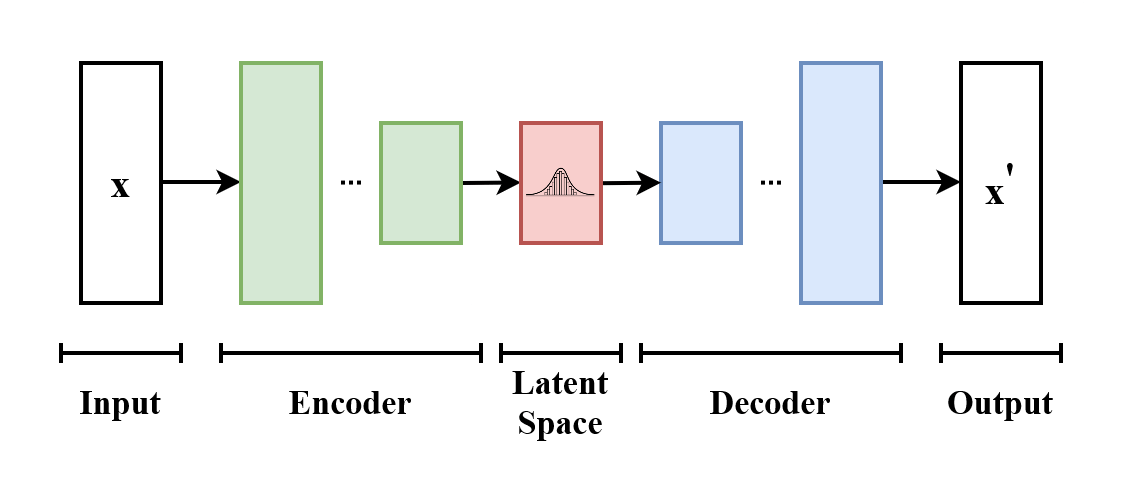
Neural network 1

Evaluation

Neural network 2

Variational auto-encoder overview

Simulated samples

Probability distribution of expression of "meta genes"

Input to other classifier

Anomaly detection

Embedding

VAEs' primary output is an "embedding." These are often most useful
as input to other models.

 

Example embedding

Example use case: cell type classification

Transformer overview

img src

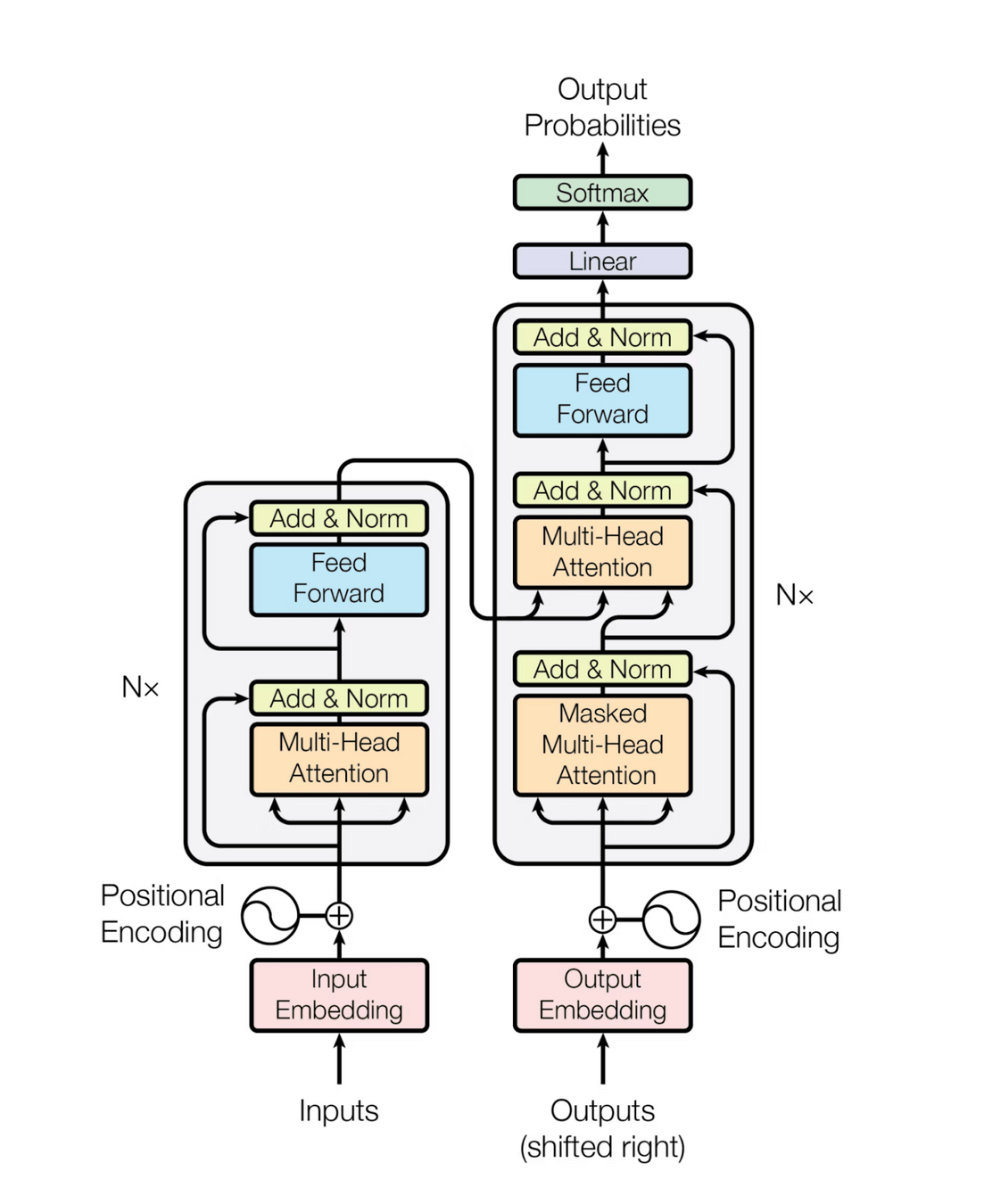
Prompt

"Attention" values are just weights applied to the input like before. They allow for:

1 - Being able to look at the whole input at once

2 - Weight the most salient bits of the input more heavily (adapted for each unique input)

"Understand-er"

"Generator"

Transformers' outputs include:

  • Generated / simulated data: 
    "Prompt" (input new data point of the same type as the original input) => generated output (type depends on architecture)
     
  • Embedding: representation learned by the encoder. Most useful as input to other models.
     
  • Attention weights: infer which parts of the input data are most relevant for which predictions

"Foundation model" is another fuzzy distinction used to imply complexity and flexibility

"Task-specific models are more accurate than foundation models, but foundation models scale."

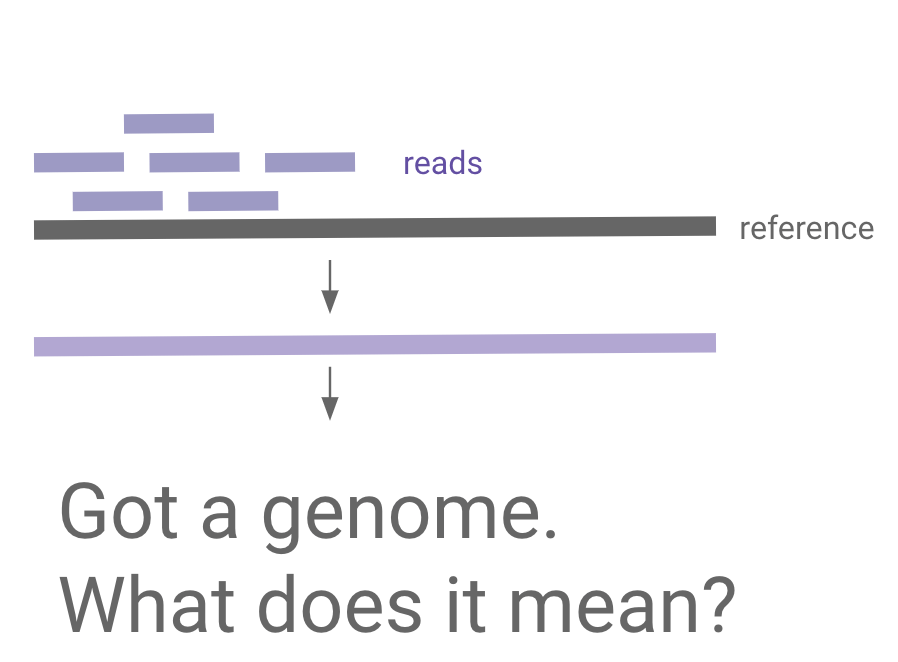
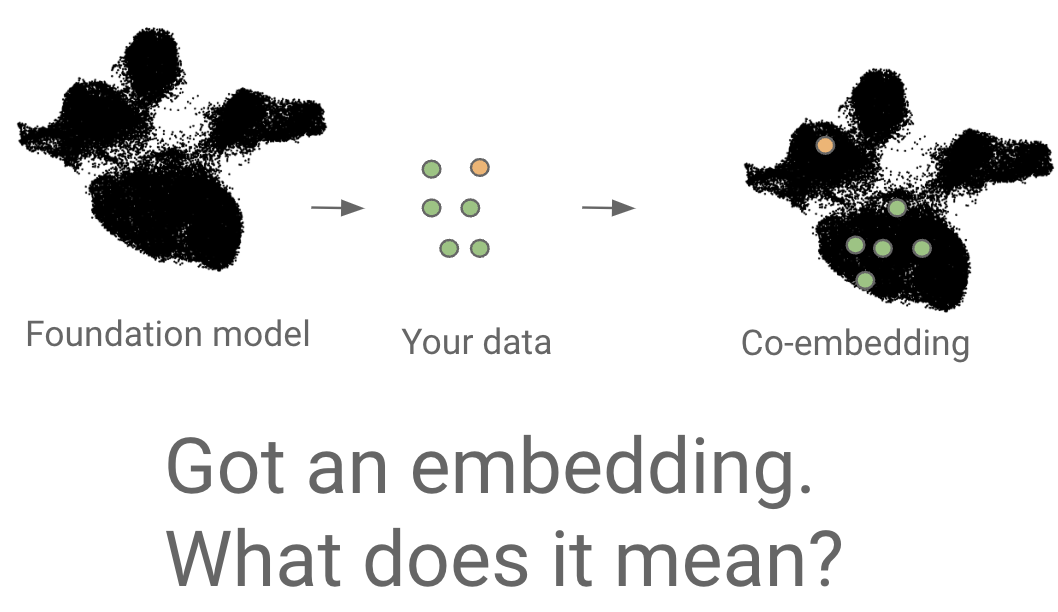
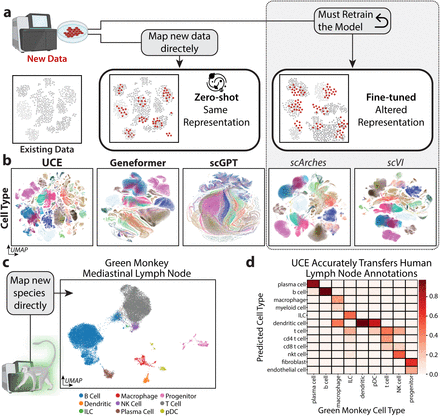
Mapping new data to reference

Transformer case study:
"universal cell embedding"

Part 2 Take-homes:

  • The terms "ML" "AI" and "Foundation Model" are all fuzzy. They're just models.
     
  • Neural networks are common in single cell analysis. They're basically a bunch of linear regressions recursively stacked on top of each other.
     
  • Neural networks come in many forms, including "variational auto encoders," "transformers," and "graph neural networks."
     
  • Most of these models output embeddings, which are most useful as input to other task-specific models

Next week

  • Landscape: what questions are biologists using these models to answer?
     
  • How are they visualizing and interpreting the outputs?
     
  • What are the key interpretability challenges in the field right now?
     
  • Where are there potential opportunities for our Apps team?