\text{Chapter 10}
\text{Chapter 10}
\text{Chapter 10}
\text{Chapter 10}
\textit{Dr. Adel Abbout}
\begin{array}{|c|}
\hline \text { Rotation } \\
\alpha=\text { constant } \\
\\
\hline\\ \omega=\omega_0+\alpha \mathrm{t} \\
\\
\hline \\ \theta-\theta_0=\omega_0 \mathrm{t}+\frac{1}{2} \alpha \mathrm{t}^2 \\
\\
\hline \\ \omega^2=\omega_0^2+2 \alpha\left(\theta-\theta_0\right) \\
\\
\hline \\ \theta-\theta_0=\frac{1}{2}\left(\omega+\omega_0\right) \mathrm{t} \\
\\
\hline \\ \theta-\theta_0=\omega \mathrm{t}-\frac{1}{2} \alpha \mathrm{t}^2 \\
\\
\hline \\ \omega_{\text {avg }}=\frac{1}{2}\left(\omega+\omega_0\right) \\
\hline
\end{array}
\text {Average angular } \text { velocity }
\theta=\frac{s}{r}
\text{Average Angular acceleration}
\omega_{\text {avg }}=\frac{\theta_f-\theta_i}{t_f-t_i}=\frac{\Delta \theta}{\Delta t} \\
\alpha_{\text {avg }}=\frac{\omega_f-\omega_i}{t_f-t_i}=\frac{\Delta \omega}{\Delta t}
\text {Linear speed }
\\
\hspace{1mm}T=\frac{2 \pi r}{v}=\frac{2 \pi}{\omega}\hspace{1mm}\\
\text{Period}
\hspace{1mm} V=\omega r\hspace{1mm}
\text { Tangential acceleration }
\hspace{1mm}a_t=\alpha r \hspace{1mm}
\hspace{1mm}a_r=\frac{v^2}{r}=\omega^2 r\hspace{1mm}
\text {Radial acceleration }
\text{Angle}
\hspace{1mm} K=\frac{1}{2} I \omega^2\hspace{1mm}
\text {Pure translation } \mathrm{K}=\frac{1}{2} \mathrm{M} \mathrm{~V}_{\text {com }}^2
\text { Moment of inertia } I=\sum_{i=1}^n m_i r_i^2
\text { Parallel-axis theorem }
\hspace{1mm}\mathrm{I}=\mathrm{I}_{\text {com }}+\mathrm{M} \mathrm{~h}^2\hspace{1mm}
\begin{aligned}
&\text { Pure rotation }\\
\end{aligned}
\hspace{1mm}\tau_{\text {net }}=I \alpha\hspace{1mm}\\
\hspace{1mm}W=\Delta K=\frac{1}{2} I \omega_f^2-\frac{1}{2} I \omega_i^2 \hspace{1mm}
\text { Power }=\frac{\mathrm{dW}}{\mathrm{dt}}=\tau \omega
\begin{align*}
&\text{A wheel initially has an angular velocity of } 18~\mathrm{rad/s} \text{ but it is slowing at a constant rate of } \\
& 2.0~\mathrm{rad/s^2}. \text{The time it takes to stop is:} \\[4pt]
&\text{A) } 0.0~\mathrm{s} \\
&\text{B) } 3.0~\mathrm{s} \\
&\text{C) } 6.0~\mathrm{s} \\
&\text{D) } 12.0~\mathrm{s} \\
&\text{E) } 9.0~\mathrm{s}
\end{align*}
\text { (Answer: E) }
\begin{align*}
&\text{At $\mathrm{t}=0$, a disk has an angular velocity of $360 \mathrm{rev} / \mathrm{min}$, and constant angular acceleration}\\
&\text{of $-0.50 \mathrm{~rad} / \mathrm{s}^2$. }\text{How many rotations does the disk make before coming to rest?}\\
&\\
&A) \hspace{2mm}226 \\
&B) \hspace{2mm}180\\
&C) \hspace{2mm}360\\
&D) \hspace{2mm}90\\
&E) \hspace{2mm}113\\
\end{align*}
\text { (Answer: A) }
\begin{align*}
&\text{Two wheels $A$ and $B$ are identical. Wheel $B$ is rotating with twice the angular velocity of }\\
&\text{wheel A. The ratio of the radial acceleration of a point on the rim of $B(a 2)$ to the radial }\\
&\text{acceleration of a point on the rim of $A$ (a1) is (a2/a1) :}\\
&\\
&A) \hspace{2mm}1 / 4\\
&B) \hspace{2mm} 2\\
&C) \hspace{2mm} 1 / 2\\
&D) \hspace{2mm} 4\\
&E) \hspace{2mm} 1\\
\end{align*}
\text { (Answer: D) }
\begin{align*}
&\text{Fig.~6 shows a pulley } (R = 3.0~\text{cm} \text{ and } I_0 = 0.0045~\text{kg.m}^2) \text{ suspended from the ceiling.} \\
&\text{A rope passes over it with a } 2.0~\text{kg block attached to one end and a } 4.0~\text{kg block attached } \\
&\text{to the other. When the speed of the heavier block is } 2.0~\text{m/s, find the total kinetic energy } \\
&\text{of the pulley and blocks.}\\
&\\[-4pt]
&\text{A) } 2~\text{J} \\
&\text{B) } 10~\text{J} \\
&\text{C) } 22~\text{J} \\
&\text{D) } 16~\text{J} \\
&\text{E) } 38~\text{J} \\
\end{align*}
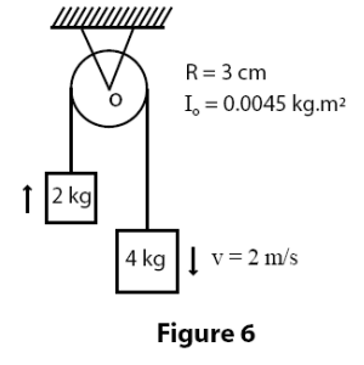
\text { (Answer: C) }
\begin{align*}
&\text{A particle of mass } 0.50~\text{kg is attached to one end of a } 1.0~\text{m long rod of mass } 3.0~\text{kg (Fig.~5).} \\
&\text{The rod and the particle are rotating around the other pivoted end of the rod with } 2.0~\text{rad/s.} \\
&\text{Find the kinetic energy of the system about the pivot.} \\
&\\[-4pt]
&\text{A) } 0.50~\text{J} \\
&\text{B) } 0.84~\text{J} \\
&\text{C) } 3.0~\text{J} \\
&\text{D) } 0.62~\text{J} \\
&\text{E) } 1.0~\text{J} \\
\end{align*}
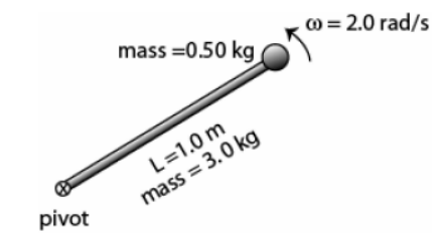
\text { (Answer: C) }
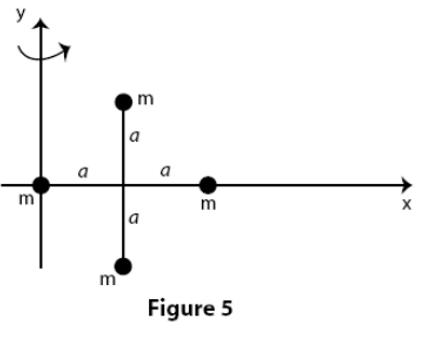
\begin{align*}
&\text{Four identical particles, each with mass } m, \text{ are arranged in the } x,y \text{ plane as shown in Fig.~5.} \\
&\text{They are connected by light sticks of negligible mass to form a rigid body.} \\
&\text{If } m = 2.0~\text{kg} \text{ and } a = 1.0~\text{m}, \text{ find the rotational inertia of this system about the y-axis.} \\
&\\[-4pt]
&\text{A) } 12~\text{kg.m}^2 \\
&\text{B) } 4.0~\text{kg.m}^2 \\
&\text{C) } 8.0~\text{kg.m}^2 \\
&\text{D) } 16~\text{kg.m}^2 \\
&\text{E) } 0~\text{kg.m}^2 \\
\end{align*}
\text { (Answer: A) }
\begin{align*}
&\text{What is the net torque about the origin on an object located at } (0, -5.0, 5.0)~\text{m} \\
&\text{when forces } \vec{F}_1 = (-3.0~\hat{k})~\text{N and } \vec{F}_2 = (2.0~\hat{j})~\text{N act on the object?} \\
&\\[-4pt]
&\text{A) } (15~\hat{i})~\text{N.m} \\
&\text{B) } (5.0~\hat{i})~\text{N.m} \\
&\text{C) } (10~\hat{j})~\text{N.m} \\
&\text{D) } (-3.0~\hat{k} + 2.0~\hat{j})~\text{N.m} \\
&\text{E) } \text{Zero} \\
\end{align*}
\text { (Answer: B) }
\begin{align*}
&\text{A } 2.0~\text{kg particle is moving such that its position vector } \vec{r} \text{ relative to the origin is} \\
&\vec{r} = (-2.0t^2~\hat{i} + 3.0~\hat{j})~\text{m.} \\
&\text{What is the torque (about the origin) acting on the particle at } t = 2.0~\text{s?} \\
&\\[-4pt]
&\text{A) } -24~\hat{k}~\text{N.m} \\
&\text{B) } -36~\hat{k}~\text{N.m} \\
&\text{C) } 24~\hat{k}~\text{N.m} \\
&\text{D) } -48~\hat{k}~\text{N.m} \\
&\text{E) } 0 \\
\end{align*}
\text { (Answer: C) }
\begin{align*}
&\text{A torque of $0.80 \mathrm{~N} \cdot \mathrm{m}$ applied to a pulley increases its angular speed from $45.0 \mathrm{~rev} / \mathrm{min}$ to}\\
&\text{$180 \mathrm{~rev} / \mathrm{min}$ in 3.00 s.}\text{ Find the moment of inertia of the pulley.}\\
&\\
&A) \hspace{2mm}0.54 \mathrm{~kg} \cdot \mathrm{m}^2 \\
&B) \hspace{2mm}0.21 \mathrm{~kg} \cdot \mathrm{m}^2\\
&C) \hspace{2mm}0.17 \mathrm{~kg} \cdot \mathrm{m}^2\\
&D) \hspace{2mm}0.42 \mathrm{~kg} \cdot \mathrm{m}^2\\
&E) \hspace{2mm}0.30 \mathrm{~kg} \cdot \mathrm{m}^2\\
\end{align*}
\text { (Answer: C) }
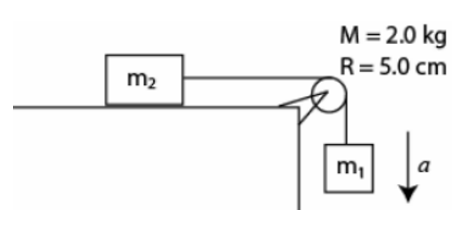
\begin{align*}
&\text{A mass } m_1 = 5.0~\text{kg} \text{ hangs from a string and descends with an acceleration $a$. The other end} \\
&\text{is attached to a mass } m_2 = 4.0~\text{kg} \text{ which slides on a frictionless horizontal table. The string } \\
&\text{goes over a pulley (a uniform disk) of mass } M = 2.0~\text{kg} \text{ and radius } R = 5.0~\text{cm (see Fig.~6).} \\
&\text{Find the value of $a$.} \\
&\\[-4pt]
&\text{A) } 1.0~\text{m/s}^2 \\
&\text{B) } 5.4~\text{m/s}^2 \\
&\text{C) } 9.8~\text{m/s}^2 \\
&\text{D) } 2.0~\text{m/s}^2 \\
&\text{E) } 4.9~\text{m/s}^2 \\
\end{align*}
\text { (Answer: E) }
\begin{align*}
&\text{A thin rod of mass } 0.23~\text{kg} \text{ and length } 1.00~\text{m} \text{ is rotated in a horizontal circle about a fixed} \\
&\text{axis passing through a point } 20.0~\text{cm from one of the edges of the rod.} \\
&\text{If it has a constant angular acceleration of } 3.0~\text{rad/s}^2, \text{ find the net torque acting on the rod.} \\
&\\[-4pt]
&\text{A) } 0.12~\text{N.m} \\
&\text{B) } 0.085~\text{N.m} \\
&\text{C) } 0.028~\text{N.m} \\
&\text{D) } 0.15~\text{N.m} \\
&\text{E) } 0.077~\text{N.m} \\
\end{align*}
\text { (Answer: A) }
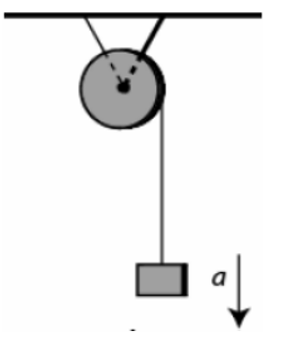
\begin{align*}
&\text{A } 16~\text{kg block is attached to a cord that is wound around the rim of a flywheel} \\
&\text{of radius } 0.20~\text{m} \text{ and hangs vertically, as shown in Fig. 4.} \\
&\text{The rotational inertia of the flywheel is } 0.50~\text{kg.m}^2. \\
&\text{When the block is released and the cord unwinds, the acceleration of the block is:} \\
&\\[-4pt]
&\text{A) } 9.8~\text{m/s}^2 \\
&\text{B) } 1.5~\text{m/s}^2 \\
&\text{C) } 8.2~\text{m/s}^2 \\
&\text{D) } 5.5~\text{m/s}^2 \\
&\text{E) } 13~\text{m/s}^2 \\
\end{align*}
\text { (Answer: D) }
\begin{align*}
&\text{A disk starts from rest and rotates around a fixed axis, subject to a constant net torque.} \\
&\text{The work done by the torque during the time interval from } t = 0 \text{ to } 2~\text{s is } W_1, \\
&\text{and the work done during the time interval from } t = 0 \text{ to } 6~\text{s is } W_2. \\
&\text{The ratio } \dfrac{W_2}{W_1} \text{ is:} \\
&\\[-4pt]
&\text{A) } 9 \\
&\text{B) } 3 \\
&\text{C) } \dfrac{1}{3} \\
&\text{D) } \dfrac{1}{9} \\
&\text{E) } 4 \\
\end{align*}
\text { (Answer: A) }
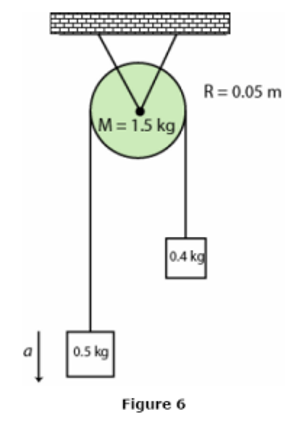
\begin{align*}
&\text{In Fig. 6, } m_1 = 0.50~\mathrm{kg},~ m_2 = 0.40~\mathrm{kg} \text{ and the pulley has a disk shape of radius } 0.05~\mathrm{m} \\
&\text{and mass } M = 1.5~\mathrm{kg}. \text{ What is the linear acceleration of the block of mass } m_2? \\[4pt]
&\text{A) } 0.59~\mathrm{m/s^2} \\
&\text{B) } 0.42~\mathrm{m/s^2} \\
&\text{C) } 1.46~\mathrm{m/s^2} \\
&\text{D) } 0.21~\mathrm{m/s^2} \\
&\text{E) } 0.0
\end{align*}
\text { (Answer: A) }
\begin{align*}
&\text{A disk has a rotational inertia of } 4.0~\mathrm{kg \cdot m^2} \text{ and a constant angular acceleration of } 2.0~\mathrm{rad/s^2}. \\
&\text{If it starts from rest, the work done during the first } 5.0~\mathrm{s} \text{ by the net torque acting on it is:} \\[4pt]
&\text{A) } 0~\mathrm{J} \\
&\text{B) } 100~\mathrm{J} \\
&\text{C) } 40~\mathrm{J} \\
&\text{D) } 200~\mathrm{J} \\
&\text{E) } 400~\mathrm{J}
\end{align*}
\text { (Answer: D) }
\begin{align*}
&\text{A disk starts from rest at } t = 0, \text{ and rotates about a fixed axis } (\text{$I$} = 0.030~\mathrm{kg \cdot m^2}) \\
&\text{with an angular acceleration of } 7.5~\mathrm{rad/s^2}. \text{ What is the rate at which work is being} \\
&\text{ done on the disk when its angular velocity is } 32~\mathrm{rad/s}? \\[4pt]
&\text{A) } 5.5~\mathrm{W} \\
&\text{B) } 7.2~\mathrm{W} \\
&\text{C) } 3.1~\mathrm{W} \\
&\text{D) } 8.7~\mathrm{W} \\
&\text{E) } 2.2~\mathrm{W}
\end{align*}
\text { (Answer: B) }
\begin{align*}
&\text{The engine delivers } 1.20 \times 10^5~\mathrm{W} \text{ to a plane propeller at } \omega = 2400~\mathrm{rev/min}. \\
&\text{How much work does the engine do in one revolution?} \\[4pt]
&\text{A) } 3000~\mathrm{J} \\
&\text{B) } 4000~\mathrm{J} \\
&\text{C) } 5000~\mathrm{J} \\
&\text{D) } 2000~\mathrm{J} \\
&\text{E) } 1000~\mathrm{J}
\end{align*}
\text { (Answer: A) }
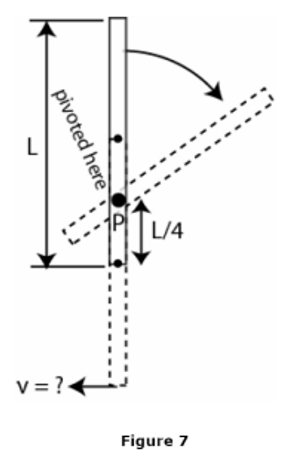
\begin{align*}
&\text{A uniform rod } (M = 2.0~\mathrm{kg},~ L = 2.0~\mathrm{m}) \text{ is held vertical about a pivot at point P, a distance } \\
&L/4 \text{ from one end}\text{(see Fig.~7). The rotational inertia of the rod about P is } 1.17~\mathrm{kg \, m^2}.\\
&\text{ If it starts rotating from rest, what is the} \text{linear speed of the lowest point of the rod as it }\\
&\text{passes again through the vertical position } (v)? \\[4pt]
&\text{A) } 2.4~\mathrm{m/s} \\
&\text{B) } 4.8~\mathrm{m/s} \\
&\text{C) } 17~\mathrm{m/s} \\
&\text{D) } 8.7~\mathrm{m/s} \\
&\text{E) } 0
\end{align*}
\text { (Answer: D) }