
\text{Adel Abbout}
\text{King Fahd University of Petroleum and Minerals, Saudi Arabia}
\text{}
\text{San Sebastian, 2023}



\displaystyle
\begin{aligned}
J(\mathbf{q})= & -J_1\left(2 \cos \left(q_x a\right)+4 \cos \left(\frac{q_x a}{2}\right) \cos \left(\frac{\sqrt{3} q_y a}{2}\right)\right) \\
& -J_2\left(2 \cos \left(\sqrt{3} q_y a\right)+4 \cos \left(\frac{3 q_x a}{2}\right) \cos \left(\frac{\sqrt{3} q_y a}{2}\right)\right)
\end{aligned}
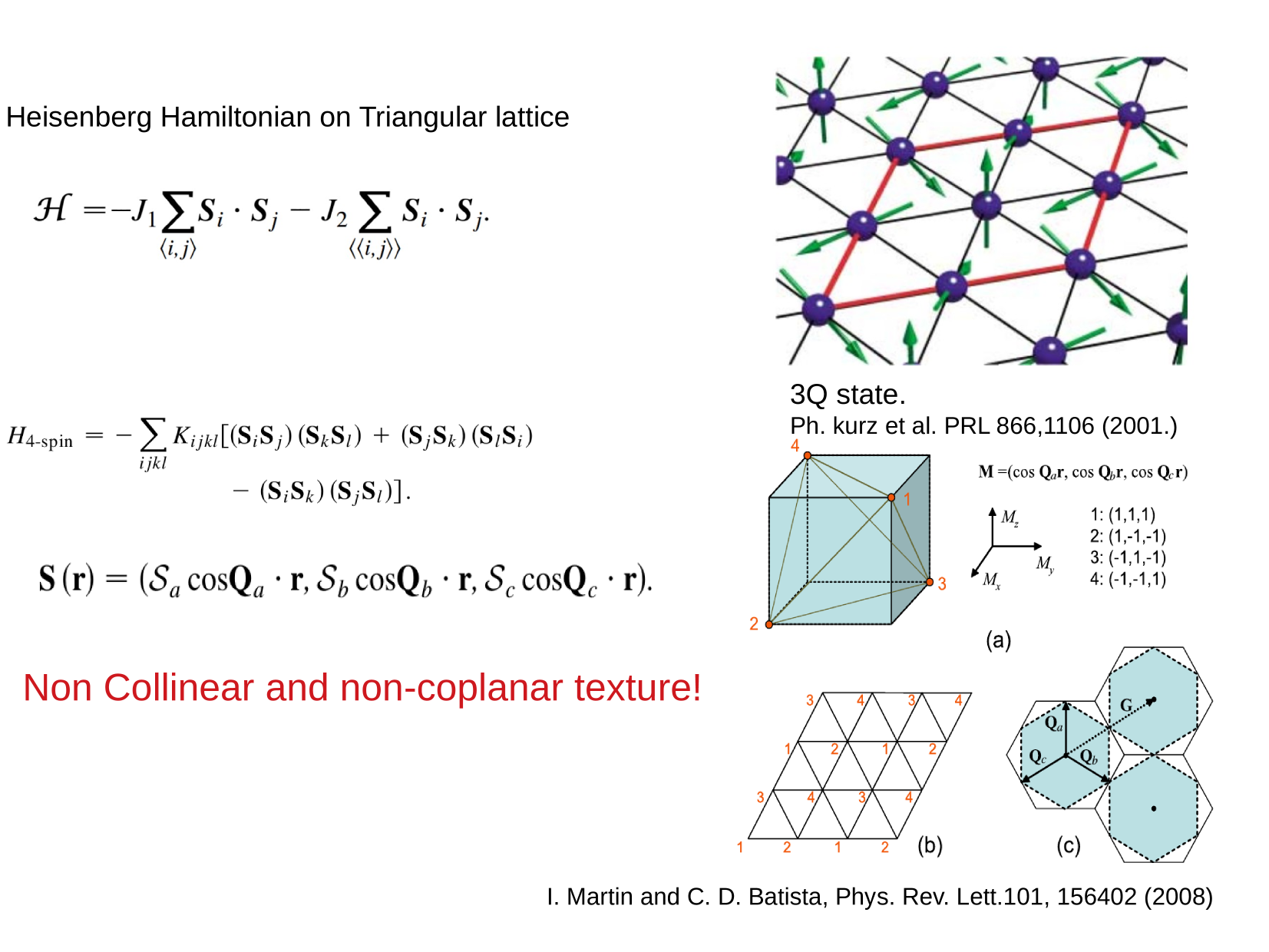
\displaystyle \mathcal{H}=-J_1 \sum_{\langle i, j\rangle} \boldsymbol{S}_i \cdot \boldsymbol{S}_j-J_2 \sum_{\langle\langle i, j\rangle\rangle} \boldsymbol{S}_i\boldsymbol{S}_j
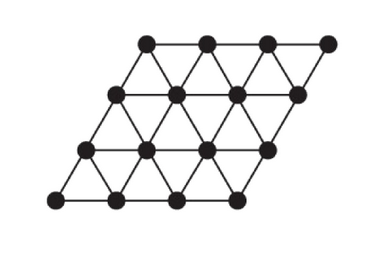
\text { Heisenberg Hamiltonian on Triangular lattice }
\text { Ground state depends on } \displaystyle {\textcolor{red}{\alpha=\frac{J_2}{J_1}}}
\text{Fourier transform}
\text { Th. Jolicoeur et al. Phys. Rev. B 42, 4800(R) }
\text { Ground state depends on } \displaystyle {\textcolor{red}{\alpha=\frac{J_2}{J_1}}}
\displaystyle \alpha<\frac{1}{8}
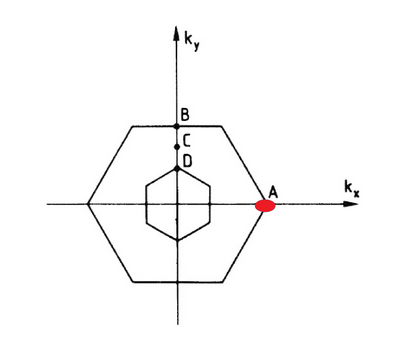
\text { Minimum at } {\textcolor{red}A}
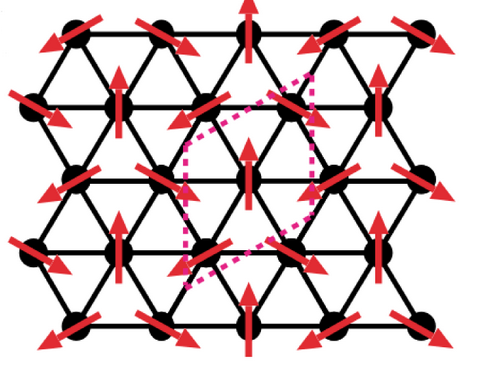
120^\circ \text { structure }
\text { Th. Jolicoeur et al. Phys. Rev. B 42, 4800(R) }

\displaystyle
\begin{aligned}
J(\mathbf{q})= & -J_1\left(2 \cos \left(q_x a\right)+4 \cos \left(\frac{q_x a}{2}\right) \cos \left(\frac{\sqrt{3} q_y a}{2}\right)\right) \\
& -J_2\left(2 \cos \left(\sqrt{3} q_y a\right)+4 \cos \left(\frac{3 q_x a}{2}\right) \cos \left(\frac{\sqrt{3} q_y a}{2}\right)\right)
\end{aligned}
\displaystyle \mathcal{H}=-J_1 \sum_{\langle i, j\rangle} \boldsymbol{S}_i \cdot \boldsymbol{S}_j-J_2 \sum_{\langle\langle i, j\rangle\rangle} \boldsymbol{S}_i\boldsymbol{S}_j
\text { Heisenberg Hamiltonian on Triangular lattice }
\text { Ground state depends on } \displaystyle {\textcolor{red}{\alpha=\frac{J_2}{J_1}}}
\displaystyle \alpha<\frac{1}{8}
\text { Minimum at } {\textcolor{red}A}
120^\circ \text { structure }
\text{Fourier transform}
\text { Th. Jolicoeur et al. Phys. Rev. B 42, 4800(R) }
\displaystyle \frac{1}{8}<\alpha<1
\text { Minimum at } {\textcolor{blue}B} \text {. The vector } Q \text { is half the reciprocal unit vector. }

\text { Ground state depends on } \displaystyle {\textcolor{red}{\alpha=\frac{J_2}{J_1}}}
\displaystyle \alpha<\frac{1}{8}
\text { Minimum at } {\textcolor{red}A}
120^\circ \text { structure }
\text { Th. Jolicoeur et al. Phys. Rev. B 42, 4800(R) }
\displaystyle \frac{1}{8}<\alpha<1
\text { Minimum at } {\textcolor{blue}B} \text {. The vector } Q \text { is half the reciprocal unit vector. }
\text { Row-wise AF}
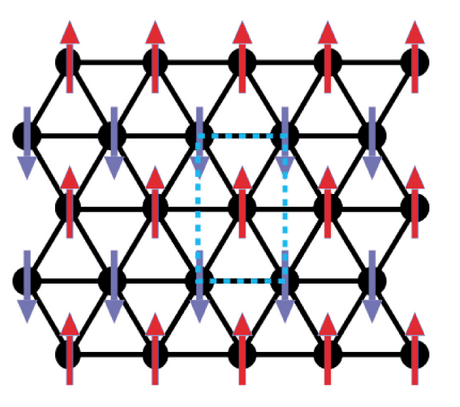

\text { Ground state depends on } \displaystyle {\textcolor{red}{\alpha=\frac{J_2}{J_1}}}
\displaystyle \alpha<\frac{1}{8}
\text { Minimum at } {\textcolor{red}A}
120^\circ \text { structure }
\displaystyle \frac{1}{8}<\alpha<1
\text { Minimum at } {\textcolor{blue}B} \text {. The vector } Q \text { is half the reciprocal unit vector. }
\text { Row-wise AF}

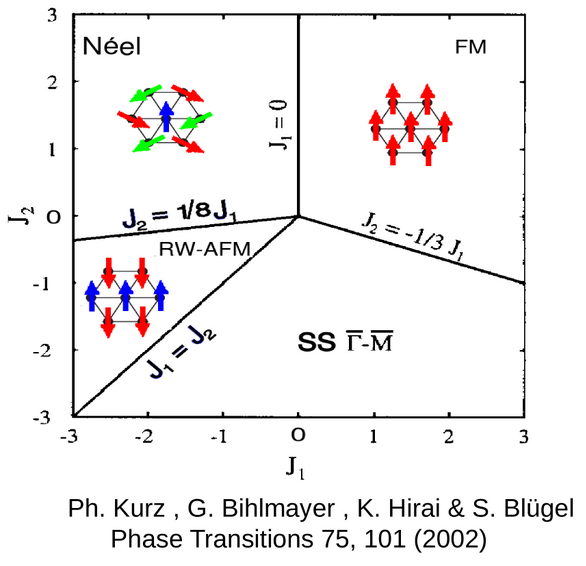
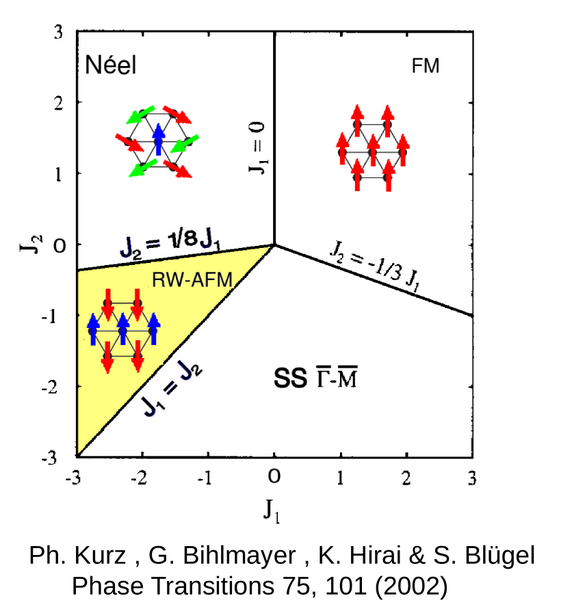
\displaystyle \alpha>1
\text { Minimum at } {\textcolor{green}C}
\text { Incommensurate spiral}
\displaystyle
\begin{aligned}
J(\mathbf{q})= & -J_1\left(2 \cos \left(q_x a\right)+4 \cos \left(\frac{q_x a}{2}\right) \cos \left(\frac{\sqrt{3} q_y a}{2}\right)\right) \\
& -J_2\left(2 \cos \left(\sqrt{3} q_y a\right)+4 \cos \left(\frac{3 q_x a}{2}\right) \cos \left(\frac{\sqrt{3} q_y a}{2}\right)\right)
\end{aligned}
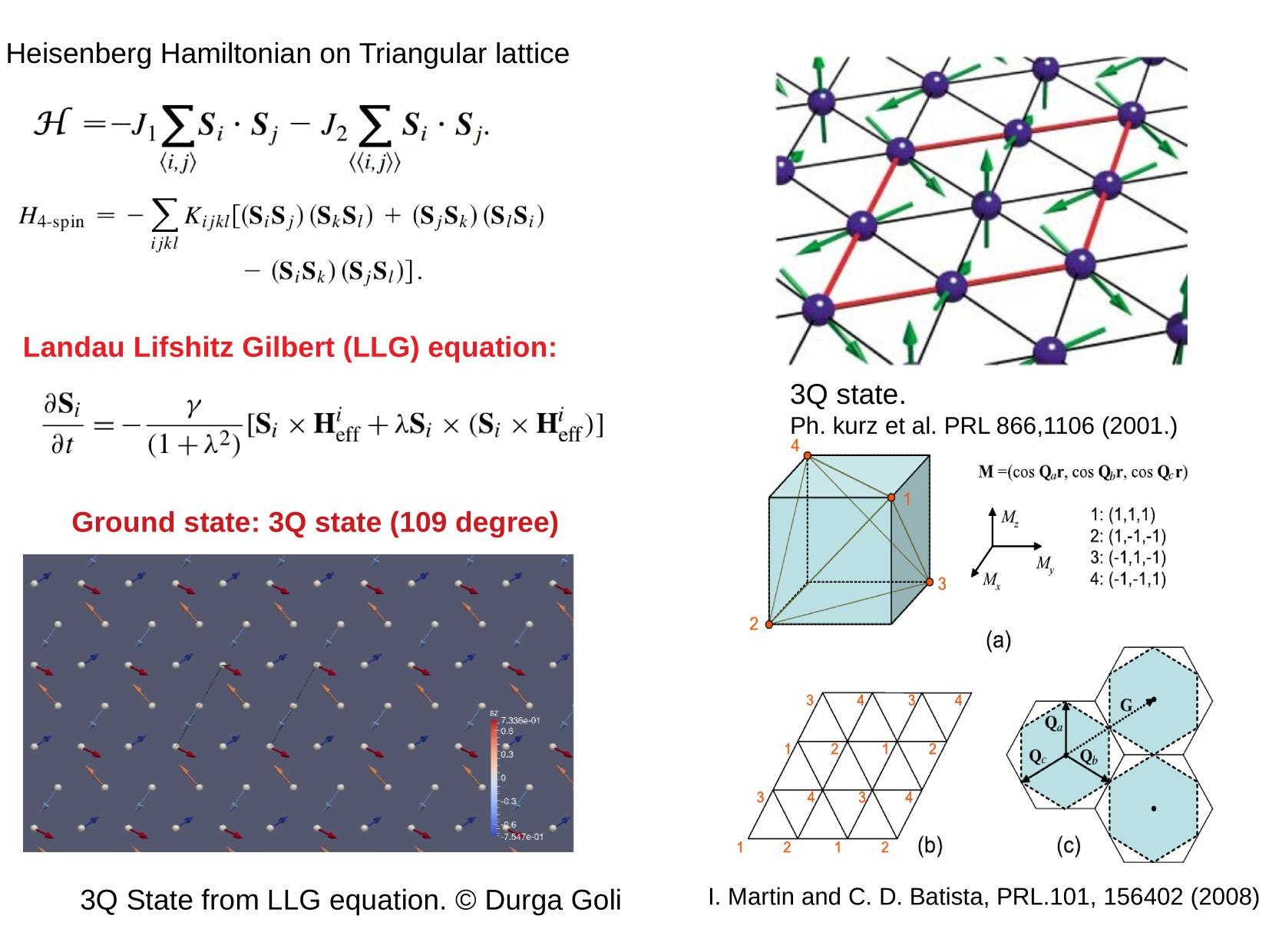
\displaystyle \mathcal{H}=-J_1 \sum_{\langle i, j\rangle} \boldsymbol{S}_i \cdot \boldsymbol{S}_j-J_2 \sum_{\langle\langle i, j\rangle\rangle} \boldsymbol{S}_i\cdot\boldsymbol{S}_j
\text { Heisenberg Hamiltonian on Triangular lattice }
\text { Ground state depends on } \displaystyle {\textcolor{red}{\alpha=\frac{J_2}{J_1}}}
\text{Fourier transform}
\displaystyle
\begin{aligned}
J(\mathbf{q})= & -J_1\left(2 \cos \left(q_x a\right)+4 \cos \left(\frac{q_x a}{2}\right) \cos \left(\frac{\sqrt{3} q_y a}{2}\right)\right) \\
& -J_2\left(2 \cos \left(\sqrt{3} q_y a\right)+4 \cos \left(\frac{3 q_x a}{2}\right) \cos \left(\frac{\sqrt{3} q_y a}{2}\right)\right)
\end{aligned}
\displaystyle \mathcal{H}=-J_1 \sum_{\langle i, j\rangle} \boldsymbol{S}_i \cdot \boldsymbol{S}_j-J_2 \sum_{\langle\langle i, j\rangle\rangle} \boldsymbol{S}_i\cdot\boldsymbol{S}_j
\text { Heisenberg Hamiltonian on Triangular lattice }
\text { Ground state depends on } \displaystyle {\textcolor{red}{\alpha=\frac{J_2}{J_1}}}
\text{Fourier transform}
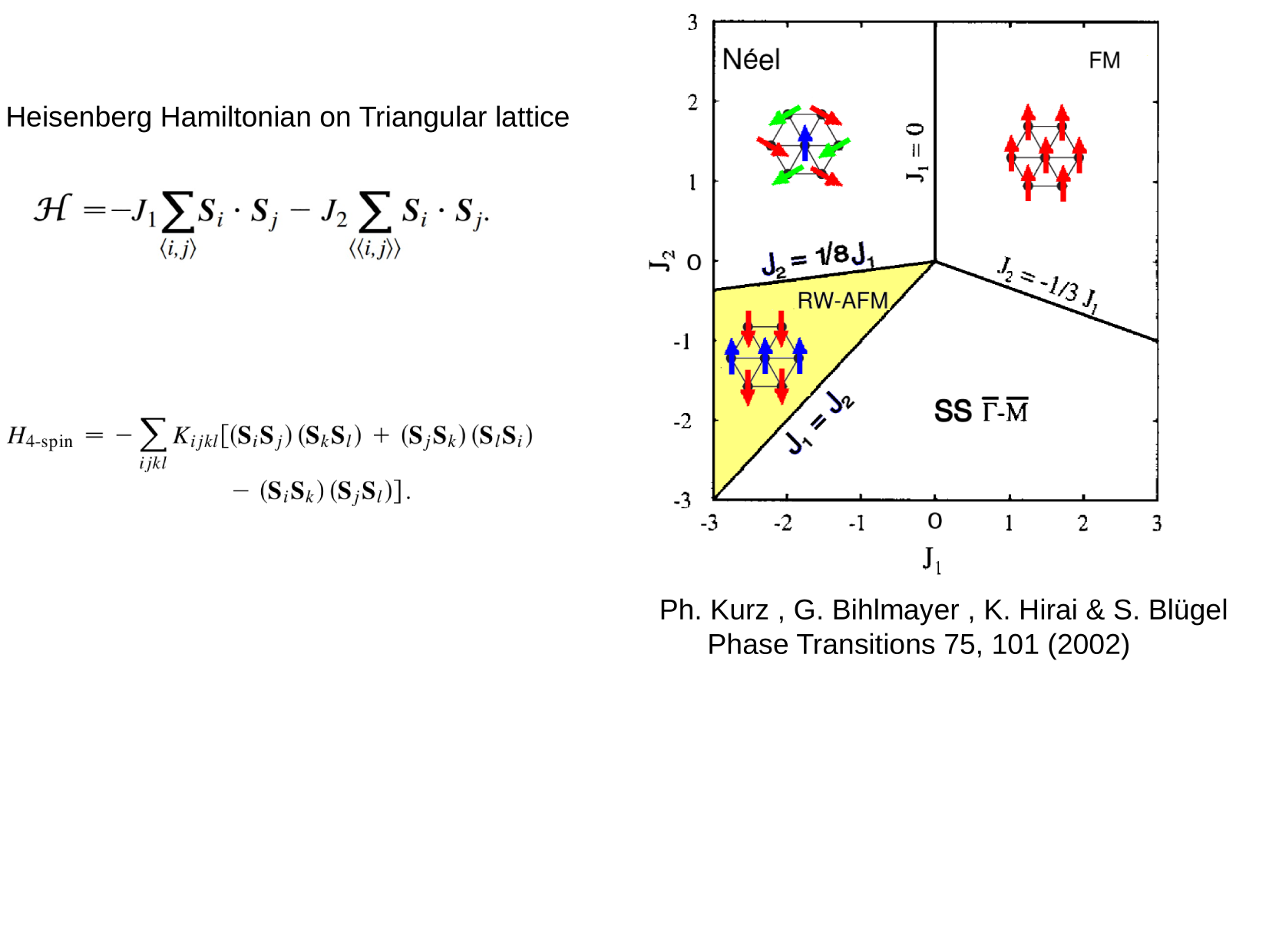
\text{4-spin interaction}
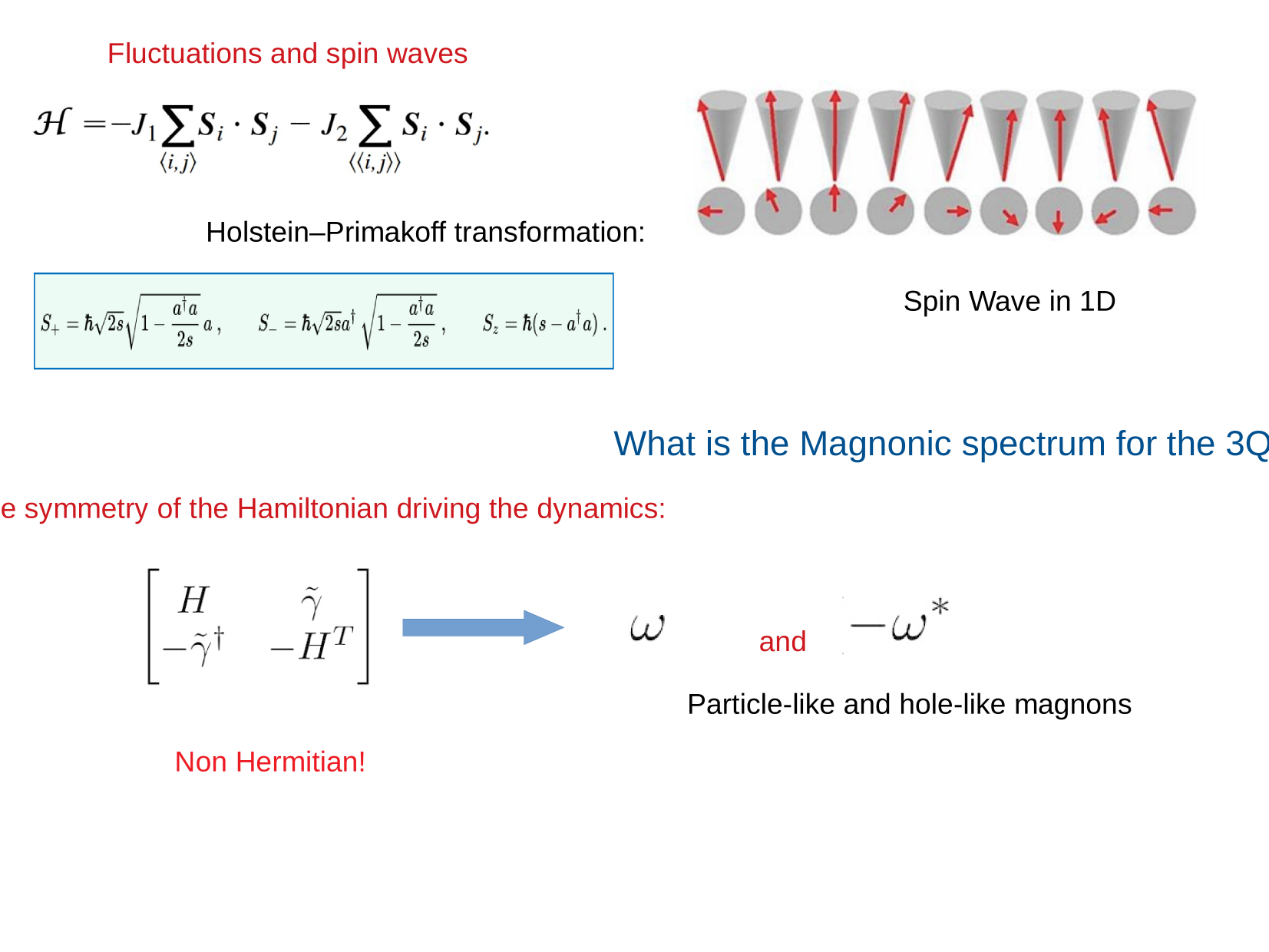

\text{Or using dynamical matrix}
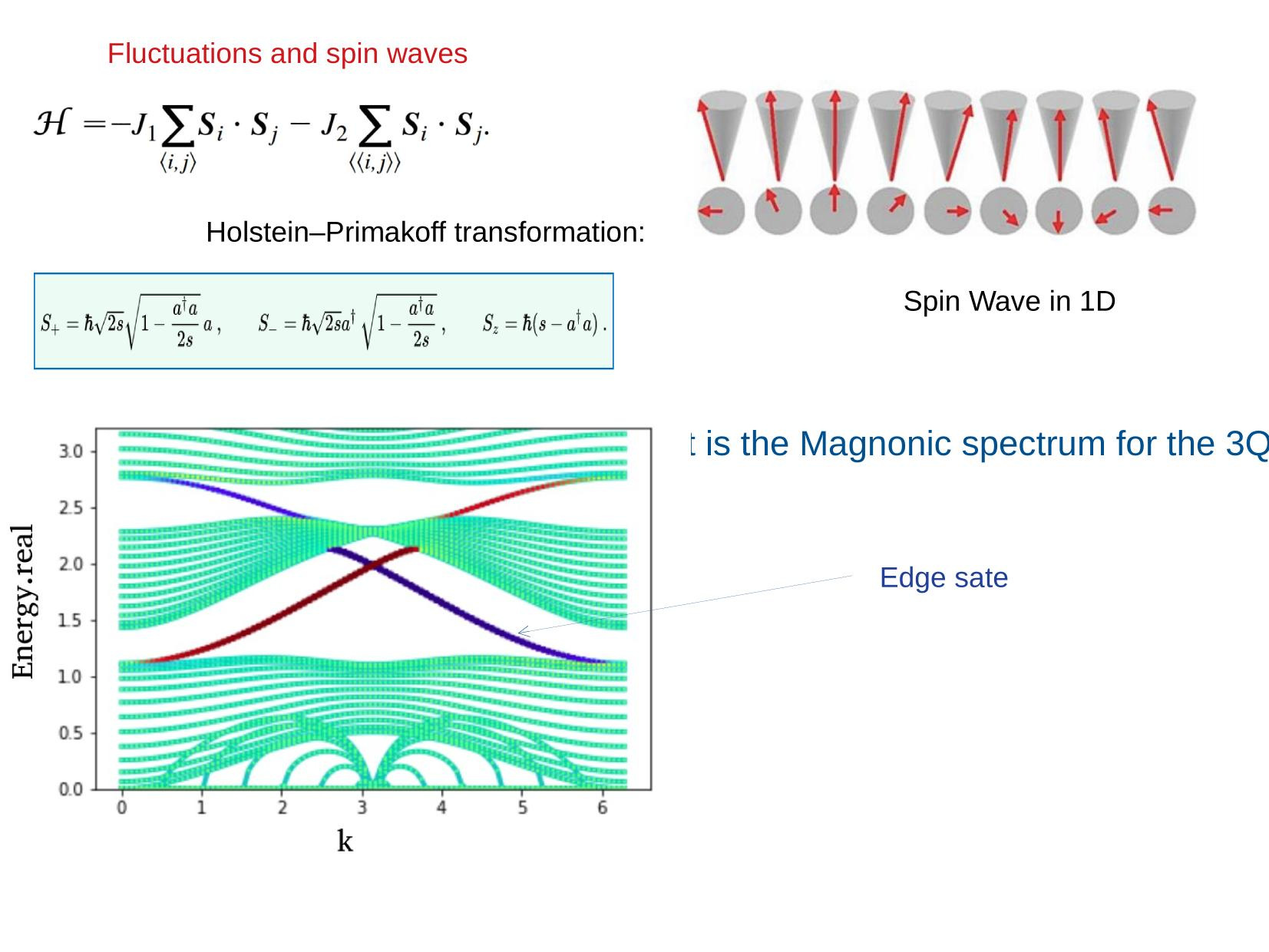

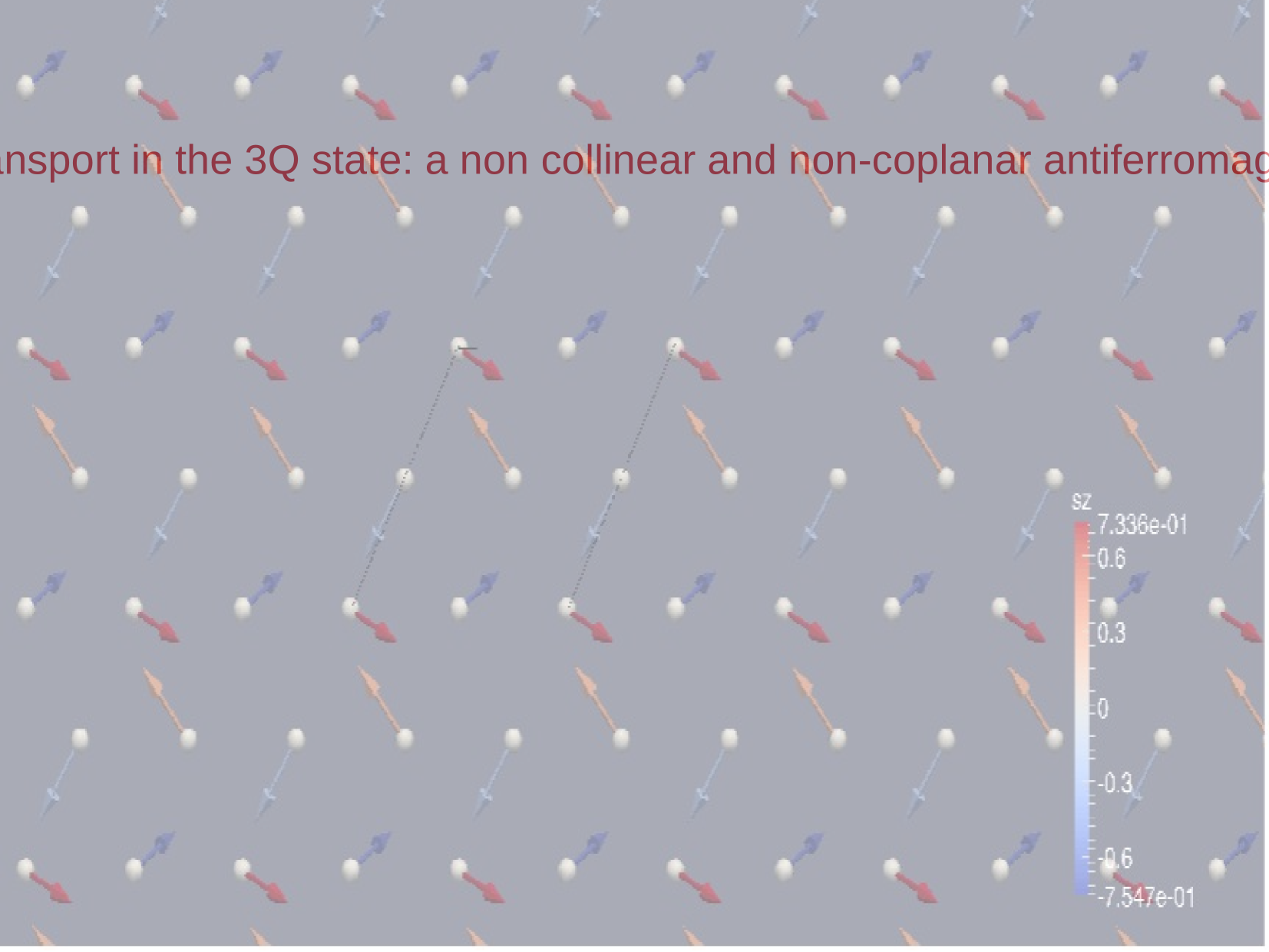

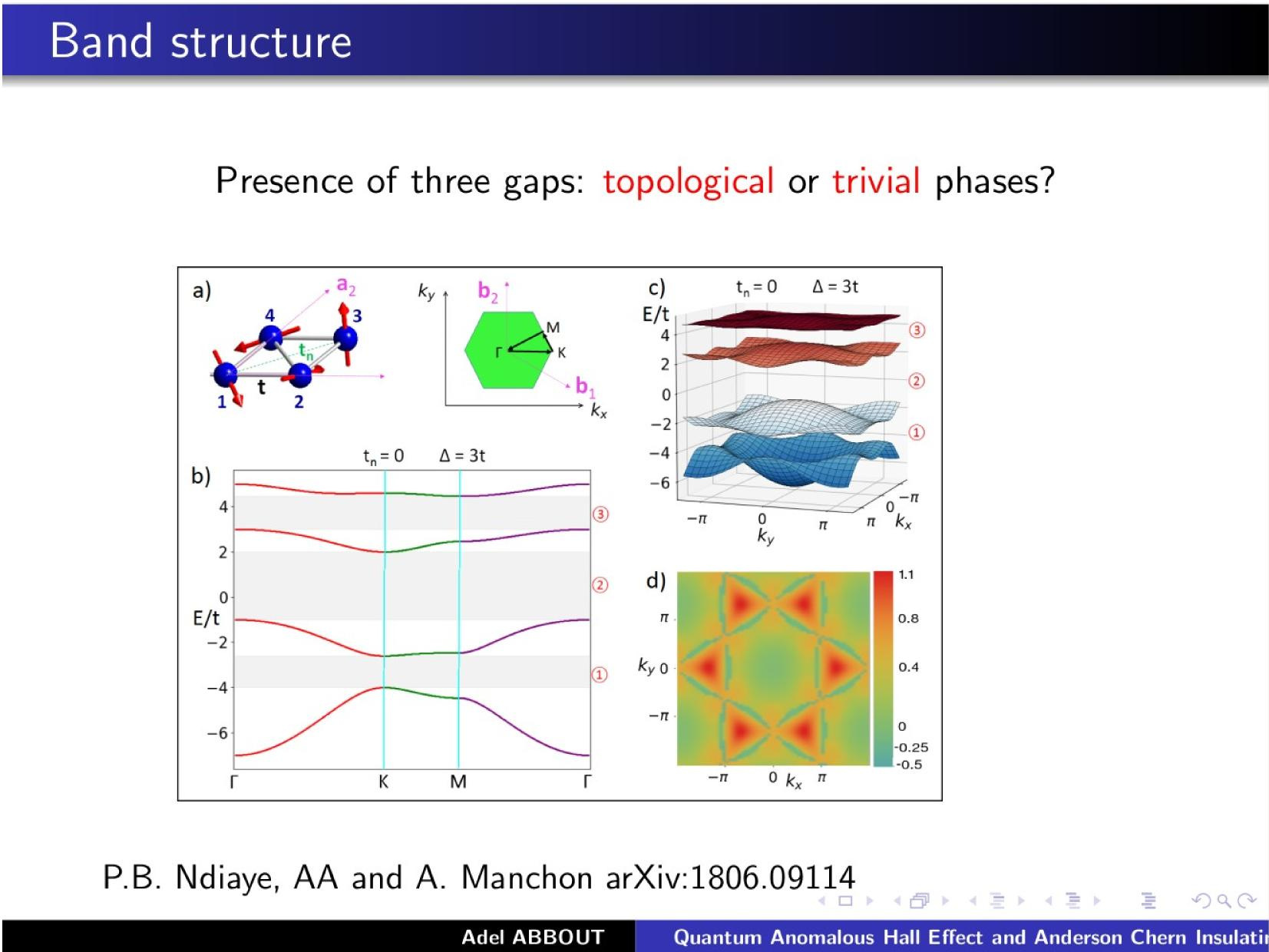
\text{Papa B. Ndiaye, Adel Abbout, Durga Goli, and Aurélien Manchon
Phys. Rev. B 100, 144440}
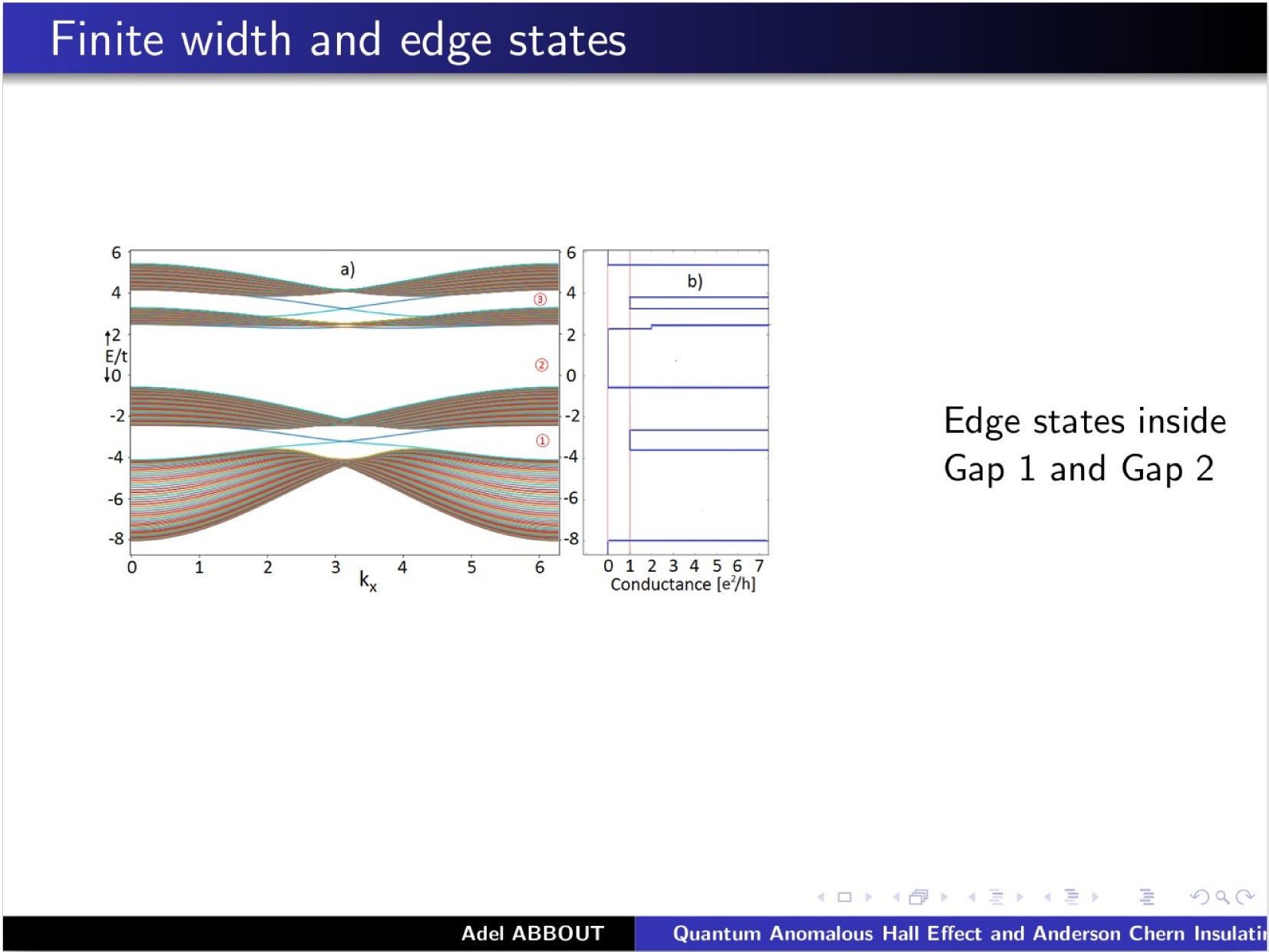
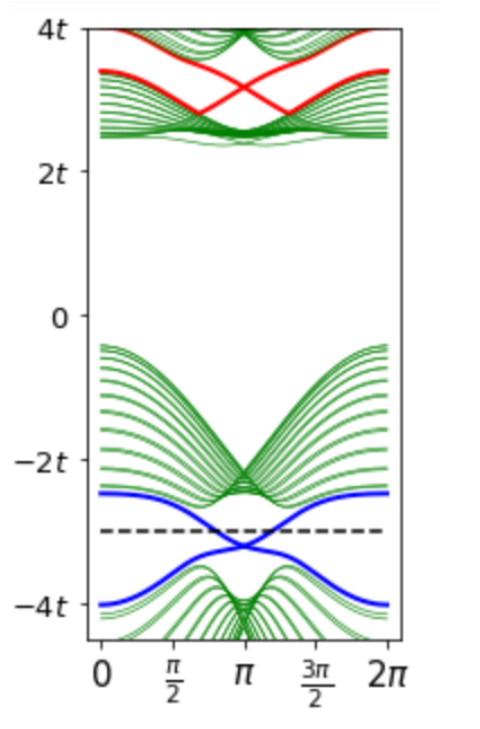


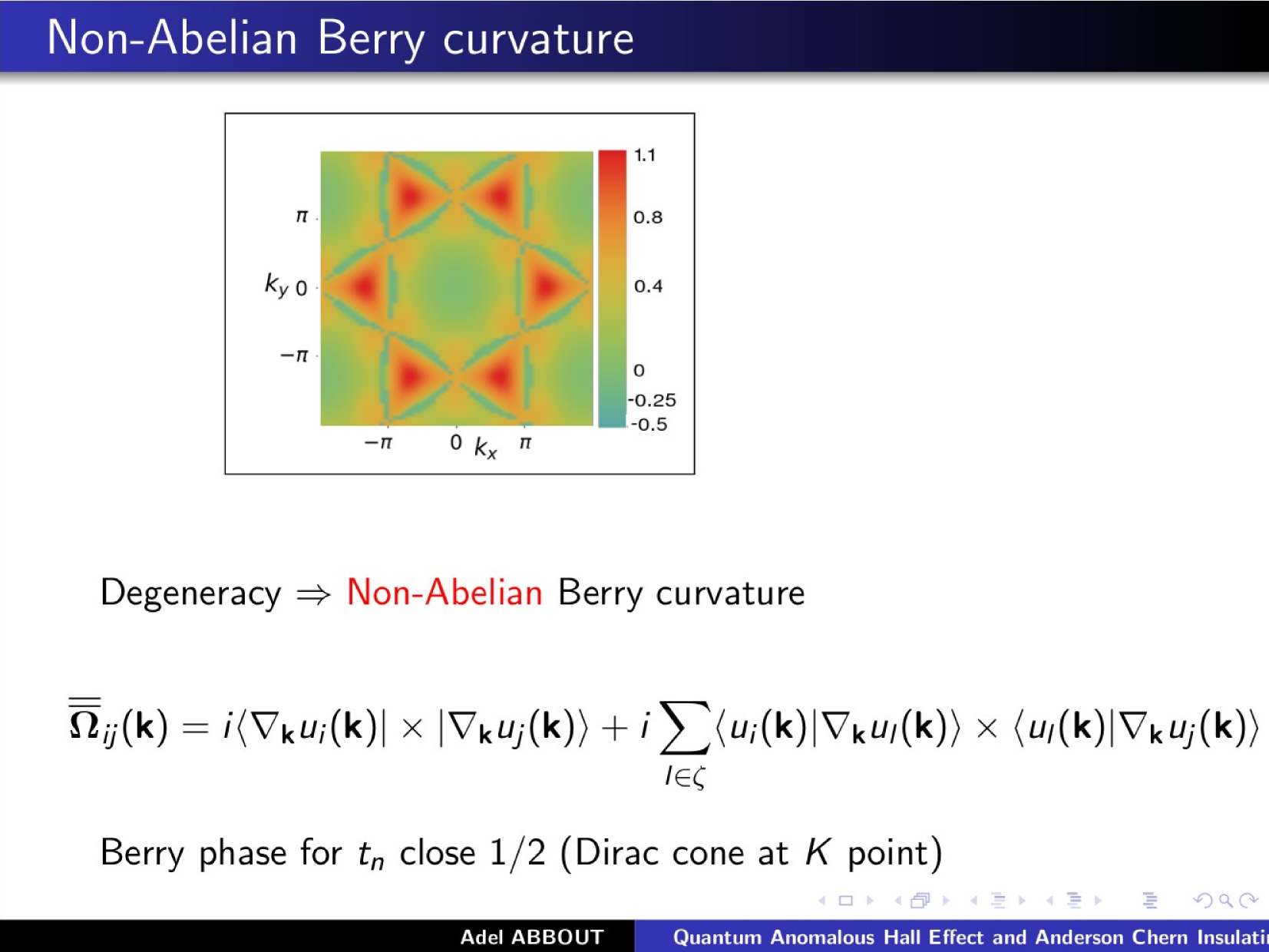

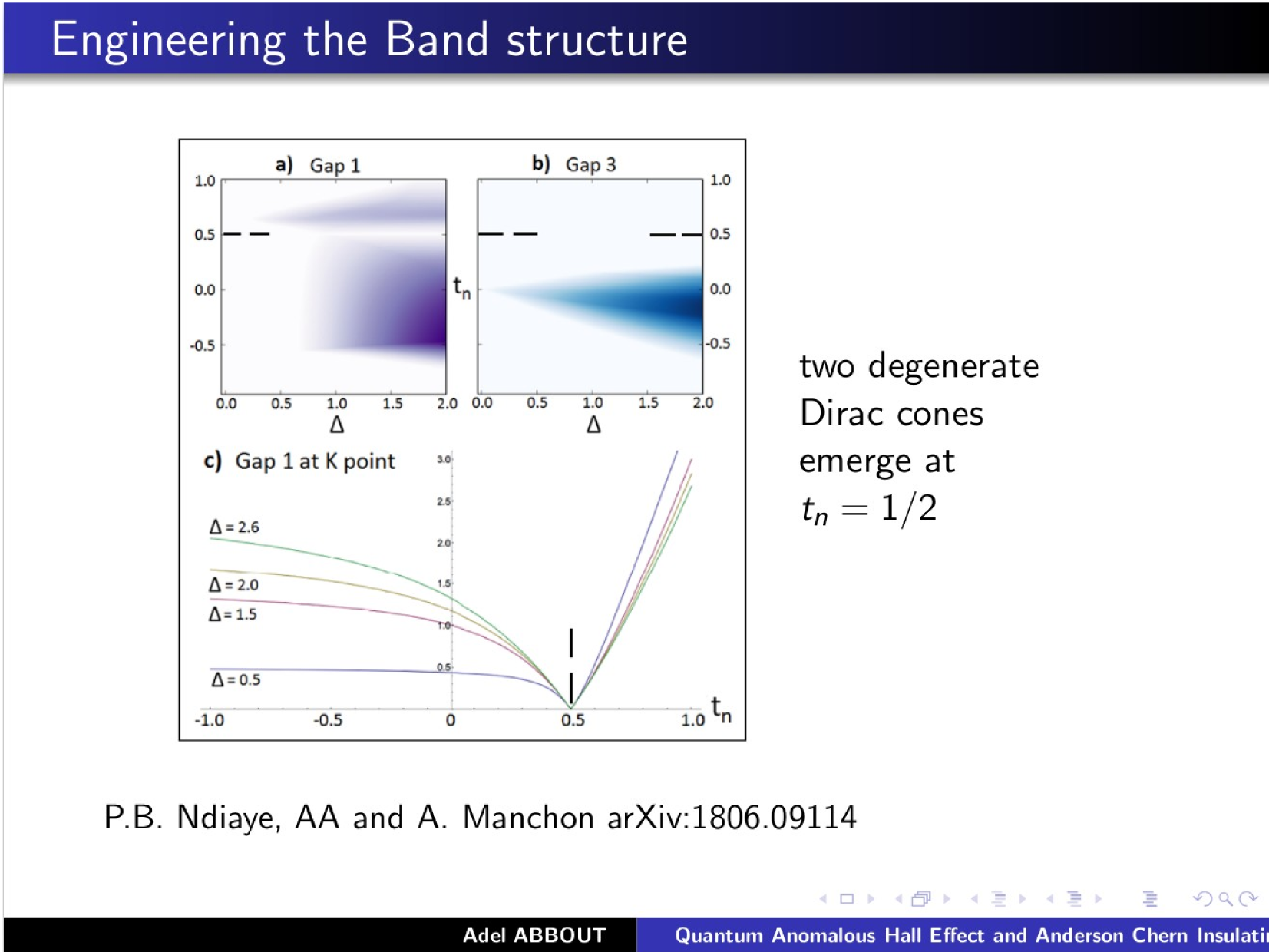
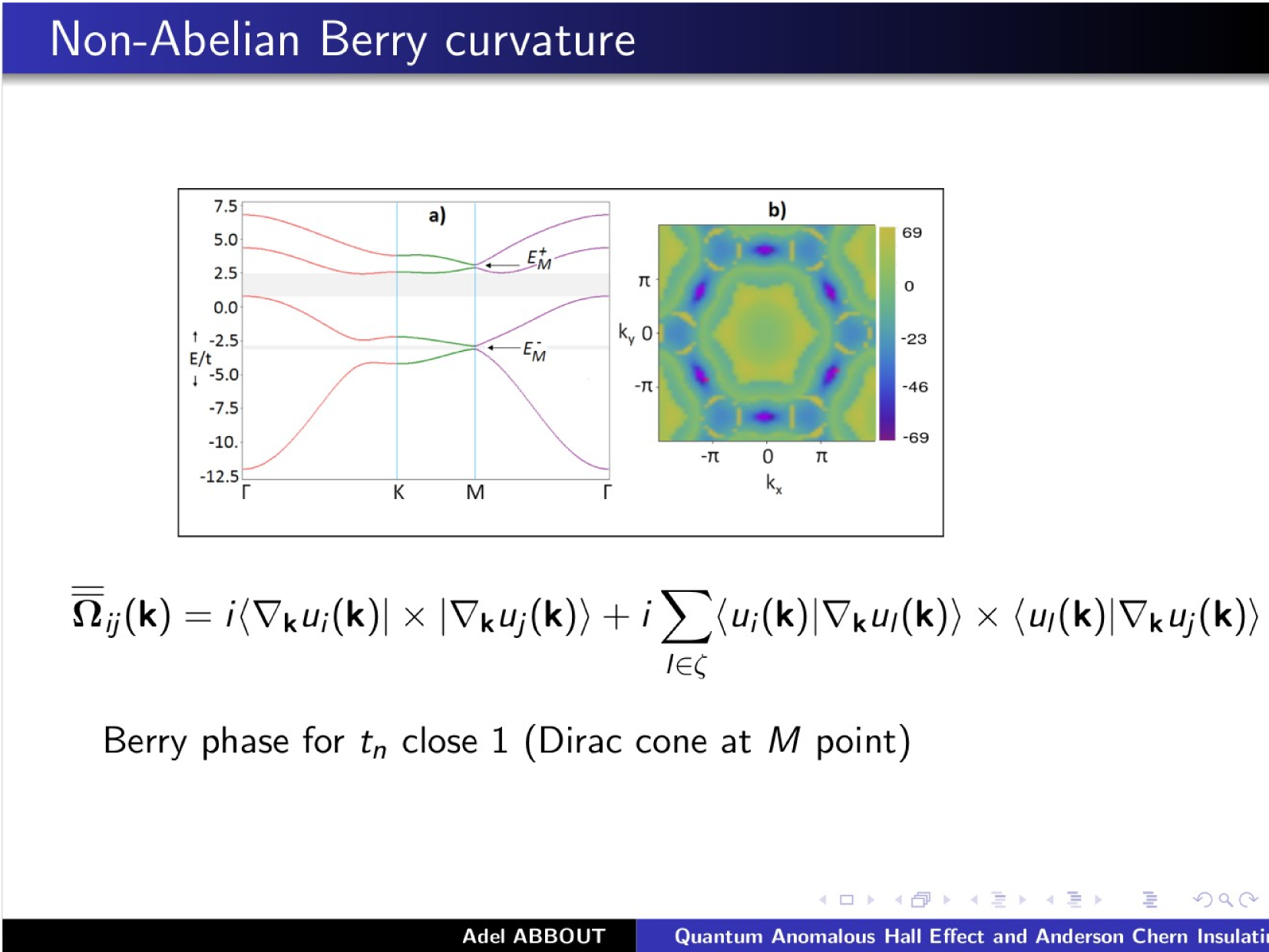
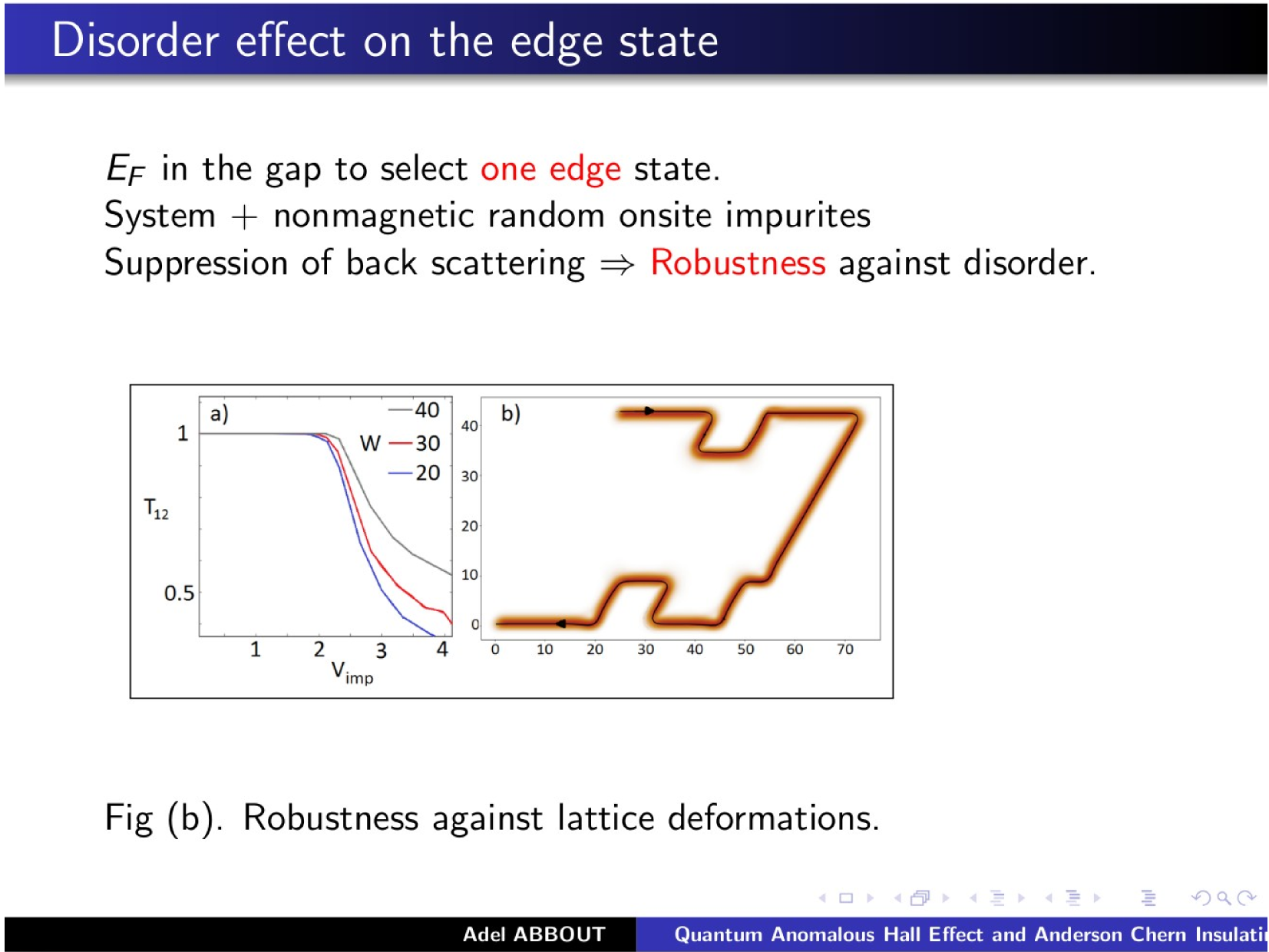


\text{\textcolor{red}{Postdoc positions }are available}
\text{Topological Systems and Quantum Computing}
\text{competitive salary}
\text{housing}
\text{health care}
\text{annual flight tickets}