\begin{aligned}
H & =\left(\begin{array}{cc}
v & t \\
t & -v
\end{array}\right) . \\
\end{aligned}
\begin{aligned}
& =\frac{1}{\left(\begin{array}{cc}
E-v-\Sigma_0 & -t \\
-t & E+v-\Sigma_0
\end{array}\right)} \\
\end{aligned}
\begin{align*}
G & =\frac{1}{\operatorname{det(E-H-\Sigma)}}\left(\begin{array}{cc}
E+v-\Sigma_0 & +t \\
+t & \epsilon-v-\Sigma_0
\end{array}\right)
\end{align*}
G=\frac{1}{E-H-\Sigma}
\begin{aligned}
\Gamma^L & =\left(\begin{array}{cc}
\Gamma^L_0 & 0 \\
0 & 0
\end{array}\right) . \\
\end{aligned}
\begin{aligned}
\Sigma & =\left(\begin{array}{cc}
\Sigma_0 & 0 \\
0 & \Sigma_0
\end{array}\right) . \\
\end{aligned}
\begin{aligned}
\Gamma^R & =\left(\begin{array}{cc}
0 & 0 \\
0 & \Gamma^R_0
\end{array}\right) . \\
\end{aligned}
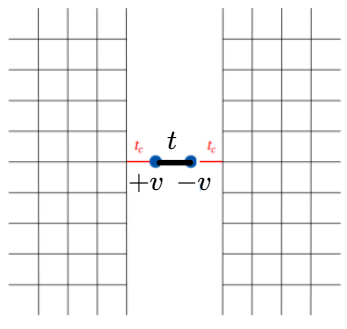
G_{12}=\frac{t}{(\epsilon-\Sigma_0-v)(\epsilon-\Sigma_0+v)-t^2}
T=\text{Trace}(\Gamma^L G\Gamma^R G^\dagger )
\Rightarrow T=\Gamma^L_0 G_{12}\Gamma^R_0 G^\dagger_{12}
T=\Gamma^2 \frac{t^2}{\left |(\epsilon-v-\Sigma_0)(\epsilon+v-\Sigma_0)-t^2\right|^2}
\text{We need to do a taylor expansion of this formula to the second order in $\Gamma$ and $\Sigma_0$ }
\Gamma_0^L=\Gamma_0^R=\Gamma
\Gamma\rightarrow \Gamma+\delta \Gamma
\Sigma_0\rightarrow \Sigma_0+\delta \Sigma
\text{(Do the expansion and try to express all the coefficients in terms of T)}
(\text{corrected})
T(E)=\frac{t^2\Gamma^2}{\left[(E-\Re\Sigma)^2-(p^2-\frac{\Gamma^2}{2})\right]^2+p^2-(p-\Gamma^2/2)^2}
p^2=v^2+b^2+t^2
\text{maximum appears at }
E=\Re\Sigma \pm\sqrt{p^2-\Gamma^2/2}
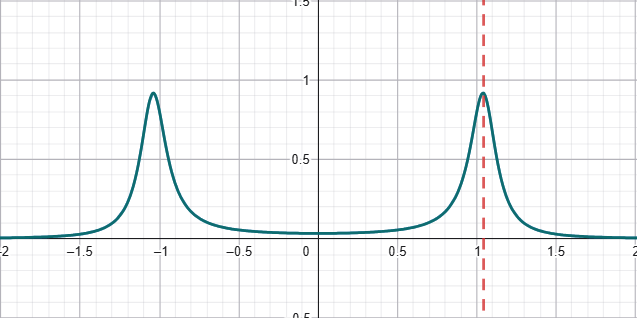
T(E)=\frac{4 t^2 b^2}{\left[(E-a)^2-(p^2-2b^2)\right]^2+p^4-(p^2-2b^2)^2}
T=\frac{4 t^2 b^2}{\left(E^2-p^2-b^2-t^2\right)^2+4 E^2 b^2}
(\text{correct})
(\text{I don't know if correct})
\Sigma=a-ib
T(E)=\frac{4 t^2 b^2}{\left[(E-a)^2-(p^2-2b^2)\right]^2+p^4-(p^2-2b^2)^2}
\text{Formula for small $b$}
T(E)\approx\frac{4 t^2 b^2}{\left[(E-a)^2-p^2\right]^2+4p^2b^2}
T_\text{max}\approx\frac{t^2}{p^2}
p^2\approx v^2+t^2
T\approx\frac{T_\text{max}}{\left[\frac{(E-a)^2-p^2}{2p b}\right]^2+1}
T(E)=\frac{4 t^2 b^2}{\left[(E-a)^2-p^2\right]^2+4b^2 (E-a)^2}
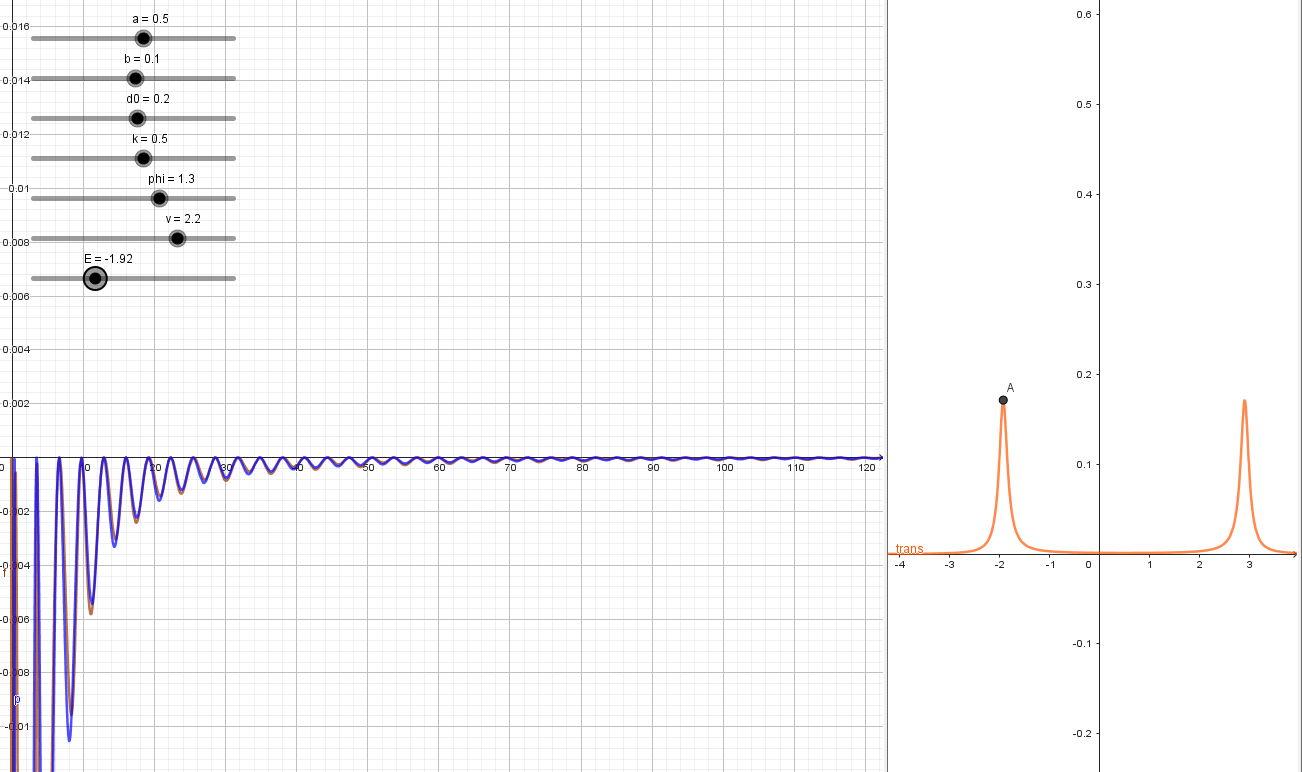
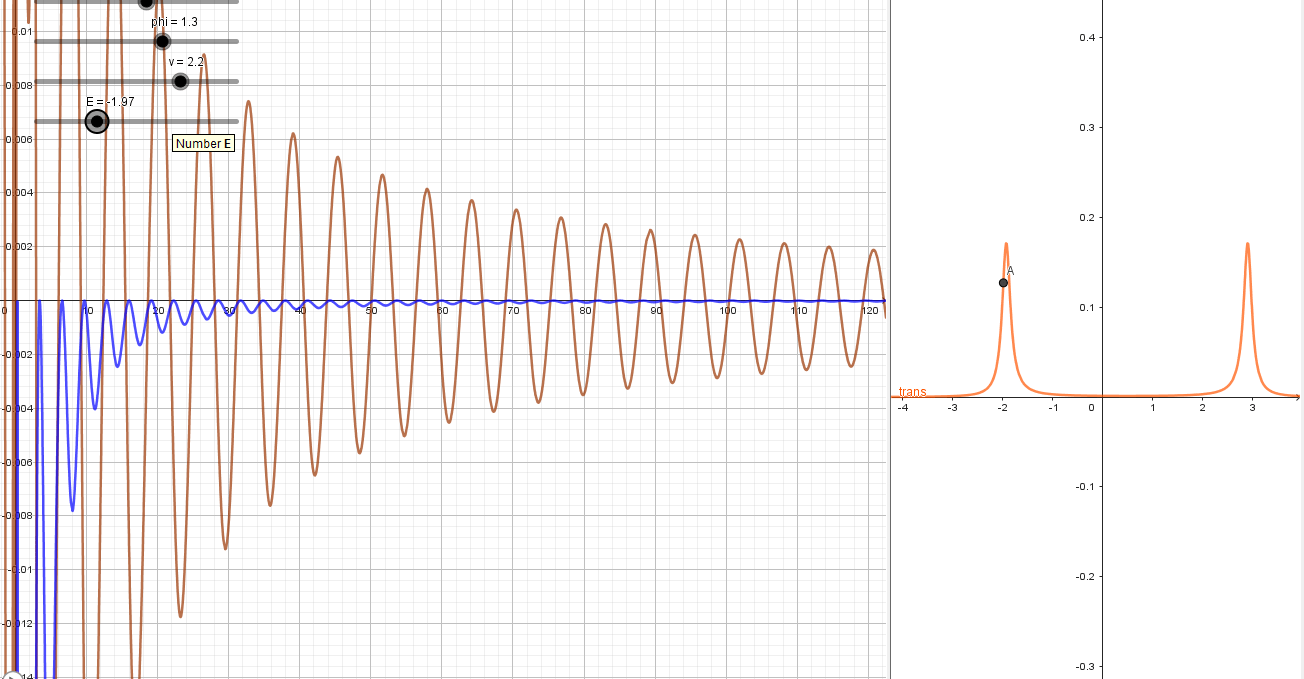
T=T_\text{max}
T\neq T_\text{max}
#!/bin/bash
#SBATCH -J pyjob
#SBATCH -N 1
#SBATCH --ntasks-per-node=3 # 64 processes on 1 node
#SBATCH --time=02:10:00 # hh:mm:ss
#SBATCH -o %x-%j.out
#SBATCH -e %x-%j.err
#SBATCH --partition=cpu_x440 ##all ###cpu_x440
#SBATCH --mem=200G
#SBATCH --exclude=node0014
# --- Python environment ---
#module load python/3.10 # or your site’s module
module use /software/modulefiles
module purge
module load conda/25.08
module load kwant/1.5-py39
module load tkwant/1.1.1-py311
# source ~/envs/myenv/bin/activate # if using a venv
# --- Run ---
# If your code uses MPI / mpi4py (one process per rank):
# srun -n 16 python -u your_script.py
srun -n 3 python -u tip.py\text{sbatch scriptname}
\text{To run the job:}
\# \text{statement}
\text{(this is comment)}
\# \text{SBATCH} \text{ something}
\text{(command)}
\text{script for the cluster}
\text{squeue \texttt{--}me}
\text{$$see my job running time}
\text{squeue -u username}
\text{similar}
\text{sbatch script}
\text{run a script}
\text{sacct -j 258058 \texttt{--}format=JobID,Elapsed,CPUTime,State}
\text{here job id:258058}
\text{scancel 258058}
\text{cancel a job}
\text{vi program.py}
\text{open a file}
\text{squeue}
\text{returns all the running jobs for different users}
\text{rm filename}
\text{removes the file: filename}
\text{rm *err}
\text{removes all the files ending with err}
\text{cp filepath .}
\text{copy the file here (the dot means here)}
# mpirun -np 4 python mpi_sin_example.py
from mpi4py import MPI
import numpy as np
import math
comm = MPI.COMM_WORLD
rank = comm.Get_rank()
size = comm.Get_size()
# Each processor takes a different angle
# Example: angles equally spaced between 0 and 2π
angles = np.linspace(0, 2*np.pi, size, endpoint=False)
my_angle = angles[rank]
# Each processor computes sin(angle)
my_value = math.sin(my_angle)
# Gather all values at root (rank 0)
all_values = comm.gather(my_value, root=0)
if rank == 0:
print("Angles:", angles)
print("Sin values from all processors:", all_values)
\text{understand how this code is working and what is it doing}