Chapter 19

\text{Chapter 19}

\text{Dr. Adel Abbout}

\text{The lowest pressure attainable in the laboratory is 5.}0\times10^{-18}\text{ Pa at 20}^{\circ} C

\text{How many gas molecules are there per m}^{3}\text{ at this pressure?}

A) 1.2 \times 10^3

B) 2.3 \times 10^3

C) 4.4 \times 10^3

D) 3.1 \times 10^3

E) 5.6 \times 10^3

\begin{aligned} & P V=N k T \\ & \frac{\mathrm{N}}{\mathrm{V}}=\frac{P}{k T}=\frac{5 \times 10^{-18}}{1.38 \times 10^{-23} \times(20+273)}=1.2 \times 10^3 \frac{\text { molelule }}{\mathrm{m}^3} \end{aligned}

\text{The lowest pressure attainable in the laboratory is 5.}0\times10^{-18}\text{ Pa at 20}^{\circ} C

\text{How many gas molecules are there per m}^{3}\text{ at this(mwessure?}

\text{Two moles of a monatomic ideal gas with an RMS speed of 254 m/s are contained in a tank }\\ \hspace{-9.2 cm}\text{that has a volume of 0.150 m}^3.\\ \hspace{-2.2 cm}\text{ If the molar mass of the gas is 0.390 kg/mole, what is the pressure of the gas?}

\begin{aligned} &\text{A) }1.12\times10^5\text{ Pa} \\ &\text{B) }7.17\times10^5\text{ Pa} \\ &\text{C})2.22\times10^4\text{ Pa}. \\ &\text{D})3.25\times10^6\text{Pa.} \\ &\text{E) }6.87\times10^4\text{ Pa}. \end{aligned}

\begin{aligned} V_{r m s} & =\sqrt{\frac{3 R T}{M}} \Rightarrow T=\frac{M V_{r m s}^2}{3 R} \\ p V & =n R T \Rightarrow p=\frac{n R T}{V}=\frac{n R}{V} \frac{M V_{r m s}^2}{3 R} \\ p & =\frac{n M V_{r m s}^2}{3 V}=\frac{2(0.390)(254)^2}{3(0.150)}=1.12 \times 10^5 \mathrm{~Pa} \end{aligned}

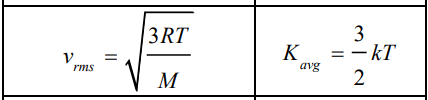
\text{Formula sheet}

\begin{aligned} &\text{An ideal gas initially at a pressure of 1.2 atm and temperature 74°C undergoes an isothermal }\\ &\text{expansion to twice its original volume. During the expansion, the gas absorbs 20 kJ of heat.}\\ &\text{Find the number of moles for this gas?}\end{aligned}

\begin{gathered} \text{A) 10} \\ \text{B) 12} \\ \text{C) 15} \\ \text{D) 18} \\ \text{E) 20} \end{gathered}

\begin{aligned} & \Rightarrow \Delta E_{\text {int }}=0=Q-W \\ & \Rightarrow Q=W=n R T \ln \frac{V_f}{V_i} \\ & n=\frac{Q}{R T \ln \frac{V_f}{V_i}}=\frac{20 \times 10^3}{(8.31)(74+273) \ln 2}=10 \text { moles } \end{aligned}

\begin{gathered} \text{A) 10} \\ \text{B) 12} \\ \text{C) 15} \\ \text{D) 18} \\ \text{E) 20} \end{gathered}

\text { Isothermal ($\Delta T=0$)}

\Delta E_{\text {int }}=n C_V \Delta T

\text{(always valid)}

\begin{aligned} &\text{When an amount of heat of 35.1 J was added to a particular ideal gas, the volume of the gas}\\ &\text{changed from $50.0\mathrm{~cm}^3$ to $100\mathrm{~cm}^3$ while the pressure remained at 1.00 atm. If the quantity }\\ &\text{of gas present was $2.00\times10^{-3}$ mol, find the value of specific heats $\mathrm{C}_V$ and $\mathrm{C}_\mathfrak{p}$ (in J/mol.K)} \end{aligned}

\text{A) 49.5 and 57.8}\\\text{B) 57.8 and 49.5}\\\text{C) 26.1 and 34.4}\\\text{D) 51.1 and 61.5}\\\text{E) 29.5 and 37.8}

Q=n C_p \Delta T \\

p V=n R T \Rightarrow p \Delta V=n R \Delta T \\

C_p=\frac{Q}{n \Delta T}=\frac{Q}{p \Delta V}=\frac{R Q}{p \Delta V}=\frac{(8.31)(35.1)}{\left(1.01 \times 10^5\right)(100-50) \times 10^{-6}} \\

C_p=57.8 \frac{\mathrm{J}}{\mathrm{mol} \cdot K} \quad C_p=C_V+R \Rightarrow C_V=49.4 \frac{\mathrm{J}}{\mathrm{mol} \cdot \mathrm{K}}

\text{$C_p=C_V+R$, so choices B) and D) are not possible }

\text { (constant pressure) }

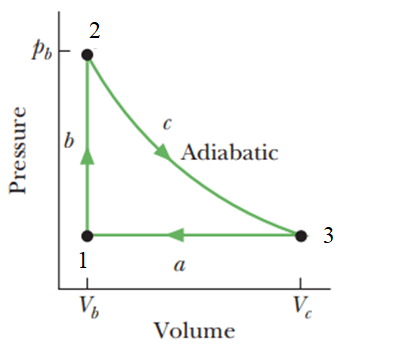
\begin{aligned} &\text{The figure shows a cycle undergone by 1.0 mole of an ideal diatomic gas. The temperatures }\\ &\text{are $T_1=400 \mathrm{ K},T_2=700 K$}, \text{and } T_3=555 \mathrm{K}. \text{ Calculate the net~work~done~in~one~cycle}. \end{aligned}

\begin{array}{l}\mathrm{A)~1.7~kJ~by~the~gas}\\\mathrm{B)~1.7~kJ~on~the~gas}\\\mathrm{C)~3.8~kJ~on~the~gas}\\\mathrm{D)~3.8~kJ~by~the~gas}\\\mathrm{E)~0.52~kJ~by~the~gas}\end{array}

\begin{array}{l}{{\Delta E_{int}=Q-W}}\\{0=Q-W\quad(cycle)}\\{{W=Q=Q_{a}+Q_{b}+Q_{c}}}\\{{W=nC_{p}\Delta T_{31}+nC_{v}\Delta T_{12}+0}}\\\end{array}

W=\frac{7}{2}R(T_{1}-T_{3})+\frac{5}{2}R(T_{2}-T_{1})

W=8.31[\frac{7}{2}(400-555)+\frac{5}{2}(700-400)]=+1.7\text{ kJ}

\text{The work we calculate along the cycle is the work done $\underline{\text{by the gas}}$}

\text{answer A}

\begin{aligned} &\text{An ideal gas with a volume }V_0\text{ and a pressure }P_0\text{ undergoes a free expansion to volume }V_1\\ &\text{and pressure } P_1\mathrm{~where~}V_1=32V_0.\text{ The gas is then compressed adiabatically to the original }\\ &\text{volume $V_0$ and pressure } 4\text{P}_0.\text{ The ratio of specific heats, }\gamma,\text{ of the ideal gas is:} \end{aligned}

\begin{array}{c}\mathrm{A)~7/5}\\\mathrm{B)~2/5}\\\mathrm{C)~3/5}\\\mathrm{D)~1/5}\\\mathrm{E)~9/5}\end{array}

\text{Reminder for free expansion:}\\ \Delta E=0, Q=0,W=0, \Delta T=0,\text{ $PV=$const}

PV=\text{const} \Rightarrow P_1V_1=P_0V_0

\Rightarrow P_1=P_0\frac{V_0}{V_1}=P_0\frac{V_0}{32 V_0}=\frac{P_0}{32}

\text{adiabatic expansion:}

PV^\gamma=\text{const}

P_1V_1^\gamma=P_2V_2^\gamma

P_2=4P_0

V_2=V_0

\frac{P_0}{32}(32 V_0)^\gamma=4P_0 V_0^\gamma\Rightarrow \frac{32^\gamma}{32}=4\Rightarrow \gamma \ln 32=\ln 128

\gamma=\frac{\ln 128}{\ln32}=1.4=7/5