\text{Chapter 16}
\text{Chapter 16}
\text{Chapter 16}
\text{Chapter 16}
\text{Dr. Adel Abbout}
y_m^{\prime}=\left|2 y_m \cos \frac{1}{2} \phi\right| \quad \text { (amplitude). }
y^{\prime}(x, t)=\left[2 y_m \sin k x\right] \cos \omega t .
y^{\prime}(x, t)=\left[2 y_m \cos \frac{1}{2} \phi\right] \sin \left(k x-\omega t+\frac{1}{2} \phi\right) \text {. }

P_{\mathrm{avg}}=\frac{1}{2} \mu \nu \omega^2 y_m^2
v=\sqrt{\frac{\tau}{\mu}}
v=\frac{\omega}{k}=\frac{\lambda}{T}=\lambda f
k=\frac{2 \pi}{\lambda}
\frac{\omega}{2 \pi}=f=\frac{1}{T}
y(x, t)=y_m \sin (k x-\omega t)
\text{propagating wave}
\text{wave on a stretched string}
\text{wave interference}
\text{wave speed doesn't depend on the frequency}
\text{standing wave}
\text{Resonance}
\text{stretched string with fixed ends}
f=\frac{v}{\lambda}=n \frac{v}{2 L}, \quad \text { for } n=1,2,3, \ldots
\text{two waves shifted by $\Delta x$ have a differnce of phase}
\Delta \phi=k\Delta x=2\pi \frac{\Delta x}{\lambda}
\text{$n=1$ is the fundamental}
\text{The displacement of a string carrying a traveling sinusoidal wave is given by:}\\
y(x, t)=y_m \sin (k x-\omega t+\varphi) .
\text{At time $t=0$ the point at $x=0$ has a displacement of zero and is moving in the positive}
\text{ $y$ direction. Find the value of the phase constant $\varphi$.}
\begin{aligned}
&\text{A) 180 degrees} \\
&\text{B) 90 degrees} \\
&\text{C) 135 degrees} \\
&\text{D) 0 degrees} \\
&\text{E) 270 degrees}
\end{aligned}
\text{The displacement of a string carrying a traveling sinusoidal wave is given by:}\\
y(x, t)=y_m \sin (k x-\omega t+\varphi) .
\text{At time $t=0$ the point at $x=0$ has a displacement of zero and is moving in the positive}
\text{ $y$ direction. Find the value of the phase constant $\varphi$.}
\displaystyle y=y_m \sin\phi=0\Rightarrow \sin \phi=0
\text{at $x=0$, $t=0$, we have }
\Rightarrow
\phi = \begin{cases}
0 \\
\pi
\end{cases}
\displaystyle u(0,0)=-\omega y_m \cos\phi>0 \Rightarrow \cos \phi<0
\text{We deduce that: $\phi=\pi$}
\text{Reminder:}
\text{The equation } \sin\theta=a
\text{has two solutions in } [0, 2\pi]:
\theta=\theta_0
\theta=\pi-\theta_0
\text{where } \theta_0=\sin^{-1}a
\text{Your calculator gives only one of them}
\text{(We use the transverse speed to find which angle is correct)}
\text{(moving upward, $\Rightarrow u>0$)}
\text{A transverse sinusoidal wave is travelling on a stretched string. The maximum transverse }
\text{speed of a particle on the string is $24.0 \mathrm{~m} / \mathrm{s}$.}
\text{The frequency of oscillations of a particle }
\text{in the string is $120 \mathrm{~Hz}$. What is the amplitude of the wave?}
\text{A) $31.8 \mathrm{~mm}$}
\text{B) $25.1 \mathrm{~mm}$}
\text{C) $12.0 \mathrm{~mm}$}
\text{D) $43.3 \mathrm{~mm}$}
\text{E) $53.2 \mathrm{~mm}$}
\text{A transverse sinusoidal wave is travelling on a stretched string. The maximum transverse }
\text{speed of a particle on the string is $24.0 \mathrm{~m} / \mathrm{s}$.}
\text{The frequency of oscillations of a particle }
\text{in the string is $120 \mathrm{~Hz}$. What is the amplitude of the wave?}
u_m=\omega y_m \Rightarrow y_m=\frac{u_m}{\omega}=\frac{u_m}{2\pi f}=\frac{24}{2 \pi\times 120}=0.0318\hspace{1mm} m
\text{The maximum transverse speed is}
\text{Figure 1 shows a snapshot graph of a wave traveling to the right along a string at 25 $\mathrm{m} / \mathrm{s}$.}
\text{At this instant, what are the velocities of points A, B , and C on the string, respectively?}
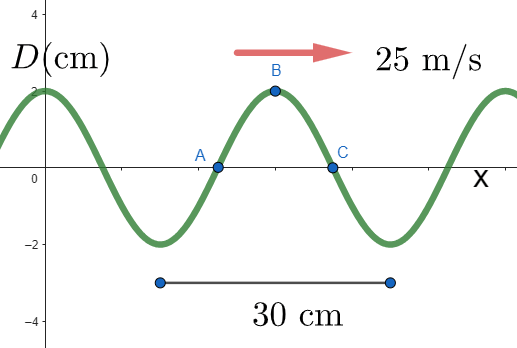
\text{A) $-11 \mathrm{~m} / \mathrm{s}, 0,+11 \mathrm{~m} / \mathrm{s}$}
\text{B) $-11 \mathrm{~m} / \mathrm{s}, 0,-11 \mathrm{~m} / \mathrm{s}$}
\text{C) $0,-11 \mathrm{~m} / \mathrm{s}, 0$}
\text{D) $0,+11 \mathrm{~m} / \mathrm{s},-11 \mathrm{~m} / \mathrm{s}$}
\text{E) $-19 \mathrm{~m} / \mathrm{s}, 0,+19 \mathrm{~m} / \mathrm{s}$}
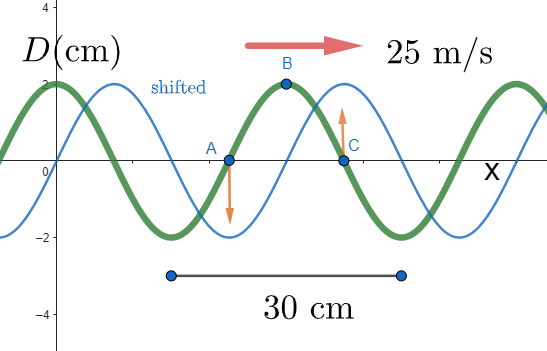
\text{We shift the wave to the \textcolor{red}{right}}
\text{(because it is a right moving wave)}
\text{We check in which direction each point moves}
\text{A: down, C: Up}
\left|u_{\max }\right|=\omega y_m=2 \pi f y_m
f=\frac{v}{\lambda}=\frac{25}{0.3}=83.33 \mathrm{~m} / \mathrm{s}
\left|u_{\max }\right|=2 \pi \times 83.33 \times 2 \times 10^{-2}=10.47 \mathrm{~m} / \mathrm{s}\approx11 \mathrm{~m} / \mathrm{s}
\text{Figure 1 shows a snapshot graph of a wave traveling to the right along a string at 25 $\mathrm{m} / \mathrm{s}$.}
\text{At this instant, what are the velocities of points A, B , and C on the string, respectively?}
\text{At B, the transverse speed=0}
\text{At A and C, the transverse speed is maximum}
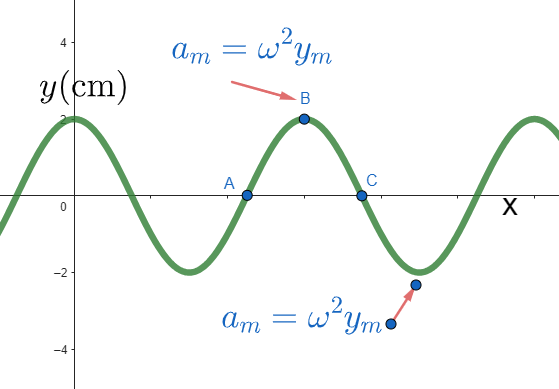
\text{The displacement of a particle moving in simple harmonic motion is given by the equation:}
\text{ $y(t)=2.0 \cos (kx-6.0 t)$, where $y$ is in meters and $t$ is in seconds. }
\text{What is the maximum acceleration of the particle and where does it occur?}
y(t)=2 \cos(kx-6.0 t)
\omega=6 \text{ rad/s}
a(t)=-\omega^2 y(t)
a(t) \text{ will be maximum for } y(t)=-y_m
a_m=\omega^2 y_m=6^2\times 2=72 \text{ $m/s^2$}
\text{ for $y(t)$ minimum}
\text{The displacement of a particle moving in simple harmonic motion is given by the equation:}
\text{ $y(t)=2.0 \cos (kx-6.0 t)$, where $y$ is in meters and $t$ is in seconds. }
\text{What is the maximum acceleration of the particle and where does it occur?}
\text{A stretched string of mass $2.0 \mathrm{~g}$ and length $10 \mathrm{~cm}$, carries a wave having the following }
\text{displacement wave: $y(x, t)=0.05 \sin (2 \pi x-400 \pi t)$, where $x$ and $y$ are in meters }
\text{and $t$ is in seconds. What is the tension in the string?}

\begin{aligned}
v=\sqrt{\frac{\tau}{\mu}} \Rightarrow \tau & =v^2 \mu=\left(\frac{\omega}{k}\right)^2 \mu=\left(\frac{\omega}{k}\right)^2 \frac{m}{l} \\
\tau & =\left(\frac{400 \pi}{2 \pi}\right)^2 \frac{2 \times 10^{-3}}{10 \times 10^{-2}}=800 \mathrm{~N}
\end{aligned}
\text{A stretched string of mass $2.0 \mathrm{~g}$ and length $10 \mathrm{~cm}$, carries a wave having the following }
\text{displacement wave: $y(x, t)=0.05 \sin (2 \pi x-400 \pi t)$, where $x$ and $y$ are in meters }
\text{and $t$ is in seconds. What is the tension in the string?}
\text{FIGURE 1 shows a graph that represents a transverse wave on a string. The wave is moving}
\text{in the $+x$ direction with a speed of $0.15 \mathrm{~m} / \mathrm{s}$. Using the information contained in the graph,}
\text{write the expression for the wave}
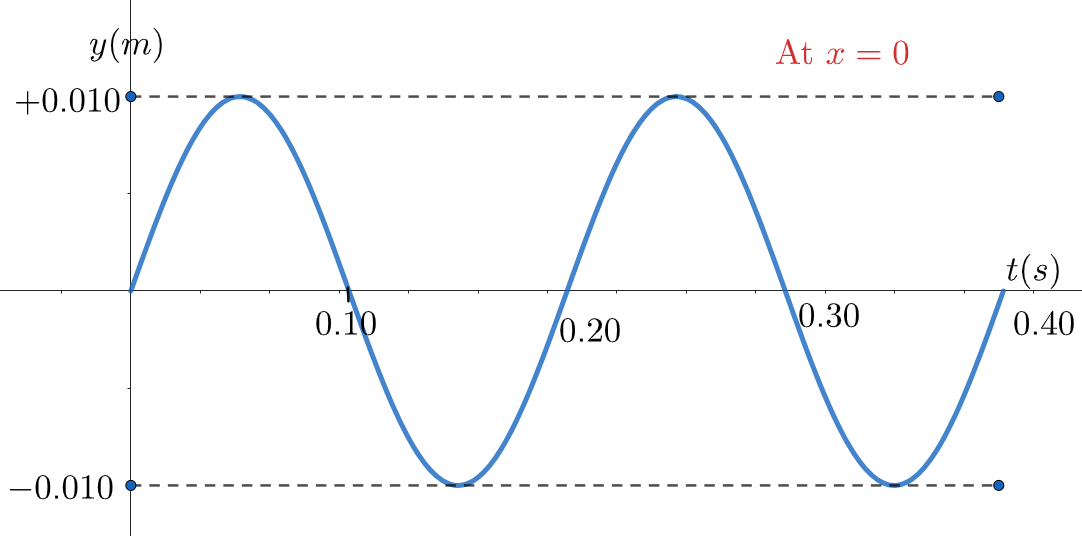
\text{A) $y=0.01 \sin (209 x-31.4 t)$}
\text{B) $y=0.01 \sin (209 x+31.4 t)$}
\text{C) $y=0.04 \sin (209 x-6.28 t)$}
\text{D) $y=0.01 \sin (0.942 x-31.4 t)$}
\text{E) $y=0.01 \sin (0.942 x+31.4 t)$}
\text{FIGURE 1 shows a graph that represents a transverse wave on a string. The wave is moving}
\text{in the $+x$ direction with a speed of $0.15 \mathrm{~m} / \mathrm{s}$. Using the information contained in the graph,}
\text{write the expression for the wave}

\begin{aligned}
& \omega=\frac{2 \pi}{T}=\frac{2 \pi}{0.2}=10 \pi=31.4 \text{ rad/s}\\
&\\
& \mathrm{~k}=\frac{\omega}{v}=\frac{10 \pi}{0.15}=\frac{200}{3} \pi=209 \text{ rad/m}
\end{aligned}
y_m=0.01 \text{ m}
\mathrm{T}=0.2\text{ s}
\text{right moving wave, so: $ y=0.01 \sin (209 x-31.4 t)$ }
\text{The amplitude is:}
\text{Graph: displacement vs time}
\text{Two pieces of string, each of length $L=1.5 \mathrm{~m}$, are joined together end to end, to make }
\text{a $3.0 \mathrm{~m}$ long combined string. The first piece of string has mass per unit length $\mu_1=100$ $\mathrm{g} / \mathrm{m}$, }
\text{the second piece has mass per unit length $\mu_2=6.0 \mu_1$.}
\text{travelling wave to travel the entire $3.0 \mathrm{~m}$ length of the string?}
\text{If the combined string is under tension $\tau=5.0 \mathrm{~N}$, how much time does it take a transverse }
\text{A) $0.73 \mathrm{~s}$}
\text{B) $1.1 \mathrm{~s}$}
\text{C) $1.7 \mathrm{~s}$}
\text{D) $1.9 \mathrm{~s}$}
\text{E) $2.8 \mathrm{~s}$}
\text{Two pieces of string, each of length $L=1.5 \mathrm{~m}$, are joined together end to end, to make }
\text{a $3.0 \mathrm{~m}$ long combined string. The first piece of string has mass per unit length $\mu_1=100$ $\mathrm{g} / \mathrm{m}$, }
\text{the second piece has mass per unit length $\mu_2=6.0 \mu_1$.}
\text{travelling wave to travel the entire $3.0 \mathrm{~m}$ length of the string?}
\text{If the combined string is under tension $\tau=5.0 \mathrm{~N}$, how much time does it take a transverse }
\displaystyle t_{\text {Tot }}=L\left(\frac{1}{v_1}+\frac{1}{v_2}\right)=L\left(\sqrt{\frac{\mu_1}{\tau}}+\sqrt{\frac{\mu_2}{\tau}}\right)=1.5\left[\sqrt{\frac{0.1}{5}}+\sqrt{\frac{0.6}{5}}\right]=0.731 \mathrm{~s}
t_\text{Tot}=t_1+t_2
\text{The cords in the three configurations are the same. All the objects have the same mass.}
\text{In which configuration, the wave speed in the cord is maximum?}
\text{The cords in the three configurations are the same. All the objects have the same mass.}
\text{In which configuration, the wave speed in the cord is maximum?}
\tau_1
\tau_2
\tau_3
\tau_1=mg
\tau_2=mg
\tau_3=2mg
\tau_2
\text{The highest speed is in configuration 3}
\text{The speeds in configurations 1 and 2 are tie}
(\text{The tension in the string is constant})
(\text{we neglect the mass of the hanging string})
mg
mg
mg
2mg
\text{A $0.550 \mathrm{~m}$ long string fixed at both ends is vibrating in its fundamental mode. }
\text{The maximum transverse acceleration of a point at the middle of the string is $8.40 \times 10^3$ $\mathrm{m} / \mathrm{s}^2$ }
\text{and the maximum transverse velocity is $3.80 \mathrm{~m} / \mathrm{s}$.}
\text{What is the wave speed of the transverse waves traveling on this string? }
\begin{aligned}
& \frac{a_{\max }}{u_{\max }}=\frac{y_m^{\prime} \omega^2}{y_m^{\prime} \omega}=\omega=\frac{8.4 \times 10^3}{3.8}=2210.5 \mathrm{rad} / \mathrm{s} \\
& \lambda=2 L=2 \times 0.55=1.1 \mathrm{~m} \\
& v=\frac{\omega}{k}=\frac{\lambda \omega}{2 \pi}=\frac{1.1 \times 2210.5}{2 \pi}=386.99 \mathrm{~m} / \mathrm{s}
\end{aligned}
\text{A $0.550 \mathrm{~m}$ long string fixed at both ends is vibrating in its fundamental mode. }
\text{The maximum transverse acceleration of a point at the middle of the string is $8.40 \times 10^3$ $\mathrm{m} / \mathrm{s}^2$ }
\text{and the maximum transverse velocity is $3.80 \mathrm{~m} / \mathrm{s}$.}
\text{What is the wave speed of the transverse waves traveling on this string? }
\text{(because it is the fundamental)}
y^{\prime}(x, t)=\left[2 y_m \sin k x\right] \cos \omega t .
\text{(standing wave equation)}
u(x, t)=-\left[2 y_m \omega \sin k x\right] \sin\omega t .
a(x, t)=-\left[2 y_m \omega^2 \sin k x\right] \cos\omega t .
\text{Two sinusoidal waves, identical except for phase, travel in the same direction along }
\text{a stretched string, producing a resultant wave $y(x, t)=0.097 \sin (15 x-2.4 t+0.78)$,}
\text{where $x$ is in meters and $t$ is in seconds. What is the amplitude of the interfering waves? }
\text{A) $0.068 \mathrm{~m}$}
\text{B) $0.052 \mathrm{~m}$}
\text{C) $0.097 \mathrm{~m}$}
\text{D) $0.035 \mathrm{~m}$}
\text{E) $0.044 \mathrm{~m}$}
\text{Two sinusoidal waves, identical except for phase, travel in the same direction along }
\text{a stretched string, producing a resultant wave $y(x, t)=0.097 \sin (15 x-2.4 t+0.78)$,}
\text{where $x$ is in meters and $t$ is in seconds. What is the amplitude of the interfering waves? }
y^{\prime}(x, t)=\left[2 y_m \cos \frac{1}{2} \phi\right] \sin \left(k x-\omega t+\frac{1}{2} \phi\right) \text {. }
\text{We can see that: }\frac{\phi}{2}=0.78 \text{ rad}
2 y_m |\cos \frac{1}{2} \phi|=0.097 \Rightarrow y_m=\displaystyle \frac{0.097}{2 |\cos \frac{1}{2} \phi|}=\frac{0.097}{2 |\cos 0.78|}=0.068 \text{ m}
\text{(resultant wave)}
\begin{gathered}
\text{A)1.83 m }\\
\text{B)1.22 m } \\
\text{C)1.12 m }\\
\text{D)2.86 m }\\
\text{E)2.12 m }
\end{gathered}
\begin{aligned}
&\text{A light string is fixed between two supports with two successive standing-wave frequencies}\\
&\text{occur at 525 Hz and 630 Hz. There are other standing-wave frequencies lower than 525 Hz}\\
&\text{and higher than 630 Hz. If the speed of transverse waves on the string is 384 m/ s, then find }\\
&\text{the length of the string?}
\end{aligned}
\begin{aligned}
& f_1=630-525=105 \mathrm{~Hz} \\
& f_1=\frac{ v}{2 L}=\frac{384}{2 L}=105 \mathrm{~Hz} \\
& \Rightarrow L=1.83 \mathrm{~m}
\end{aligned}
\text{The difference between successive frequencies gives the fundamental}
\begin{aligned}
&\text{A light string is fixed between two supports with two successive standing-wave frequencies}\\
&\text{occur at 525 Hz and 630 Hz. There are other standing-wave frequencies lower than 525 Hz}\\
&\text{and higher than 630 Hz. If the speed of transverse waves on the string is 384 m/ s, then find }\\
&\text{the length of the string?}
\end{aligned}
\text{A string oscillates in a third -harmonic standing wave pattern. The amplitude at a point }
\text{$30 \mathrm{~cm}$ from one end of the string is half the maximum amplitude. How long is the string?}

\text{A string oscillates in a third -harmonic standing wave pattern. The amplitude at a point }
\text{$30 \mathrm{~cm}$ from one end of the string is half the maximum amplitude. How long is the string?}
L=\frac{3 \lambda}{2} \Rightarrow k=\frac{2 \pi}{\lambda}=2 \pi \times \frac{3}{2 L}=\frac{3 \pi}{L}
\operatorname{Amplitude}\text{ at }(x=0.3 m) ; y'_m=2 y_m \operatorname{sin}k x=2 y_m \sin \left(\frac{3 \pi}{L} \times 0.3\right)=y_m
1=2 \sin \left(\frac{0.9 \pi}{L}\right)
L=\frac{0.9 \pi}{\sin ^{-1}\left(\frac{1}{2}\right)}=\frac{0.9 \pi}{30^{\circ}}=\frac{0.9 \pi}{\pi / 6}=6 \times 0.9=5.4 \mathrm{~m}
\text{(maximum amplitude is $2y_m$)}
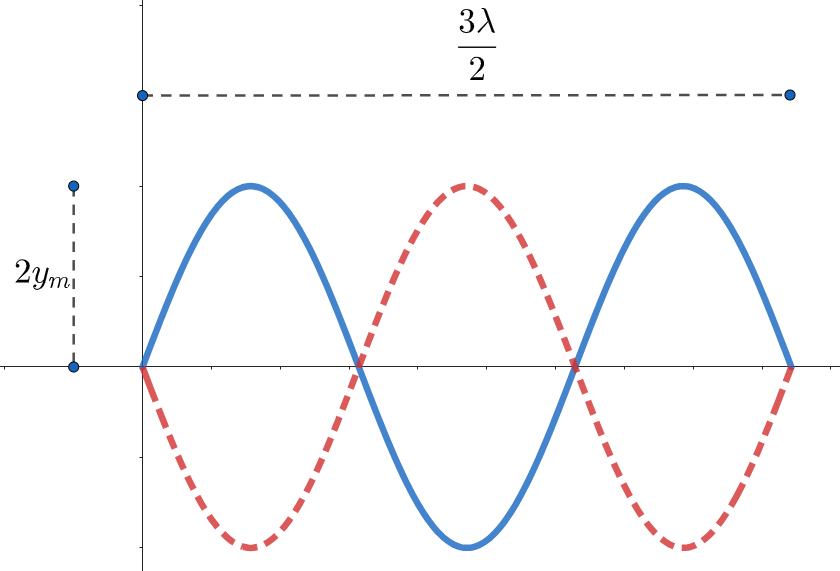
\text{A string oscillates in a third -harmonic standing wave pattern. The amplitude at a point }
\text{$30 \mathrm{~cm}$ from one end of the string is half the maximum amplitude. How long is the string?}
y'_m=2 y_m |\operatorname{sin}k x|=2 y_m \Big|\sin \left(\frac{3 \pi}{L} \times 0.3\right)\Big|=y_m
\frac{1}{2}=\Big| \sin \left(\frac{0.9 \pi}{L}\right)\Big|
L=\frac{0.9 \pi}{\sin ^{-1}\left(\displaystyle\textcolor{red}{\pm}\frac{1}{2}\right)}

\text{The previous solution is actually incomplete.}
\text{The correct way is to do it as follows}
\sin^{-1}(\frac{1}{2})=\frac{\pi}{6}+2\pi n
\sin^{-1}(\frac{1}{2})=\frac{5\pi}{6}+2\pi n
\text{ or }
\text{with $n$ integer}
\text{A string oscillates in a third -harmonic standing wave pattern. The amplitude at a point }
\text{$30 \mathrm{~cm}$ from one end of the string is half the maximum amplitude. How long is the string?}
L=\frac{0.9 \pi}{\sin ^{-1}\left(\displaystyle\pm\frac{1}{2}\right)}

\sin^{-1}(\frac{1}{2})=\frac{\pi}{6}+2\pi n
a)
L=\frac{5.4}{1+12n}
\text{the acceptable $n$ for which $L>(x=0.3)$ are}
n=0,1
\text{So, $L=5.4 $ m or $L=0.42 $ m}
\sin^{-1}(\frac{1}{2})=\frac{5\pi}{6}+2\pi n
L=\frac{5.4}{5+12n}
\text{the acceptable $n$ for which $L>(x=0.3)$ are}
n=0,1
\text{So, $L=1.08 $ m or $L=0.32 $ m}
b)
\text{A string oscillates in a third -harmonic standing wave pattern. The amplitude at a point }
\text{$30 \mathrm{~cm}$ from one end of the string is half the maximum amplitude. How long is the string?}
L=\frac{0.9 \pi}{\sin ^{-1}\left(\displaystyle\pm\frac{1}{2}\right)}

\sin^{-1}(-\frac{1}{2})=-\frac{\pi}{6}+2\pi n
c)
L=\frac{5.4}{-1+12n}
\text{the acceptable $n$ for which $L>(x=0.3)$ are}
n=1
\text{So, $L=0.42 $ m}
\sin^{-1}(-\frac{1}{2})=-\frac{5\pi}{6}+2\pi n
L=\frac{5.4}{-5+12n}
\text{the acceptable $n$ for which $L>(x=0.3)$ are}
n=1,2
\text{So, $L=0.77 $ m}
d)
\cdot
\cdot
\cdot
\cdot
\cdot
\cdot
\text{(as we can see from the figure, there are 6 possible points)}
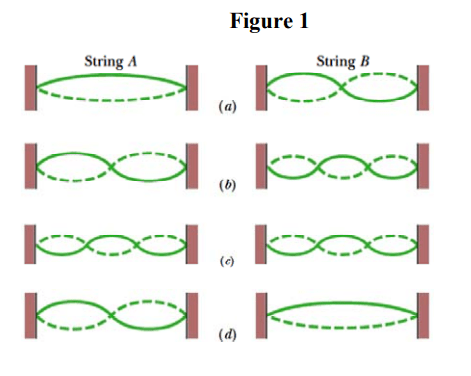
\text{Strings A and B have identical lengths and linear densities, but string A is under greater tension }
\text{than string B. Figure 1 shows four situations, in which standing wave patterns exist on the two }
\text{strings. In which situation(s) is there the possibility that strings A and B are oscillating at the}
\text{ same resonant frequency? }
\text{Strings A and B have identical lengths and linear densities, but string A is under greater tension }
\text{than string B. Figure 1 shows four situations, in which standing wave patterns exist on the two }
\text{strings. In which situation(s) is there the possibility that strings A and B are oscillating at the}
\text{ same resonant frequency? }
\begin{aligned}
& v=\sqrt{\frac{\tau}{\mu}} \\
& v_A>v_B \\
& f_{n A}=\frac{n_A v_A}{2 L}, f_{n B}=\frac{n_B v_B}{2 L} \\
& \frac{n_A v_A}{2 L}=\frac{n_B v_B}{2 L}
\end{aligned}

n_B=\frac{v_A}{v_B} n_A
\Rightarrow
n_B> n_A
\text{because $(v_A>v_B$)}
\Rightarrow
\text{The possible situations are a and b}


\begin{aligned}
& P_1=\frac{1}{2} \mu_1 v_1\omega^2 y_m^2 \\
& \mu_2=2 \mu_1 ; v_2=\sqrt{\frac{\tau}{\mu_2}}=\frac{v_1}{\sqrt{2}} \\
& P_2=\frac{1}{2} 2 \mu_1 \frac{v_1}{\sqrt{2}} \omega^2 y_m^2 \\
& P_2=\frac{2}{\sqrt{2}}\left[\frac{1}{2} \mu_1 v_1\omega^2 y_m^2 \right]=\sqrt{2} P_1 \approx 1.4 P_1
\end{aligned}
\text{Standing waves are created in a $160 \mathrm{~cm}$ long string. The string has two adjacent resonances }
\text{at frequencies of $85.0 \mathrm{~Hz}$ and $102 \mathrm{~Hz}$.}
\text{What is the length of each loop at the $85.0 \mathrm{~Hz}$ resonance?}
\text{A) $32.0 \mathrm{~cm}$}
\text{B) $10.4 \mathrm{~cm}$}
\text{C) $68.0 \mathrm{~cm}$}
\text{D) $83.5 \mathrm{~cm}$}
\text{E) $25.7 \mathrm{~cm}$}
\text{Standing waves are created in a $160 \mathrm{~cm}$ long string. The string has two adjacent resonances }
\text{at frequencies of $85.0 \mathrm{~Hz}$ and $102 \mathrm{~Hz}$.}
\text{What is the length of each loop at the $85.0 \mathrm{~Hz}$ resonance?}
\text{Adjacent resonances} \Rightarrow f_{n+1}-f_n=102-85.0=17 \text{ Hz}
\text{So, the fundamental frequency is}: f_1=17 \text{ Hz}
f_n=n f_1\Rightarrow n=\frac{f_n}{f_1}=\frac{85.0}{17}=5
85.0 \text{ Hz}\text{ is the frequency of the $5^{th}$ harmonic}
\text{The $5^\text{th}$ harmonics has 5 loops. The length of one loop is }d=L/5=160/5=32 \text{ cm}