\text{Review Session }
\text{Major I}
\text{Phys 102}



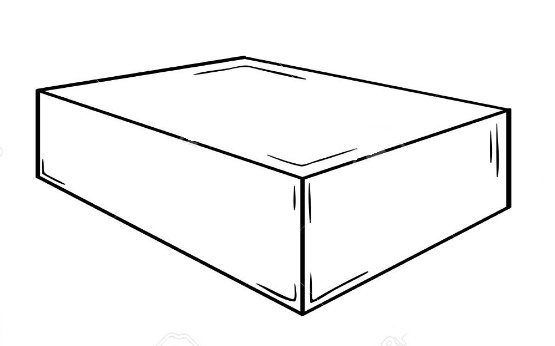
\text{We have }
Q=kA \frac{T_H-T_L}{L}
\text{This is valid on each surface of the box}
\text{ice}
\text{room}
\text{Insulating box}
\text{the system (ice) is loosing heat through each surface of the box}
\text{since $T_H$, $T_L$, $k$, and the thikness $L$ are the same for all the surfaces}
Q'=kA' \frac{T_H-T_L}{L}
\text{We can write}
\text{$Q'$ is the total heat,and $A'$ is the total surface area}


\text{ice}
\text{room}
\text{Insulating box}
Q'=kA' \frac{T_H-T_L}{L}
\text{total heat= conduction rate$\times$time}
mL_F=k A'\frac{(T_H-T_L)}{L}\times \text{ time}
\text{time}=\frac{mL_F \times L}{k A'{(T_H-T_L)}}=\frac{100 \times 333\times 0.04}{2.22\times 10^{-2}\times 1.2 \times 15}=3333 s
\text{time}=55.6\text{ min}
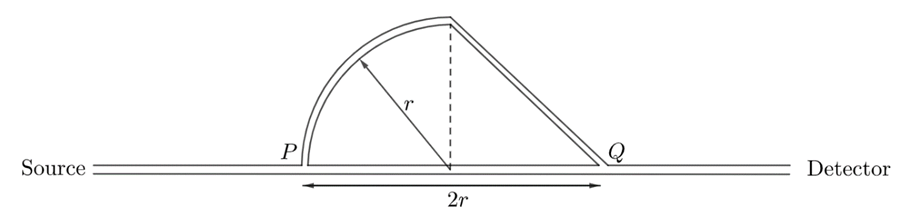
\text{A sound wave enters a tube at the source end, as shown in figure 1. At point $P$, the sound }
\text{wave splits into two waves that recombine at point $Q$. The radius $r$ of the quarter circle is }
\text{varied until the first minimum is observed at the detector when $r=50.0 \mathrm{~cm}$.}
\text{What is the wavelength of sound?}
A) 114 \text{ cm}
B) 228 \text{ cm}
C) 456 \text{ cm}
D) 99 \text{ cm}
E) 304 \text{ cm}

\text{A sound wave enters a tube at the source end, as shown in figure 1. At point $P$, the sound }
\text{wave splits into two waves that recombine at point $Q$. The radius $r$ of the quarter circle is }
\text{varied until the first minimum is observed at the detector when $r=50.0 \mathrm{~cm}$.}
\text{What is the wavelength of sound?}
\Delta L=\frac{\pi}{2}r+\sqrt{r}-2r
\text{first minimum: }\Delta L=\frac{\lambda}{2}
\frac{\lambda}{2}=\frac{\pi}{2}r+\sqrt{2}r-2r\Rightarrow{\lambda}=({\pi}+2\sqrt{2}-4)r=0.985 \text{ m}
\text{Answer D}
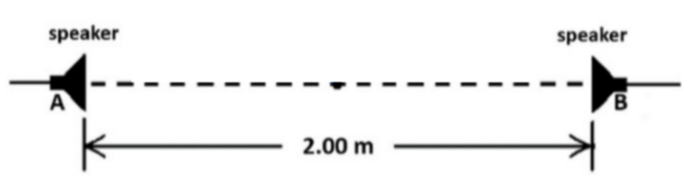
\text{Two speakers, placed $2.0 \mathrm{~m}$ apart, are in phase and emit sound waves with a frequency of $1000 \mathrm{~Hz}$.}
\text{Starting at the midpoint $\mathrm{P}$, a detector is moved along the line joining the two detectors toward}
\text{speaker A. How far (from the midpoint) should the detector move to observe the first maximum }
\text{in sound intensity? }
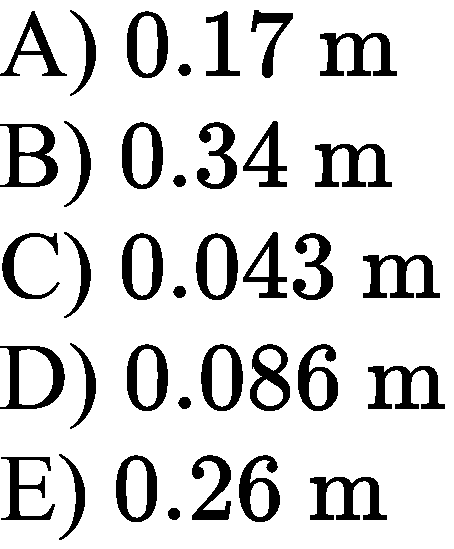
\text{Two speakers, placed $2.0 \mathrm{~m}$ apart, are in phase and emit sound waves with a frequency of $1000 \mathrm{~Hz}$.}
\text{Starting at the midpoint $\mathrm{P}$, a detector is moved along the line joining the two detectors toward}
\text{speaker A. How far (from the midpoint) should the detector move to observe the first maximum }
\text{in sound intensity? }

x
d/2-x
d/2+x
\text{We suppose the first maximum appears at a distance $x$ from the middle}
L_1=d/2-x
L_2=d/2+x
\Delta L=L_2-L_1=2x
\text{first constructive interference: }
\Delta L=\lambda \Rightarrow 2x=\lambda \Rightarrow x=\lambda/2= v/2f=343/(2\times 1000)=0.17 \text{ m}




\text{since the odd harmonics are missing, the difference }
\text{between successive harmonics is $2F_1$}
750-450=2f_1\Rightarrow f_1=150 \text{ Hz}
f_1=\frac{v}{4L}\Rightarrow L=\frac{v}{4f_1}=\frac{343}{4\times 150}=0.572 \text{m}

\text{The texts asks how much water evaporated. This insinuates that we have a mixture }
\text{water at $20^0$}
\rightarrow
\rightarrow
Q_c
\text{heating}
\text{water at $100^0$}
Q_\text{water}+Q_\text{c}=0
(m_{w}c_{w}\Delta T_w+m'_wL_V)+ m_c \text{c}_\text{c}\Delta T_\text{c}=0
\text{$m'$ is the mass of water that has evaporated}
{Q_\text{1}}
(\text{only exchange, no heat is lost})
\text{of water and steam the final temperature is therefore $100^0$}
\text{steam at $100^0$}
\rightarrow
{Q_\text{2}}
\text{Copper at $100^0$}
\text{Copper at $800^0$}
\text{The texts asks how much water evaporated. This insinuates that we have a mixture }
\text{water at $20^0$}
\rightarrow
\rightarrow
Q_c
\text{heating}
\text{water at $100^0$}
Q_\text{water}+Q_\text{c}=0
(m_{w}c_{w}\Delta T_w+m'_wL_V)+ m_c \text{c}_\text{c}\Delta T_\text{c}=0
\text{$m'$ is the mass of ice that has evaporated}
{Q_\text{1}}
(\text{only exchange, no heat is lost})
\text{of water and steam the final temperature is therefore $100^0$}
\text{steam at $100^0$}
\rightarrow
{Q_\text{2}}
\text{Copper at $100^0$}
\text{Copper at $800^0$}
\text{The texts asks how much water evaporated. This insinuates that we have a mixture }
\text{water at $20^0$}
\rightarrow
\rightarrow
Q_c
\text{heating}
\text{water at $100^0$}
m'_w=-\frac{ m_c \text{c}_\text{c}\Delta T_\text{c}+m_{w}c_{w}\Delta T_w}{L_V}=-\frac{0.100\times 4190\times 100-0.200\times386\times 700}{2256\times 10^3}
{Q_\text{1}}
\text{of water and steam the final temperature is therefore $100^0$}
\text{steam at $100^0$}
\rightarrow
{Q_\text{2}}
\text{Copper at $100^0$}
\text{Copper at $800^0$}
(m_{w}c_{w}\Delta T_w+m'_wL_V)+ m_c \text{c}_\text{c}\Delta T_\text{c}=0
\text{The ends of the two brass and steel rods, each $1.00 \mathrm{~m}$ long; as shown in the Figure 4, are separated}
\text{by $5.00 \mathrm{~mm}$ at $25.0^{\circ} \mathrm{C}$. Assuming that the outside ends of both rods rest firmly against rigid supports,}
\text{at what temperature will the inside ends of the rods just touch?}\\
\text{$\left(\alpha_{\text {steel }}=13.0 \times 10^{-6} /{ }^{\circ} \mathrm{C} ; \alpha_{\text {Brass }}=19.0 \times 10^{-6} / \mathrm{C}^{\circ}\right)$.}


\text{The ends of the two brass and steel rods, each $1.00 \mathrm{~m}$ long; as shown in the Figure 4, are separated}
\text{by $5.00 \mathrm{~mm}$ at $25.0^{\circ} \mathrm{C}$. Assuming that the outside ends of both rods rest firmly against rigid supports,}
\text{at what temperature will the inside ends of the rods just touch?}\\
\text{$\left(\alpha_{\text {steel }}=13.0 \times 10^{-6} /{ }^{\circ} \mathrm{C} ; \alpha_{\text {Brass }}=19.0 \times 10^{-6} / \mathrm{C}^{\circ}\right)$.}

\Delta L_{\text {Brass }}+\Delta L_{\text {Steel }}=d
\Delta T=\frac{d}{L\left(\alpha_{\text {Brass }}+\alpha_{\text {Steel }}\right)}=\frac{5 \times 10^{-3}}{1(19+13) \times 10^{-6}}=156.3
T_f=T_i+\Delta T=25+156.3=181.25^{\circ} \mathrm{C}
L \alpha_\text {Brass }\Delta T+L\alpha_\text {Steel }\Delta T=d
\text{The touching condition is}
\text{A quantity of an ideal gas is compressed to half its initial volume. The process may be }
\text{E) isobaric, adiabatic, isothermal}
\text{D) isothermal, adiabatic, isobaric}
\text{C) adiabatic, isobaric, isothermal}
\text{B) adiabatic, isothermal, isobaric}
\text{A) isobaric, isothermal, adiabatic}
\text{adiabatic, isothermal, or isobaric. Rank those three processes in order of the work done on }
\text{the gas by an external force, {LEAST to GREATEST}.
}
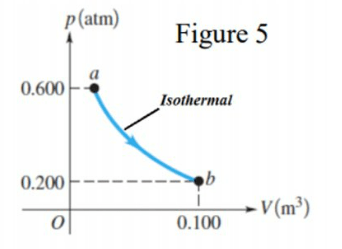
\text{In the isothermal process $\boldsymbol{a} \rightarrow \boldsymbol{b}$ shown in Figure 5, the temperature of an ideal gas remains constant}
\text{at $85.0^{\circ} \mathrm{C}$. Find the magnitude of the work done by the gas during the process $a \rightarrow b$.}
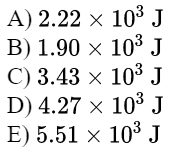

\text{In the isothermal process $\boldsymbol{a} \rightarrow \boldsymbol{b}$ shown in Figure 5, the temperature of an ideal gas remains constant}
\text{at $85.0^{\circ} \mathrm{C}$. Find the magnitude of the work done by the gas during the process $a \rightarrow b$.}
\begin{aligned}
& W=n R T \ln \left(\frac{V_f}{V_i}\right)=P_b V_b \ln \left(\frac{P_a}{P_b}\right) \\
& =0.2 \times 1.01 \times 10^5 \times 0.1 \times \ln \left(\frac{0.6}{0.2}\right)=2219.2 \mathrm{~J}
\end{aligned}
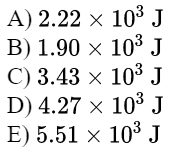
PV=nRT
P_aV_a=P_bV_b
(T=\text{const})
\text{we can keep "atm"}
\text{we need to change "atm" to "Pa"}