Conditioning branching shape processes
Stefan Sommer, University of Copenhagen

Faculty of Science, University of Copenhagen
(simple) shape processes
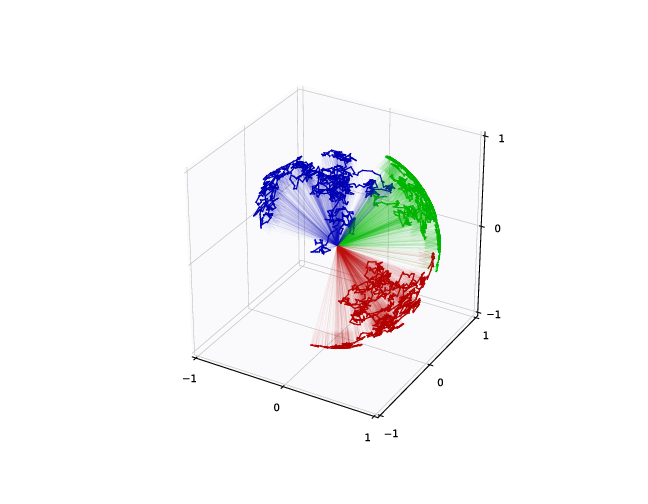
Stochastic shape process:
\[dX_t=K(X_t)\circ dW_t\]
Kernel matrix:
\[K(X_t)^i_j=k(x_i,x_j)\]
\(X_t\) landmarks at time \(t\):
\[X_t=\begin{pmatrix}x_{1,t}\\y_{1,t}\\\vdots\\x_{n,t}\\y_{n,t}\end{pmatrix}\]
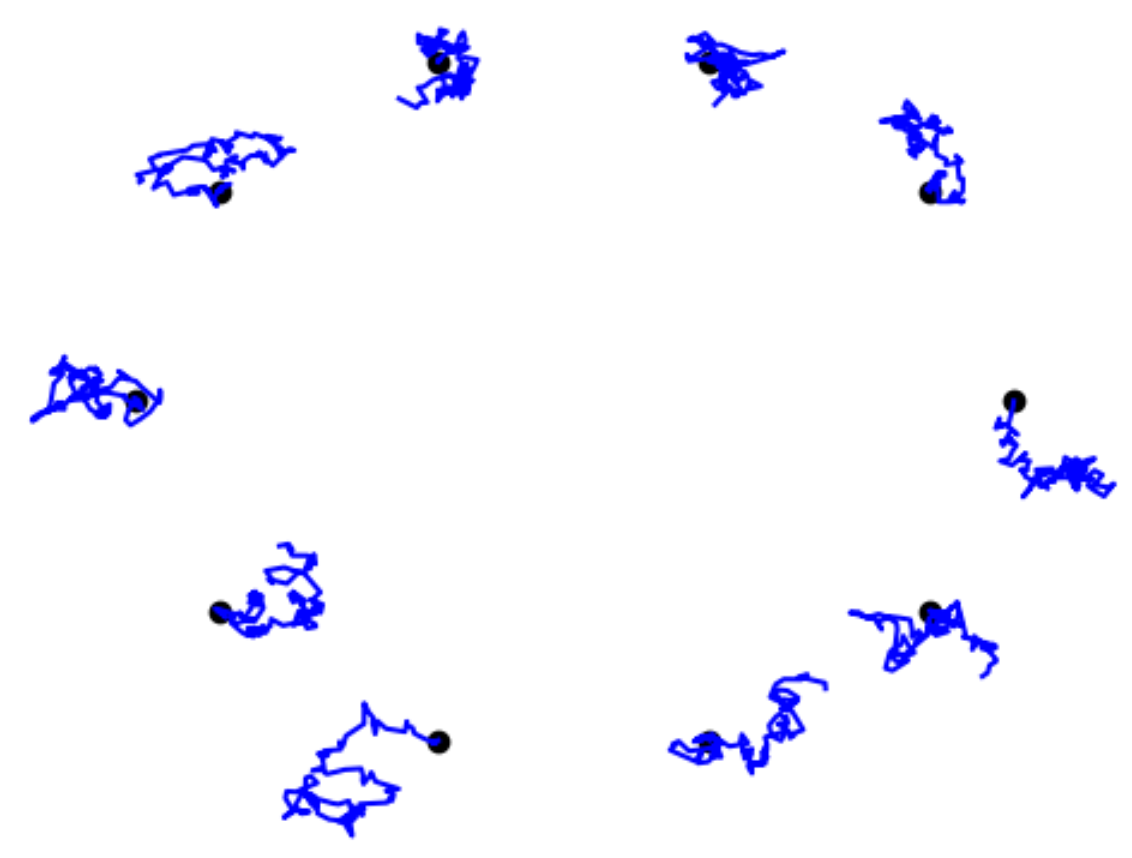

\(X_0\)
\(t=\frac12\)
\(t=3\)
Bridges: conditioned processes
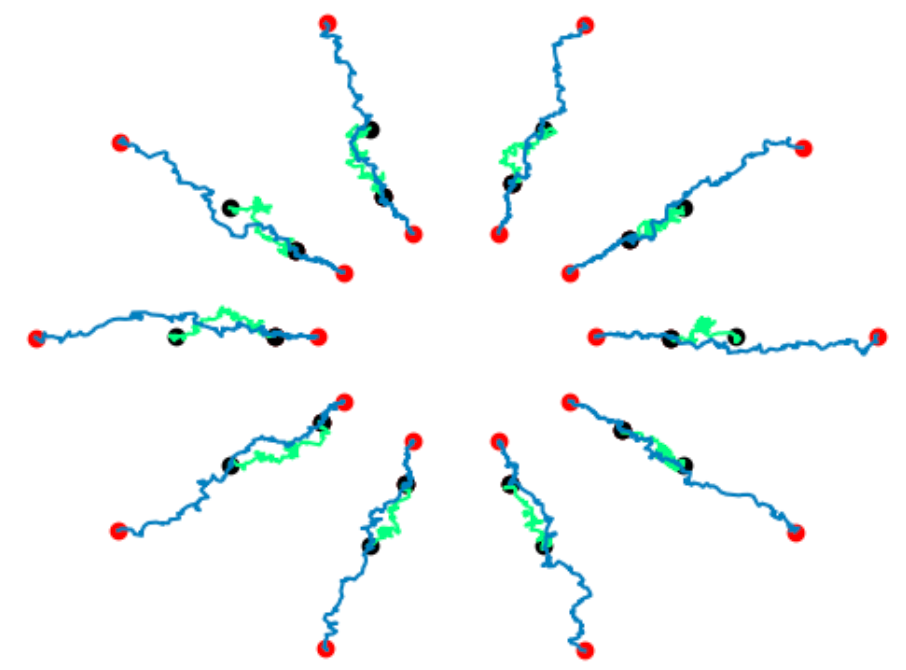
Conditioning on hitting target \(v\) at time \(T>0\):
\[X_t|X_T=v\]
Ito stochastic process:
\[dx_t=b(t,x_t)dt\qquad\qquad\qquad\\+\sigma(t,x_t)dW_t\]
Bridge process:
\[dx^*_t=b(t,x^*_t)dt+a(t,x^*_t)\nabla_x\log \rho_t(x^*_t)dt\\+\sigma(t,x^*_t)dW_t\]
Score \(\nabla_x\log \rho_t\) intractable....
\[\rho_t(x)=p_{T-t}(v;x)\]
\[a(t,x)=\sigma(t,x)\sigma(t,x)^T\]
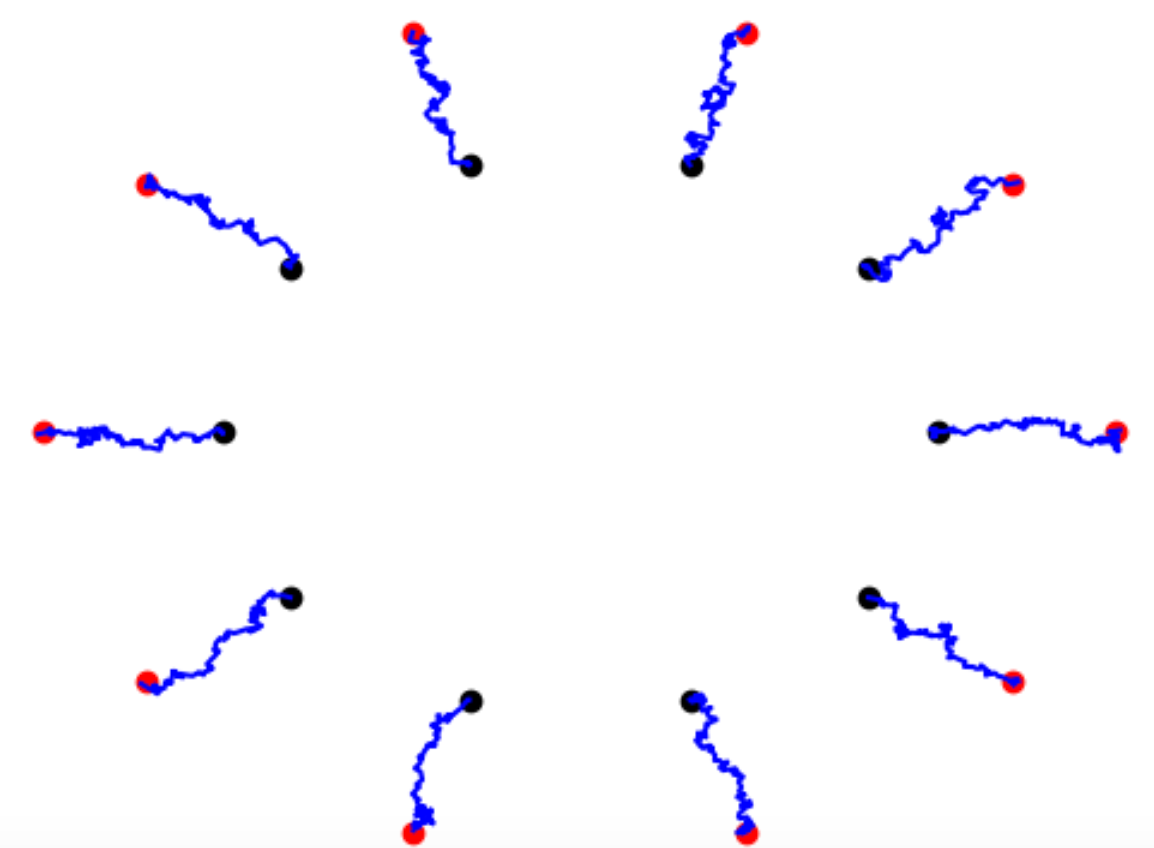
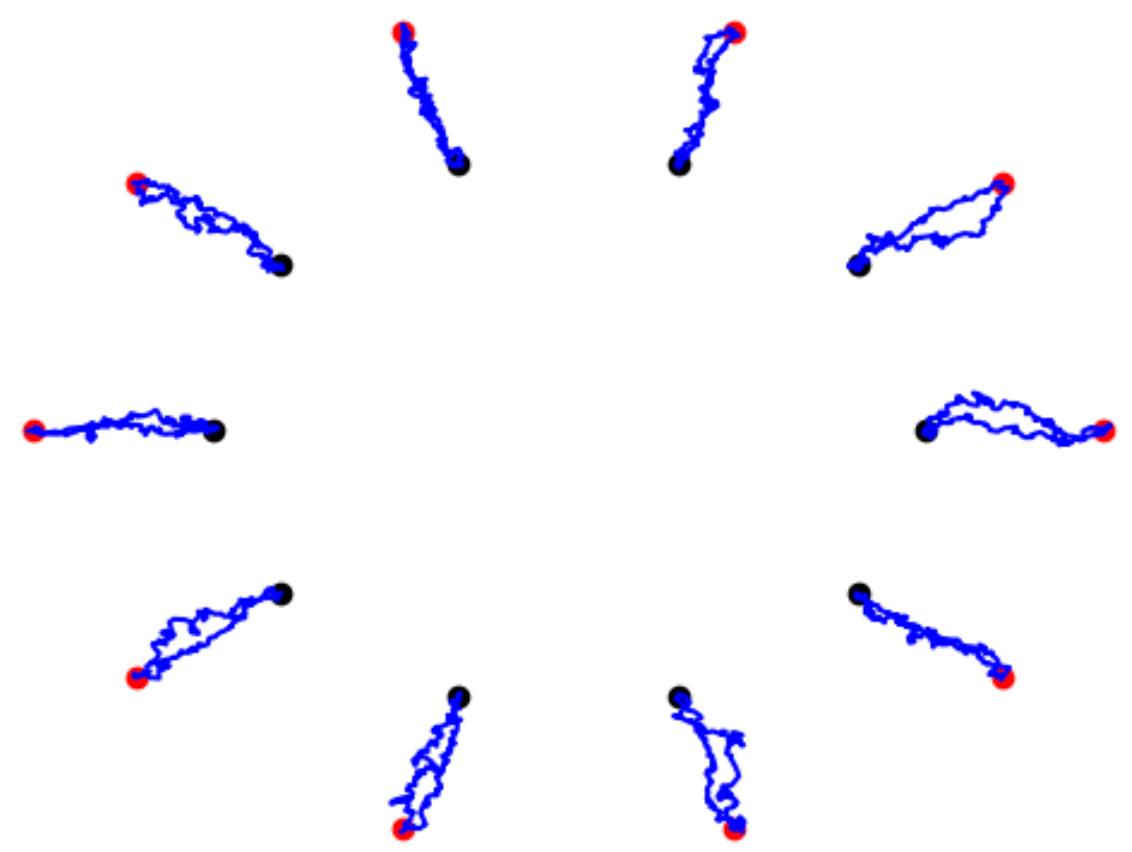
black: \(X_0\), red: \(v\)
Approximate simulation
Auxilary process:
\[d\tilde{x}_t=\tilde{b}(t,\tilde{x}_t)dt+\tilde{\sigma}(t,\tilde{x}_t)dW_t\]
Approximate bridge:
\[d\tilde{x}_t=\tilde{x}(t,\tilde{x}_t)dt\\+\tilde{a}(t,\tilde{x}_t)\nabla_x\log \tilde{\rho}_t(\tilde{x})dt+\tilde{\sigma}(t,\tilde{x}_t)dW_t\]
E.g. linear process so that score \(\nabla_x\log \tilde{\rho}_t\) is known in closed from
(almost) explicitly computable likelihood ratio:
\[\frac{d\mathbb P^*}{d\tilde\mathbb P}=\frac{\tilde{\rho}_0(v)}{\rho_0(v)}\Psi(\tilde{x}_t)\]
van der Meulen, Schauer et al.
Ito stochastic process:
\[dx_t=b(t,x_t)dt+\sigma(t,x_t)dW_t\]
Bridge process:
\[dx^*_t=b(t,x^*_t)dt\\+a(t,x^*_t)\nabla_x\log \rho_t(x^*_t)dt+\sigma(t,x^*_t)dW_t\]
Score \(\nabla_x\log \rho_t\) intractable....
v.d. Meulen/Schauer bridges
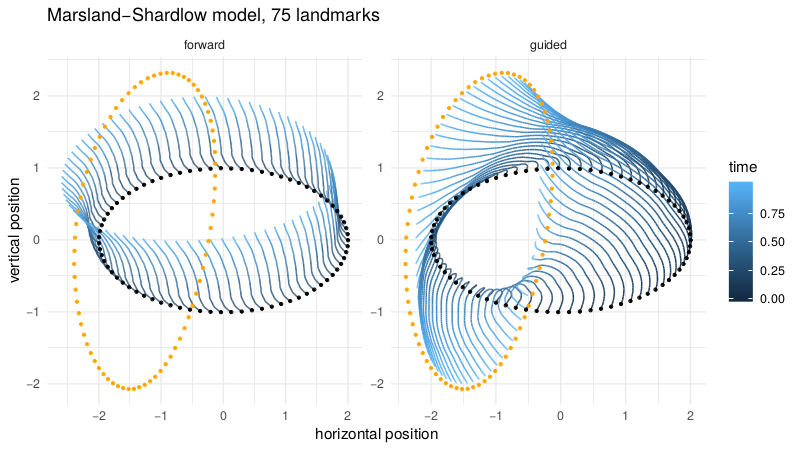
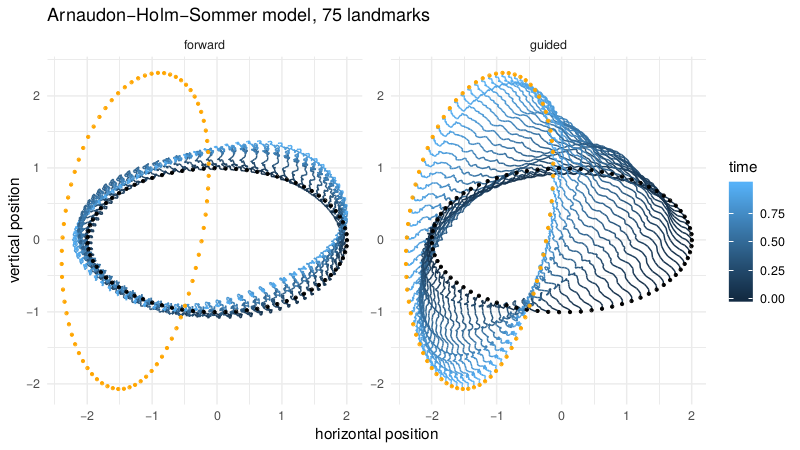
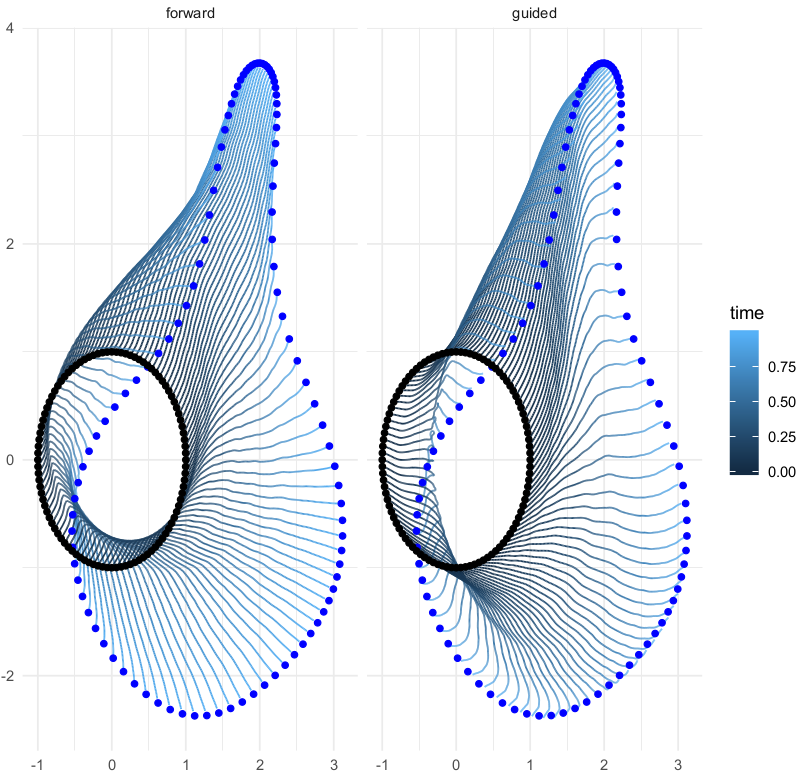
v.d. Meulen,Schauer,Arnaudon,Sommer,arxiv'21
Explicit guiding term
Delyon/Hu 2006:
\(\sigma\) invertible:
- guided bridge proposal$$dy_t = b(t,y_t)dt - \frac{y_t-v}{T-t}dt + \sigma(t,y_t)dW_t$$
- \(y_T=v\) a.s.
- \(x_t|x_T=v\) absolute continuous wrt. \(y_t\)
- \(\mathbb E_{x_t|x_T=v}[f(x_t)]\propto \mathbb E_{y_t}[f(y_t)\varphi(y_t)]\)

\(v\)
\(x_0\)
\(x_t\)
Simulation of Conditioned Semimartingales on Riemannian Manifolds
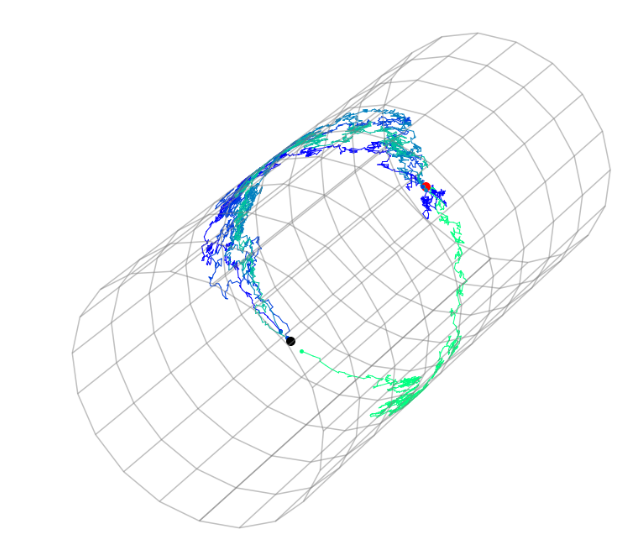
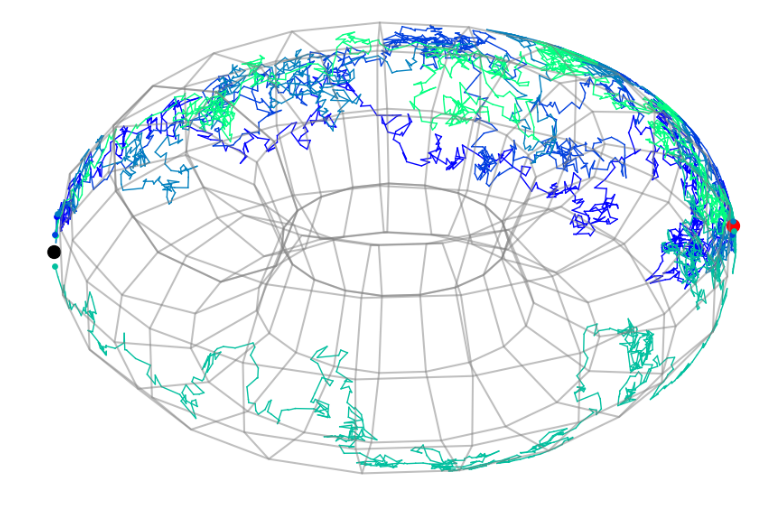
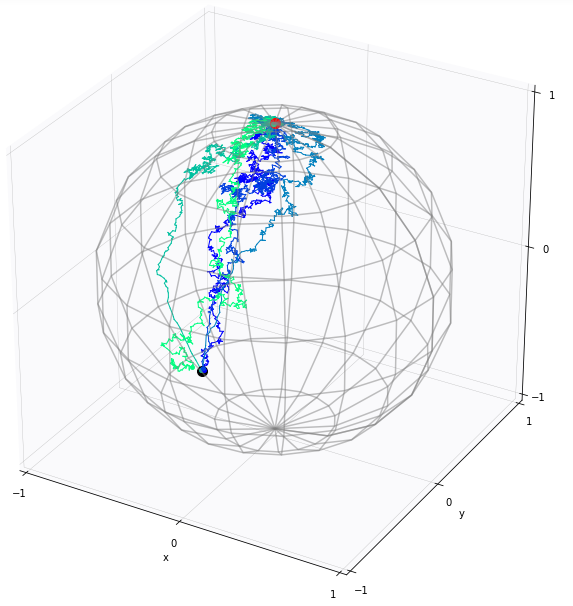
Jensen, Mallasto, Sommer 2019 ; Jensen, Sommer 2021, 2022
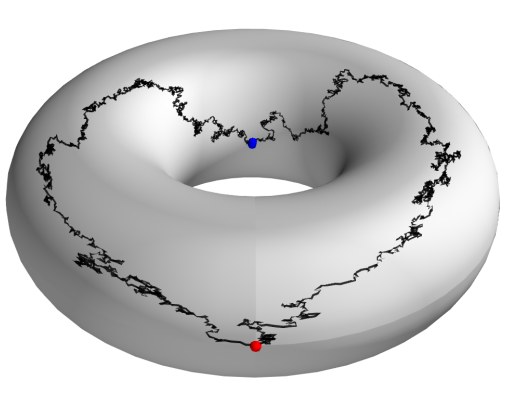
Simulation of Conditioned Semimartingales on Riemannian Manifolds

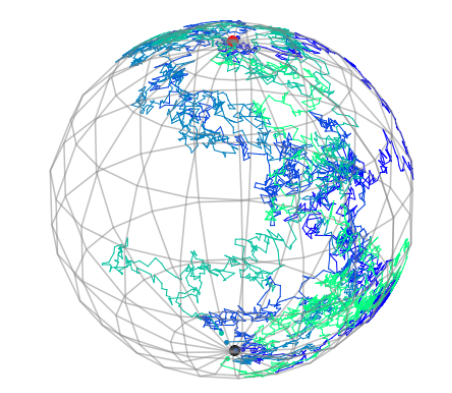
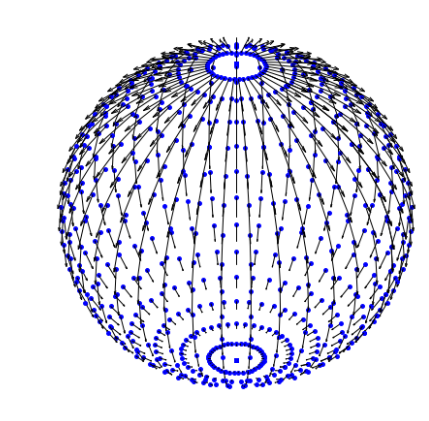
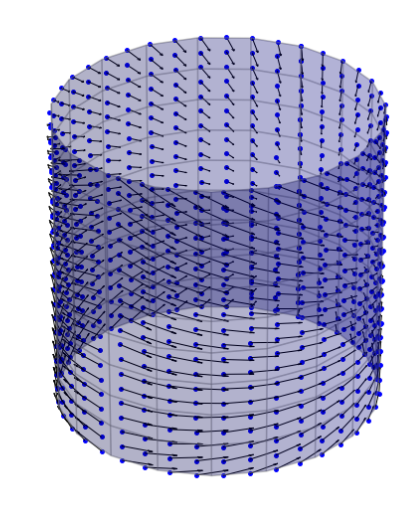
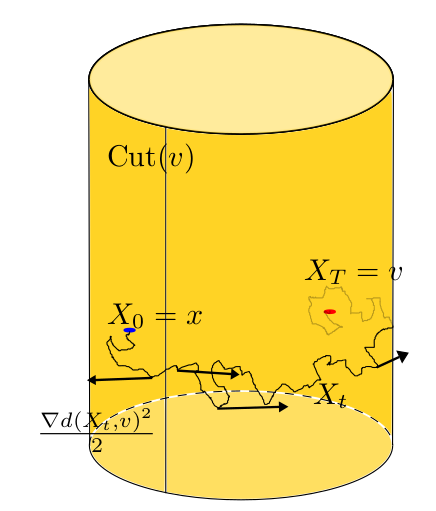
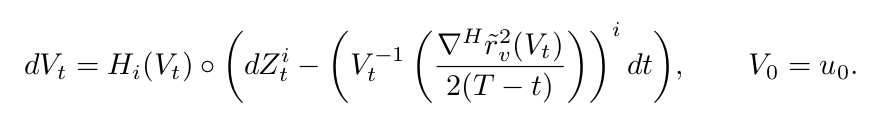
From edges to graphs
Bridge:
Leaf conditioning:
\(x_0\)
\(v\)
\(x_0\)
\(h\)
\(v_1\)
\(v_2\)

van der Meulen, Schauer + Soustrup, Nielsen, van der Meulen, Sommer
\(v_2\)
Backwards filtering, forward guiding
\(x_0\)
\(h\)
\(v_1\)
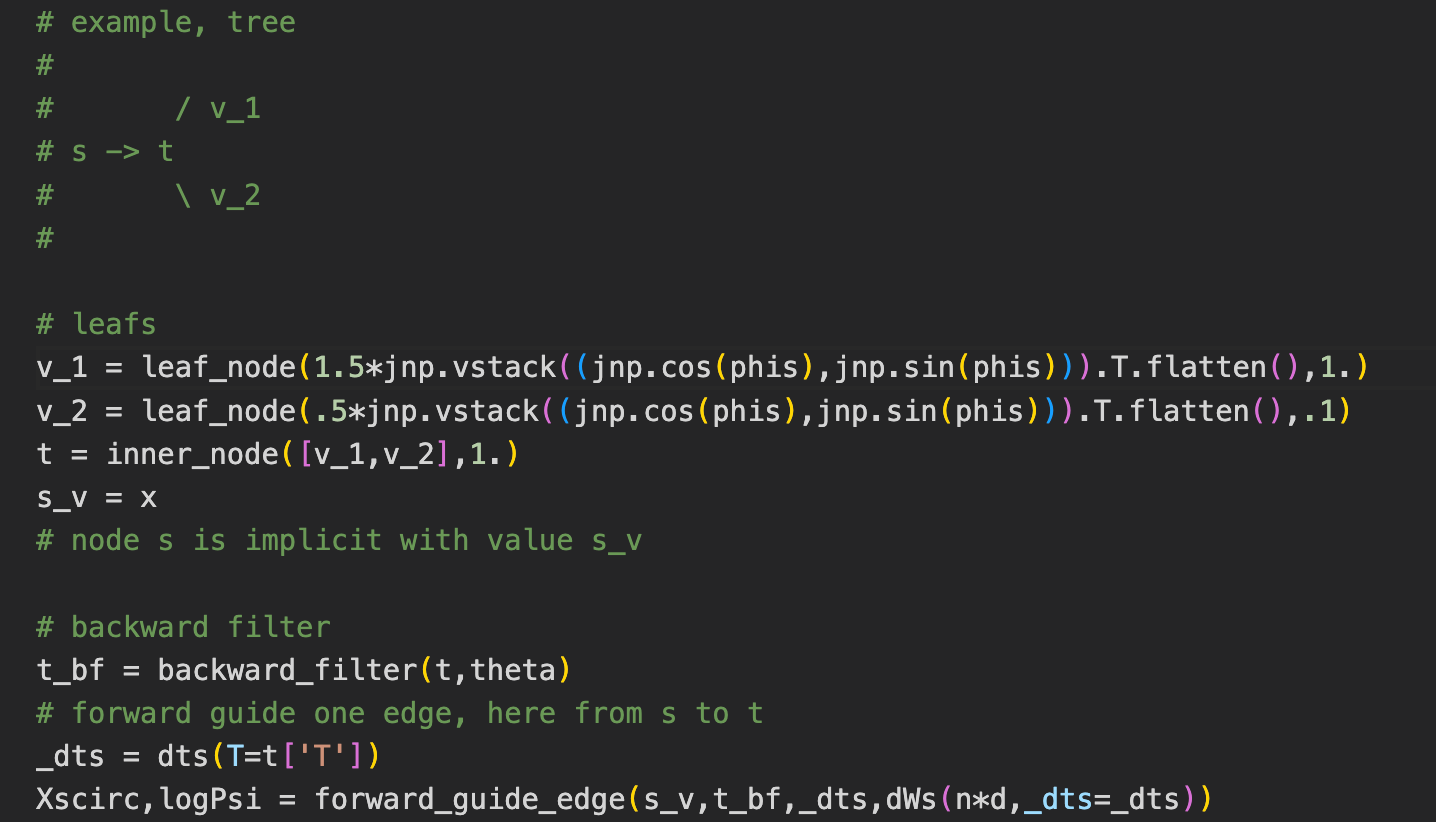

\(v_2\)
MCMC


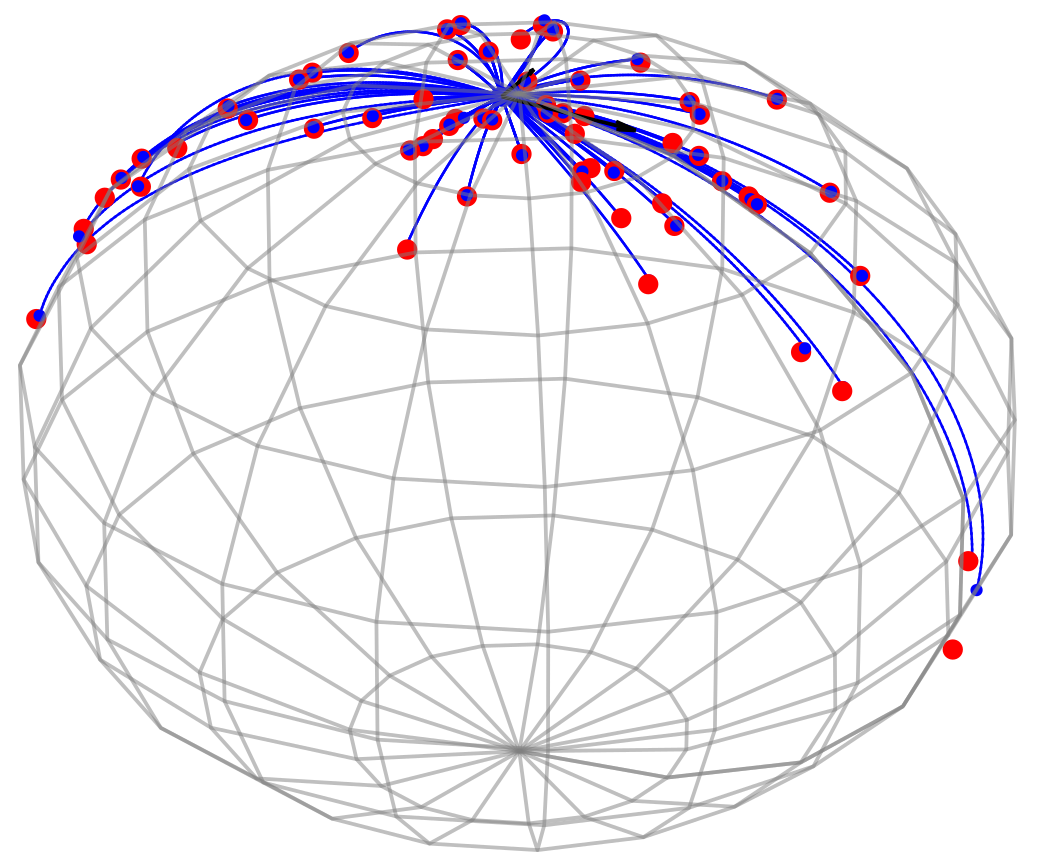
Diffusion mean on \(\mathbb S^2\)
- \(x_t\in M\) Brownian motion
- \(\theta=x_0\), \(y\sim x_T\)
- \(\bar{x}_{\mathrm{diffusion}}=\mathrm{argmax}_\theta\mathcal{L}(\theta)\)
Brownian motion starting point
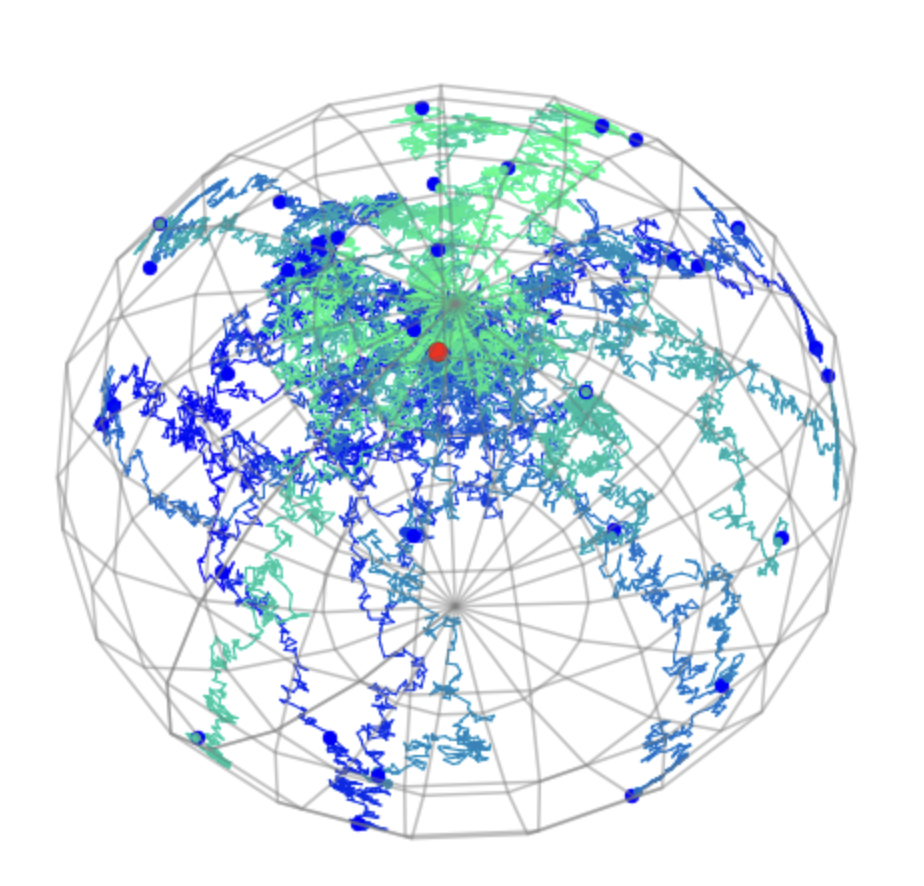
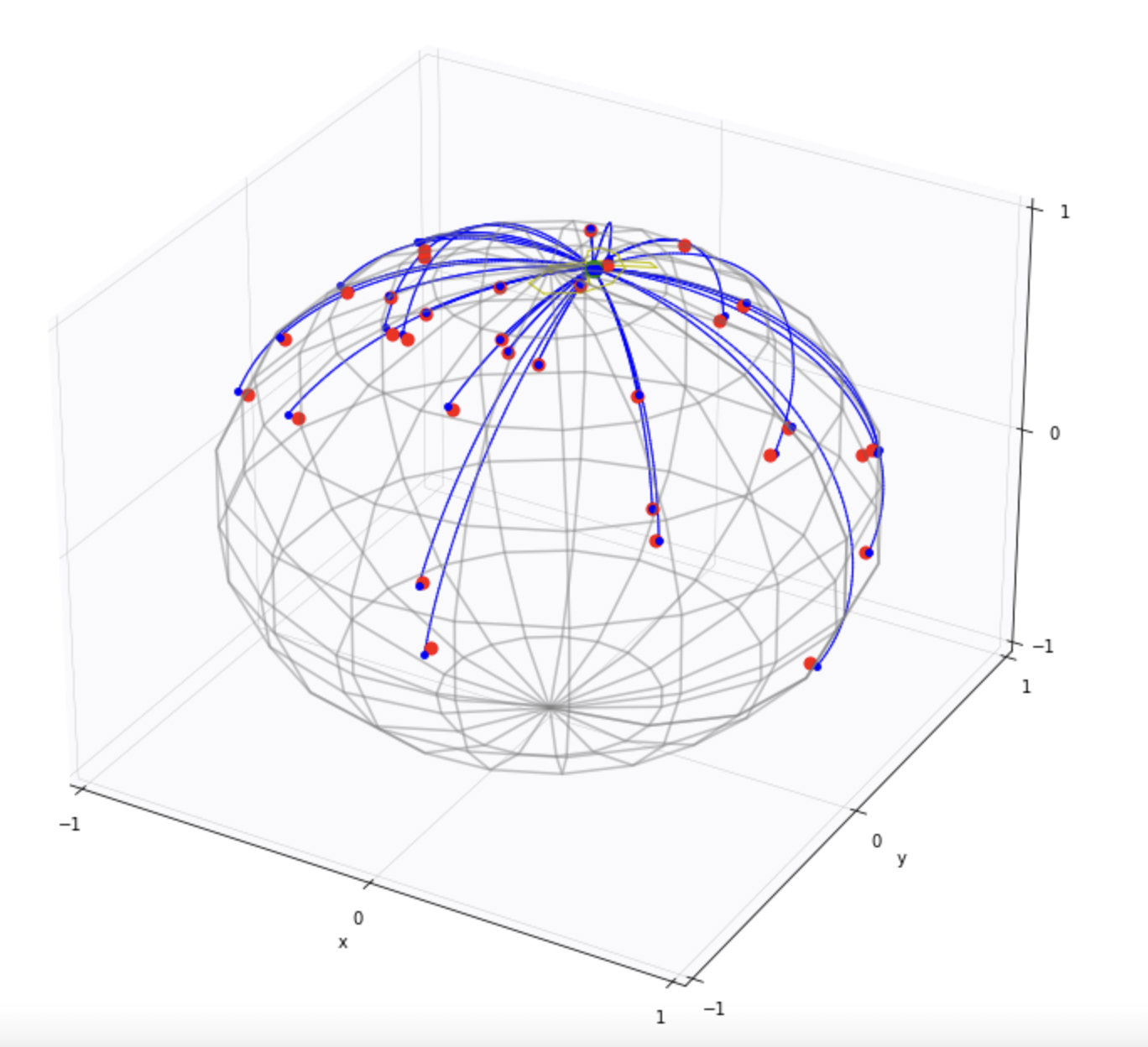
Geometry, stochastics, geometric statistics
code: http://bitbucket.com/stefansommer/jaxgeometry Centre for Computational Evolutionary Morphometry: http://www.ccem.dk
slides: https://slides.com/stefansommer Stochastic Morphometry: https://www.ccem.dk/stochastic-morphometry/
References:
- Eltzner, Hansen, Huckemann, Sommer: Diffusion Means in Geometric Spaces, Bernoulli, 2022, arXiv:2105.12061.
- Grong, Sommer: Most probable paths for anisotropic Brownian motions on manifolds, FoCM 2022, arXiv:2110.15634
- Højgaard, Joshi, Sommer: Discrete-Time Observations of Brownian Motion on Lie Groups and Homogeneous Spaces: Sampling and Metric Estimation, Algorithms, 2022, https://www.mdpi.com/1999-4893/15/8/290
- Jensen, Sommer: Mean Estimation on the Diagonal of Product Manifolds, Algorithms, 2022, https://www.mdpi.com/1999-4893/15/3/92
- Arnaudon, v.d. Meulen, Schauer, Sommer: Diffusion bridges for stochastic Hamiltonian systems and shape evolutions, SIIM, 2022, arXiv:2002.00885
- Hansen, Eltzner, Sommer: Diffusion Means and Heat Kernel on Manifolds, 2021, GSI 2021, arXiv:2103.00588.
- Højgaard Jensen, Sommer: Simulation of Conditioned Diffusions on Riemannian Manifolds, 2021, arXiv:2105.13190.
- Sommer, Bronstein: Horizontal Flows and Manifold Stochastics in Geometric Deep Learning, TPAMI, 2020, doi: 10.1109/TPAMI.2020.2994507
- Arnaudon, Holm, Sommer: A Geometric Framework for Stochastic Shape Analysis, Foundations of Computational Mathematics, 2019, arXiv:1703.09971.
- Højgaard Jensen, Mallasto, Sommer: Simulation of Conditioned Diffusions on the Flat Torus, GSI 2019., arXiv:1906.09813.
- Sommer, Svane: Modelling Anisotropic Covariance using Stochastic Development and Sub-Riemannian Frame Bundle Geometry, JoGM, 2017, arXiv:1512.08544.
- Sommer: Anisotropically Weighted and Nonholonomically Constrained Evolutions, Entropy, 2017, arXiv:1609.00395 .
- Sommer, Svane: Modelling Anisotropic Covariance using Stochastic Development and Sub-Riemannian Frame Bundle Geometry, JoGM, 2017, arXiv:1512.08544.
- Sommer: Anisotropically Weighted and Nonholonomically Constrained Evolutions, Entropy, 2017, arXiv:1609.00395 .
- Arnaudon, Holm, Sommer: A Stochastic Large Deformation Model for Computational Anatomy, IPMI 2017, arXiv:1612.05323.
- Sommer: Anisotropic Distributions on Manifolds: Template Estimation and Most Probable Paths, IPMI 2015, doi: 10.1007/978-3-319-19992-4_15.

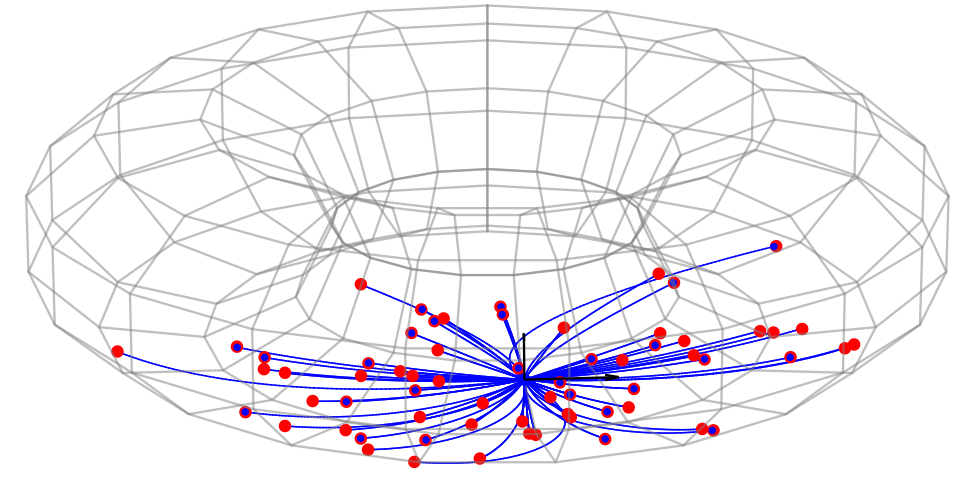


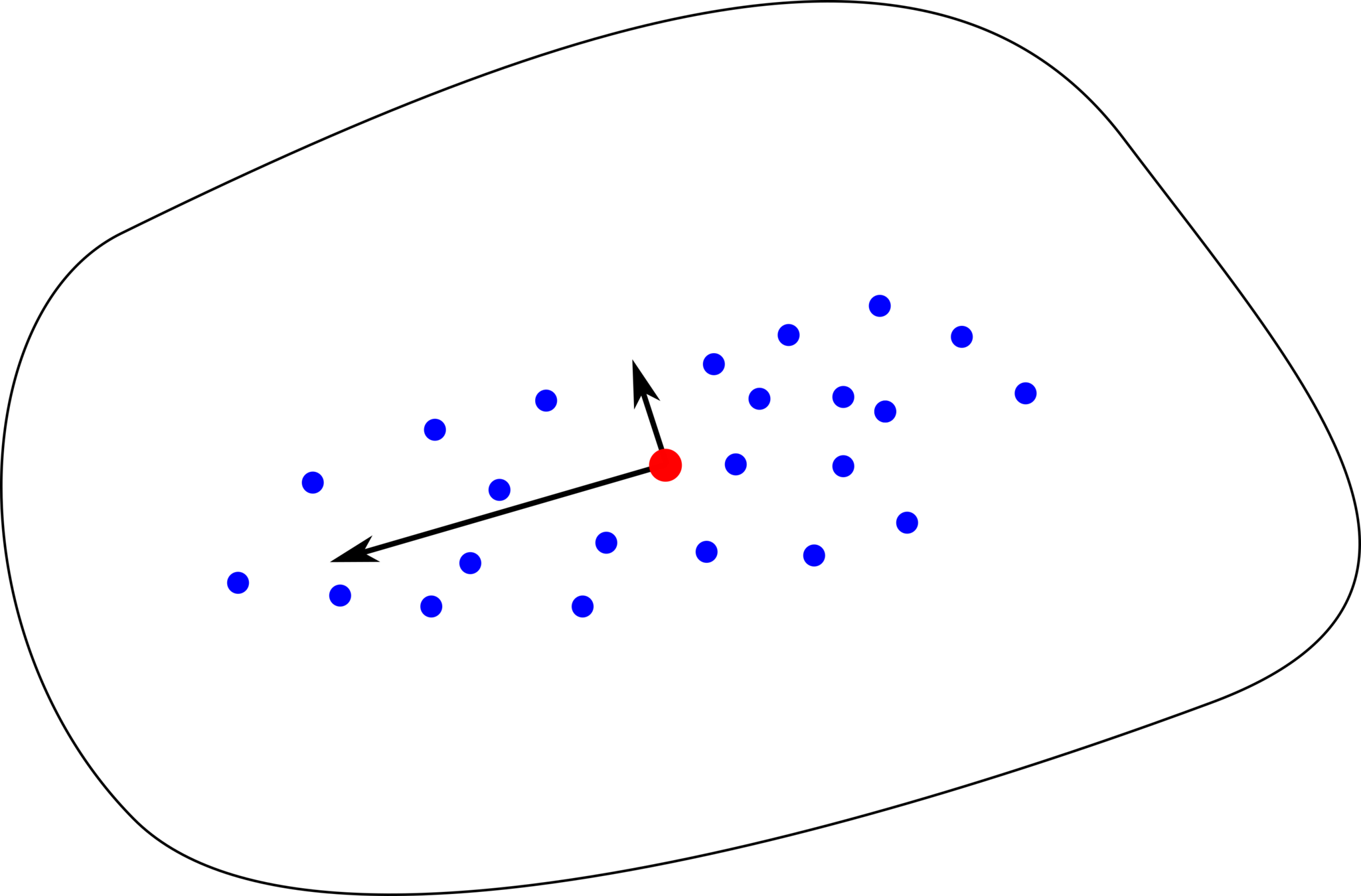
- parametric families of probability distributions \(\mu_\theta\)
- likelihood from density:
\(\quad\mathcal{L}(\theta; y_1,\ldots,y_N)=\prod_{i=1}^Np_\theta(y_i)\) - ML/MAP estimates:
\(\quad\bar{\theta}=\mathrm{argmax}_\theta\mathcal{L}(\theta; y_1,\ldots,y_N)\)
- Diffusion mean:
\(\quad x_t\in M\) Brownian motion
\(\quad\theta=x_0\) - assume \(y\sim x_T\):
\(\quad\bar{x}_{\mathrm{diffusion}}=\mathrm{argmax}_\theta\mathcal{L}(\theta)\)
Generalization of Euclidean statistical notions and techniques.
- i.i.d. samples \(y_1,\ldots,y_N\in M\)
- Fréchet mean:
\(\bar{x}=\mathrm{argmin}_{x\in M}\sum_{i=1}^Nd(x,y_i)^2\)
Nye, White, JMIV'14;
Sommer,IPMI'15; Sommer,Svane,JGM'15;
Hansen,Eltzner,Huckemann,Sommer,GSI'21,'21
Means in geometric statistics
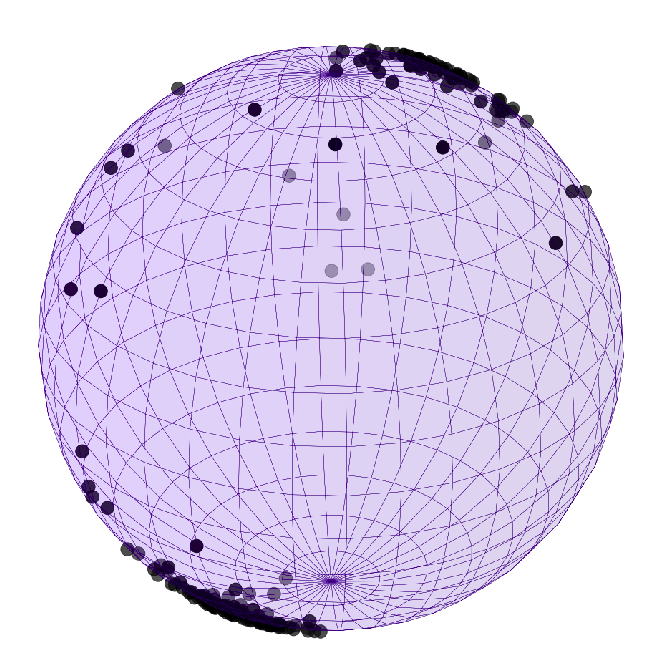
Uniqueness and asymptotics
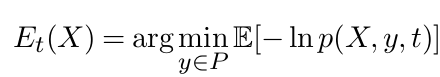
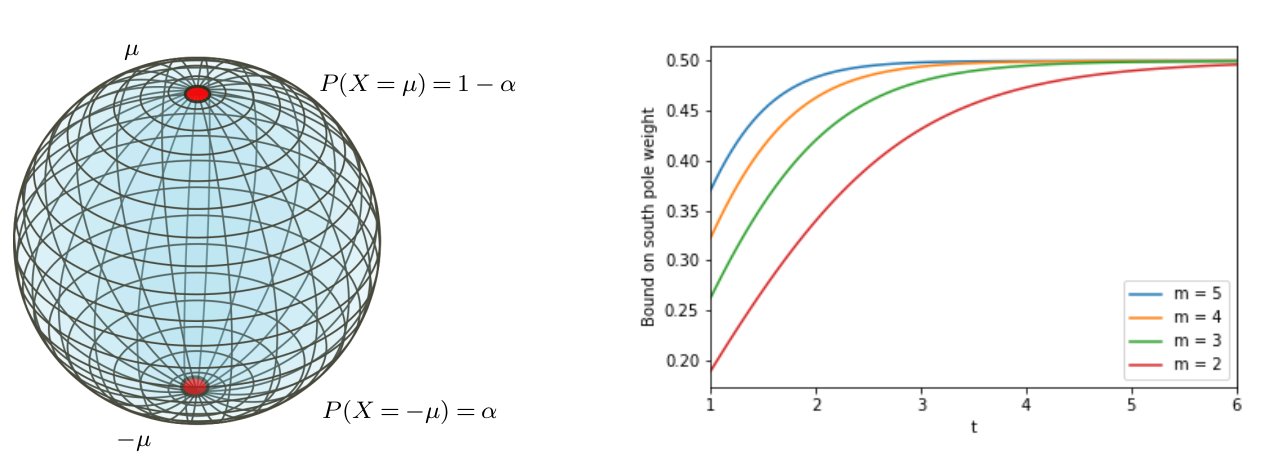
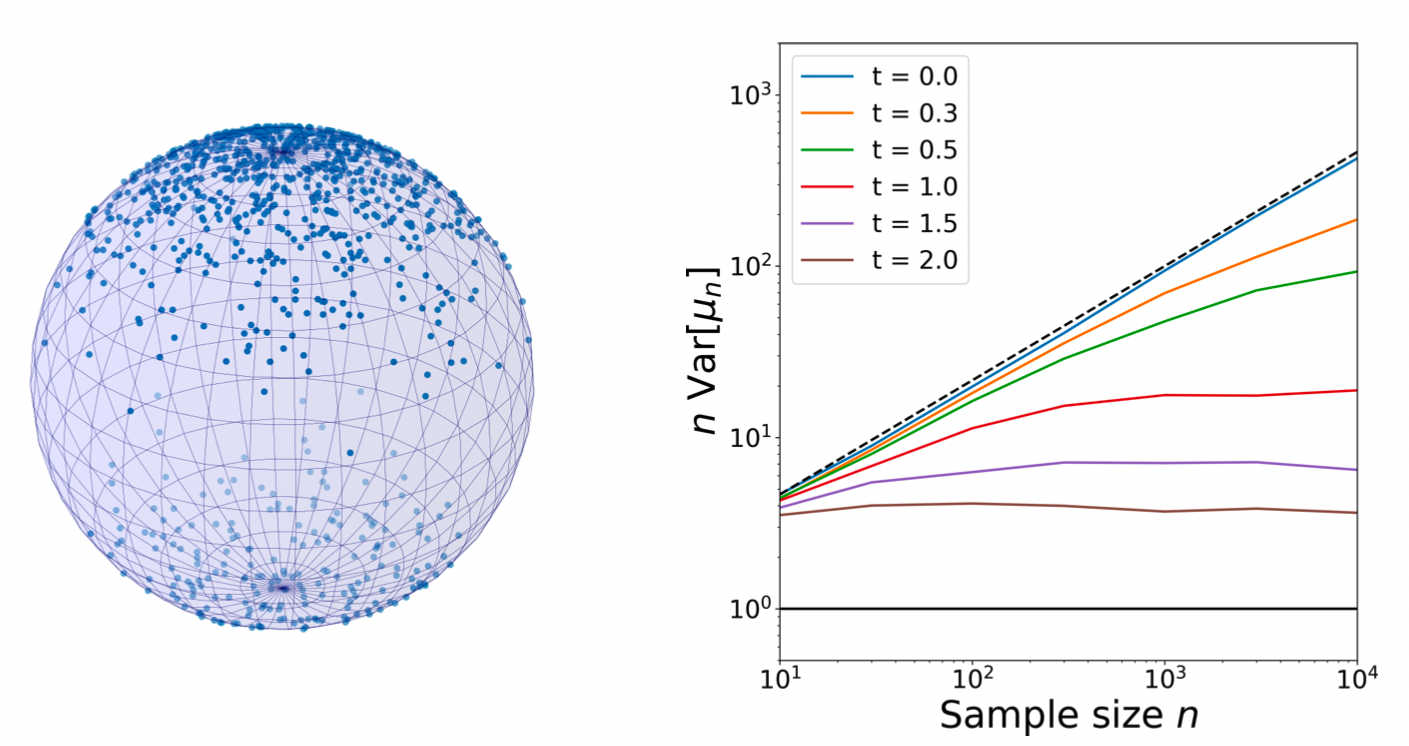
Estimating diffusion mean and diffusion variance
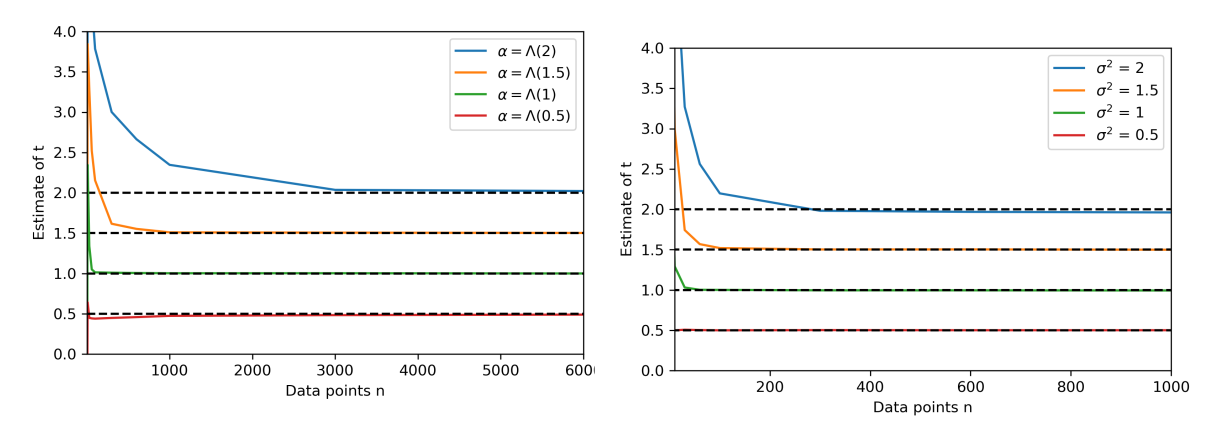
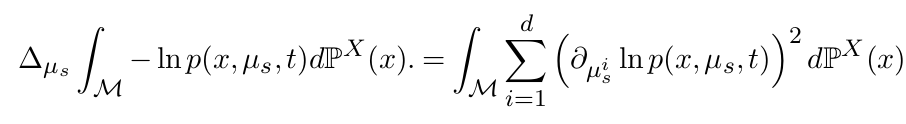
smeary at optimal \(t\)?
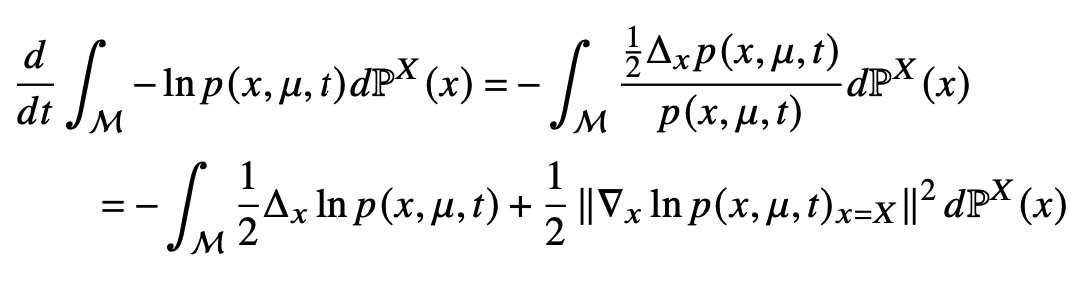
Brownian motion samples
two-pole distribution
Finite sample size smeariness
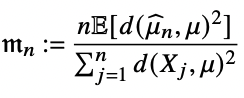
variance modulation:
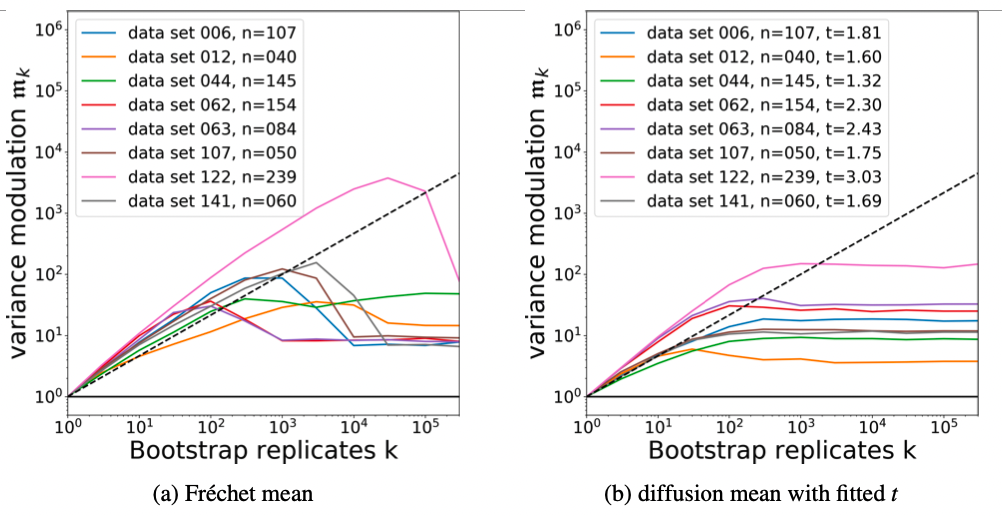
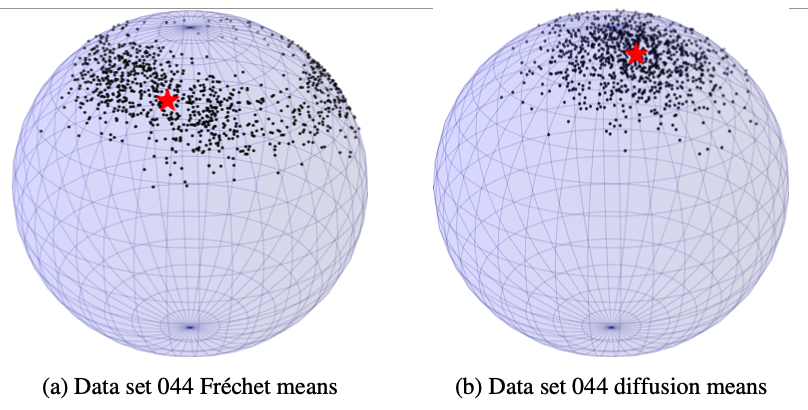
Can we avoid directional smeariness?
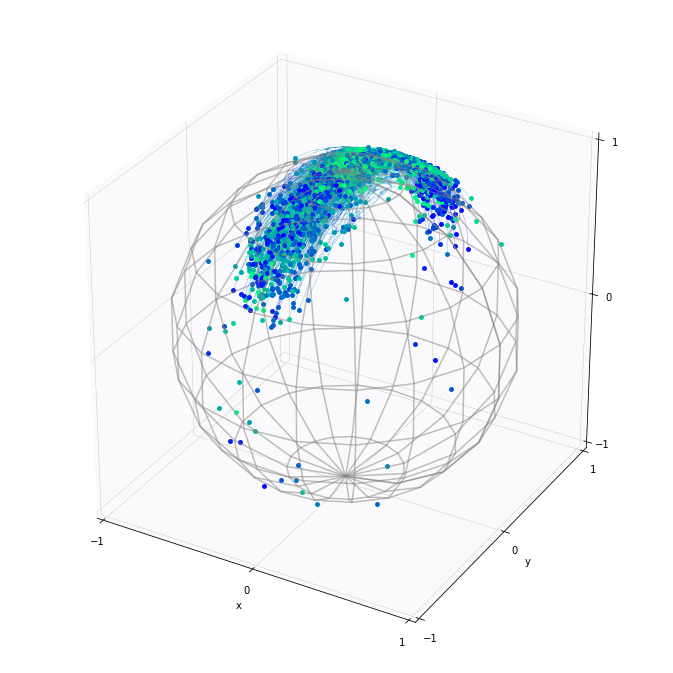
non-trivial covariance: fit anisotropic normal distributions