Diffusions means in geometric statistics

Stefan Sommer, University of Copenhagen

Faculty of Science, University of Copenhagen

BIMSA, Yanqi Lake, 2023

shapes - geometric statistics - stochastics - diffusion means

w/ Erlend Grong, Alexis Arnaudon, Darryl Holm, Sarang Joshi, Frank v.d. Meulen, Moritz Schauer, Benjamin Eltzner, Stephan Huckemann, Line Kuhnel, Mathias H. Jensen, Pernille E.H. Hansen, Mads Nielsen, Rasmus Nielsen, Christy Hipsley

Villum foundation

Novo nordisk foundation

University of Copenhagen

Statistical shape analysis

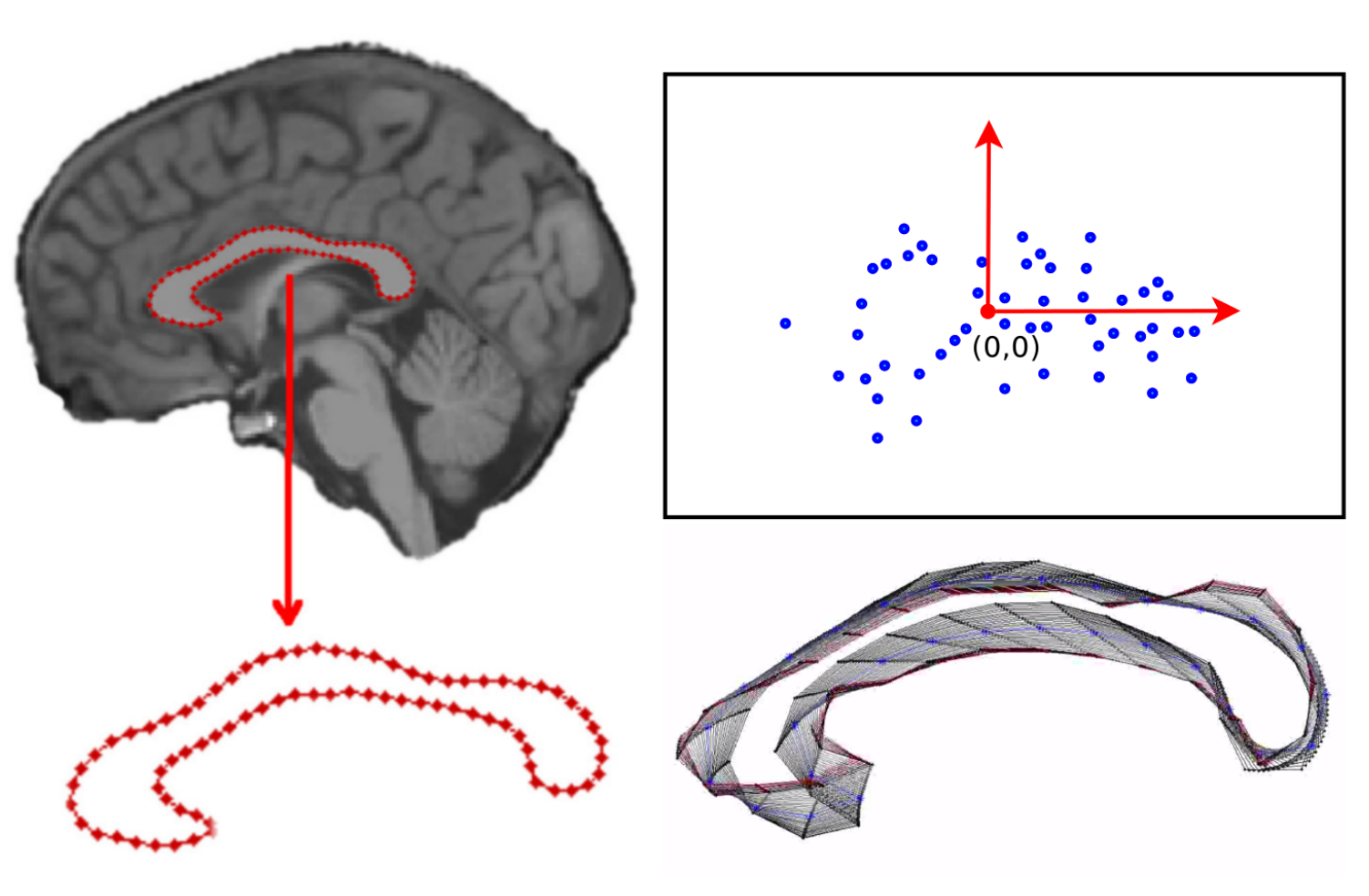
Deformations and shape

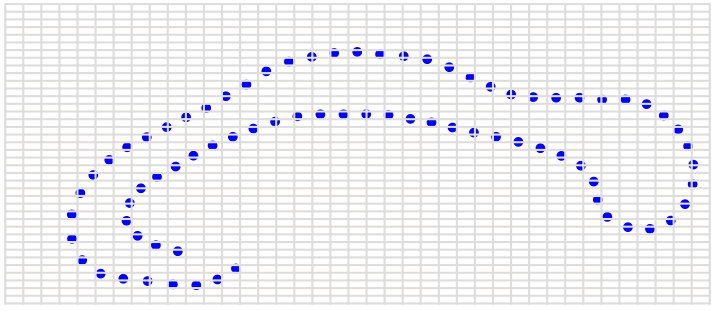
E_{s_0,s_1}(\phi)=R(\phi)+\frac1\lambda S(\phi.s_0,s_1)

action: \(\phi.s=\phi\circ s\)         (shapes)
             \(\phi.s=s\circ\phi^{-1}\)     (images)

\( \phi \)

\( \phi \) warp of domain \(\Omega\) (2D or 3D space)

landmarks: \(s=(x_1,\ldots,x_n)\)

curves: \(s: \mathbb S^1\to\mathbb R^2\)

surfaces: \(s: \mathbb S^2\to\mathbb R^3\)

Riemannian view

R(\phi_t)=\int_0^T\|\partial_t \phi_t\|_{\phi_t}^2dt

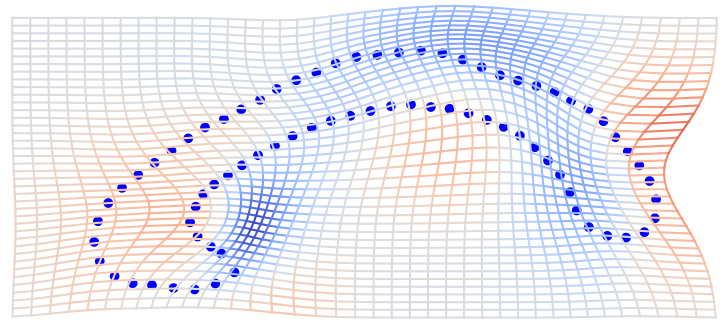
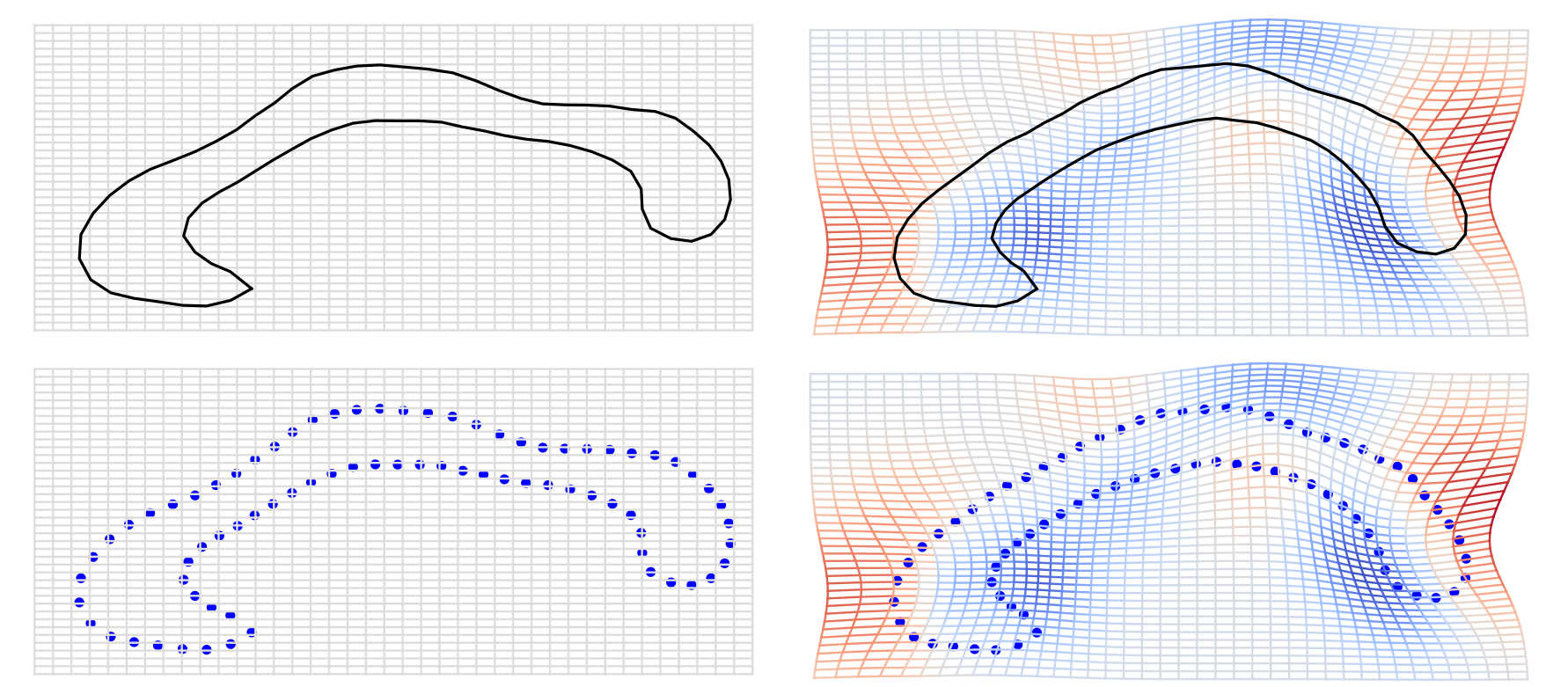
\( \phi_t:[0,T]\to\mathrm{Diff}(\Omega) \) path of diffeomorphisms (parameter t)

\mathrm{Diff}(\Omega)
\mathrm{Id}_{\mathrm{Diff}(\Omega)}
\varphi_t

LDDMM: Grenander, Miller, Trouve, Younes, Christensen, Joshi, et al.

Evolution with noise

\partial_t \phi_t = F(\phi_t)\ \to\ d\phi_t=F(\phi_t)dt\color{blue}{+\sigma(\phi_t) dW_t}
\mathrm{Diff}(\Omega)
\mathrm{Id}_{\mathrm{Diff}(\Omega)}
\phi_t

Markussen,CVIU'07; Budhiraja,Dupuis,Maroulas,Bernoulli'10
Trouve,Vialard,QAM'12;Vialard,SPA'13;Marsland/Shardlow,SIIMS'17
Arnaudon,Holm,Sommer,IPMI'17; FoCM'18; JMIV'19
Arnaudon,v.d. Meulen,Schauer,Sommer'21

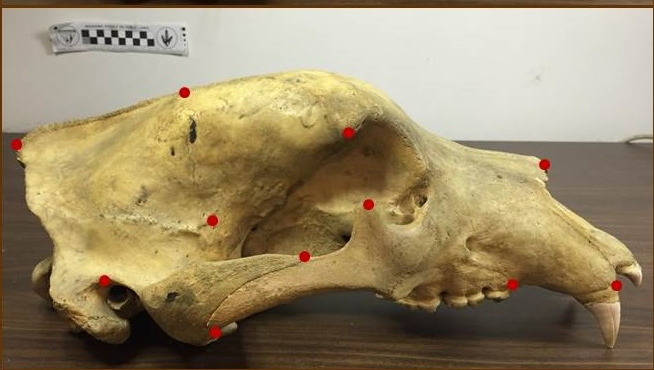
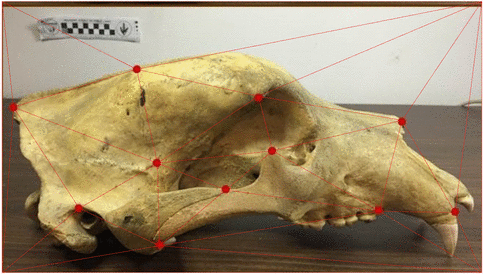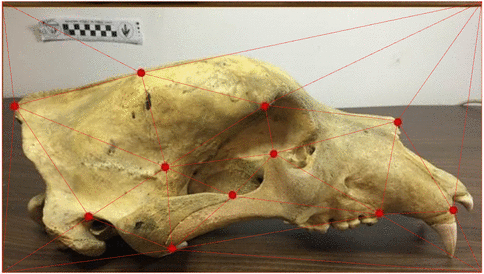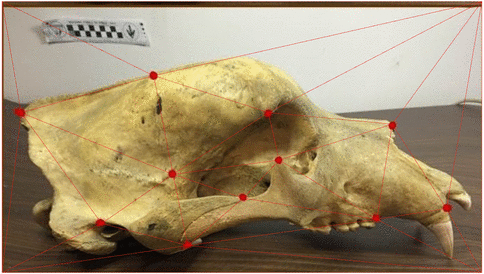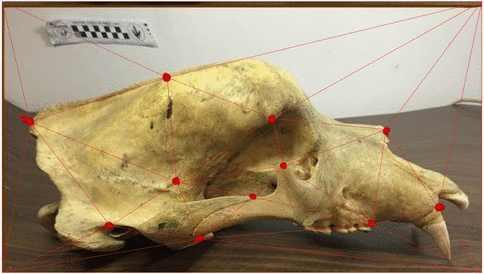
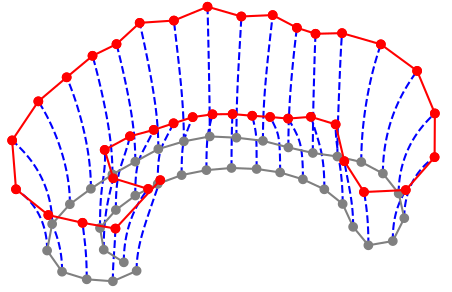
Stochastic morphometry along phylogenies

v.d. Meulen,Schauer,Arnaudon,Sommer, SIIMS 21

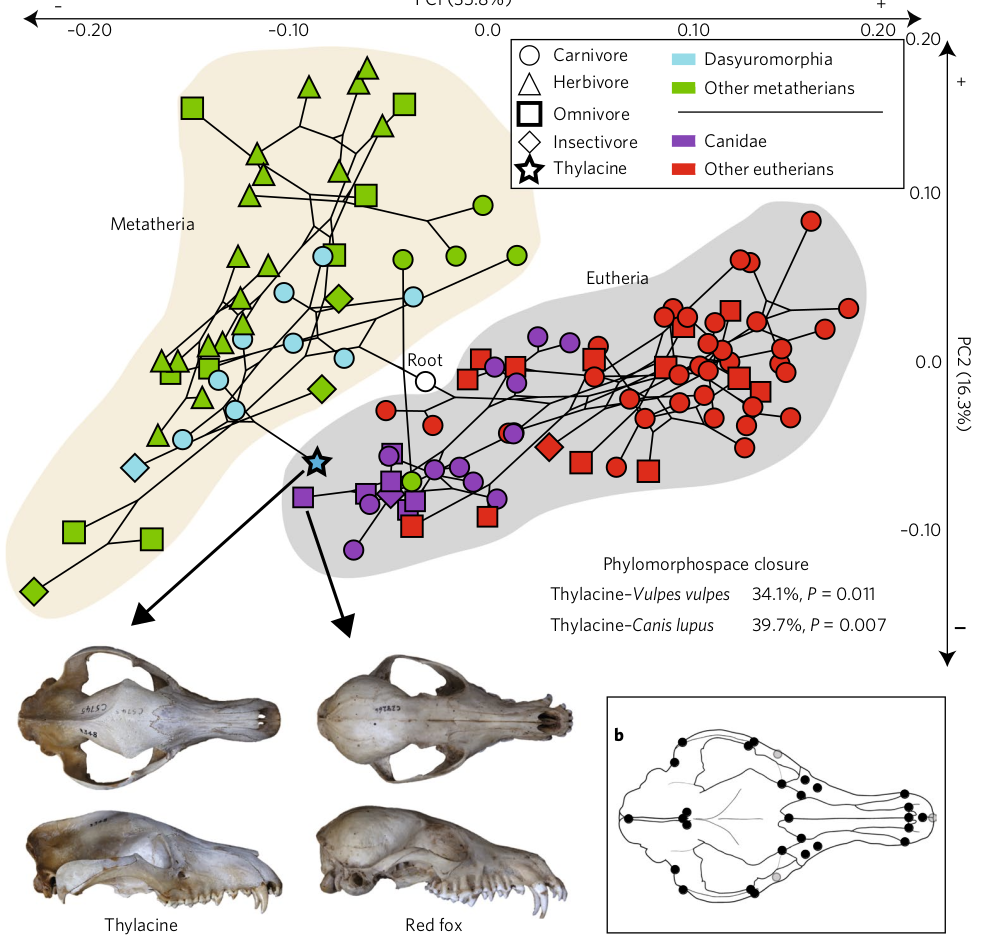
Center for Computational Evolutionary Morphometrics

w/ Rasmus Nielsen

Least-squares \(\leftrightarrow\) probabilistic

Deterministic:

  • \(\phi_t\) geodesic evolution
  • square distances:
    \(\quad d(s_0,s1)^2\)
  • Riemannian least-
    squares

Stochastic:

  • \(\phi_t\) stochastic process
  • (log) transition density
    \(\quad -\log p_T(s_1; s_0)\)
  • ML/MAP
  • bridge:
    \(\quad \phi_t|\phi_T.s_0=s_1\)
  • bridge + noise in observation:
    \(\quad \phi_t|\phi_T.s_0+\epsilon=s_1\)

Geometric data: Directional statistics

Plane directions:      \(\mathbb{S}^1\)

Geographical data:  \(\mathbb{S}^2\)

3D directions:           \(\mathrm{SO}(3), \mathbb{S}^2\)

Angles:                       \(\mathbb{T}^N\)

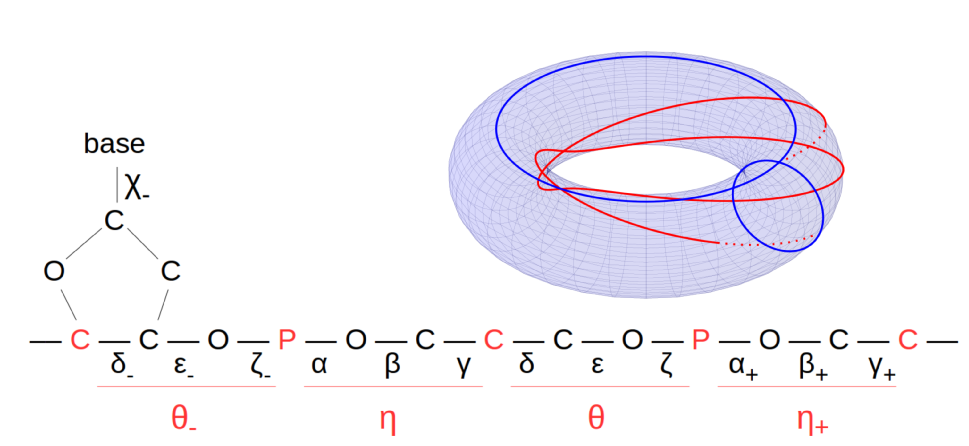
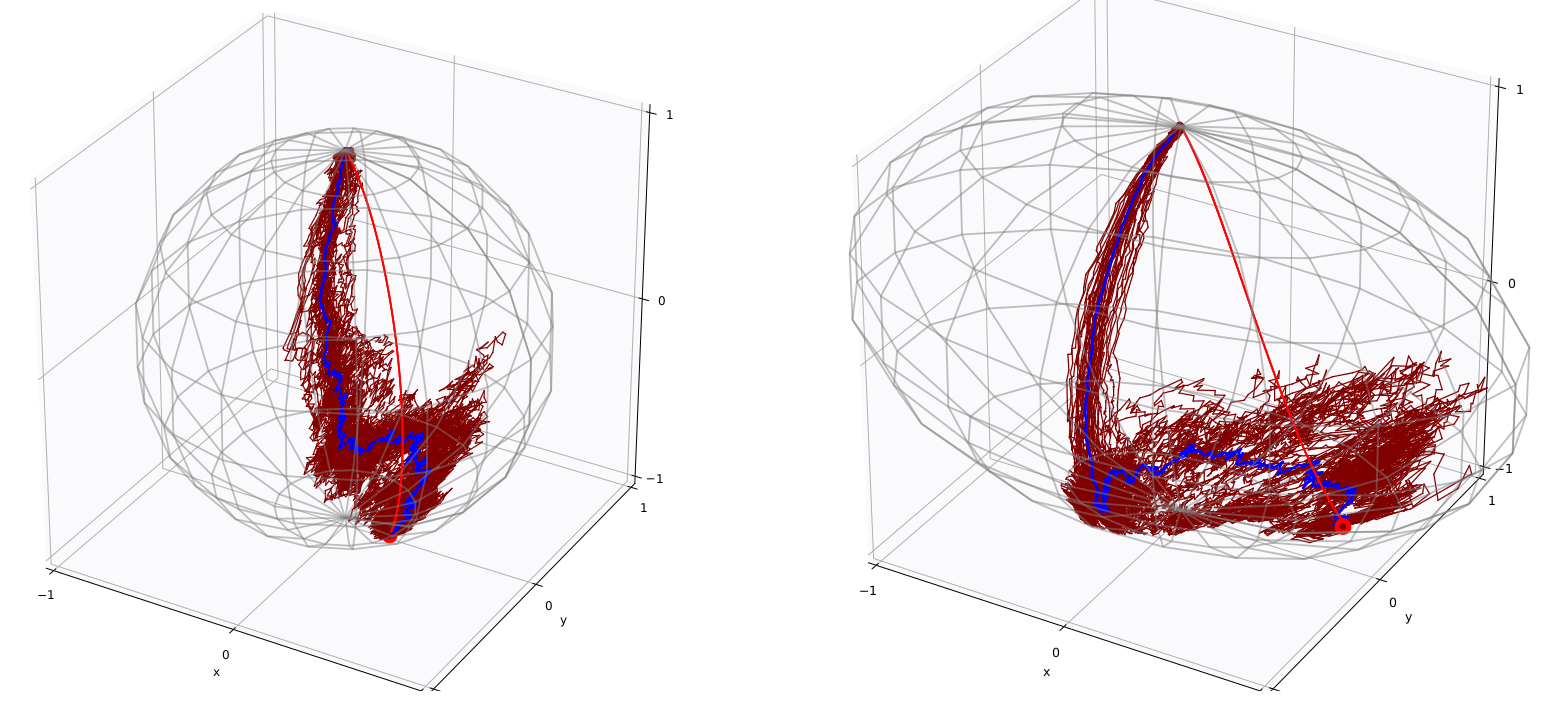
Simulation of Conditioned Semimartingales on Riemannian Manifolds

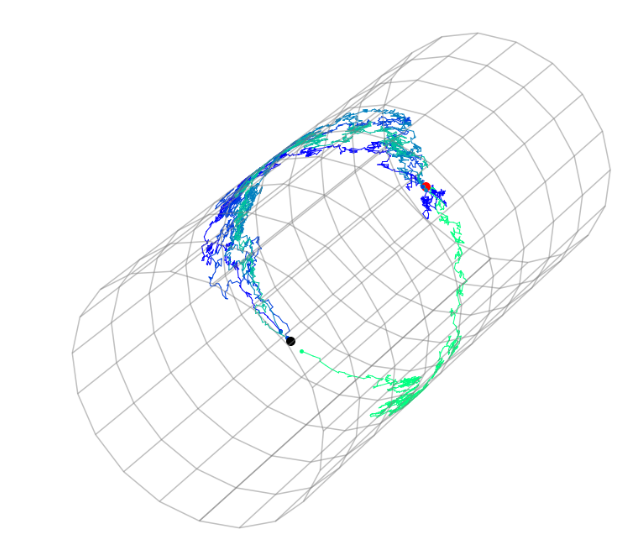
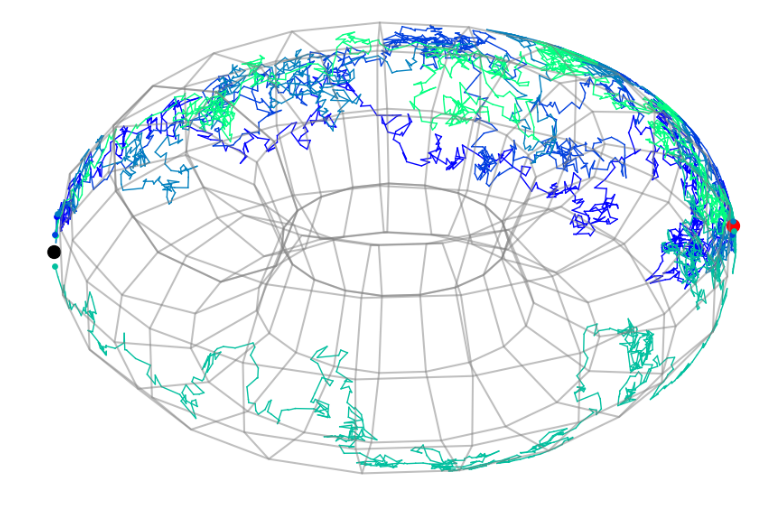
Jensen, Mallasto, Sommer 2019 ; Jensen, Sommer 2021, 2022

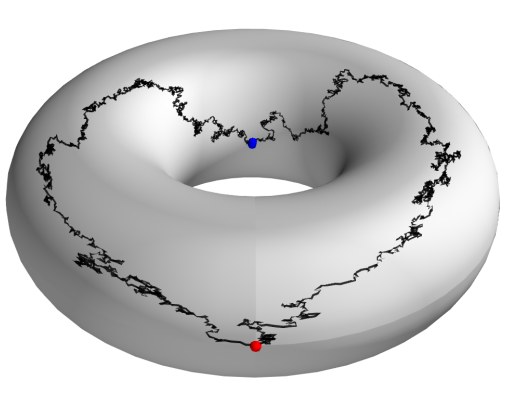
Bridges without auxiliary processes

dx_t = b(t,x_t)dt +\sigma(t,x_t)dW_t

Delyon/Hu 2006:

\(\sigma\) invertible:

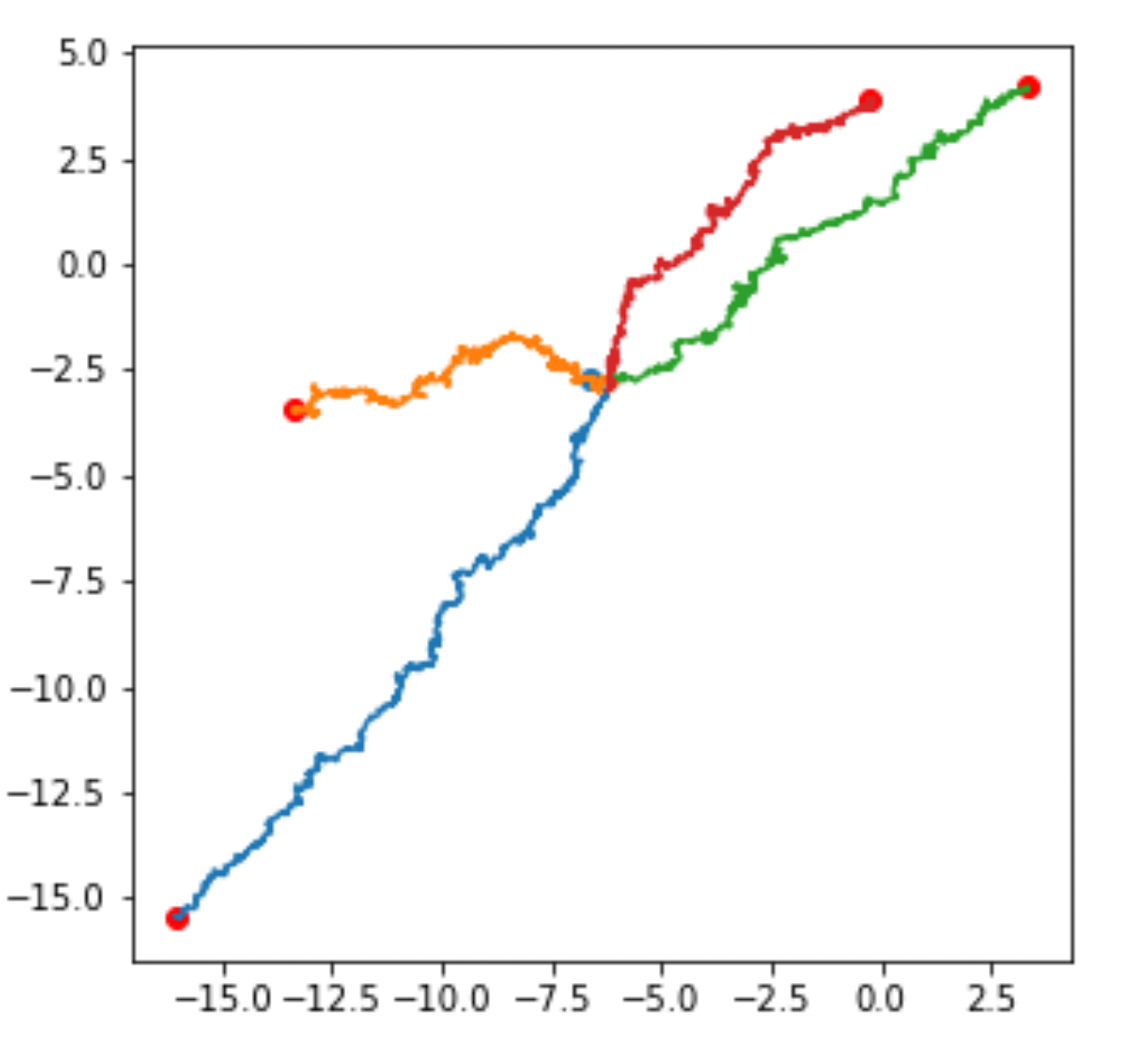
  • guided bridge proposal$$dy_t = b(t,y_t)dt - \frac{y_t-v}{T-t}dt + \sigma(t,y_t)dW_t$$
  • \(y_T=v\) a.s.
  • \(x_t|x_T=v\) absolute continuous wrt. \(y_t\)
  • \(\mathbb E_{x_t|x_T=v}[f(x_t)]\propto \mathbb E_{y_t}[f(y_t)\varphi(y_t)]\)

\(v\)

\(x_0\)

\(x_t\)

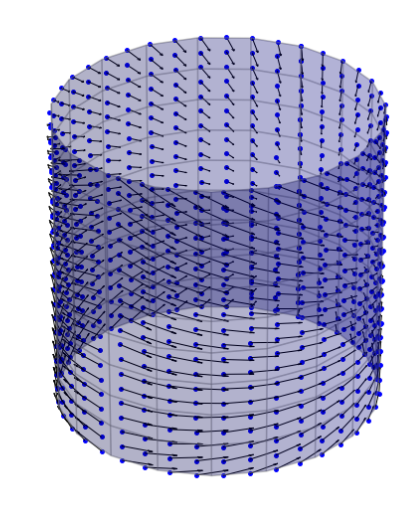
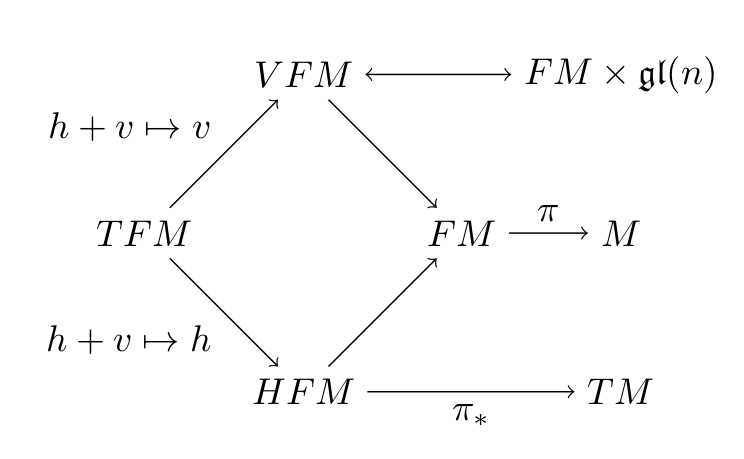
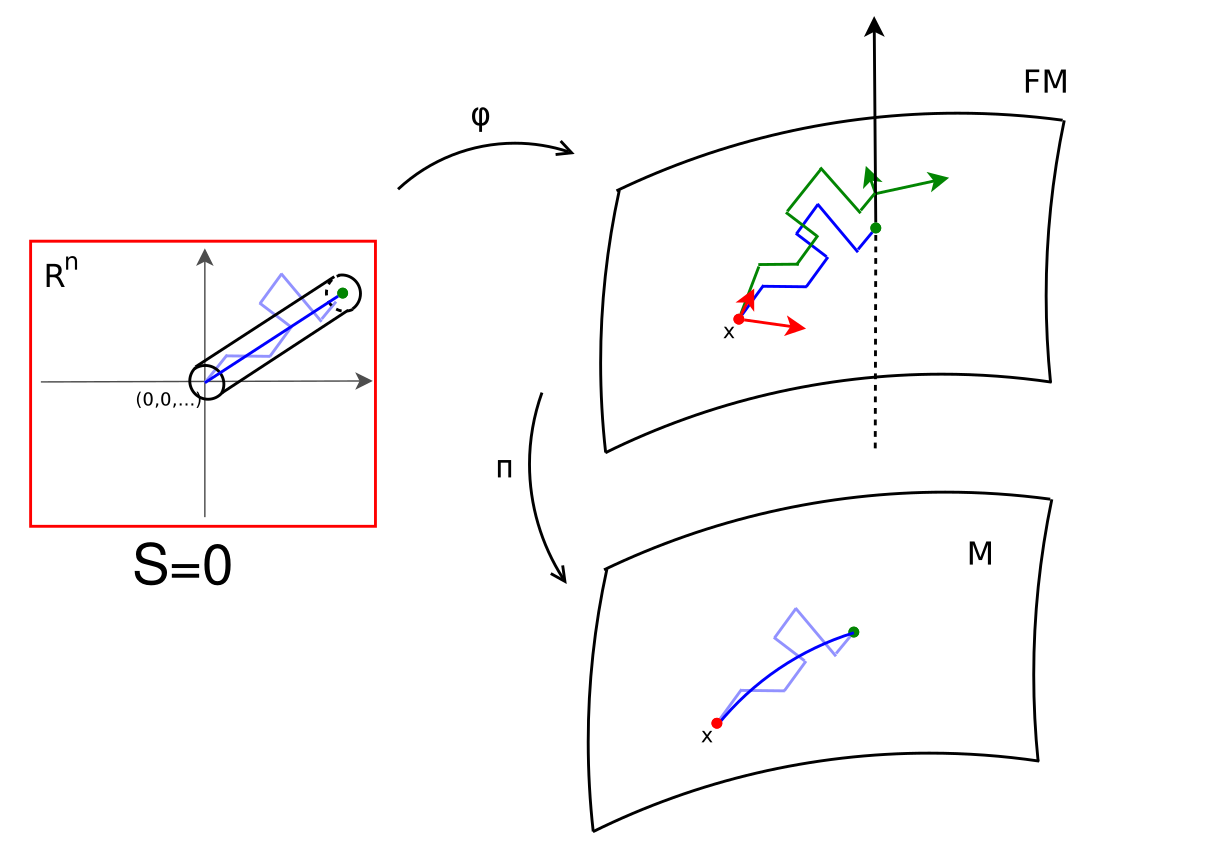
Frame bundles

  • \(\pi:FM\to M\) is the bundle of linear frames, i.e.
    \(u=(u_1,\ldots,u_d)\in FM\) is an ordered basis for \(T_xM\), \(x=\pi(u)\)
  • \(FM\) is a \(\mathrm{GL}(n)\) principal bundle: \(u:\mathbb R^d\to T_x M\) linear, invertible
  • \(OM\) the subbundle of orthonormal frames (orientations)
  • horizontal lift \(h_u:T_xM\to H_uFM\) and fields: \(H_i:FM\to TFM\)

          \(h_u=(\pi_*|_{H_uFM})^{-1}\)
          \(H_i(u)=h_u(ue_i)\)

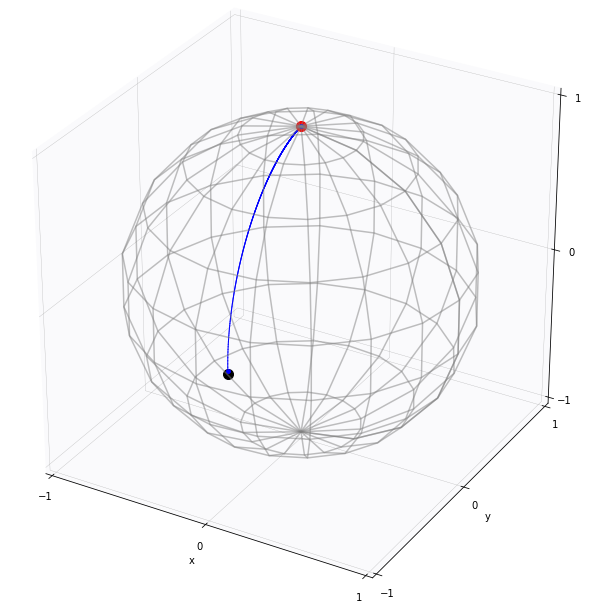
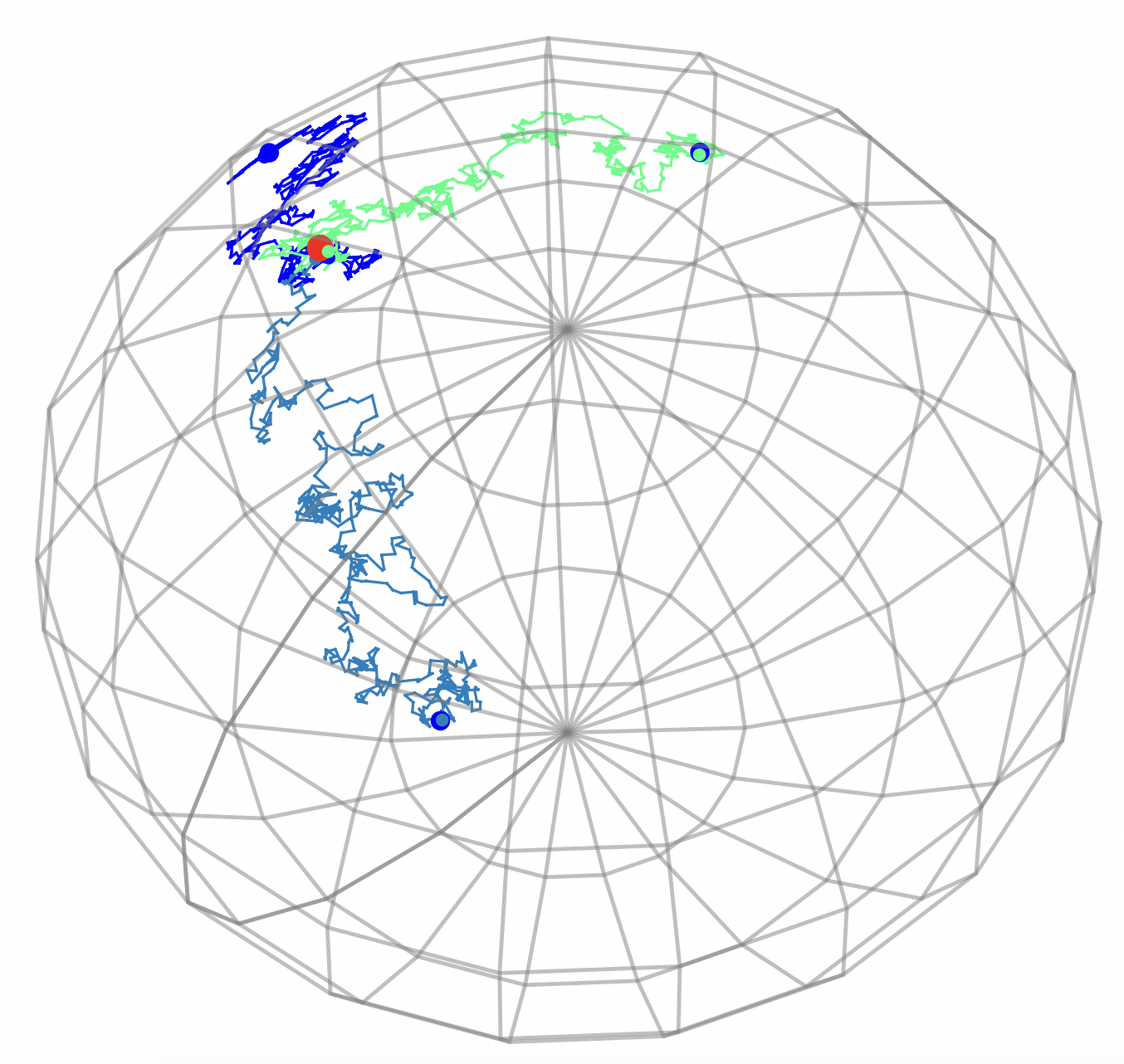
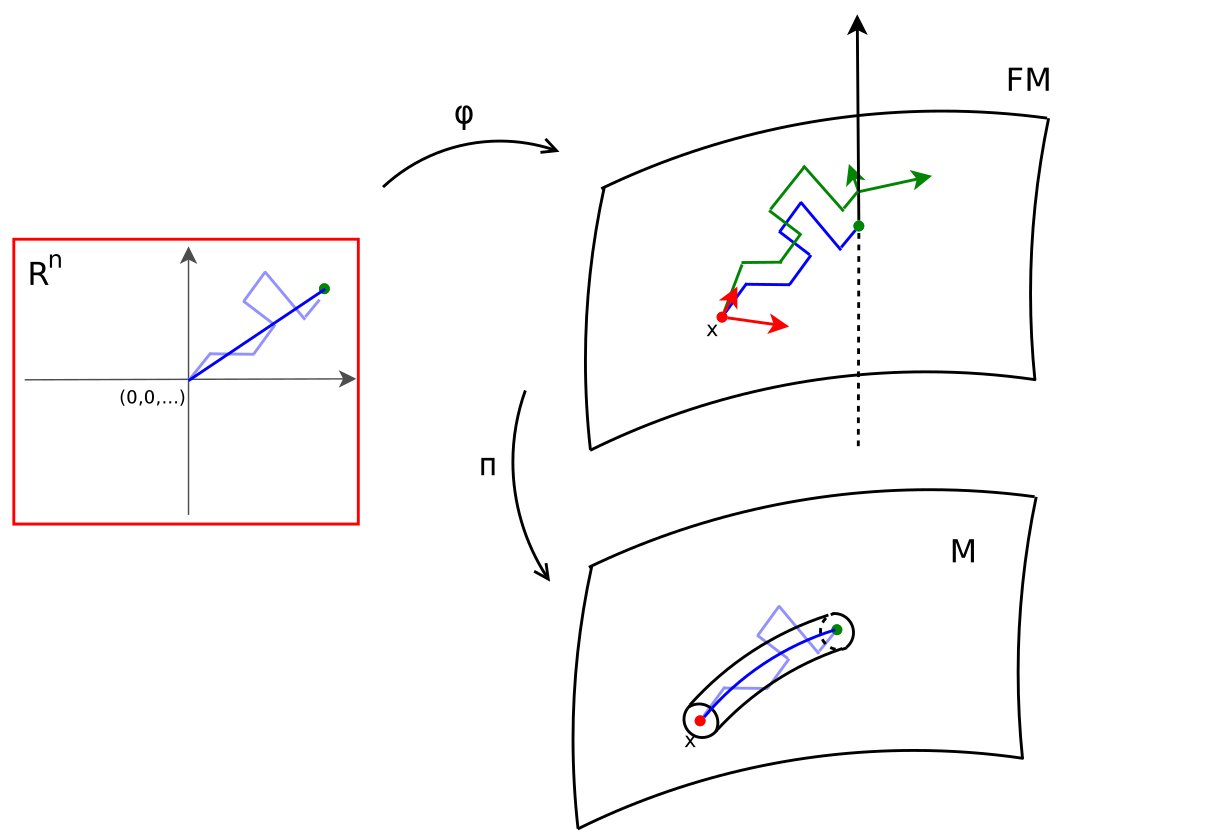
Stochastic development

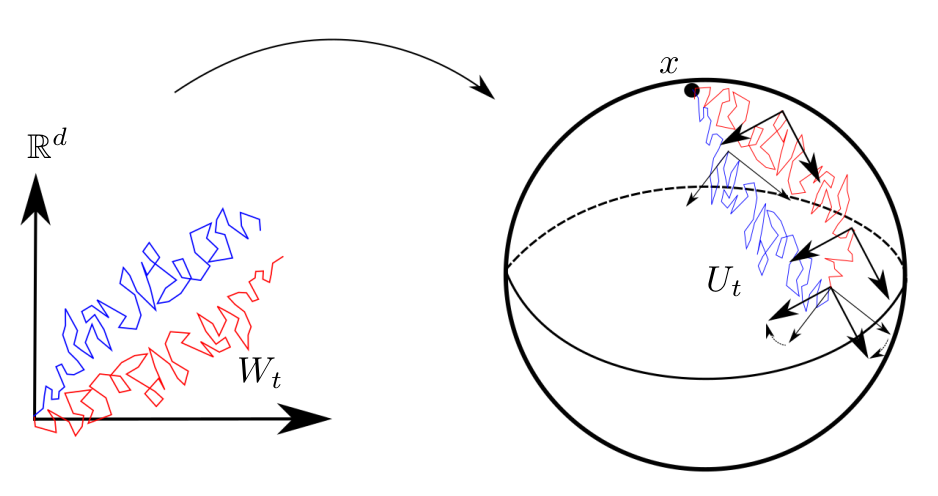
Stochastic development:

    \(dU_t=\sum_{i=1}^d H_i(U_t)\circ_{\mathcal S} dW_t^i\)

\(W_t\) Euclidean Brownian motion

\(X_t=\pi(U_t)\) Riemannian Brownian motion

\(U_t\) is stochastically parallel transported

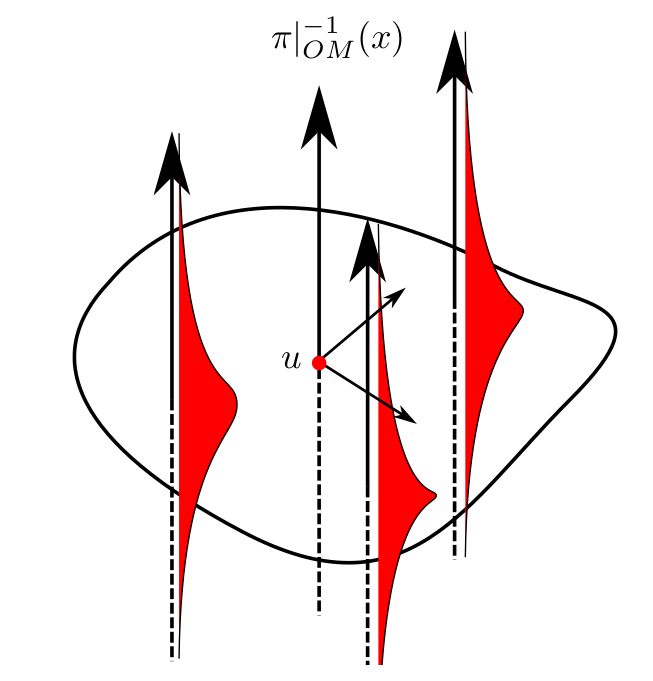
Fix \(T>0\): \(U_T\) probability distribution in \(FM\)

Rolling without slipping

Simulation of Conditioned Semimartingales on Riemannian Manifolds

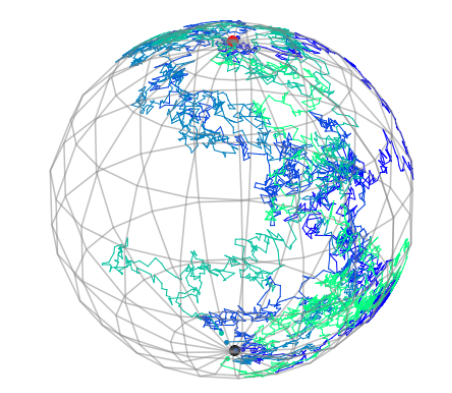
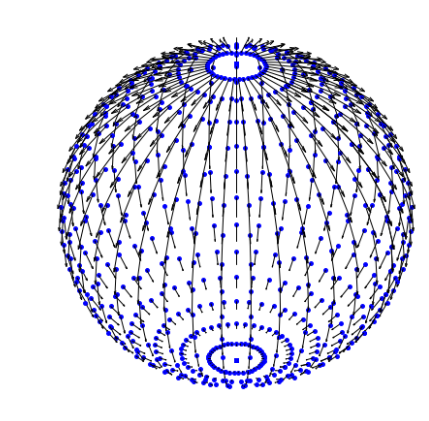
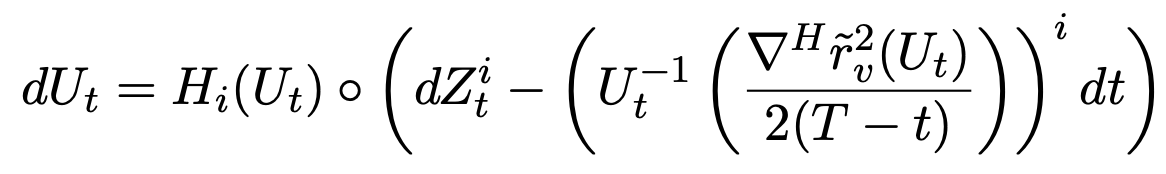
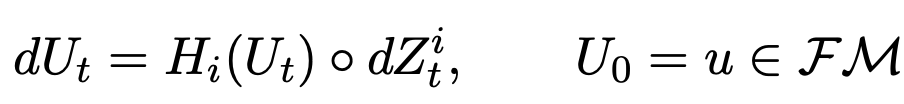
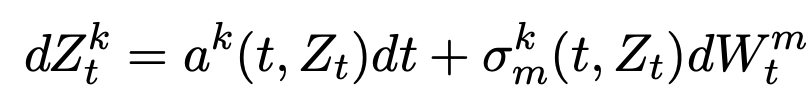
Driving semi-martingale:

 

developed process:

 

Fermi bridge:

 

 

Heat kernel approximations

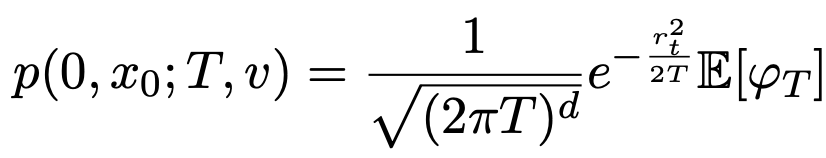
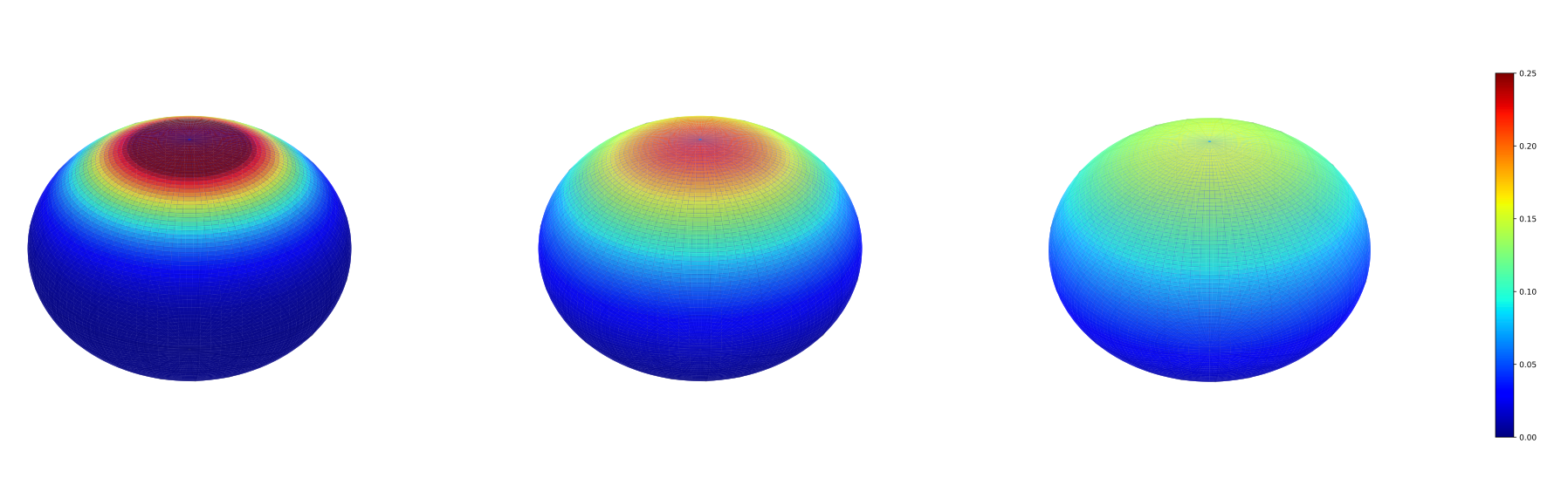
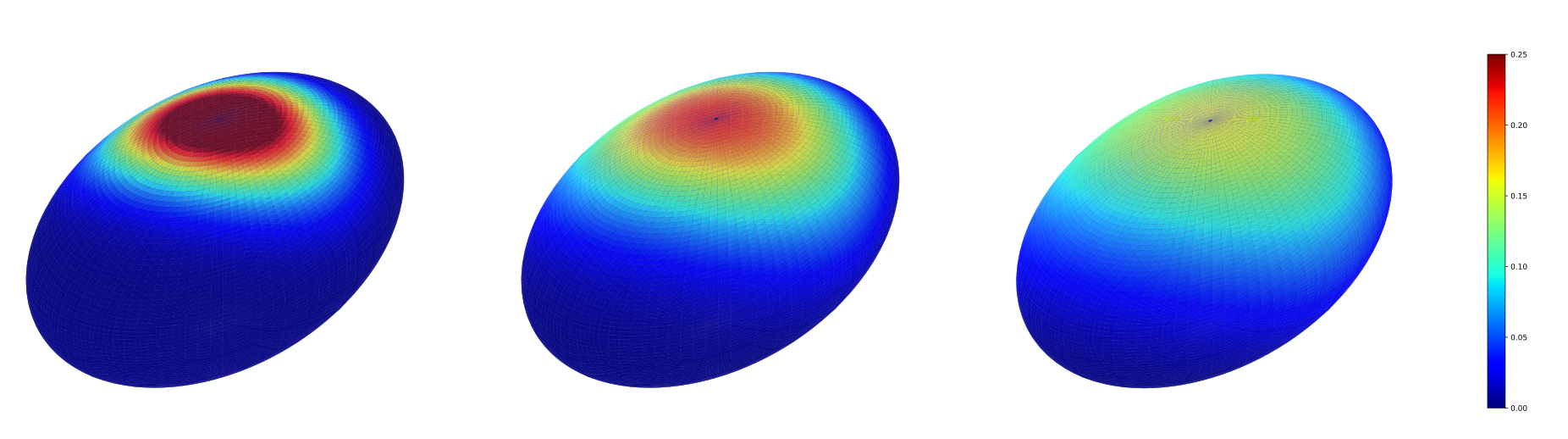
Bridges on Lie groups and homogenous spaces

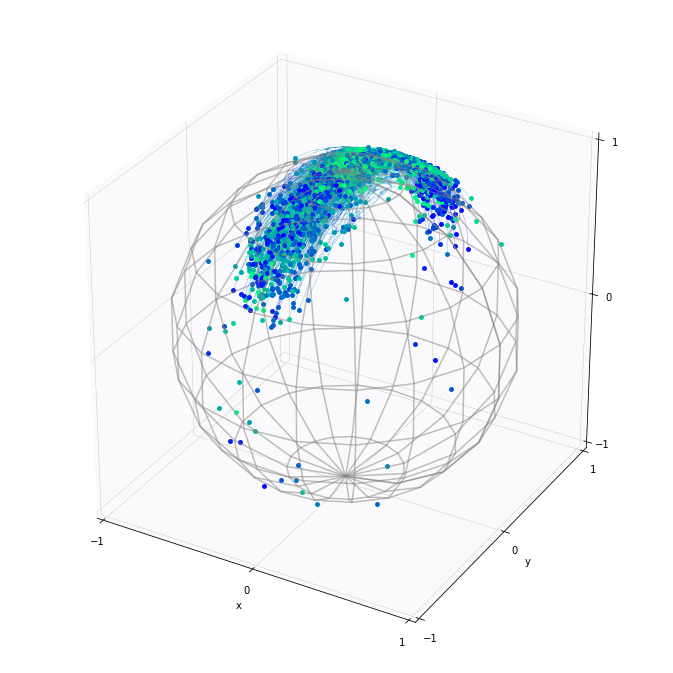
  • \(A\) quadratic form on \(so(3)\)
  • \(x_t\in SO(3)\) Brownian motion
  • \(\theta=(x_0,A)\)
  • \((\bar{x},\bar{A})=\mathrm{argmax}_\theta\mathcal{L}(\theta)\)

\(\pi\)

Thompson'16, Sommer,Joshi,Højgaard,'22

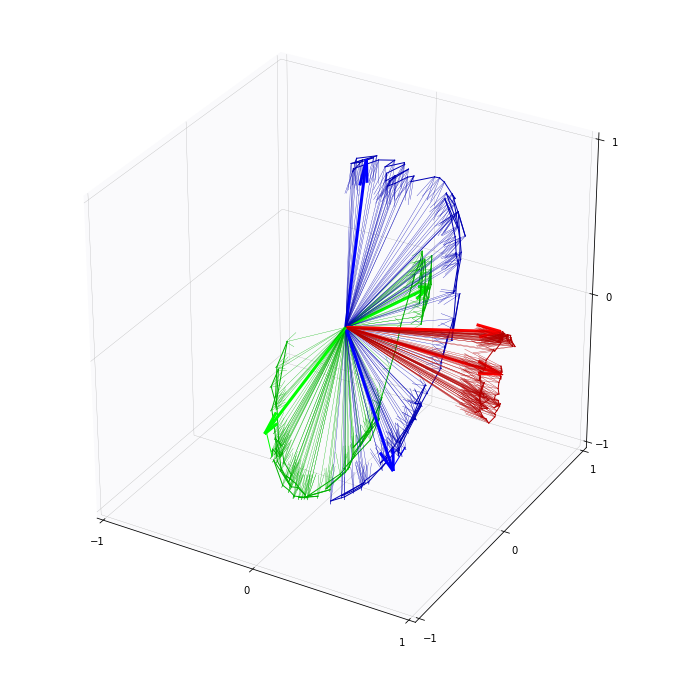
Left-invariant frame:

      \(V_i(g)=(dL_g)_ev_i,\quad v_i\in\mathfrak g\)

Brownian motion:

      \(dg_t=-\frac12V_0(g_t)dt+V_i(g_t)\circ dW_t^i\)

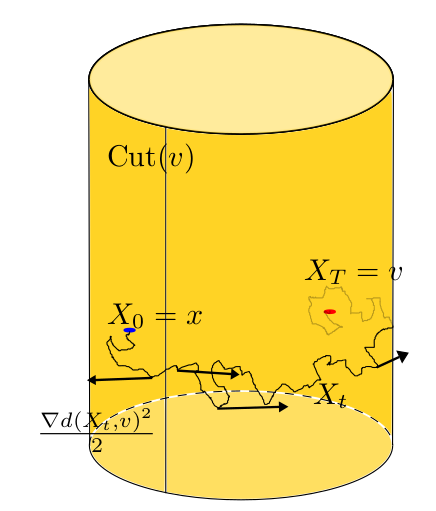
Fermi bridge:

    \(dg_t=-\frac12V_0(g_t)dt+V_i(g_t)\circ \left(dW_t^i-\frac{\mathrm{log}_{g_t}(v)^i}{T-t}dt\right)\)

Fermi bridge to fiber:

    \(dg_t=-\frac12V_0(g_t)dt+V_i(g_t)\circ \left(dW_t^i-\frac{\left(\nabla d(g_t,\pi^{-1}(v))^2\right)^i}{2(T-t)}dt\right)\)

  • parametric families of probability distributions \(\mu_\theta\)
  • likelihood from density:
    \(\quad\mathcal{L}(\theta; y_1,\ldots,y_N)=\prod_{i=1}^Np_\theta(y_i)\)
  • ML/MAP estimates:
    \(\quad\bar{\theta}=\mathrm{argmax}_\theta\mathcal{L}(\theta; y_1,\ldots,y_N)\)
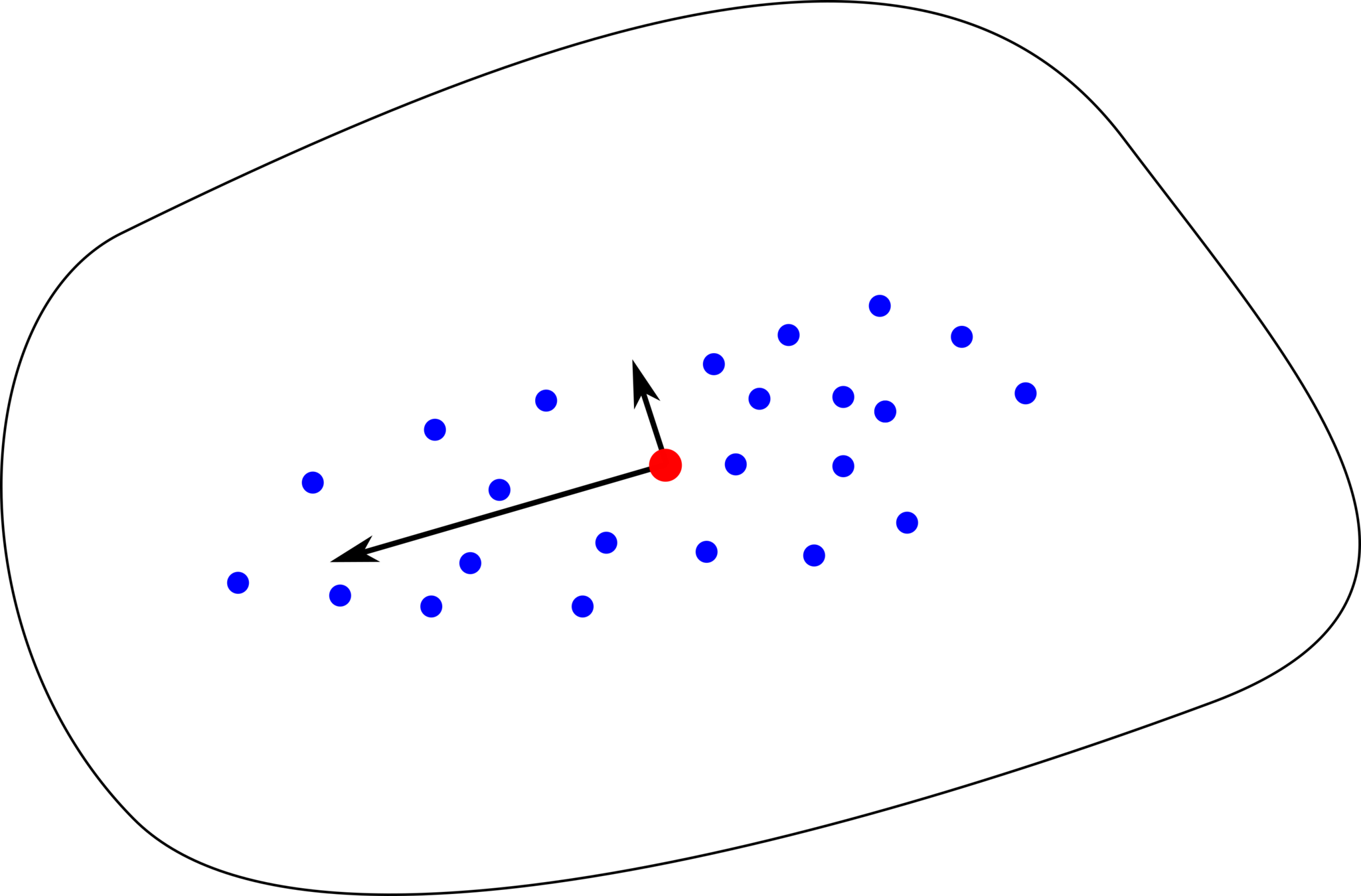
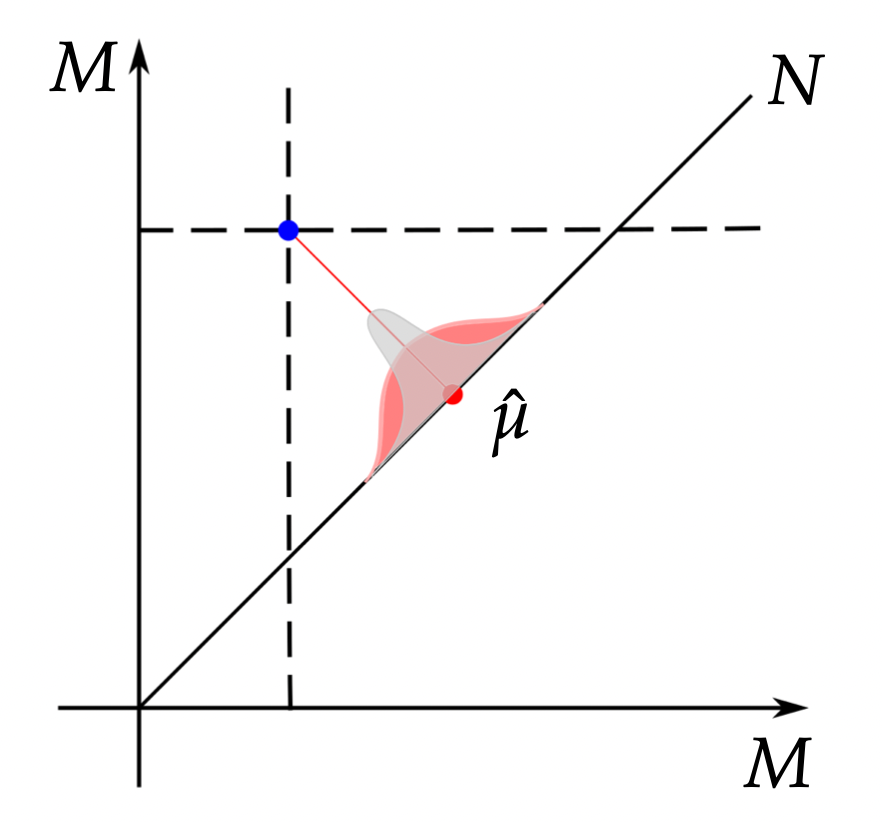
  • Diffusion mean:
    \(\quad x_t\in M\) Brownian motion
    \(\quad\theta=x_0\)
  • assume \(y\sim x_T\):
    \(\quad\bar{x}_{\mathrm{diffusion}}=\mathrm{argmax}_\theta\mathcal{L}(\theta)\)

 

 

Generalization of Euclidean statistical notions and techniques.

  • i.i.d. samples \(y_1,\ldots,y_N\in M\)
  • Fréchet mean:
    \(\bar{x}=\mathrm{argmin}_{x\in M}\sum_{i=1}^Nd(x,y_i)^2\)

Nye, White, JMIV'14;
Sommer,IPMI'15; Sommer,Svane,JGM'15;
Hansen,Eltzner,Huckemann,Sommer,GSI'21,Bernoulli'23

Means in geometric statistics

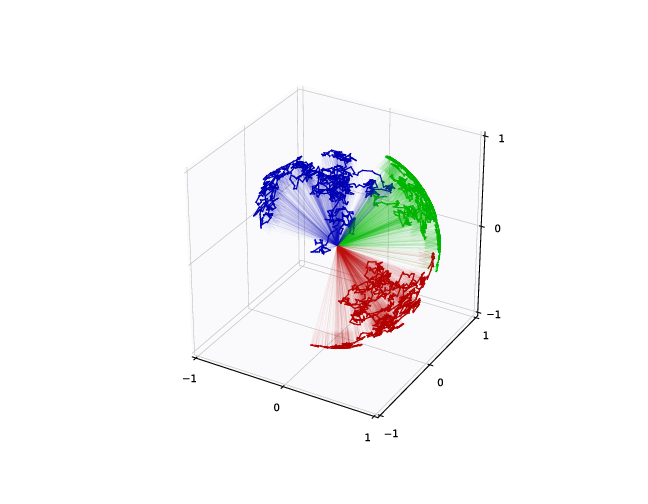
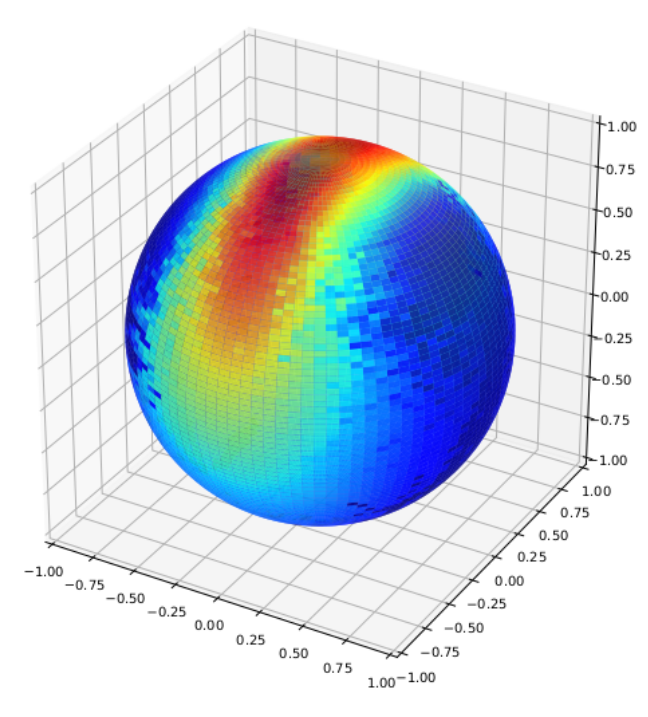
Diffusion mean on \(\mathbb S^2\)

  • \(x_t\in M\) Brownian motion
  • \(\theta=x_0\), \(y\sim x_T\)
  • \(\bar{x}_{\mathrm{diffusion}}=\mathrm{argmax}_\theta\mathcal{L}(\theta)\)
dx_t= -\frac12g(x_t)^{kl}\Gamma(x_t)_{kl}dt + \sqrt{g(x_t)^*}dW_t

Brownian motion starting point

Uniqueness and asymptotics

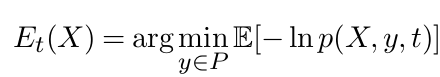
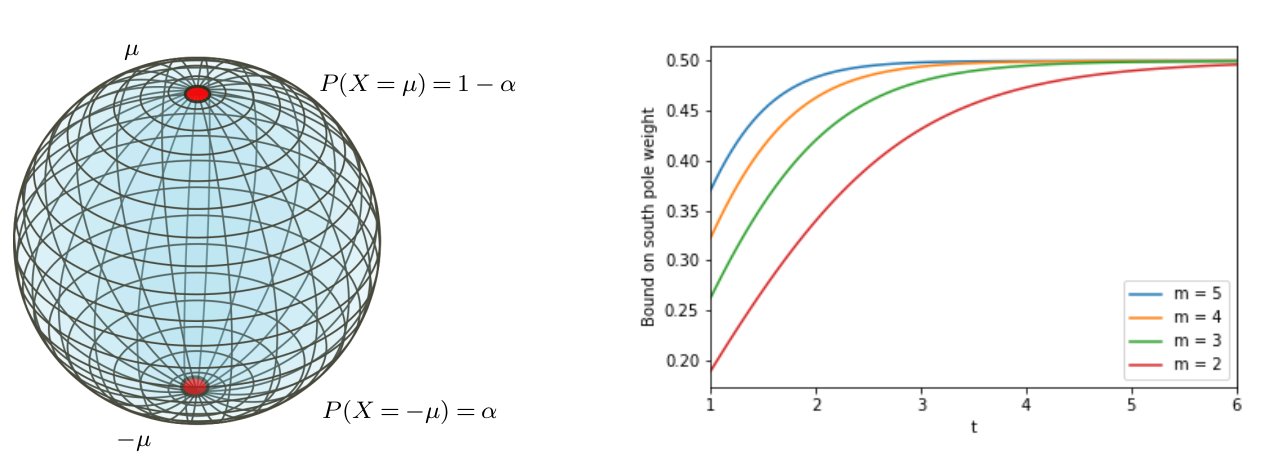
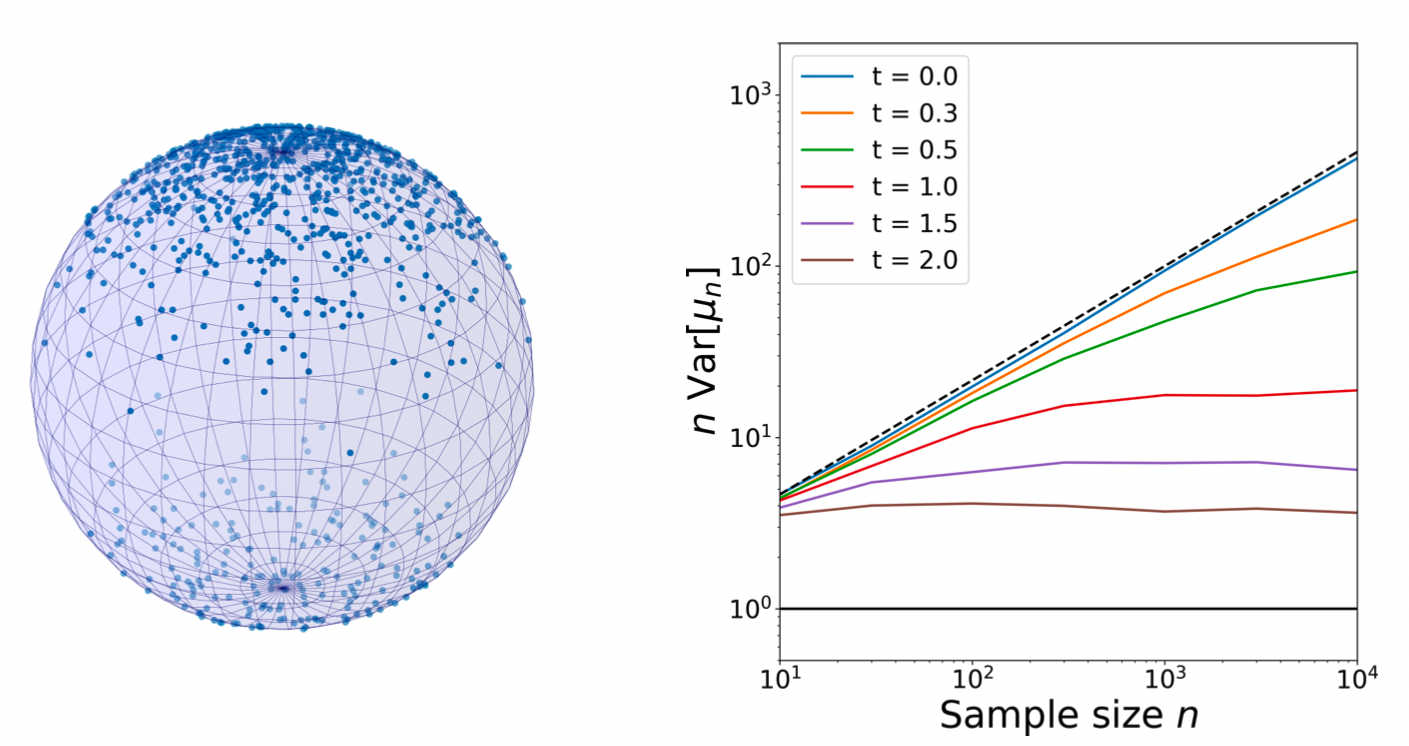
Estimating diffusion mean and diffusion variance

smeary at optimal \(t\)?

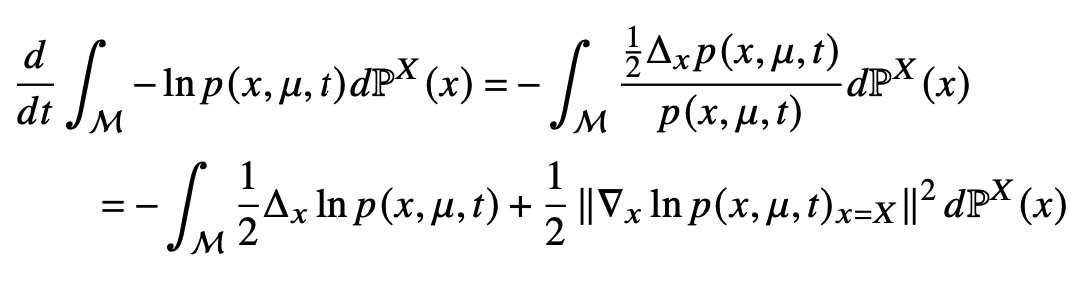
Brownian motion samples

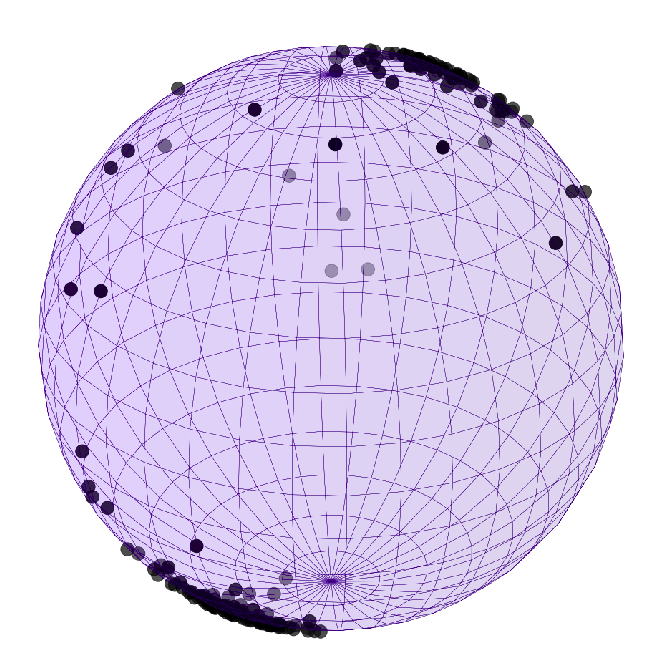
two-pole distribution

Finite sample size smeariness

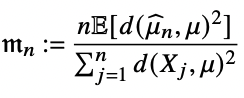
variance modulation:

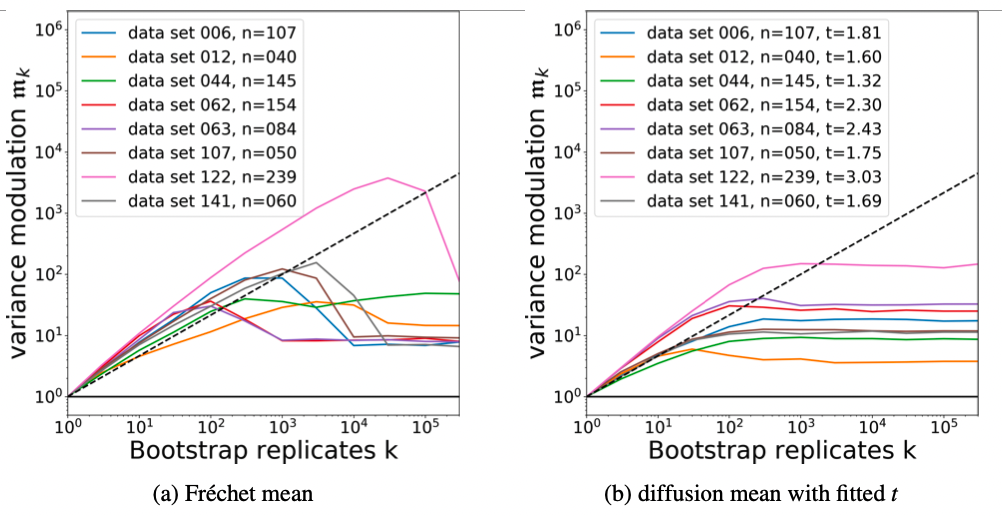
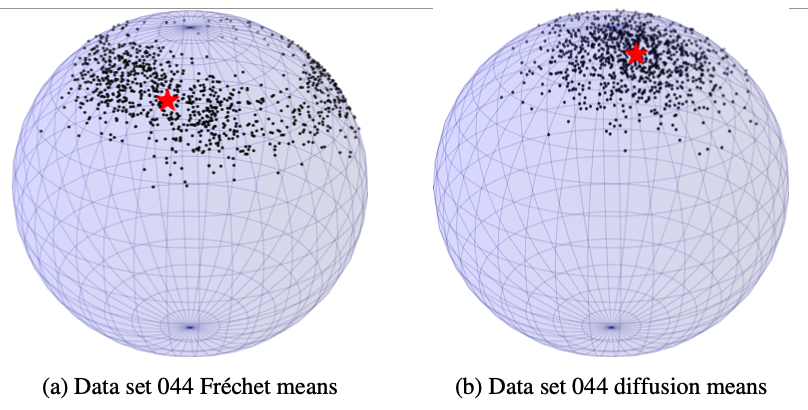
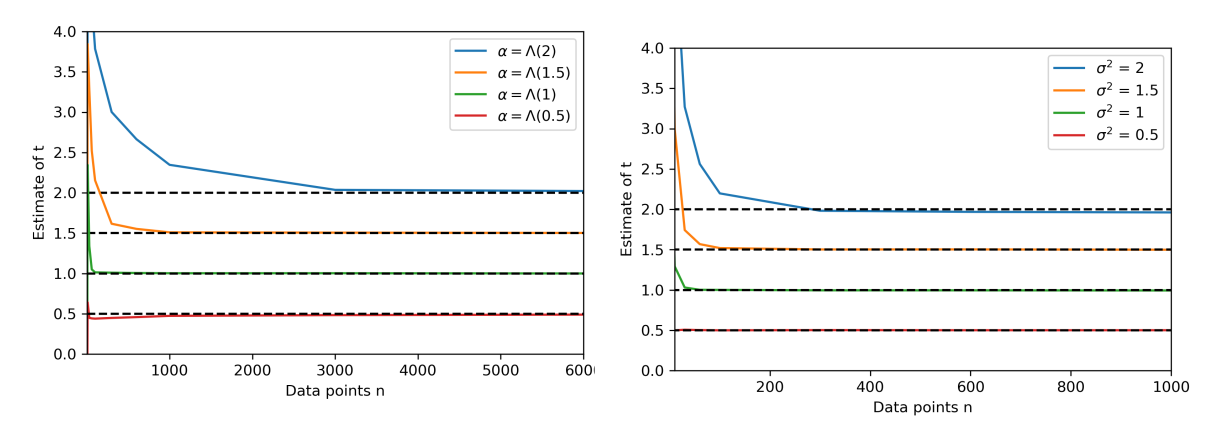
Estimation

Direct optimzation of \(\mathcal{L}(\theta; y_1,\ldots,y_N)\):

  • heat kernel expansion
  • bridge sampling
     

Direct sampling:

  • reverse time and condition on diagonal

Diagonally conditioned distribution

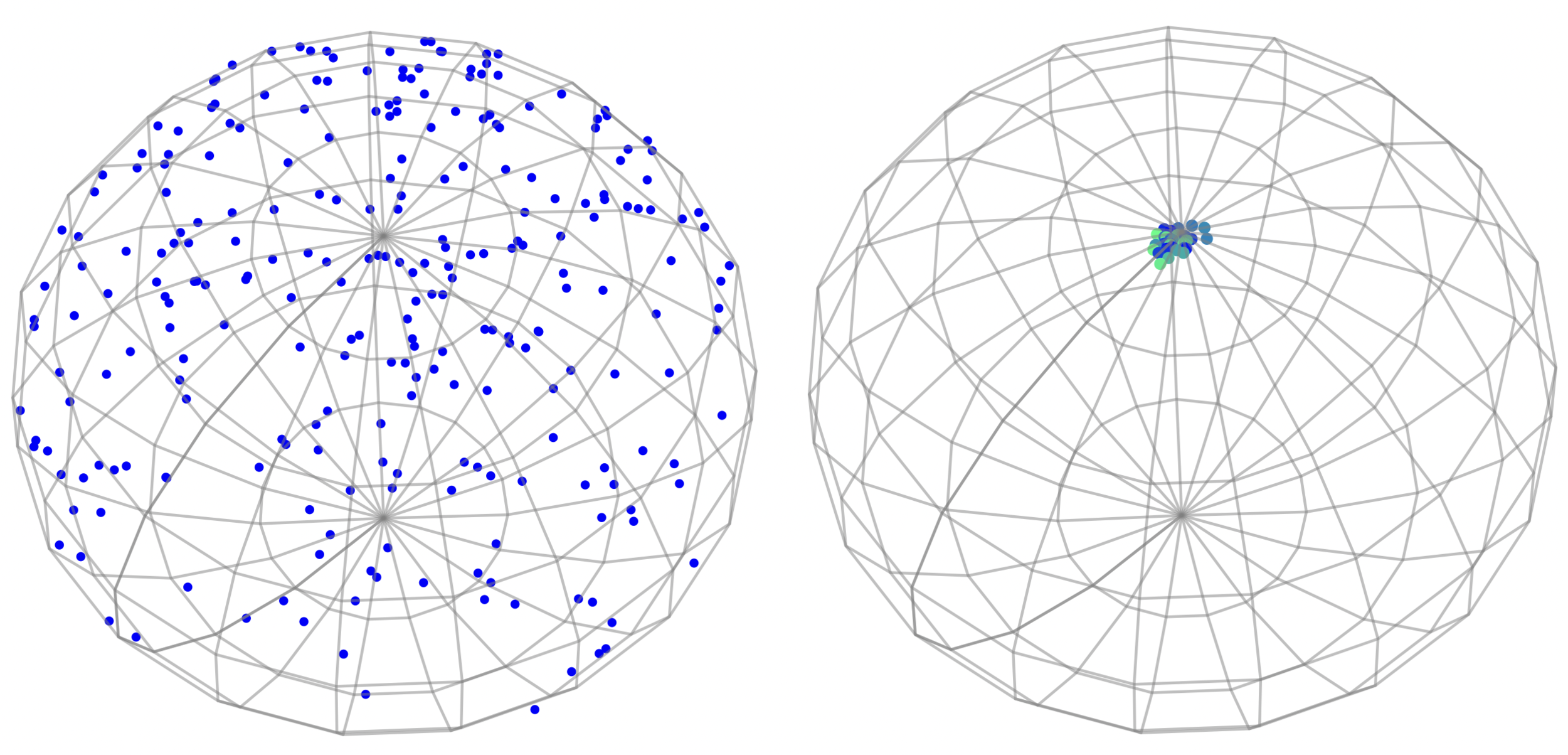
Sommer, Bronstein, TPAMI 2021; Jensen, Sommer, Algorithms 2022

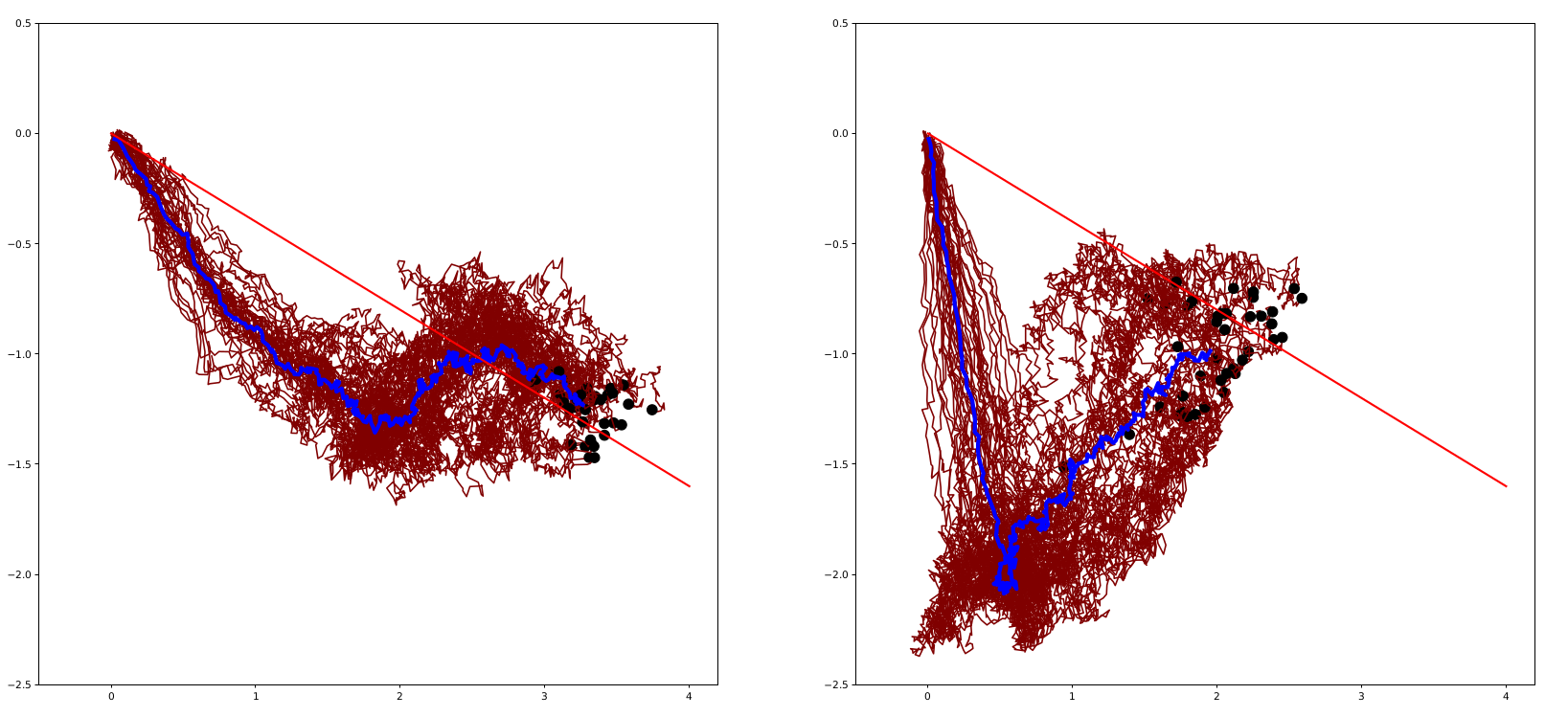
Fast mean estimation

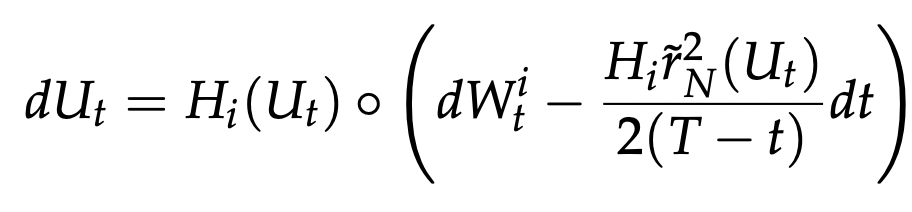
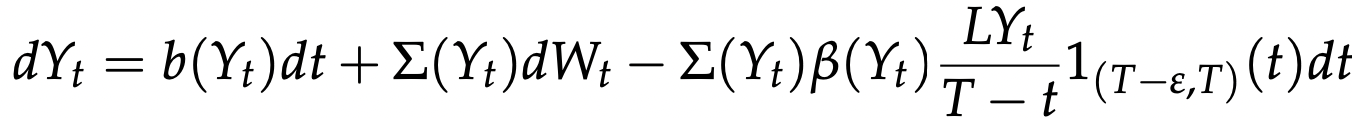
Fermi bridge:

Coordinate bridge:

One (or few) forward samples - compared to nested optimization

Added variance on top of CLT - gain in computational speed

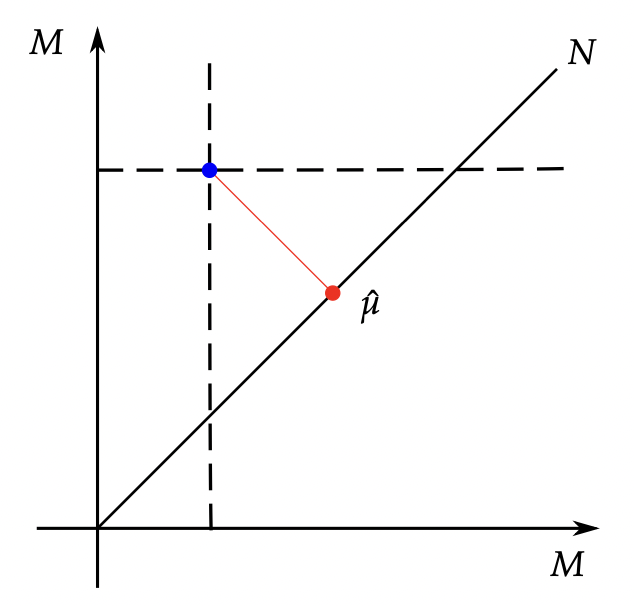
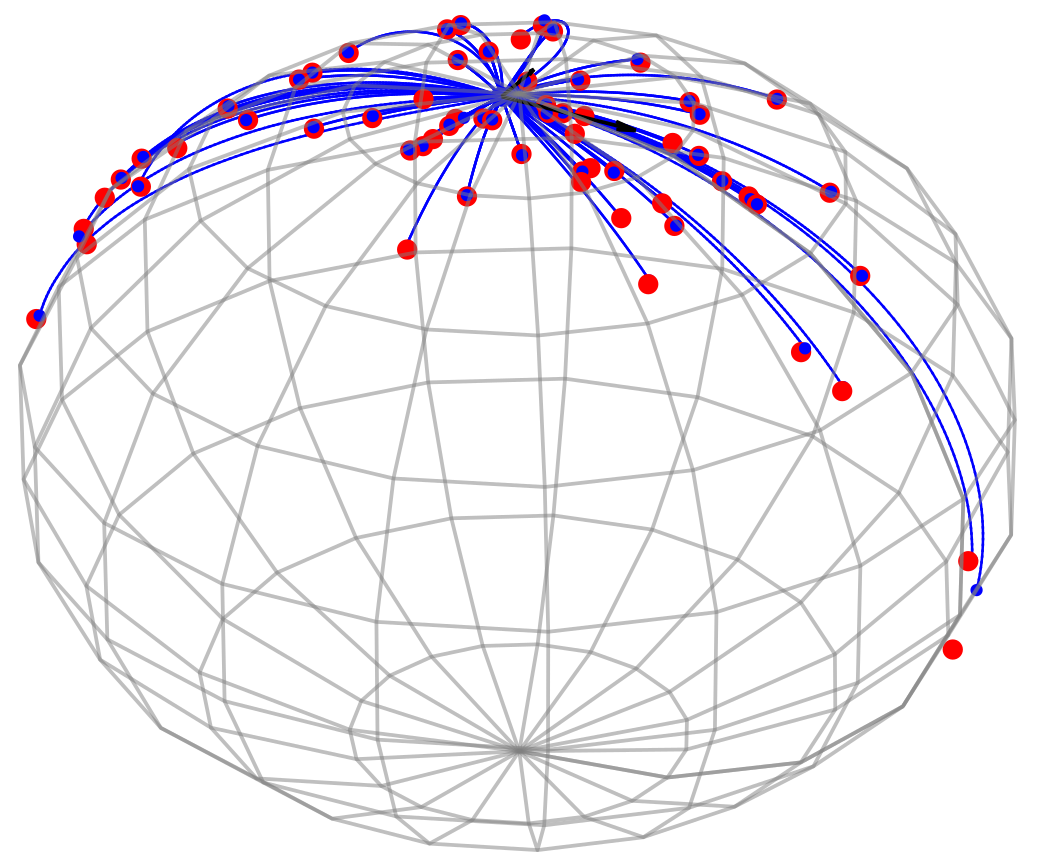
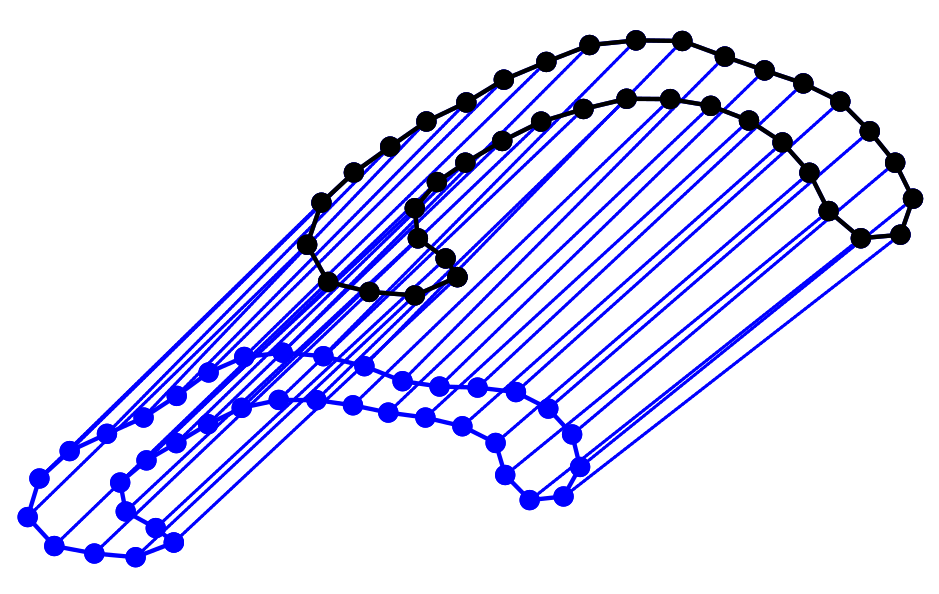
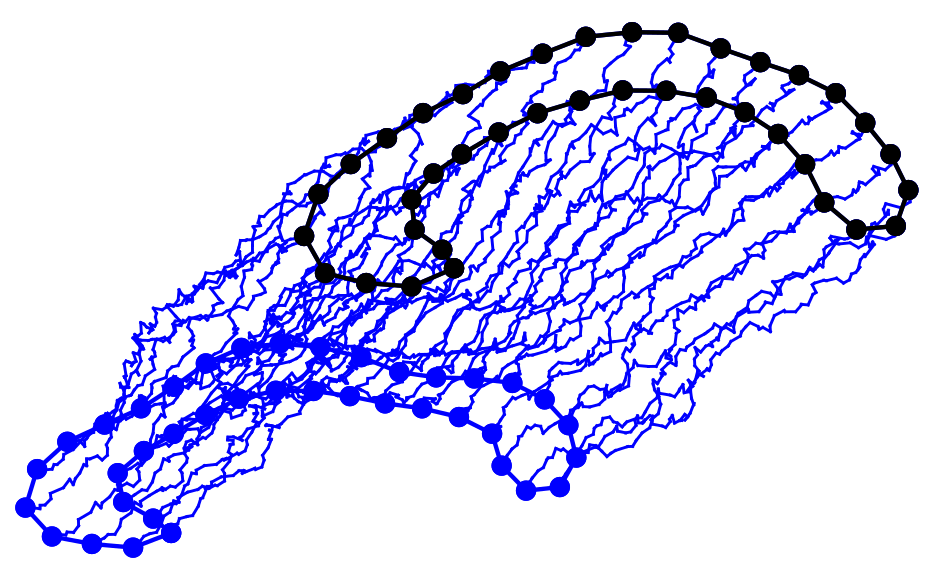
Sampled landmark means

Diagonally conditioned process:

Frechet mean (green), diffusion mean (blue)

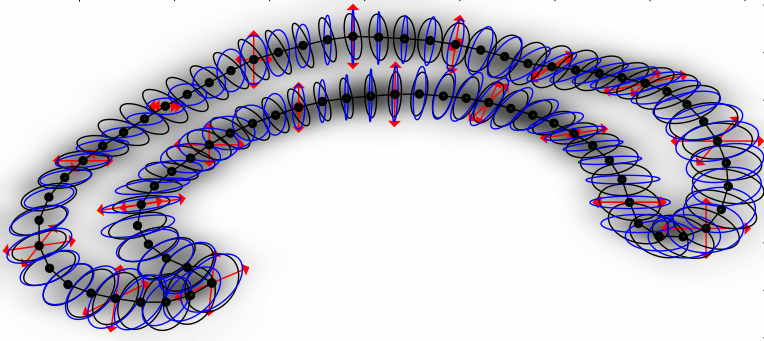
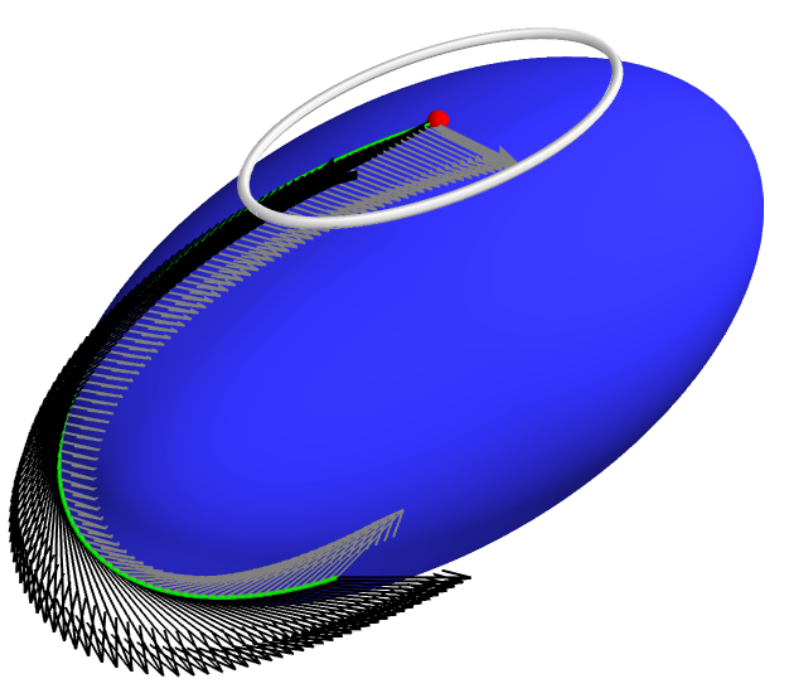
Can we model anisotropy?

non-trivial covariance: fit anisotropic normal distributions

Covariance transport

du_t=H_i(u_t)\circ dW_t^i
u_t\in FM

development

anti-development

Curvature and covariance

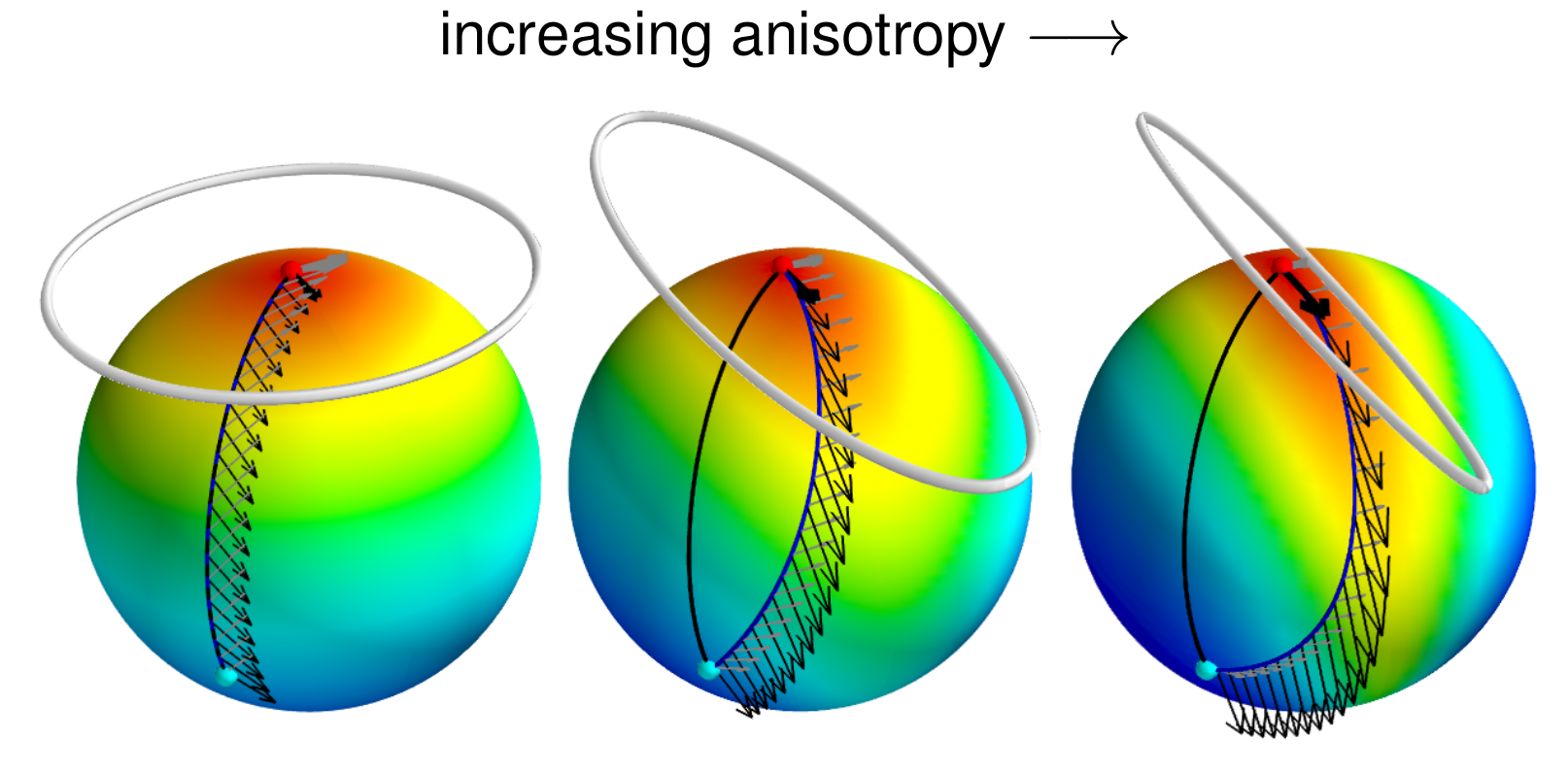
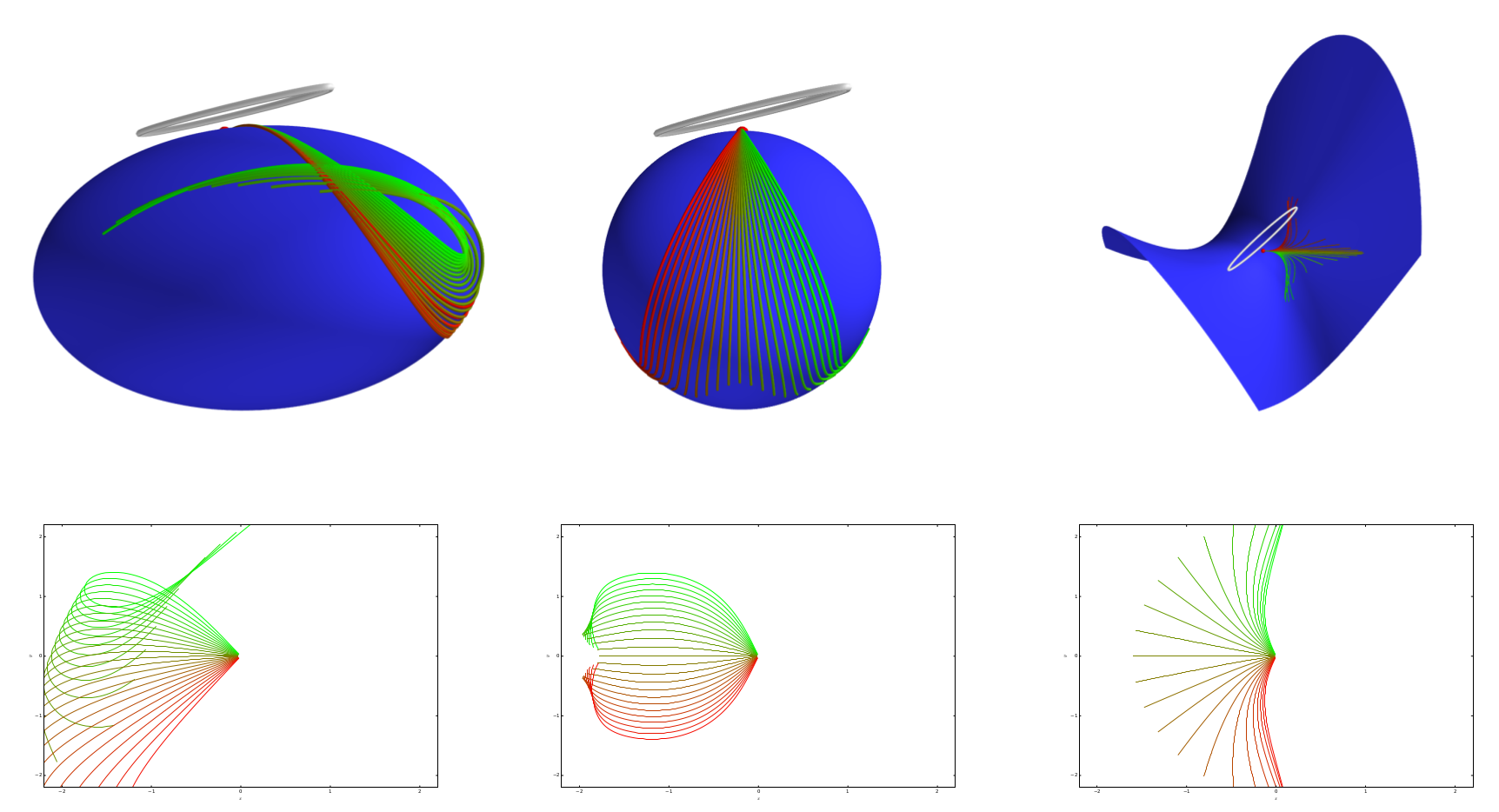
Sommer,Svane,JGM'15; Sommer,Entropy,'16

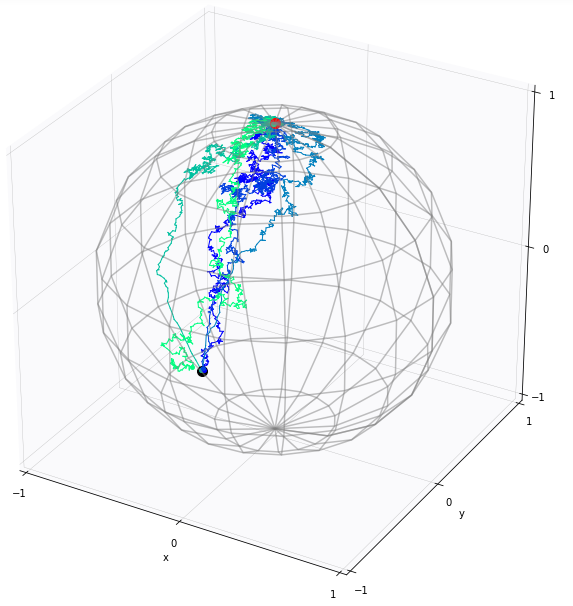
Most probable paths

  • in \(\mathbb R^d\), straight lines are most probable for stationary (isotropic) diffusion processes
  • Onsager-Machlup functional, \(\gamma_t\in M\):\[L_M(\gamma(t),\dot{\gamma}(t))=-\frac{1}{2}\|\dot{\gamma}(t)\|^2_g+\frac{1}{12}S(\gamma(t))\]
  • most probable paths maximize \(L_M(\gamma)\):\[\int_0^1 L_M(\gamma(t),\dot{\gamma}(t))dt = -E(\gamma)+ \frac{1}{12}\int_0^1S(\gamma(t))dt\]

 

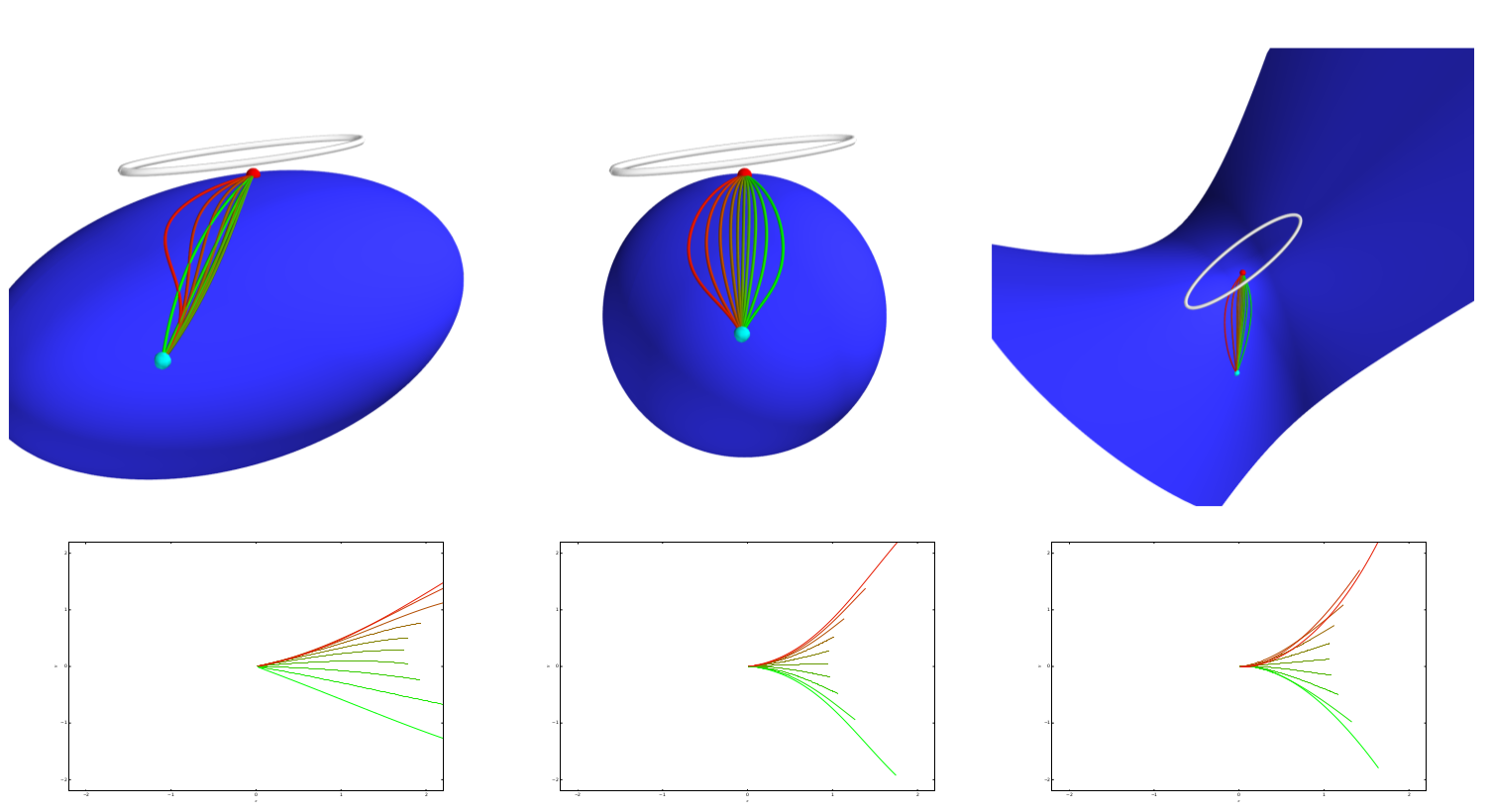
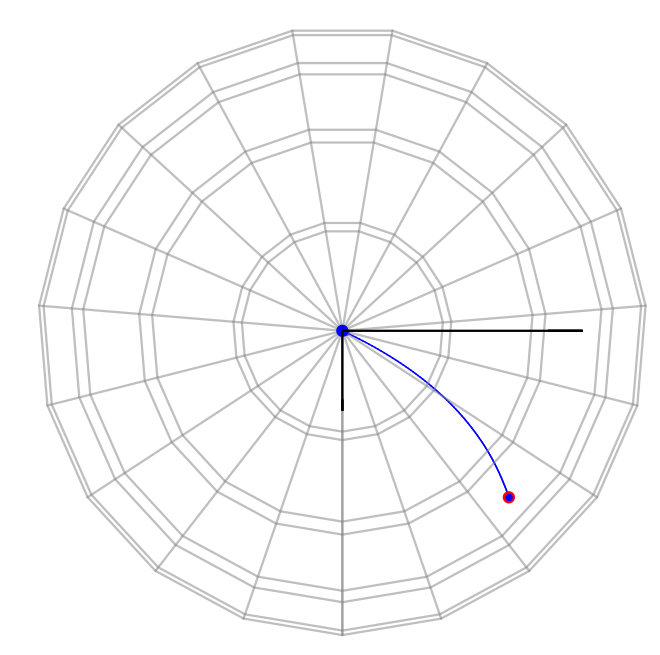
Most probable paths

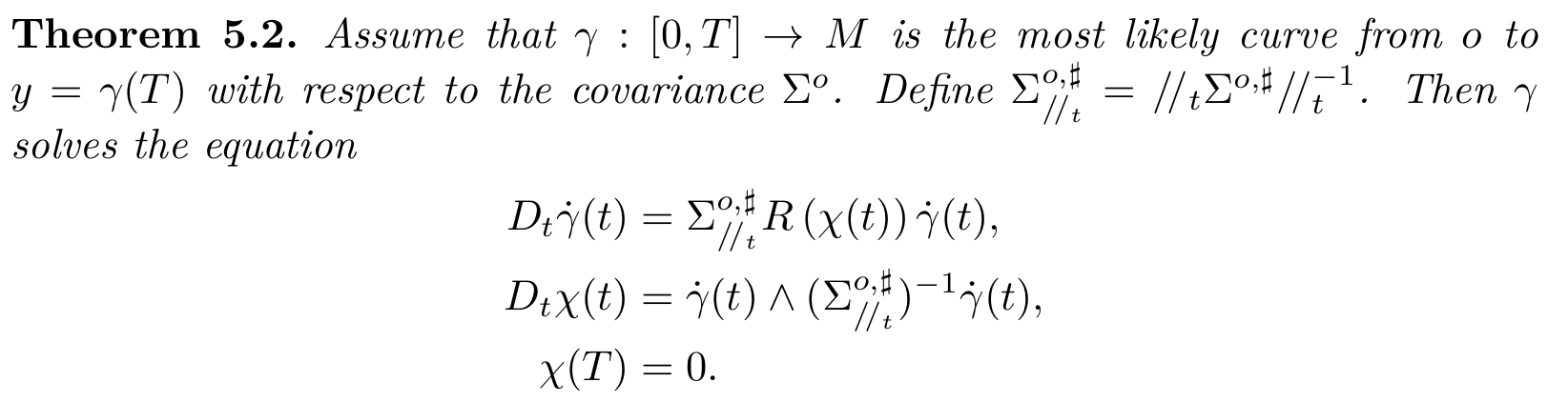
Grong, Sommer, FoCM 2022

Grong, 2021

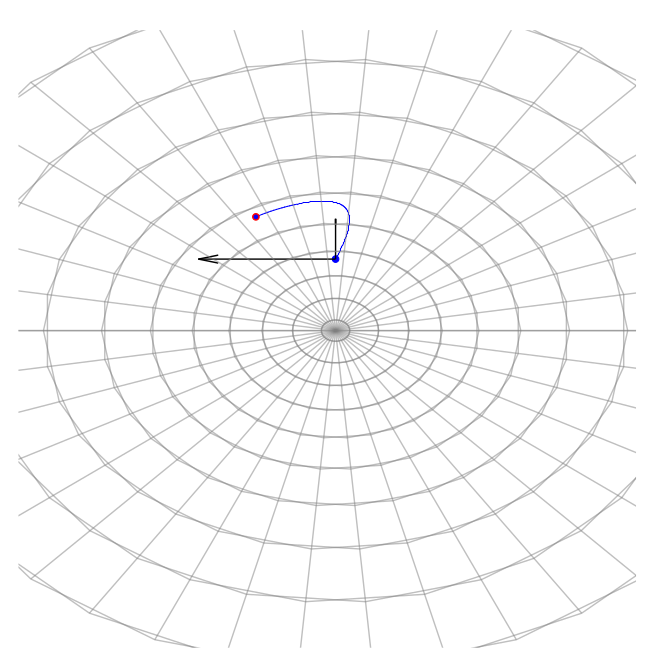
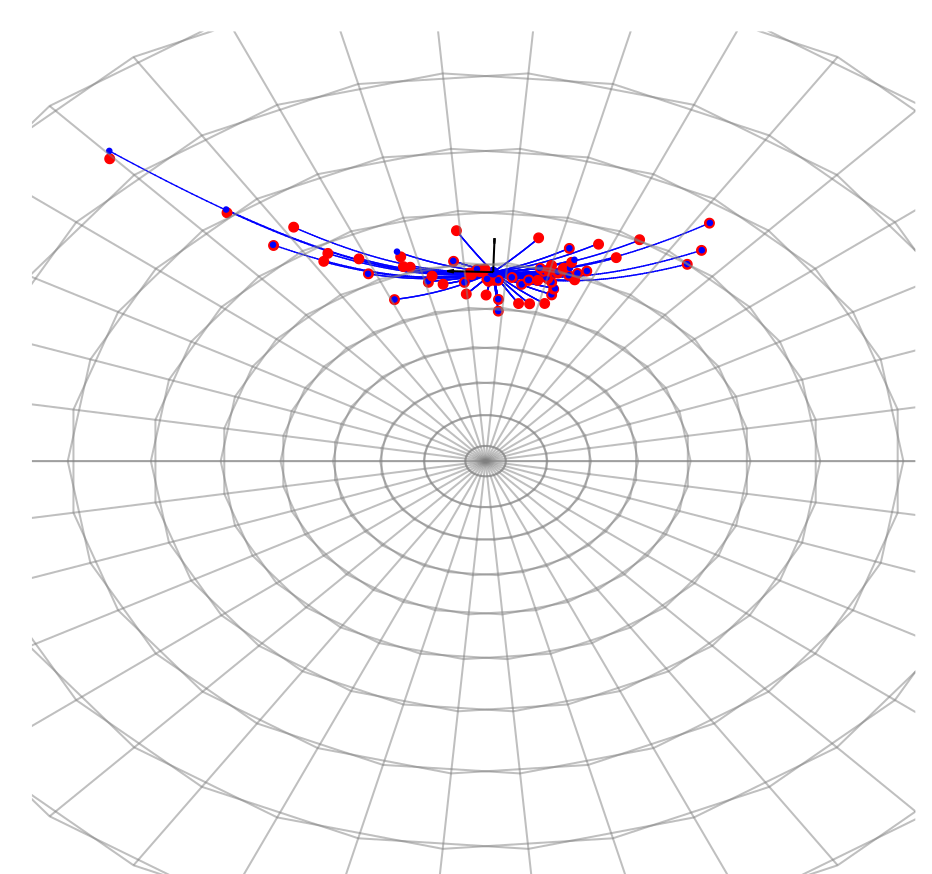
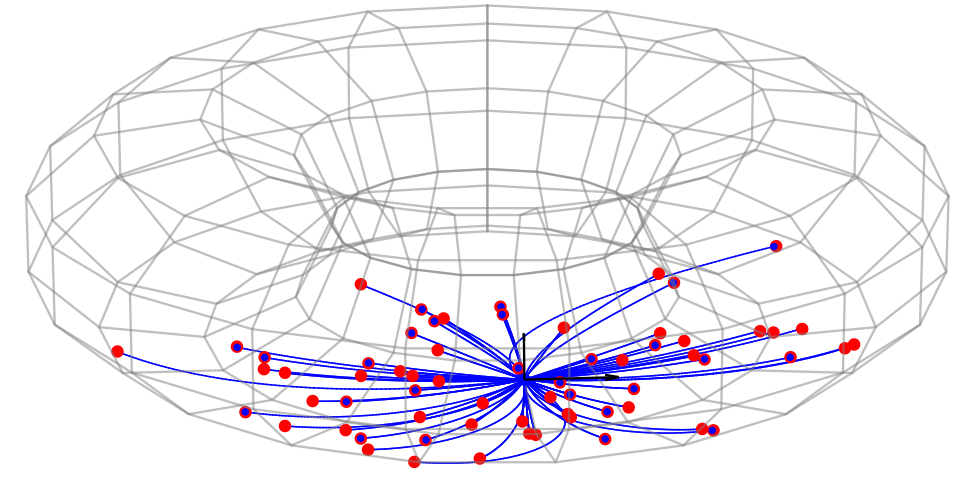
Directional smeariness and anisotropic diffusion mean

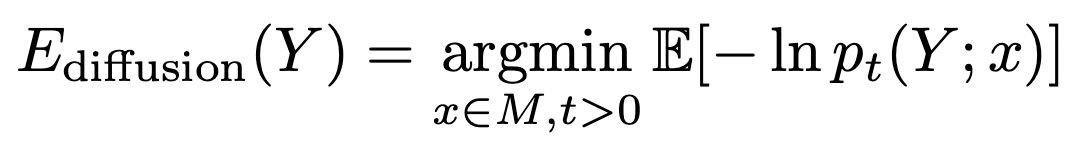
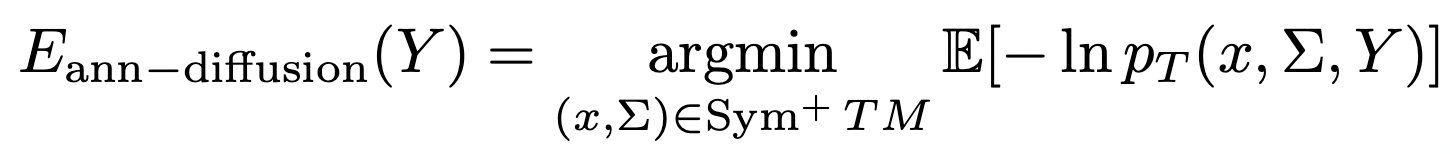
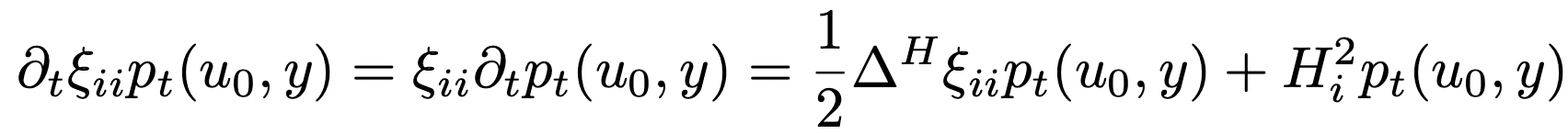
Vertical derivative of heat equation:

 

 

Geometry, stochastics, geometric statistics

code: http://bitbucket.com/stefansommer/jaxgeometry                          Centre for Computational Evolutionary Morphometry: http://www.ccem.dk

slides: https://slides.com/stefansommer                                                     Stochastic Morphometry: https://www.ccem.dk/stochastic-morphometry/

References:

  • Philipp Harms, Peter W. Michor, Xavier Pennec, Stefan Sommer: Geometry of sample spaces, Diff. Geom. and its Appl., 2023, arXiv:2010.08039
  • Hansen, Eltzner, Huckemann, Sommer: Diffusion Means in Geometric Spaces, Bernoulli, in press, 2023, arXiv:2105.12061
  • Grong, Sommer: Most probable paths for anisotropic Brownian motions on manifolds, FoCM 2022, arXiv:2110.15634
  • Højgaard, Joshi, Sommer: Discrete-Time Observations of Brownian Motion on Lie Groups and Homogeneous Spaces: Sampling and Metric Estimation, Algorithms, 2022, 
  • Jensen, Sommer: Mean Estimation on the Diagonal of Product Manifolds, Algorithms, 2022, https://www.mdpi.com/1999-4893/15/3/92
  • Arnaudon, v.d. Meulen, Schauer, Sommer: Diffusion bridges for stochastic Hamiltonian systems and shape evolutions, SIIM, 2022, arXiv:2002.00885
  • Hansen, Eltzner, Sommer: Diffusion Means and Heat Kernel on Manifolds, 2021, GSI 2021, arXiv:2103.00588.
  • Højgaard Jensen, Sommer: Simulation of Conditioned Diffusions on Riemannian Manifolds, 2021, arXiv:2105.13190.
  • Sommer, Bronstein: Horizontal Flows and Manifold Stochastics in Geometric Deep Learning, TPAMI, 2020, doi: 10.1109/TPAMI.2020.2994507
  • Arnaudon, Holm, Sommer: A Geometric Framework for Stochastic Shape Analysis, Foundations of Computational Mathematics, 2019, arXiv:1703.09971.
  • Højgaard Jensen, Mallasto, Sommer: Simulation of Conditioned Diffusions on the Flat Torus, GSI 2019., arXiv:1906.09813.
  • Sommer, Svane: Modelling Anisotropic Covariance using Stochastic Development and Sub-Riemannian Frame Bundle Geometry, JoGM, 2017, arXiv:1512.08544.
  • Sommer: Anisotropically Weighted and Nonholonomically Constrained Evolutions, Entropy, 2017, arXiv:1609.00395 .
  • Sommer, Svane: Modelling Anisotropic Covariance using Stochastic Development and Sub-Riemannian Frame Bundle Geometry, JoGM, 2017, arXiv:1512.08544.
  • Sommer: Anisotropically Weighted and Nonholonomically Constrained Evolutions, Entropy, 2017, arXiv:1609.00395 .
  • Arnaudon, Holm, Sommer: A Stochastic Large Deformation Model for Computational Anatomy, IPMI 2017, arXiv:1612.05323.
  • Sommer: Anisotropic Distributions on Manifolds: Template Estimation and Most Probable Paths, IPMI 2015, doi: 10.1007/978-3-319-19992-4_15.