Currents and K-functions for Fiber Point Processes
Geometric Science of Information 2021
Pernille Hansen, Rasmus Waagepetersen, Anne Marie Svane, Jon Sporring, Hans Stephensen , Jon Sporring, Stine Hasselholt, Stefan Sommer
Analysis of fiber point processes
- Point processes and Ripley's K-function
- Fiber/shape valued processes
- Fiber K-function using currents metric
- Simulation and myelin fibers results

Point processes
A point process \(X\) on a metric space \(S\) is a measurable map from some probability space \((\Omega, F, P )\) into the space of locally finite subsets of \( S\).
Usually \( S= \mathbb R^n \)
Ripley's K-function for point processes \(X\) on \(\mathbb R^n\):
\(K(t) = \frac{1}{\lambda} \mathbb E\)[#events within distance \(t\) from a point]
\(\lambda \) is the intensity (number per unit area) of events.
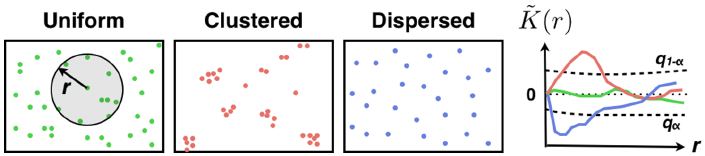
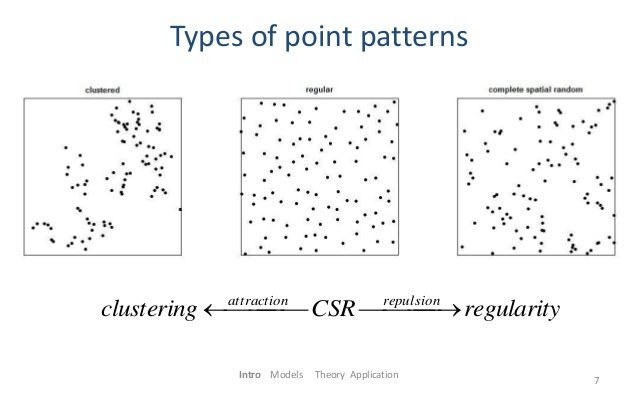
Ripley’s K-function is standard statistical tool for
- analyzing second order moment
structure of point processes - measuring deviance from complete
spatial randomness in point sets.
Ripley's K-function
\(t\)
Ripley's K-function
\(t\)
\( K(t)\)
Ripley’s K-function is standard statistical tool for
- analyzing second order moment
structure of point processes - measuring deviance from complete
spatial randomness in point sets.
clustered
dispersed

Aim
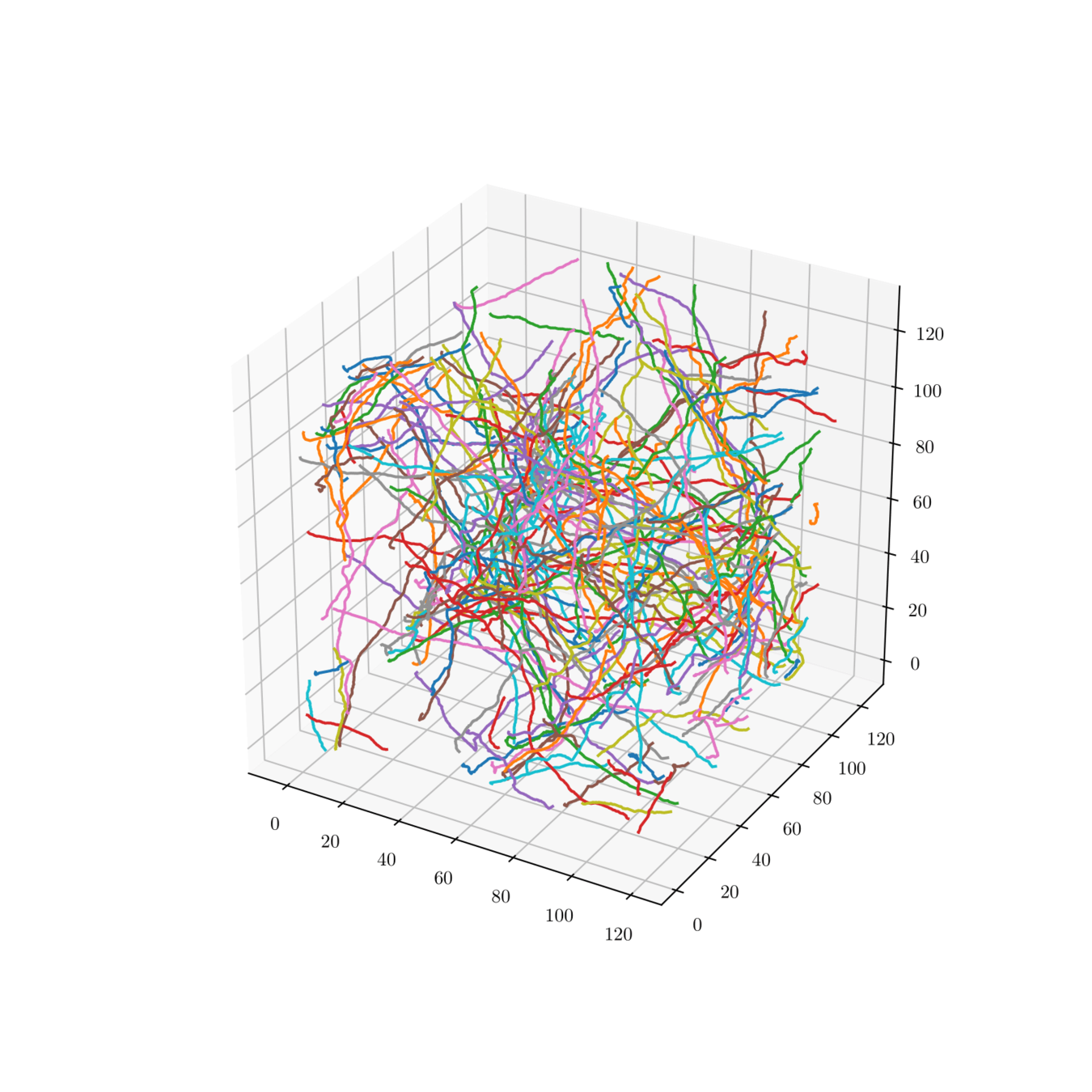
Define a K-function for point processes where every point is a shape, for example fibers in \( \mathbb R^3\)
Issues
- Metric
- Well-posed K-function
- Uniform shape process - equivalent to Poisson point processes
K-function for fibers and shapes
\(\hat{K}(t) = \frac{1}{\hat{\lambda}}\sum_{i\not=j}\frac{1[\mathrm{dist}(p_i,p_j)<t]}{n}\)
\(\hat{\lambda}=\frac{n}{|W|}\)
Metric: Currents
A piece-wise smooth curve \( \gamma \) is characterized by the path-integral over vector fields \(w\)
where \( \tau(x)_\gamma \) is the unit tangent of \( \gamma \) at \(x\).
\(V_\gamma(w) = \int_\gamma w(x)^t\tau_\gamma(x)d \lambda(x) \)
The shape \( \gamma \) is considered a functional
\(V_\gamma\in W^* = \{ f:W\to \mathbb R | \text{linear and cont} \}. \)
This representation is a current and formally the space of \(m\)-currents is the dual space of the differential \(m\)-forms.
By considering W as a RKHS gives the inner product on \(W^*\)
\( \langle V_{\gamma_1}, V_{\gamma_2} \rangle = \int_{\gamma_1}\int_{\gamma_2} \tau_{\gamma_1}(x)^tK(x,y) \tau_{\gamma_2}(x) d\lambda(x)\lambda(y) \)
where \(K\) is the kernel of \(W\) and the induced distance measure
\( d_c(V_{\gamma_1}, V_{\gamma_2}) = ||V_{\gamma_1} - V_{\gamma_2} || \)
Define the empirical K-function on shapes \(S\)
\(c:S\to\mathbb R^d\) gives curve center points (\(c\) translation equivariant),
\(\gamma_c:=\gamma-c(\gamma)\) are centered curves,
\(\nu(S_0) \) is a measure on centered curves,
and \( |W| \) size of the observation window
Currents based K-function
\( \hat{K}(t,s) = \frac{1}{|W|\nu(S_0)} \sum \sum 1[||c(\gamma)-c(\gamma')|| \leq t, d_c(\gamma_c,\gamma_c')\leq s]\)
\( \gamma\in X:c(\gamma)\in W\)
\( \gamma' \neq \gamma \in X \)
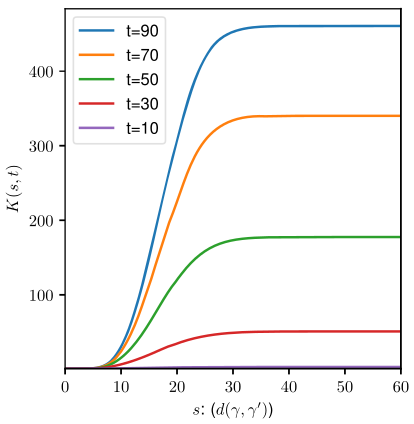
\(K(s,t)\) measures both spatial (\(t\)) and shape (\(s\)) homogeneity
The shape K-function is the expectation
\[K(t,s)=\mathbb E[\hat{K}(t,s)]\]
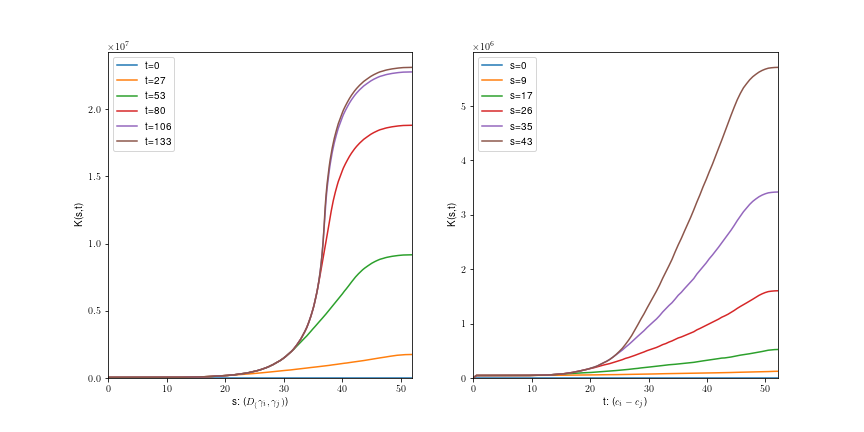
Currents based K-function
\( s \) shape parameter
\( \hat{K}(s,t) = \frac{1}{|W|\nu(S_0)} \sum \sum 1[||c(\gamma)-c(\gamma')|| \leq t, d_c(\gamma_c,\gamma_c')\leq s]\)
\( \gamma\in X:c(\gamma)\in W\)
\( \gamma' \neq \gamma \in X \)
\(K(s,t)\) measures both spatial (\(t\)) and shape (\(s\)) homogeneity
\(t\) spatial parameter
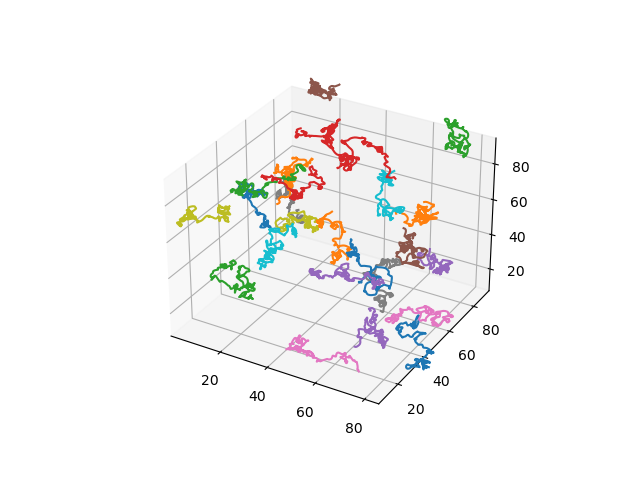
Poisson centers \(c(\gamma)\) and fiber Brownian motion:
Analogue of Poisson point process
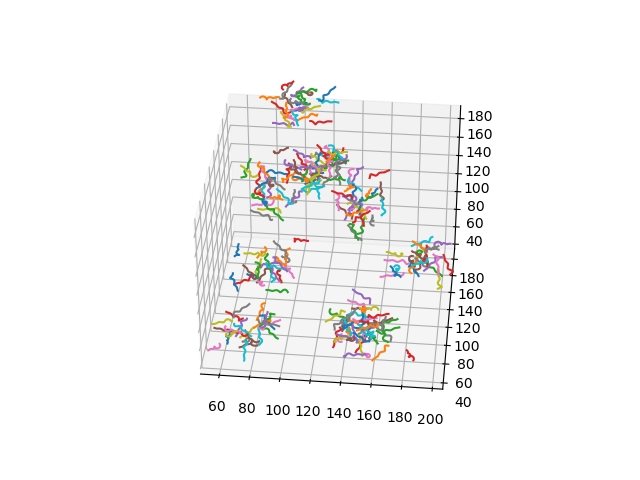
Uniform random fiber process
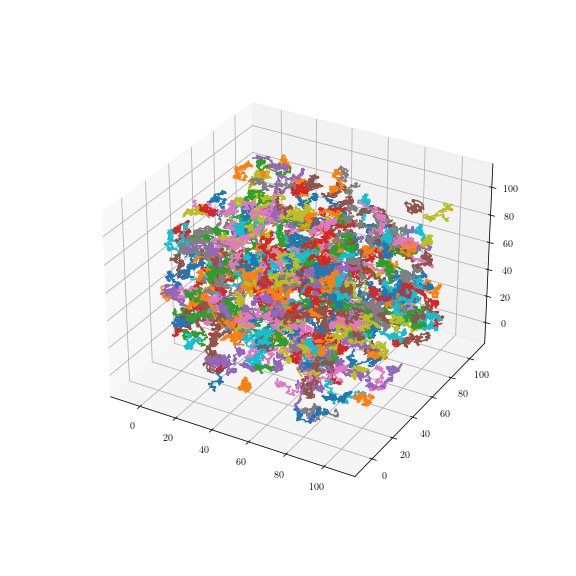
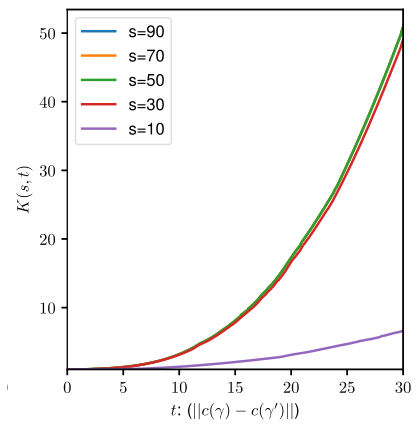
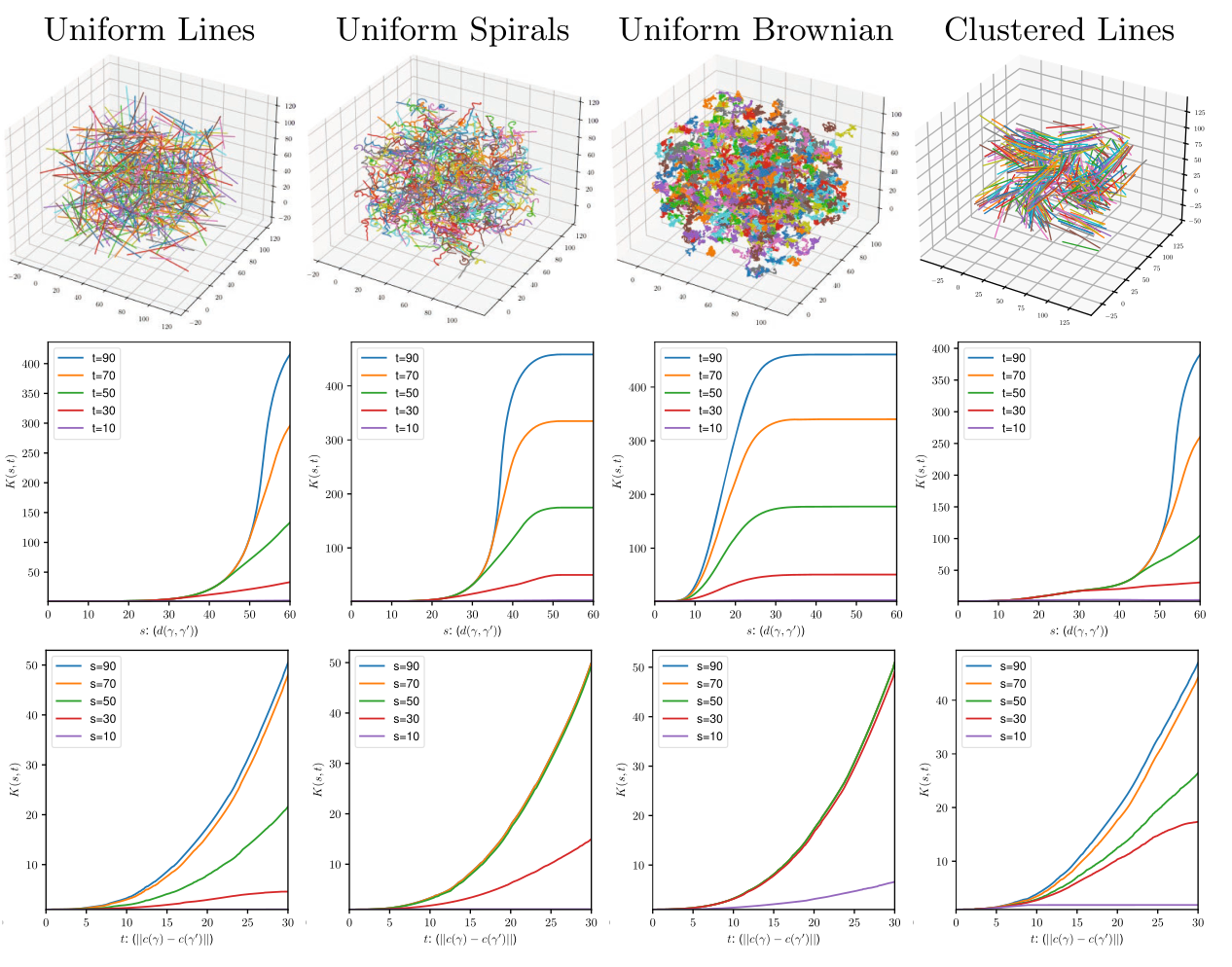
Synthetic data
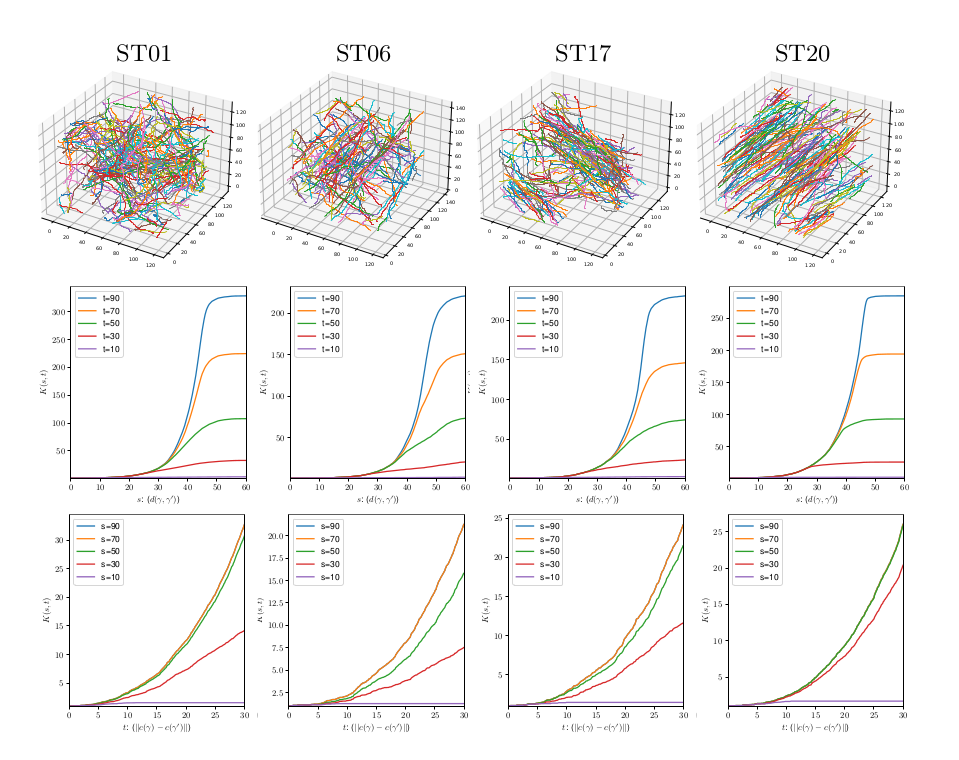
Myelin fibers
Currents and K-functions for Fiber Point Processes
code: http://bitbucket.com/stefansommer/theanogeometry
http://bitbucket.com/stefansommer/jaxgeometry
slides: https://slides.com/stefansommer
References:
- Hansen, Waagepetersen, Svane, Sporring, Stephensen, Hasselholt, Sommer: Currents and K-functions for Fiber Point Processes, GSI 2021, arXiv:2102.05329
- Sporring, Waagepetersen, Sommer: Generalizations of Ripley's K-function with application to space of curves, IPMI 2019, arXiv:1812.06870
Acknowledgements: We thank Zhiheng Xu and Yaqing Wang from Institute of Genetics and Developmental Biology, Chinese Academy of Sciences for providing the mouse tissue used for generation of the dataset. The work was supported by the Novo Nordisk Foundation grant NNF18OC0052000.


