Kunita flows, shape stochastics, and phylogenetic inference

Stefan Sommer, University of Copenhagen

Faculty of Science, University of Copenhagen

Chalmers University, May, 2025

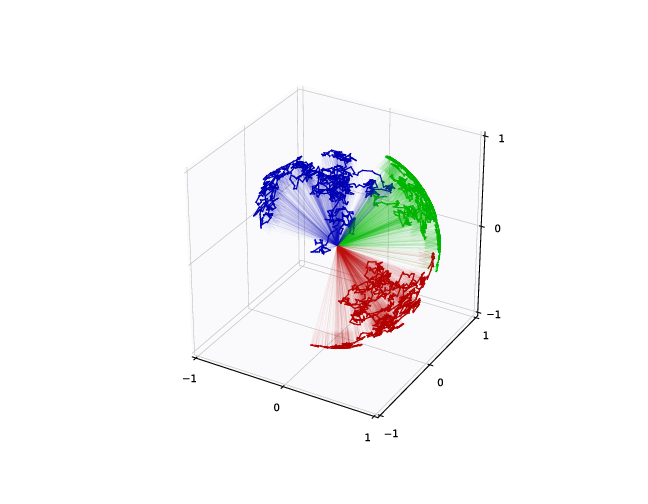
Shape stochastics, conditional processes and inference

w/ Frank v.d. Meulen, Rasmus Nielsen, Christy Hipsley, Sofia Stoustrup, Libby Baker, Gefan Yang, Michael Severinsen

Villum foundation

Novo nordisk foundation

University of Copenhagen

Center for Computational Evolutionary Morphometrics

w/ Rasmus Nielsen

Brownian motion model of trait evolution

Brown. motion

branch (independent children)

incorporate leaf observations $x_{V_T}$ into probabilistic model:
$p(X_t|x_{V_T})$

Felsenstein's pruning algorithm for shapes

Brown. motion

1) What is a shape Brownian motion?

2) How do we condition the nonlinear process on shape observations?

3) How do we perform inference in the full model?

Stochastics of shapes

Stochastic processes that

apply to landmarks, curves, surfaces and images
are independent of discretization
preserve shape structure
model correlation between points
are nonlinear
are invariant to acting groups

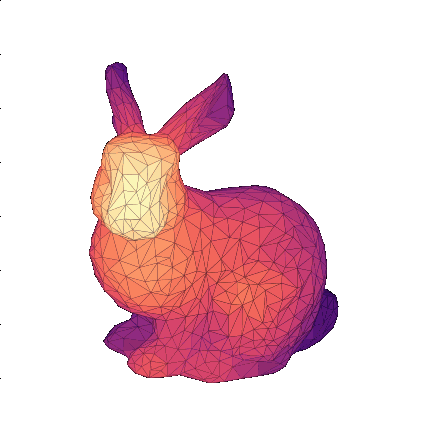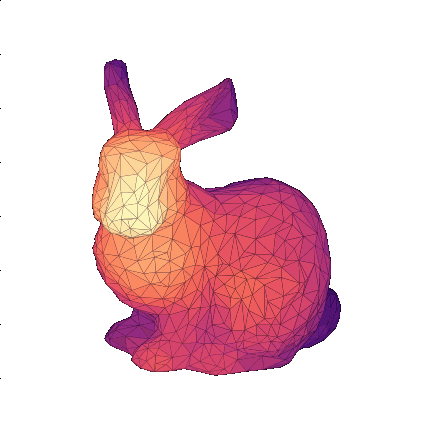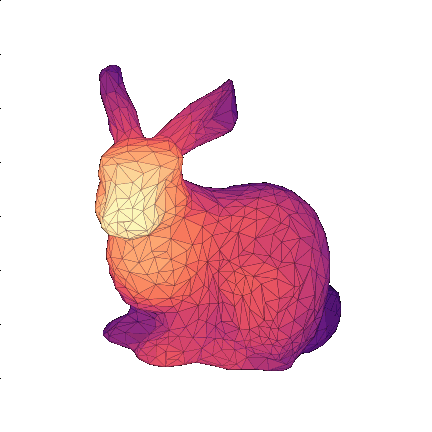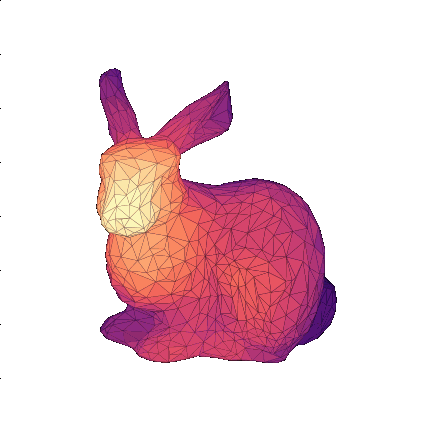
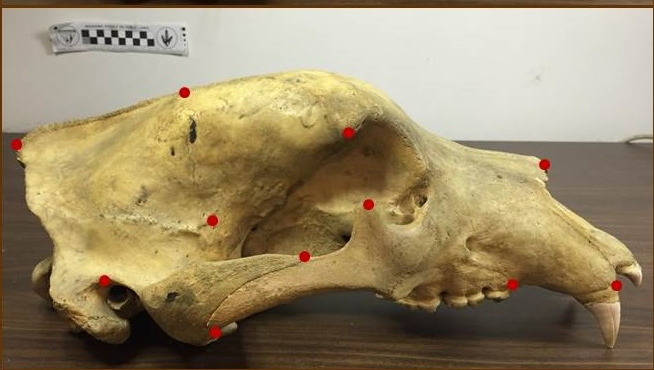
shape $s_0$

shape $s_1$

stoch. evolution $s_0\rightarrow s_1$

dx_t= -\frac12g(x_t)^{kl}\Gamma(x_t)_{kl}dt + \sqrt{g(x_t)^*}dW_t

Riemannian Brownian motion:

Stochastics of shapes

Shapes, deformations and nonlinearity

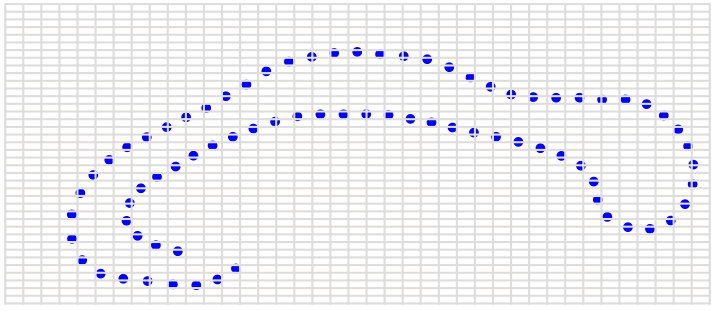
E_{s_0,s_1}(\phi)=R(\phi)+\frac1\lambda S(\phi.s_0,s_1)

action: $\phi.s=\phi\circ s$ (shapes)
$\phi.s=s\circ\phi^{-1}$ (images)

$ \phi $

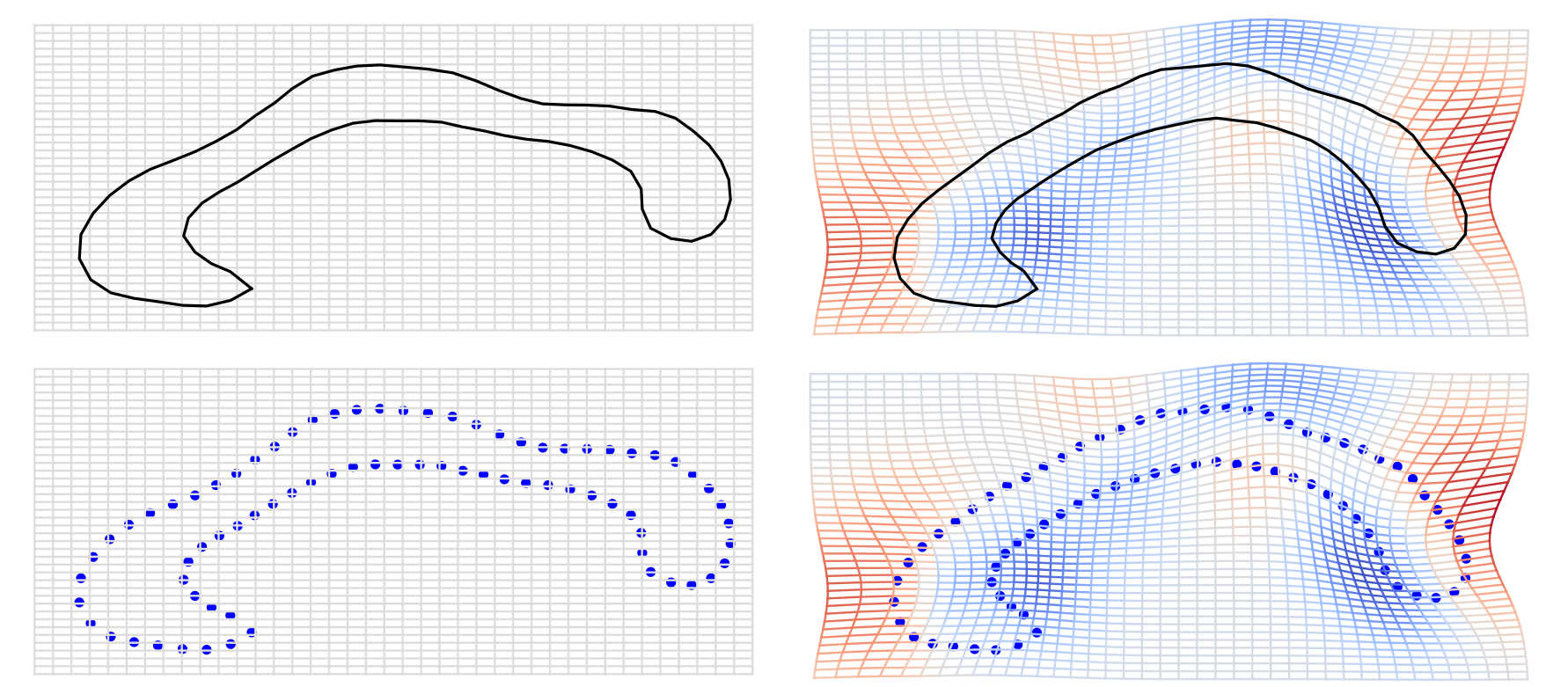
$ \phi $ warp of domain $\Omega$ (2D or 3D space)

landmarks: $s=(x_1,\ldots,x_n)$

curves: $s: \mathbb S^1\to\mathbb R^2$

surfaces: $s: \mathbb S^2\to\mathbb R^3$

s_0

s_1

Geometric + metric view

R(\phi_t)=\int_0^T\|\partial_t \phi_t\|_{\phi_t}^2dt

$ \phi_t:[0,T]\to\mathrm{Diff}(\Omega) $ path of diffeomorphisms (parameter t)

\mathrm{Diff}(\Omega)

\mathrm{Id}_{\mathrm{Diff}(\Omega)}

\phi_t

LDDMM: Grenander, Miller, Trouve, Younes, Christensen, Joshi, et al.

\partial_t \phi_t

\phi

Evolution with noise

\partial_t \phi_t = F(\phi_t)\ \to\ d\phi_t=F(\phi_t)dt\color{blue}{+\sigma(\phi_t) dW_t}

\mathrm{Diff}(\Omega)

\mathrm{Id}_{\mathrm{Diff}(\Omega)}

\phi_t

Markussen,CVIU'07; Budhiraja,Dupuis,Maroulas,Bernoulli'10
Trouve,Vialard,QAM'12;Vialard,SPA'13;Marsland/Shardlow,SIIMS'17
Arnaudon,Holm,Sommer,IPMI'17; FoCM'18; JMIV'19
Arnaudon,v.d. Meulen,Schauer,Sommer'21

geodesic ODE

perturbed SDE

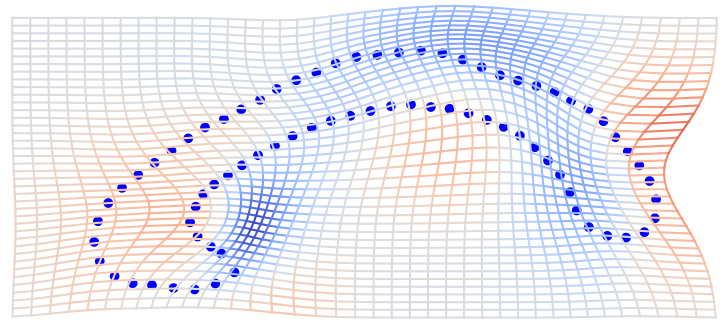
Eulerian shape process / Kunita flow

Shape process:

\[dX_t=K(X_t)\circ dW_t\]

Kernel matrix:

\[K(X_t)^i_j=k(x_i,x_j)\]

Infinite noise:

\[dX_t = Q^{1/2}(X_t) \circ dW_t\]

$Q^{1/2}(X_t)v(x) =\\\qquad \int_{D} k^{Q^{1/2}}(X_t(x)+x,y) v(y) \, dy$

$X_t$ landmarks at time $t$:

\[X_t=\begin{pmatrix}x_{1,t}\\y_{1,t}\\\vdots\\x_{n,t}\\y_{n,t}\end{pmatrix}\]

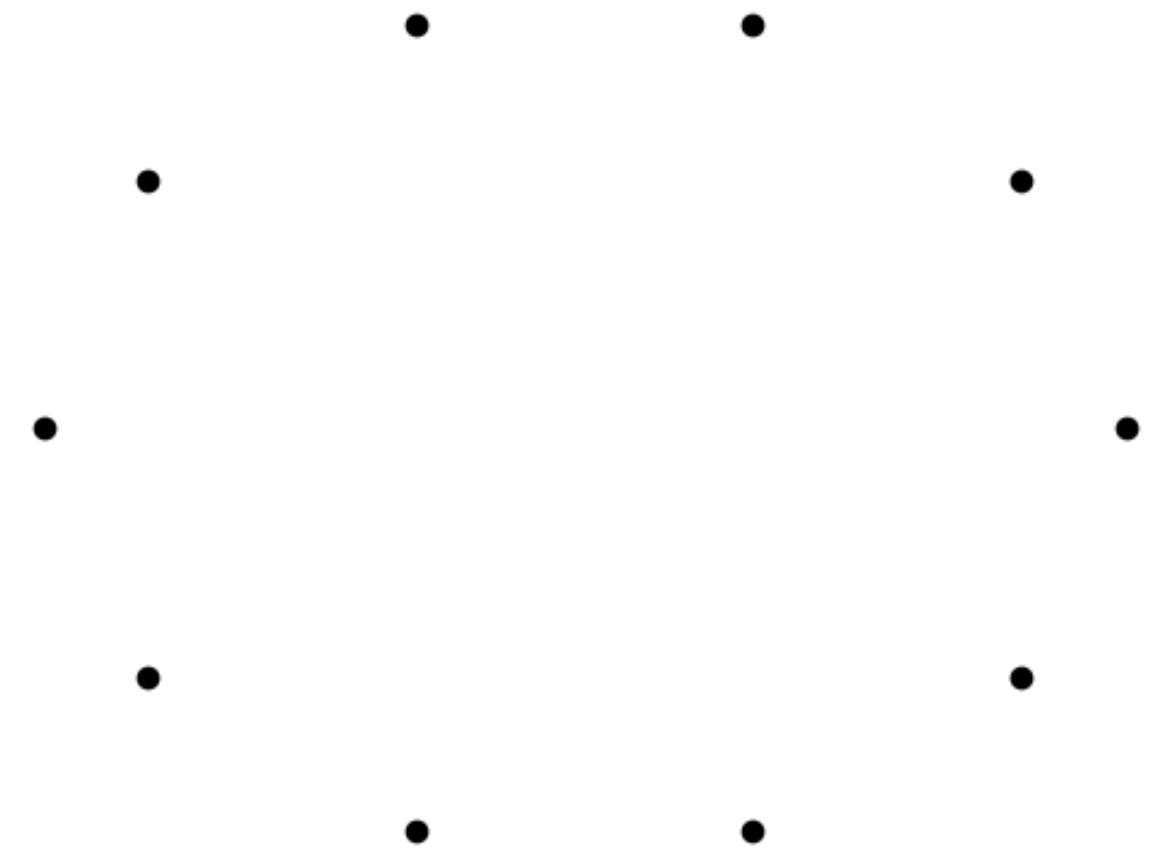
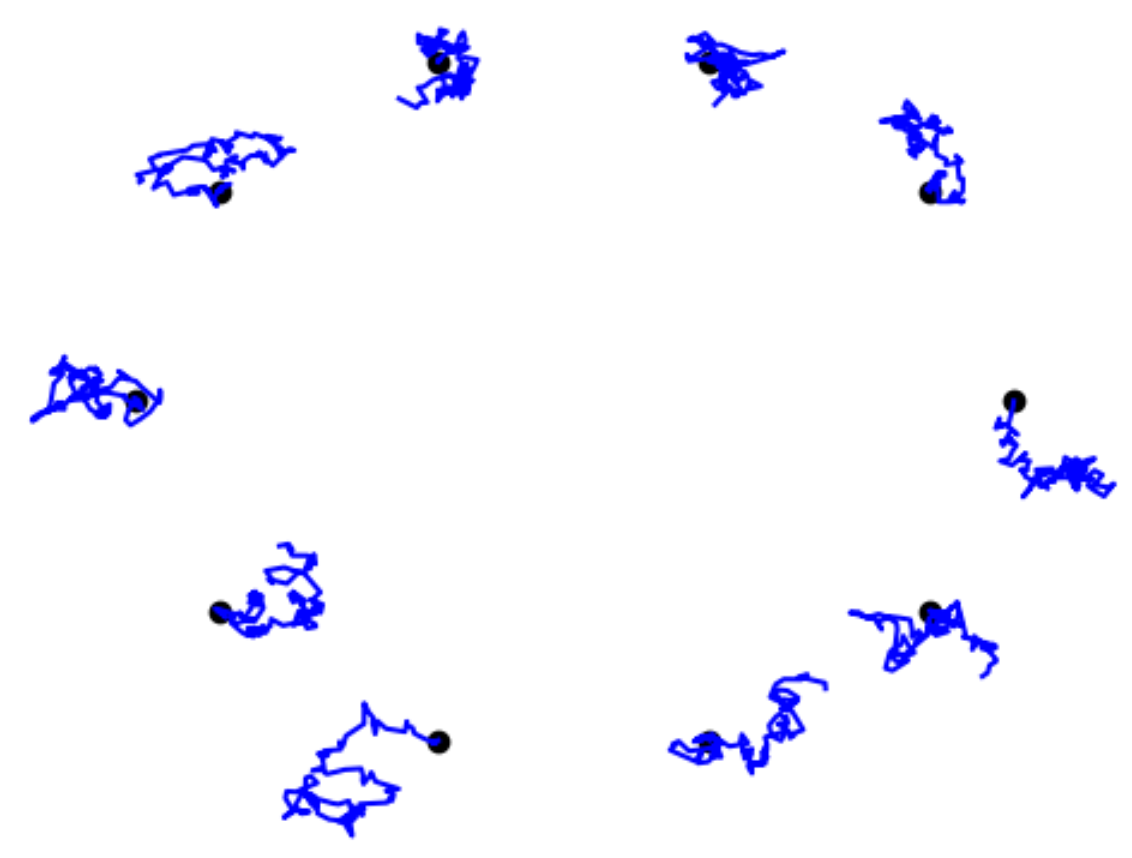
$t=\frac12$

$t=3$

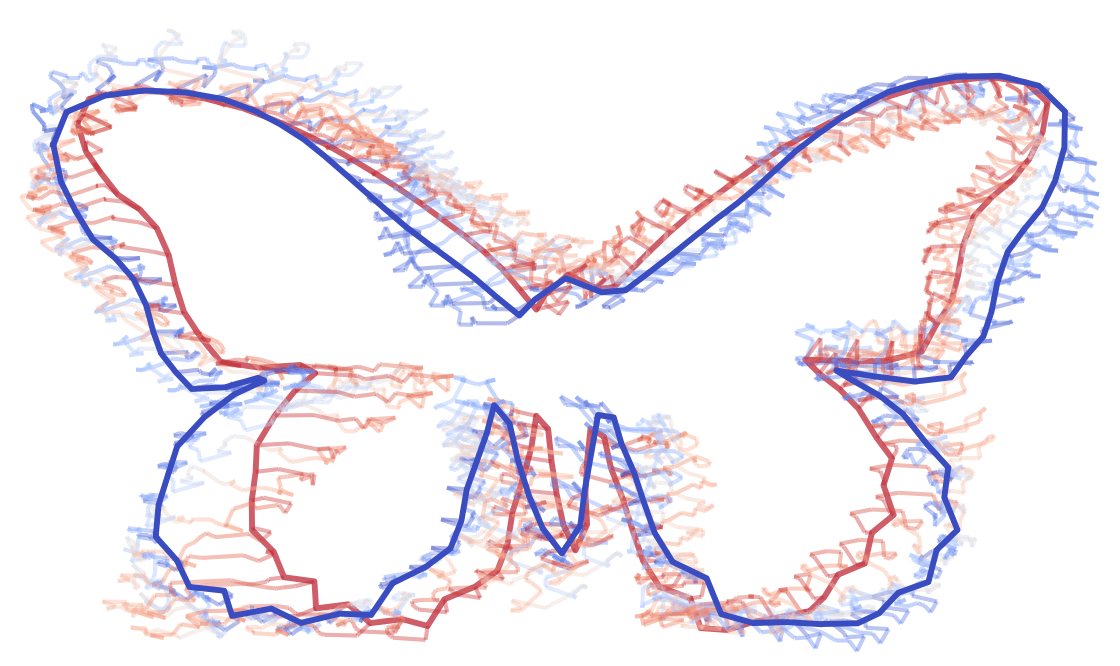
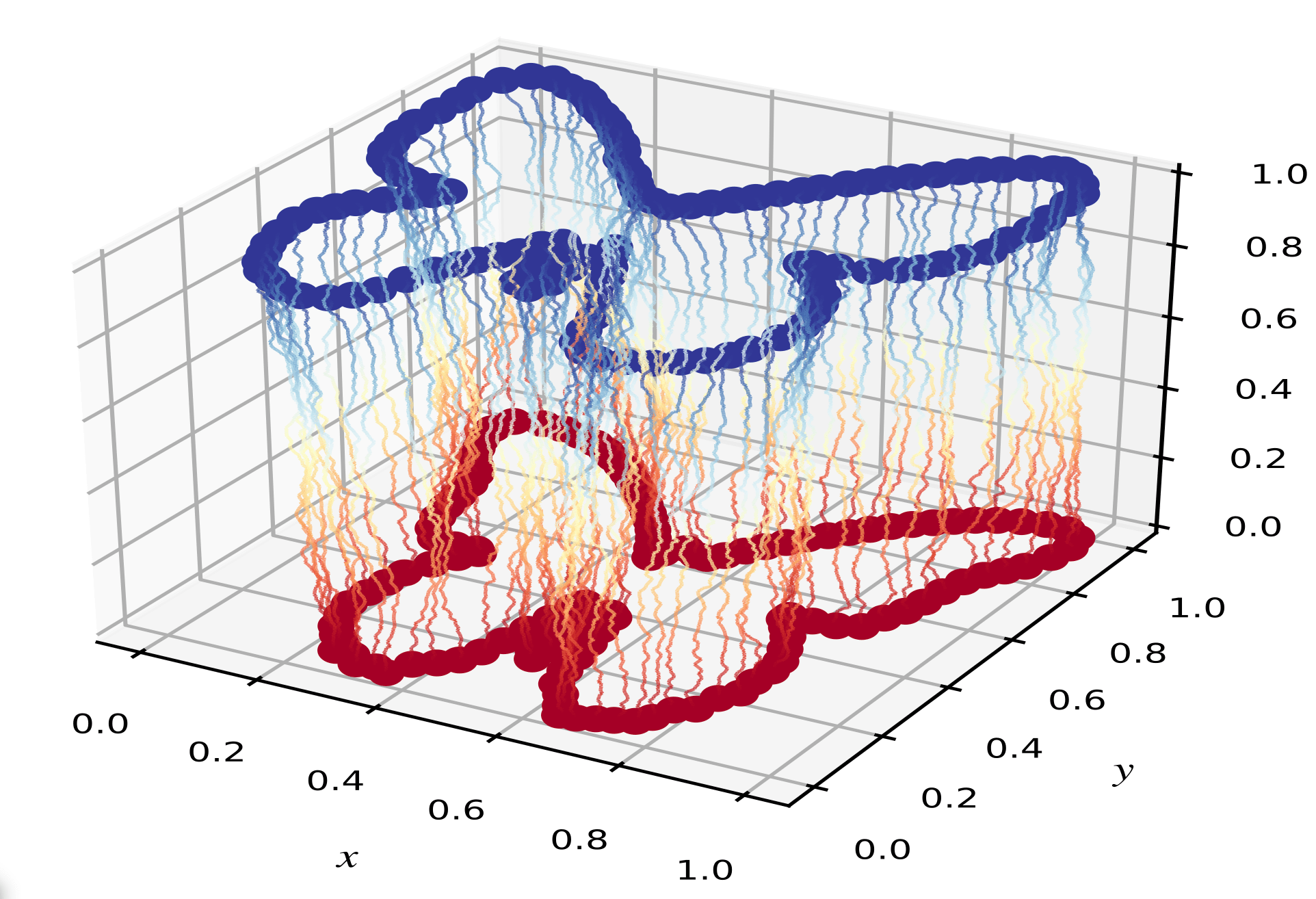
Inference: Data conditional processes

$X_t$ generates distribution $p(\cdot|X_0)$
given observed shape $v$, we wish for $T>0$ to generate $X_t|X_T=v$ - a bridge

$X_t$ (no conditioning)

$X_t|X_T=v$ (conditioned)

Guided bridges

dx_t = b(t,x_t)dt +\sigma(t,x_t)dW_t

Delyon/Hu 2006:

$\sigma$ invertible:

guided bridge proposal$$dy_t = b(t,y_t)dt - \frac{y_t-v}{T-t}dt + \sigma(t,y_t)dW_t$$
$y_T=v$ a.s.
$x_t|x_T=v$ absolute continuous wrt. $y_t$
$\mathbb E_{x_t|x_T=v}[f(x_t)]\propto \mathbb E_{y_t}[f(y_t)\varphi(y_t)]$

$v$

$x_0$

$x_t$

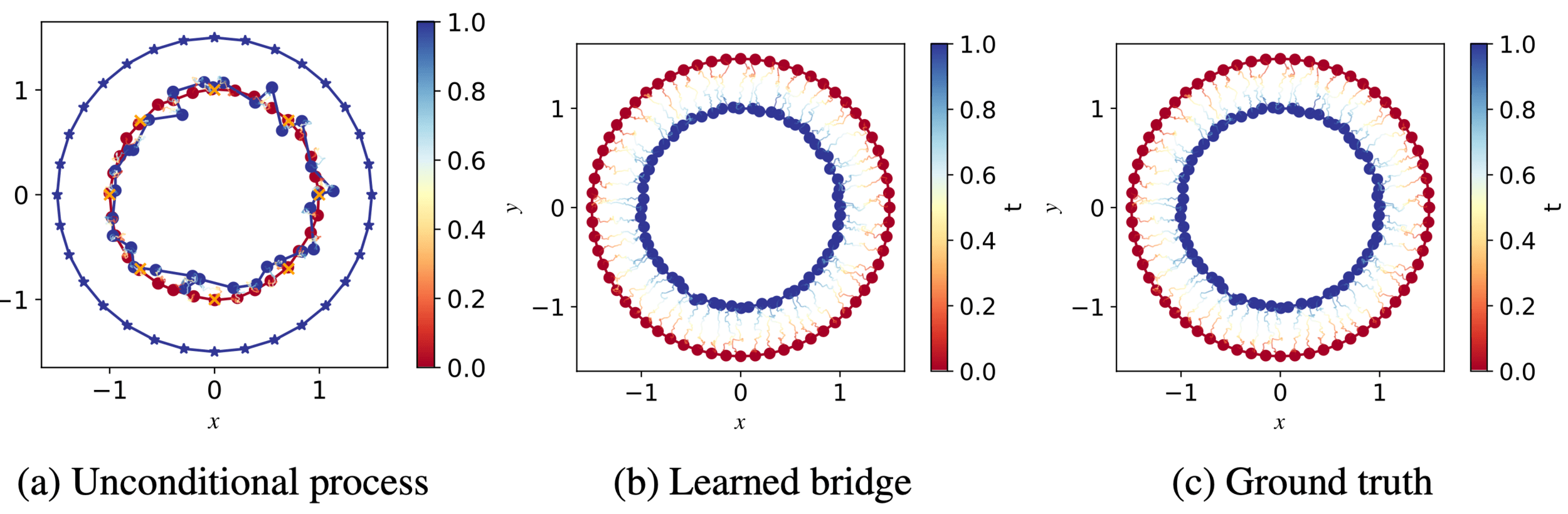
Guided bridges on manifolds

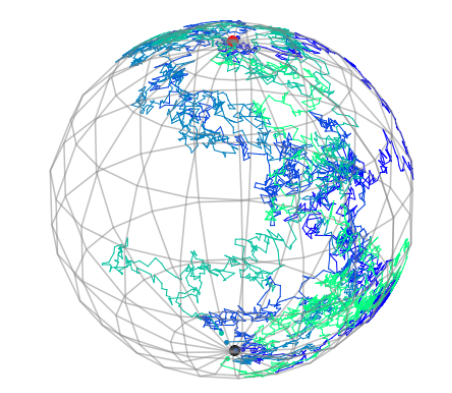
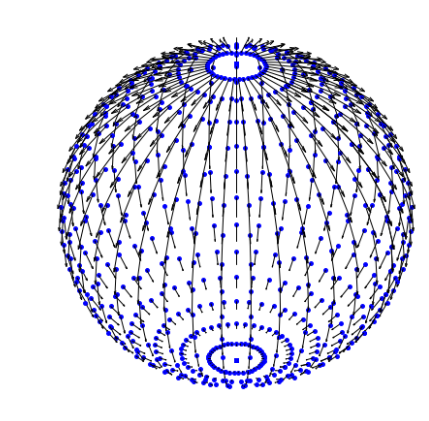
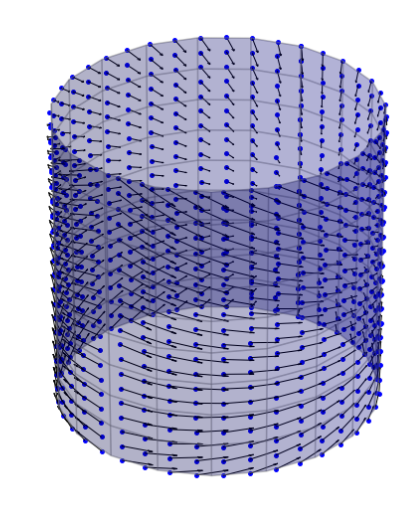
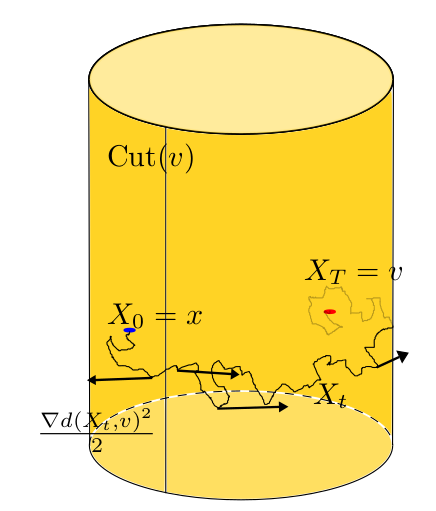
Jensen, Sommer 2021, 2022

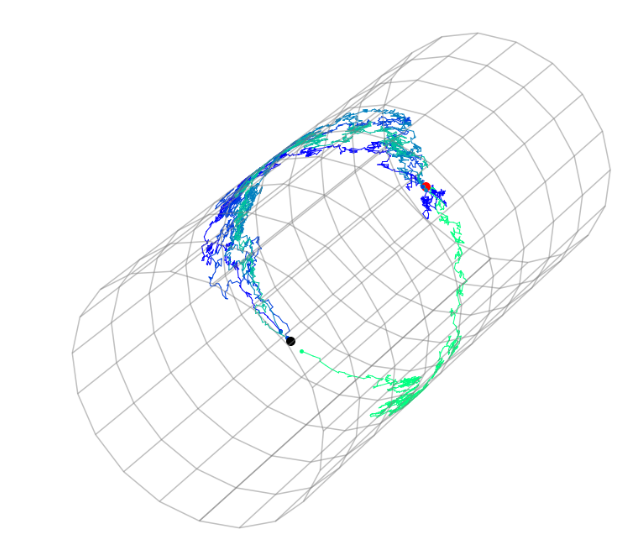
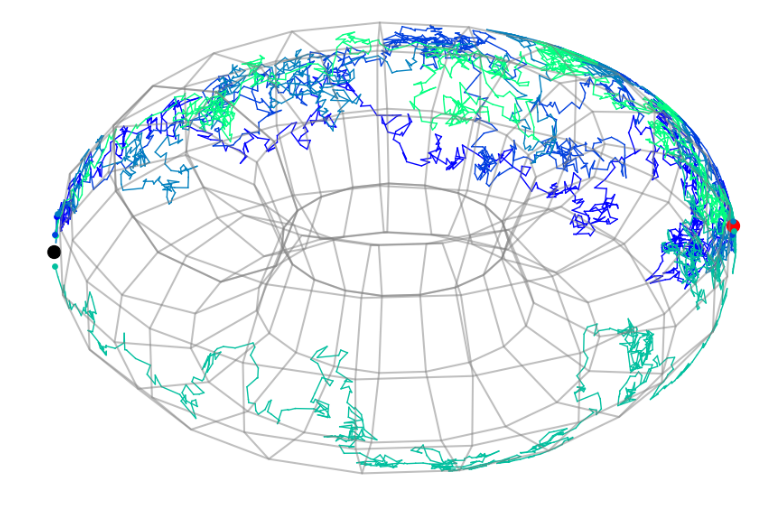
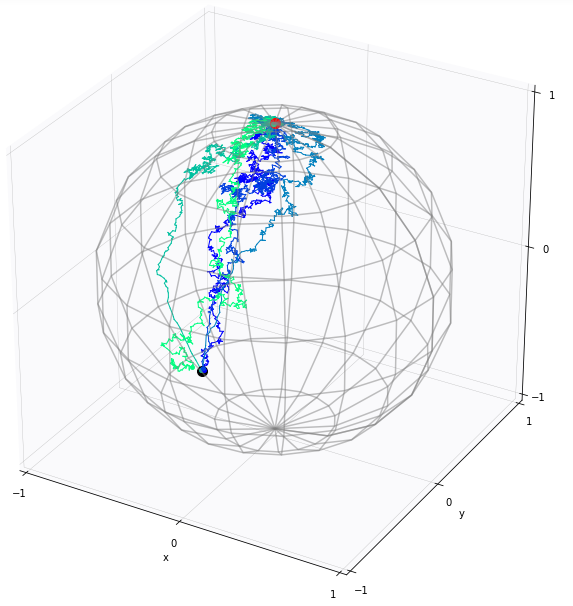
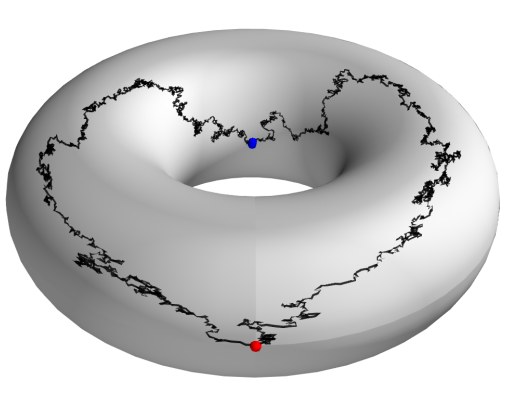
Guided bridges on manifolds

Heat kernel approximations

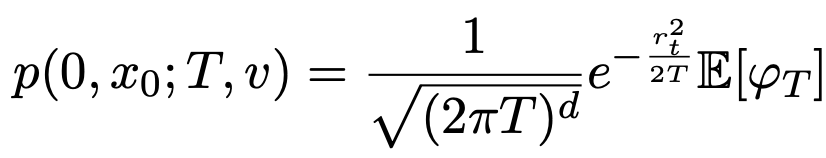
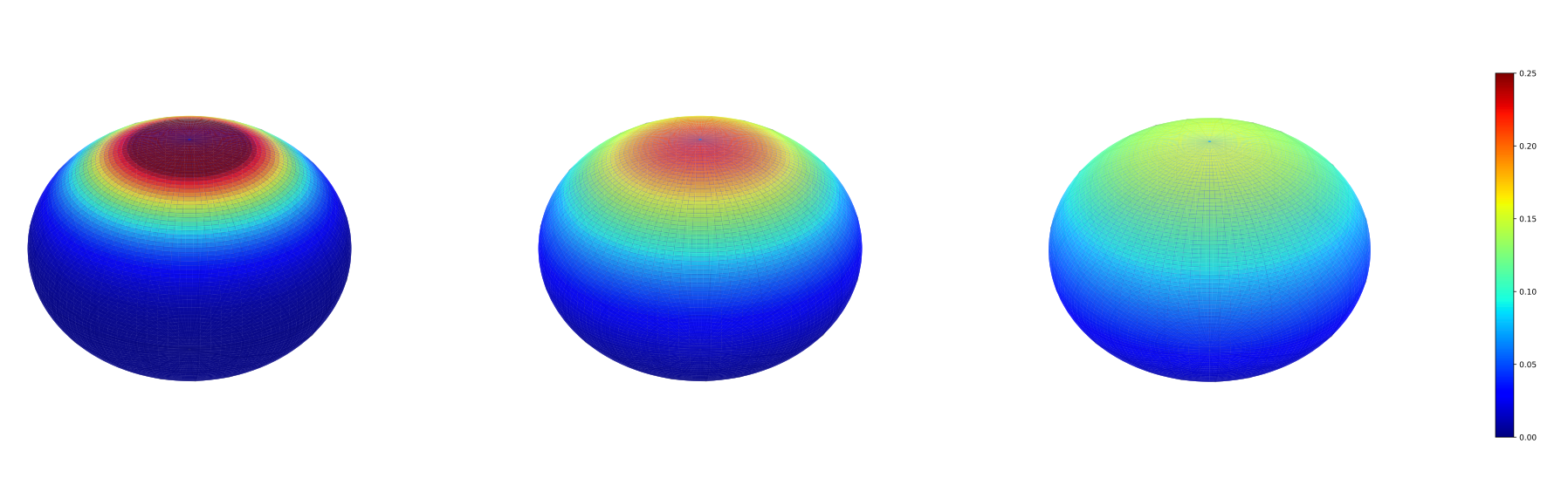
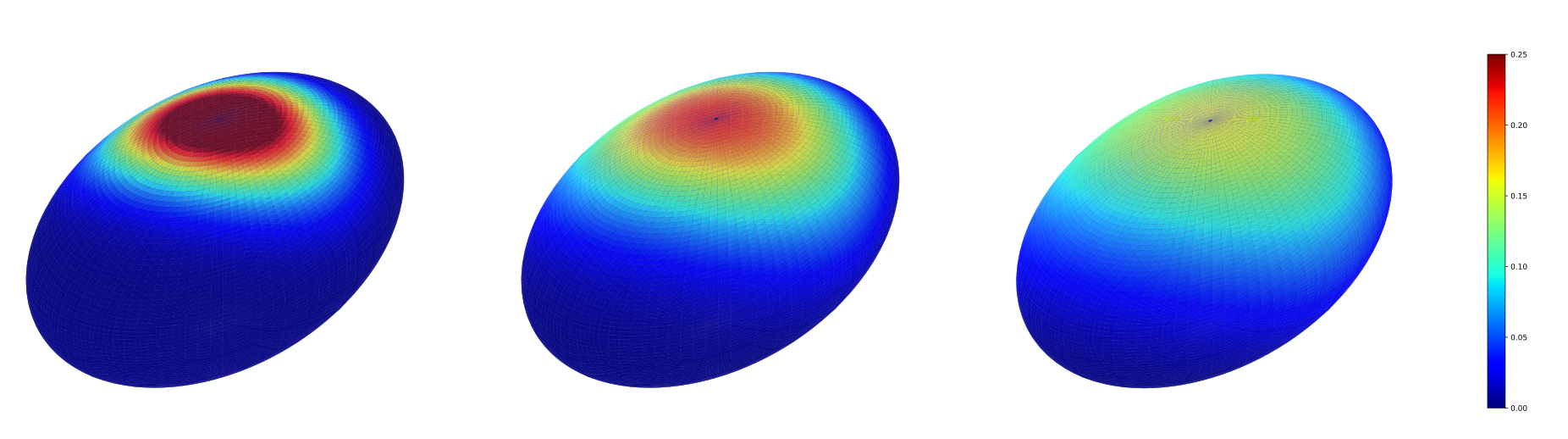
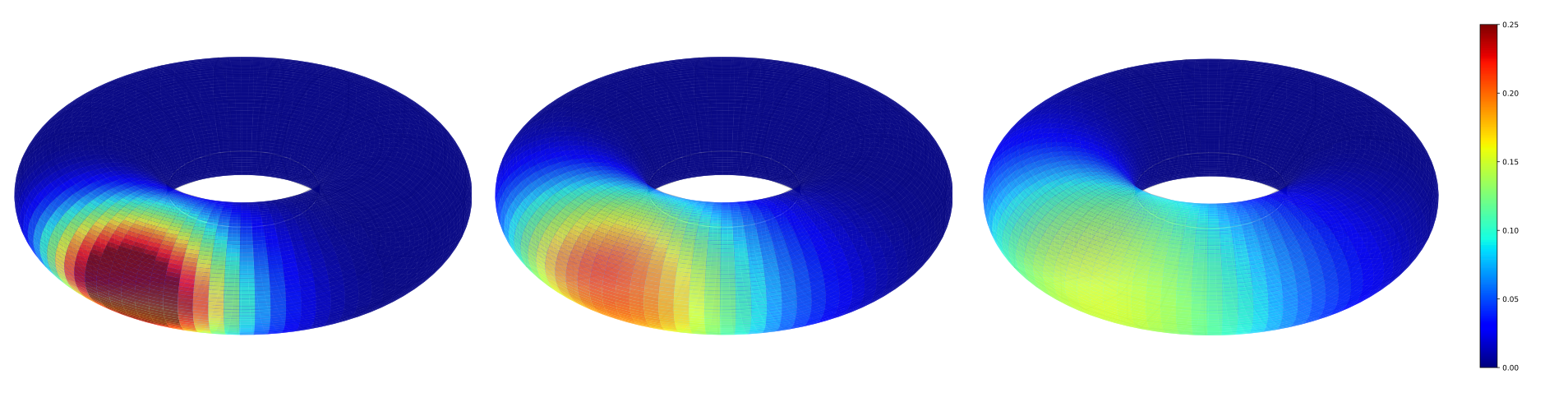
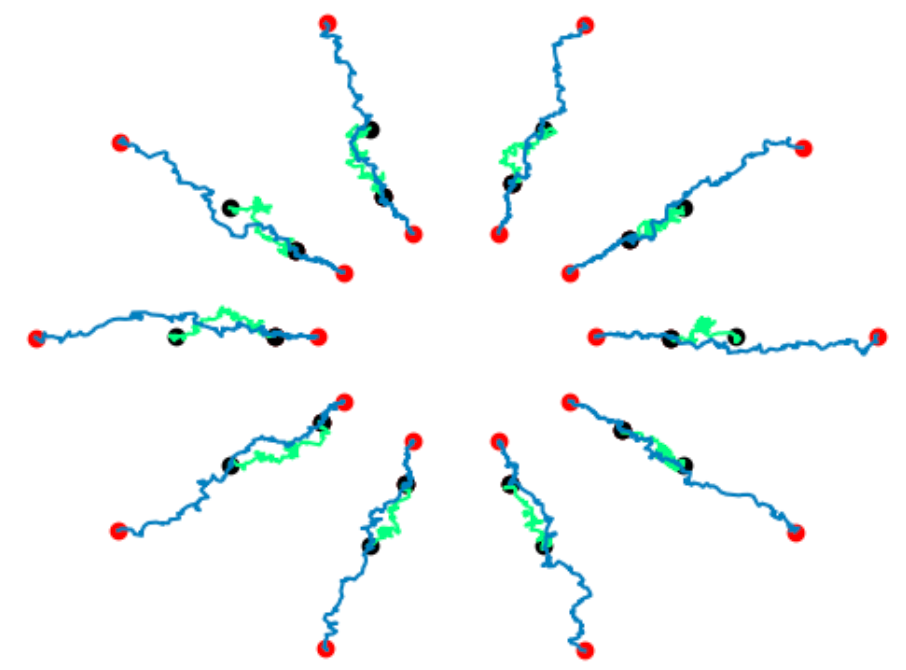
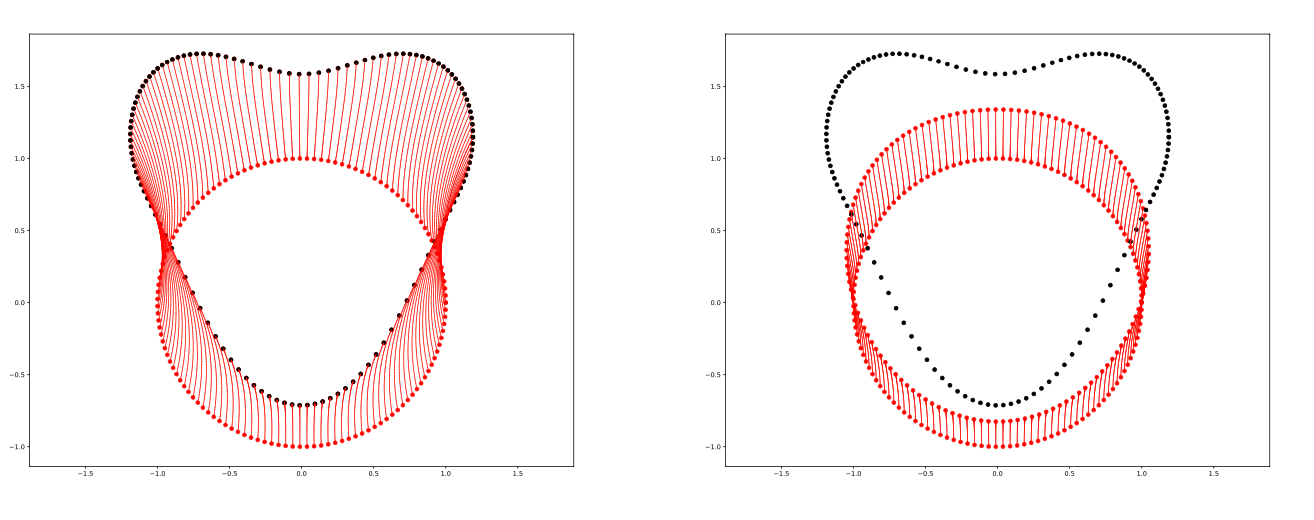
Conditioned shape process

Conditioning on hitting target $v$ at time $T>0$:

\[X_t|X_T=v\]

Ito stochastic process:

\[dx_t=b(t,x_t)dt\qquad\qquad\qquad\qquad\quad\\+\sigma(t,x_t)dW_t\]

True bridge:

\[dx^*_t=b(t,x^*_t)dt+a(t,x^*_t)\nabla_x\log \rho_t(x^*_t)dt\\+\sigma(t,x^*_t)dW_t\]

Score $\nabla_x\log \rho_t$ intractable....

\[\rho_t(x)=p_{T-t}(v;x)\]

\[a(t,x)=\sigma(t,x)\sigma(t,x)^T\]

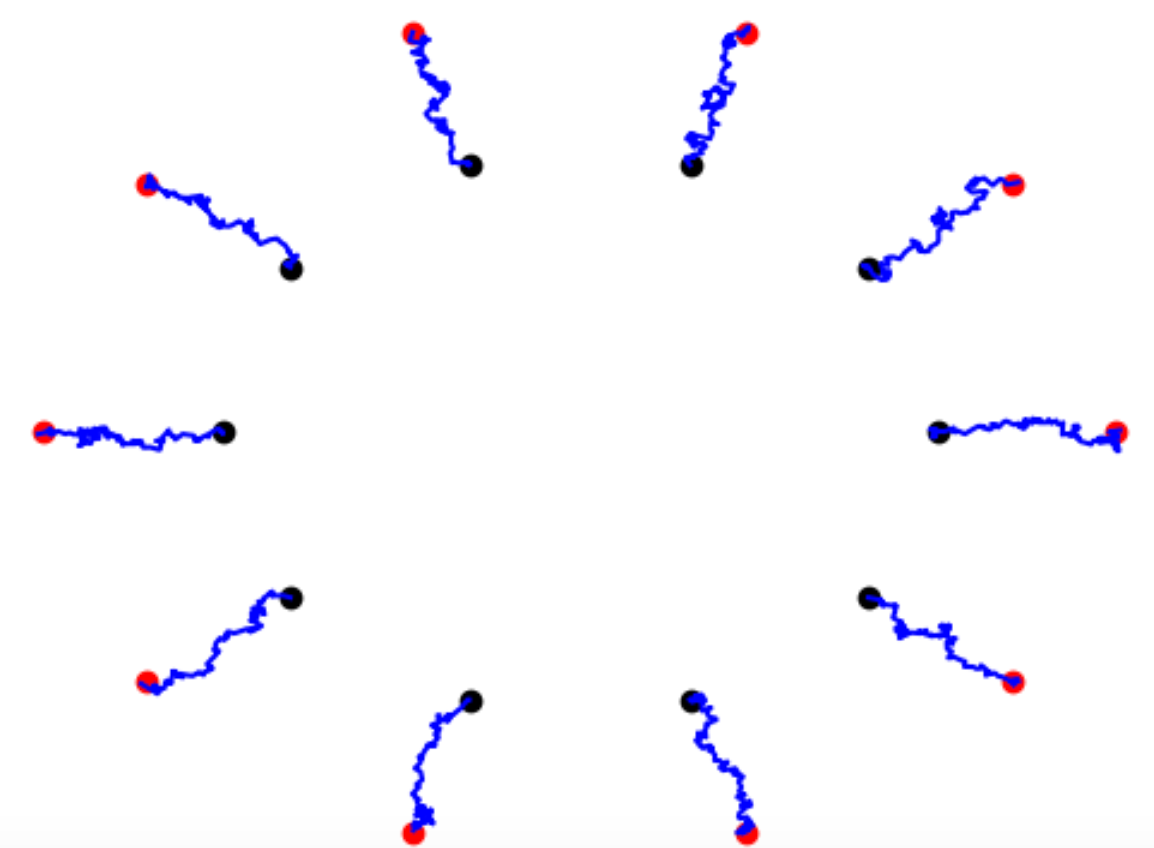
black: $X_0$, red: $v$

Auxilary process:

\[d\tilde{x}_t=\tilde{b}(t,\tilde{x}_t)dt+\tilde{\sigma}(t,\tilde{x}_t)dW_t\]

Approximate bridge:

\[dx_t^\circ=b(t,x_t^\circ)dt+a(t,x_t^\circ)\nabla_x\log \tilde{\rho}_t(x_t^\circ)dt\\+\sigma(t,x_t^\circ)dW_t\]

E.g. linear process, score $\nabla_x\log \tilde{\rho}_t$ is known in closed from

(almost) explicitly computable likelihood ratio:

\[\frac{d\mathbb P^*}{d\mathbb P^\circ}=\frac{\tilde{\rho}_T(v)}{\rho_T(v)}\Psi(x_t^\circ)\]

Backward filtering, forward guiding: van der Meulen, Schauer et al.

Ito stochastic process:

\[dx_t=b(t,x_t)dt+\sigma(t,x_t)dW_t\]

Bridge process:

\[dx^*_t=b(t,x^*_t)dt+a(t,x^*_t)\nabla_x\log \rho_t(x^*_t)dt\\+\sigma(t,x^*_t)dW_t\]

Score $\nabla_x\log \rho_t$ intractable....

Backwards filtering, forward guiding bridges

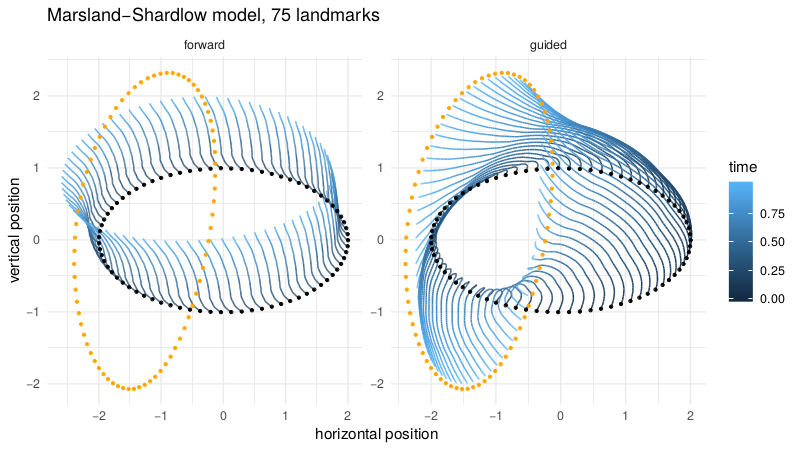
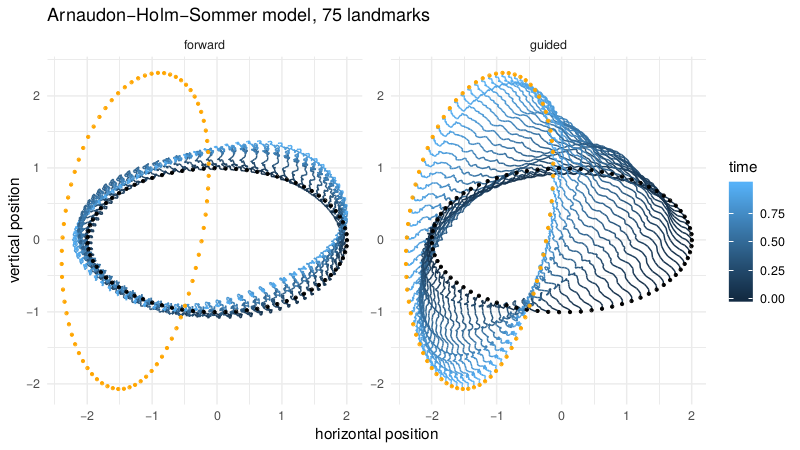
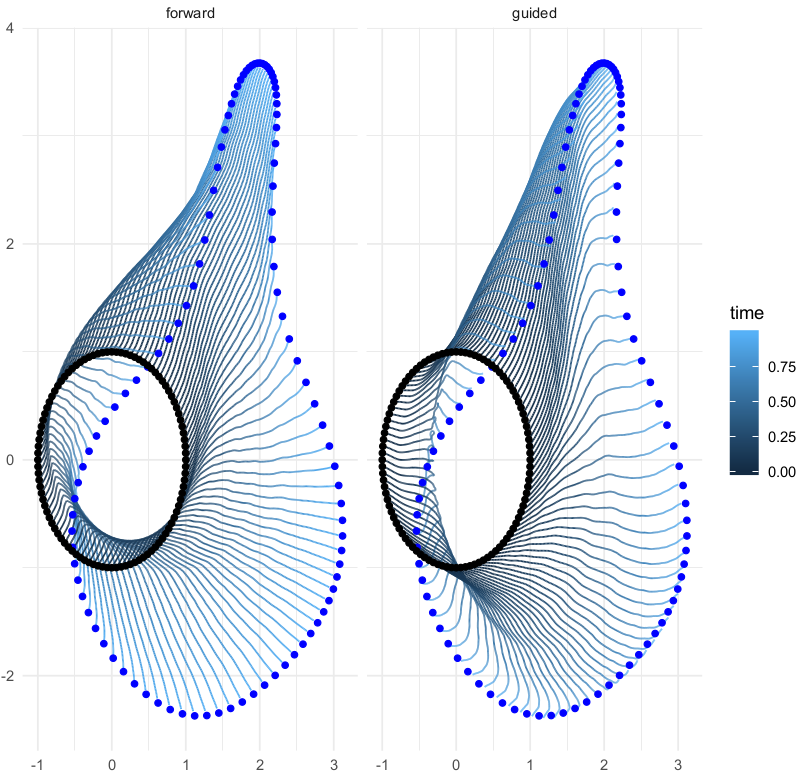
v.d. Meulen,Schauer,Arnaudon,Sommer,SIIMS'22

From single edges to trees

Bridge:

Leaf conditioning:

$x_0$

$v$

$x_0$

$h$

$v_1$

van der Meulen, Schauer'20; van der Meulen'22
Stoustrup, Nielsen, van der Meulen, Sommer

$v_2$

recursive,leaves to root

Backwards filter:

root to leaves

Forward guiding:

$v$

$v_1$

$v_2$

$h$

$x_0$

Felsenstein's pruning algorithm for shapes

Brown. motion

branch (independent children)

incorporate leaf observations $x_{V_T}$ into probabilistic model:
$p(X_t|x_{V_T})$

Doob’s h-transform

$h_s(x)=\prod_{t\in\mathrm{ch(s)}}h_{s\to t}(x)$

conditioned process $X^*_t$

approximations $\tilde{h}$

guided process $X^\circ_t$

Upwards message passing

Messages:

approximation of h-transform \[h(x,t)=e^{c+Fx+x^THx}\](Doob's h function)

Up:

propagate c,F,H

Fuse:

sum c,F,H

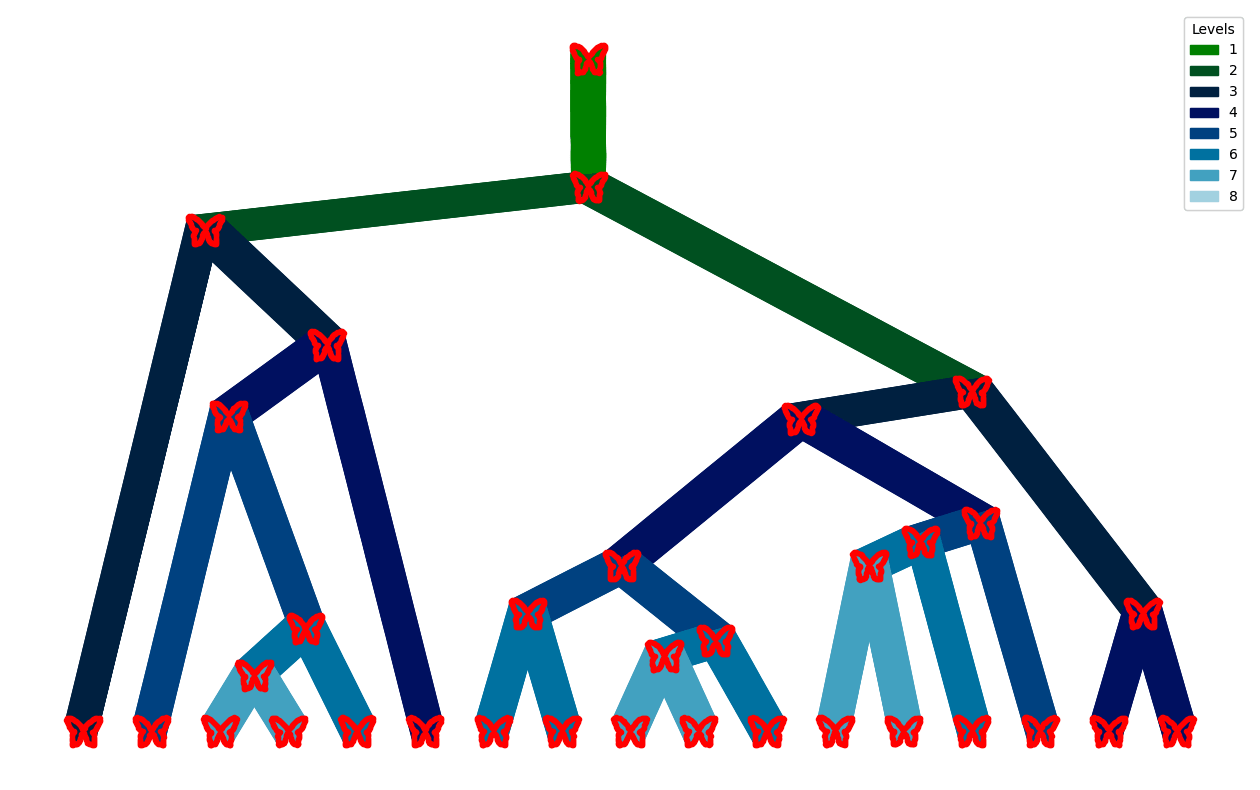
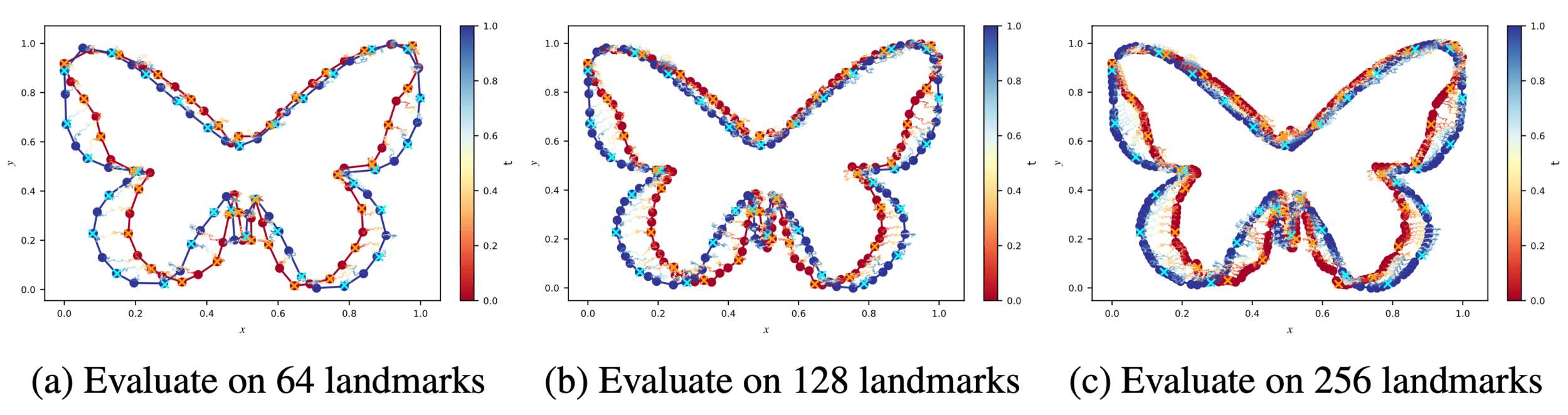
Backwards filtering, forward guiding butterflies

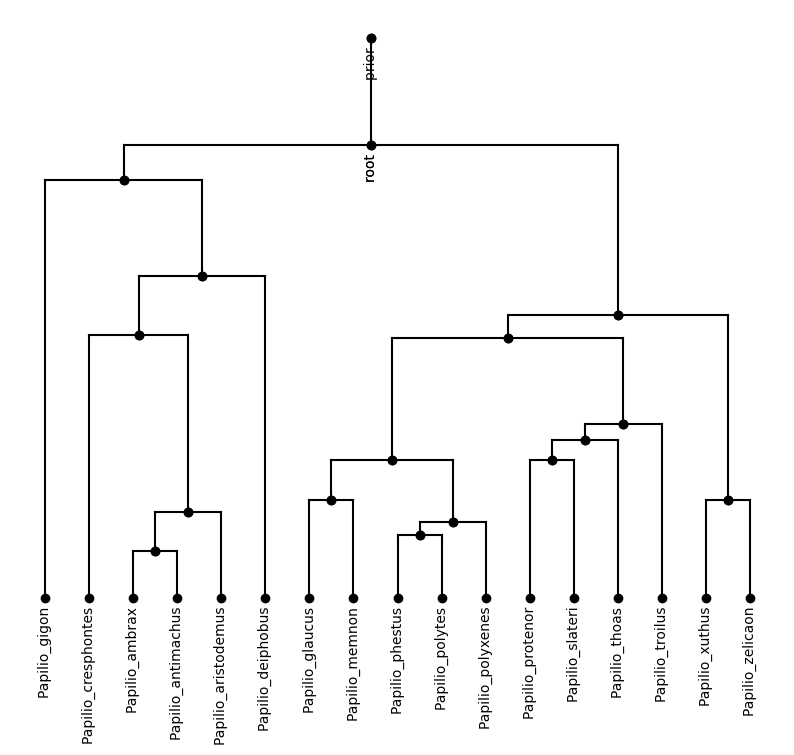
v.d. Meulen,Schauer,Sommer,'25

Parameter inference with MCMC

sample parameters (e.g. kernel width, amplitude)

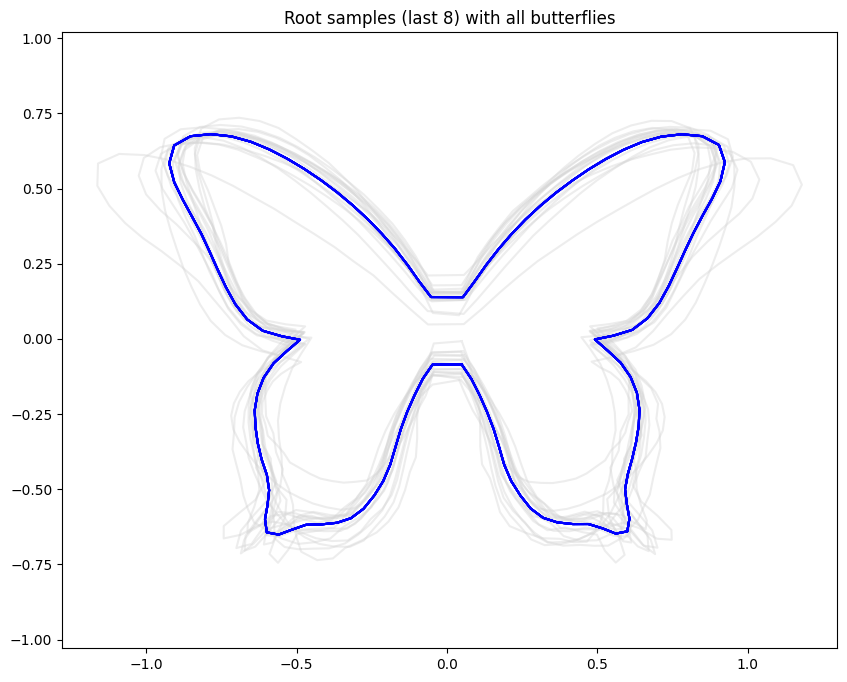
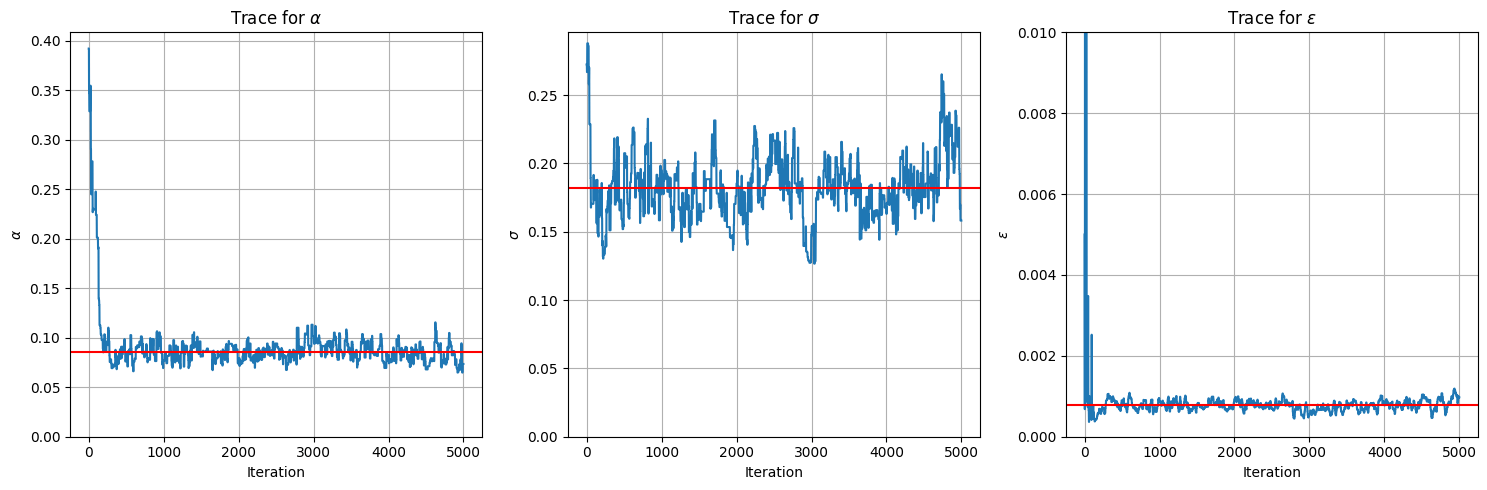
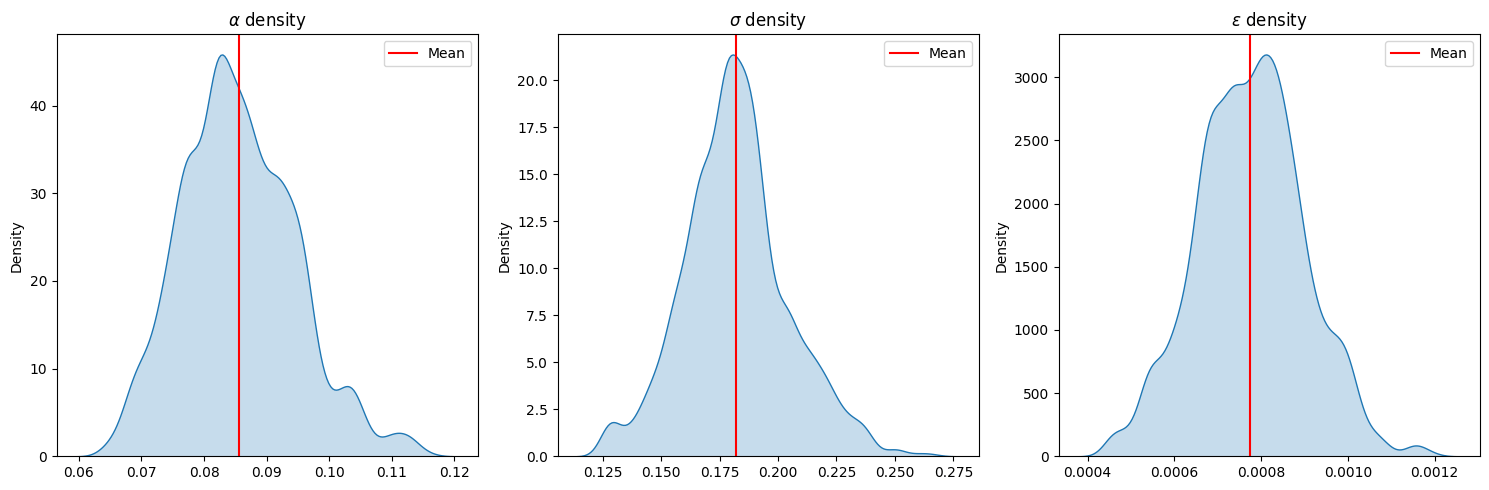
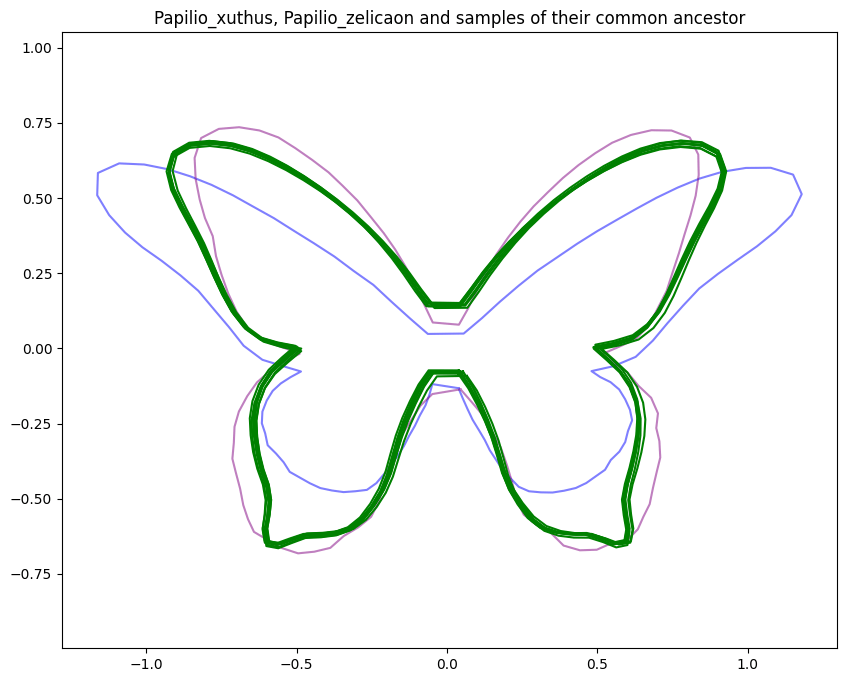
v.d. Meulen,Schauer,Arnaudon,Sommer,SIIMS'22

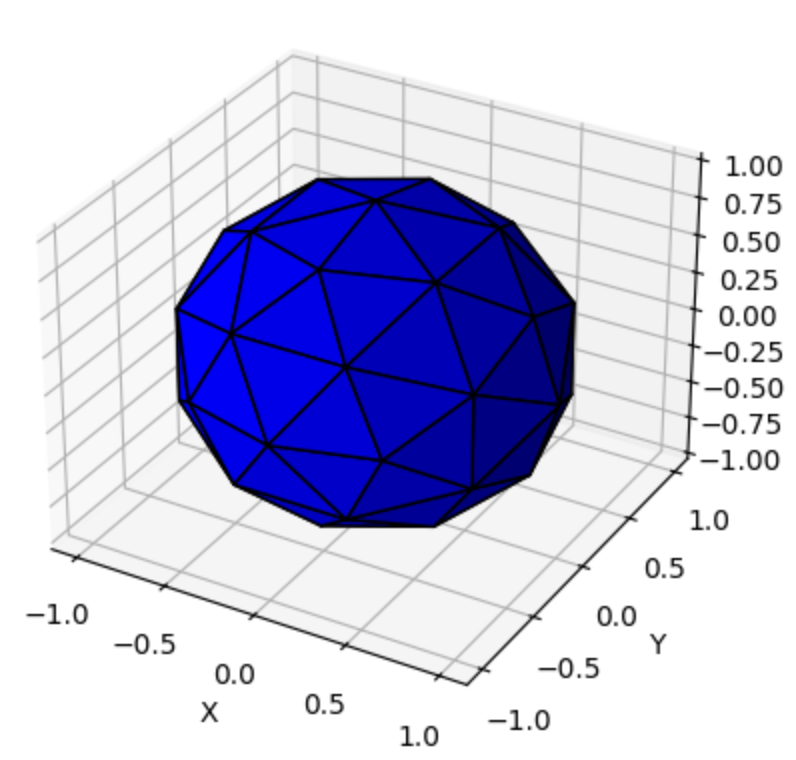
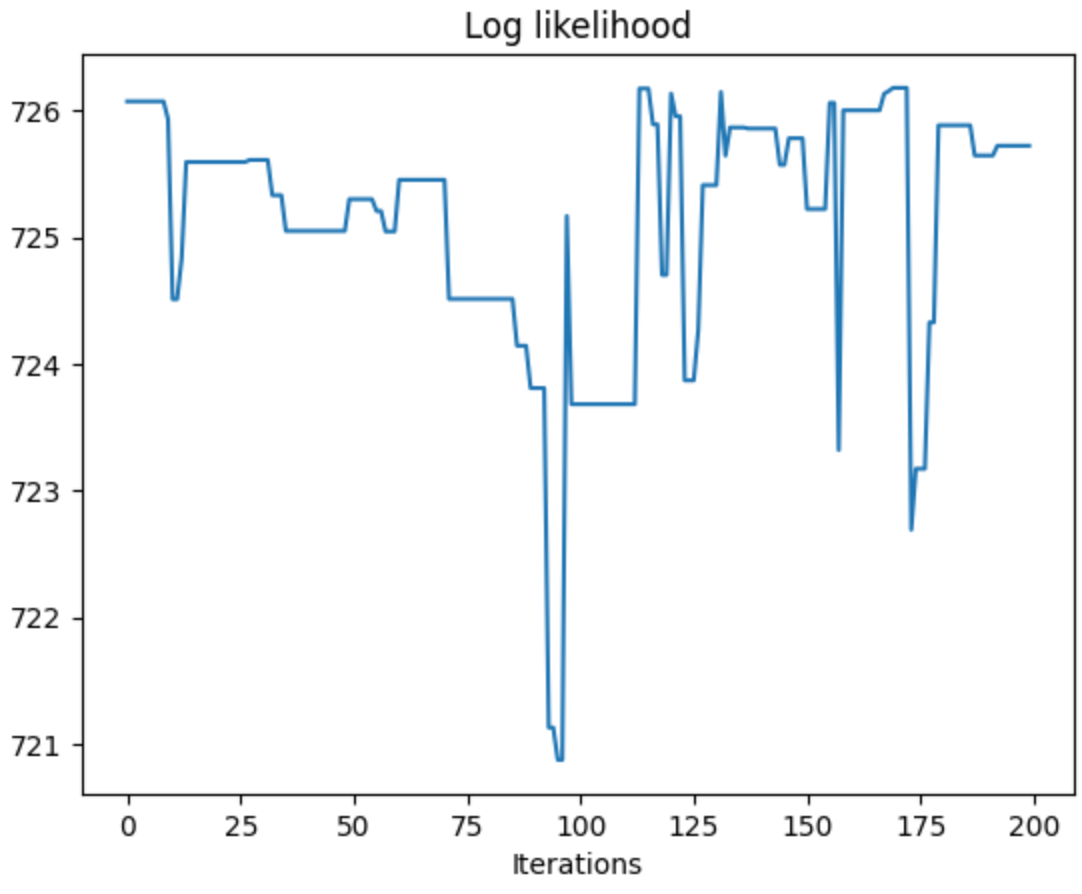
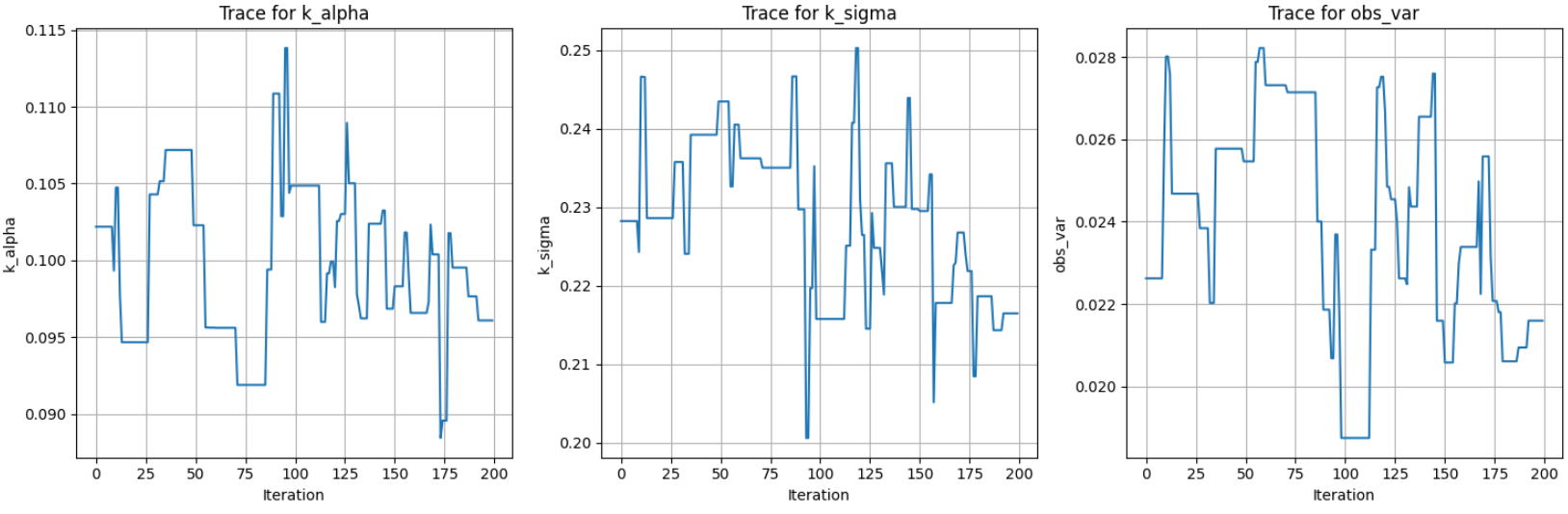
Parameter inference with MCMC

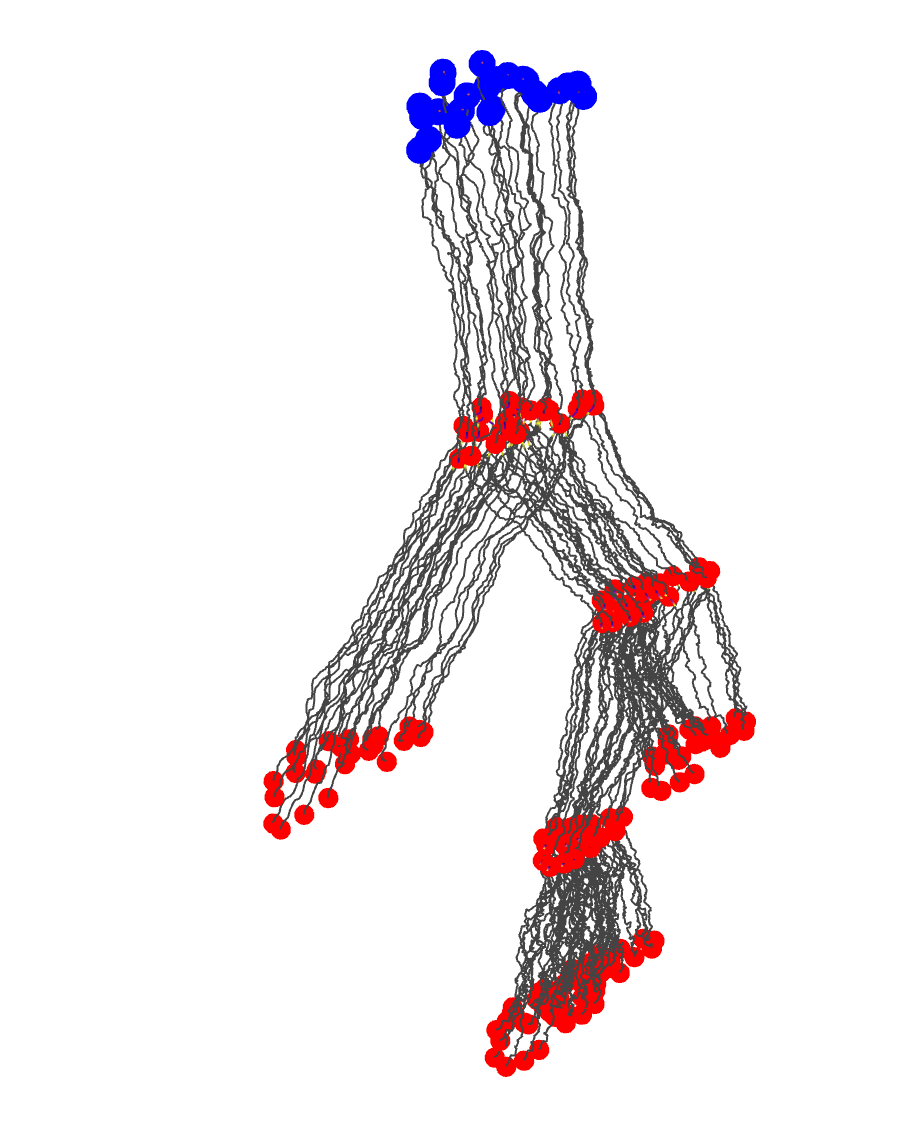
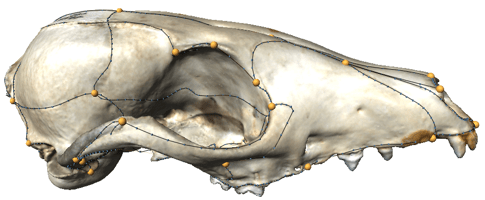
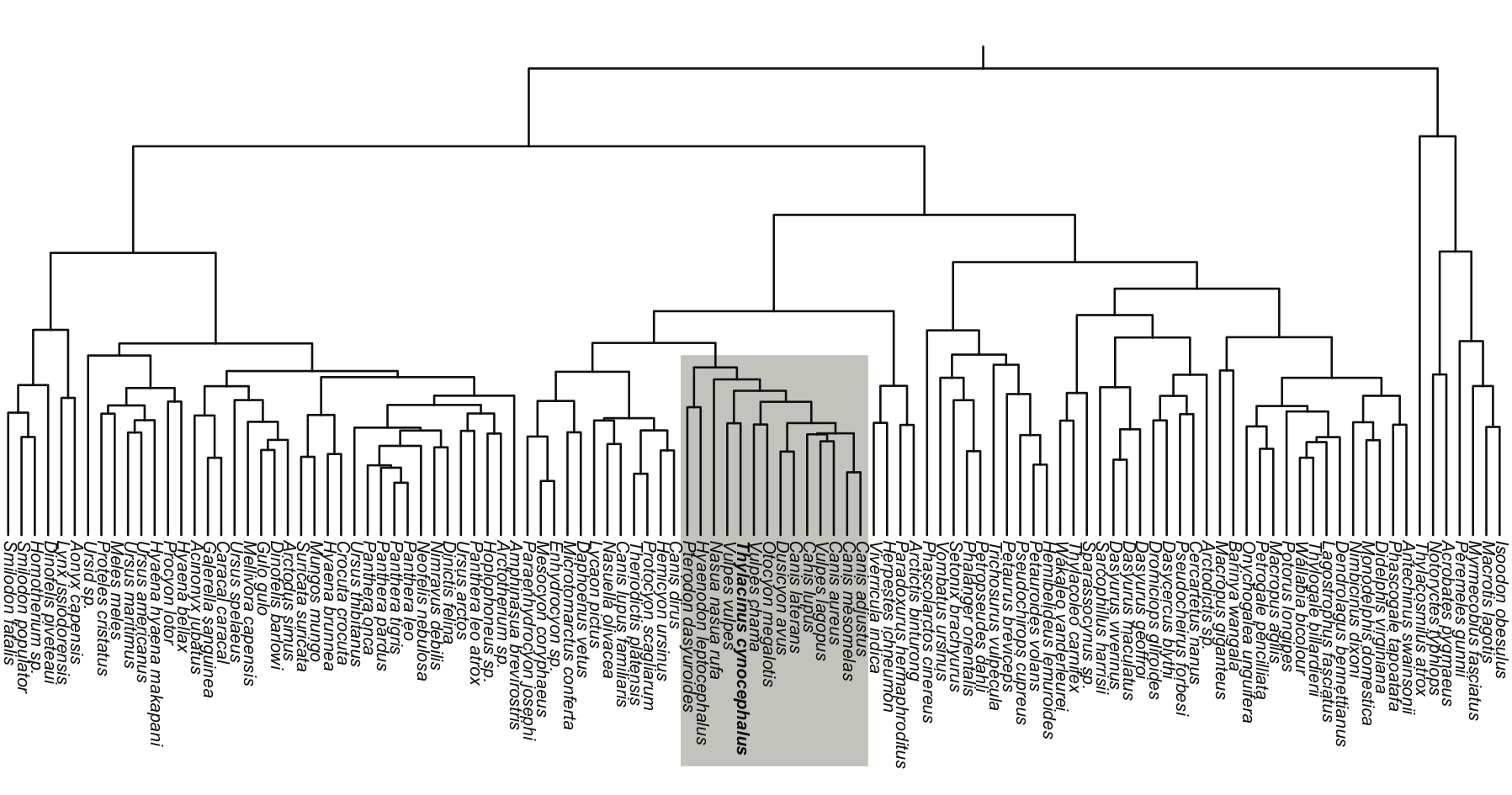
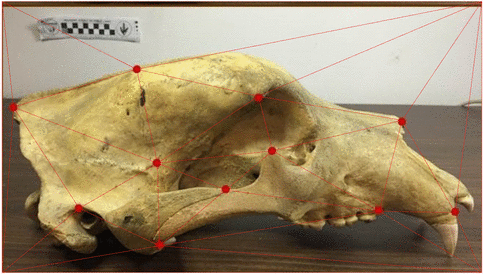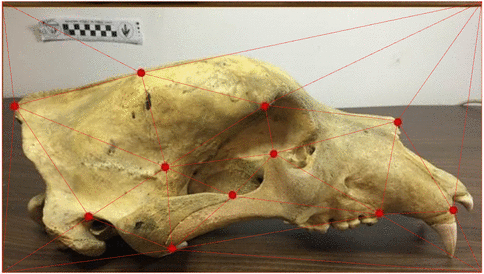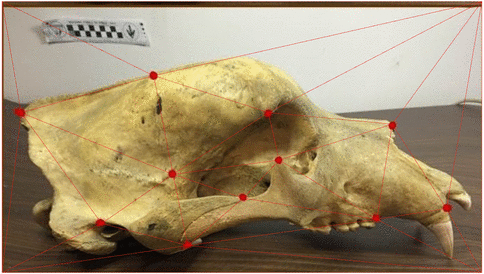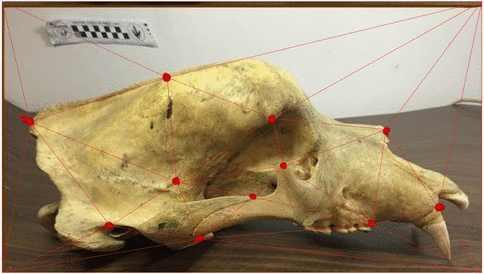
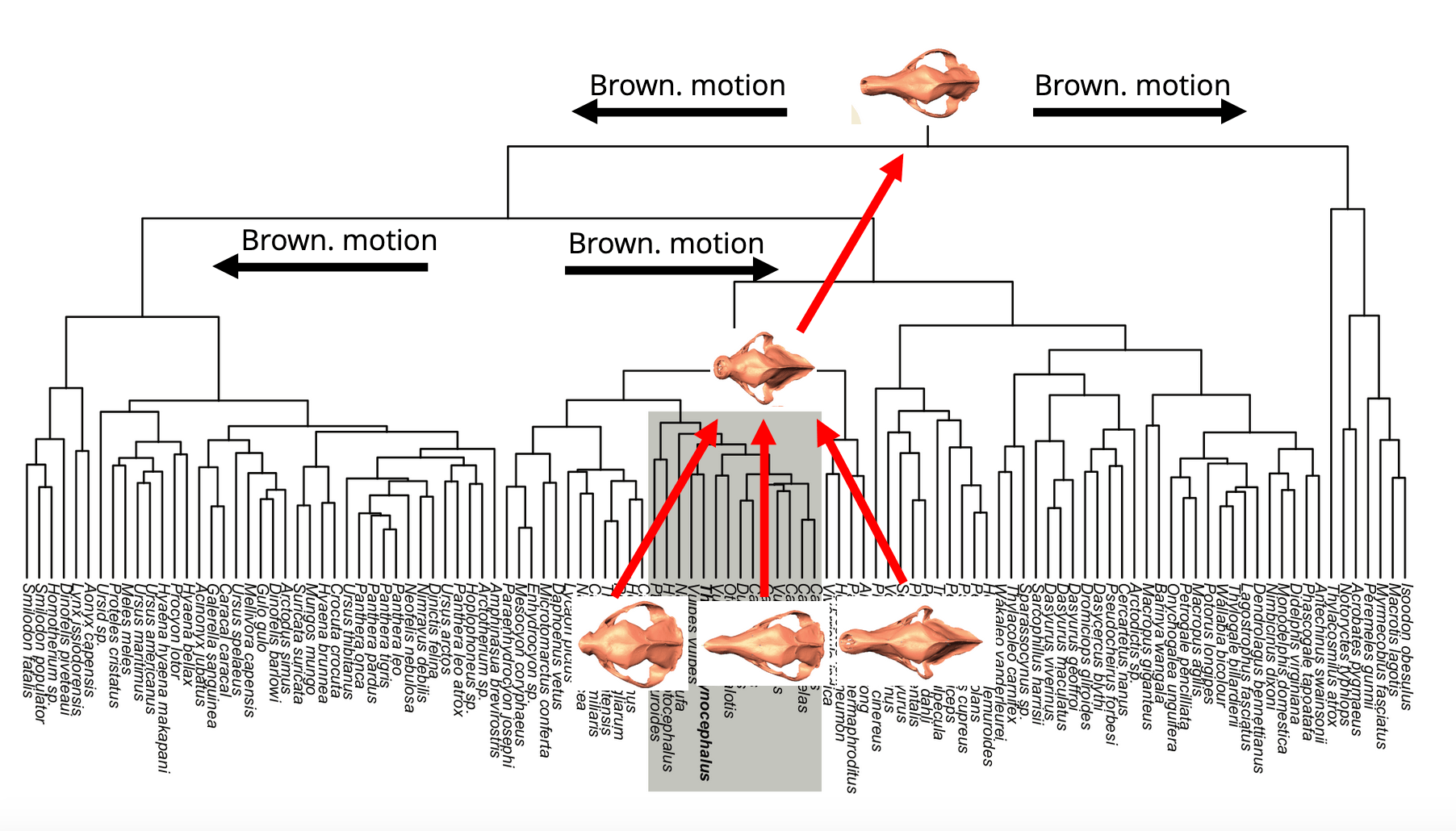
Canidae skulls

Severinsen, Hipsley, Nielsen, Sommer

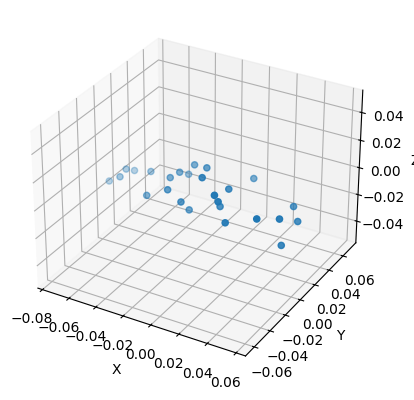
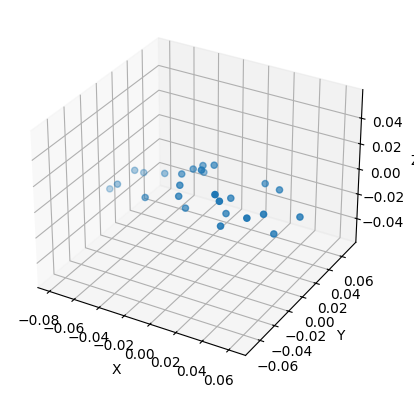
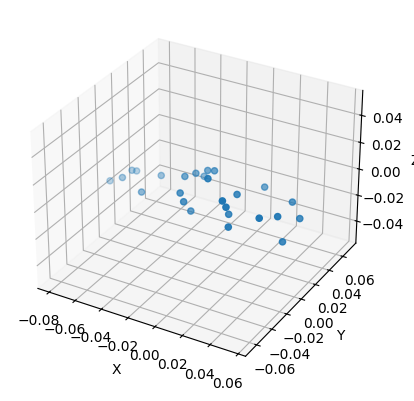
Felsenstein's pruning algorithm for shapes

Brown. motion

1) What is a shape Brownian motion?

2) How do we condition the nonlinear process on shape observations?

3) How do we perform inference in the full model?

Other takes:
Upwards LDDMM: recursive shape matching

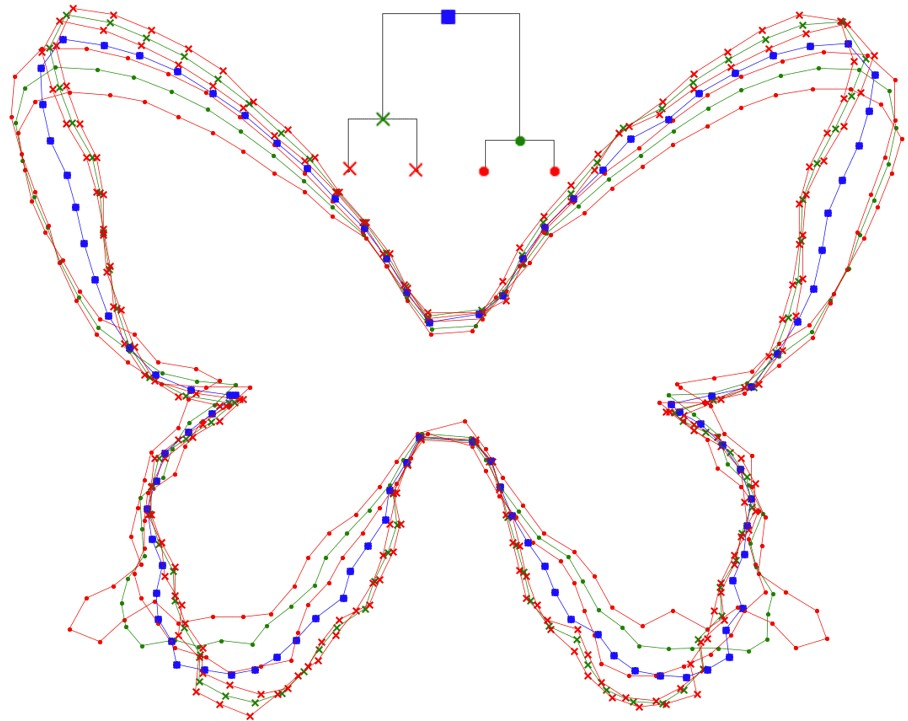
Severinsen, Hipsley, Nielsen, Sommer

Infinite dimensions and score learning

Train a neural network to learn the score in the bridge SDE:

\[dx^*_t=b(t,x^*_t)dt+a(t,x^*_t)\nabla_x\log \rho_t(x^*_t)dt\\+\sigma(t,x^*_t)dW_t\]

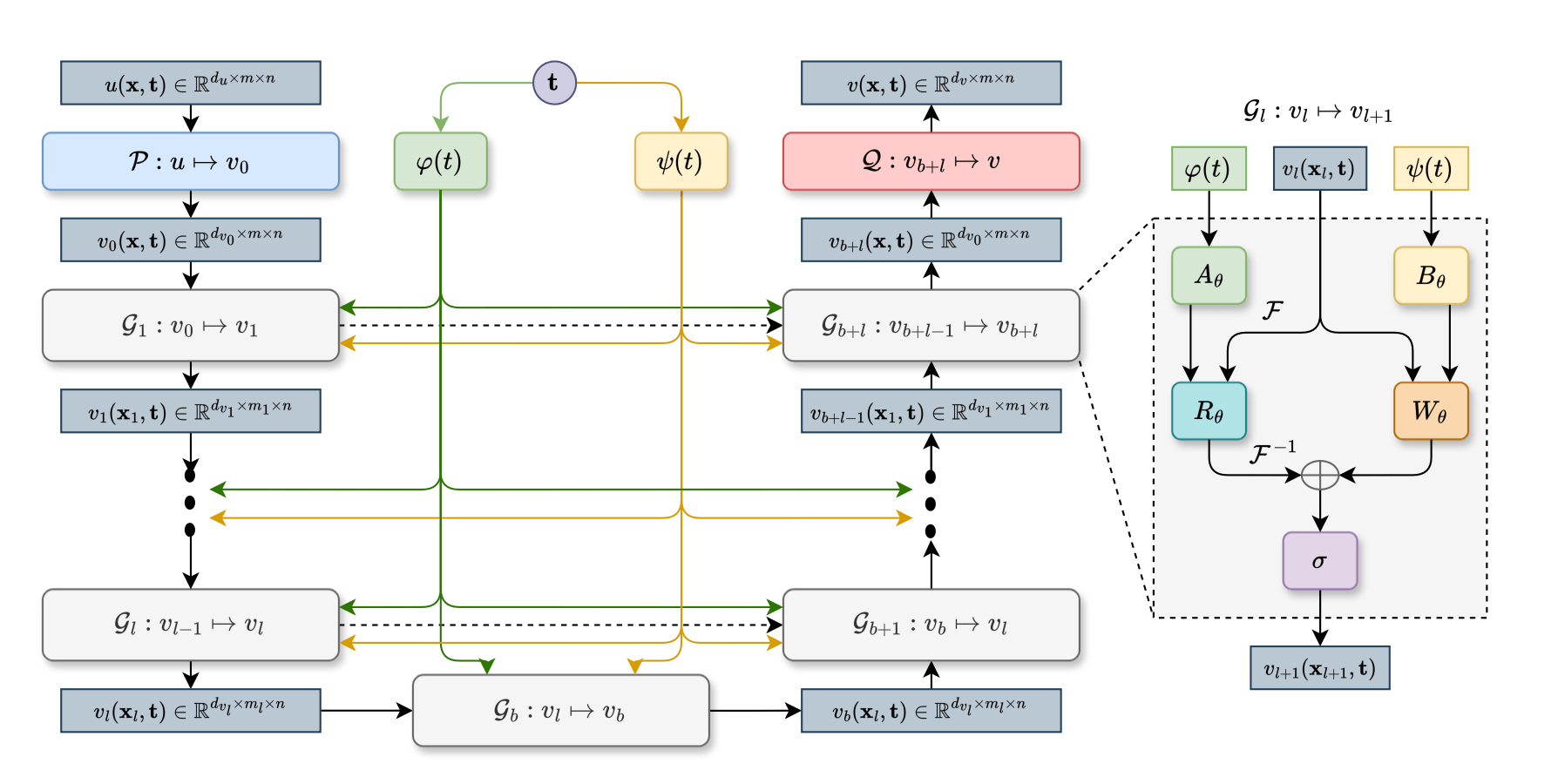
Intrinsic shape processes

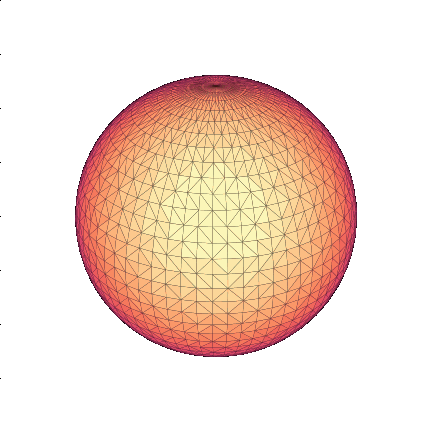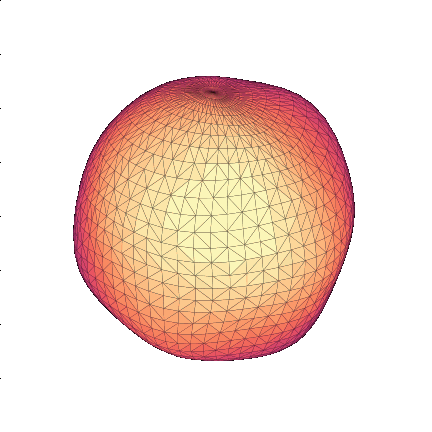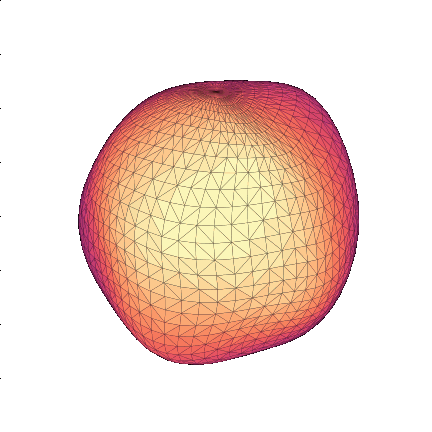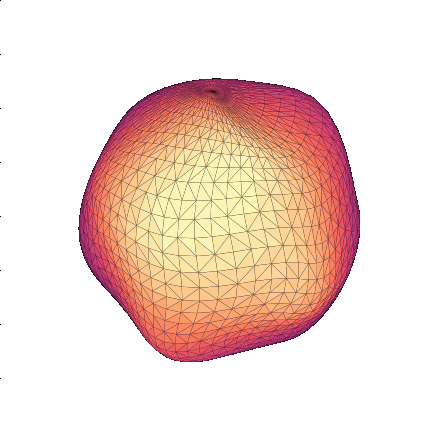
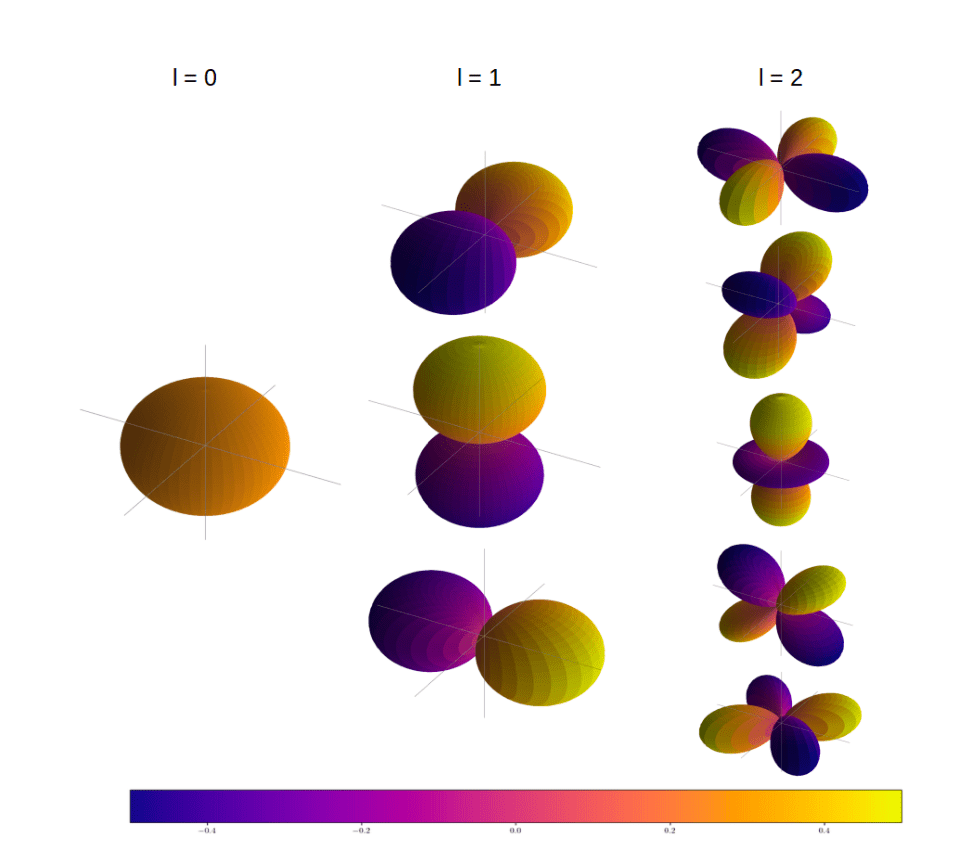
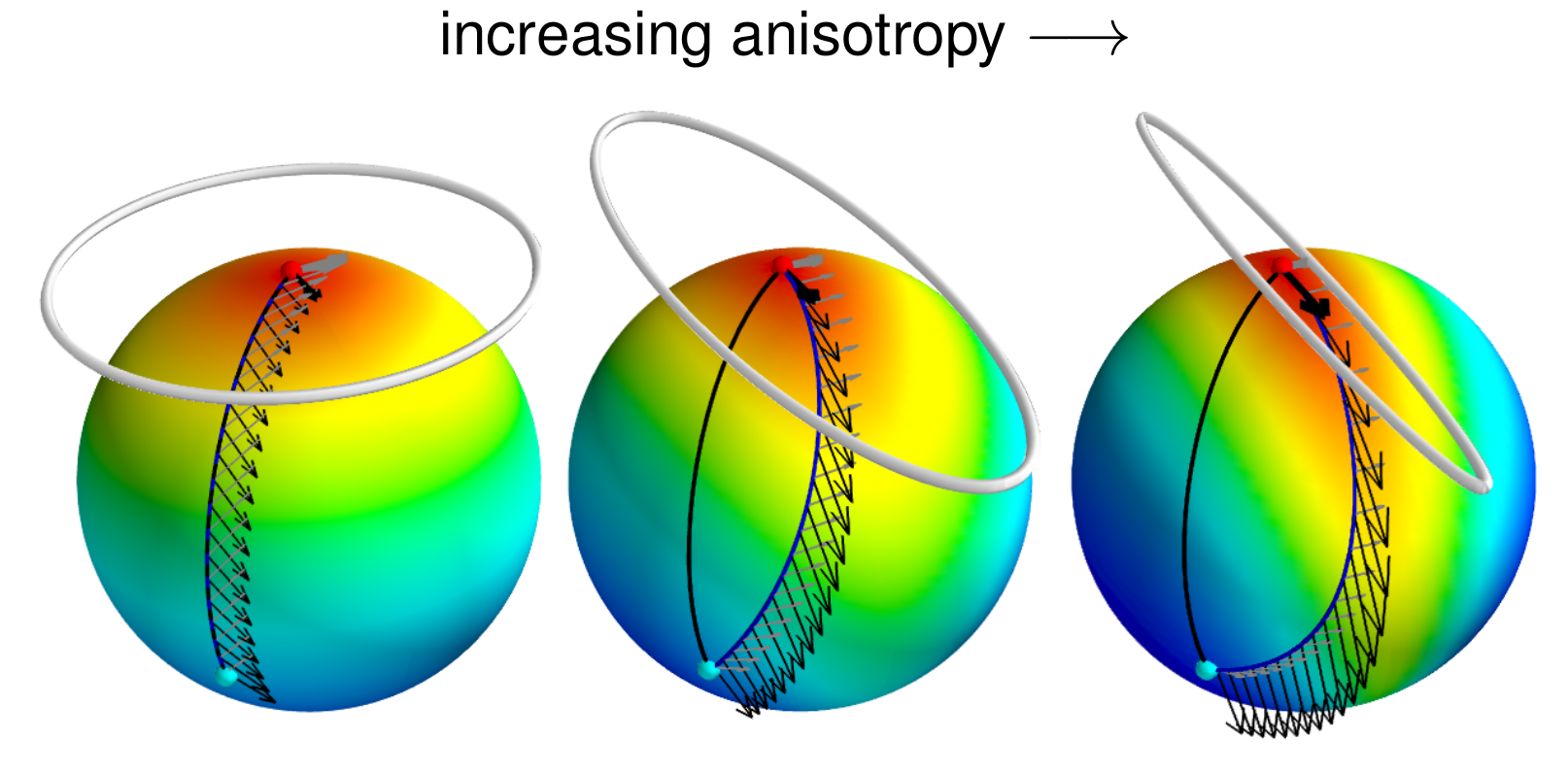
Most probable flows

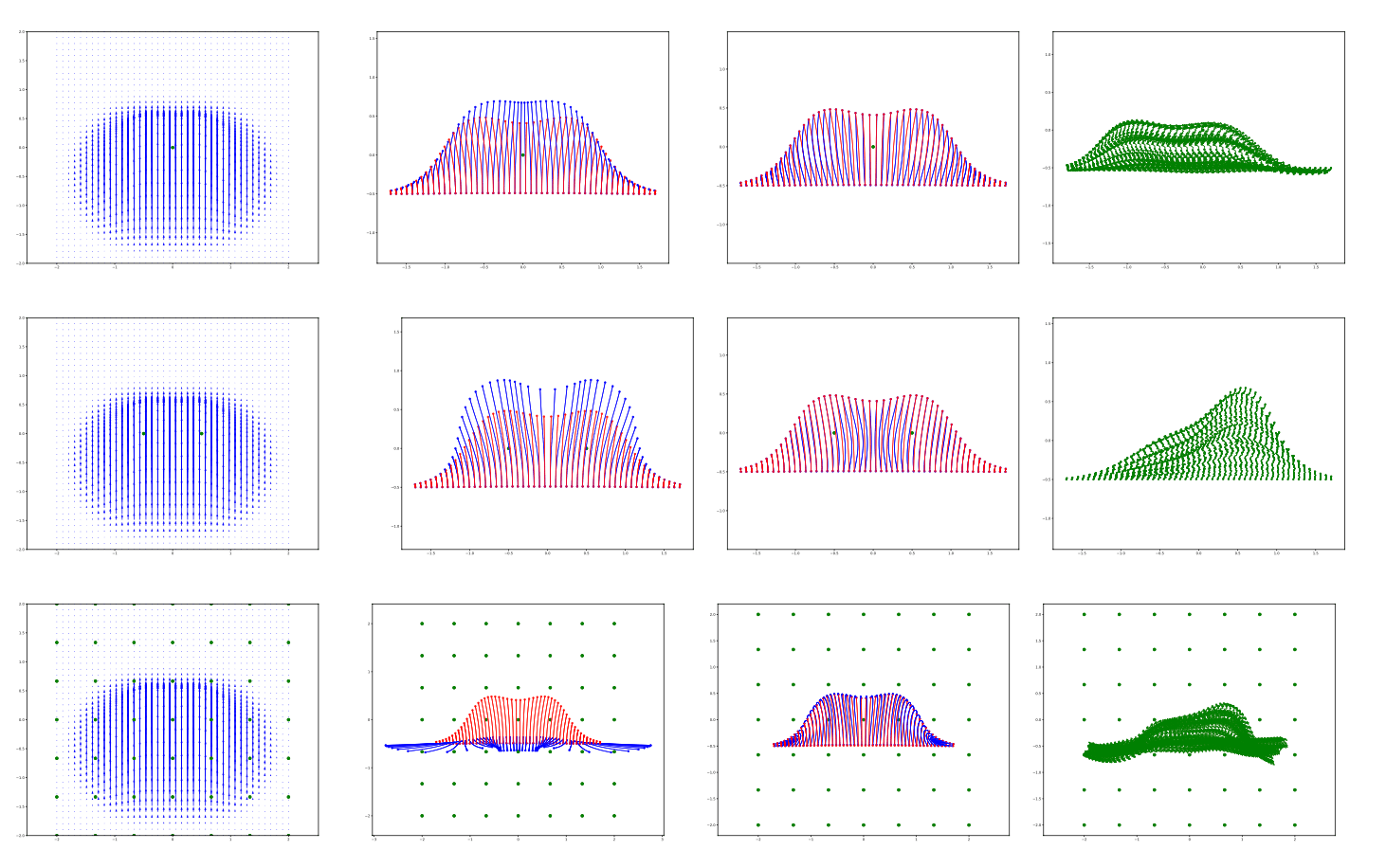
Geometric statistics

Diffusion mean

Most probable paths

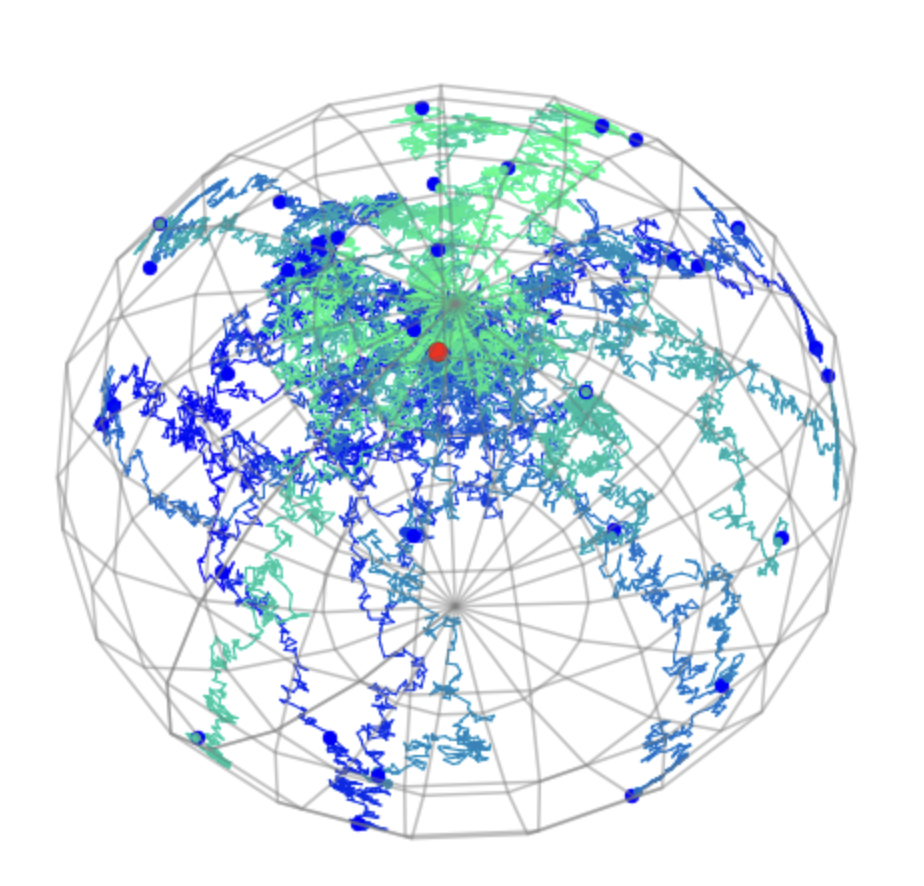
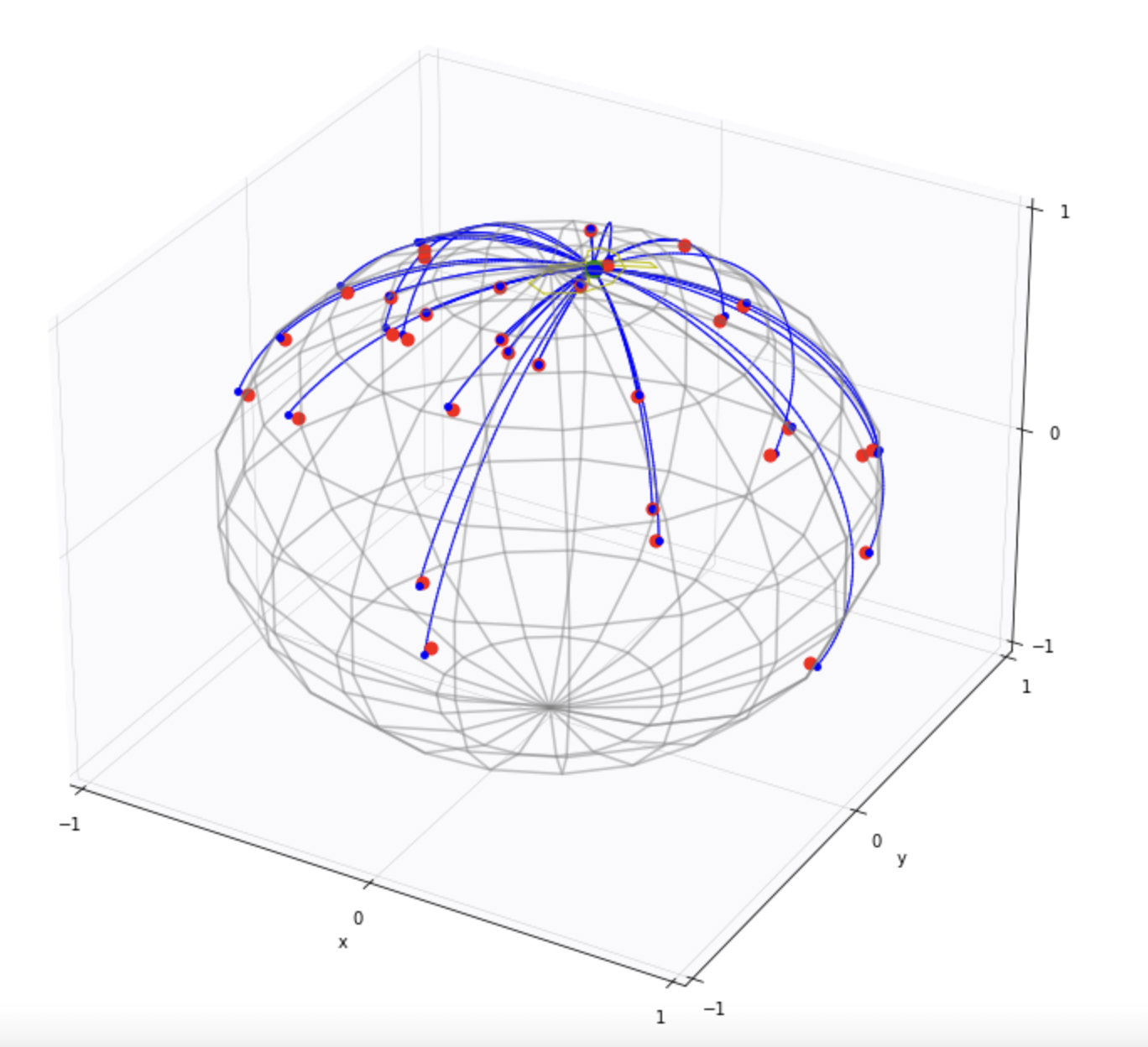
Eltzner, Huckemann, Grong, Corstanje,van der Meulen,Schauer,Sommer et al.

Manifold bridges

Software

Jax magic... in milliseconds:

Trees with millions of nodes
shapes with millions of landmarks

Geometry, stochastics, geometric statistics

JaxGeometry: https://github.com/computationalevolutionarymorphometry/jaxgeometry CCEM: http://www.ccem.dk

Hyperiax: https://github.com/computationalevolutionarymorphometry/hyperiax slides: https://slides.com/stefansommer

References:

Grong, Sommer: Most probable paths for developed processes, https://arxiv.org/abs/2211.15168
Grong, Sommer: Most probable flows for Kunita SDEs, https://arxiv.org/abs/2209.03868
Sommer, Schauer, v. d. Meulen: Stochastic flows and shape bridges, Oberwolfach, 2021
Baker, Besnier, Sommer: A function space perspective on stochastic shape evolution, https://arxiv.org/abs/2302.05382
Yang, Baker, Severinsen, Hipsley, Sommer: Simulating infinite-dimensional nonlinear diffusion bridges, https://arxiv.org/abs/2405.18353
Baker, Yang, Severinsen, Hipsley, Sommer: Conditioning non-linear and infinite-dimensional diffusion processes, https://arxiv.org/abs/2402.01434
Hansen, Eltzner, Huckemann, Sommer: Diffusion Means in Geometric Spaces, Bernoulli, 2023, arXiv:2105.12061
Grong, Sommer: Most probable paths for anisotropic Brownian motions on manifolds, FoCM 2022, arXiv:2110.15634
Philipp Harms, Peter W. Michor, Xavier Pennec, Stefan Sommer: Geometry of sample spaces, Diff. Geom. and its Appl., 2023, arXiv:2010.08039
Arnaudon, v.d. Meulen, Schauer, Sommer: Diffusion bridges for stochastic Hamiltonian systems and shape evolutions,SIIMS,2022,arXiv:2002.00885
Højgaard Jensen, Sommer: Simulation of Conditioned Diffusions on Riemannian Manifolds, 2021, arXiv:2105.13190.
Arnaudon, Holm, Sommer: A Geometric Framework for Stochastic Shape Analysis, Foundations of Computational Mathematics, 2019, arXiv:1703.09971.
Sommer, Svane: Modelling Anisotropic Covariance using Stochastic Development and Sub-Riemannian Frame Bundle Geometry, JoGM, 2017, arXiv:1512.08544.
Arnaudon, Holm, Sommer: A Stochastic Large Deformation Model for Computational Anatomy, IPMI 2017, arXiv:1612.05323.

Kunita flows, shape stochastics, and phylogenetic inference

Shape stochastics, conditional processes and inference

Brownian motion model of trait evolution

Felsenstein's pruning algorithm for shapes

Stochastics of shapes

Stochastics of shapes

Shapes, deformations and nonlinearity

Geometric + metric view

Evolution with noise

Eulerian shape process / Kunita flow

Inference: Data conditional processes

Guided bridges

Guided bridges on manifolds

Guided bridges on manifolds

Heat kernel approximations

Conditioned shape process

Backwards filtering, forward guiding bridges

Backwards filtering, forward guiding bridges

From single edges to trees

Felsenstein's pruning algorithm for shapes

Upwards message passing

Backwards filtering, forward guiding butterflies

Parameter inference with MCMC

Parameter inference with MCMC

Canidae skulls

Felsenstein's pruning algorithm for shapes

Other takes: Upwards LDDMM: recursive shape matching

Infinite dimensions and score learning

Intrinsic shape processes

Most probable flows

Geometric statistics

Software

Geometry, stochastics, geometric statistics

Other takes:
Upwards LDDMM: recursive shape matching