Shape analysis and actions of the diffeomorphism group

Faculty of Science, University of Copenhagen

Stefan Sommer

Department of Computer Science, University of Copenhagen

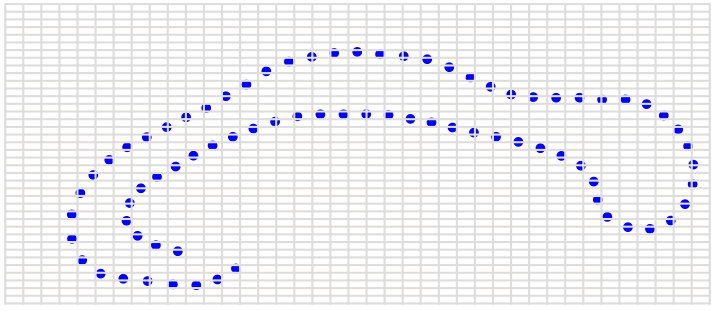
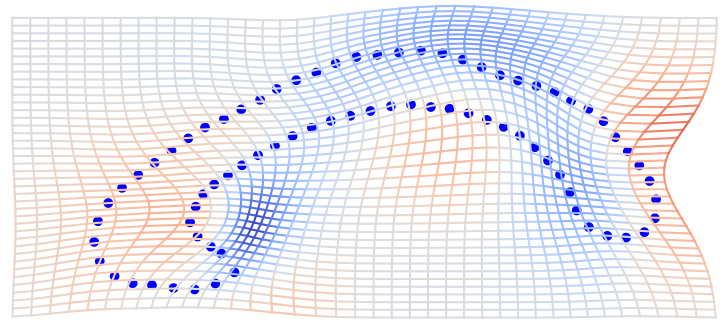
\( \phi \)

Statistical Shape models

Session 1: (L 9-9:45) Shape analysis and actions of the  diffeomorphism group

Session 2: (E 10-10:45) Landmark analysis in Theano Geometry

Session 3: (L 11-11:45) Linear representations and random orbit model

Session 4: (E 12:30-13:15) Landmarks statistics in Theano Geometry

Session 5: (L 13:30-14:15) Shape spaces of images, curves and surfaces

Session 6: (E 14:30-15:15) Analysis of continuous shapes

Slides: https://slides.com/stefansommer/shape-analysis-X/ (X=1,2,3)

Shapes

Objects on which the diffeomorphism group acts

 

\(d=2,3\)

 

  • landmarks in \(\mathbb{R}^d\): \(\mathbf{q}=(q_1,\ldots,q_n)\)
  • curves: \(\gamma:\mathbb{S}^1\to\mathbb{R}^d\)
  • surfaces: \(\gamma:\mathbb{S}^2\to\mathbb{R}^d\)
  • images: \(I:\Omega\to\mathbb{R}\), \(\Omega\subset\mathbb{R}^d\)
  • tensor fields: \(\Omega\to\mathcal{T}^k_l\), \(\Omega\subset\mathbb{R}^d\)
  • ...

Shape analysis via actions

move analysis from

  • the complicated, nonlinear shape space to
  • the (less complicated) space of diffeomorphisms

 

treat all shape types with in one framework

Shape analysis via actions

LDDMM: Large Deformation Diffeomorphic Metric Mapping

Grenander, Christensen, Trouve, Younes, Miller, Joshi, Holm, etc.

Shape analysis from deformations

\( \phi \)

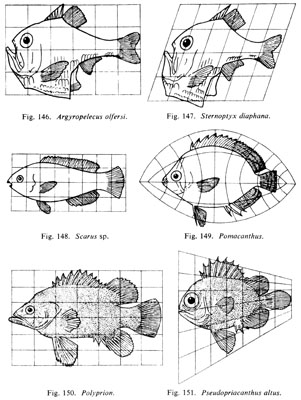
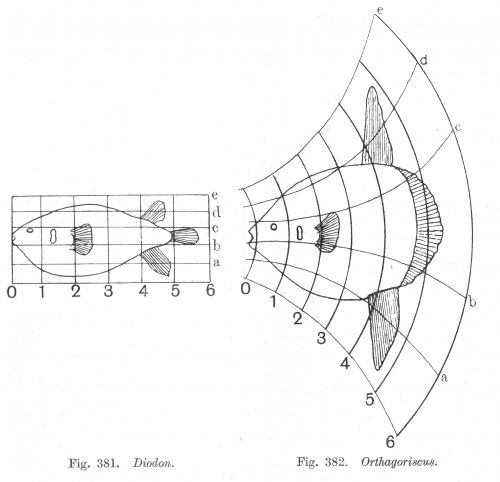
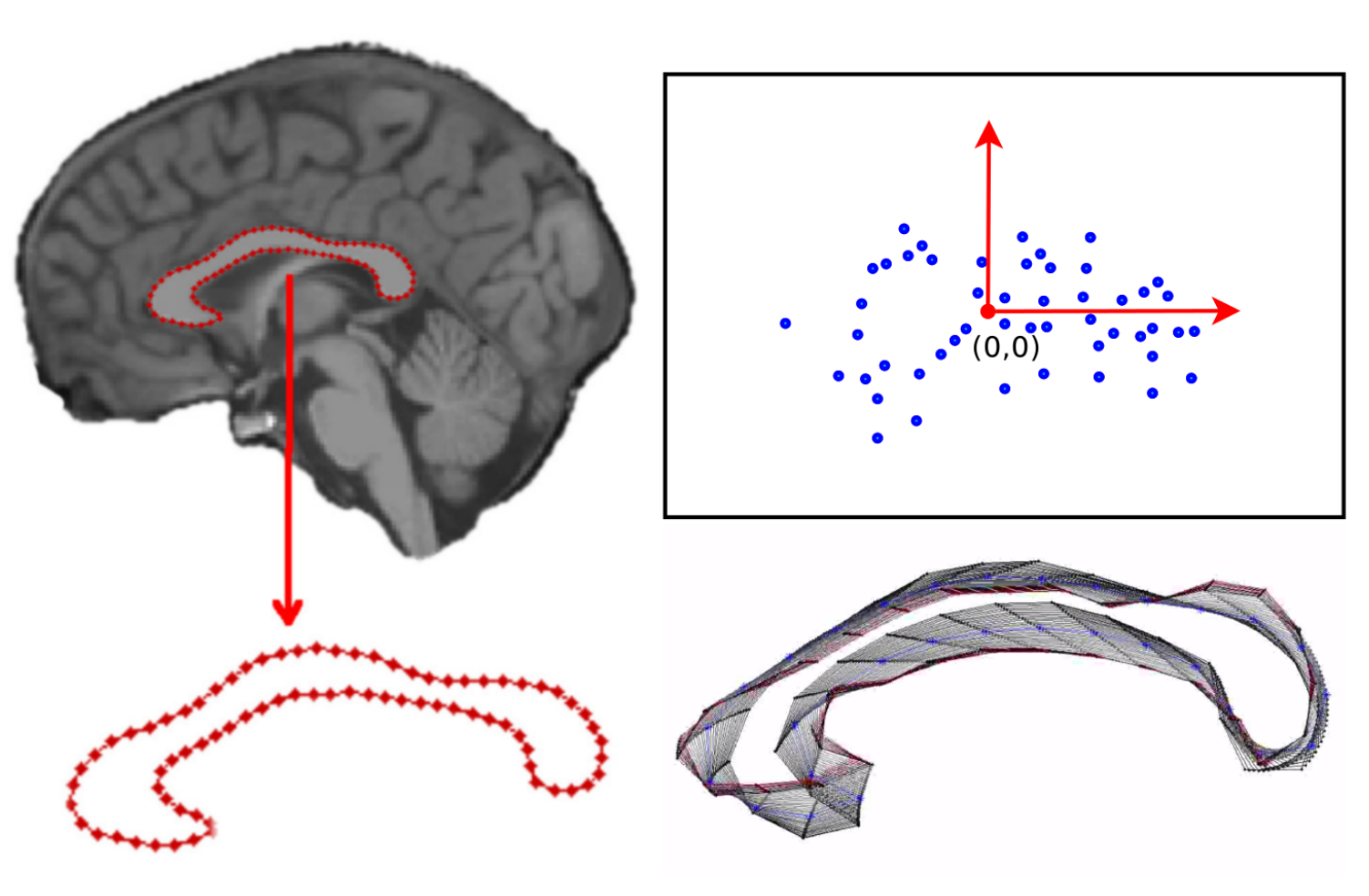
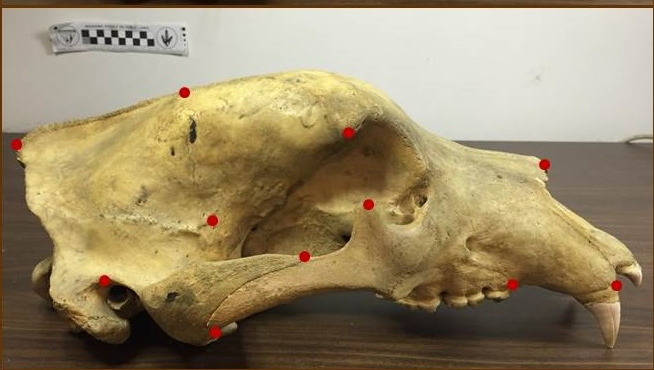
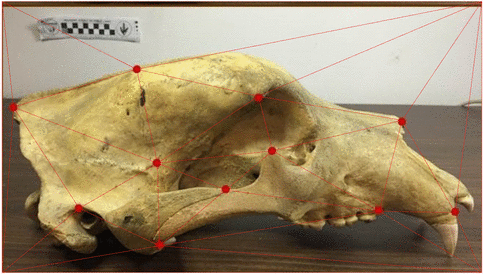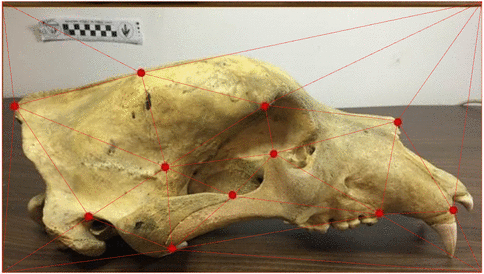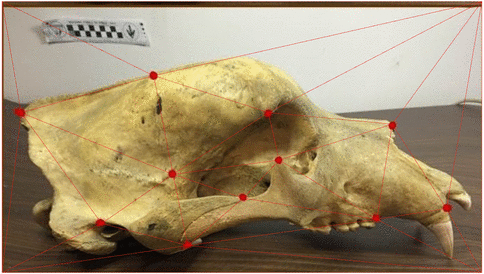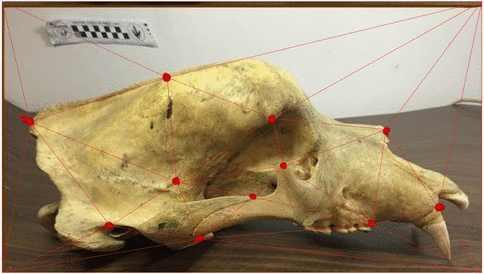
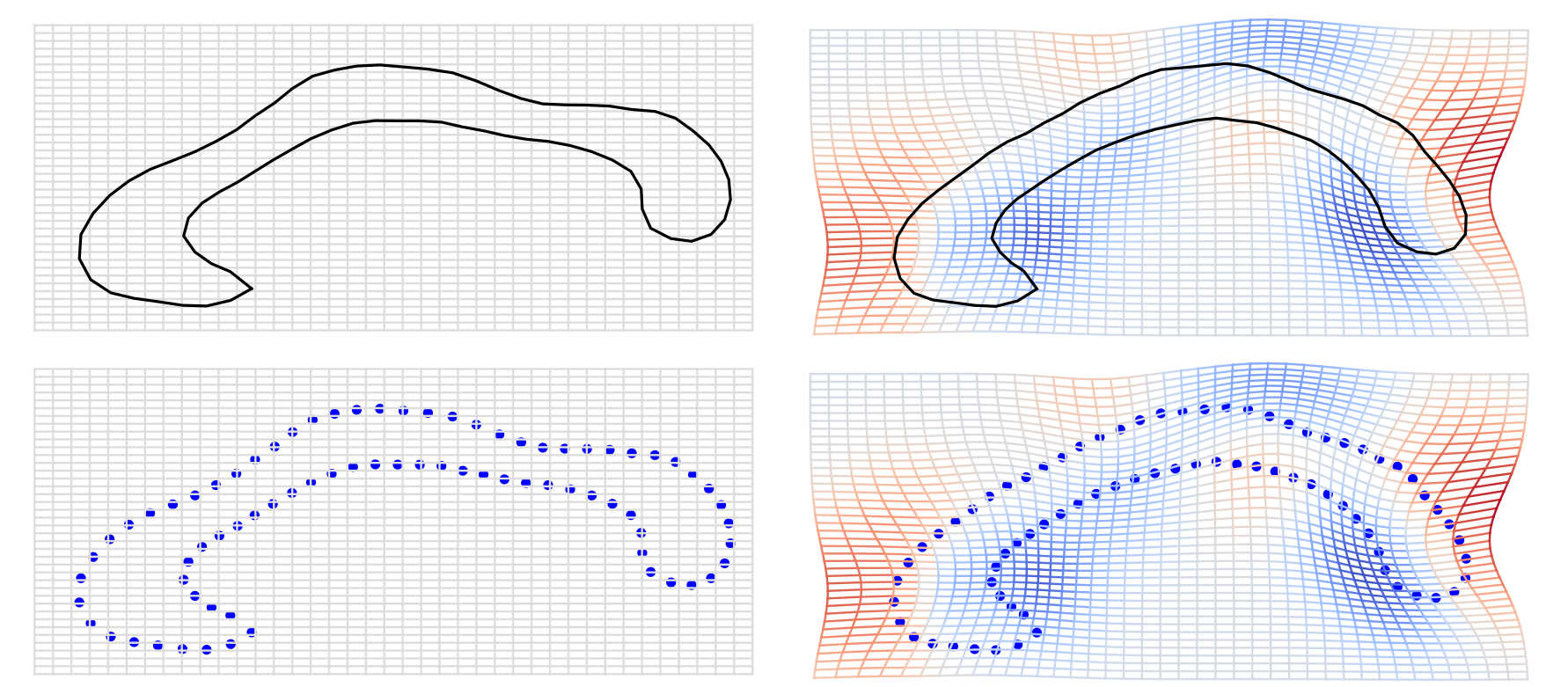
One framework - multiple shape types

Actions

\( \phi \)

\(\phi\) deformation of domain \(\Omega\)

action: shape follows deformation

Actions

\(G = \mathrm{Diff}(\Omega)\)

\(\phi\in G\): smooth (\(C^k\)), invertible, smooth inverse

 

Actions:

  • \(\phi.\mathbf{q}:=(\phi(q_1),\ldots,\phi(q_N))\)
  • curves: \(\phi.\gamma:=\phi\circ\gamma\)
  • surfaces: \(\phi.\gamma:=\phi\circ\gamma\)
  • images: \(\phi.I:=I\circ\phi^{-1}\)
  • tensor fields: \(\phi.T:=\phi_*T\) (push-forward action)
  • ...

Actions

shape \(s\) (e.g. \(s=\mathbf{q}\) or \(s=I\))

left actions satisfy

  • Identity: e.s = s
  • compatibility: (gh).s=g.(h.s)

 

Landmark action:

  • \(\phi.\mathbf{q}:=(\phi(q_1),\ldots,\phi(q_N))\)
    \((\psi\circ\phi).\mathbf{q}:=((\psi\circ\phi)(q_1),\ldots,(\psi\circ\phi)(q_N))\)
    \(                                =(\psi(\phi(q_1)),\ldots,\psi(\phi(q_N)))\)
    \(                                =\psi.(\phi(q_1),\ldots,\phi(q_N))=\psi.(\phi.\mathbf{q})\)

Shape Matching

E_{s_0,s_1}(\phi)=R(\phi)+\frac1\lambda S(\phi.s_0,s_1)

\( \phi\in\mathrm{Diff}(\Omega) \) diffeomorphism of domain \(\Omega\)

\( \phi \)

Variational problem to find optimal \(\phi\in G\):

Group and quotient

Hamilton's Equations for Landmarks

\[ \frac{d}{dt} q = \quad \frac{\partial H(q,p)}{\partial p} \]

\[ \frac{d}{dt} p = -\frac{\partial H(q,p)}{\partial q} \]

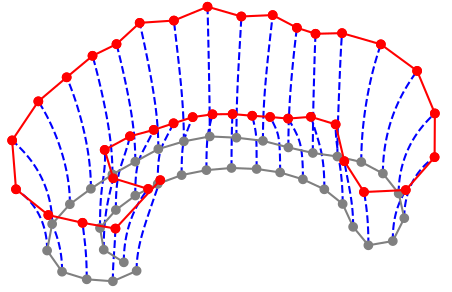
LDDMM landmark matching:

  • \(q=(q_1,\ldots,q_n)\) configuration of \(n\) landmarks
  • \(p\) landmark momentum
  • matching of \(q_0\) to \(q_1\) by finding optimal trajectory \(q(t)\) with \(q(0)=q_0\)

Hamilton's Equations for Landmarks

\[ \frac{d}{dt} q = \quad \frac{\partial H(q,p)}{\partial p} \]

\[ \frac{d}{dt} p = -\frac{\partial H(q,p)}{\partial q} \]

Geodesics for Riemannian metric on landmark shape space:

  • Landmarks \(\mathbf{q}=(q_1,\ldots,q_n),\,q_i\in\Omega\subseteq\mathbb R^d\)
  • LDDMM cometric \( \left<\xi,\eta\right>_{\mathbf q}=\xi^T K(\mathbf q,\mathbf q)\eta\)
  • \(p(0)\) (or \(v(0)\)) determines the entire evolution

Hamiltonian

\[ \frac{d}{dt} q = \quad \frac{\partial H(q,p)}{\partial p} \]

\[ \frac{d}{dt} p = -\frac{\partial H(q,p)}{\partial q} \]

LDDMM landmark matching:

  • \(q=(q_1,\ldots,q_n)\) configuration of \(n\) landmarks
  • \(p\) landmark momentum

Hamiltonian:

\[ H(q,p) = \sum_{i,j=1}^n p_i^TK(x_i,x_j)p_j\]

\(K\) RKHS kernel, e.g. \(K(q_i,q_j)=\alpha e^{-\frac{\|q_i-q_j\|^2}{2\sigma^2}}\)

Landmark geodesic equations

Hamiltonian:

\[ H(q,p) = \sum_{i,j=1}^n p_i^TK(q_i,q_j)p_j\]

\(K\) RKHS kernel, e.g. \(K(q_i,q_j)=\alpha e^{-\frac{\|q_i-q_j\|^2}{2\sigma^2}}\)

\frac{d}{dt} p = \, -\frac{\partial H(q,p)}{\partial q} = - \sum_{j=1}^n p_j^T D_1K (q_i , q_j )^T p_i
\frac{d}{dt} q = \quad \frac{\partial H(q,p)}{\partial p} = \quad \sum_{j=1}^n K (q_i , q_j) p_j

Entire evolution \((q(t),p(t)\) determined by \((q_0,p_0)\) or \((q_0,v_0)\), \(v_0=Kp_0\)

Hamilton's Equations in Theano

x = T.tensor3('x')

# landmark RKHS kernel
def K(q1,q2):
    r_sq = T.sqr(q1.dimshuffle(0,'x',1)-q2.dimshuffle('x',0,1)).sum(2)
    return T.exp( - r_sq / (2.*sigma**2) )

#Hamiltonian
def H(q,p):
    return 0.5*T.tensordot(p,T.tensordot(K(q,q),p,[[1],[0]]),[[0,1],[0,1]])

# Hamiltons equations
dq = lambda q,p: T.grad(H(q,p),p)
dp = lambda q,p: -T.grad(H(q,p),q)

# ODE
def ode_f(x):
    dqt = dq(x[0],x[1])
    dpt = dp(x[0],x[1])
        
    return T.stack((dqt,dpt))

# Euler step
def euler(x,dt):    
    return x+dt*ode_f(x)

# Euler integration: symbolic loop
(cout, updates) = theano.scan(fn=euler,outputs_info=[x],non_sequences=[dt],
                              n_steps=n_steps)

# compile it
simf = function(inputs=[x],outputs=cout,updates=updates)

# and loss function for matching
loss = 1./N*T.sum(T.sqr(cout[-1,0]-qtarget0))

# gradient
dloss = T.grad(loss,x)

# compile
lossf = function(inputs=[x],outputs=loss,updates=updates)
dlossf = function(inputs=[x],outputs=[loss, dloss],updates=updates)


# shooting
from scipy.optimize import minimize,fmin_bfgs,fmin_cg
def shoot(q0,p0):
    def fopts(x):
        [y,gy] = dlossf(np.stack([q0,x.reshape([N.eval(),DIM])]).astype(theano.config.floatX),)
        return (y,gy[1].flatten())
    
    res = minimize(fopts, p0.flatten(), method='L-BFGS-B', jac=True)
    
    return(res.x,res.fun)

Theano Geometry

https://colab.research.google.com/drive/1_QWs9YnpBGDRmLGUbYapAPoo5NzjwT0r

https://colab.research.google.com/drive/1ufGJygLWE3Sk63RgzHkDlxhLrgEHf8t8

Theano Geometry: Hamiltonian Dynamics

# # This file is part of Theano Geometry
#
# ...

from src.setup import *
from src.utils import *

###############################################################
# geodesic integration, Hamiltonian form                      #
###############################################################

def initialize(M):
    q = M.coords()
    p = M.coordscovector()

    dq = lambda q,p: T.grad(M.H(q,p),p)
    dp = lambda q,p: -T.grad(M.H(q,p),q)

    def ode_Hamiltonian(t,x):
        dqt = dq(x[0],x[1])
        dpt = dp(x[0],x[1])
        return T.stack((dqt,dpt))
    M.Hamiltonian_dynamics = lambda q,p: integrate(ode_Hamiltonian,T.stack((q,p)))
    M.Hamiltonian_dynamicsf = theano.function([q,p], M.Hamiltonian_dynamics(q,p))

    ## Geodesic
    M.Exp_Hamiltonian = lambda q,p: M.Hamiltonian_dynamics(q,p)[1][-1,0]
    M.Exp_Hamiltonianf = theano.function([q,p], M.Exp_Hamiltonian(q,p))

Hamilton's Equations in Theano

Exercise session:

  • download Theano geometry
  • open notebook courses/shape19-E1.ipynb. It contains template code you can base your solutions on
  • forward integrate with different momenta + kernel parameters
  • what happens when shooting landmarks together?
  • define two nontrivial shapes and match them
  • plot underlying grid deformation and discuss the result. Try varying the kernel width. How is the result related to lifting from shape space to \(\mathrm{Diff}(\Omega)\)?

Slides: https://slides.com/stefansommer/shape-analysis-X/ (X=1,2,3)