Stochastic Shape Analysis and Probabilistic Geometric Statistics

Stefan Sommer, University of Copenhagen

Faculty of Science, University of Copenhagen

University of Bergen, 2020

stochastic shapes and probabilistic geometric statistics

w/ Alexis Arnaudon, Darryl Holm, Sarang Joshi, Tom Fletcher, Frank v.d. Meulen, Moritz Schauer, Benjamin Eltzner, Line Kuhnel, Mathias H. Jensen, Pernille E.H. Hansen

Novo nordisk foundation

Villum foundation

Carlsberg foundation

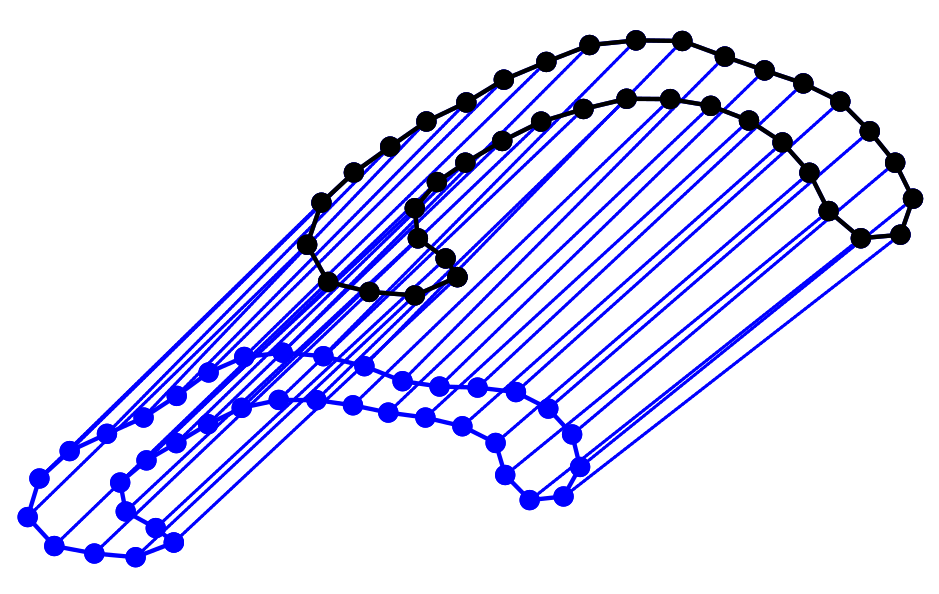
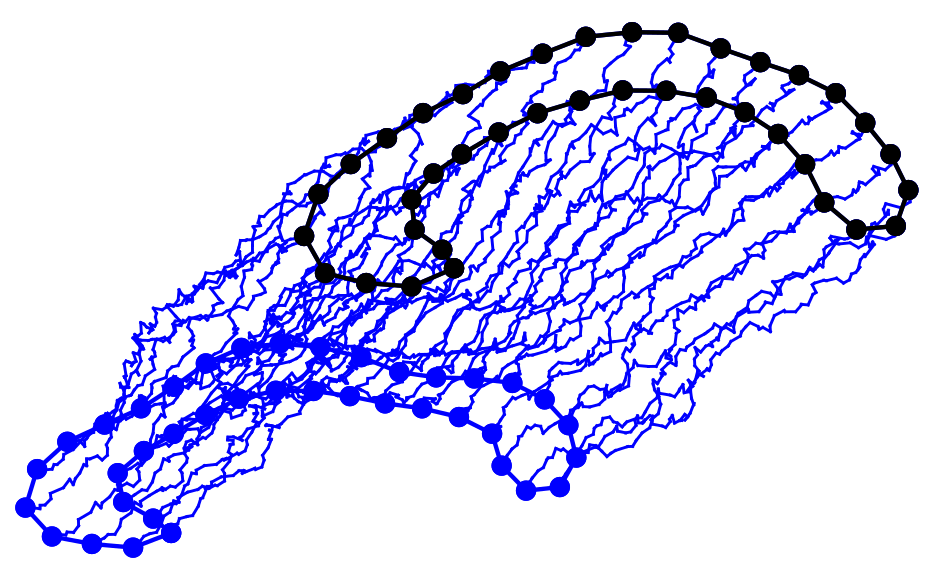
Statistical shape analysis

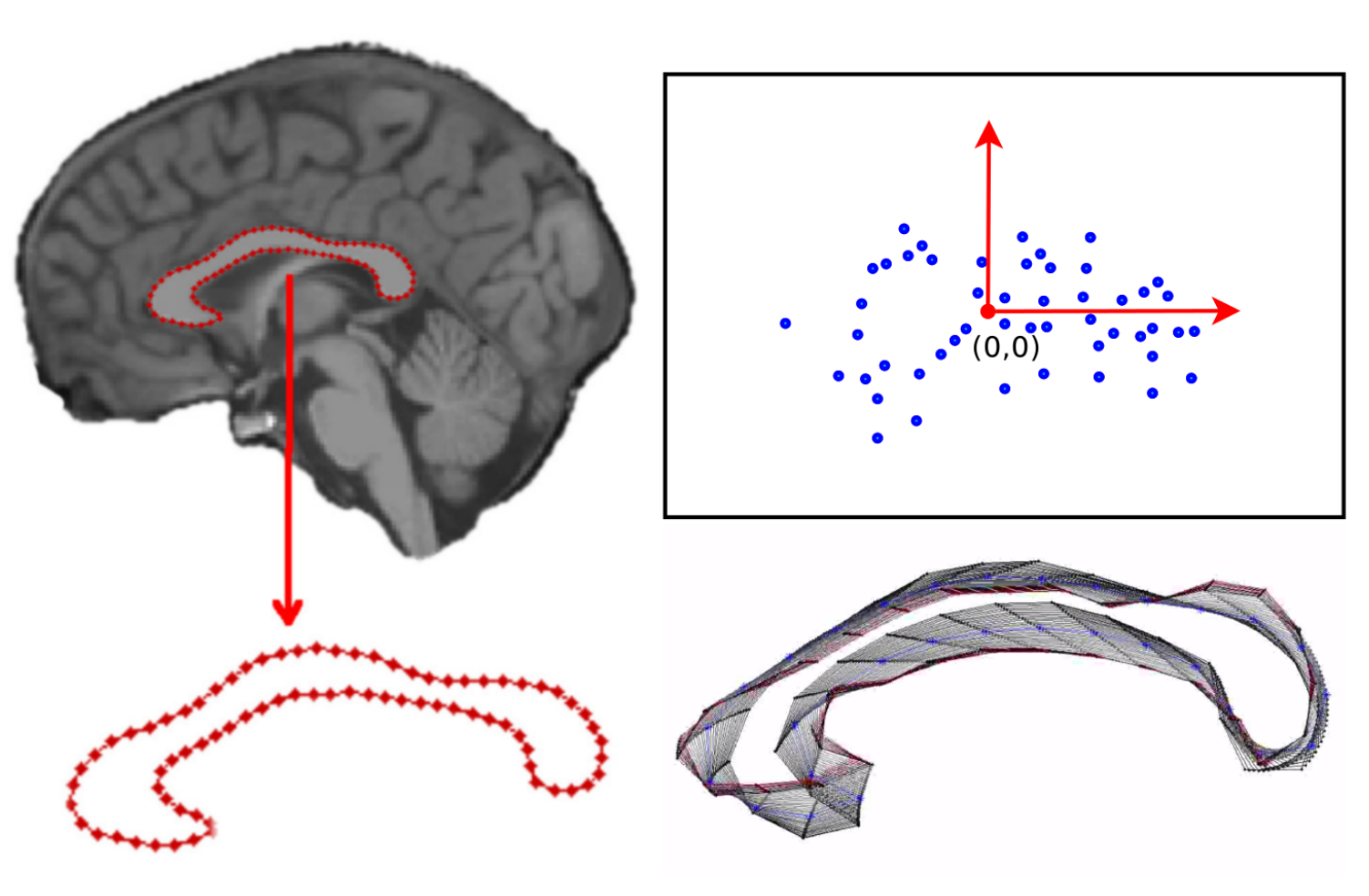
Geometric statistics

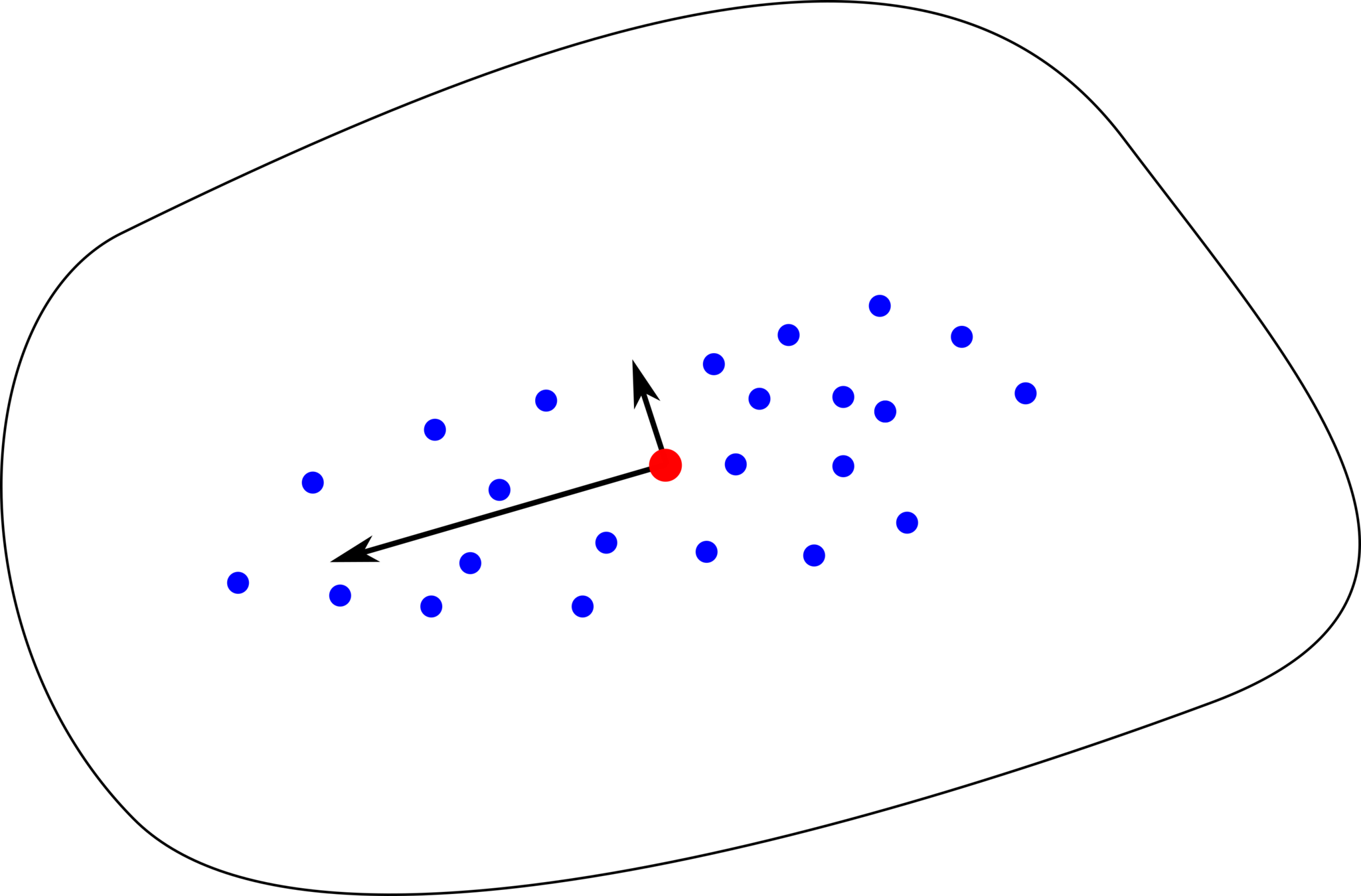
Generalization of Euclidean statistical notions and techniques to spaces without vector space structure

  • i.i.d. samples \(y_1,\ldots,y_N\in M\)
  • Fréchet mean
    \(\bar{x}=\mathrm{argmin}_{x\in M}\sum_{i=1}^Nd(x,y_i)^2\)

The Fréchet mean is not an expected value.

There is no equivalence between different characterizations of means

- in contrast to Euclidean statistics

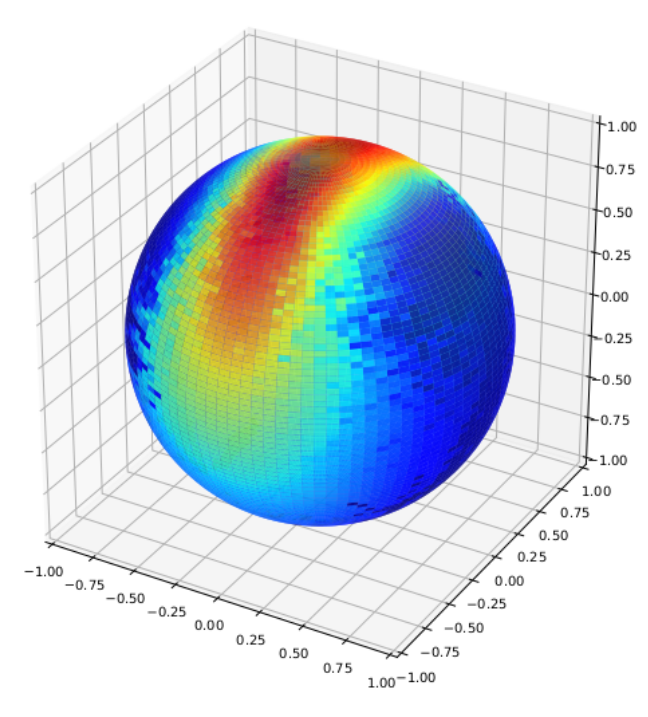
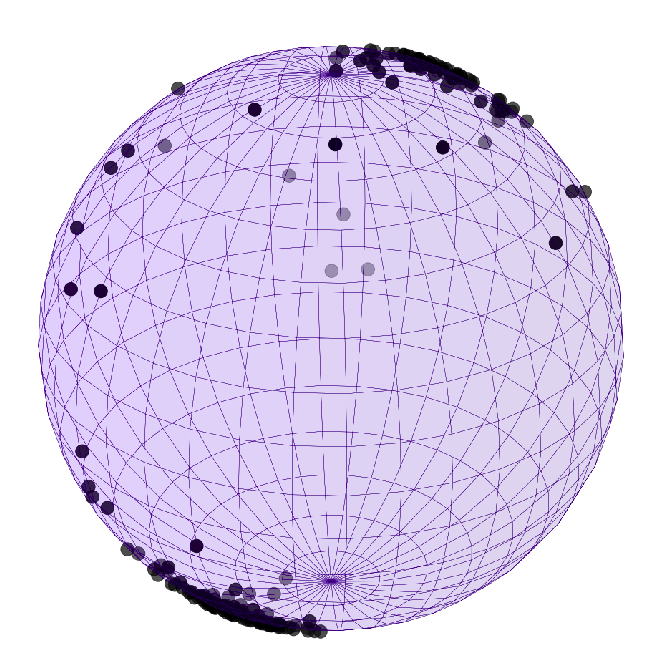
Geometric data: Directional statistics

Plane directions:      \(\mathbb{S}^1\)

Geographical data:  \(\mathbb{S}^2\)

3D directions:           \(\mathrm{SO}(3), \mathbb{S}^2\)

Angles:                       \(\mathbb{T}^N\)

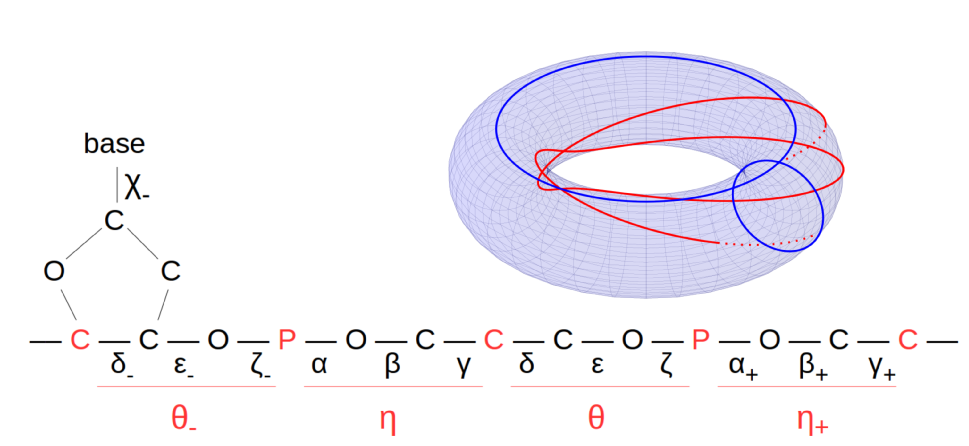
Geometric data: Diffusion MRI

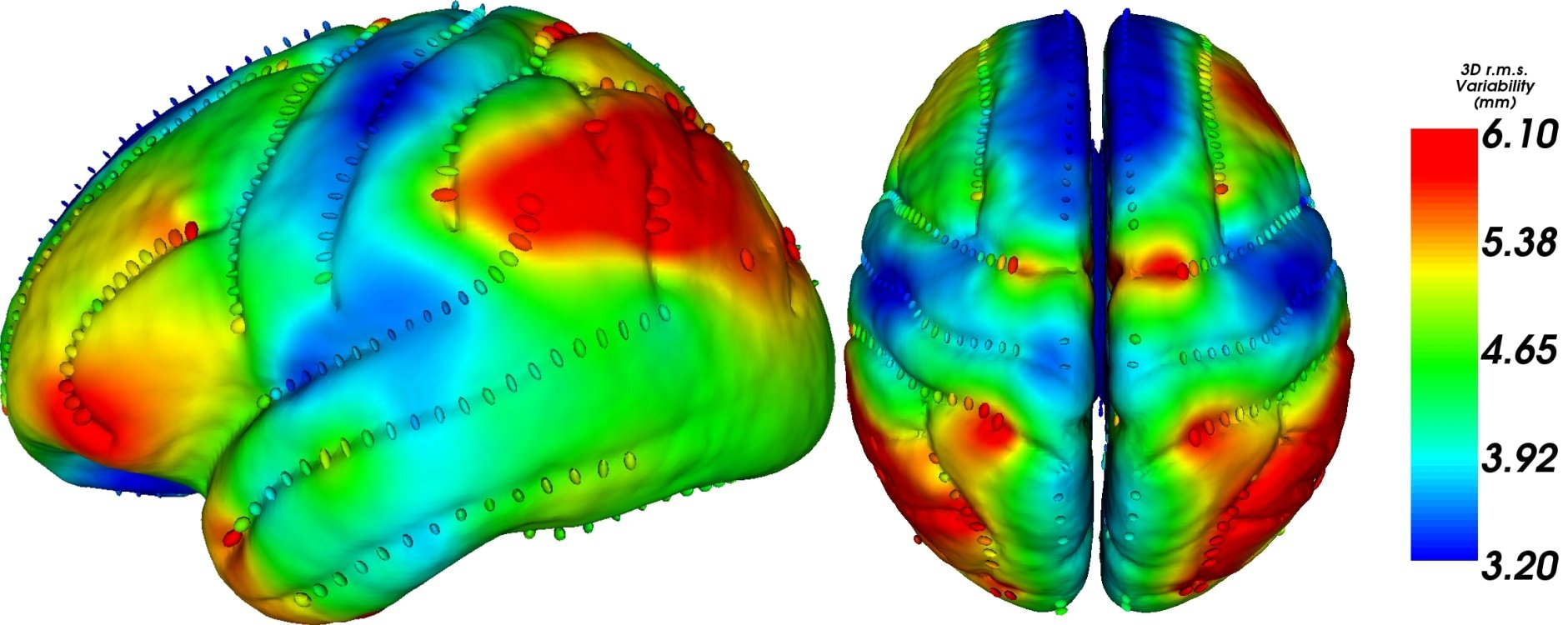
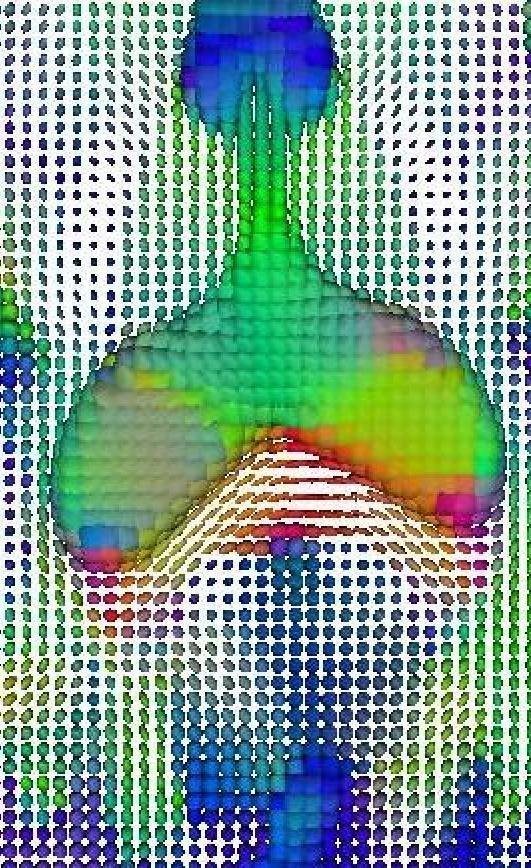
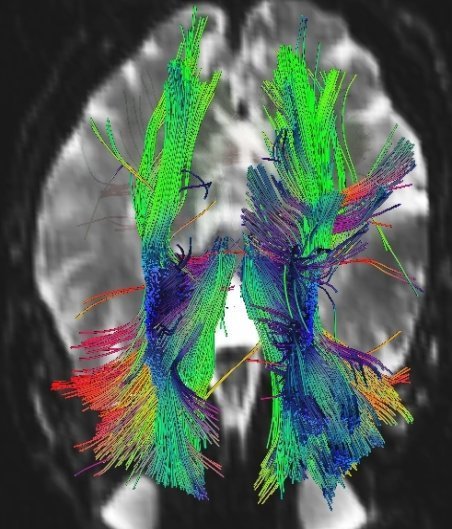
Positive, symmetric 3 tensors:   SPD(3)

Geometric data: Functional signals

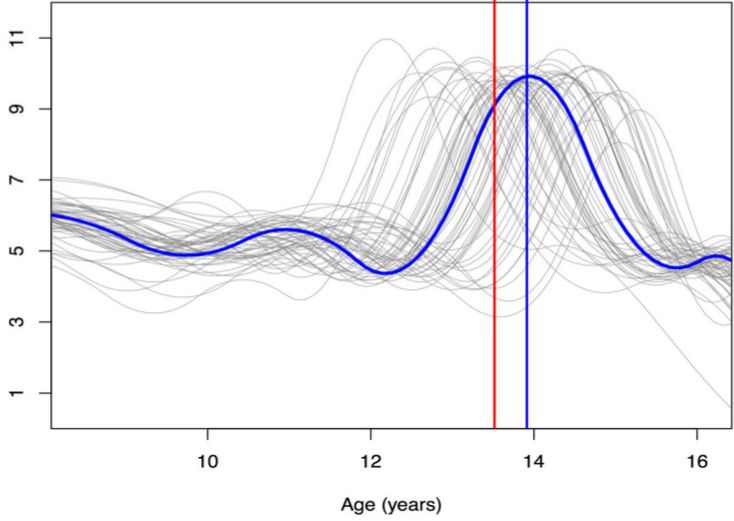
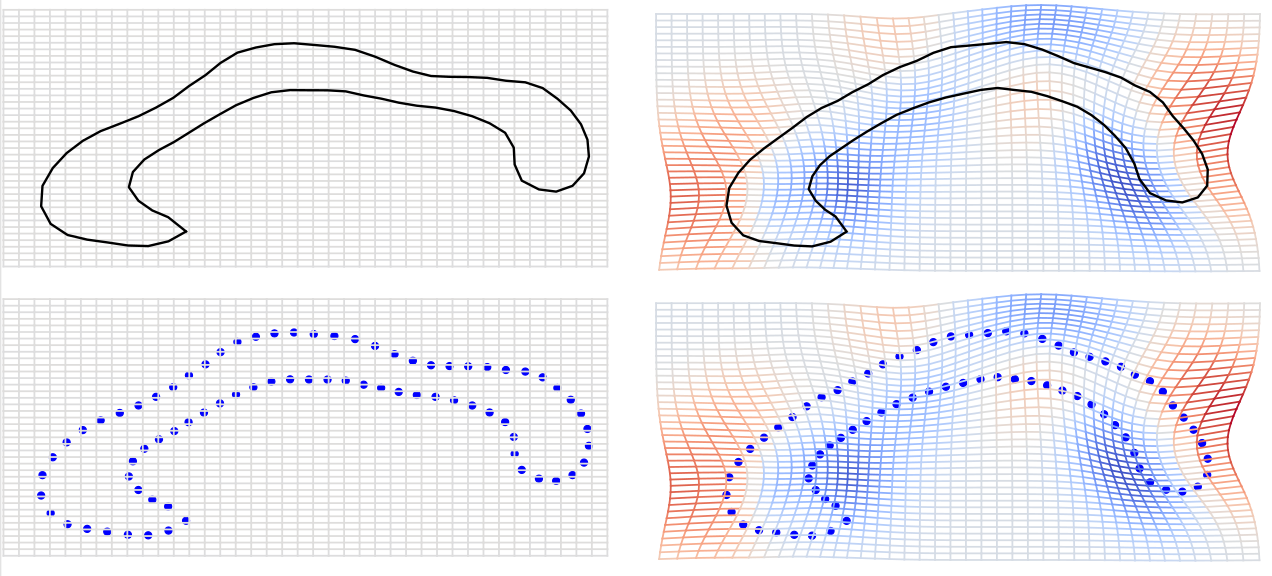
 continuous curves: \(\mathrm{Emb}(\mathbb S^1,\mathbb R^2)/\mathrm{Diff}(\mathbb S^1) \)

Mieritz et al.,JCEM'15

Shape matching

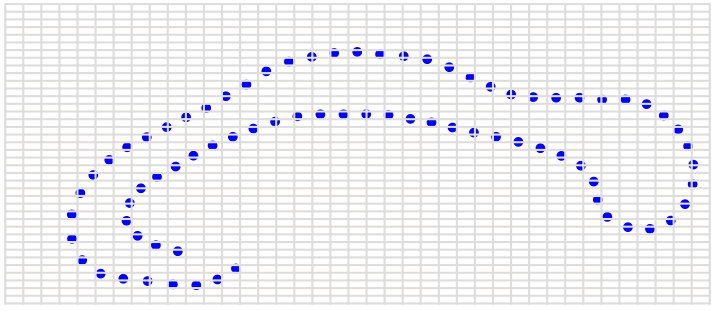
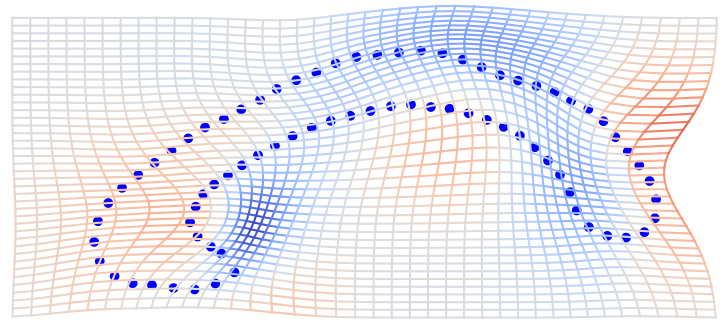
E_{s_0,s_1}(\phi)=R(\phi)+\frac1\lambda S(\phi.s_0,s_1)

\( \phi\in\mathrm{Diff}(\Omega) \) diffeomorphism of domain \(\Omega\)
action: \(\phi.s=\phi\circ s\)         (shapes)
             \(\phi.s=s\circ\phi^{-1}\)     (images)

\( \phi \)

Riemannian view

R(\phi_t)=\int_0^T\|\partial_t \phi_t\|_{\phi_t}^2dt

\( \phi_t:[0,T]\to\mathrm{Diff}(\Omega) \) path of diffeomorphisms (parameter t)

\mathrm{Diff}(\Omega)
\mathrm{Id}_{\mathrm{Diff}(\Omega)}
\varphi_t

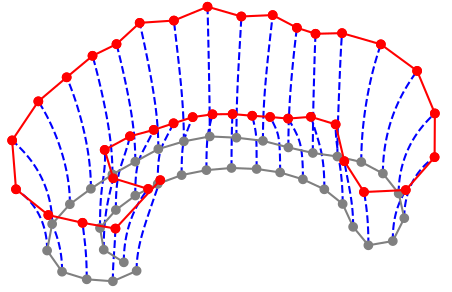
LDDMM: Grenander, Miller, Trouve, Younes, Christensen, Joshi, et al.

Evolution with noise

\partial_t \phi_t = F(\phi_t)\ \to\ d\phi_t=F(\phi_t)dt\color{blue}{+\sigma(\phi_t) dW_t}
\mathrm{Diff}(\Omega)
\mathrm{Id}_{\mathrm{Diff}(\Omega)}
\phi_t

Trouve,Vialard,QAM'12;Vialard,SPA'13;Marsland/Shardlow,SIIMS'17
Arnaudon,Holm,Sommer,IPMI'17; FoCM'18; JMIV'19

Least-squares \(\leftrightarrow\) probabilistic

Deterministic:

  • \(\phi_t\) geodesic evolution
  • exact matching:
    \(\quad\mathrm{argmin}_{\phi_1.s_0=s_1} E(\phi_t)\)
  • inexact matching:
    \(\quad\mathrm{argmin}_{\phi_t} E(\phi_t)\)
  • distance:
    \(\quad d(s_0,s1)^2=E(\phi_t)\)
  • Riemannian least-
    squares

Stochastic:

  • \(\phi_t\) stochastic process
  • bridge:
    \(\quad \phi_t|\phi_T.s_0=s_1\)
  • bridge + noise in observation:
    \(\quad \phi_t|\phi_T.s_0+\epsilon=s_1\)
  • (log) transition density
    \(\quad -\log p_T(s_1; s_0)\)
  • ML/MAP

Inferring geometry of landmarks spaces

  • Landmarks \(\mathbf{q}=(q_1,\ldots,q_n),\,q_i\in\Omega\subseteq\mathbb R^d\)
  • LDDMM cometric \( \left<\xi,\eta\right>_{\mathbf q}=\xi^T K(\mathbf q,\mathbf q)\eta\)
  • kernel \(K(\mathbf q_1,\mathbf q_2)=\alpha e^{-1\frac12 x^T\Sigma^{-1}x}\mathrm{Id}_d\)
  • Riemannian Brownian motion
    $$dq_t^i=g^{kl}\Gamma(\mathbf q_t)^i_{kl}dt+\sqrt{g^*(\mathbf q_t)}^idW_t$$
  • Brownian motion transition density
    $$p_{T,\theta}(\mathbf v)=\frac1{\sqrt{|K(\mathbf v,\mathbf v)|(2\pi T)^{Nd}}}e^{-\frac{\|(\mathbf q_0-\mathbf v)^TK(\mathbf q_0,\mathbf q_0)^{-1}(\mathbf q_0-\mathbf v)\|^2}{2T}}\mathbb E_{\mathbf y_\theta}[\varphi_{\theta}(\mathbf y)]$$

 

 

 

 

 

 

 

 

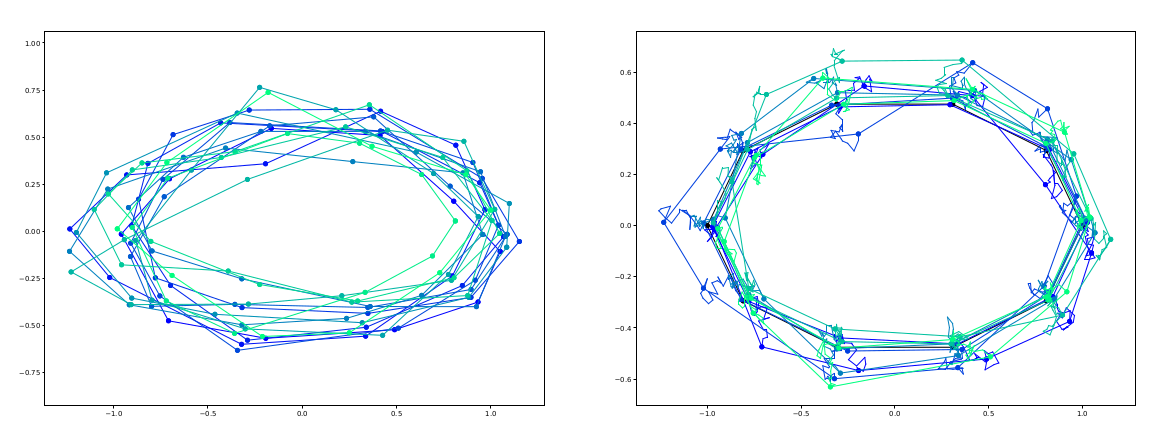
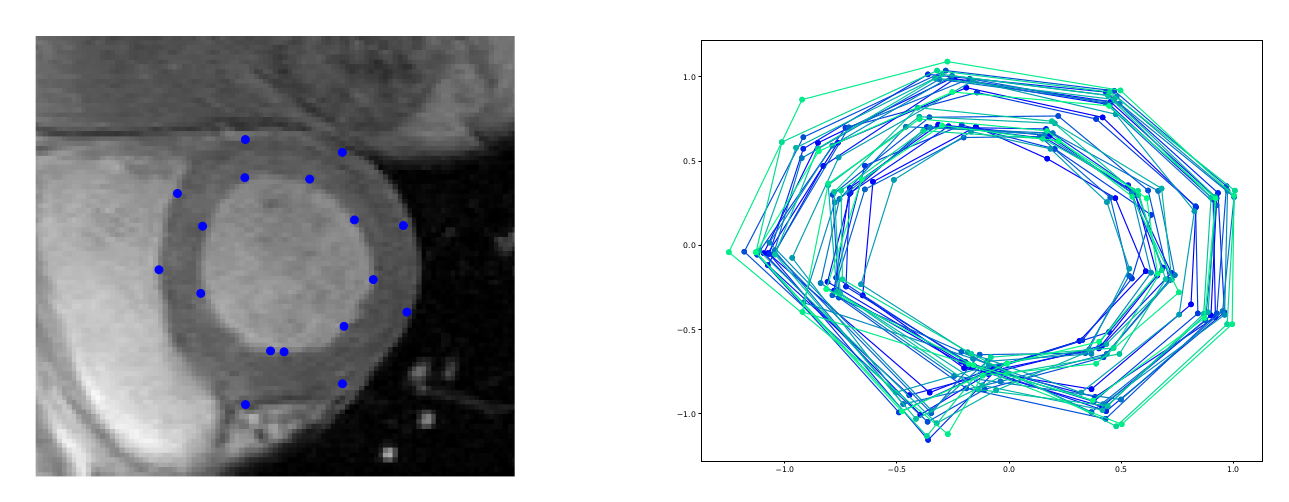
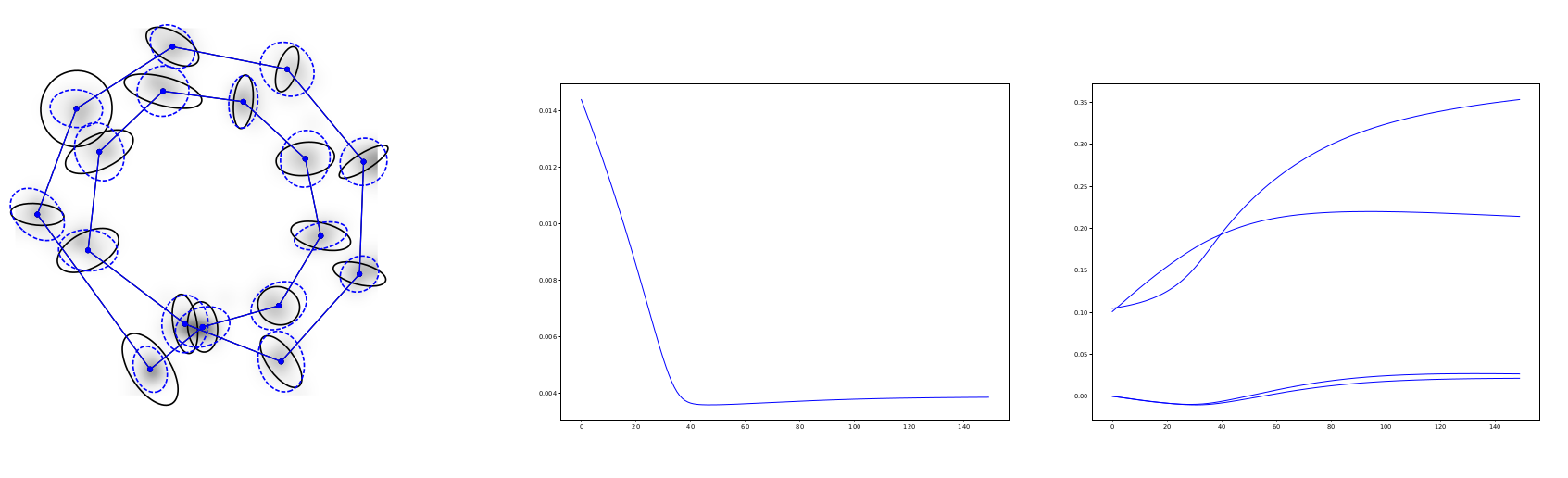
Sommer,Arnaudon,Kuhnel,Josh,MFCA'17

Stochastic matching

geometric bridge sampling

dx_t = b(t,x_t)dt +\sigma(t,x_t)dW_t

Delyon/Hu 2006 + v.d. Meulen, Schauer:

\(\sigma\) invertible:

  • guided bridge proposal$$dy_t = b(t,y_t)dt - \frac{y_t-v}{T-t}dt + \sigma(t,y_t)dW_t$$
  • \(y_T=v\) a.s.
  • \(x_t|x_T=v\) absolute continuous wrt. \(y_t\)
  • \(\mathbb E_{x_t|x_T=v}[f(x_t)]\propto \mathbb E_{y_t}[f(y_t)\varphi(y_t)]\)

\(v\)

\(x_0\)

\(x_t\)

Schauer/v.d. Meulen shape bridges

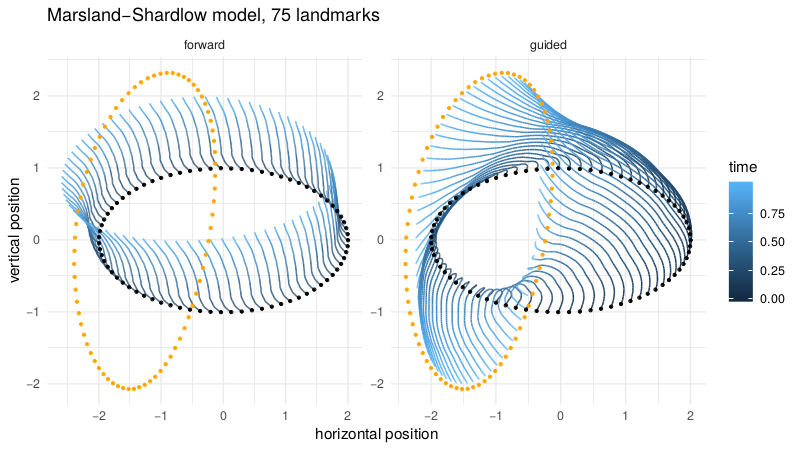
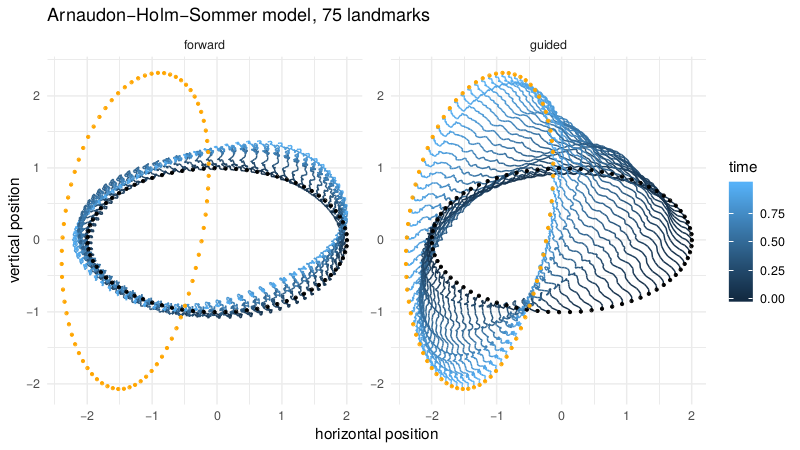
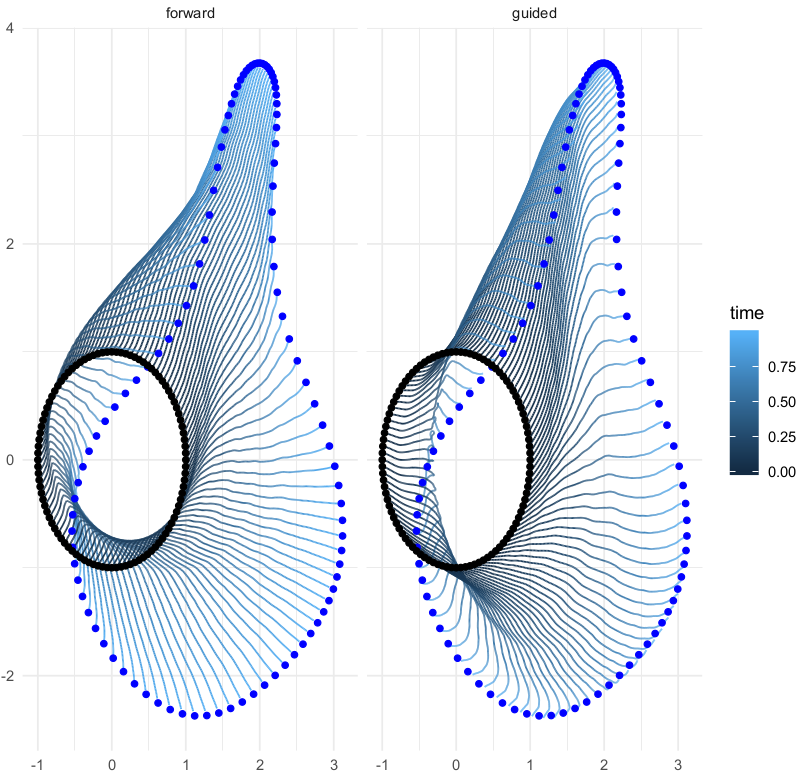
v.d. Meulen,Schauer,Arnaudon,Sommer,arxiv'20

Stochastic Euler-Poincaré equations

Stochastic perturbation of the reconstruction equation

  • right-invariant noise, momentum map preserved
  • stochastic Euler-Poincare principle
  • landmark equations​:
    \(\quad q_i = \frac{\partial h}{\partial p_i} dt+\sum_{l=1}^J\frac{\partial\phi_l}{\partial p_i}\circ dW_t^l\)
    \(\quad p_i = -\frac{\partial h}{\partial q_i} dt+\sum_{l=1}^J\frac{\partial\phi_l}{\partial q_i}\circ dW_t^l\)
  • image equations:
    \(\quad 0=d\mathbf m+\big( (\mathbf u\cdot\nabla)\mathbf m+\mathbf m\cdot(D\mathbf v)^T+\mathrm{div}(\mathbf u)\mathbf m\big)dt\)
    \(\quad\quad+\sum_{l=1}^J\big(\mathbf\sigma_l\cdot\nabla)\mathbf m+\mathbf m\cdot(D\mathbf\sigma_l)^T+\mathrm{div}(\mathbf\sigma_l)\mathbf m\big)\circ dW^l_t\)
    \(\quad dI=-\nabla I\cdot\mathbf udt+\sum_{l=1}^J\nabla I\cdot\mathbf\sigma_l\circ dW_t^l\)
d\frac{\delta l}{\delta u} + \mathrm{ad}^*_{u_t} \frac{\delta l}{\delta u}dt + \color{blue}{\sum_{l=1}^J \mathrm{ad}^*_{\sigma_l} \frac{\delta l}{\delta u}\circ dW^l_t=0}
dg_t = u_t( g_t) dt + \color{blue}{\sum_{l=1}^J \sigma_l( g_t) \circ dW^l_t}

Arnaudon,Holm,Sommer,IPMI'17; FoCM'18; JMIV'19

d\frac{\delta l}{\delta u} + \mathrm{ad}^*_{u_t} \frac{\delta l}{\delta u}dt=0
dg_t = u_t( g_t) dt

Landmark E-P bridges

  • conditioning on \(\mathbf v=(v_1,\ldots,v_N)\)
  • \(\phi_{t,T}\) approximates expected endpoint
  • \(\Sigma\) is not invertible, using \(\Sigma_{\mathbf q}^\dagger\) pseudo-inverse
  • appropriate continuity of density \(p(\mathbf q_0,\mathbf p_0; \mathbf q,T)\)

Theorem:


 

 

 

 

\begin{pmatrix} d\hat{\mathbf q} \\ d\hat{\mathbf p} \end{pmatrix} = b(\hat{\mathbf q},\hat{\mathbf p})dt - \frac{\Sigma(\hat{\mathbf q},\hat{\mathbf p})\Sigma_{\mathbf q}(\hat{\mathbf q})^\dagger(\phi_{t,T}(\hat{\mathbf q},\hat{\mathbf p})-\mathbf v)} {T-t}dt + \Sigma(\hat{\mathbf q},\hat{\mathbf p}) \circ dW
\mathbb E_{(\mathbf q,\mathbf p)|\mathbf v}[f(\mathbf q,\mathbf p)] = \lim_{t\rightarrow T} \frac{ \mathbb E_{(\hat{\mathbf q},\hat{\mathbf p})}\left [ f(\hat{\mathbf q},\hat{\mathbf p}) \varphi(\hat{\mathbf q},\hat{\mathbf p},t) \right ] }{\mathbb E_{(\hat{\mathbf q},\hat{\mathbf p})}[\varphi(\hat{\mathbf q},\hat{\mathbf p},t)]}
p(\mathbf q_0,\mathbf p_0; \mathbf q,T) = \left(\frac{\left|A(\mathbf v)\right|}{2\pi T}\right)^{\frac d2} e^{-\frac{\|\Sigma_\mathbf q(\mathbf q_0)^\dagger(\mathbf q_0-v)\|^2}{2T}} \lim_{t\to T} \mathbb E_{(\hat{\mathbf q},\hat{\mathbf p})} [\varphi(\hat{\mathbf q},\hat{\mathbf p},t)]

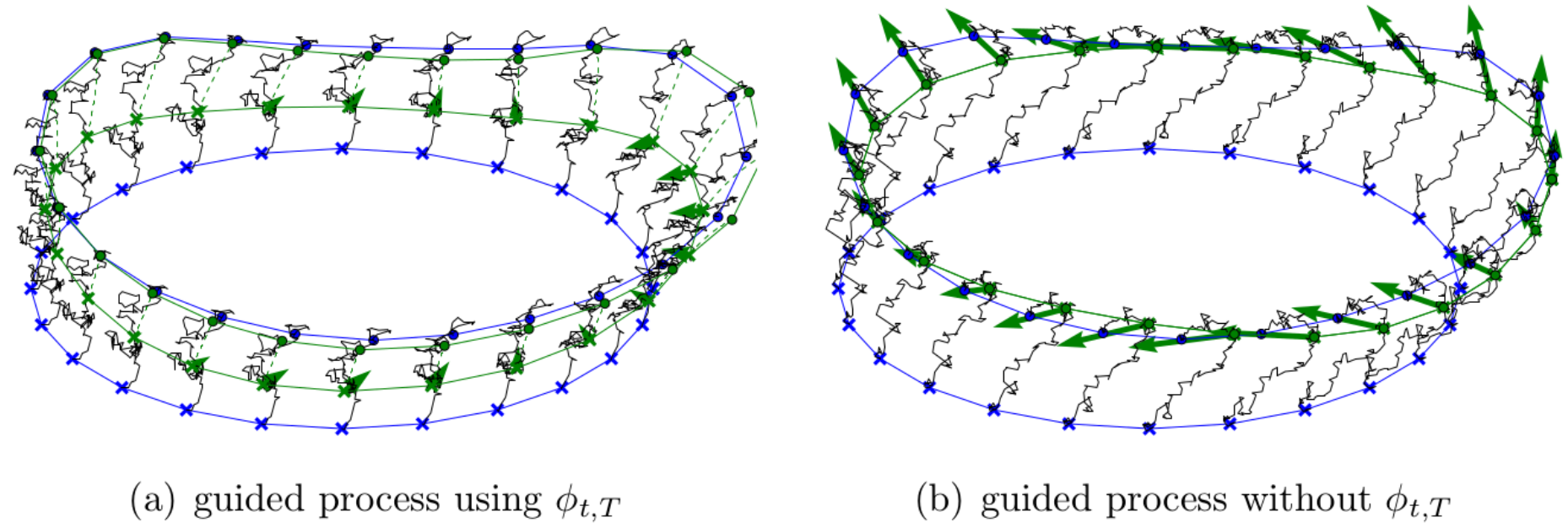
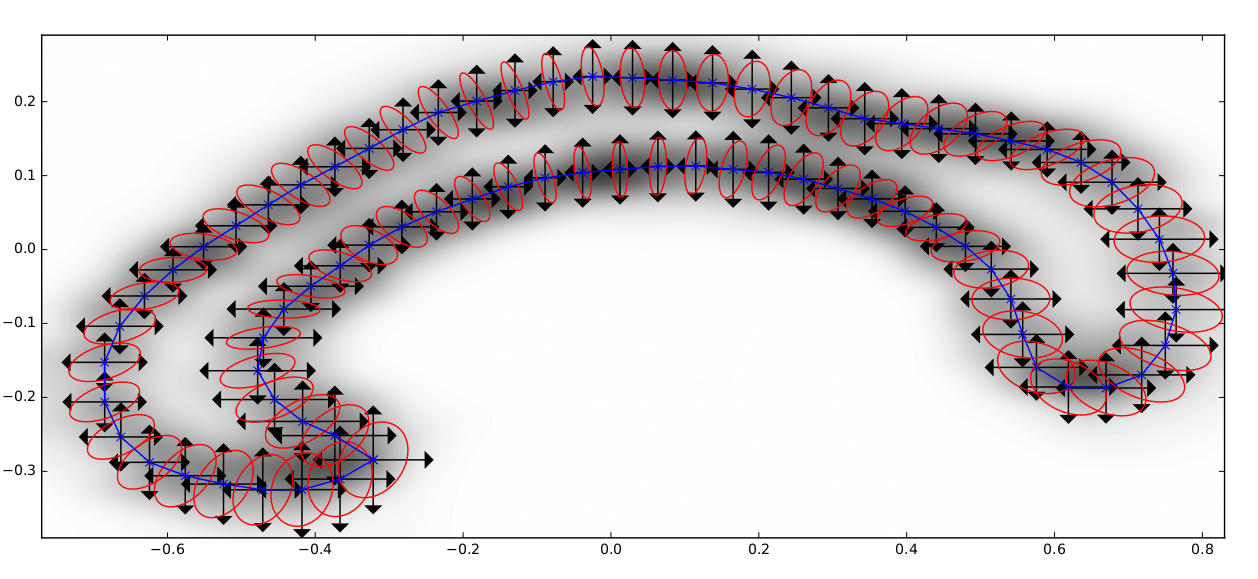
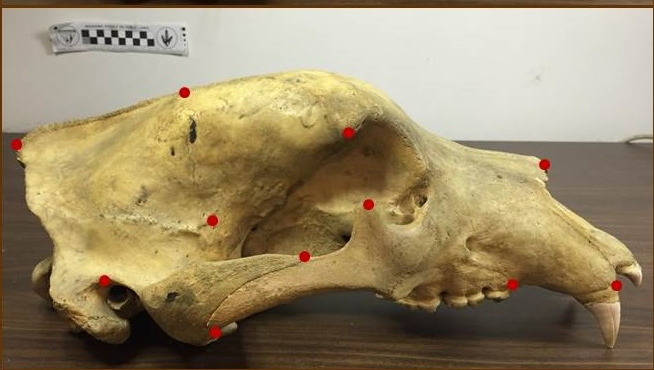
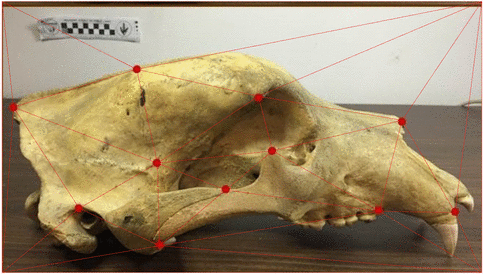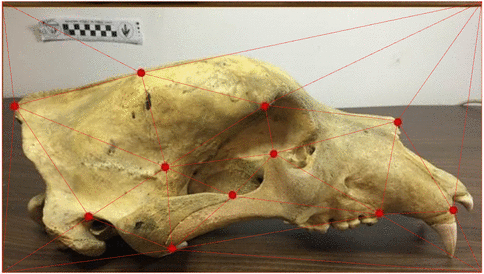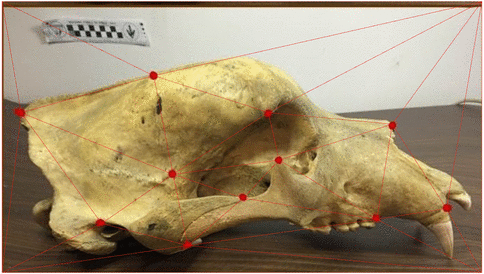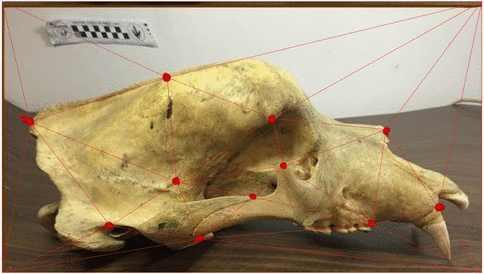
Landmark E-P bridges

v.d. Meulen,Schauer,Arnaudon,Sommer,arxiv'20

  • parametric families of probability distributions \(\mu_\theta\)
  • likelihood from density:
    \(\quad\mathcal{L}(\theta; y_1,\ldots,y_N)=\prod_{i=1}^Np_\theta(y_i)\)
  • ML/MAP estimates:
    \(\quad\bar{\theta}=\mathrm{argmax}_\theta\mathcal{L}(\theta; y_1,\ldots,y_N)\)
  • Diffusion mean:
    \(\quad x_t\in M\) Brownian motion
    \(\quad\theta=x_0\)
  • assume \(y\sim x_T\):
    \(\quad\bar{x}_{\mathrm{ML}}=\mathrm{argmax}_\theta\mathcal{L}(\theta)\)

 

Generalization of Euclidean statistical notions and techniques.

  • i.i.d. samples \(y_1,\ldots,y_N\in M\)
  • Fréchet mean:
    \(\bar{x}=\mathrm{argmin}_{x\in M}\sum_{i=1}^Nd(x,y_i)^2\)

Sommer,IPMI'15; Sommer,Svane,JGM'15;
Sommer,GSI'17; Sommer,Sankhya A'19

The Fréchet mean is not an expected value.

There is no equivalence between different characterizations of means

- in contrast to Euclidean statistics

Geometric statistics

Diffusion mean on \(\mathbb S^2\)

  • \(x_t\in M\) Brownian motion
  • \(\theta=x_0\), \(y\sim x_T\)
  • \(\bar{x}_{\mathrm{ML}}=\mathrm{argmax}_\theta\mathcal{L}(\theta)\)
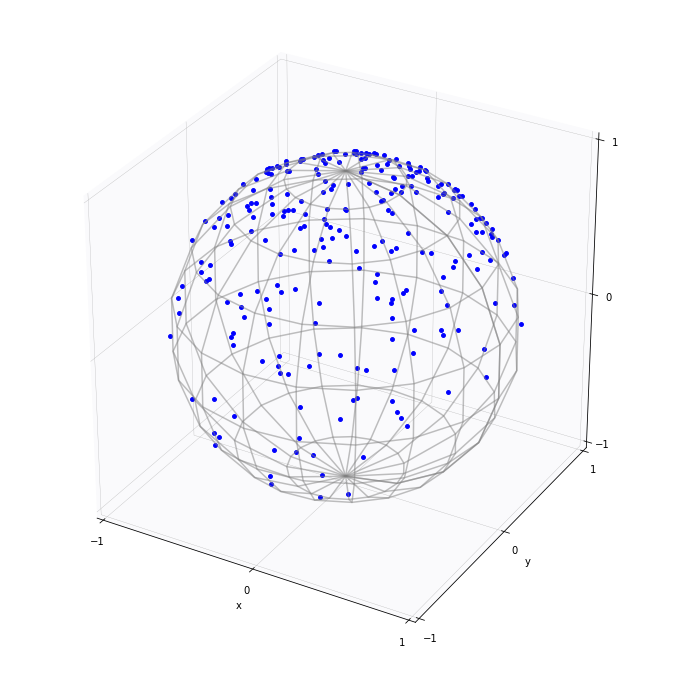
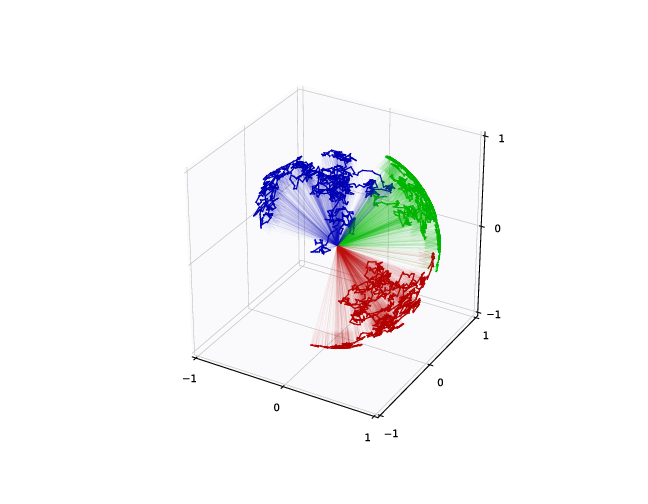
dx_t= -\frac12g(x_t)^{kl}\Gamma(x_t)_{kl}dt + \sqrt{g(x_t)^*}dW_t

Brownian motion starting point

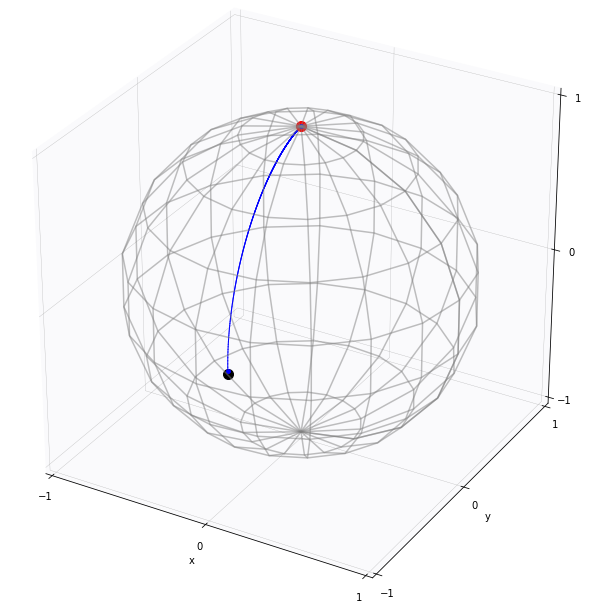
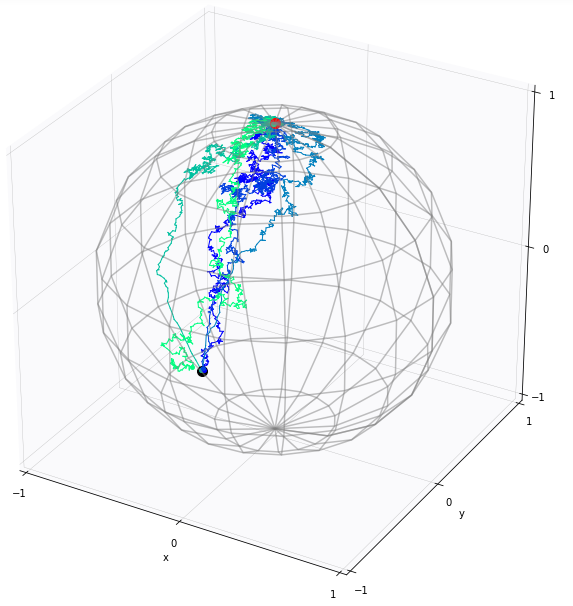
Manifold bridges

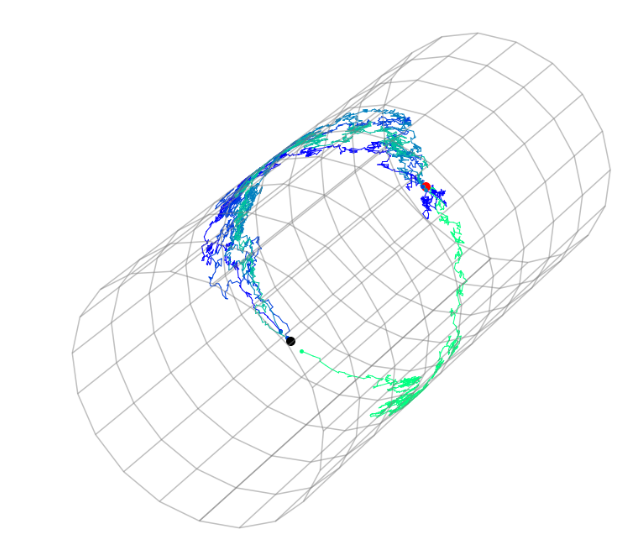
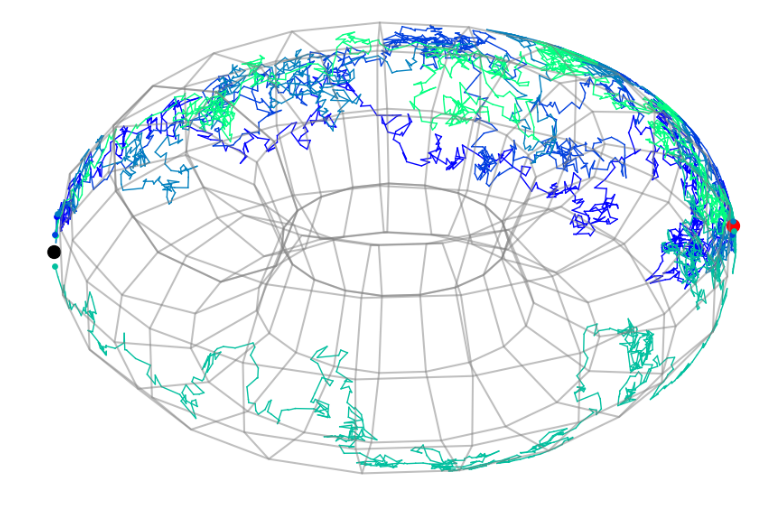
Højgaard,Sommer,in preparation

From means to covariance
\(SO(3)\) and \(\mathbb S^2\)

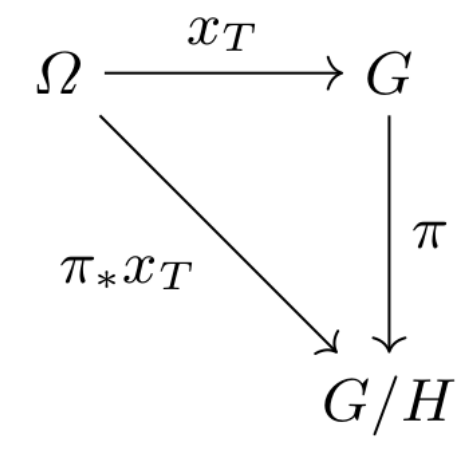
  • \(A\) quadratic form on \(so(3)\)
  • \(x_t\in SO(3)\) Brownian motion
  • \(\theta=(x_0,A)\)
  • \((\bar{x}_{\mathrm{ML}},\bar{A})=\mathrm{argmax}_\theta\mathcal{L}(\theta)\)

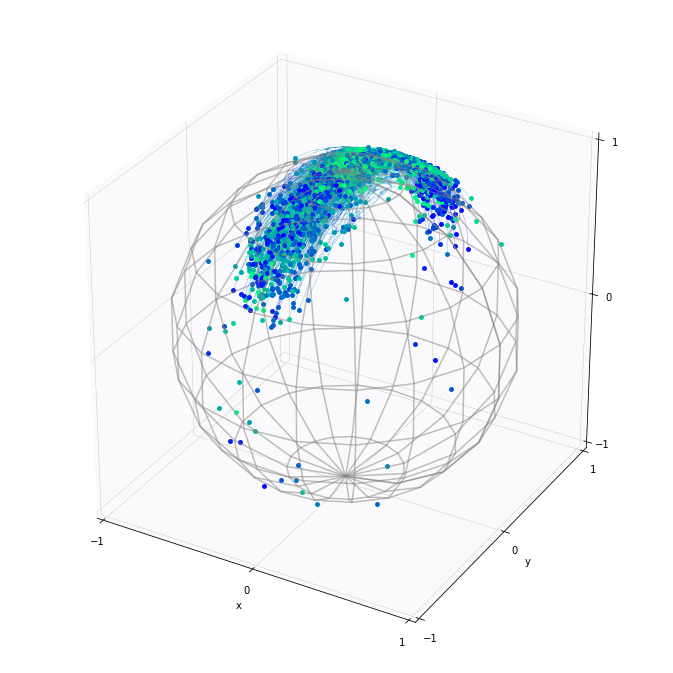
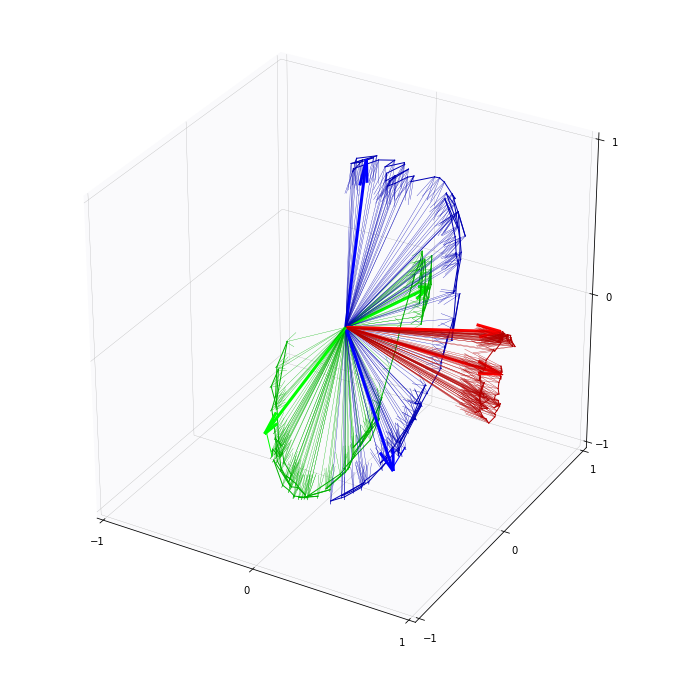
\(\pi\)

Sommer,Joshi,Højgaard, in preparation

Beyond the mean: PCA

Non-Euclidean generalizations of PCA:

  • Principal Geodesic Analysis (PGA, Fletcher et al., ’04)
  • Geodesic PCA (GPCA, Huckeman et al., ’10)
  • Horizontal Component Analysis (HCA, Sommer, ’13)
  • Principal Nested Spheres ((C)PNS, Jung et al., ’12)
  • Barycentric Subspaces (BS, Pennec, ’15)

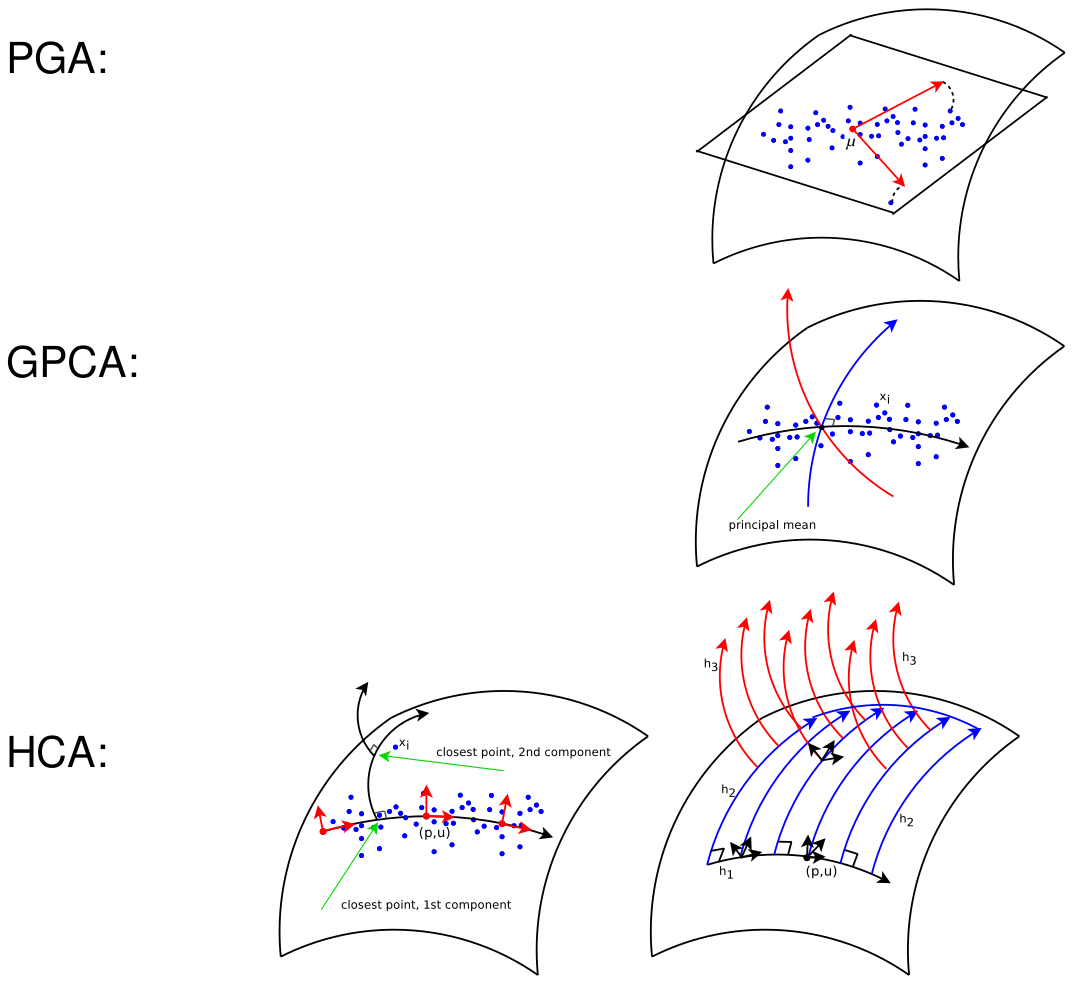
Covariance and principal components

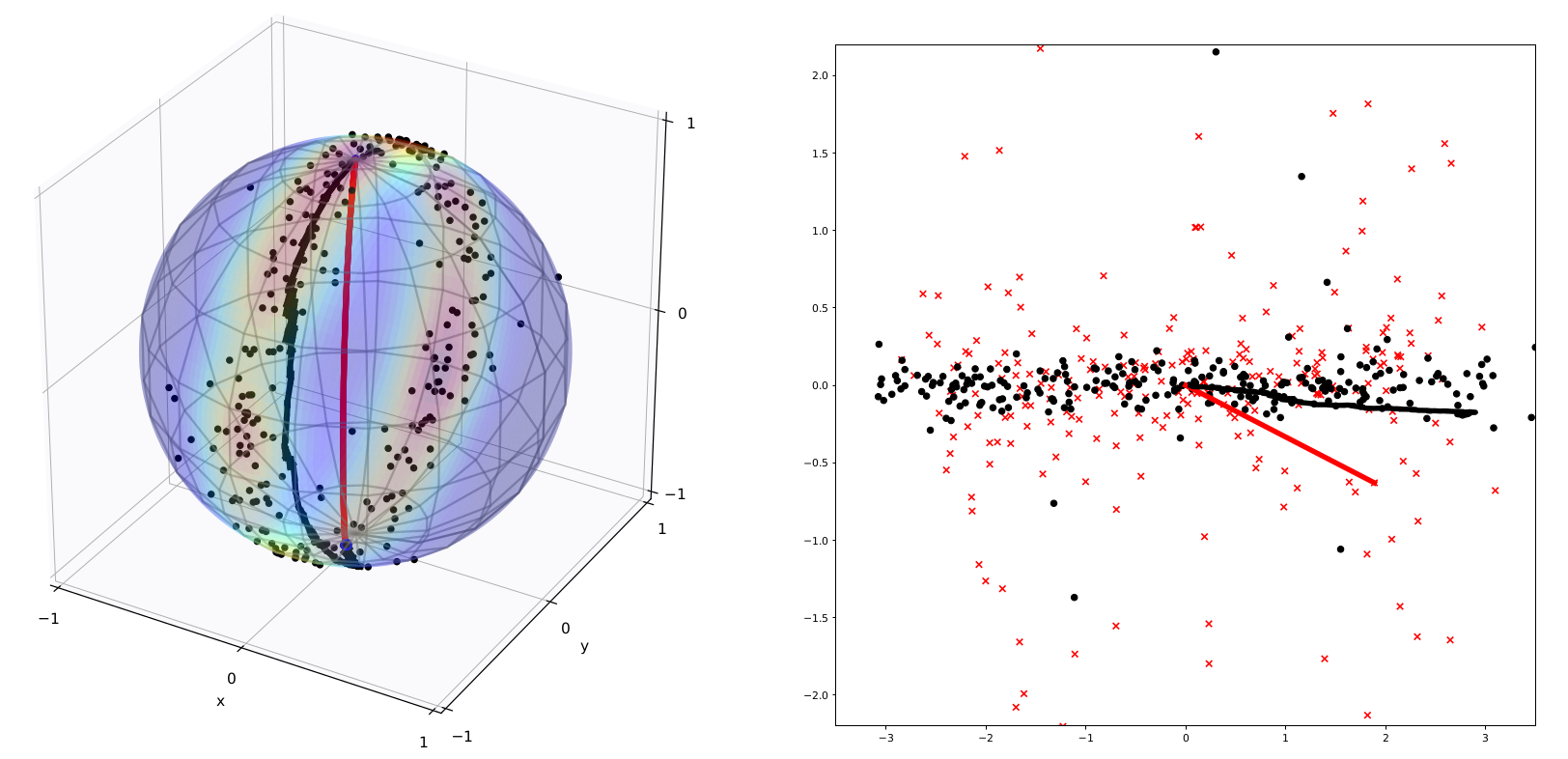
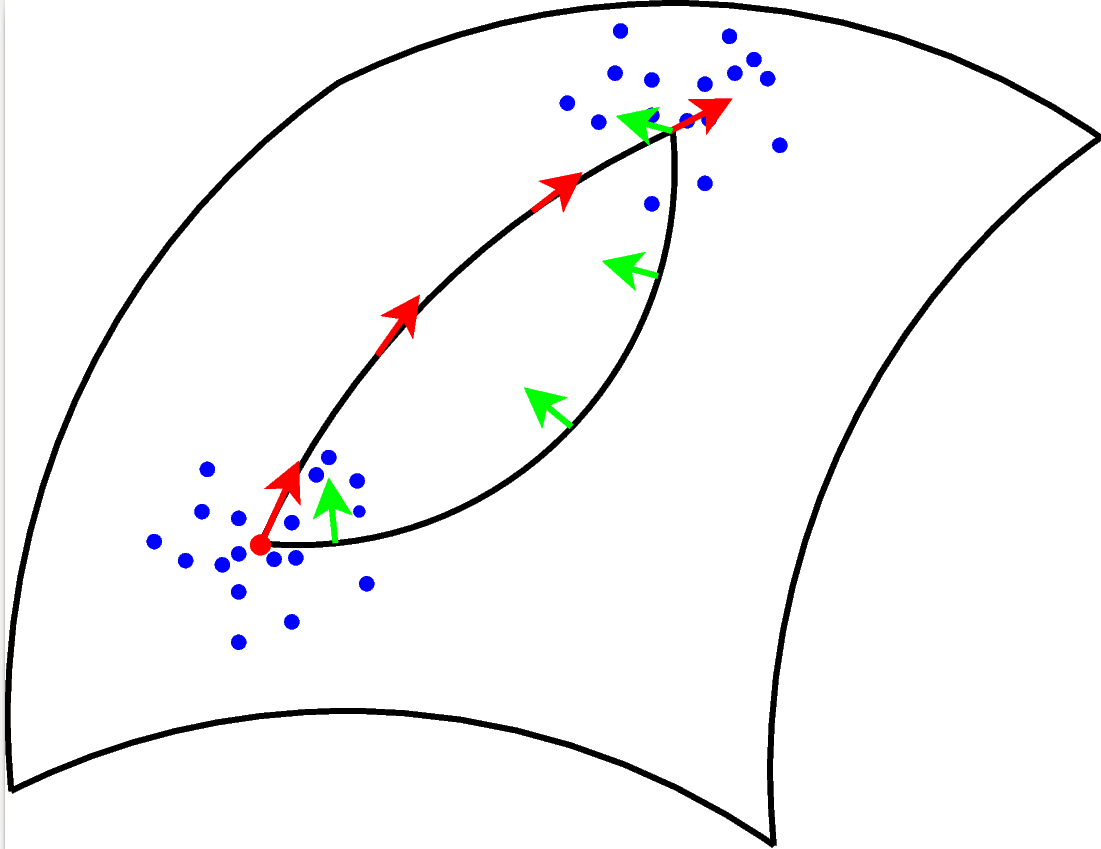
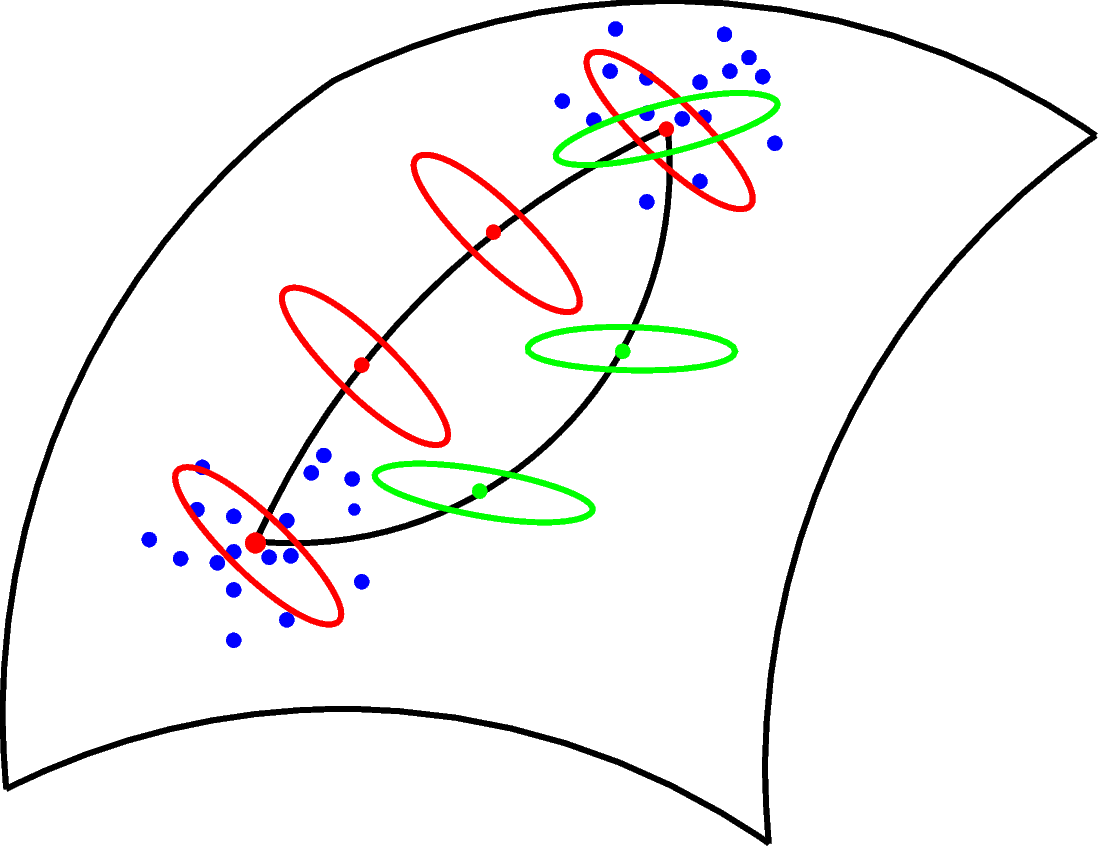
Infinitesimal Probabilistic principal components (PPCA)

  • map of Euclidean Brownian motion \(W_t\) to \(M\) via the frame bundle \(FM\): \(\qquad\qquad du_t=H_i(u_t)\circ dW_t\)
  • \(\theta=u_0\), \(u_0=(x,\sigma)\in FM\)
    \(x\in M\) mean, \(\Sigma=\sigma\sigma^T\) (infinitesimal) covariance
  • \((\bar{x}_{\mathrm{ML}},\bar{\sigma})=\mathrm{argmax}_\theta\mathcal{L}(\theta)\)

Frame bundles

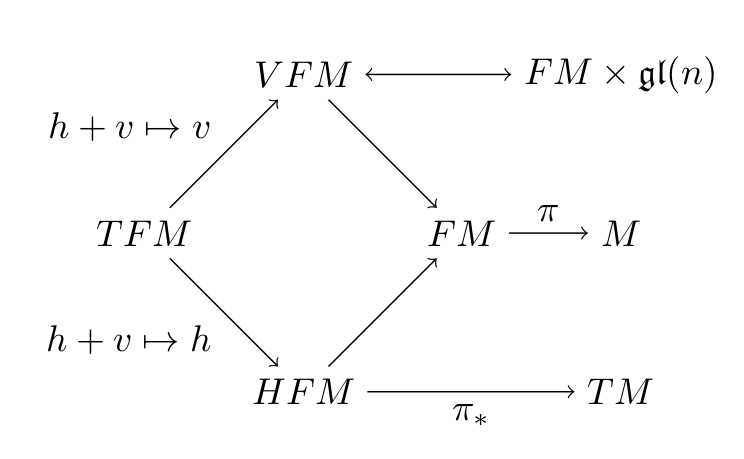
  • \(\pi:FM\to M\) is the bundle of linear frames, i.e.
    \(u=(u_1,\ldots,u_d)\in FM\) is an ordered basis for \(T_xM\), \(x=\pi(u)\)
  • \(FM\) is a \(\mathrm{GL}(n)\) principal bundle: \(u:\mathbb R^d\to T_x M\) linear, invertible
  • \(OM\) the subbundle of orthonormal frames (orientations)
  • horizontal lift \(h_u:T_xM\to H_uFM\) and fields: \(H_i:FM\to TFM\)

          \(h_u=(\pi_*|_{H_uFM})^{-1}\)
          \(H_i(u)=h_u(ue_i)\)

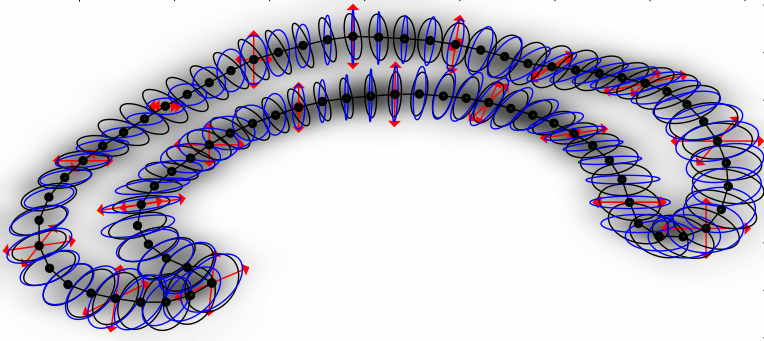
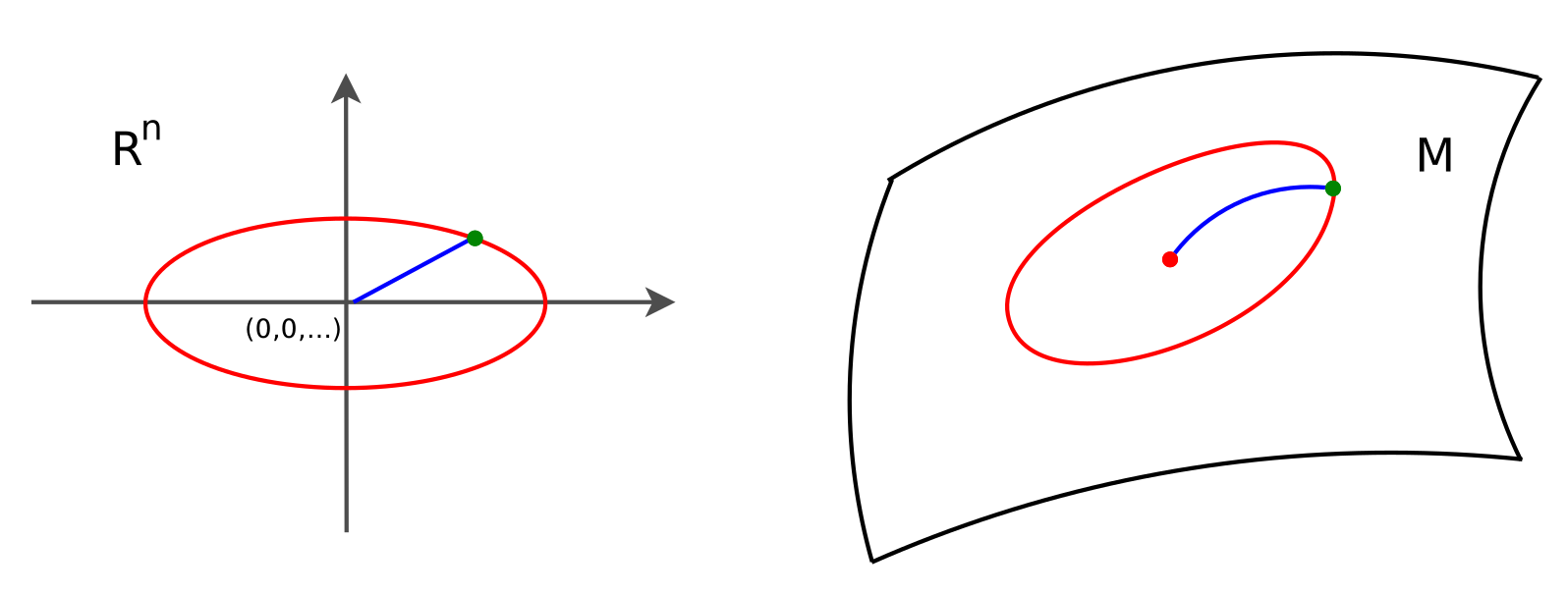
Transporting along all paths

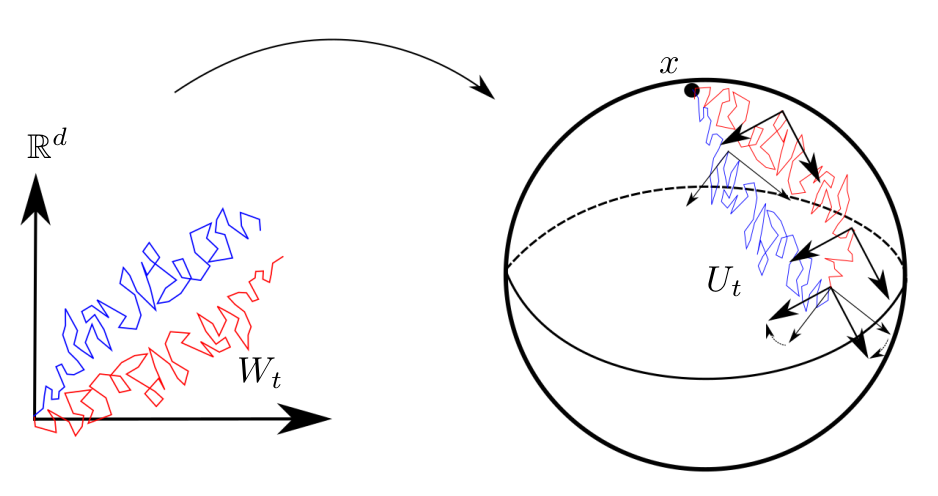
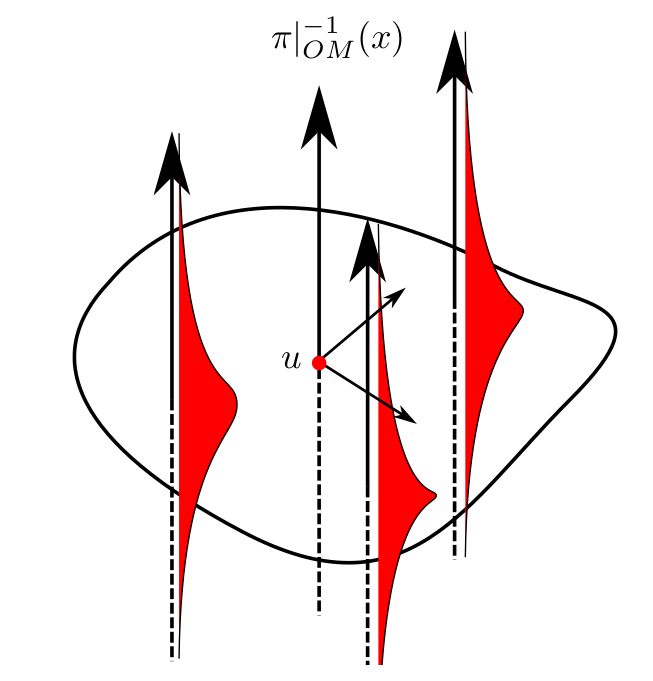
Stochastic development:

    \(dU_t=\sum_{i=1}^d H_i\circ_{\mathcal S} dW_t^i\)

\(W_t\) Euclidean Brownian motion

\(X_t=\pi(U_t)\) Riemannian Brownian motion

\(X_t\) supports stochastic parallel transport

Fix \(T>0\): \(U_T\) probability distribution in \(FM\)

... as opposed to geodesics only

Need measure on path space  \(W ([0, T ], M )\)

Covariance transport

du_t=H_i(u_t)\circ dW_t^i
u_t\in FM

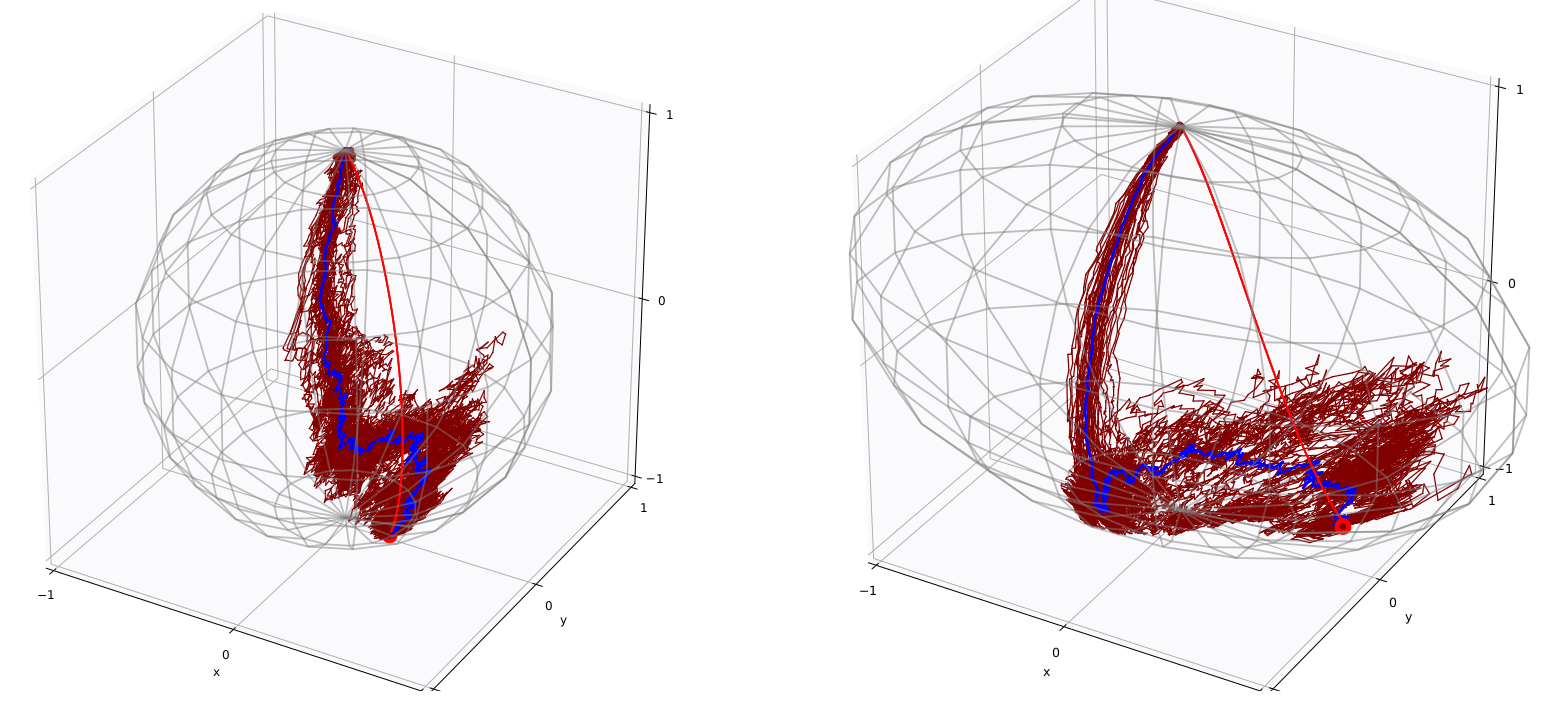
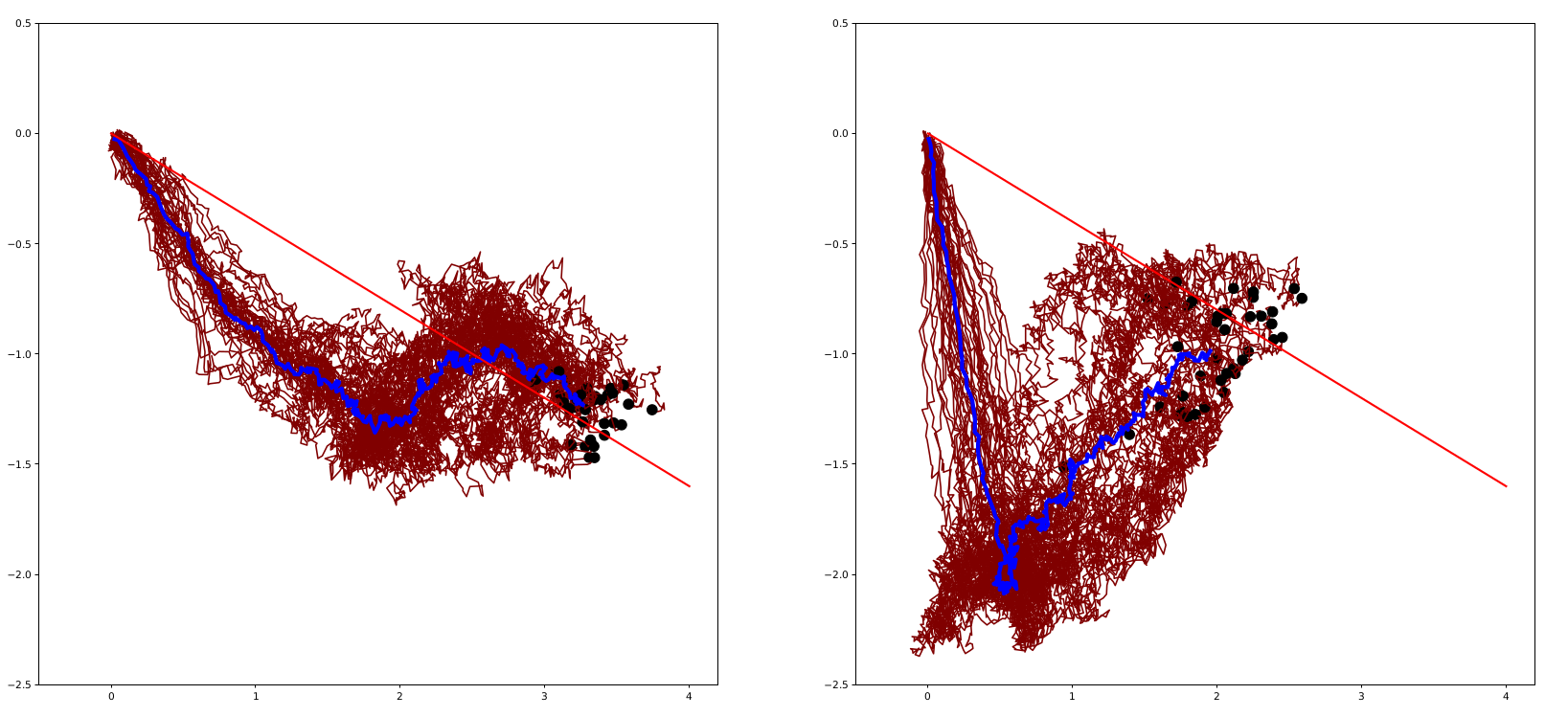
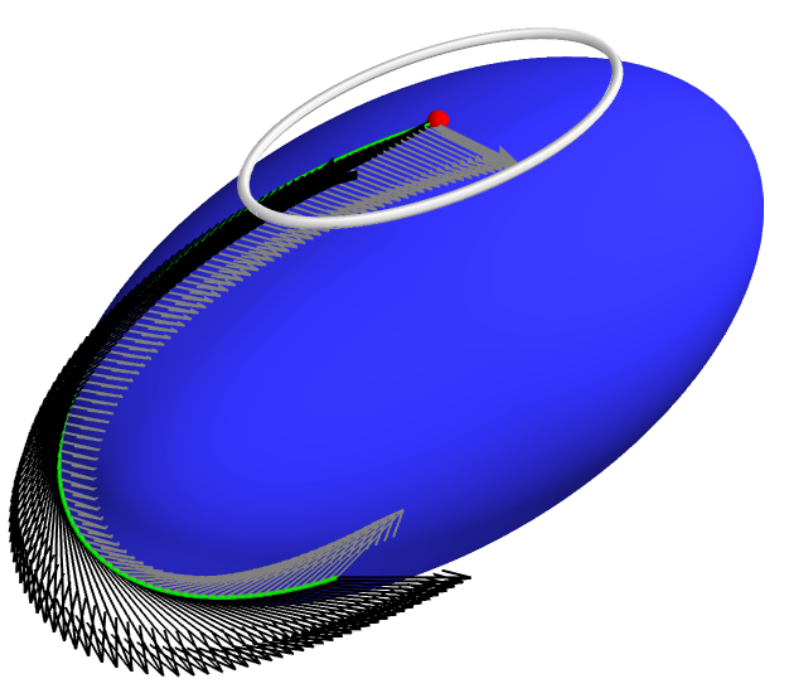
Most probable paths

  • in \(\mathbb R^d\), straight lines are most probable for stationary (isotropic) diffusion processes
  • Onsager-Machlup functional, \(\gamma_t\in M\):\[L_M(\gamma(t),\dot{\gamma}(t))=-\frac{1}{2}\|\dot{\gamma}(t)\|^2_g+\frac{1}{12}S(\gamma(t))\]
  • most probable paths maximize \(L_M(\gamma)\):\[\int_0^1 L_M(\gamma(t),\dot{\gamma}(t))dt = -E(\gamma)+ \frac{1}{12}\int_0^1S(\gamma(t))dt\]

 

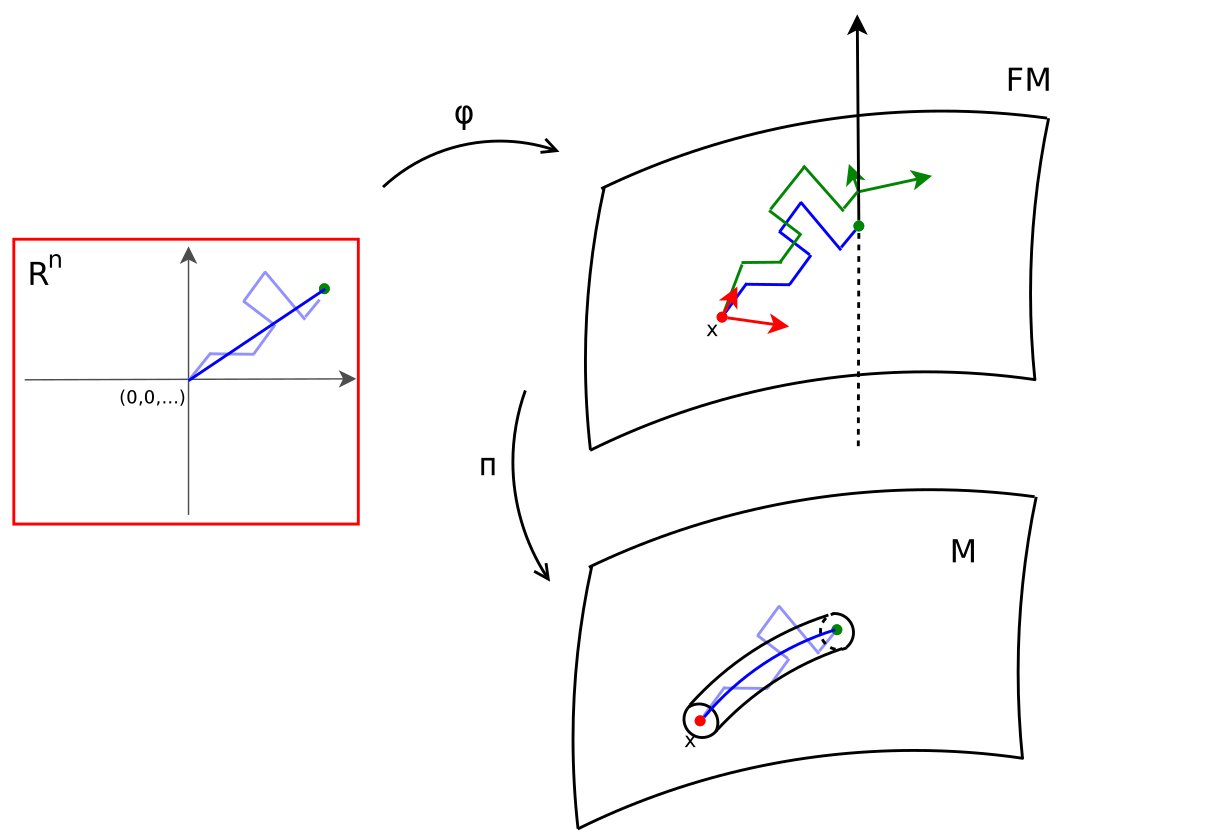
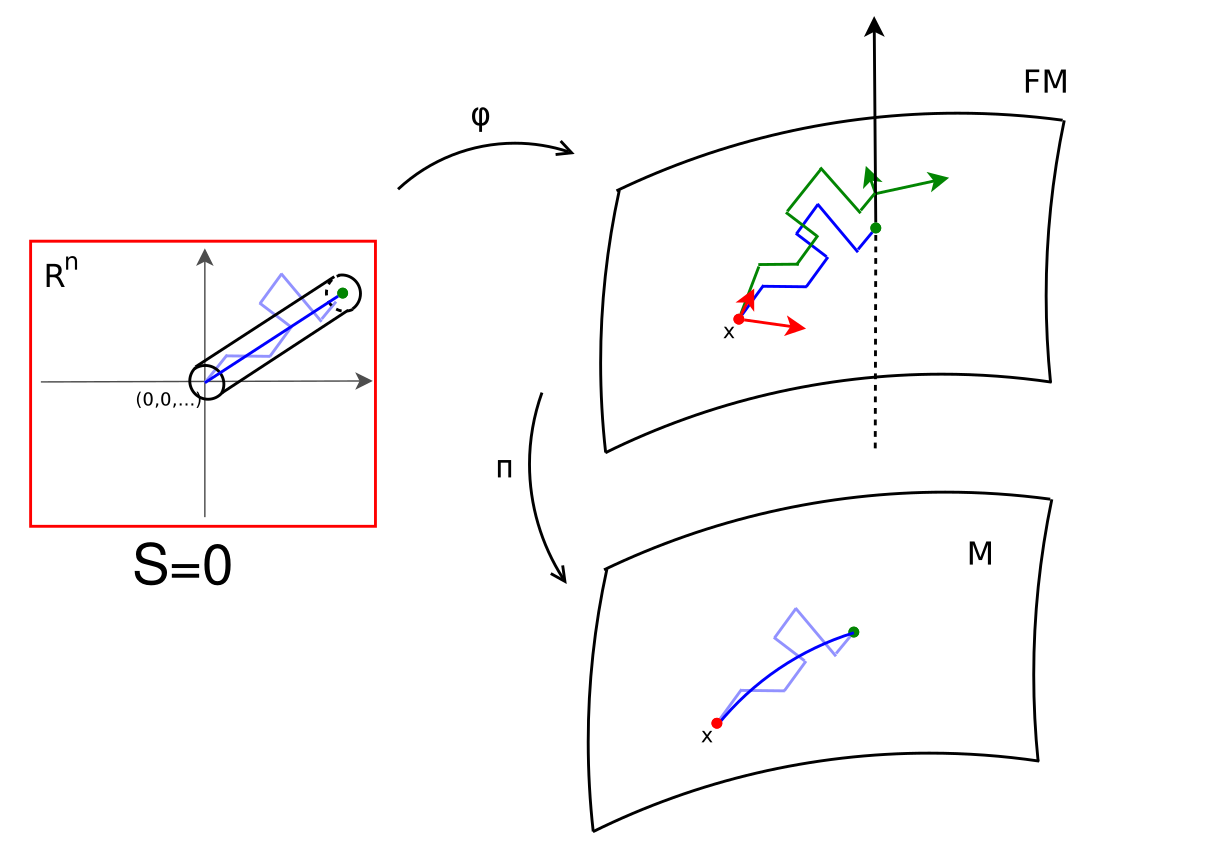
sub-Riemannian geodesics

Curvature and covariance

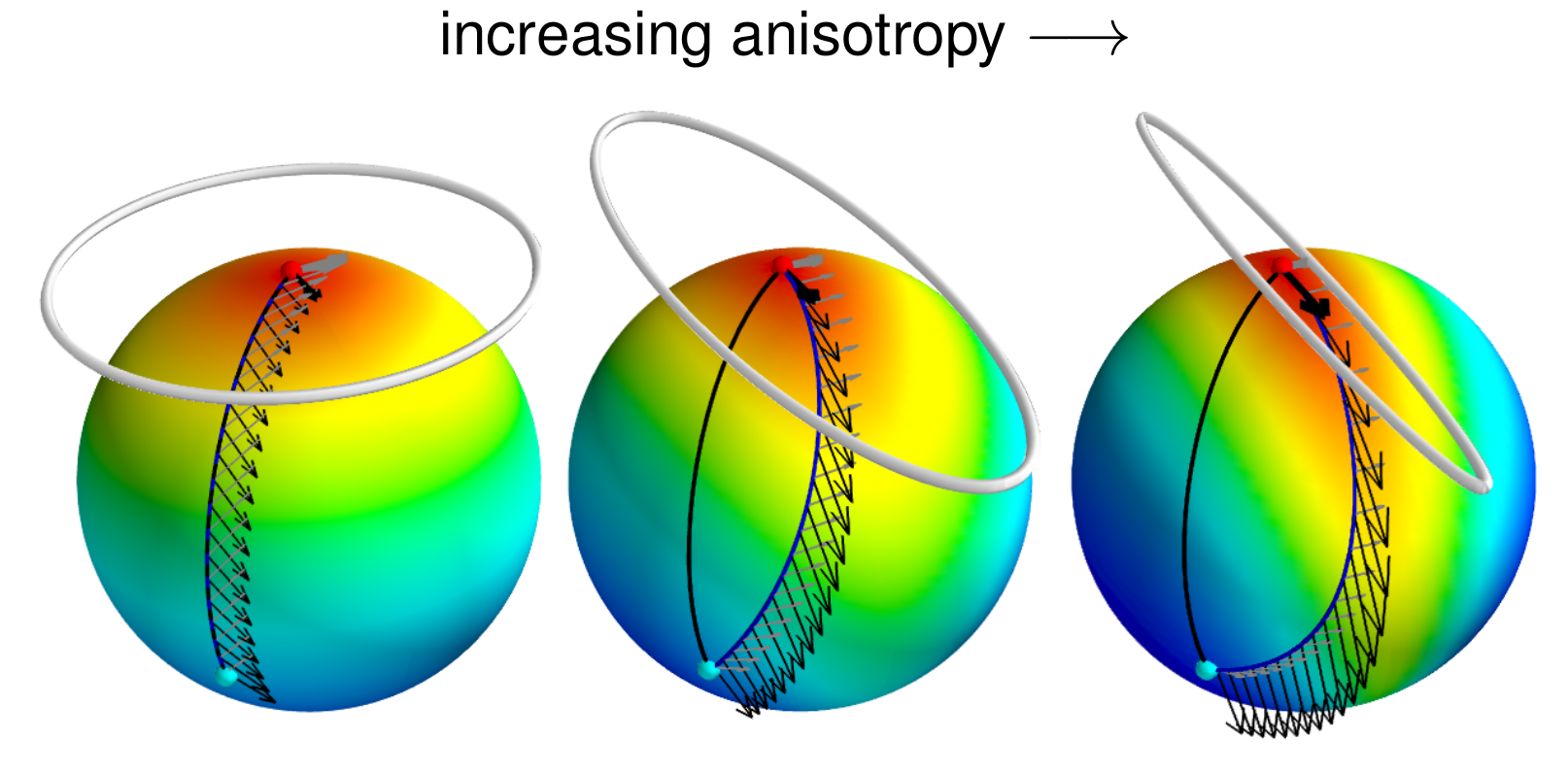
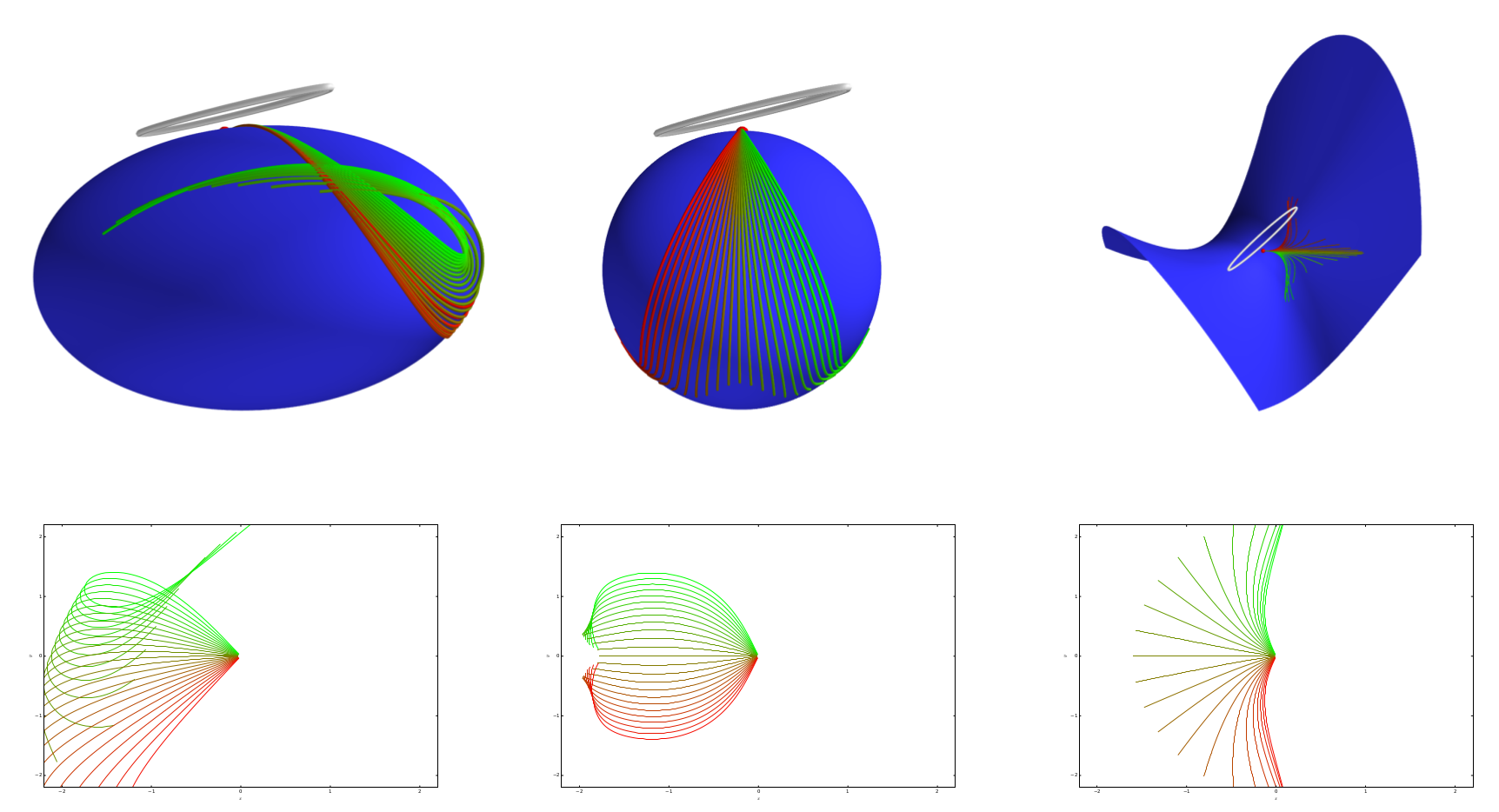
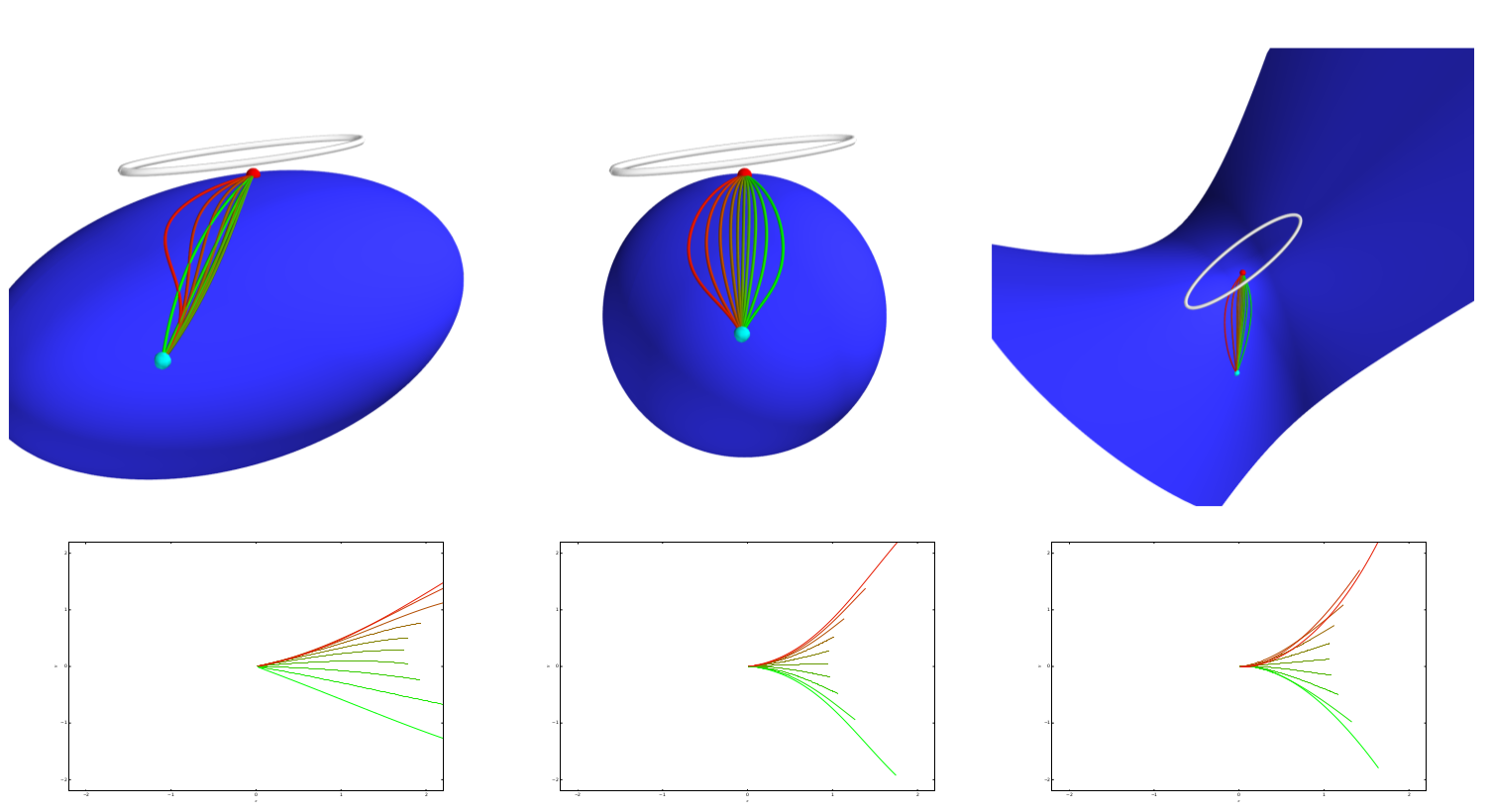
Sommer,Svane,JGM'15; Sommer,Entropy,'16

sub-Riemannian structure

Hörmander condition

Smooth density

Small time asymptotics

 

  • smooth, global support
  • Composition:
    \(k_2\ast_{W_{T/2}} (k_1\ast_{W_{T/2}} f)(u)=\)
        \(\mathrm{E}[k_2(-W_{T/2})k_1(-(W_T-W_{T/2}))f(U_T^u)]\)
  • Tensors: \(k^n_m\), \(f:OM\to\mathbb R^m\)
         \(y^n=\mathrm{E}[k^n(-W_t)f(U_T^u)]\)
  • Equivariance: \(a\in O(d)\)
        \(k\ast_{W_T} (a.f)(u)=a.(k\ast_{W_T} f)(u)\)
  • Non-linearities \(\phi_i\):
        \(\phi_n(k_n\ast_{W_{T/n}} \phi_{n-1}(\cdots \phi_1(k_1\ast_{W_{T/n}} f))(u)\)
  • precomputed density \(\rho\)

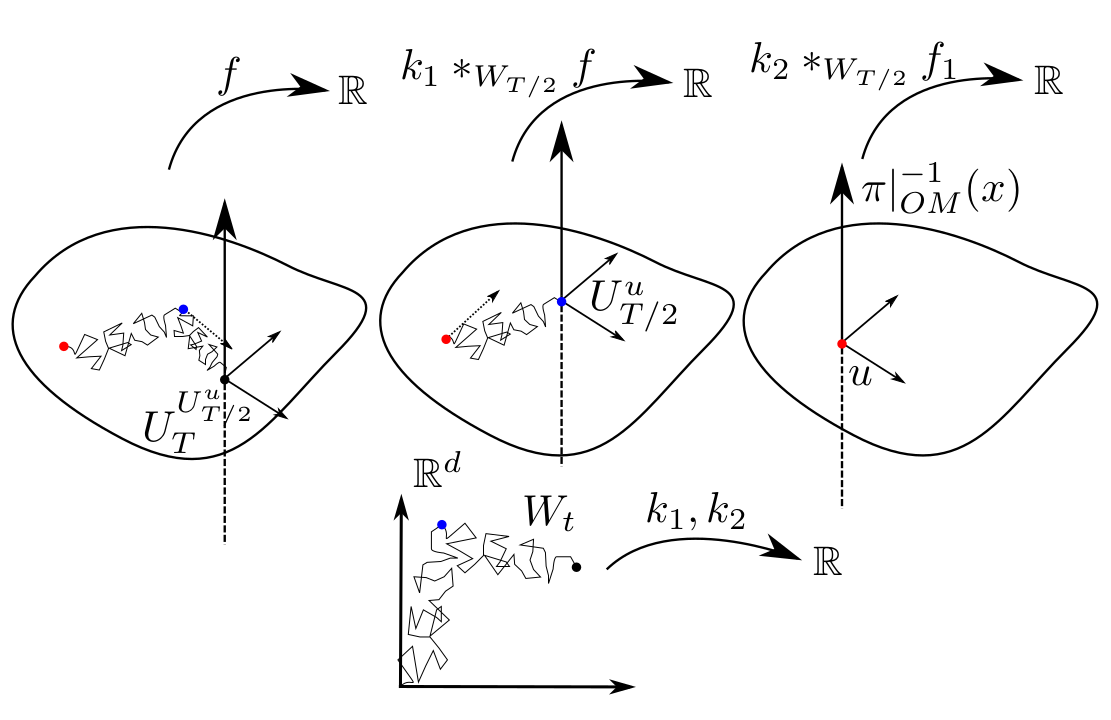
Geometry and deep learning:

Intrinsic convolutions

Sommer,Bronstein,TPAMI'20

Stochastic Shapes and Probalistic Geometric Statistics

code: http://bitbucket.com/stefansommer/theanogeometry

slides: https://slides.com/stefansommer

References:

  • Sommer, Bronstein: Horizontal Flows and Manifold Stochastics in Geometric Deep Learning, TPAMI, 2020, doi: 10.1109/TPAMI.2020.2994507
  • Hansen, Eltzner, Huckemann, Sommer: Diffusion Means on Riemannian Manifolds, in preparation, 2020.
  • Højgaard Jensen, Sommer: Simulation of Conditioned Diffusions on Riemannian Manifolds, in preparation, 2020.
  • Sommer: Anisotropic Distributions on Manifolds: Template Estimation and Most Probable Paths, IPMI 2015, doi: 10.1007/978-3-319-19992-4_15.
  • Sommer, Svane: Modelling Anisotropic Covariance using Stochastic Development and Sub-Riemannian Frame Bundle Geometry, JoGM, 2017, arXiv:1512.08544.
  • Sommer: Anisotropically Weighted and Nonholonomically Constrained Evolutions, Entropy, 2017, arXiv:1609.00395 .
  • Sommer: Anisotropic Distributions on Manifolds: Template Estimation and Most Probable Paths, IPMI 2015, doi: 10.1007/978-3-319-19992-4_15.
  • Sommer, Svane: Modelling Anisotropic Covariance using Stochastic Development and Sub-Riemannian Frame Bundle Geometry, JoGM, 2017, arXiv:1512.08544.
  • Sommer: Anisotropically Weighted and Nonholonomically Constrained Evolutions, Entropy, 2017, arXiv:1609.00395 .
  • Arnaudon, Holm, Sommer: A Stochastic Large Deformation Model for Computational Anatomy, IPMI 2017, arXiv:1612.05323.
  • Arnaudon, Holm, Sommer: A Geometric Framework for Stochastic Shape Analysis, Foundations of Computational Mathematics, arXiv:1703.09971.
  • Arnaudon, Holm, Sommer: String Methods for Stochastic Image and Shape Matching. JMIV, 2018, arXiv:1805.06038.
  • Sommer, Joshi: Brownian Bridge Simulation and Metric Estimation on Lie Groups and Homogeneous Spaces, in preparation, 2018.
  • Sommer: An Infinitesimal Probabilistic Model for Principal Component Analysis of Manifold Valued Data, Sankhya A, arXiv:1801.10341.
  • Kuhnel, Fletcher, Joshi, Sommer: Latent Space Non-Linear Statistics, arXiv:1805.07632, 2018.
  • Højgaard Jensen, Mallasto, Sommer: Simulation of Conditioned Diffusions on the Flat Torus, GSI 2019., arXiv:1906.09813.

http://ipmi2021.org