Stochastic shapes and mean sampling

Stefan Sommer, University of Copenhagen

Faculty of Science, University of Copenhagen

Stochastic Morphometrics 2022

shapes - geometric statistics - bridges - mean sampling

w/ Alexis Arnaudon, Darryl Holm, Sarang Joshi, Frank v.d. Meulen, Moritz Schauer, Benjamin Eltzner, Stephan Huckemann, Line Kuhnel, Mathias H. Jensen, Pernille E.H. Hansen, Mads Nielsen, Rasmus Nielsen, Christy Hipsley

Villum foundation

Novo nordisk foundation

University of Copenhagen

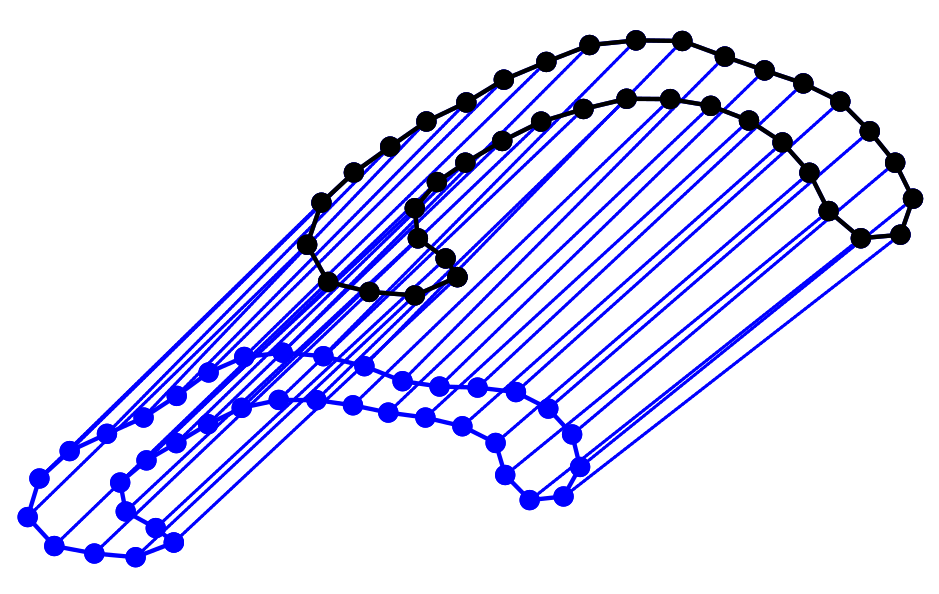
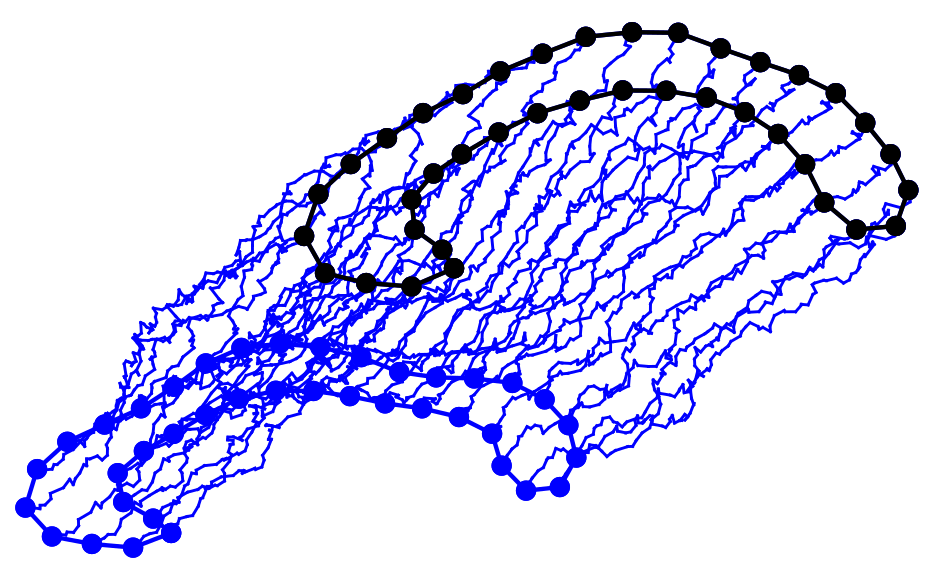
Statistical shape analysis

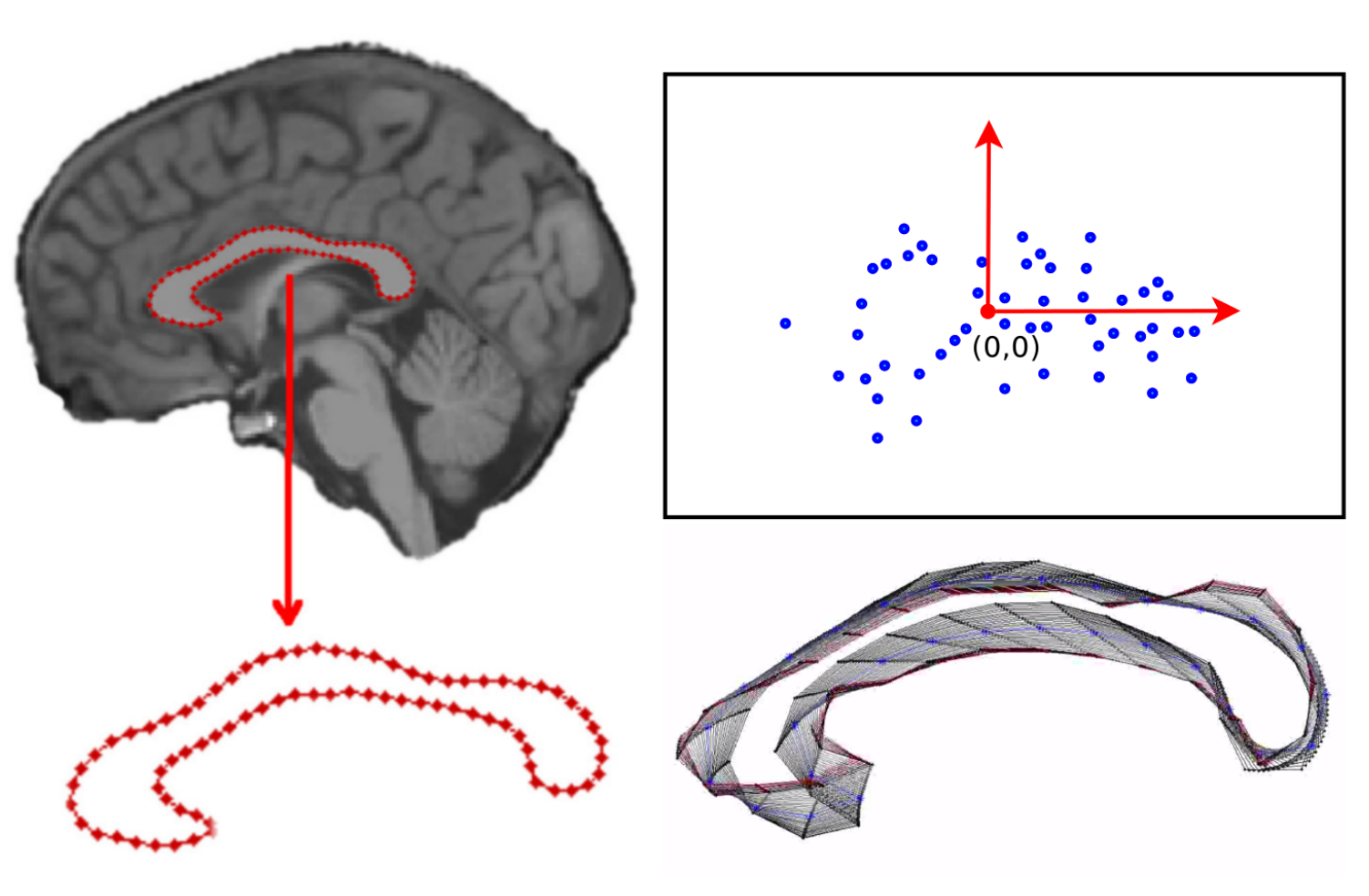
Deformations and shape

E_{s_0,s_1}(\phi)=R(\phi)+\frac1\lambda S(\phi.s_0,s_1)

action: $\phi.s=\phi\circ s$ (shapes)
$\phi.s=s\circ\phi^{-1}$ (images)

$ \phi $

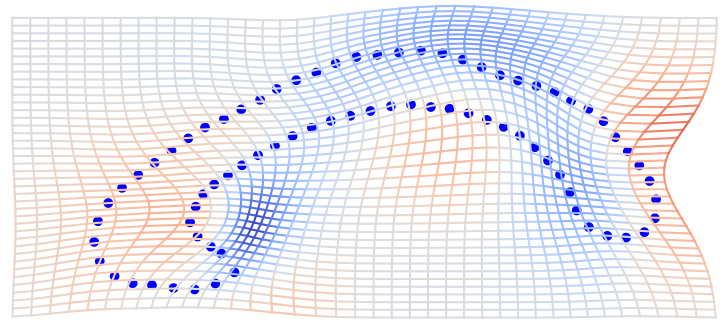
$ \phi $ warp of domain $\Omega$ (2D or 3D space)

landmarks: $s=(x_1,\ldots,x_n)$

curves: $s: \mathbb S^1\to\mathbb R^2$

surfaces: $s: \mathbb S^2\to\mathbb R^3$

Riemannian view

R(\phi_t)=\int_0^T\|\partial_t \phi_t\|_{\phi_t}^2dt

$ \phi_t:[0,T]\to\mathrm{Diff}(\Omega) $ path of diffeomorphisms (parameter t)

\mathrm{Diff}(\Omega)

\mathrm{Id}_{\mathrm{Diff}(\Omega)}

\varphi_t

LDDMM: Grenander, Miller, Trouve, Younes, Christensen, Joshi, et al.

Evolution with noise

\partial_t \phi_t = F(\phi_t)\ \to\ d\phi_t=F(\phi_t)dt\color{blue}{+\sigma(\phi_t) dW_t}

\mathrm{Diff}(\Omega)

\mathrm{Id}_{\mathrm{Diff}(\Omega)}

\phi_t

Markussen,CVIU'07; Budhiraja,Dupuis,Maroulas,Bernoulli'10
Trouve,Vialard,QAM'12;Vialard,SPA'13;Marsland/Shardlow,SIIMS'17
Staneva,Younes'17; Sommer,Arnaudon,Kuhnel,Joshi,MFCA'17
Arnaudon,Holm,Sommer,IPMI'17; FoCM'18; JMIV'19
Arnaudon,v.d. Meulen,Schauer,Sommer'21

Least-squares $\leftrightarrow$ probabilistic

Deterministic:

$\phi_t$ geodesic evolution
exact matching:
$\quad\mathrm{argmin}_{\phi_1.s_0=s_1} E(\phi_t)$
inexact matching:
$\quad\mathrm{argmin}_{\phi_t} E(\phi_t)$
distance:
$\quad d(s_0,s1)^2=E(\phi_t)$
Riemannian least-
squares

Stochastic:

$\phi_t$ stochastic process
bridge:
$\quad \phi_t|\phi_T.s_0=s_1$
bridge + noise in observation:
$\quad \phi_t|\phi_T.s_0+\epsilon=s_1$
(log) transition density
$\quad -\log p_T(s_1; s_0)$
ML/MAP

Inferring geometry of landmarks spaces

Landmarks $\mathbf{q}=(q_1,\ldots,q_n),\,q_i\in\Omega\subseteq\mathbb R^d$
LDDMM cometric $ \left<\xi,\eta\right>_{\mathbf q}=\xi^T K(\mathbf q,\mathbf q)\eta$
kernel $K(\mathbf q_1,\mathbf q_2)=\alpha e^{-1\frac12 x^T\Sigma^{-1}x}\mathrm{Id}_d$
Riemannian Brownian motion
$$dq_t^i=g^{kl}\Gamma(\mathbf q_t)^i_{kl}dt+\sqrt{g^*(\mathbf q_t)}^idW_t$$

Riemannian Brownian motion transition density:
$$p_{T,\theta}(\mathbf v)=\frac1{\sqrt{|K(\mathbf v,\mathbf v)|(2\pi T)^{Nd}}}e^{-\frac{\|(\mathbf q_0-\mathbf v)^TK(\mathbf q_0,\mathbf q_0)^{-1}(\mathbf q_0-\mathbf v)\|^2}{2T}}\mathbb E_{\mathbf y_\theta}[\varphi_{\theta}(\mathbf y)]$$

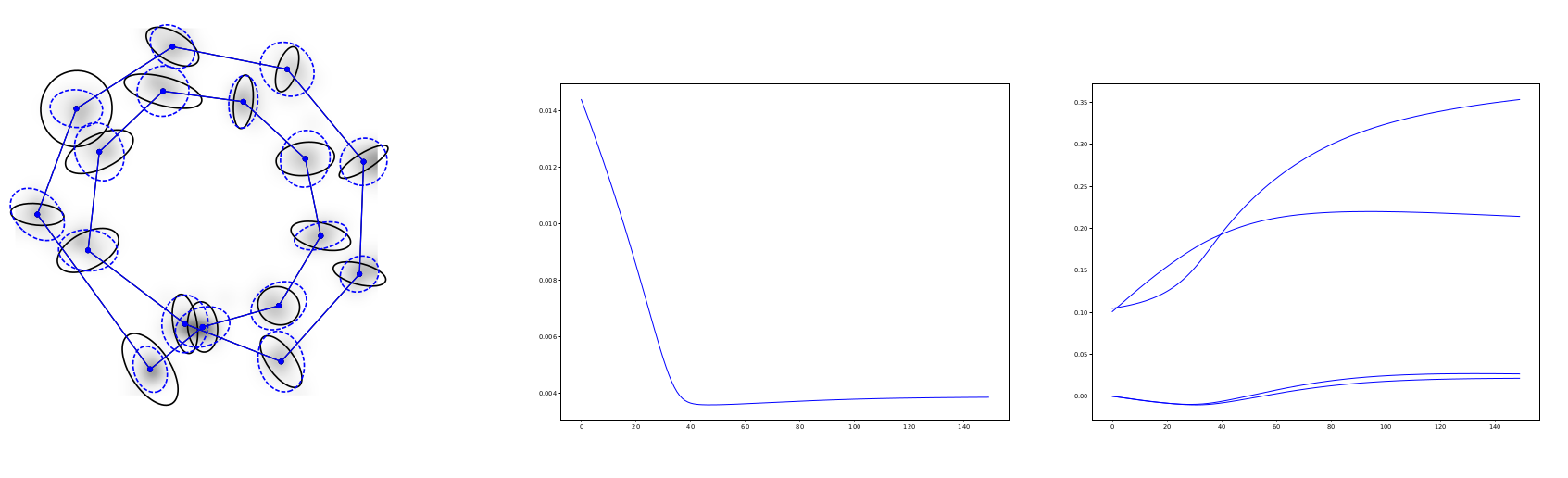
Sommer,Arnaudon,Kuhnel,Josh,MFCA'17

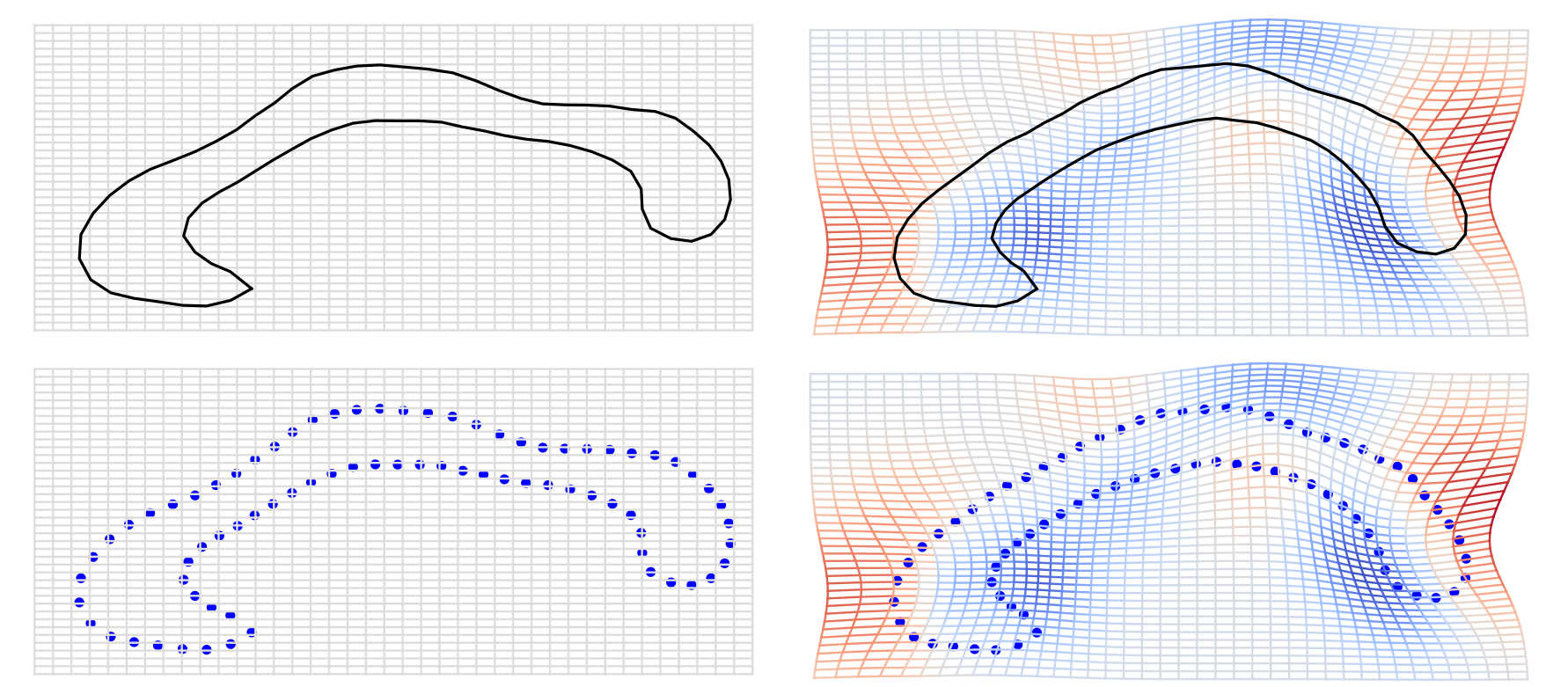
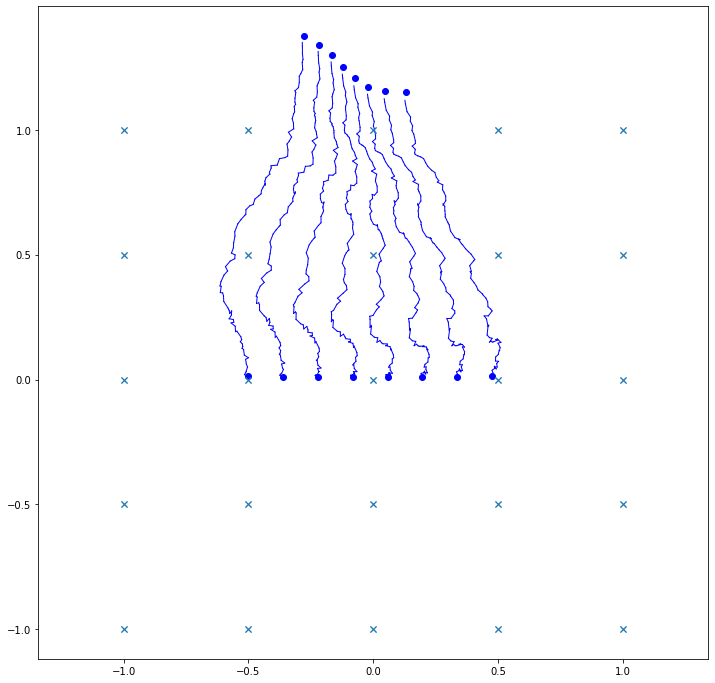
Approximating $p_T(v)$: Stochastic matching

bridge sampling

dx_t = b(t,x_t)dt +\sigma(t,x_t)dW_t

Delyon/Hu 2006:

$\sigma$ invertible:

guided bridge proposal$$dy_t = b(t,y_t)dt - \frac{y_t-v}{T-t}dt + \sigma(t,y_t)dW_t$$
$y_T=v$ a.s.
$x_t|x_T=v$ absolute continuous wrt. $y_t$
$\mathbb E_{x_t|x_T=v}[f(x_t)]\propto \mathbb E_{y_t}[f(y_t)\varphi(y_t)]$

$v$

$x_0$

$x_t$

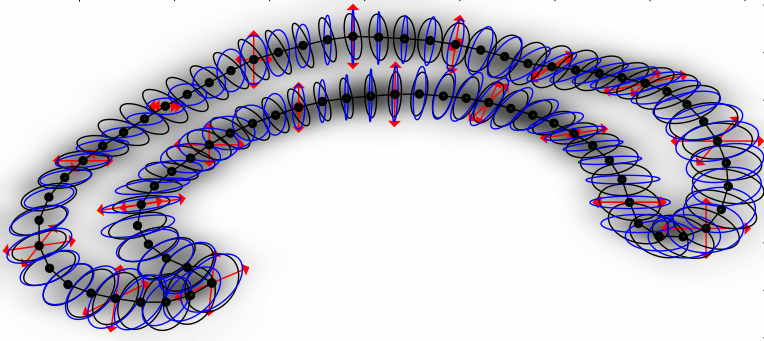
Stochastic Euler-Poincaré model

Stochastic perturbation of the reconstruction equation

right-invariant noise, momentum map preserved
stochastic Euler-Poincare principle
landmark equations:
$\quad q_i = \frac{\partial h}{\partial p_i} dt+\sum_{l=1}^J\frac{\partial\phi_l}{\partial p_i}\circ dW_t^l$
$\quad p_i = -\frac{\partial h}{\partial q_i} dt+\sum_{l=1}^J\frac{\partial\phi_l}{\partial q_i}\circ dW_t^l$
image equations:
$\quad 0=d\mathbf m+\big( (\mathbf u\cdot\nabla)\mathbf m+\mathbf m\cdot(D\mathbf v)^T+\mathrm{div}(\mathbf u)\mathbf m\big)dt$
$\quad\quad+\sum_{l=1}^J\big(\mathbf\sigma_l\cdot\nabla)\mathbf m+\mathbf m\cdot(D\mathbf\sigma_l)^T+\mathrm{div}(\mathbf\sigma_l)\mathbf m\big)\circ dW^l_t$
$\quad dI=-\nabla I\cdot\mathbf udt+\sum_{l=1}^J\nabla I\cdot\mathbf\sigma_l\circ dW_t^l$

d\frac{\delta l}{\delta u} + \mathrm{ad}^*_{u_t} \frac{\delta l}{\delta u}dt + \color{blue}{\sum_{l=1}^J \mathrm{ad}^*_{\sigma_l} \frac{\delta l}{\delta u}\circ dW^l_t=0}

dg_t = u_t( g_t) dt + \color{blue}{\sum_{l=1}^J \sigma_l( g_t) \circ dW^l_t}

Arnaudon,Holm,Sommer,IPMI'17; FoCM'18; JMIV'19

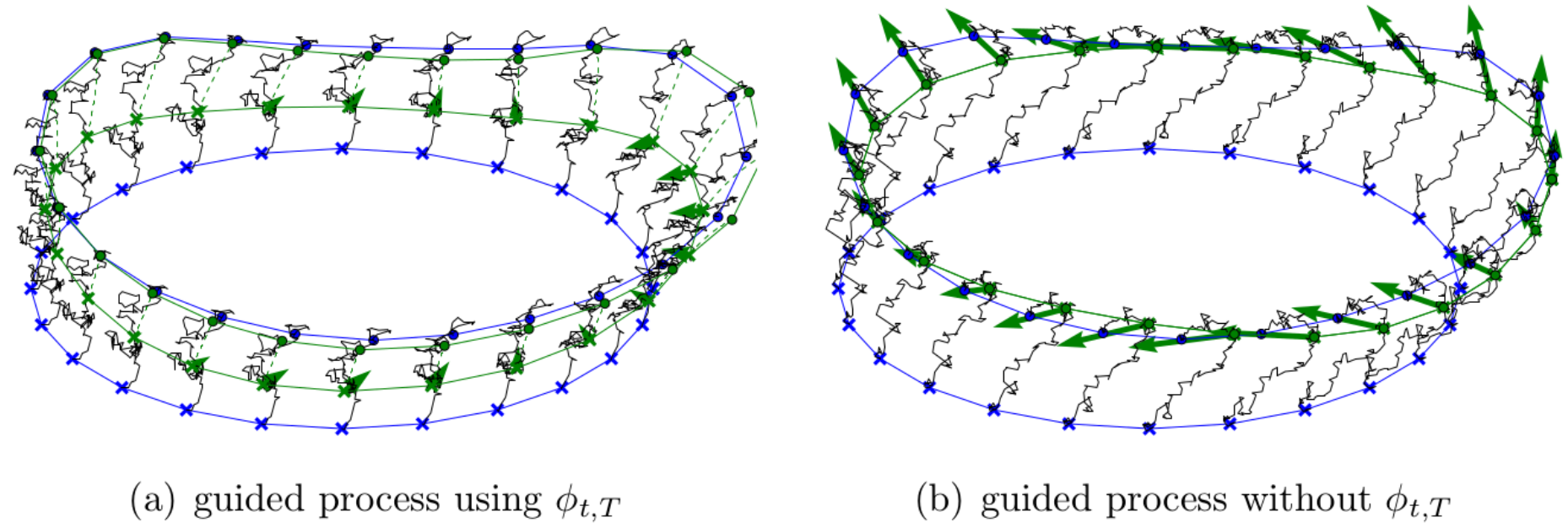
d\frac{\delta l}{\delta u} + \mathrm{ad}^*_{u_t} \frac{\delta l}{\delta u}dt=0

dg_t = u_t( g_t) dt

Landmark E-P bridges

conditioning on $\mathbf v=(v_1,\ldots,v_N)$
$\phi_{t,T}$ approximates expected endpoint
$\Sigma$ is not invertible, using $\Sigma_{\mathbf q}^\dagger$ pseudo-inverse
appropriate continuity of density $p(\mathbf q_0,\mathbf p_0; \mathbf q,T)$

Theorem:

\begin{pmatrix} d\hat{\mathbf q} \\ d\hat{\mathbf p} \end{pmatrix} = b(\hat{\mathbf q},\hat{\mathbf p})dt - \frac{\Sigma(\hat{\mathbf q},\hat{\mathbf p})\Sigma_{\mathbf q}(\hat{\mathbf q})^\dagger(\phi_{t,T}(\hat{\mathbf q},\hat{\mathbf p})-\mathbf v)} {T-t}dt + \Sigma(\hat{\mathbf q},\hat{\mathbf p}) \circ dW

\mathbb E_{(\mathbf q,\mathbf p)|\mathbf v}[f(\mathbf q,\mathbf p)] = \lim_{t\rightarrow T} \frac{ \mathbb E_{(\hat{\mathbf q},\hat{\mathbf p})}\left [ f(\hat{\mathbf q},\hat{\mathbf p}) \varphi(\hat{\mathbf q},\hat{\mathbf p},t) \right ] }{\mathbb E_{(\hat{\mathbf q},\hat{\mathbf p})}[\varphi(\hat{\mathbf q},\hat{\mathbf p},t)]}

p(\mathbf q_0,\mathbf p_0; \mathbf q,T) = \left(\frac{\left|A(\mathbf v)\right|}{2\pi T}\right)^{\frac d2} e^{-\frac{\|\Sigma_\mathbf q(\mathbf q_0)^\dagger(\mathbf q_0-v)\|^2}{2T}} \lim_{t\to T} \mathbb E_{(\hat{\mathbf q},\hat{\mathbf p})} [\varphi(\hat{\mathbf q},\hat{\mathbf p},t)]

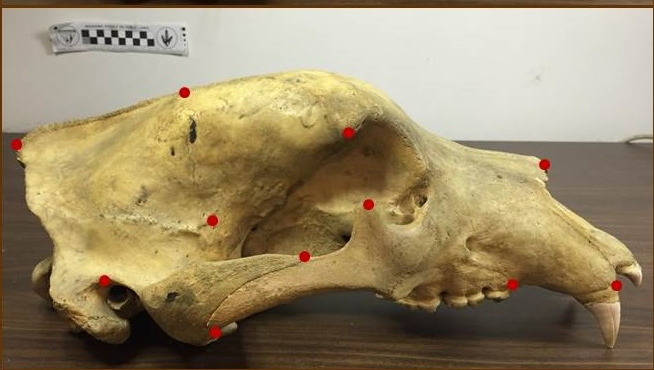
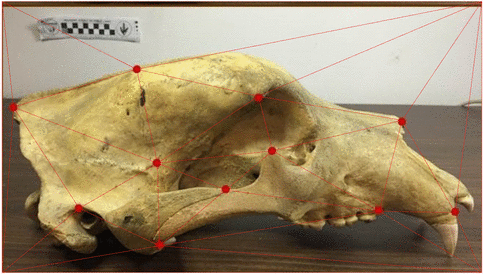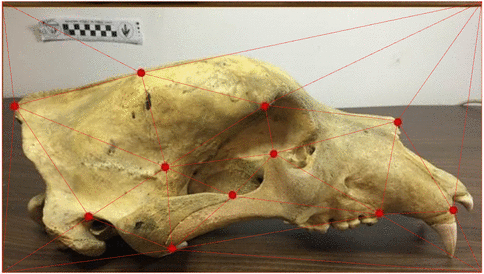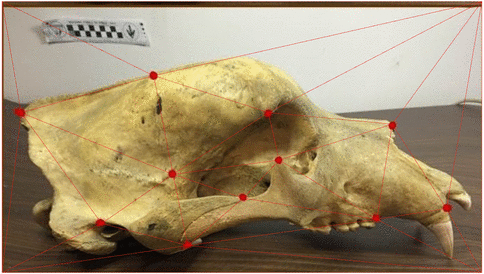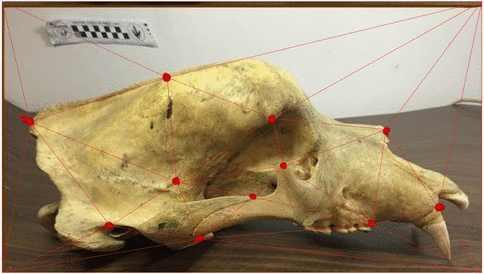
Stochastic morphometry along phylogenies

v.d. Meulen,Schauer,Arnaudon,Sommer, SIIMS 21

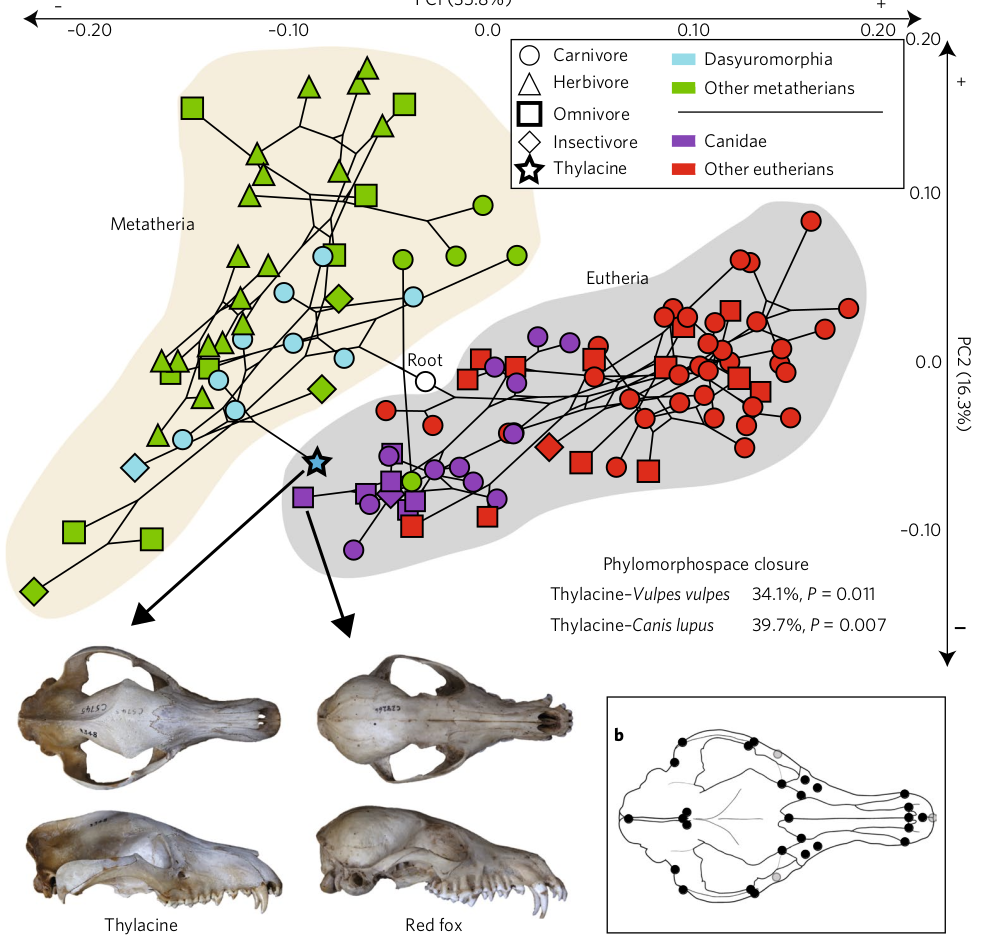
Simulation of Conditioned Semimartingales on Riemannian Manifolds

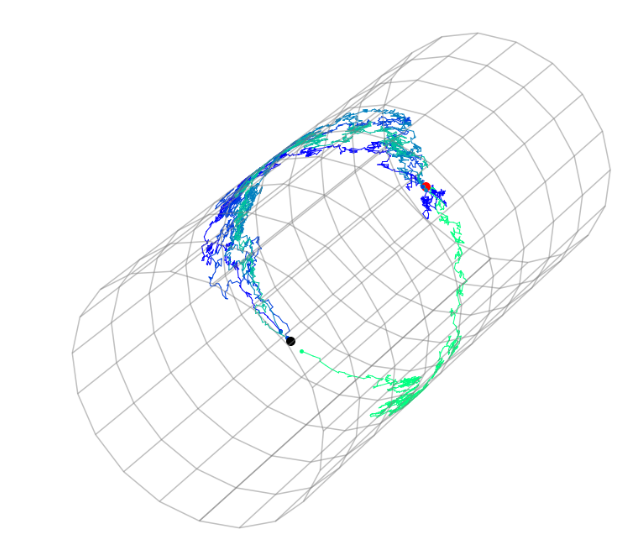
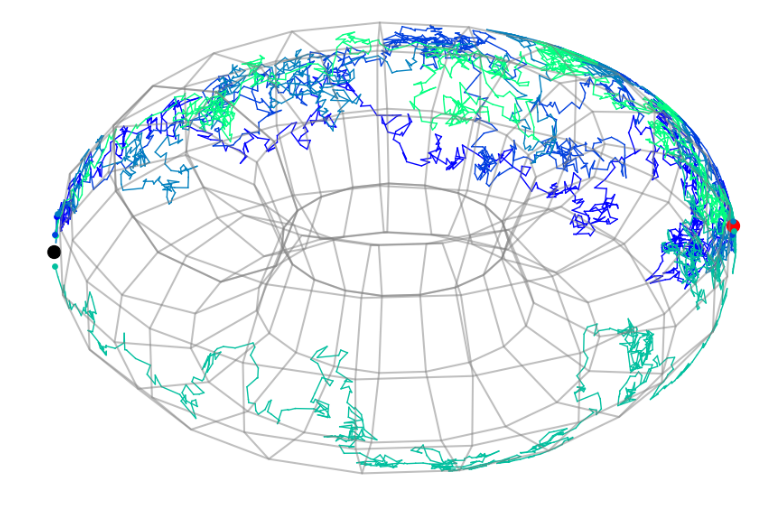
Jensen, Mallasto, Sommer, GSI 2019 ; Jensen, Sommer, GSI 2021; Jensen, Sommer, arxiv 2021

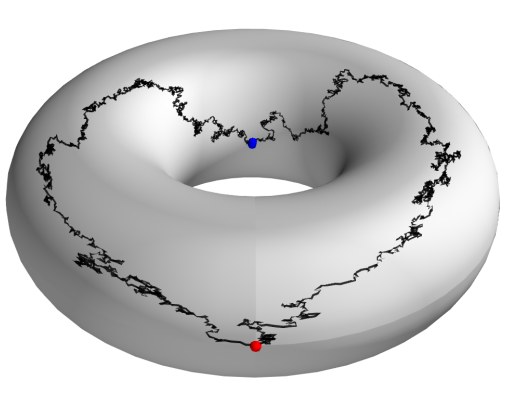
Stochastic forcing

perturbation of Hamiltonian system

Lagrangian coordinates

$dq_i^\alpha=\frac{\partial H}{\partial p_i^\alpha}dt$

$dp_i^\alpha=-\frac{\partial H}{\partial q_i^\alpha}dt+\gamma_idW^i_t$

$dp_i^\alpha=-\lambda\frac{\partial H}{\partial p_i^\alpha}dt-\frac{\partial H}{\partial q_i^\alpha}dt+\gamma_idW^i_t$

Marsland/Shardlow,SIIMS'17

Trouve,Vialard,QAM'12;Vialard,SPA'13

Schauer/v.d. Meulen bridges

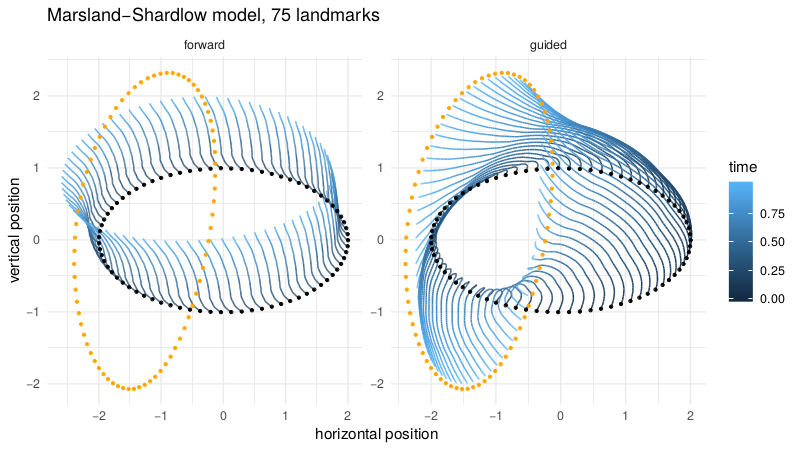
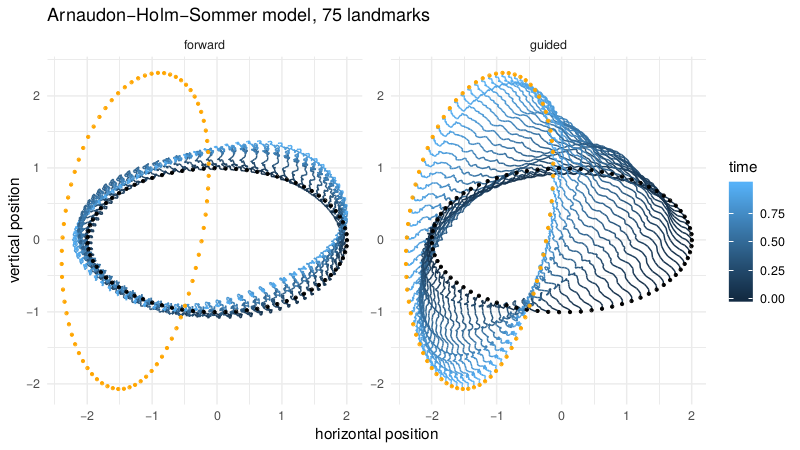
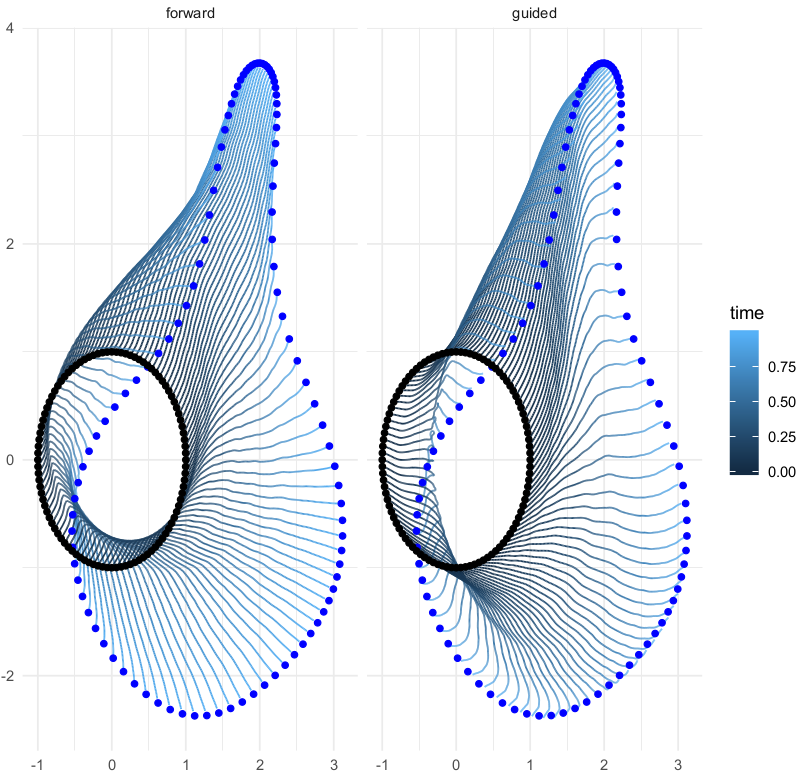
v.d. Meulen,Schauer,Arnaudon,Sommer,arxiv'21

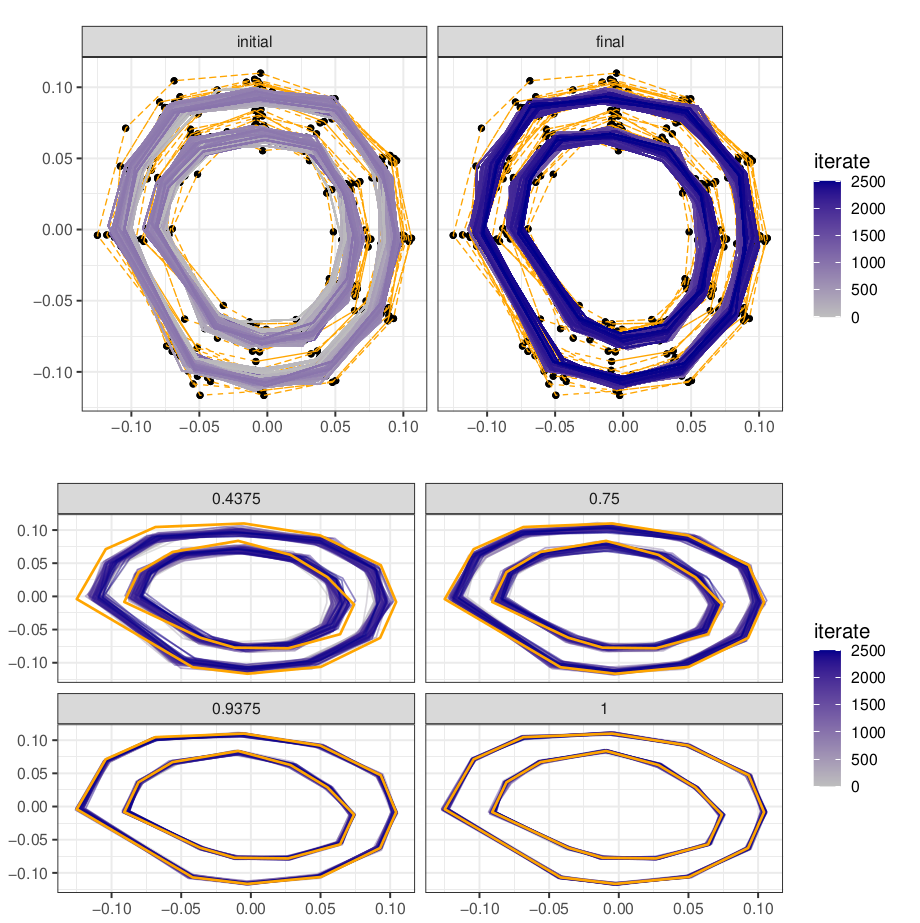
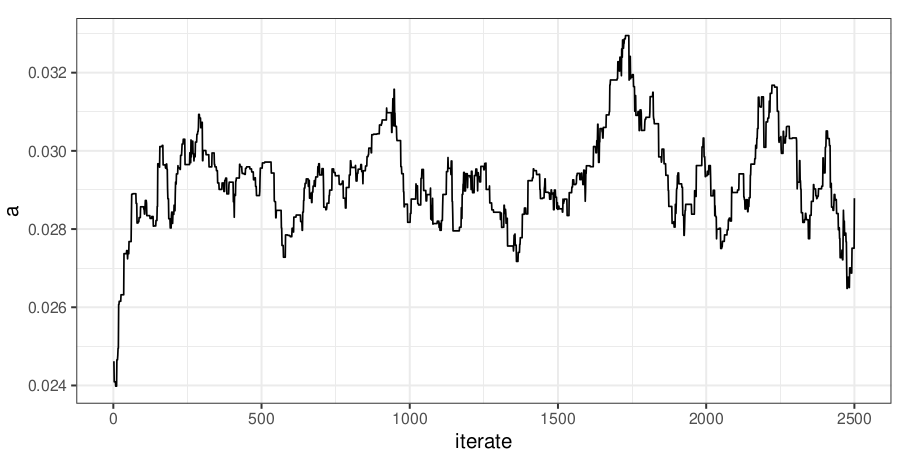
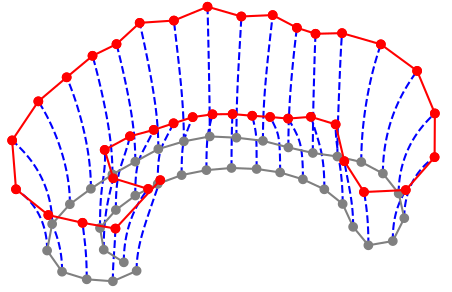
Hamiltonian kernel parameter

corpus callosum bridge

ventricles

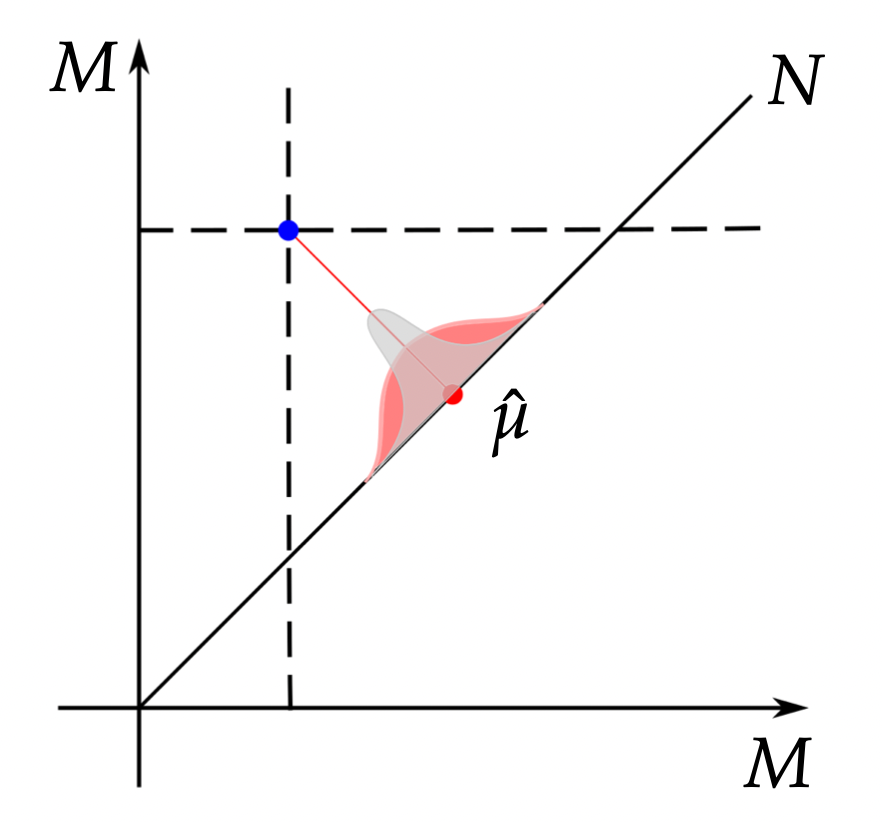
parametric families of probability distributions $\mu_\theta$
likelihood from density:
$\quad\mathcal{L}(\theta; y_1,\ldots,y_N)=\prod_{i=1}^Np_\theta(y_i)$
ML/MAP estimates:
$\quad\bar{\theta}=\mathrm{argmax}_\theta\mathcal{L}(\theta; y_1,\ldots,y_N)$

Diffusion mean:
$\quad x_t\in M$ Brownian motion
$\quad\theta=x_0$
assume $y\sim x_T$:
$\quad\bar{x}_{\mathrm{ML}}=\mathrm{argmax}_\theta\mathcal{L}(\theta)$

Generalization of Euclidean statistical notions and techniques.

i.i.d. samples $y_1,\ldots,y_N\in M$
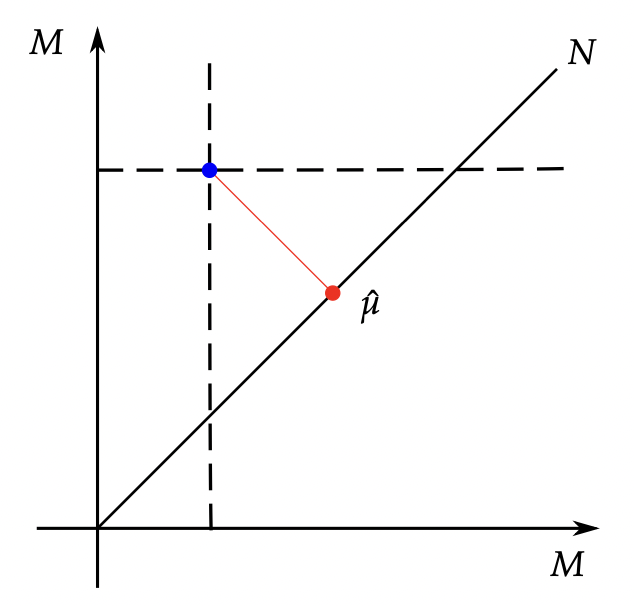
Fréchet mean:
$\bar{x}=\mathrm{argmin}_{x\in M}\sum_{i=1}^Nd(x,y_i)^2$

Nye, White, JMIV'14;
Sommer,IPMI'15; Sommer,Svane,JGM'15;
Hansen,Eltzner,Huckemann,Sommer,GSI'21,'21

Geometric statistics

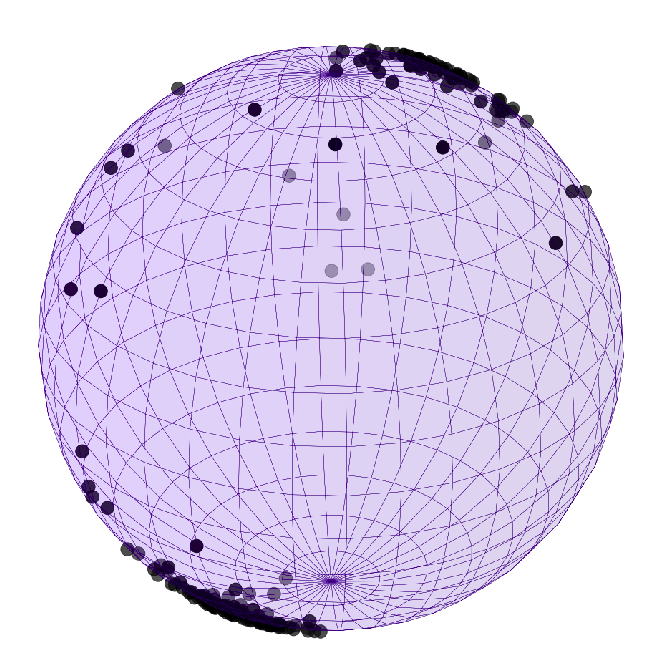
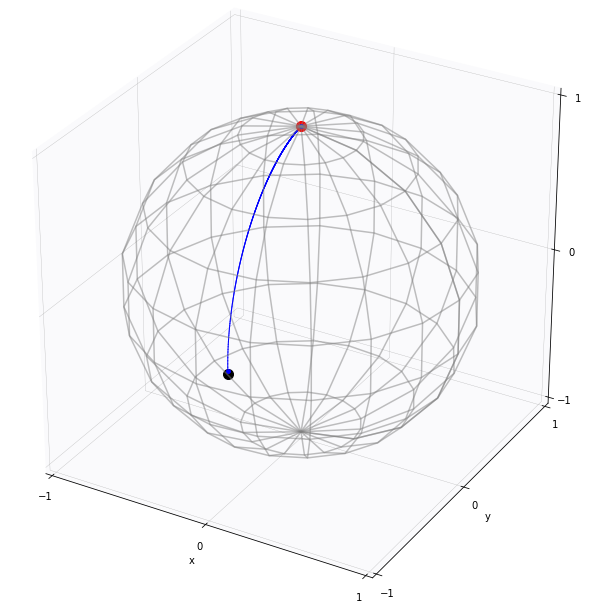
Diffusion mean on $\mathbb S^2$

$x_t\in M$ Brownian motion
$\theta=x_0$, $y\sim x_T$
$\bar{x}_{\mathrm{ML}}=\mathrm{argmax}_\theta\mathcal{L}(\theta)$

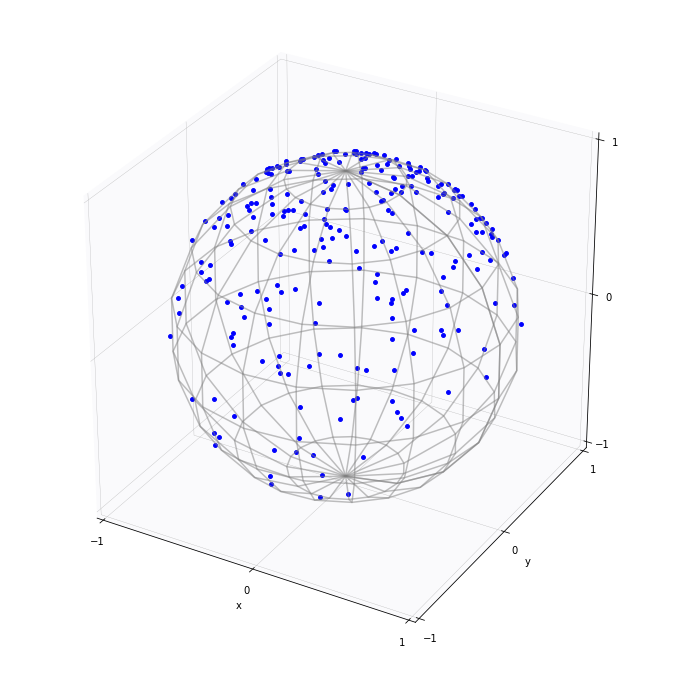
dx_t= -\frac12g(x_t)^{kl}\Gamma(x_t)_{kl}dt + \sqrt{g(x_t)^*}dW_t

Brownian motion starting point

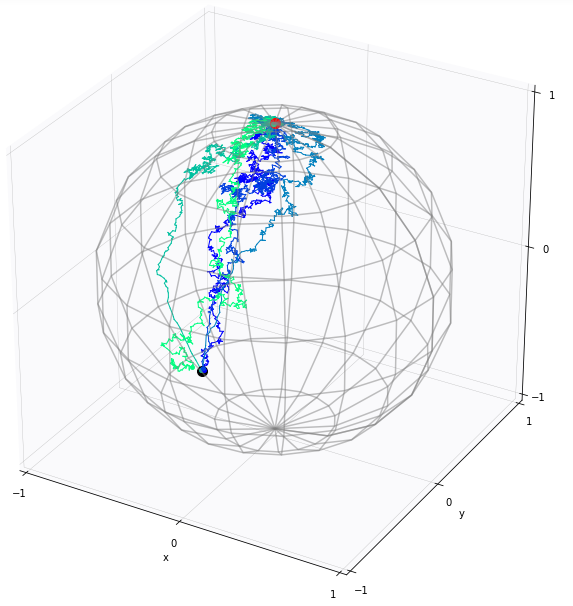
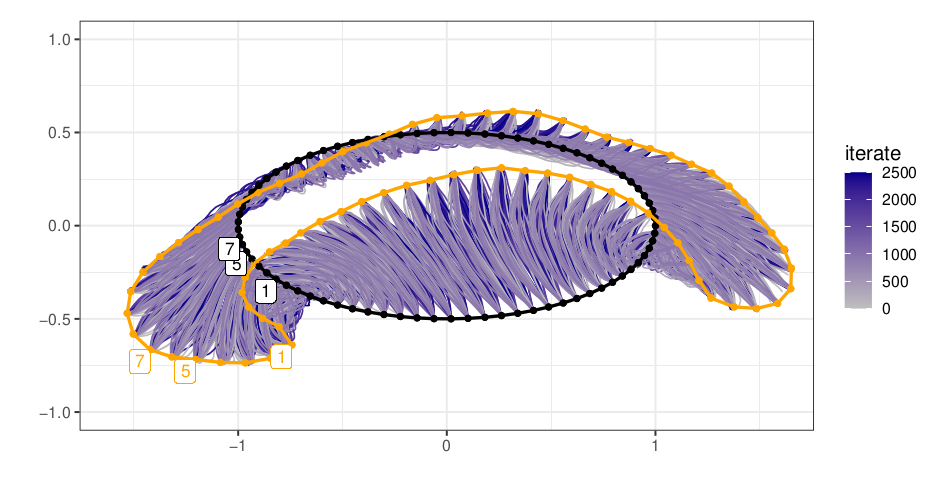
Sampling means

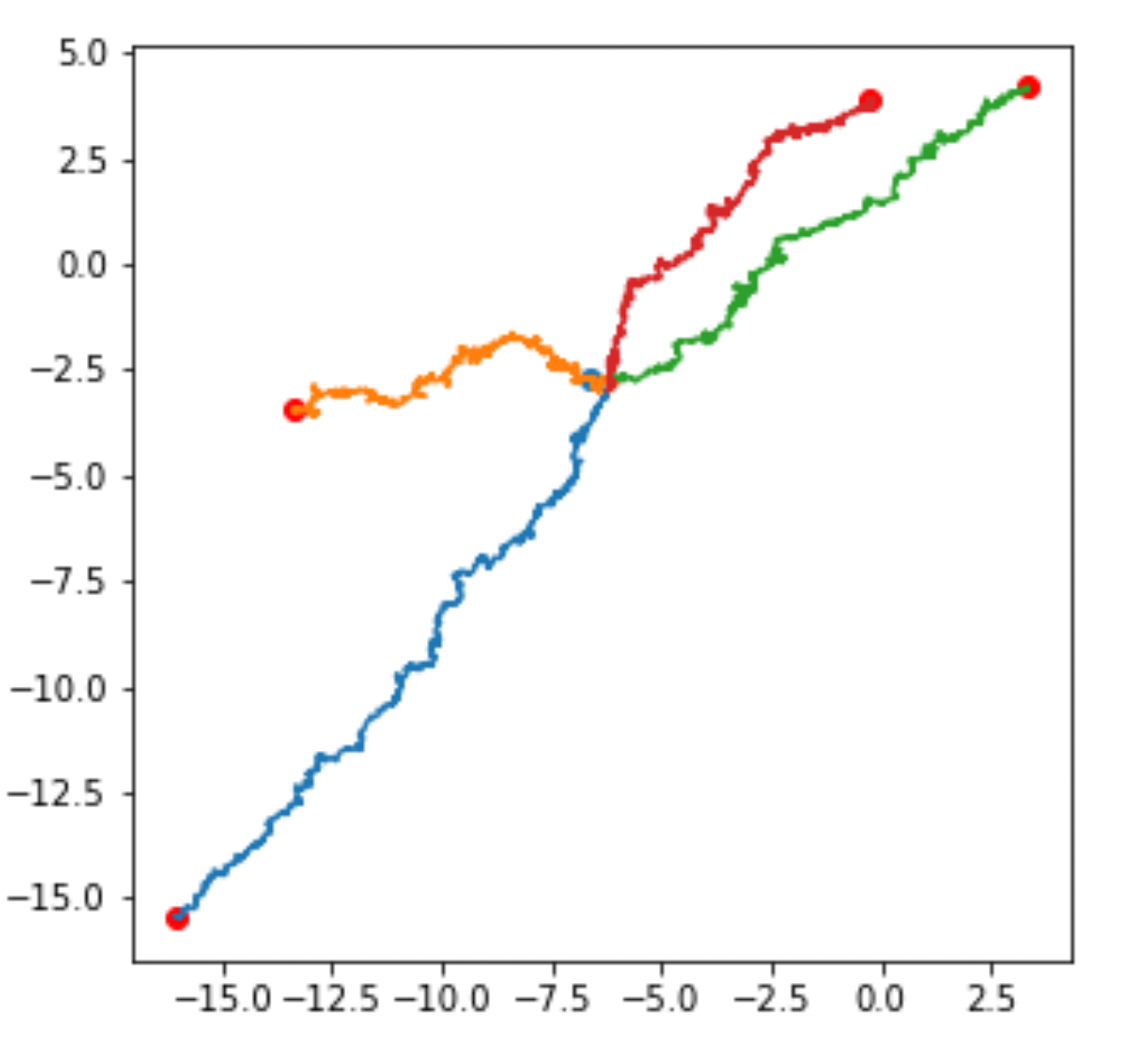
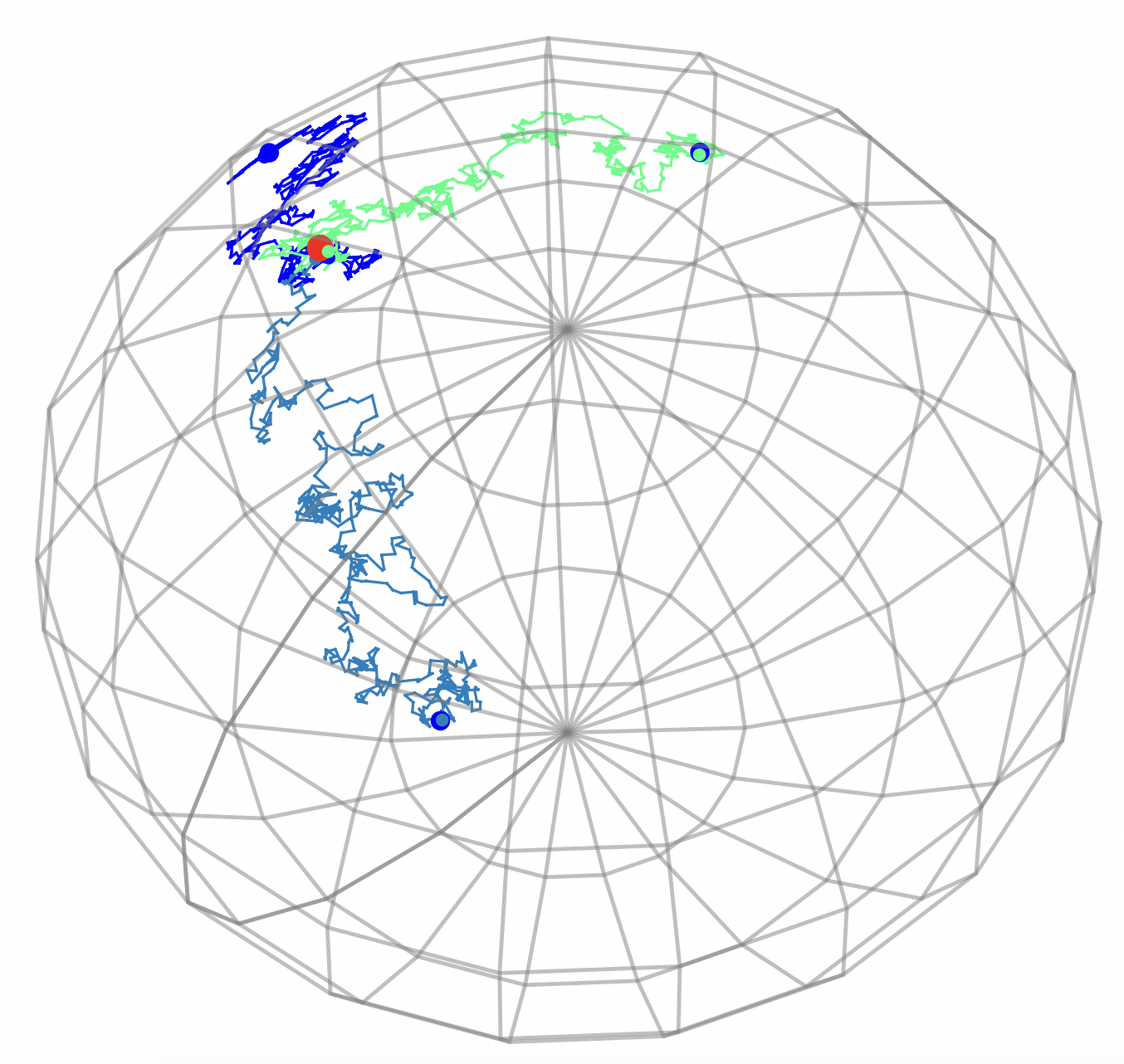
Diagonally conditioned distribution

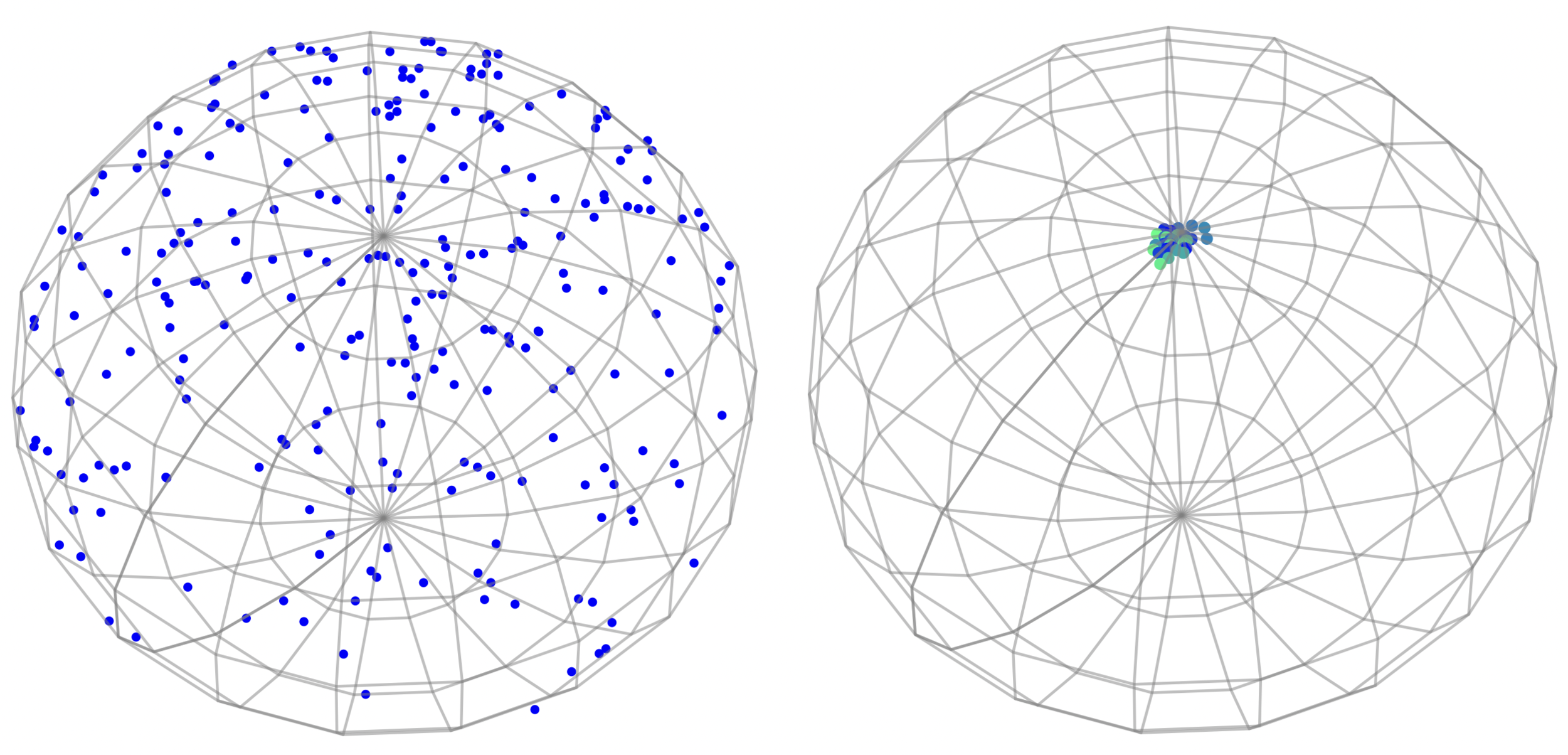
Sommer, Bronstein, TPAMI 2021; Jensen, Sommer, Algorithms 2022

Fast mean estimation

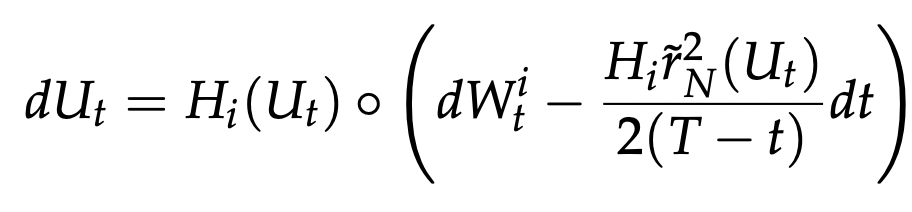
Fermi bridge:

Coordinate bridge:

One (or few) forward samples - compared to nested optimization

Added variance on top of CLT - gain in computational speed

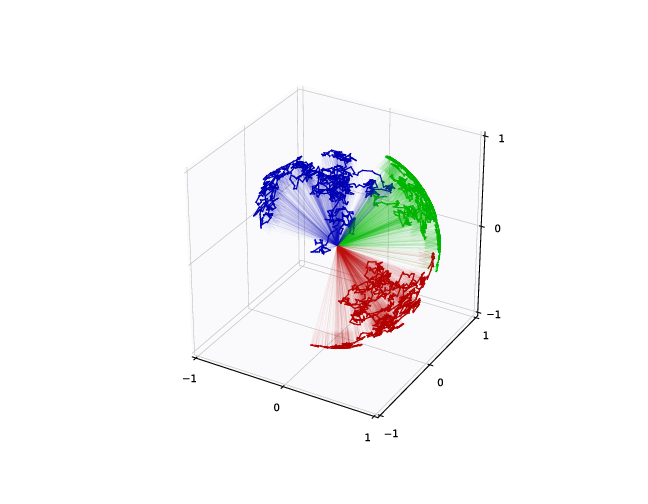
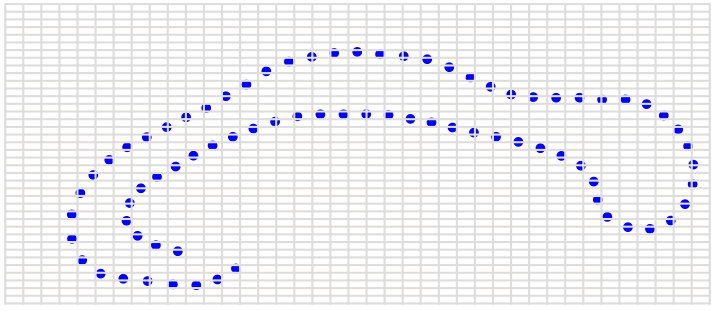
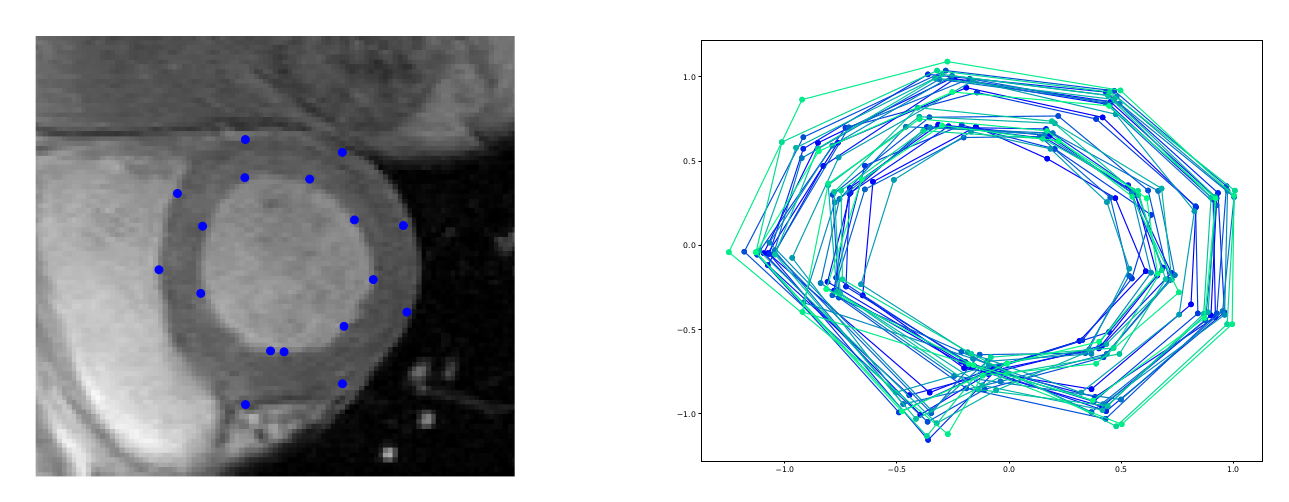
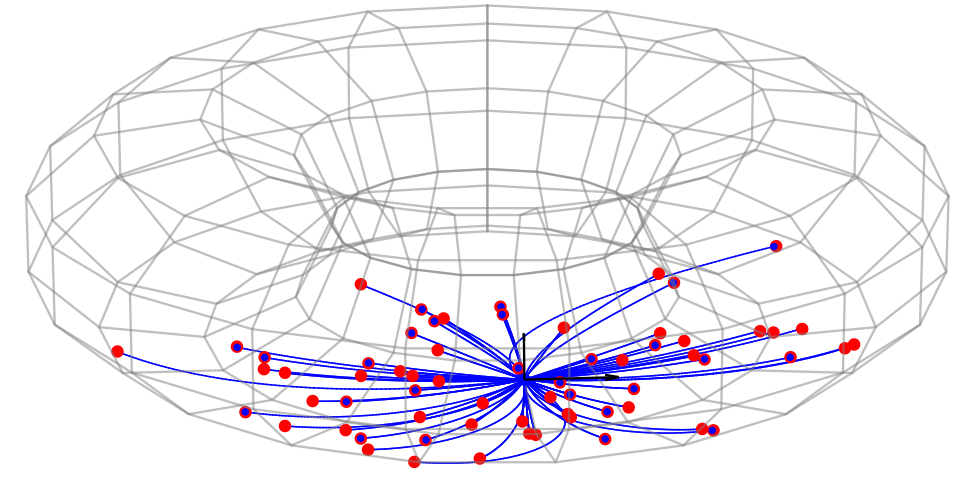
Sampled landmark means

Diagonally conditioned process:

Frechet mean (green), diffusion mean (blue)

Shape stochastics, bridges, mean sampling

code: http://bitbucket.com/stefansommer/jaxgeometry

slides: https://slides.com/stefansommer

References:

Jensen, Sommer: Mean Estimation on the Diagonal of Product Manifolds, Algorithms, 2022, https://www.mdpi.com/1999-4893/15/3/92
Arnaudon, v.d. Meulen, Schauer, Sommer: Diffusion bridges for stochastic Hamiltonian systems and shape evolutions, SIIM, 2022, arXiv:2002.00885
Hansen, Eltzner, Huckemann, Sommer: Diffusion Means in Geometric Spaces, 2021, arXiv:2105.12061.
Hansen, Eltzner, Sommer: Diffusion Means and Heat Kernel on Manifolds, 2021, arXiv:2103.00588.
Højgaard Jensen, Sommer: Simulation of Conditioned Diffusions on Riemannian Manifolds, 2021, arXiv:2105.13190.
Højgaard, Joshi, Sommer: Brownian Bridge Simulation and Metric Estimation on Lie Groups and Homogeneous Spaces,
Sommer, Bronstein: Horizontal Flows and Manifold Stochastics in Geometric Deep Learning, TPAMI, 2020, doi: 10.1109/TPAMI.2020.2994507
Arnaudon, Holm, Sommer: A Geometric Framework for Stochastic Shape Analysis, Foundations of Computational Mathematics, 2019, arXiv:1703.09971.
Højgaard Jensen, Mallasto, Sommer: Simulation of Conditioned Diffusions on the Flat Torus, GSI 2019., arXiv:1906.09813.
Sommer, Svane: Modelling Anisotropic Covariance using Stochastic Development and Sub-Riemannian Frame Bundle Geometry, JoGM, 2017, arXiv:1512.08544.
Sommer: Anisotropically Weighted and Nonholonomically Constrained Evolutions, Entropy, 2017, arXiv:1609.00395 .
Sommer, Svane: Modelling Anisotropic Covariance using Stochastic Development and Sub-Riemannian Frame Bundle Geometry, JoGM, 2017, arXiv:1512.08544.
Sommer: Anisotropically Weighted and Nonholonomically Constrained Evolutions, Entropy, 2017, arXiv:1609.00395 .
Arnaudon, Holm, Sommer: A Stochastic Large Deformation Model for Computational Anatomy, IPMI 2017, arXiv:1612.05323.
Sommer: Anisotropic Distributions on Manifolds: Template Estimation and Most Probable Paths, IPMI 2015, doi: 10.1007/978-3-319-19992-4_15.

Open phd/pd positions on shape stochastics and morphometry