Lecture 3:
Tabular Reinforcement Learning
Artyom Sorokin | 19 Feb
Previous Lecture: Value Functions
Reward-to-go / Return:
State Value Function / V-Function:
State-Action Value Function / Q-Function:
Previous Lecture: Bellman Equations
Bellman Expectation Equations for policy \(\pi\):
Bellman Optimality Equations:
Previous Lecture: Bellman Equations
Bellman Expectation Equations for policy \(\pi\):
Bellman Optimality Equations:
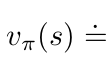
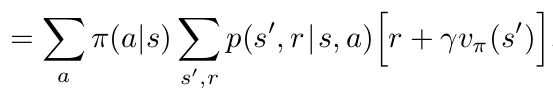
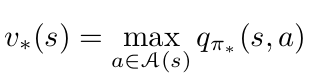
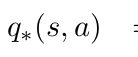
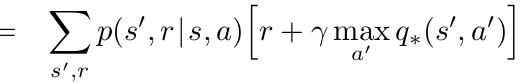
Previous Lecture: Policy Iteration

Use Belman Expectation Equations to learn \(V\)/\(Q\) for current policy
Greedily Update policy w.r.t. V/Q-function
Previous Lecture: Policy Iteration
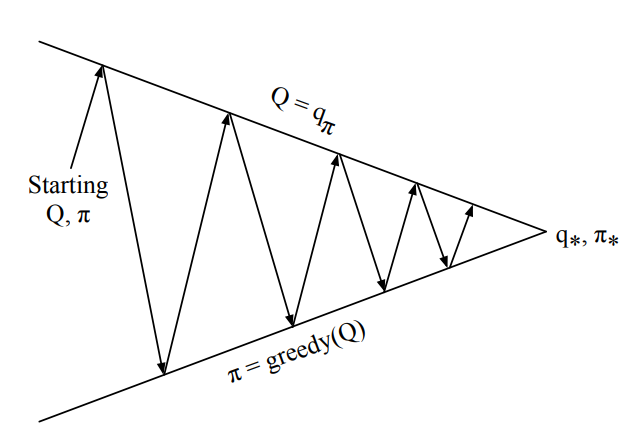
Policy Evaluation steps
Policy Improvement steps
Generalized Policy Iteration

Imporves value function estimate for current policy \(\pi\)
Imporves policy \(\pi\)
w.r.t current value function
Previous Lecture: Value Iteration

Use Belman Optimality Equations to learn \(V\)/\(Q\) for current policy
Policy Improvement is implicitly used here
But we don't know the model
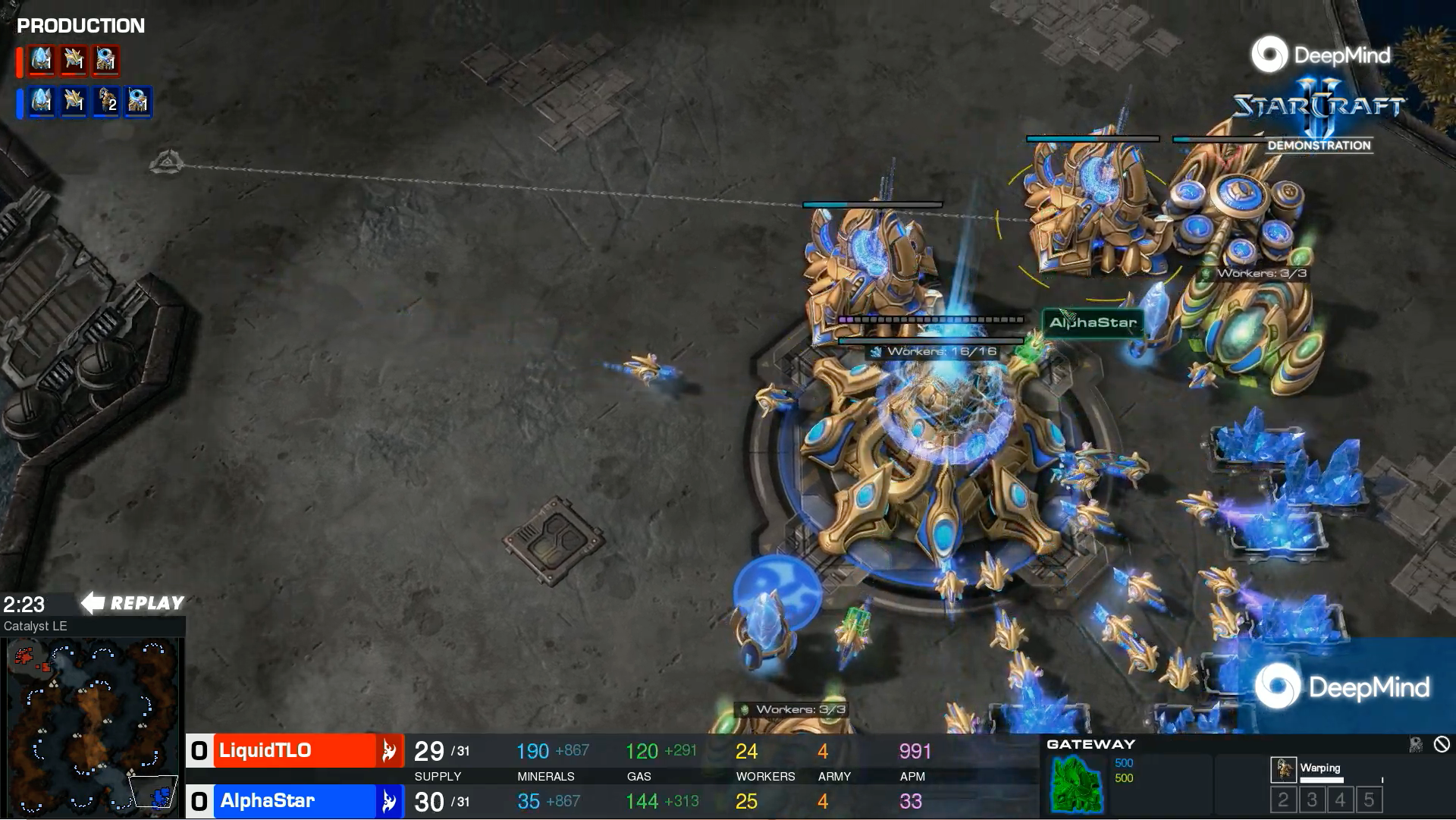

Solution: Use Sampling
- The model of the environment is unknown! :(
- But you still can interact with it!

Monte-Carlo Methods
GOAL: Learn value functions \(Q_{\pi}\) or \(V_{\pi}\) without knowing \(p(s'|s,a)\) and \(R(s,a)\)
RECALL that value function is the expected return:
First Visit Monte-Carlo
By Law of Large Numbers, \(q(s,a) \rightarrow Q_{\pi}(s,a)\) as \(N(s,a) \rightarrow \infty\)
IDEA: Estimate expectation \(Q_{\pi}(s,a)\) with empirical mean \(q(s,a)\):
- Generate an episode with \(\pi\)
- The first time-step \(t\) that state-action \((s,a)\) is visited
- Increment counter \(N(s,a) = N(s,a) + 1\)
- Increment total return \(S(s,a) = S(s,a) + G_t\)
- Value is estimated by mean return \(q(s,a) = S(s,a)/N(s,a)\)
Monte-Carlo Methods: Prediction
We can update mean values incrementally:
Incremental Monte Carlo Update:
Prediction error
Old estimate
Learning rate
In non-stationary problems we can fix learning rate:
Monte-Carlo Methods
- MC methods learn directly from episodes of experience
- MC is model-free: no knowledge of MDP transitions / rewards
- MC learns from complete episodes: no bootstrapping
- MC uses the simplest possible idea: value = mean return
- Caveat: can only apply MC to episodic MDPs:
- All episodes must terminate
Monte-Carlo Methods: Control
Remember Policy Iteration?
How would look PI version with Monte-Carlo Policy Evaluation?
Questions:
- Why we estimate \(Q_{\pi}\) and not \(V_{\pi}\)?
- Do you see any problem with policy improvement step?

- Policy Evaluation: Monte-Carlo Evaluation, \(q = Q_{\pi}\)
- Policy Improvement: Greedy policy improvement, i.e. \(\pi'(s) = argmax_a q(s,a)\)
Eploration-Exploitation Problem
Agent can't visit every \((s,a)\) with greedy policy!
Agent can't get correct \(q(s,a)\) estimates without visiting \((s,a)\) frequently!
(i.e. remember law of large numbers)
Monte-Carlo Methods: Control

Use \(\epsilon\)-greedy policy:
- Simplest idea for ensuring continual exploration
- All \(m\) actions are tried with non-zero probability
- With probability \(1 − \epsilon\) choose the greedy action
- With probability \(\epsilon\) choose an action at random
Monte-Carlo Methods: Control

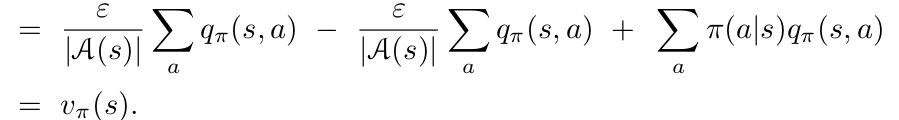
Monte-Carlo Method
Policy Iteration with Monte-Carlo method:
For every episode:
- Policy Evaluation: Monte-Carlo Evaluation, \(q = Q_{\pi}\)
- Policy Improvement: \(\epsilon\)-greedy policy improvement
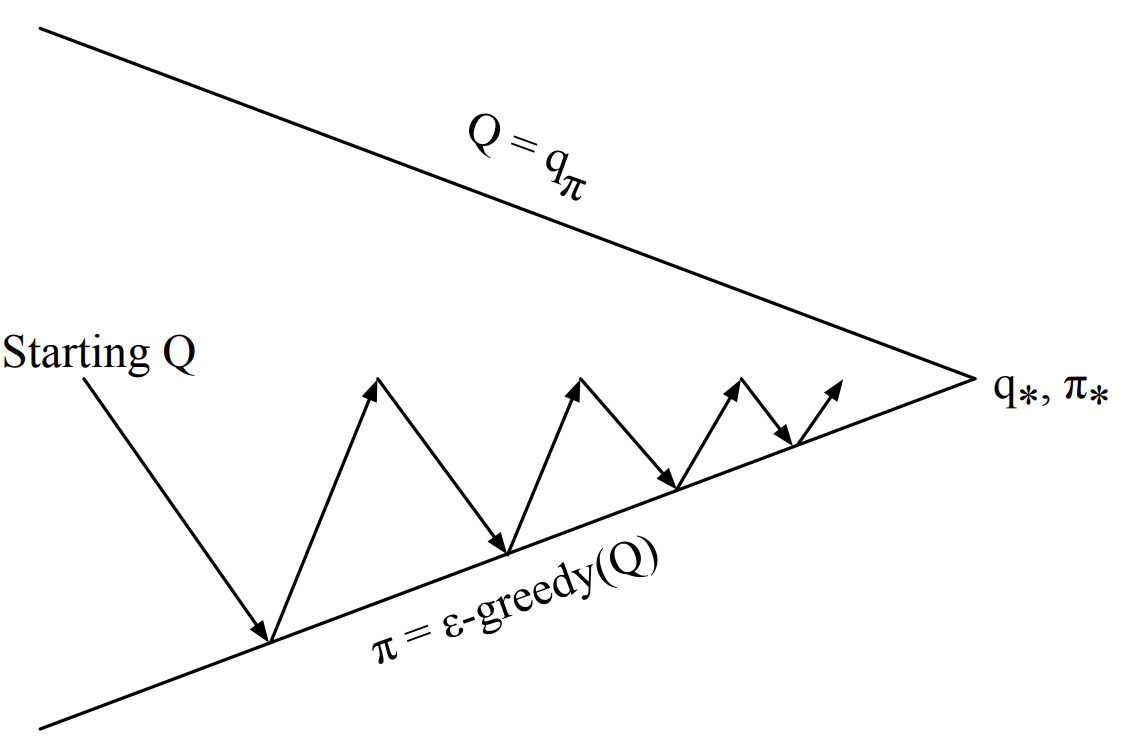
Monte-Carlo Methods: GLIE

Monte-Carlo Methods: GLIE

GLIE Mont-Carlo Control:
- Sample k-th episode using curent policy \(\pi\)
- Update with \(q(s,a)\) with \(1/N(s,a)\) learning rate
- Set \(\epsilon = 1/k\)
- Use \(\epsilon\)-greedy policy improvement
Temporal Difference Learning
Problems with Monte-Carlo method:
- Updates policy only once per episode, i.e. only episodic MDPs
- Doesn't use MDP properties
Solution:
- Recall Bellman equation:
- Use sampling instead of knowledge about the model:
TD-learning: Prediction
Goal: learn \(Q_{\pi}\) online from experience
Incremental Monte-Carlo:
- Update value \(q(s_t, a_t)\) toward actual return \(G_t\)
Temporal-Difference learning:
- Update value \(q(s_t, a_t)\) toward estimated return \(r_{t+1} + \gamma q(s_{t+1}, a_{t+1})\)
\(r_{t+1} + \gamma q(s_{t+1}, a_{t+1})\) is called the TD target
\(\delta_t = r_{t+1} + \gamma q(s_{t+1}, a_{t+1}) - q(s_t, a_t)\) is called the TD error
Temporal Difference Learning
Temporal Difference Learning:
- TD methods learn directly from episodes of experience
- TD is model-free: no knowledge of MDP transitions / rewards
- TD learns from incomplete episodes, by bootstrapping
- TD updates a guess towards a guess
TD-learning: SARSA update
This update is called SARSA: State, Action, Reward, next State, next Action

TD-learning: SARSA as Policy Iteration
Policy Iteration with Temporal Difference Learning:
For every step:
- Policy Evaluation: SARSA Evaluation, \(q = Q_{\pi}\)
- Policy Improvement: \(\epsilon\)-greedy policy improvement

TD-learning: SARSA algorithm

TD-learning: SARSA

TD-learning: Q-Learning
We approximate Bellman Expectation Equation with SARSA update:
Can we utilize Bellman Optimality Equation for TD-Learning?
Yes, of course:
TD-learning: Q-Learning vs SARSA
From Bellman Expectation Equation (SARSA) :
From Bellman Optimality Equation (Q-Learning):
\(a'\) comes from the policy \(\pi\) that generated this experience!
No connection to the actual policy \(\pi\)
TD-learning: Q-Learning vs SARSA
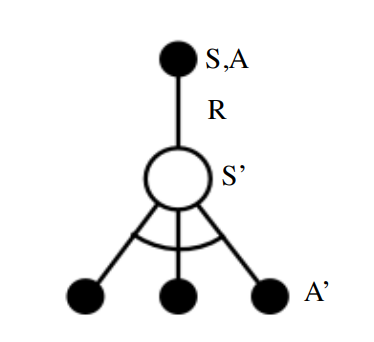
Q-Learning Update:
SARSA Update:
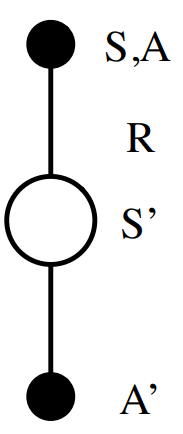
TD-learning: Q-Learning


On-policy vs Off-Policy Algorithms
SARSA and Monte-Carlo are on-policy algorithms:
- Improve policy \(\pi_k\) only from experience sampled with this policy \(\pi_k\)
- Can't use old trajectories sampled with \(\pi_{k-i}\)
Q-Learning is off-policy algorithm:
- Can Learn policy \(\pi\) using experience generated with other policy \(\mu\)
- Learn from observing humans or other agents
- Re-use experience generated from old policies
- Learn about optimal policy while following exploratory policy
- Learn about multiple policies while following one policy
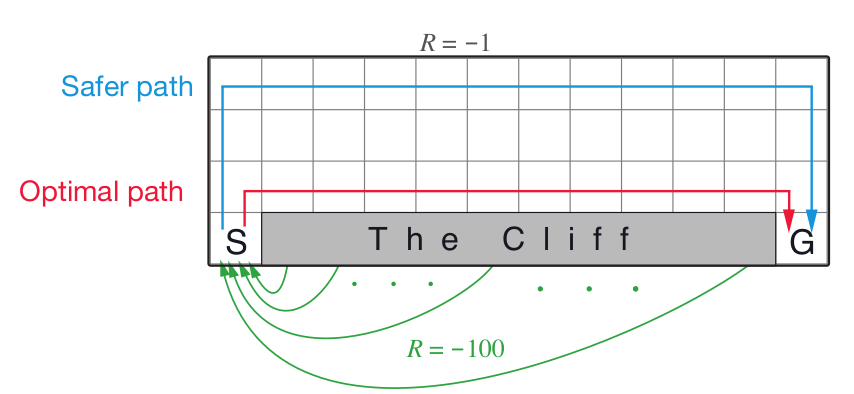
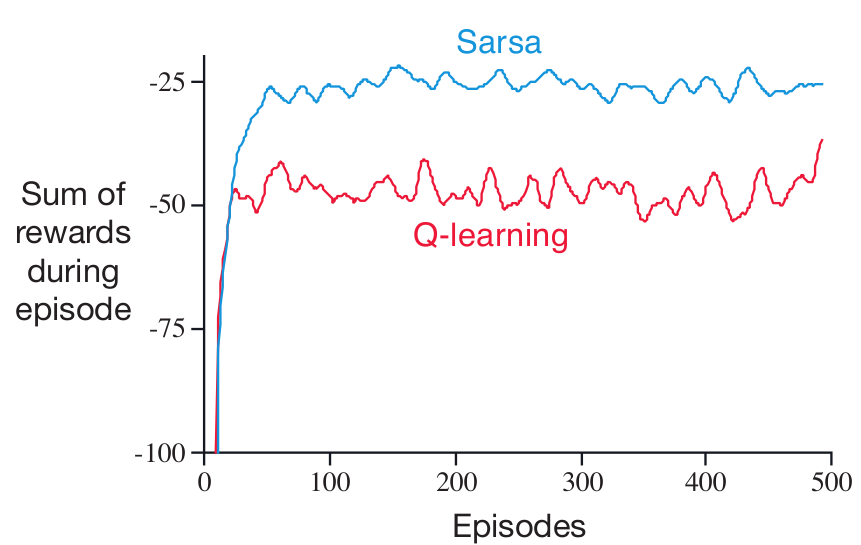
TD-learning: Cliff Example
TD vs MC: Driving Home Example
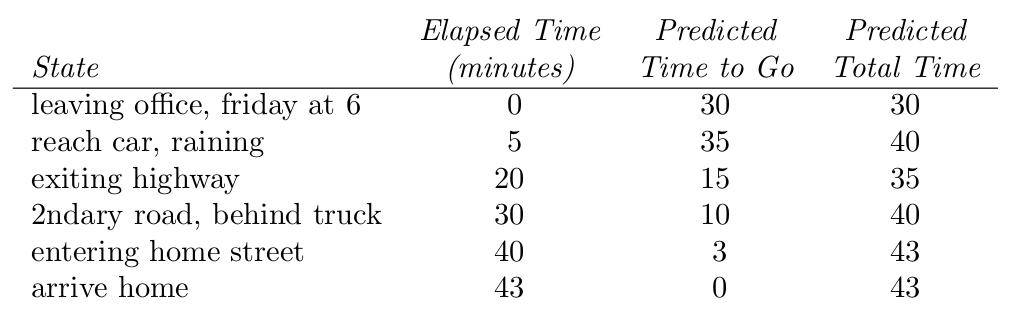
TD vs MC: Driving Home Example
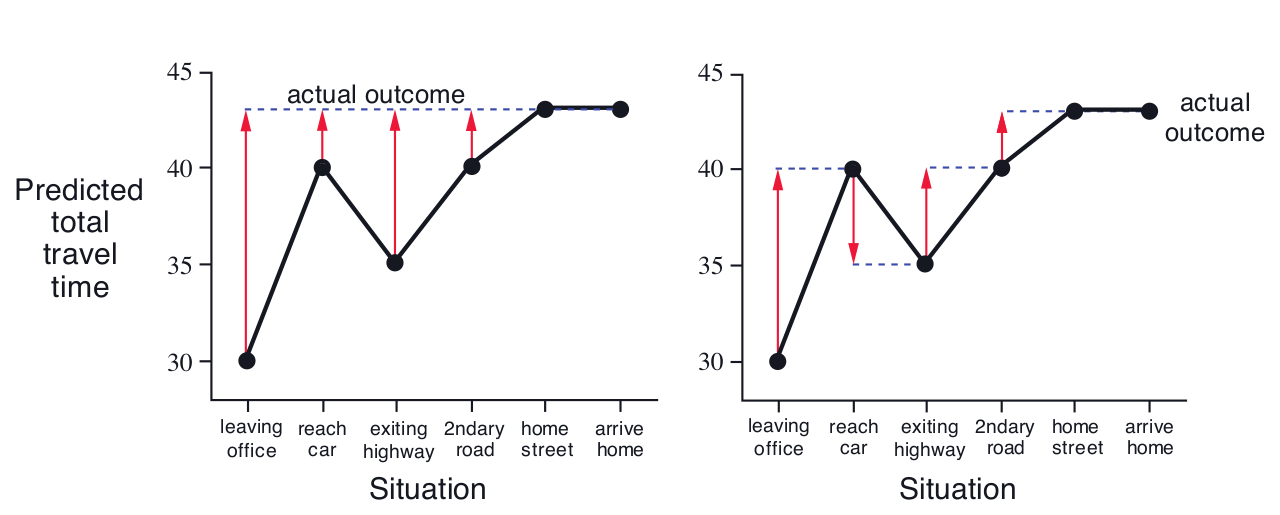
Monte Carlo
Temporal Difference
TD vs MC: Bias-Variance Tradeoff
- Return \(G_t = R_{t+1} + \gamma R_{t+2} + ... + \gamma^{T-t-1}R_{T}\) is unbiased estimate of \(Q_{\pi}(s_t, a_t)\)
- True TD target \( R_{t+1} + \gamma Q_{\pi}(s_{t+1},a_{t+1}) \) is unbiased estimate of \(Q_{\pi}(s_t, a_t)\)
- TD target \( R_{t+1} + \gamma q(s_{t+1},a_{t+1}) \) is biased estimate of \(Q_{\pi}(s_t, a_t)\)
- TD target has lower variance than the return:
- Return depends on many random actions, transitions, rewards
- TD target depends on one random action, transition, reward
- Monte-Carlo Methods: high variance, no bias
- TD-Обучение: low variance, has bias
TD vs MC: Bias-Variance Tradeoff
- MC has high variance, zero bias
- Good convergence properties
- (even with function approximation)
- Not very sensitive to initial value
- Very simple to understand and use
- TD has low variance, some bias
- Usually more efficient than MC
- TD converges to \(Q_{\pi}(s,a)\)
- (but not always with function approximation)
- More sensitive to initial value
TD vs MC: AB Example

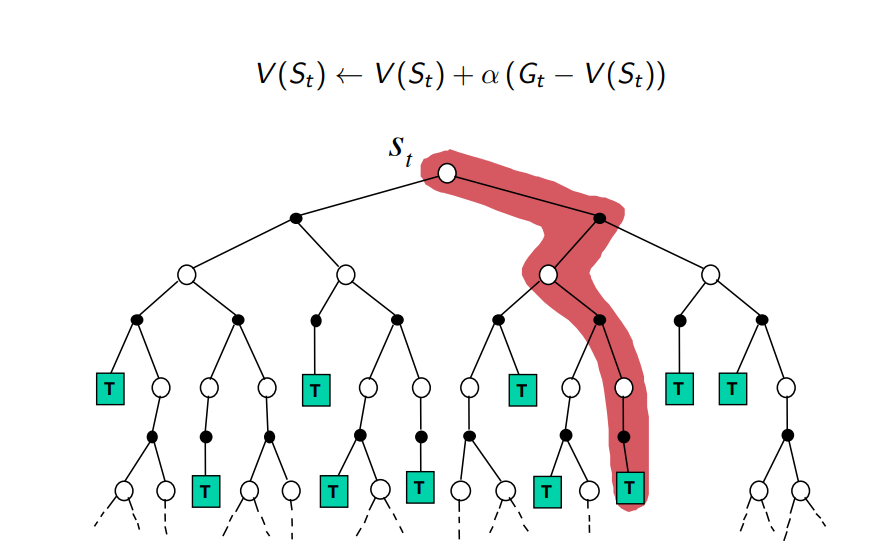
Monte-Carlo Backup
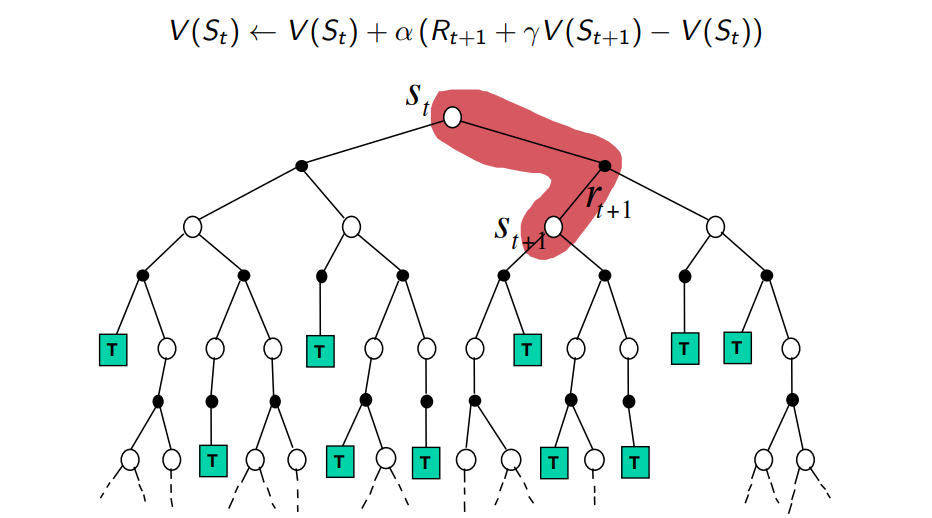
Temporal-Difference Backup
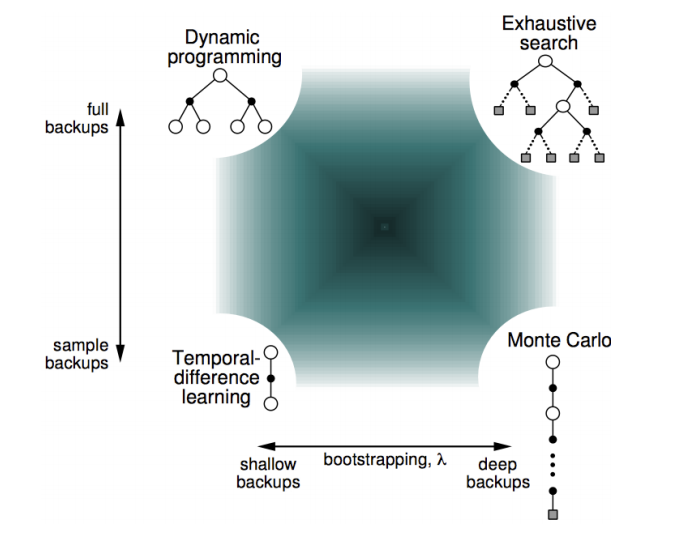
Sampling and Bootstrapping
-
Bootstrapping: update involves an estimate
- MC does not bootstrap
- DP bootstraps
- TD bootstraps
-
Sampling: update samples an expectation
- MC samples
- DP does not sample
- TD samples
Sampling and Bootstrapping
N-step Returns
Consider the following n-step returns for n = 1, 2, ...:
n-step Temporal Difference Learning:
.
.
.
.
.
.
(MC)
(TD: SARSA)
Combining N-step Returns

We can average n-step returns over different n,
e.g. average the 2-step and 4-step returns:
- Can we combine information from all n-step returns?
- Yes! Turns out that it is easier to use this combination than selecting right value of \(n\) for n-step return.
TD(\(\lambda\))
- The \(\lambda\)-return \(G^{\lambda}_t\) combines all n-step returns \(G^{(n)}_t\)
- Using weight \((1 −\lambda) \lambda^{n-1}\)
- Forward-view TD(\(\lambda\))... actually SARSA(\(\lambda\)):
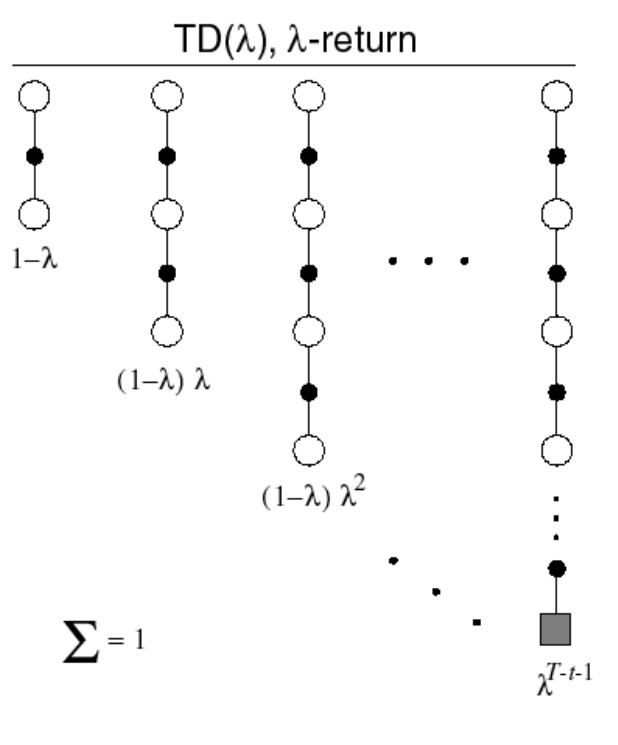
TD(0) and TD(1):
But why?
What happens when \(\lambda = 0\)?
i.e. TD target
What happens when \(\lambda = 1\)?
We can rewrite \(G^{\lambda}_t\) as:
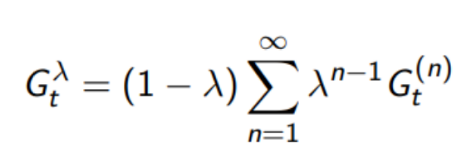
i.e. MC target
TD(0) and TD(1):
What happens when \(\lambda = 0\)?
i.e. just TD-learning
What happens when \(\lambda = 1\)?
i.e. Monte-Carlo learning
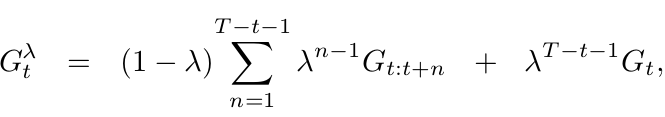
We can rewrite \(G^{\lambda}_t\) as:
HOW?
TD(\(\lambda\)): Forward view
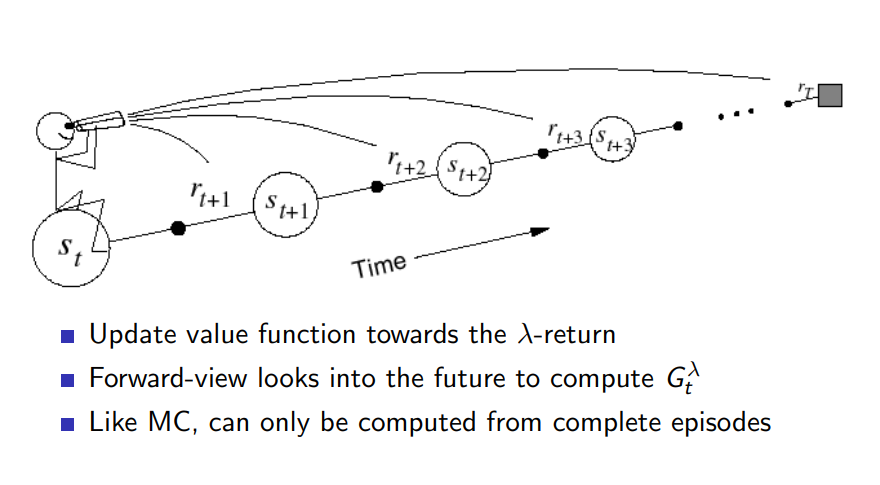
- Update value function towards the \(\lambda\)-return
- Forward-view looks into the future to compute \(G^{\lambda}_{t}\)
- Like MC, can only be computed from complete episodes
Text
TD(\(\lambda\)): Backward View
- Credit assignment problem: did bell or light cause shock?
- Frequency heuristic: assign credit to most frequent states
- Recency heuristic: assign credit to most recent states
- Eligibility traces combine both heuristics

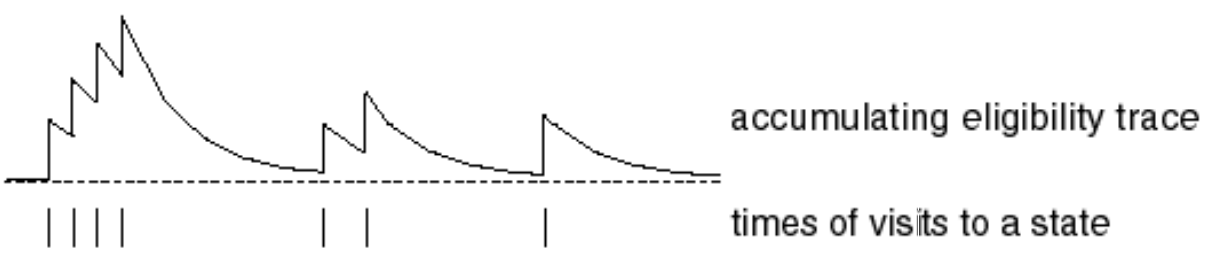
Eligibility Traces: SARSA(\(\lambda\))
- Keep an eligibility trace for every state \(s\)
- Update value \(q(s, a)\) for every (\(s, a\)) with non zero \(E_t(s,a)\)
- In proportion to TD-error \(\delta_t\) and eligibility trace \(E_t(s,a)\)
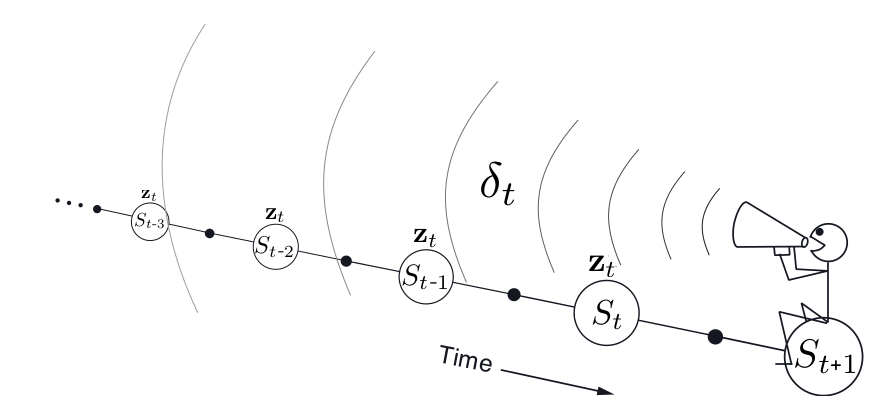

SARSA(\(\lambda\)) vs SARSA
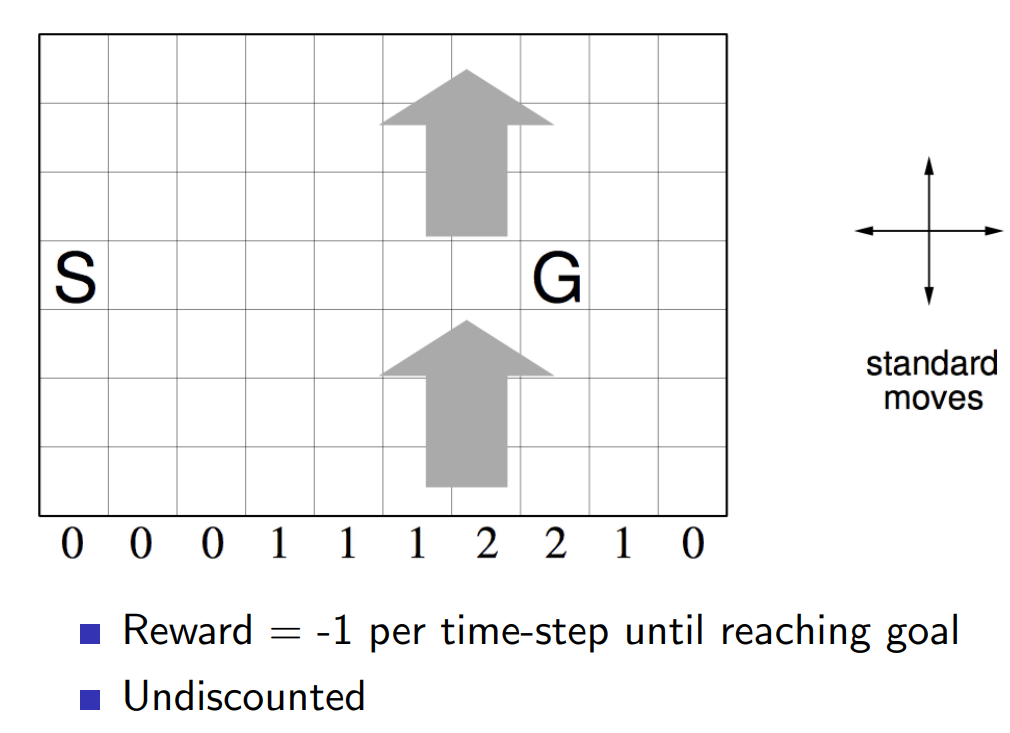
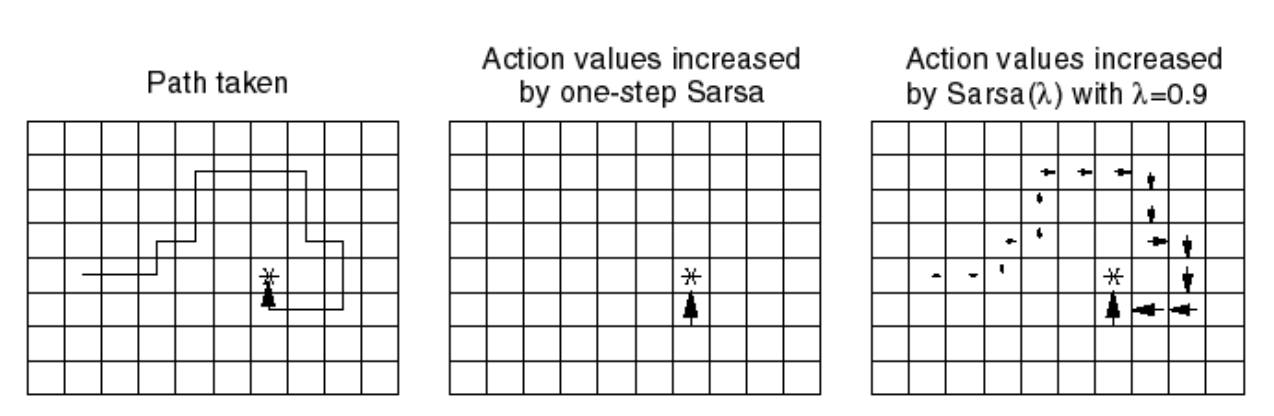
SARSA(\(\lambda\)) vs SARSA
Tabular RL: Resume
- Monte-Carlo and Temporal-Difference learning use sampling to approximate Dynamic Programming Methods
- TD learning assumes MDP and use bootstraping updates