Lecture 12:
Exploration
Artyom Sorokin |4 May
What is the problem?
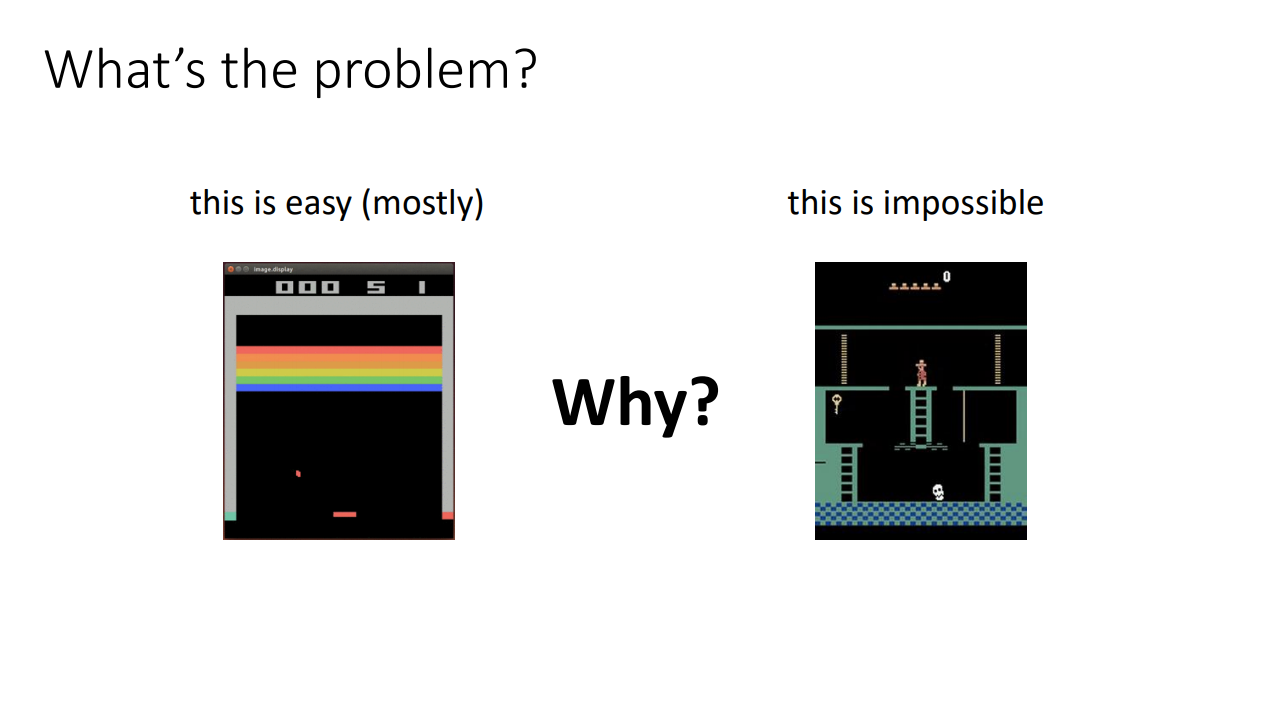
Monstezuma's Revenge
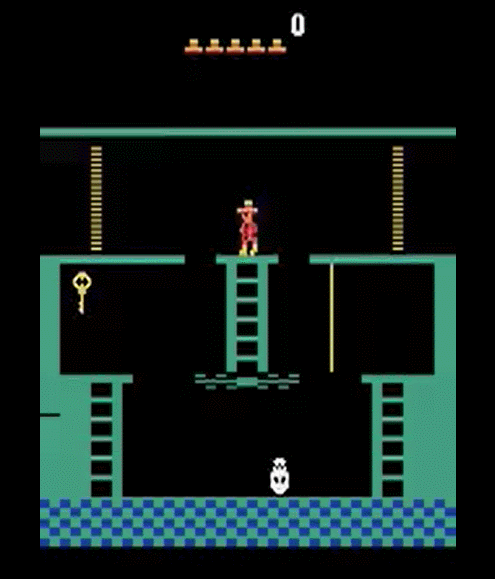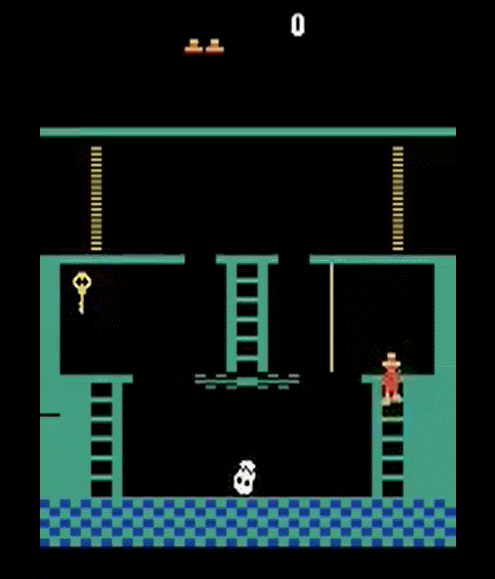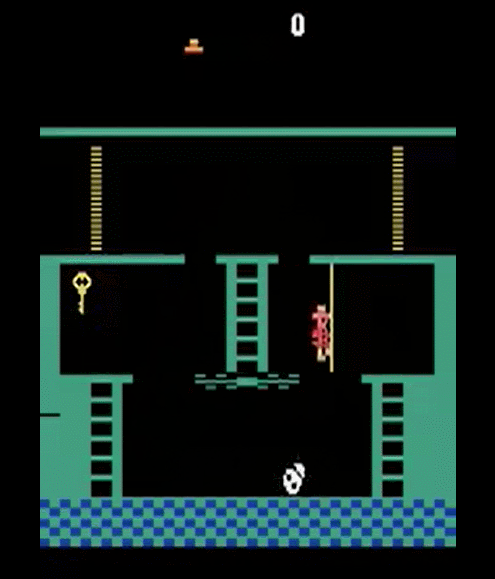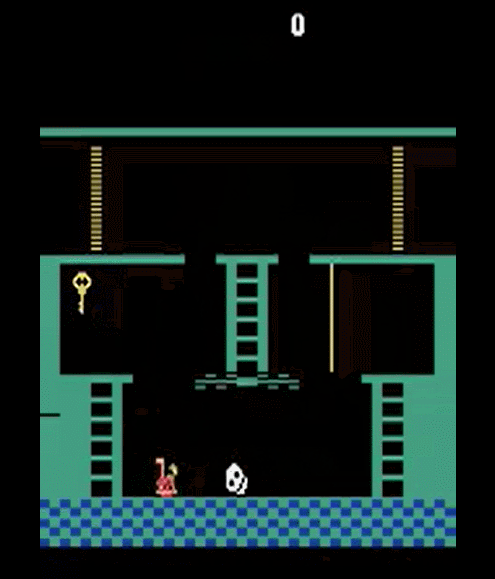
- Getting key = reward
- Opening door = reward
- Getting killed by skull = nothing (is it good? bad?)
- Finishing the game only weakly correlates with rewarding events
- We know what to do because we understand what these sprites mean!
To get the first reward:
go down the first ladder -> jump on the rope -> jump on the second ladder -> go down the second ladder -> avoid skull -> ...
Exploration and exploitation
-
Two potential definitions of exploration problem
- How can an agent discover high-reward strategies that require a temporally extended sequence of complex behaviors that, individually, are not rewarding?
- How can an agent decide whether to attempt new behaviors (to discover ones with higher reward) or continue to do the best thing it knows so far?
-
Actually the same problem:
- Exploitation: doing what you know will yield highest reward
- Exploration: doing things you haven’t done before, in the hopes of getting even higher reward
Exploration is Hard
Can we derive an optimal exploration strategy?
Yes (theoretically tractable)
No ( theoretically intractable)
multi-armed bandits
contextual bandits
small, finite MDPs
large, infinite MDPs
can formalize exploration as POMDP identification
optimal methods don’t work …but can take inspiration from optimal methods
Muliti-Armed Bandits: Reminder

Solving Exploration in Bandits
Bandit Example:
- assume \(r(a_i) \sim p_{\theta_i}(r_i)\),
- e.g. \(p(r_i=1) = \theta_i\) and \(p(r_i=0) = 1- \theta_i\)
- prior on \(\theta\) : \(\theta \sim p(\theta)\)
This defines a POMDP with states: \(s = [\theta_1, ..., \theta_n]\),
where belief states are \(\hat{p}(\theta_1,..., \theta_n)\)
- solving the POMDP yields the optimal exploration strategy
- but that’s overkill: belief state is huge!
- we can do very well with much simpler strategies
How to measure goodness of exploration algorithm?
Regret: difference between optimal policy and ours
How can we beat the bandit?
- Variety of relatively simple strategies
- Often can provide theoretical guarantees on regret
- Variety of optimal algorithms (up to a constant factor)
- But empirical performance may vary…
- Exploration strategies for more complex MDP domains will be inspired by these strategies
Optimimism in Face of Uncertainty
keep track of average reward \(\hat{\mu}_a\) for each action \(a\)
exploitation: pick \(a = argmax\,\hat{\mu}_a\)
optimistic estimate: \(a = argmax\,\hat{\mu}_a + C \sigma_a\)
Intuition: try each arm until you are sure it's not great
how uncertain we are about this action
Example:
\(Reg(T)\) is \(O(log\,T)\) as good as possible
Posterior Sampling

Bandit Example:
- assume \(r(a_i) \sim p_{\theta_i}(r_i)\),
- this defines a POMDP with states: \(s = [\theta_1, ..., \theta_n]\),
- belief states are \(\hat{p}(\theta_1,..., \theta_n)\)
- This is called posterior sampling or Thompson sampling
- Harder to analyze theoretically
- Can work very well empirically
Correction:
Thompson sampling is asymptotically optimal!
https://arxiv.org/abs/1209.3353
Information Gain
We want to determine some latent variable \(z\)
(e.g. optimal action, q-value, parameters of a model)
Which action do we take to determine \(z\) ?
let \( H(\hat{p}(z))\) be the current entropy of our \(z\) estimate
let \( H(\hat{p}(z)|y)\) be the entropy of our \(z\) estimate after observation \(y\)
Entropy measures lack of information.
Then Information Gain measures how much information about \(z\) we can get by observing \(y\)
Information Gain Example
\(y=r_a\), \(z = \theta_a\) (parameters of a model)
\(g(a) = IG(\theta_a; r_a|a)\) - information gain for action \(a\)
\(\Delta(a) = E[r(a^*) - r(a)]\) - expected suboptimality of a
Policy: choose actions according to:
General Ideas

- Most exploration strategies require some kind of uncertainty estimation (even if it’s naïve)
- Usually assumes some value to new information
- Assume unknown = good (optimism)
- Assume sample = truth
- Assume information gain = good
UCB:
Thompson sampling:
Info Gain:
Why Should We Care?
- Bandits are easier to analyze and understand
- Can derive foundations for exploration methods
- Then apply these methods to more complex MDPs
- Not covered here:
- Contextual bandits (bandits with state, essentially 1-step MDPs)
- Optimal exploration in small MDPs
- Bayesian model-based reinforcement learning (similar to information gain)
- Probably approximately correct (PAC) exploration
Exploration in Deep RL
-
Optimistic exploration / Curiocity:
- new state = good state
- requires estimating state visitation frequencies or novelty
- typically realized by means of exploration bonuses
-
Thompson sampling style algorithms:
- learn distribution over Q-functions or policies
- sample and act according to sample
-
Information gain style algorithms:
- reason about information gain from visiting new states
Curiocity /Optimistic Exploration
Can we use this idea with MDPs?
UCB:
Yes! Add exploration bonus (based on \(N(s,a)\) or \(N(s)\)) to the reward:
This should work as long as \(\mathbf{B}(N(s,a))\) decrease with \(N(s,a)\)
Use \(r^{+}(s,a)\) with any model-free algorithm!
But the is one problem...
The Trouble with Counts
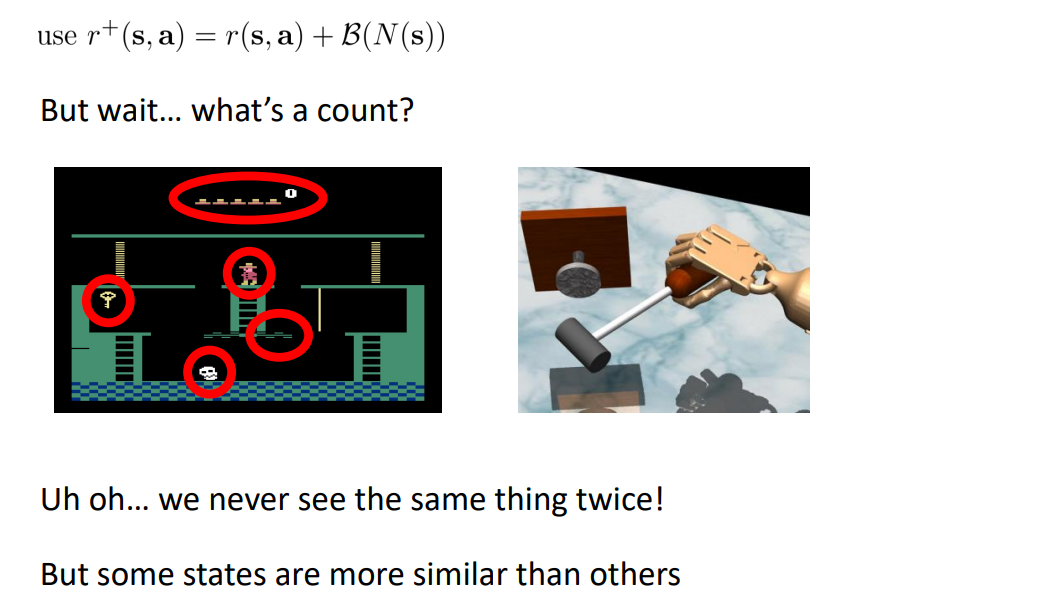
- We never see the same thing twice!
- But some states are more similar than others
But wait… what’s a count?
Fitting Generative Models
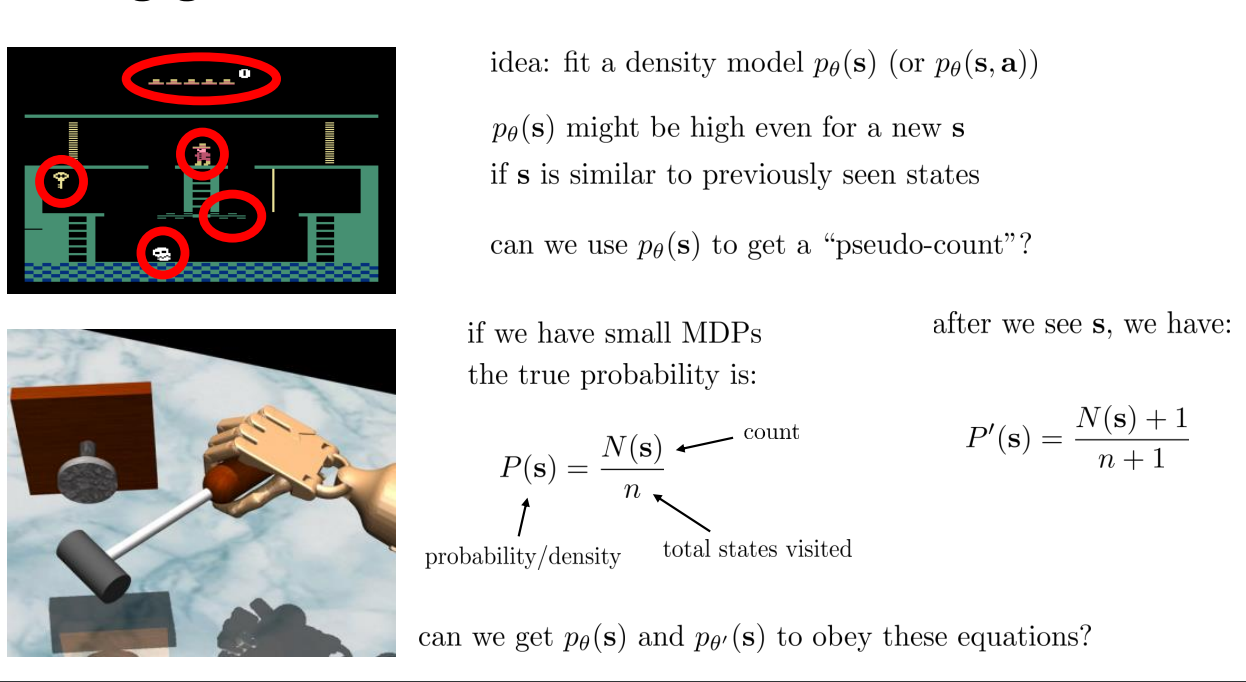
Idea: fit a density model \(p_{\theta}(s)\)
\(p_{\theta}(s)\) might be high even for a new \(s\) if \(s\) is similar to previously seen states.
Can we \(p_{\theta}(s)\) to get a "pseudo-count"?
The true probability is:
After visiting \(s\):
GOAL:
To create \(p_{\theta}(s)\) and \(p_{\theta'}(s)\) that obey these equations!
Exploring with Pseudo-Counts
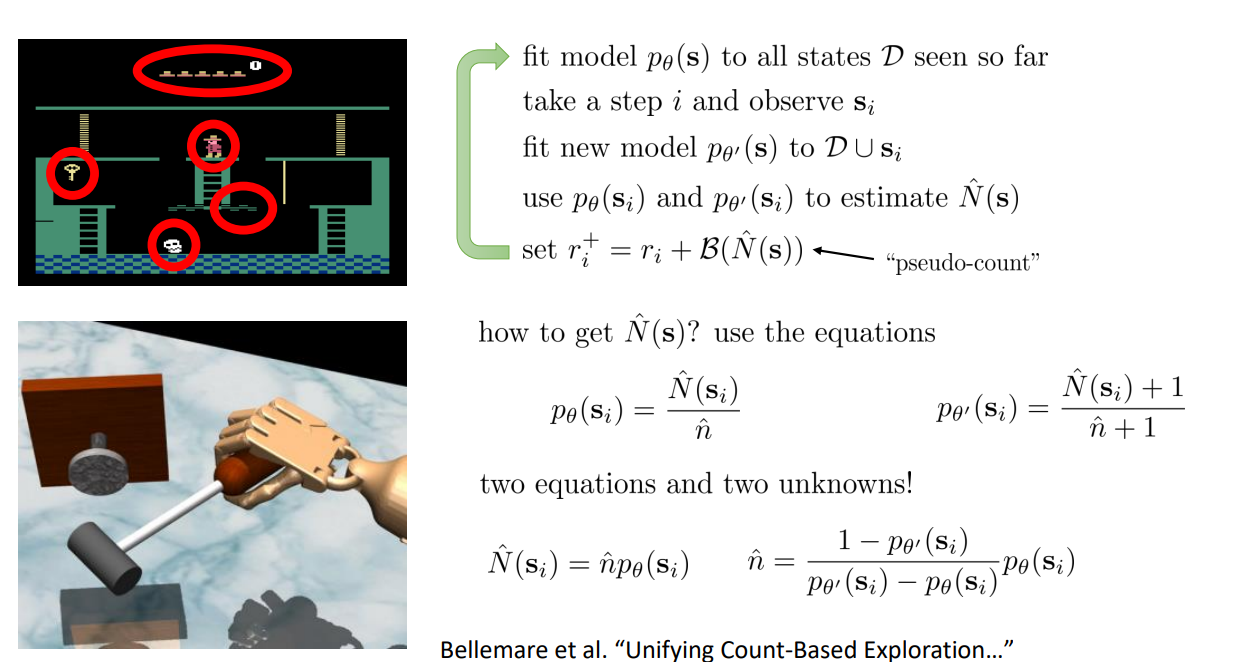

Solve a system of two linear equations:
GOAL:
To create \(p_{\theta}(s)\) and \(p_{\theta'}(s)\) that obey these equations!
Dencity Model:
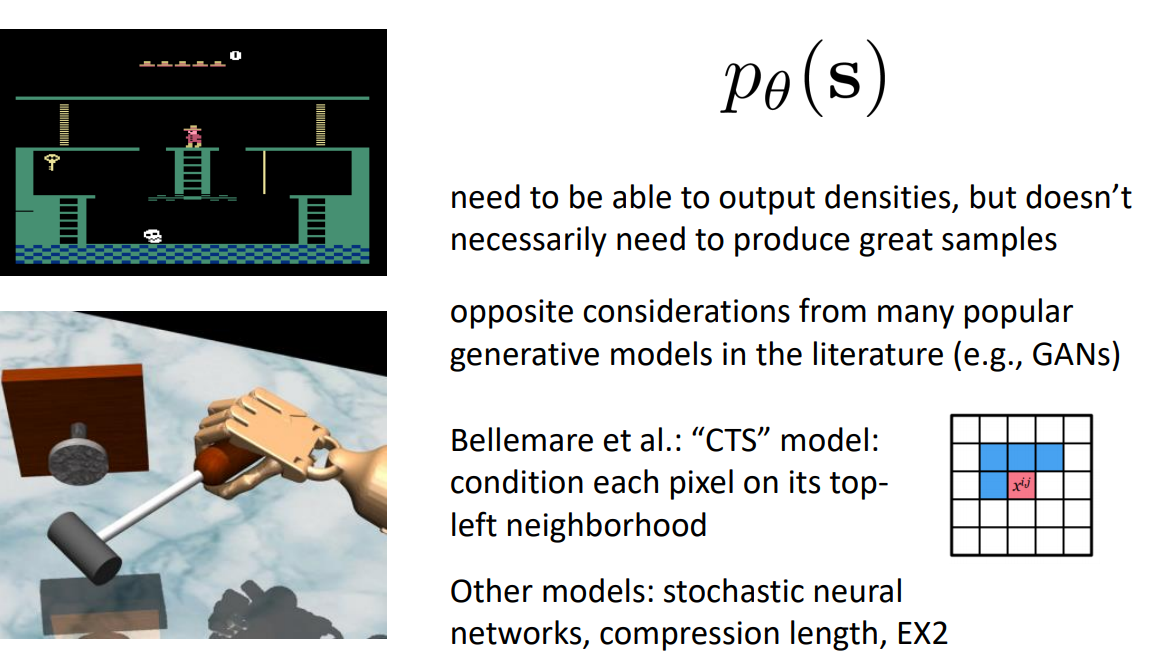
- Need to be able to output densities, but doesn’t necessarily need to produce great samples. Opposite considerations from many popular generative models in the literature (e.g., GANs)
- Bellemare et al.: “CTS” model: condition each pixel on its topleft neighborhood

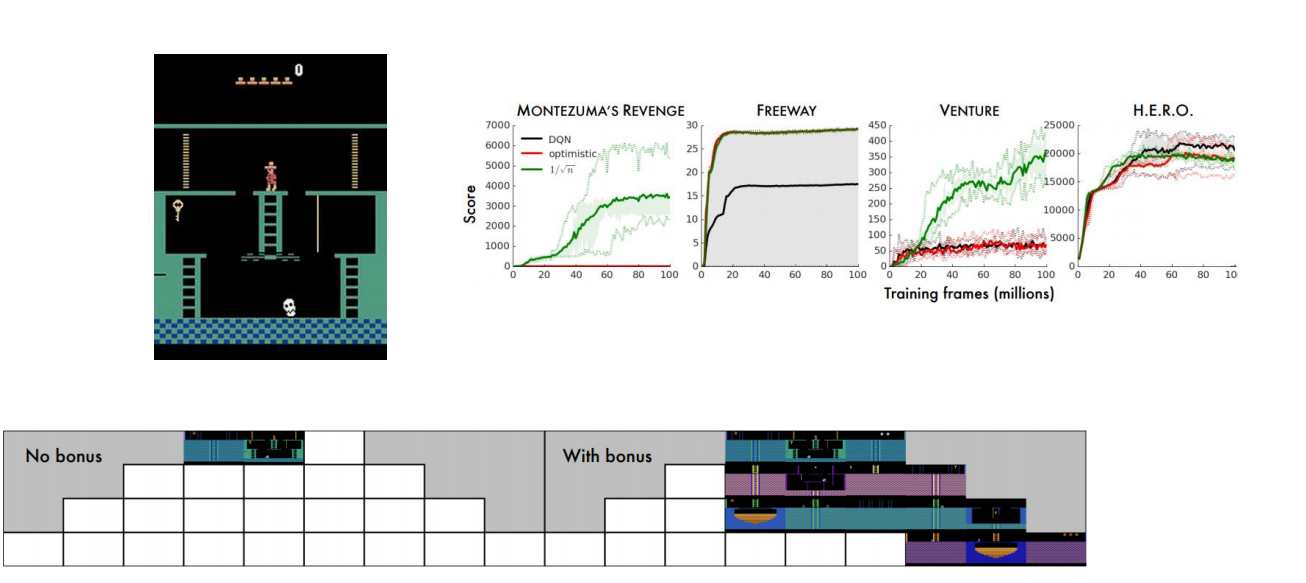
Different Bonus Versions:

Results:
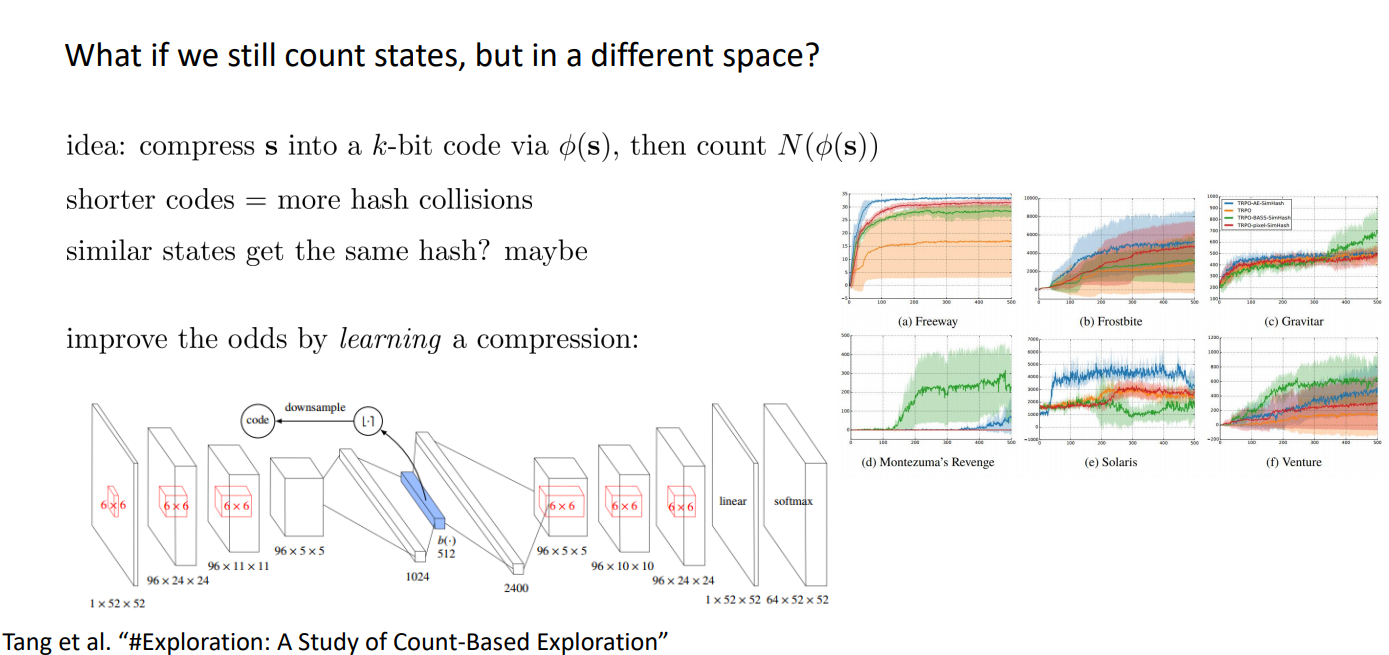
Counting with Hashes:
Idea: compress states into k-bit code via \(\phi(s)\), then count \(N(\phi(s))\)
Shorter codes = more hash collisions,
probably similar states get the same hash...
Improve the odds by learning a compression:

Implicit Density Modeling:
\(p_{\theta}(s)\) need to be able to output densities, but doesn’t necessarily need to produce great samples
Intuition: the state is novel if it is easy to distinguish from all previous seen states by a classifier
For each observation state \(s\), fit a classifier to classify that state against past states \(D\), use classifier error to obtain density:
probability that classifier assigns that \(s\) is not in past states \(D\)
Implicit Densities:
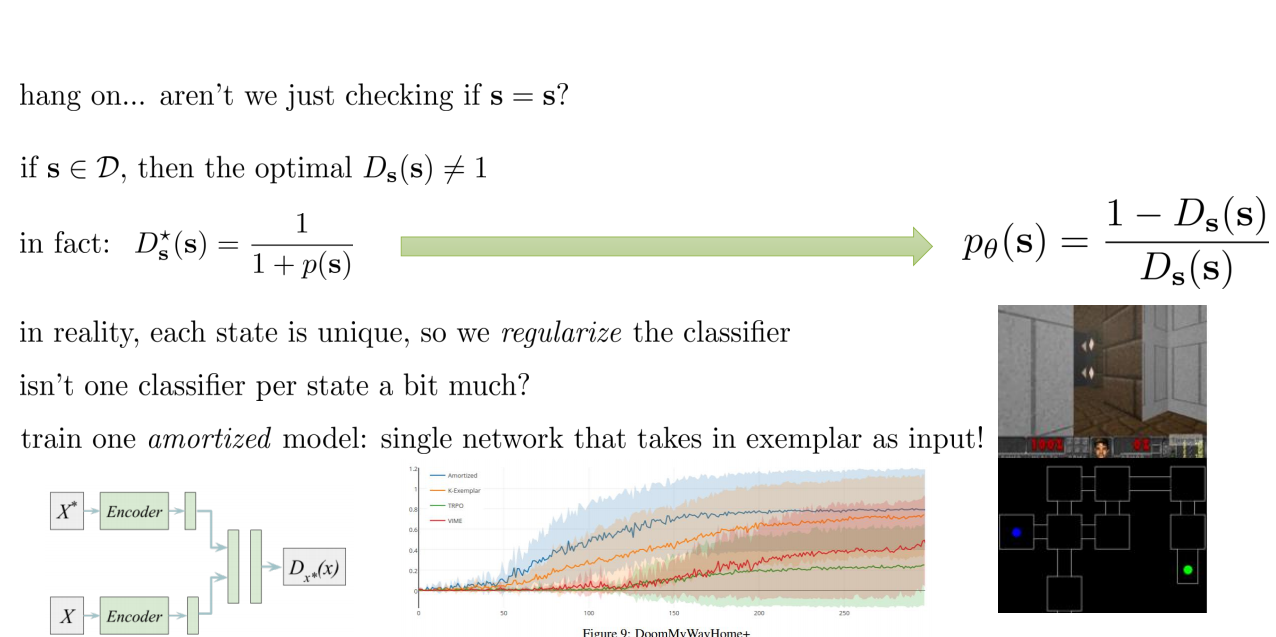
- if \(s \in D \), then the optimal \(D_s(s) \ne 1\)
- in fact \(D^{*}_s(s) = 1/(1 + p_{\theta}(s))\)
That is where we get:
Fitting a new classifier for each new state is abit to much,
therefore we train a single network that takes s as input:

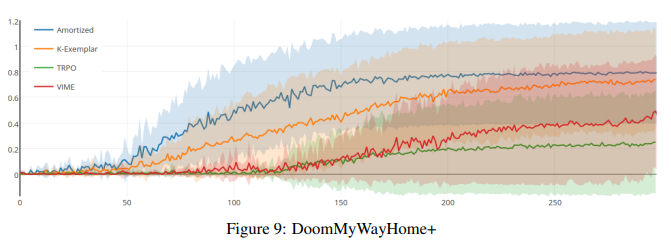
Heuristic estimation of counts via errors

- \(p_{\theta}(s)\) need to be able to output densities, but doesn’t necessarily need to produce great samples
- And doesn’t even need to output great densities
- Just need to tell if state is novel or not!

Heuristic estimation of counts via errors
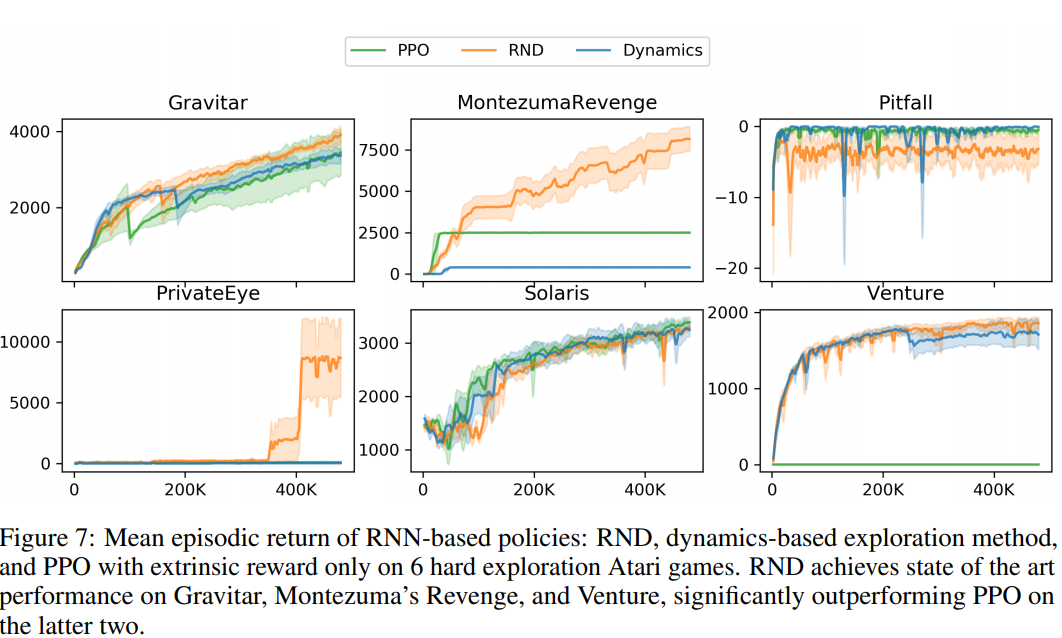
Random Network Distillation: Results
Thompson Sampling in Deep RL

Bootstrapped DQN

Bootstrapped DQN
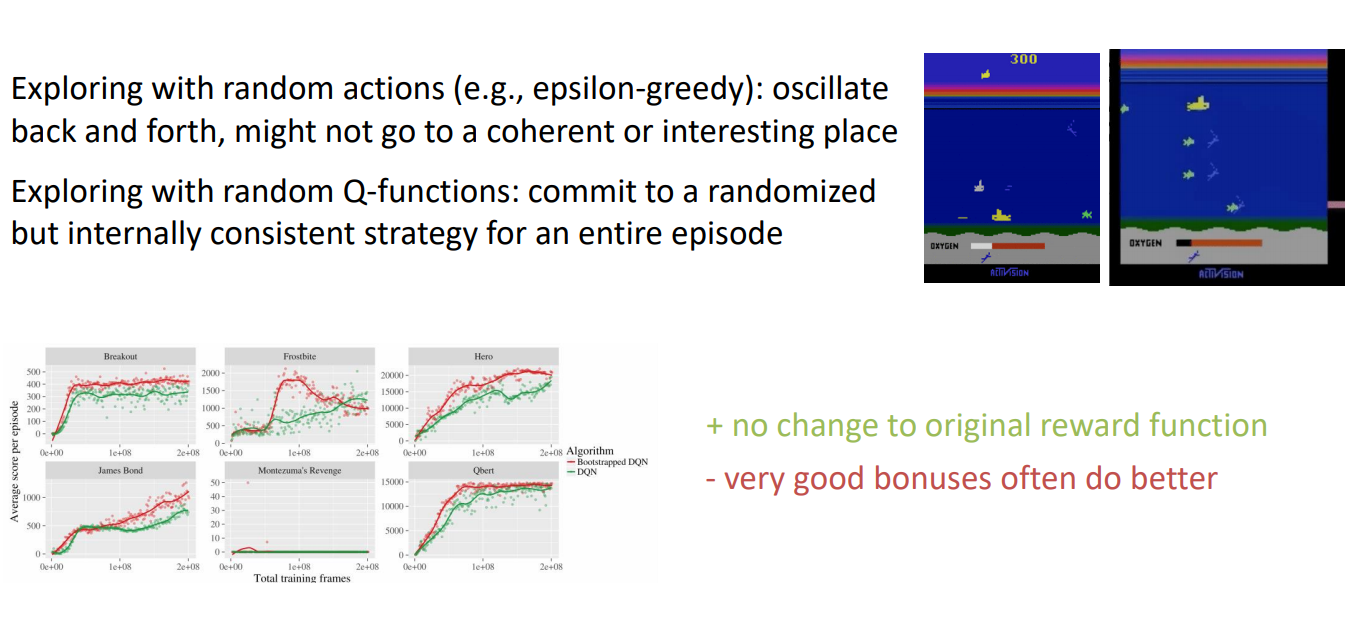
- Exploring with random actions (e.g., epsilon-greedy): oscillate back and forth, might not go to a coherent or interesting place
- Exploring with random Q-functions: commit to a randomized but internally consistent strategy for an entire episode

Information Gain in Deep RL....

