Лекция 3:
Табличное обучение с подкреплением
Артём Сорокин | 23 Ноября
Прошлая лекция: Функции Ценности
Доход или Return, или "reward to go" :
V-функция:
Q-функция:
Прошлая лекция: Уравнения Беллмана
Уравнение Белмана для стратегии \(\pi\):
Уравнения оптимальности Беллмана:
Прошлая лекция: Policy Iteration

Прошлая лекция: Policy Iteration
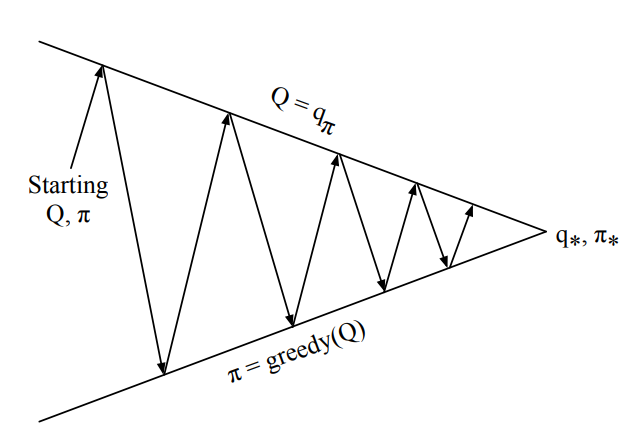
Прошлая Лекция: Value Iteration

Что делать если модель не известна?

Решение: Используем сэмплирование!
- Модель среды может быть недоступна, поэтому нельзя "честно" посчитать вероятности и мат. ожидание :(
- Но со средой можно взаимодействовать!

Методы Монте-Карло
Цель:
Выучить функции ценности \(Q_{\pi}\) и \(V_{\pi}\), когда \(p(s'|s,a)\) и \(R(s,a)\) неизвестны!
Вспоминаем определение:
Функция ценности это мат. ожидание будущей дисконтированной награды.
Метод Монте-Карло первого посещения
По закону больших чисел: \(q(s,a) \rightarrow Q_{\pi}(s,a)\), если \(N(s,a) \rightarrow \infty\)
Идея: Оценим мат. ожидание \(Q_{\pi}(s,a)\), при помощи выборочного среднего \(q(s,a)\):
- Генерируем эпизод стратегией \(\pi\)
- При первом посещений пары состояние-действие \((s,a)\):
- Увеличим счетчик \(N(s,a) = N(s,a) + 1\)
- увеличим сумарный доход по всем эпизодам \(S(s,a) = S(s,a) + G_t\)
- Оценка Q-функции определяется по формуле \(q(s,a) = S(s,a)/N(s,a)\)
Метод Монте-Карло: Оценка
Мы можем обновлять выборочное среднее инкрементально:
Инкрементальное правило обновления МК:
Ошибка предсказания
Старая оценка
Скорость обучения
Для нестационарных задач лучше взять фиксированную скорость обучения:
Свойства Методов Монте-Карло
- МК напрямую обучается из эпизодов взаимодействия со средой
- MК учится без модели /model-free
- Не нужно знать функцию переходов или функцию наград МППР
- MК учится только на полных эпизодах: нет бутстрэппинга
- МК использует 1 простое свойство:
- Функция ценности = мат. ожидание дохода
- Ограничение: МК можно применять только к эпизодическим МППР:
- Все эпизоды должны заканчиваться
Методы Монте-Карло: Управление
Кто помнит Policy Iteration?
Как будет выглядеть PI если для оценки использовать МК?
Вопросы:
- Почему мы оцениваем именно \(Q_{\pi}\), а не \(V_{\pi}\)?
- Есть ли какие-то проблемы с шагом Policy Improvement?

-
Policy Evaluation:
- Оценка Методом Монте-Карло, \(q = Q_{\pi}\)
-
Policy Improvement:
- Жадное улучшение политики \(\pi'(s) = argmax_a q(s,a)\)
Диллема Использования - Исследования
Агент не сможет посетить все пары \((s,a)\) используя жадную стратегию!
Агент не сможет получить хорошую оценку \(q(s,a)\), если не будет посещать \((s,a)\) достаточно часто!
(вспоминаем закон больших чисел)
Методы Монте-Карло: Управление

Policy Improvement step:
Улучшаем любую \(\epsilon\)-мягкую до \(\epsilon\)-жадной стратегии в соответствии с оценкой Q-функции
Для исследования можно использовать любую \(\epsilon\)-мягкую стратегию:
- \(\epsilon\)-мягкая стратегия выбирает любое действие с вероятностью не меньше чем \(\epsilon/m\)
- Простейшая идея обеспечивающая посещение всех пар \((s,a)\)
\(m\) - число доступных действий
Monte-Carlo Methods: Control

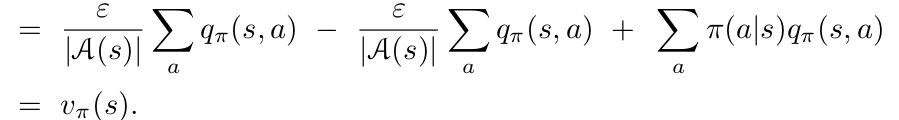

Monte-Carlo Method
Policy Iteration методами Монте-Карло:
Для каждого эпизода:
- Policy Evaluation: Оценка методами Монте-Карло, \(q \sim Q_{\pi}\)
- Policy Improvement: \(\epsilon\)-жадное улучшение стратегии
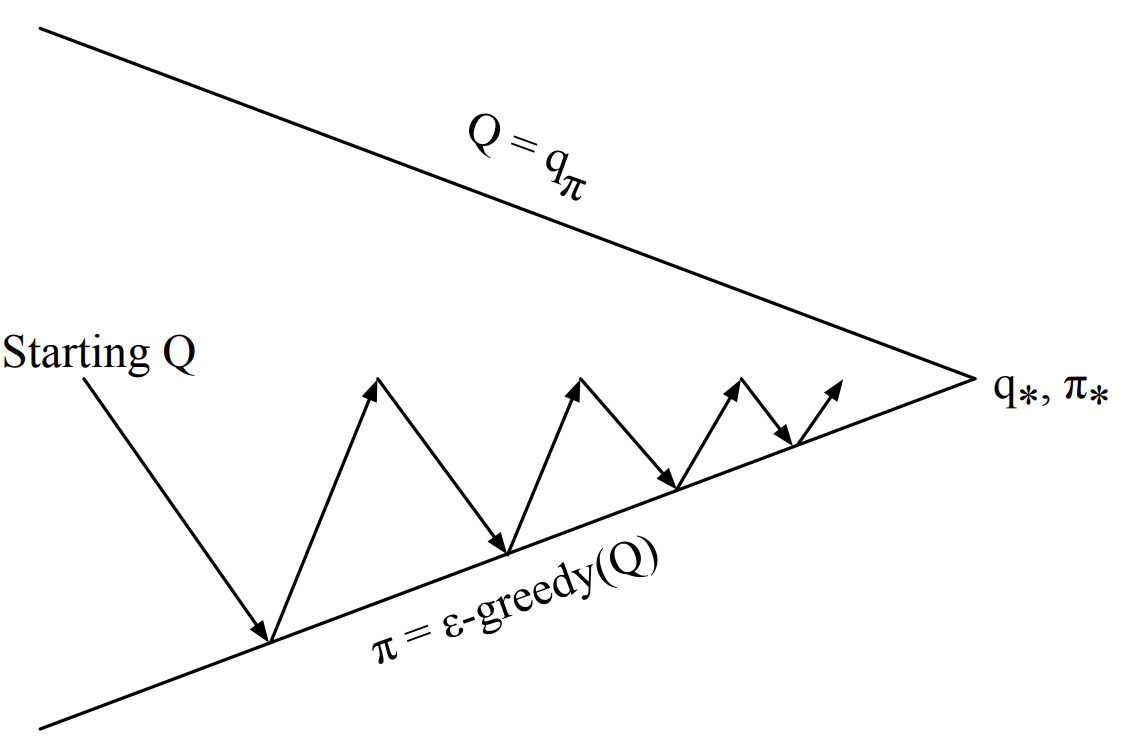
GLIE Метод Монте-Карло

GLIE Метод Монте-Карло

GLIE Метод Монте-Карло:
- Сэмплируем k-ый эпизод используя текщую стратегию \(\pi_k\)
- Обновляем \(q(s,a)\) используя скорость обучения равную \(1/N(s,a)\)
- Ставим параметр \(\epsilon = 1/k\)
- Улучшаем \(\epsilon\)-жадную стратегию
Обучение на основе временных различий
Проблема с Методами Монте-Карло:
- Обновляем стратегию только раз за эпизод ( и только эпизодические МППР)
- Не использует свойства МППР
Решение:
- Вспоминаем уравнения Беллмана:
- Используем сэмплирование чтобы оценить мат. ожидание:
TD-Обучение
TD-Обучение: Оценка
Цель: выучить \(Q_{\pi}\) на основе опыта взаимодействия со средой
Инкрементальный Метод Монте-Карло:
- Обновляем оценку \(q(s_t, a_t)\) при помощи дохода \(G_t\)
ТD-Обучение:
- Обновляем q(s_t, a_t) при помощи 1-шаговой оценки дохода \(r_{t+1} + \gamma q(s_{t+1}, a_{t+1})\)
\(r_{t+1} + \gamma q(s_{t+1}, a_{t+1})\) - это называется TD-целью
\(\delta_t = r_{t+1} + \gamma q(s_{t+1}, a_{t+1}) - q(s_t, a_t)\) - это называется TD-ошибкой
TD-Обучение
Обучение на основе временных различий:
- TD учатся по эпизодам взаимодействия со средой
- TD это model-free алгоритм
- не нужно знать функцию переходов и функцию наград МППР.
- Бутстрэппинг
- TD-обучение обновляет оценку при помощи чуть более точной оценки
- TD-методы могут учиться на неполных эпизодах, через будтстрэппинг
TD-learning: SARSA update
Правило обновления SARSA: State, Action, Reward, next State, next Action

TD-Обучение: Policy Iteration
Policy Iteration на основе TD-обучения:
На каждом шаге:
- Policy Evaluation: Правило обновления SARSA для оценки, \(q \sim Q_{\pi}\)
- Policy Improvement: \(\epsilon\)-жадное улучшение стратегии

TD-Обучение: Алгоритм SARSA

SARSA: теоретические гарантии

TD-Обучение: Q-Learning
SARSA использует уравнение Беллмана (Bellman Expectation Equation) для обновления оценки:
А как насчет TD-Обучения на основе уравнения оптимальности Беллмана (Bellman Optimality Equation):
Все очень просто:
TD-Обучение: Q-Learning vs SARSA
Уравнения Беллмана для стратегии \(\pi\) (SARSA) :
Уравнение оптимальности Беллмана (Q-Learning):
\(a'\) берется из стратеги \(\pi\) которая генерирует эпизоды
Нет связи со стратегией \(\pi\)
TD-Обучение: Q-Learning vs SARSA
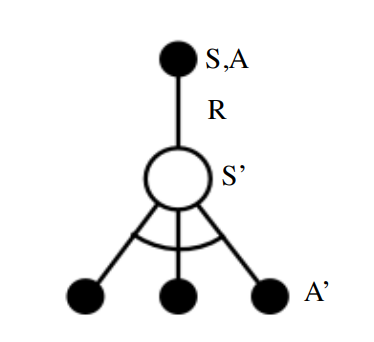
Правило обновления Q-Learning:
Правило обновления SARSA:
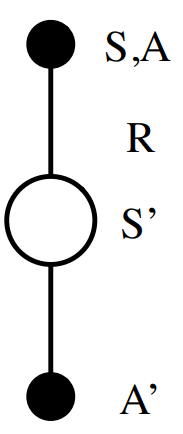
TD-Обучение: Q-Learning


On-policy и Off-Policy Алгоритмы
SARSA и МК являются on-policy алгоритмами:
- Улучшаем стратегию \(\pi_k\) только при помощи опыта собранного этой самой стратегией \(\pi_k\)
- Не можем использовать старые эпизоды сэмплированные при помощи \(\pi_{k-i}\)
Q-Learning это off-policy алгоритм:
- Можем учить стратегию \(\pi_k\) при помощи опыта собранного другой стратегией \(\mu\)
- Позволяет использовать траектории созданные человеком
- Позволяет переиспользовать траектории сгенерированные старой версией стратегии \(\pi_{k-i}\)
- Учим оптимальную стратегию собирая опыт исследовательской стратегией
- Можно выучить разные стратегии на основе одного опыта.
TD-Обучение: Задача с Обрывом
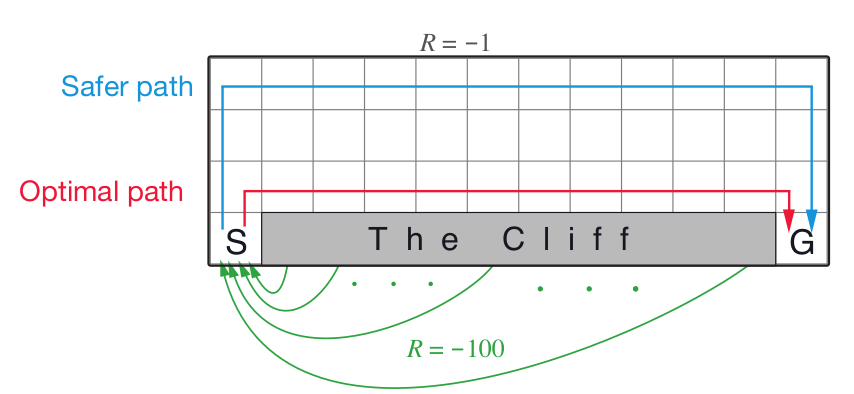
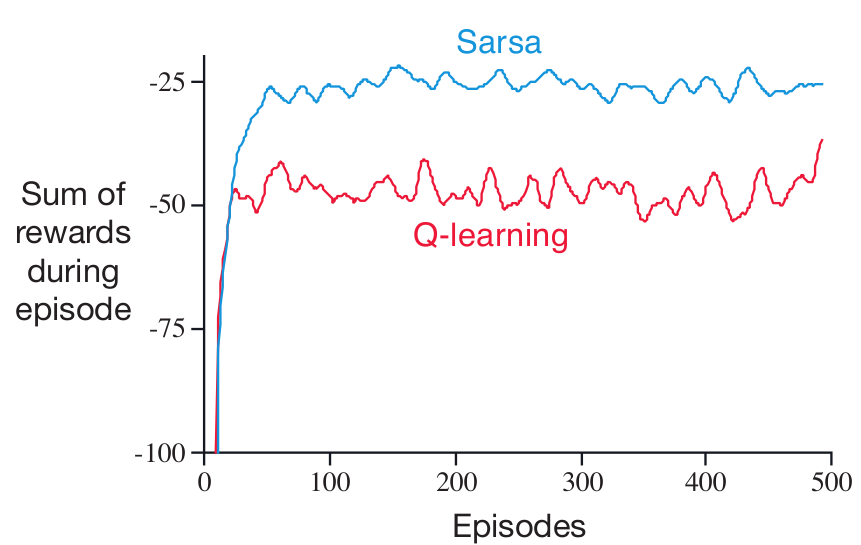
Пример: Дорога домой
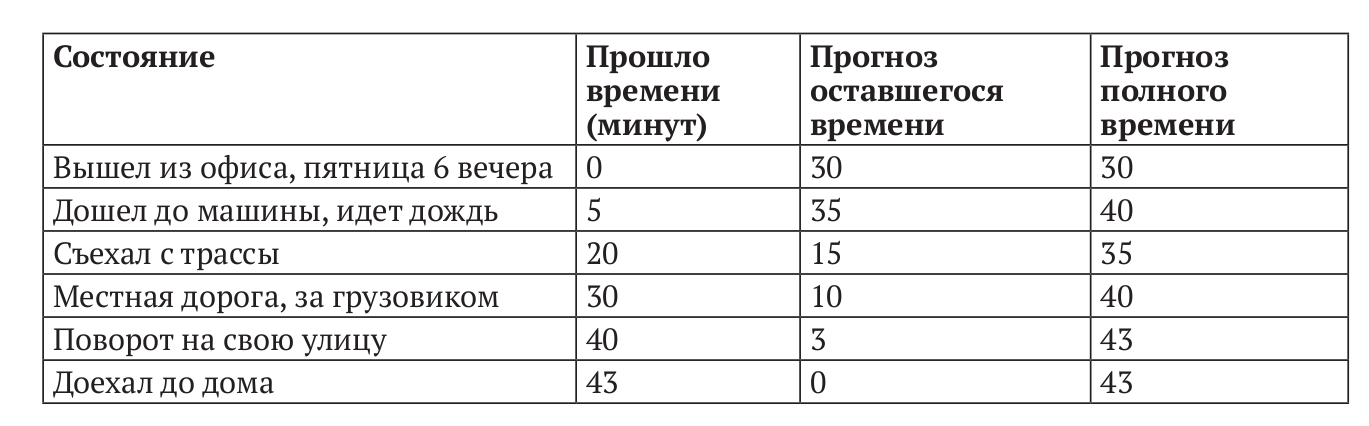
Монте-Карло и TD-Обучение: TD vs MC
Monte Carlo
Temporal Difference
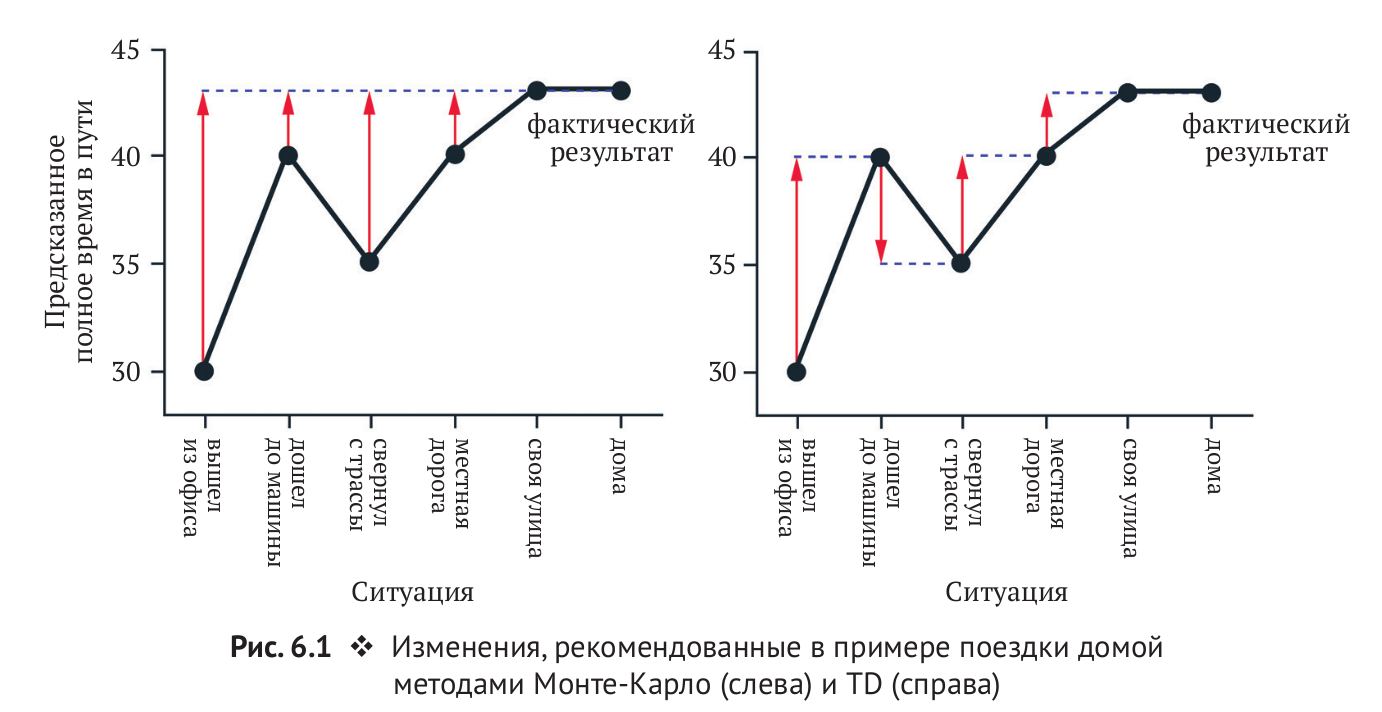
TD vs MC: Диллема Смещения-Дисперсии
- Доход \(G_t = r_{t} + \gamma r_{t+q} + ... + \gamma^{T-t-1}r_{T}\) это несмещенная оценка \(Q_{\pi}(s_t, a_t)\)
- Истинная TD-цель \( r_{t} + \gamma Q_{\pi}(s_{t+1},a_{t+1}) \) это несмещенная оценка \(Q_{\pi}(s_t, a_t)\)
- TD-цель \( r_{t} + \gamma q(s_{t+1},a_{t+1}) \) это смещенная оценка \(Q_{\pi}(s_t, a_t)\)
-
TD-цель имеет значительно меньщую дисперсию чем доход:
- Доход зависит от множества вероятностей связанных с выбором дейсвий, переходами в новые состояния и определением наград.
- TD-цель зависит только от одного действия, одной награды и одного перехода
- Методы Монте-Карло: большая дисперсия, нет смещения
- TD-Обучение: малая дисперсия, есть смещение
TD vs MC: AB Example

Диаграмма обновления Монте-Карло
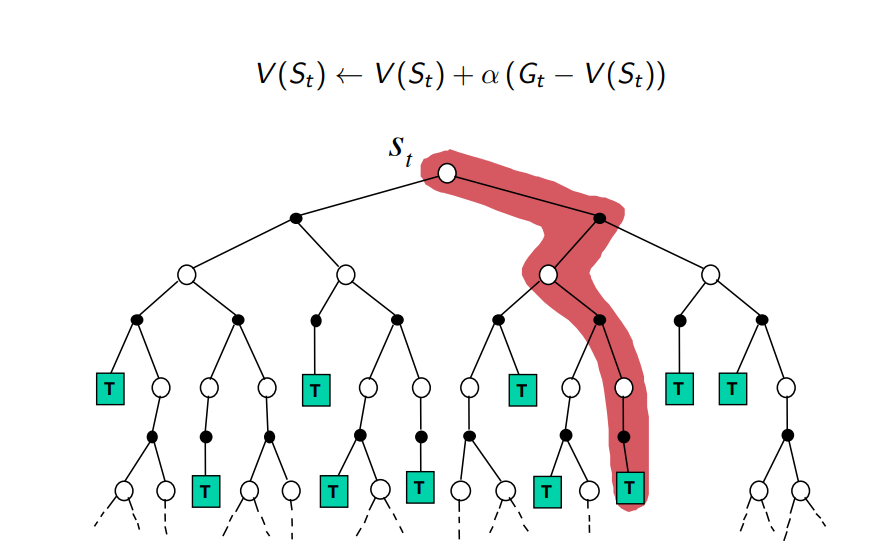
Диаграмма обновления TD-Обучения
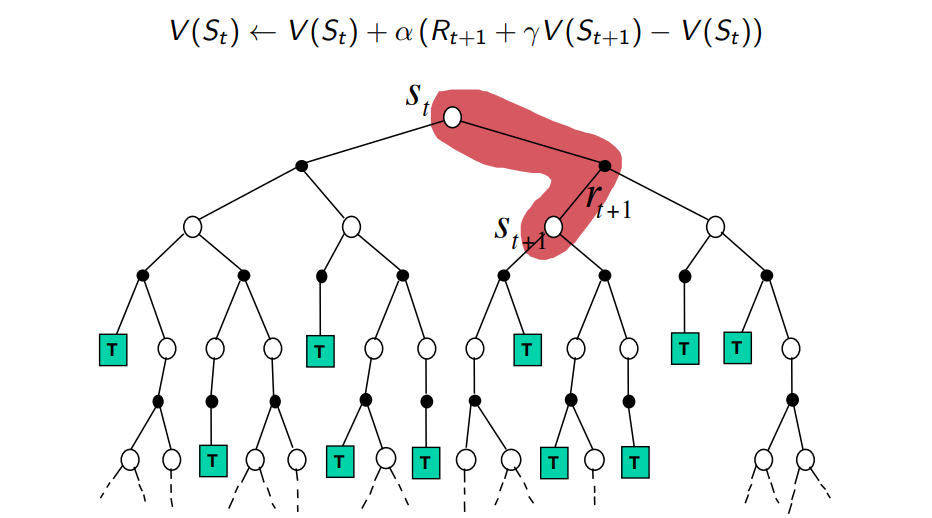
Sampling и Bootstrapping
-
Bootstrapping: обновление оценки за счет другой оценки
- Mонте-Карло не использует бутстрэппинг
- Динамическое Программирование использует бутстрэппинг
- TD-обучение использует бутстрэппинг
-
Sampling: Оцениваем мат. ожидание распределения при помощи выборки
- Монте-Карло использует сэмплирование
- Динамическое программирование не сэмплирует
- TD-обучение использует сэмплирование
Sampling и Bootstrapping
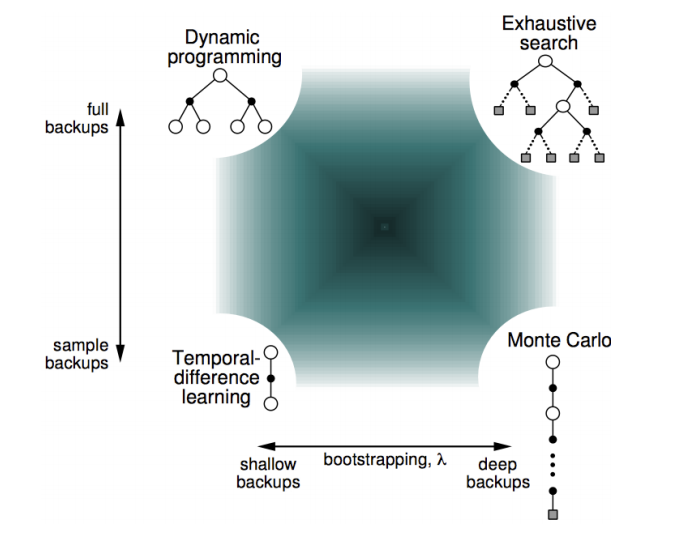
N-шаговый Bootstrapping
Рассмотрим n-шаговые цели для обновления оценки:
n-шаговое TD-обучение:
.
.
.
.
.
.
(MC)
(TD)
Объединим N-шаговые оценки

Можно комбинировать несклько n-шаговых доходов. Например, взять среднее между 2-шаговым и 4-шаговым:
Облегчает подбор правильной цели для обновления функции ценности.
Можно ли эффективно скомбинировать информацию от всех n-шаговых доходов?
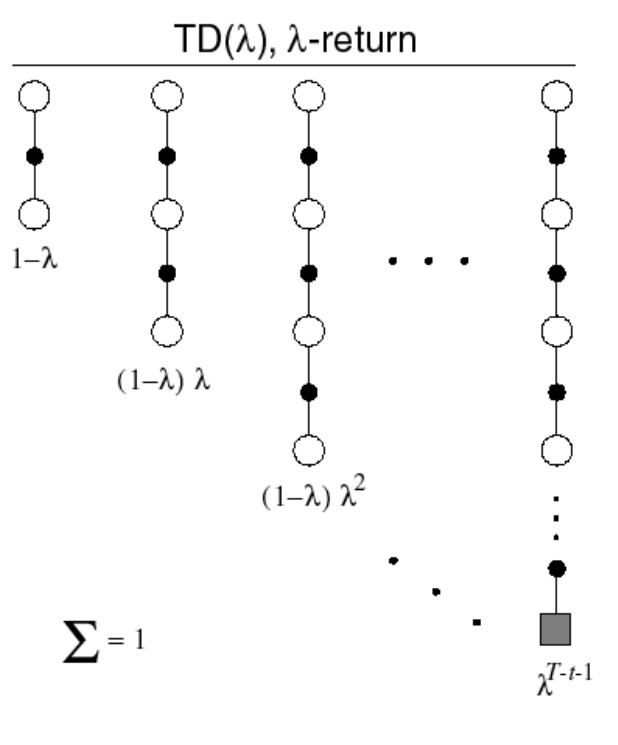
TD(\(\lambda\))
- The \(\lambda\)-оценка \(G^{\lambda}_t\) объединяет все n-шаговые оценки \(G^{(n)}_t\)
- Оценка \(G^{(n)}_t\) берется с весом \((1 −\lambda) \lambda^{n-1}\)
- Forward-view TD(\(\lambda\))... или по другому SARSA(\(\lambda\)):
TD(0) and TD(1):
Почему так?
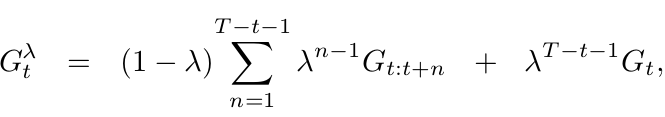
Что случится если \(\lambda = 0\)?
получим TD-цель
Что будет если \(\lambda = 1\)?
Потому что мы можем переписать \(G^{\lambda}_t\) как:
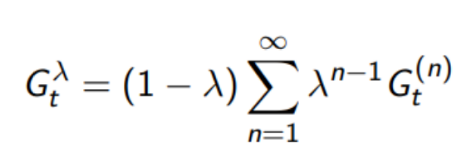
получим Доход/ цель для МК
TD(0) and TD(1):
But why?
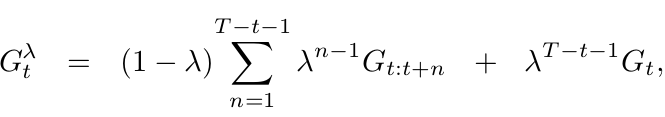
Что случится если \(\lambda = 0\)?
получим TD-цель
Что будет если \(\lambda = 1\)?
We can rewrite \(G^{\lambda}_t\) as:
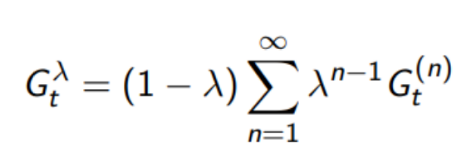
получим Доход/ цель для МК
TD(0) and TD(1):
What happens when \(\lambda = 0\)?
i.e. just TD-learning
What happens when \(\lambda = 1\)?
i.e. Monte-Carlo learning
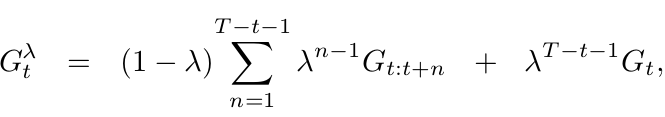
We can rewrite \(G^{\lambda}_t\) as:
HOW?
TD(\(\lambda\)): Прямая перспектива
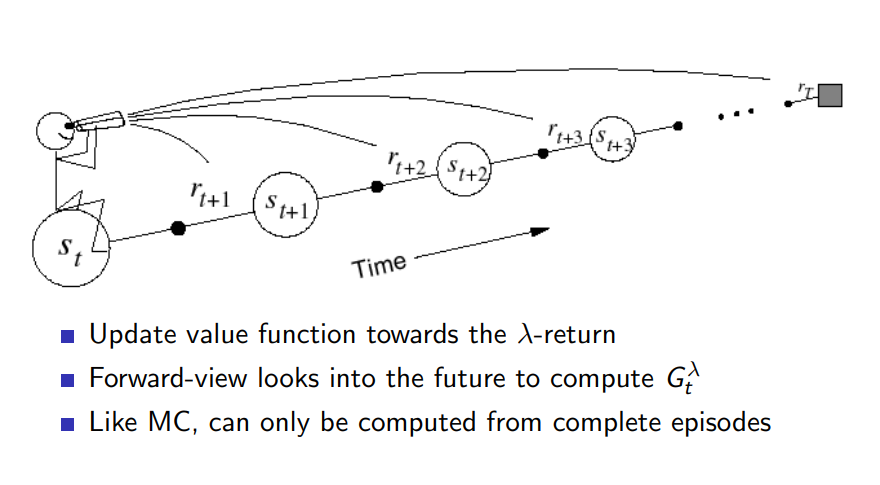
- Обновляем функцию ценности в сторону \(\lambda\)-дохода
- Forward-view TD(\(\lambda\)) должен "заглядывать" в будущее чтобы вычислять \(G^{\lambda}_{t}\)
- Как и МК, может быть вычислен только для завершенных эпизодов.
Text
TD(\(\lambda\)): Обратная Перспектива
- Проблема присвоения заслуг: Что из четырех наблюдений выше вызвало удар током?
- Частотная эвристика: влияют самые частые состояния
- Эвристика новизны: влияют последние состояния
- Eligibility traces/Следы Приемлемости объединяют обе эвристики:

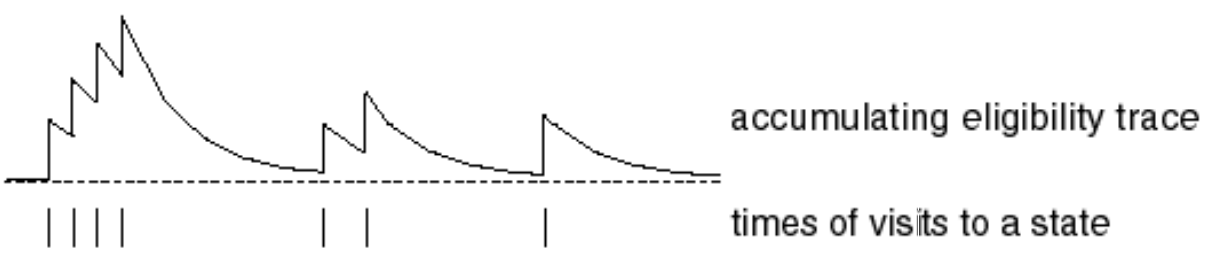
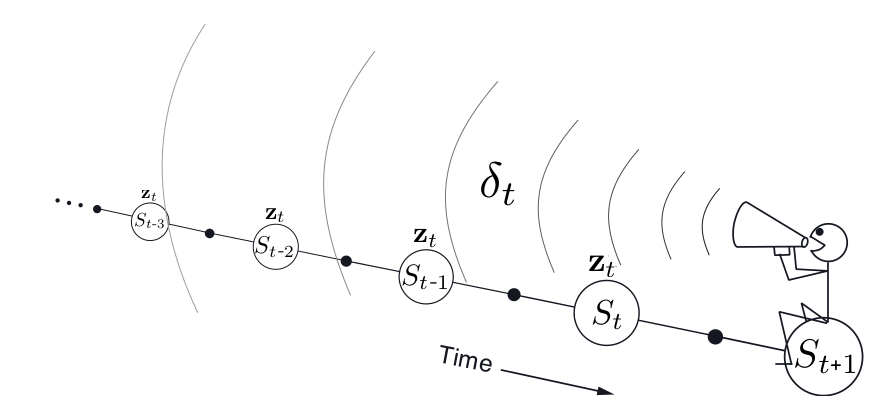
Следы приемлемости: SARSA(\(\lambda\))
- Храним следы приемлемости для каждого состояния \(s\)
- Обновляем \(q(s, a)\) для каждого \(s\) пропорционально TD-ошибке \(\delta_t\) и следу приемлимости \(E_t(s,a)\)

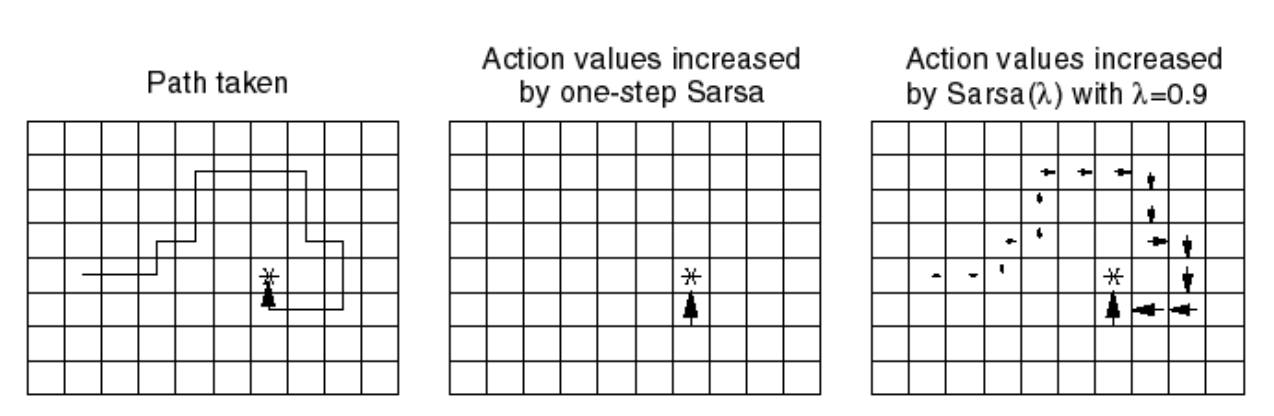
SARSA(\(\lambda\)) и SARSA
SARSA(\(\lambda\)) vs SARSA
Tabular RL: Resume
- Monte-Carlo and Temporal-Difference learning use sampling to approximate Dynamic Programming Methods
- TD learning assumes MDP and use bootstraping updates