Predicting High Uncertainty Events to Train Working Memory ( выжимка )

Artyom Sorokin | Dec 2021

Theory

Memory's Objective

Мы бы хотели чтобы наша память максимизировала следующую сумму: 

argmax_{\theta} \sum_{t=0}^{T} I(f_{t} ; m_t = \textcolor{blue}{g_{\theta} (c_0, ..., c_t)} | с_t)
argmax_{\theta} \sum_{t=0}^{T} I(f_{t} ; m^{\textcolor{blue}{\theta}}_t| с_t)

Для простоты буду писать так: 

Memory's Objective

Проблема: учить память предсказывать будущее \(f_t\) на шаге t может быть уже поздно: 

argmax_{\theta} \sum_{t=0}^{T} I(f_{t} ; m^{\textcolor{blue}{\theta}}_t| с_t)

Цель обучения памяти: 

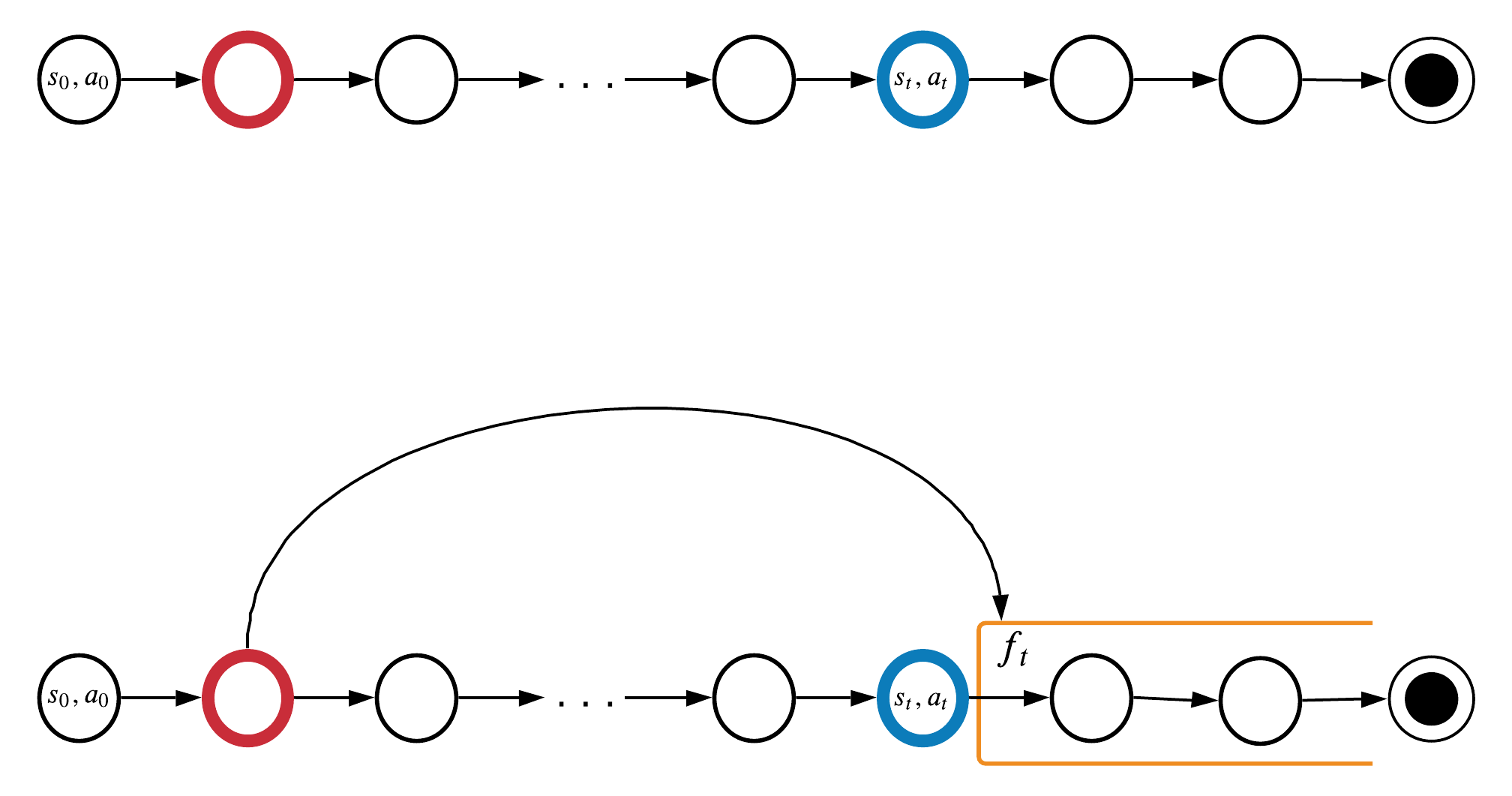
информация с шага \(t-k\) уже потеряна на шаге \(t\)

c_0 = [s_0, a_0]
c_t = [s_t, a_t]
f_t

Memory's Objective

Чтобы выучится не выкидывать старую информацию придется на каждом шаге оптимизировать память относительно всех будущих шагов:  

\(O(T^2)\) по времени

Идея MemUP:
вместо того, чтобы оптимизировать  вторую сумму полностью, выберем шаги когда обучение памяти  может дать наибольший вклад в предсказание будущего!

\sum_{t=0}^{T} \textcolor{blue}{\sum_{i=t}^{T}} I(f_\textcolor{blue}{i} ; m_\textcolor{black}{t} | с_\textcolor{blue}{i})

все еще нужно обрабатвать всю последовательность длинны \(T\)

Если поменять порядок сумм то получится 1 в 1 как учатся трансформер в RL

Finding Important Moments

насколько память может быть важна  для предсказания \(f_t\)

\textcolor{black}{\sum_{t=0}^{T}} I(f_\textcolor{black}{t} ; m^\textcolor{black}{*}_t | c_\textcolor{black}{t})
= \textcolor{black}{\sum_{t=0}^{T}} [H(f_\textcolor{black}{t}| c_\textcolor{black}{t}) - H(f_\textcolor{black}{t}|m^*, c_\textcolor{black}{t})]

Найдем моменты в будущем, когда выучивание памяти потенциально может принести максимальную пользу

Вообразим, что у нас есть идеальная память \(m^{\theta^*}\), тогда: 

мелкая игнорим

оцениваем детектором

Общая схема обучения:

  • Учим детектор \(d_{\psi}\) предсказывать \(f_t\) на каждом шаге на основе \(c_t\). Важно уметь давать оценку  неопределенности предсказаний детектора \(\hat{H}_{\psi}(f_t| с_t)\).

 

  • Учим память \(g_{\theta}\) для каждого шага t предсказывать будущие события \(U_t\), где память может быть наиболее важна:​
argmax_{\theta} \sum_{t=0}^{T} \textcolor{green}{\sum_{k \in U_t}} I(f_\textcolor{green}{k} ; m^{\theta}_\textcolor{black}{t} | с_\textcolor{green}{k})\,,

\(U_t\) это набор шагов из эпизода для, которых детектор дал наибольшую оценку \(\hat{H}_{\psi}(f_i| с_i)\); \(|U| \ll T\).

При обучении памяти мы используем информацию из будущего, которой не будем владеть во время её применения, поэтому нужна отдельная сетка для обьединения шагов k и t: предиктор

Общая схема обучения:

argmax_{\theta} \sum_{t=0}^{T} \textcolor{black}{\sum_{k \in U_t}} I(f_\textcolor{black}{k} ; m^{\theta}_\textcolor{black}{t} | с_\textcolor{black}{k})\,,
\theta^* = argmax_{\theta} \sum_{t=0}^{T} \textcolor{black}{\sum_{k \in U_t}} I(f_\textcolor{black}{k} ; m_{t} = g_{\theta}(c_0,..., c_t) | с_\textcolor{black}{k})\,,
I(f_\textcolor{black}{k} ; m^\textcolor{black}{\theta}_t | с_\textcolor{black}{k}) = H(f_k|c_k) - H(f_k|m^\textcolor{black}{\theta}_t, c_k)
\ge H(f_k|c_k) - CE(p(f_k|m^\textcolor{black}{\theta}_t, c_k), \textcolor{black}{q_{\phi}}(f_k|m^\textcolor{black}{\theta}_t, c_k))
\theta^*, \phi^* = argmin_{\theta, \phi}\, CE(p(f_k|m^\textcolor{black}{\theta}_t, c_k), \textcolor{black}{q_{\phi}}(f_k|m^\textcolor{black}{\theta}_t, c_k)) = argmin_{\theta, \phi}\, \mathbf{E}_{p(f_k, m^\textcolor{black}{\theta}_t|c_k)}[ -log\, q_\textcolor{black}{\phi}(f_k| m^\textcolor{black}{\theta}_t, c_t)]
\psi^* = argmin_{\psi}\, CE(p(f_k|c_k), d_{\psi}(f_k| c_k))
I(f_\textcolor{black}{t} ; \hat{m}_t | c_\textcolor{black}{t})
= H(f_\textcolor{black}{t}| c_\textcolor{black}{t}) - H(f_\textcolor{black}{t}|\hat{m_t}, c_\textcolor{black}{t})
\textbf{D}_{KL} (p(f_t|c_t) || \textcolor{black}{d_{\psi}(f_t| c_t)}) = \textbf{CE}(p(f_t|c_t), \textcolor{black}{d_{\psi}(f_t|c_t)}) - H(p(f_t|c_t))

Optimization

Учим детектор

Нужно чтобы детектор \(d_{\psi}\) умел оценивать энтропию \(H(f_t|c_t)\):

H(f_t|c_t) = \mathbb{E}_{p(f_t|c_t)}[\textcolor{blue}{-log\, p(f_t|c_t)}]
\textbf{D}_{KL} (p(f_t|c_t) || \textcolor{green}{d_{\psi}(f_t|| c_t)}) = \textbf{CE}(p(f_t|c_t), \textcolor{green}{d_{\psi}(f_t|c_t)}) - H(p(f_t|c_t))

Чтобы оценить \(-log\, p(f_t|c_t)\), достаточно использовать Cross-Entropy Loss: 

Мы не можем повлиять на \(H(f_t|c_t)\), поэтому минимизируя CE loss мы минимизируем \(D_{KL}\) между нашей моделькой и настроящим распределением. 

\textcolor{green}{- log \, d_{\psi}(f_t|c_t)}

если не сработает, будем искать более честную оценку энтропии

Наша оценка энтропии для бедных:

То что CE минимизурует \(D_{KL}\), результат супер известный, можно даже не расписывать в статье.

(1)

оценка энтропии по одному сэмплу или удивление

Учим детектор

Нужно чтобы детектор \(d_{\psi}\) умел оценивать энтропию \(H(f_t|c_t, m_t)\):

H(f_t|c_t) = \mathbb{E}_{p(f_t|c_t)}[\textcolor{blue}{-log\, p(f_t|c_t)}]
\textbf{D}_{KL} (p(f_t|c_t) || \textcolor{green}{d_{\psi}(f_t|| c_t)}) = \textbf{CE}(p(f_t|c_t), \textcolor{green}{d_{\psi}(f_t|c_t)}) - H(p(f_t|c_t))

Чтобы оценить \(-log\, p(f_t|c_t)\), достаточно использовать Cross-Entropy Loss: 

Мы не можем повлиять на \(H(f_t|c_t)\), поэтому минимизируя CE loss мы минимизируем \(D_{KL}\) между нашей моделькой и настроящим распределением. 

\textcolor{green}{- log \, d_{\psi}(f_t|s_t)}

если не сработает, будем искать более честную оценку энтропии

Наша оценка энтропии для бедных:

оценка энтропии по одному сэмплу или удивление

(1)

Учим память+предиктор

Память \(g_{\theta}\) и предиктор \(q_{\phi}\)  должны максимизировать взаимную информацию :

Barber, Agakov (2004) доказали Lower Bound для взаимной информации

(перепишем для нашего случая):

\sum_{t=0}^{T} \textcolor{black}{\sum_{k \in U_t}} I(f_\textcolor{black}{k} ; m_t = \textcolor{green}{ g_{\theta}(h_{1:t})} | с_\textcolor{black}{k})\, = \sum_{t=0}^{T} \textcolor{black}{\sum_{k \in U_t}} I(f_\textcolor{black}{k} ; m^\textcolor{green}{\theta}_t | с_\textcolor{black}{k})
I(f_\textcolor{black}{k} ; m^\textcolor{green}{\theta}_t | с_\textcolor{black}{k}) = H(f_k|c_k) - H(f_k|m^\textcolor{green}{\theta}_t, c_k)

вспоминаем ур.1 между \(CE\) и \(KL\) только для распределения \(p(f_k|m^{\theta}_t, c_k)\):

\textbf{D}_{KL} (p(f_k|m^\textcolor{green}{\theta}_t, c_k)|| \textcolor{blue}{q_{\phi}}(f_k|m^\textcolor{green}{\theta}_t, c_k)) = \textbf{CE}(p(f_k|m^\textcolor{green}{\theta}_t, c_k), \textcolor{blue}{q_{\phi}}(f_k|m^\textcolor{green}{\theta}_t, c_k)) - H(p(f_k|m^\textcolor{green}{\theta}_t, c_k))

Т.к.

D_{KL} \ge 0

, значит

CE(p_\textcolor{black}{\theta}, q_{\phi,\theta}) \ge H(p_\theta)

 получается:  

(2)

H(f_k|c_k) - H(f_k|m^\textcolor{green}{\theta}_t, c_k)
\ge H(f_k|c_k) - CE(p(f_k|m^\textcolor{green}{\theta}_t, c_k), \textcolor{blue}{q_{\phi}}(f_k|m^\textcolor{green}{\theta}_t, c_k))

Учим память+предиктор

Память \(g_{\theta}\) и предиктор \(q_{\phi}\)  должны максимизировать взаимную информацию :

Barber, Agakov (2004) доказали Lower Bound для взаимной информации

(перепишем для нашего случая):

\sum_{t=0}^{T} \textcolor{black}{\sum_{k \in U_t}} I(f_\textcolor{black}{k} ; m_t = \textcolor{green}{ g_{\theta}(h_{1:t})} | с_\textcolor{black}{k})\, = \sum_{t=0}^{T} \textcolor{black}{\sum_{k \in U_t}} I(f_\textcolor{black}{k} ; m^\textcolor{green}{\theta}_t | с_\textcolor{black}{k})
H(f_k|c_k) - H(f_k|m^\textcolor{green}{\theta}_t, c_k)
\ge H(f_k|c_k) - CE(p(f_k|m^\textcolor{green}{\theta}_t, c_k), \textcolor{blue}{q_{\phi}}(f_k|m^\textcolor{green}{\theta}_t, c_k))
\ge H(f_k|c_k) - \mathbb{E}_{p(f_k, m^\textcolor{green}{\theta}_t|c_k)}[ -log\, q_\textcolor{blue}{\phi}(f_k| m^\textcolor{green}{\theta}_t, c_t)]
I(f_\textcolor{black}{k} ; m^\textcolor{green}{\theta}_t | с_\textcolor{black}{k})

от нас не зависит, игнор

NLL loss, минимизируем её  и разом обновляем \(\theta\) и \(\phi\)

Итог: \(d_\psi\), \(g_\theta\), \(q_\phi\)  учим предсказывать будущее \(f_t\) при помощи NLL loss

Учим память+предиктор

На всякий случай для проверки, можно прочитать следующие 2 статьи из которых взято доказательство для функции memory+predictor: 

Architecture

Architecture

 

  • TrajGenerator создаем последовательности
    • TargetCreator: может потрбоваться создавать цели предсказания (RL, self-supervision) 
  • UncertaintyDetector: оцениваем неопределенность шагов в траектории
    • СontextEncoder: нужен здесь и для предиктора
  • EventSelector: Чтобы по неопределенности выбрать события для предсказаний памяти
  • EpisodeBuffer: Выбирает батчи эпизодов, запускает на них UncertaintyDetector, EventSelector
    • ​Возможно нужен отдельный класс чтобы все собрать в батч 
  • MemoryModule: учится хранить информацию
  • Predictor: позволяет учить памят на событиях из будущего. 

 

Чтобы учить память используем всё. Чтобы учить детектор достаточно только первых 4ех

 

ContextEncoder

* Из данных эпизода нужно сформировать нормальные наблюдения. Причем, когда эпизод уже разбит на роллауты, может быть уже поздно что-то делать.

* Применяется перед использованием Detector'а и Predictor'а (должен быть одинаковый для этой пары)

Context

TrajGenerator

Какие варианты могут быть:

  • Просто создавать, как copy-task: CopyGenerator(<аргументы задачи>)
  • Загружать из датасета: DatasetLoader(<путь и тд.>)
  • RL версия: RLGenerator( env, policy, etc.)
    • SequentialRLGenerator(env, policy, etc.)
    • ParallelRLGenerator(env, policy, MultiprocessingQueue?)

 

Поля:
* get_trajs(n?)

* TrajIterator