Исследование рабочей памяти и механизмов быстрой
адаптации в обучении с подкреплением
Выступающий: А. Ю. Сорокин
Руководитель: к. ф., -м. н. М. С. Бурцев
Представление на соискание учёной степени кандидата
физико-математических наук по специальности
05.13.17 Теоретические основы информатики
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«Московский физико-технический институт (национальный исследовательский университет)»
(МФТИ, Физтех)
Долгопрудный, 2022
Содержание
-
Введение
-
Стохастические графы и быстрая адаптация
- Сеть функциональных систем (FSN)
- TD-обучение + FSN
- Стохастические графы
- Q-обучение с памятью
-
Общая рабочая память для многозадачного и непрерывного обучения
- Мета обучение и многозадачное обучение
- Архитектура задаче-независимой памяти
- f-LSTM: факторизация LSTM слоя
- Эксперименты
- Результаты
-
Обучение долговременной памяти через предсказание событий высокой неопределенности
- Временные зависимости
- Обучение памяти через максимизацию взаимной информации
- Локальное обнаружение временных зависимостей
- Эксперименты
- Результаты
Введение
Мотивация
Современные алгоритмы обучения с подкреплением требуют миллионов эпизодов взаимодействия для успешного выучивания нового навыка или изменения поведения.
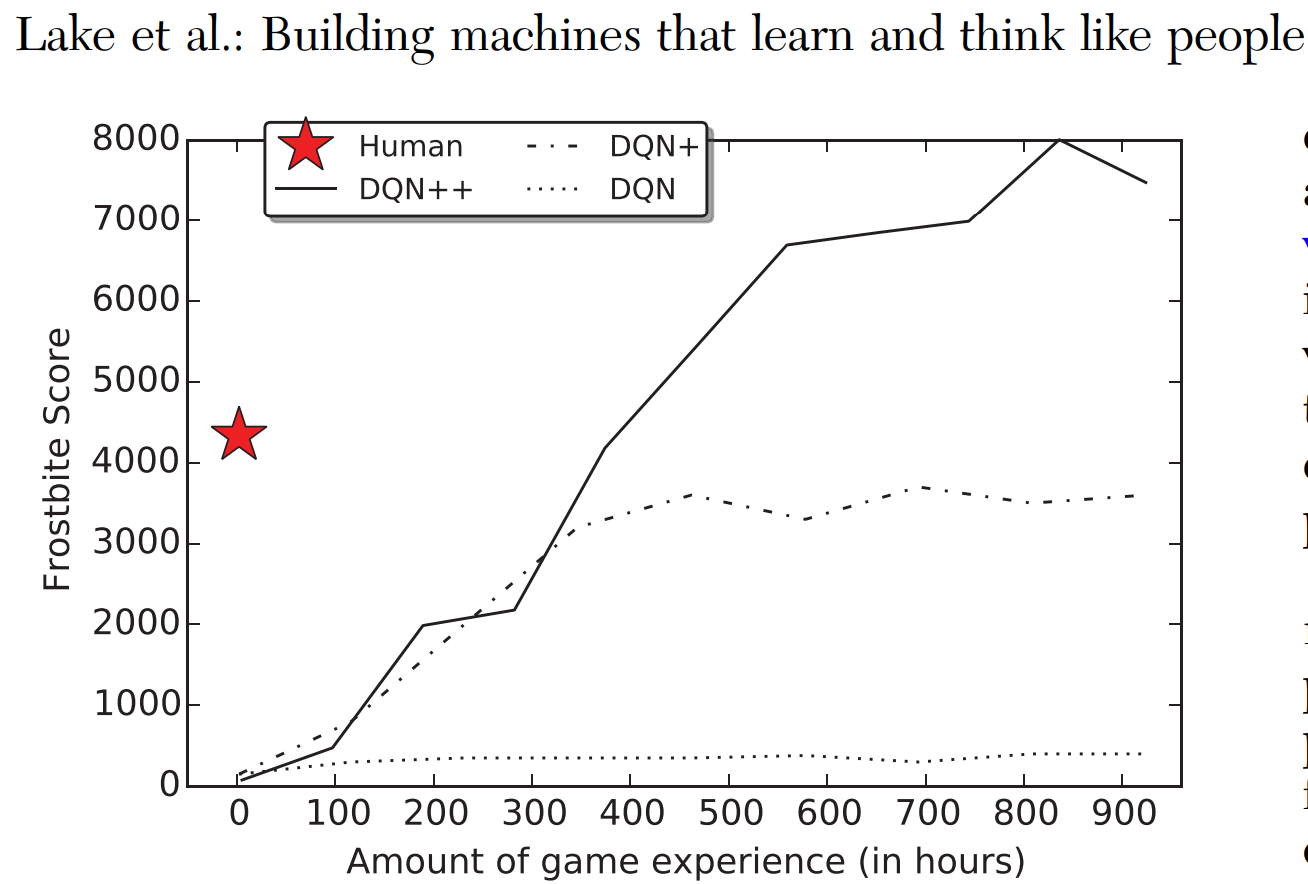
Причины быстрой адаптации[1-3]:
-
Позитивный перенос знаний между задачами (перенос представлений)
-
Иерархическая декомпозиция (перенос подстратегий)
-
Запоминание изменений[2-3]
-
Lake, B. M., Ullman, T. D., Tenenbaum, J. B., & Gershman, S. J. (2017). Building machines that learn and think like people. Behavioral and brain sciences, 40.
-
McClelland, J. L., McNaughton, B. L., & O'Reilly, R. C. (1995). Why there are complementary learning systems in the hippocampus and neocortex: insights from the successes and failures of connectionist models of learning and memory. Psychological review, 102(3), 419.
-
Kumaran, D., Hassabis, D., & McClelland, J. L. (2016). What learning systems do intelligent agents need? Complementary learning systems theory updated. Trends in cognitive sciences, 20(7), 512-534.
Стохастические графы и быстрая адаптация
Мотивация
Проблемы современного обучения с подкреплением:
-
Позитивный перенос знаний
-
Добавление навыков без потери старых
-
Быстрая адаптация
-
Иерархическая декомпозиция задач

Сеть функциональных систем[1-3]:
-
Легко строить иерархию.
-
Легко переносить знания на новую задачу
-
Нет catastrophic forgetting
Функциональные системы
Функциональная система - модуль целенаправленного поведения.
- Может распознавать проблемное состояние и активироваться
- Если активна то старается достичь целевого состояния
- Учит стратегию достижения состояния
- Может уставать и распознавать неудачу
- Может активировать и подавлять другие ФС, образуя сеть.
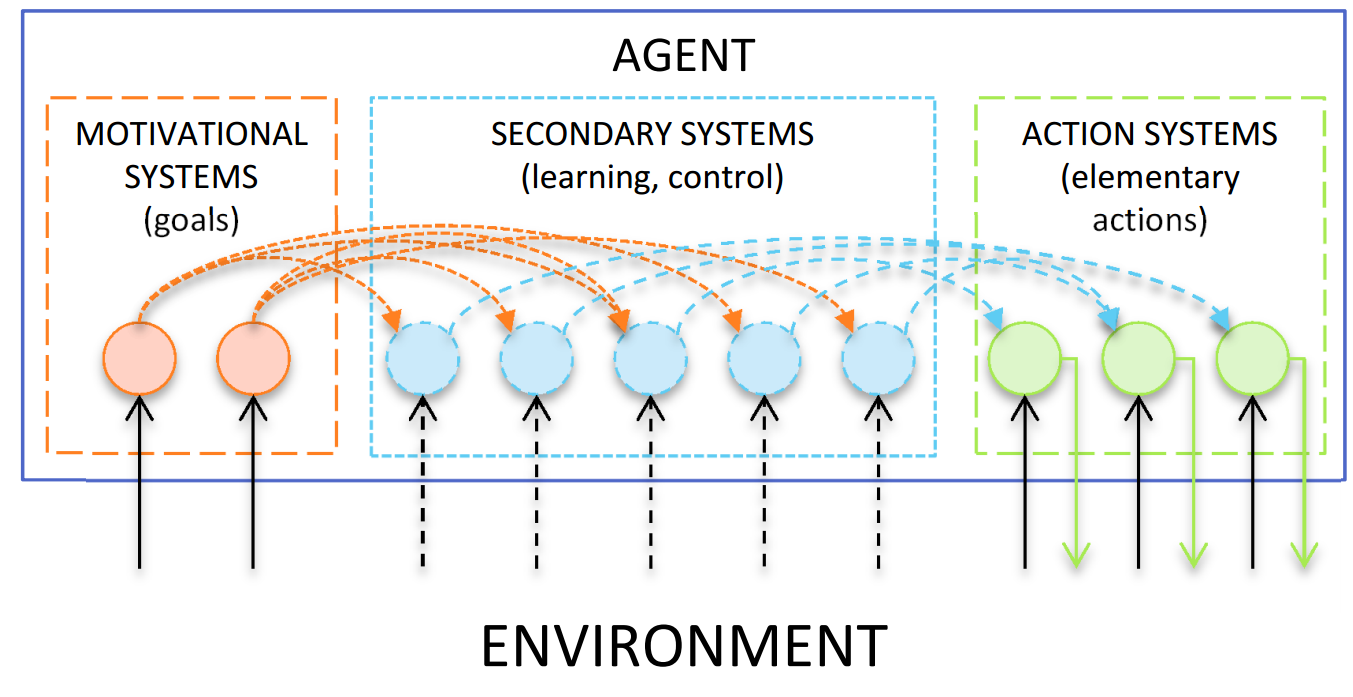
Плюсы сети функциональных систем[1-3]:
-
Легко строить иерархию.
-
Легко переносить знания на новую задачу
-
Нет catastrophic forgetting
-
Red'ko, Vladimir G. et al. "Theory of functional systems, adaptive critics and neural networks." 2004.
-
Komarov, M. A., G. V. Osipov, and M. S. Burtsev. "Adaptive functional systems: Learning with chaos." (2010)
-
Sorokin, Artyom Y., and Mikhail S. Burtsev. "Functional Systems Network Outperforms Q-learning in Stochastic Environment." (2016) [работа автора]
Задача
Проблема:
Агент не делает различий между альтернативными вариантами поведения, даже если один путь значительнее надежнее/эффективнее другого.
Цель:
Модифицировать агента, для того чтобы он мог обучаться в условиях изменяющейся стохастической среды выбирая более эффективные из выученных стратегий.
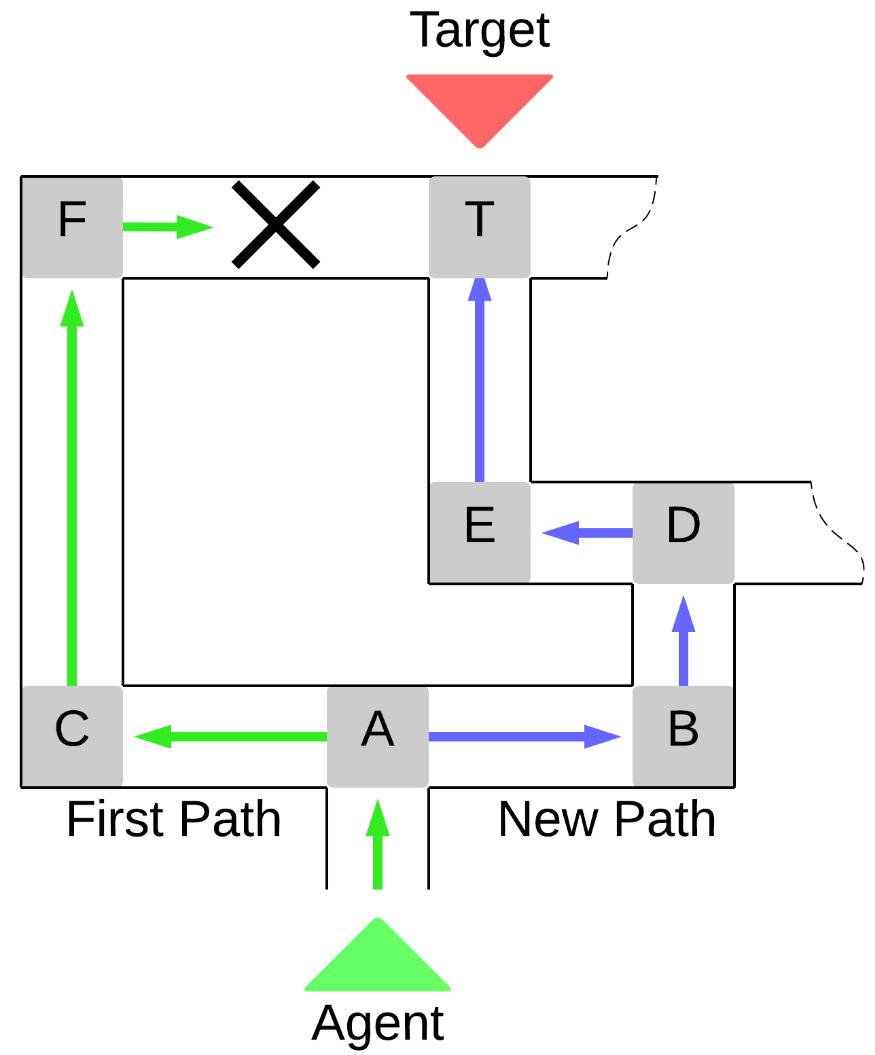
мотивирующие связи
подавляющие связи
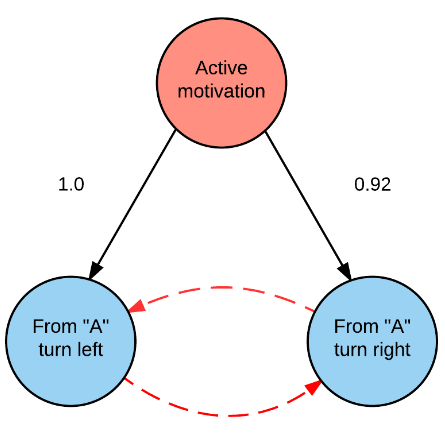
Обучение связи между ФС
Воспользуемся подходом, аналогичным тому, который используется в TD-learning. Каждой новой выученной ФС сопоставим значение , которое будет отображать её полезность для ФС уровнем выше.
Правило обновления полезности :

Обучающий сигнал \(r_i\) высчитывается следующим образом:
- \(𝑟_𝑖 = 1\), если активация привела агента в целевое состояние текущей ;
- \(𝑟_𝑖 = 0\), если активация не привела не достигла собственной цели;
- \(𝑟_𝑖 = 𝑞^{𝑘+1}_{𝑗𝑔}\), если приводит агента в состояние в, котором может быть активирована хотя бы одна выученная ФС, где 𝑔 – это индекс последней активированной в этом состоянии ФС .
высчитываем веса из значений \(q\)
Sorokin, Artyom Y., and Mikhail S. Burtsev. "Functional Systems Network Outperforms Q-learning in Stochastic Environment." (2016) [работа автора]
Моделирование стохастической изменчивости на графе
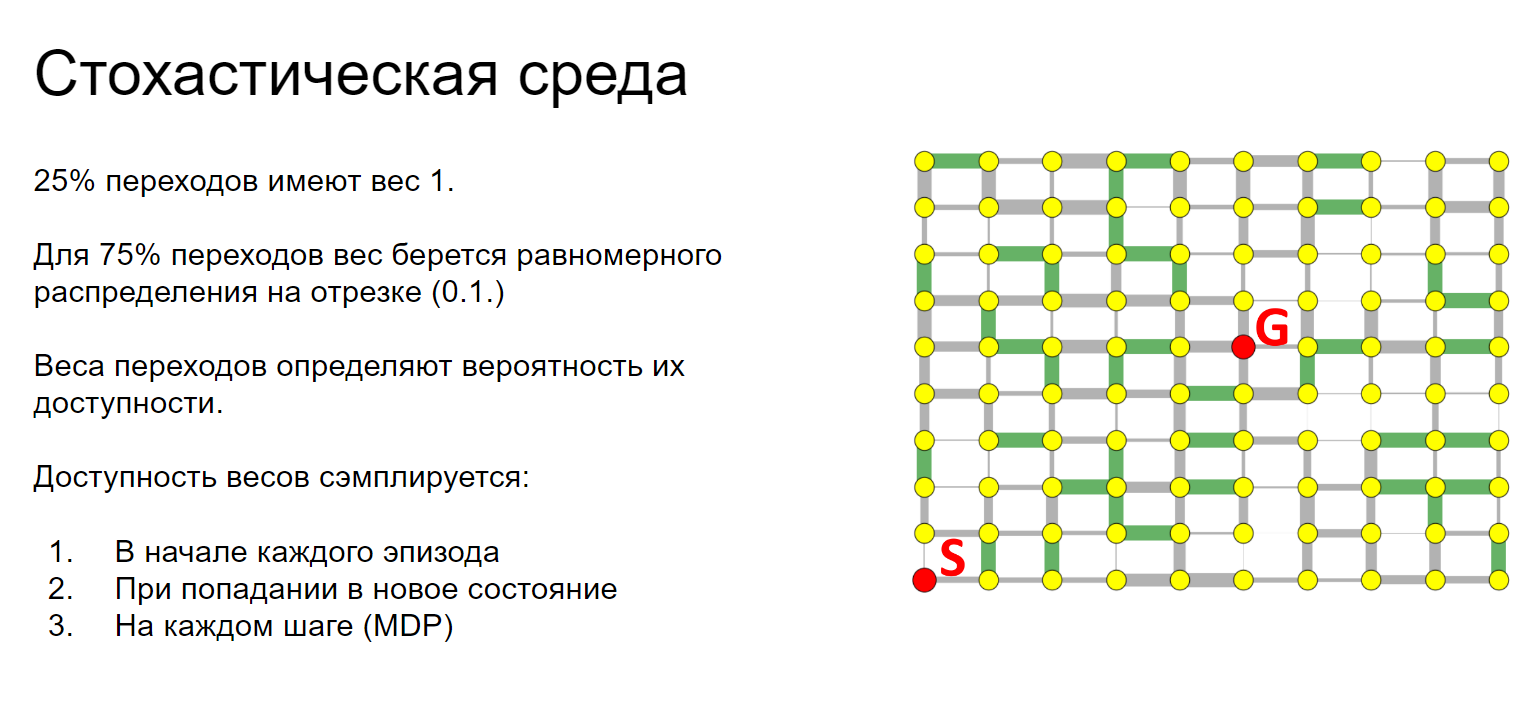
Цель Агента: из случайной стартовой вершины добраться до целевой
Стохастичность в среде:
- 25% переходов (ребра в графе) имеют вес 1;
- для 75% переходов вес берется равномерного распределения на отрезке [0, 1].
Веса переходов определяют вероятность их доступности.
В экспериментах использовались среды с разной частотой стохастической изменчивости:
-
Доступность ребер разыгрывается в начале эпизода.
-
Доступность разыгрывается при попадании в новое состояние.
-
Доступность разыгрывается на каждом шаге ( = MDP).
Sorokin, Artyom Y., and Mikhail S. Burtsev. "Functional Systems Network Outperforms Q-learning in Stochastic Environment." (2016) [работа автора]
Эксперименты
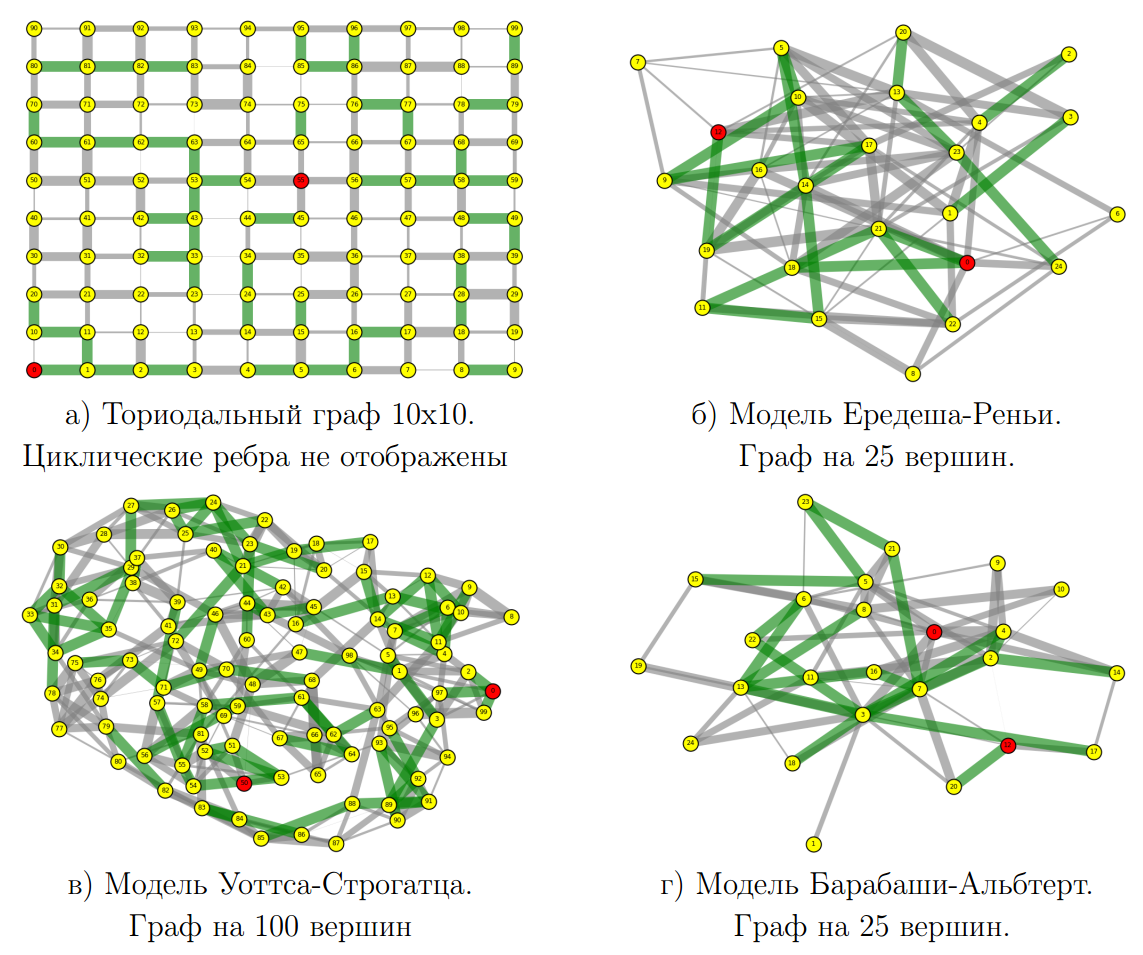
Было сгенерировано 120 графов среды различающихся:
-
Топологией (4 типа)
-
Размером (25, 100 и 400 состояний)
Всем ребрам в графах были сопоставлены вероятности в соответствии с описанным выше распределением
На каждом из графов и для всех видов стохастичности были запущены тестируемые алгоритмы:
-
Сеть Функциональных Систем + TD (наш вариант)
-
SARSA (с лучшими параметрами)
-
Q-обучение (с лучшими параметрами)
-
Алгоритм случайного поиска (качеству FSN без TD)
Sorokin, Artyom Y., and Mikhail S. Burtsev. "Functional Systems Network Outperforms Q-learning in Stochastic Environment." (2016) [работа автора]
Результаты 1/2
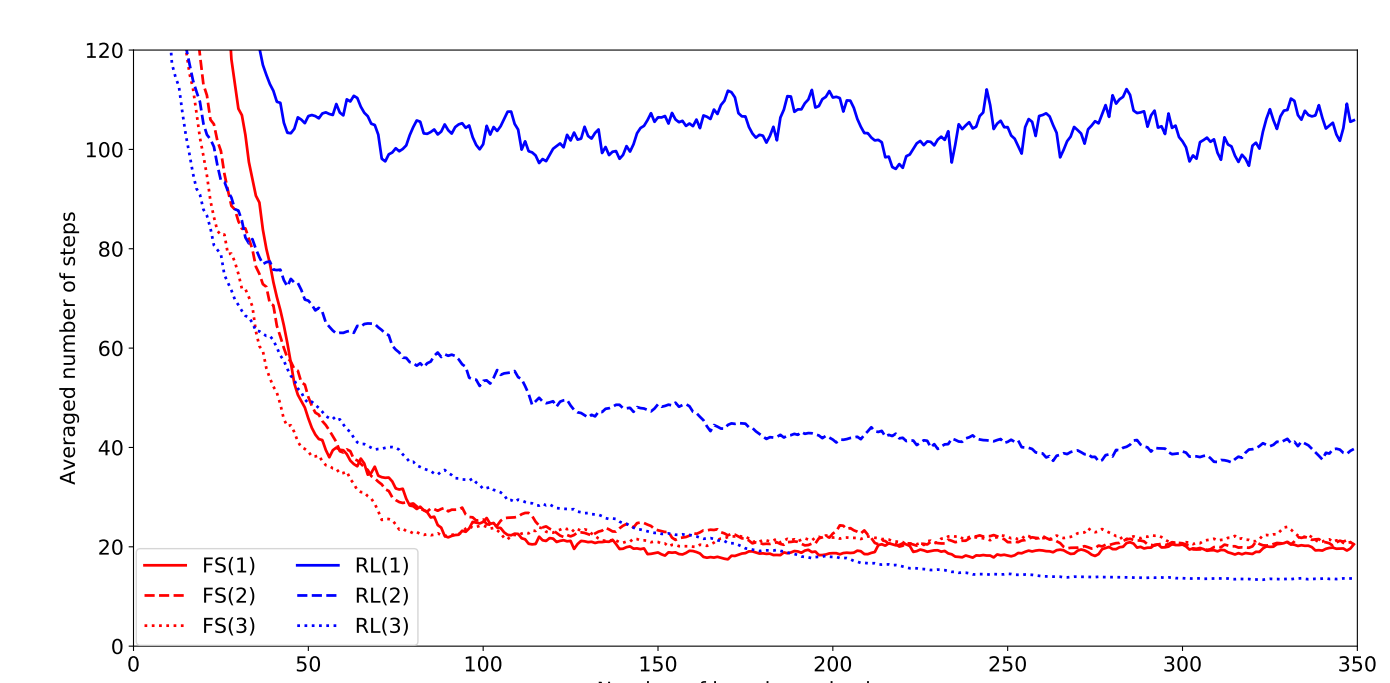
Кривые обучения агентов в средах на основе тороидального решетчатого графа (𝑁 = 100). Буквы FS обозначают результаты, полученные под управлением сети ФС, а RL — результаты алгоритма обучения с подкреплением. Цифры в скобках показывают для какого вида стохастичности среды получены эти результаты. Подобный рисунок наблюдается практически для любой другой конфигурации сред.
Sorokin, Artyom Y., and Mikhail S. Burtsev. "Functional Systems Network Outperforms Q-learning in Stochastic Environment." (2016) [работа автора]
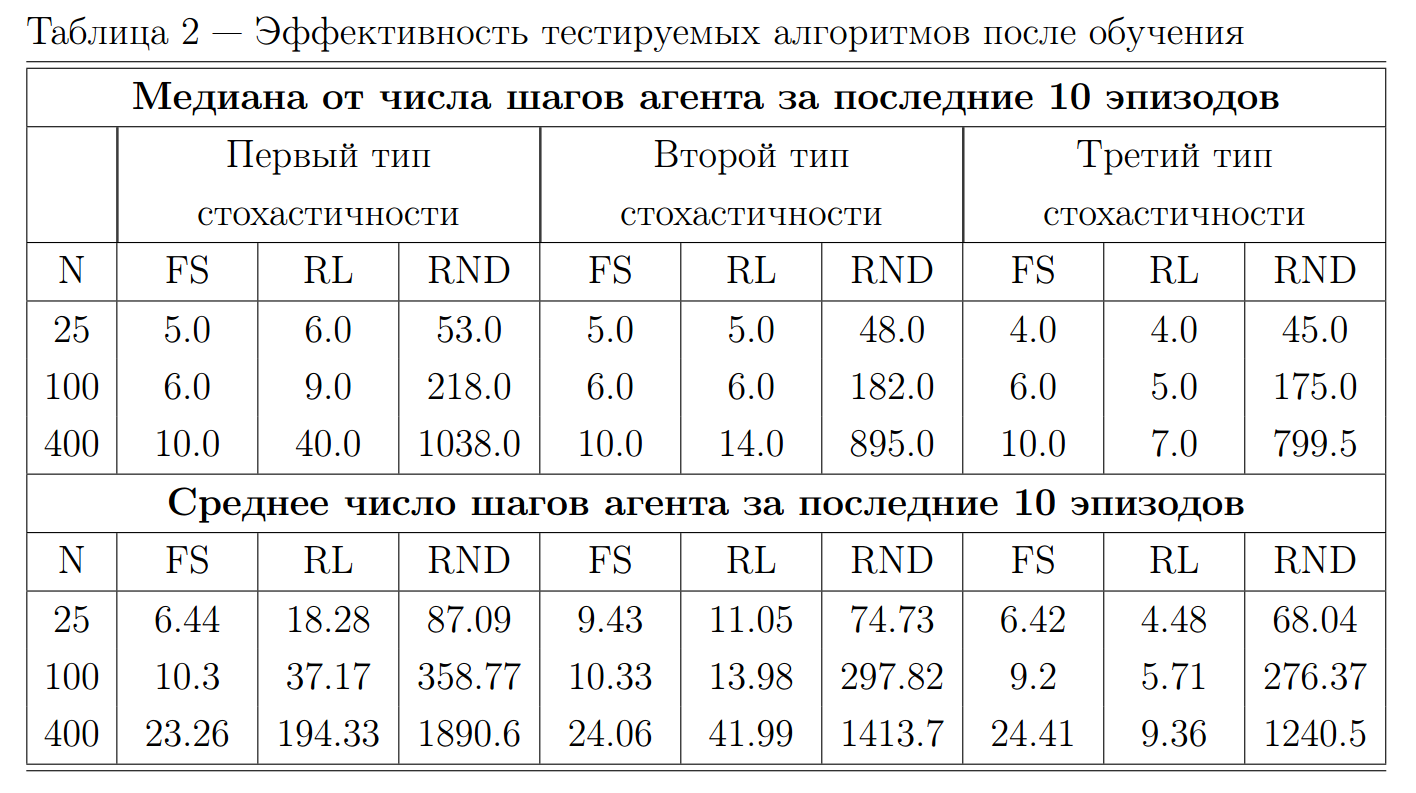
Результаты 2/2
Sorokin, Artyom Y., and Mikhail S. Burtsev. "Functional Systems Network Outperforms Q-learning in Stochastic Environment." (2016) [работа автора]
Упрощаем алгоритм FSN устраняя все отличия межу FSN и TD-обучением:
- Создание новых функциональных систем [Cразу есть все. ФС равна паре (s,a) в Q-обучении]
- Моделирование динамики Функциональных систем [Выбираем активную ФС как в Q-обучении]
- Правила обновления q [Эквивалентно Q-обучению]
- Накопление "усталости" ФС во время активности [Оставляем]
Итоговый Алгоритм MQ почти эквивалентен Q-обучению.
С с тем отличием, что для выбора действия вместо функции ценности 𝑄(𝑠,𝑎) используется:
где \(L_𝑖(S, A)\) - время последнего выполнения действия А в состоянии S, а \(𝑍_𝑖(𝑠_𝑡, 𝑎_𝑡)\) - это усталость (аналогично деактивации ФС) от выполнения действия:
Здесь \(\beta\) - пенальти за разовое использование действия, \(\lambda\) - коэффициент дисконтрирования.
MQ: Q-обучение с памятью
Sorokin, Artyom Y., and Mikhail S. Burtsev. "Functional Systems Network Outperforms Q-learning in Stochastic Environment." (2016) [работа автора]
Результаты: MQ vs FSN
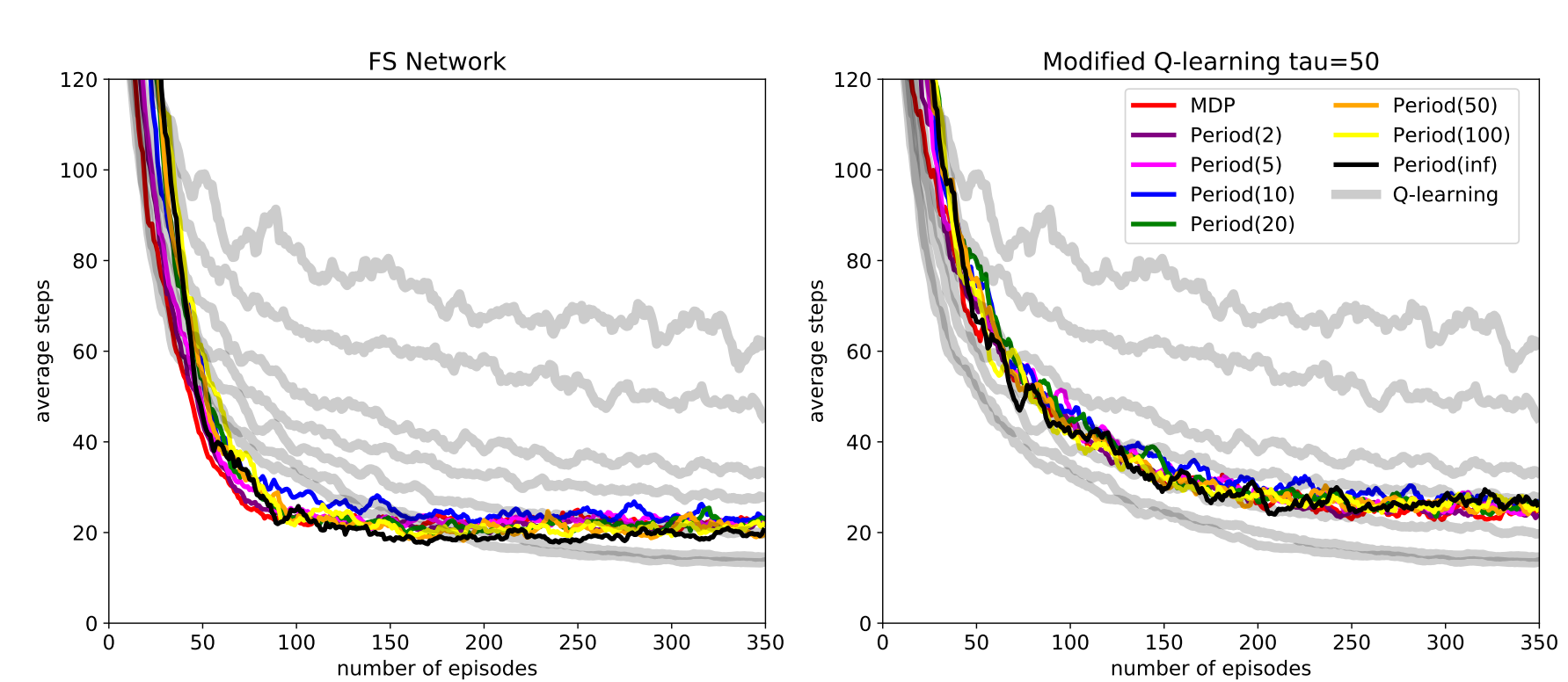
Period(T) - обозначает среду в которой состояние переходов обновляется каждые T шагов.
Выводы:
- FSN и MQ способны быстро адаптироваться к изменяющимся условиям в среде.
- Главный механизмом быстрой адаптации в FSN и MQ оказывается использование рабочей памяти (запоминание совершенных действий).
- FSN сложно применить к более сложным средам, так-как формирование новых FS это нерешенная задача, эквивалентная задаче Иерархического RL
- [Индексируется базами данных Scopus и Web of Science] A. Y. Sorokin, M. S. Burtsev., Functional Systems Network Outperforms Q-learning in Stochastic Environment // Procedia Computer Science. — 2016. — т. 88. — с. 397—402
- Сорокин, А. Ю. Алгоритм обучения сети функциональных систем в стохастической среде // ЛОМОНОСОВ-2016. —2016. — с. 134—136
Общая рабочая память для многозадачного и непрерывного обучения
Мотивация
Multi-Task Learning in RL:
-
Выучивание нескольких навыков одновременно [1,2].
-
Последовательное приобретение новых навыков [3,4].
Memory in RL:
-
Ускорение обучения и адаптации к изменениям [5,6,7]
-
Хранение важной информации на протяжении многих шагов [8,9, 10].
-
Rusu, Andrei A., et al. "Policy distillation." arXiv preprint arXiv:1511.06295 (2015).
-
Teh, Yee, et al. "Distral: Robust multitask reinforcement learning." Advances in Neural Information Processing Systems. 2017.
-
Schwarz, Jonathan, et al. "Progress & Compress: A scalable framework for continual learning." arXiv preprint arXiv:1805.06370(2018).
-
Shu, Tianmin, Richard Socher, et al. "Hierarchical and Interpretable Skill Acquisition in Multi-task Reinforcement Learning." (2017).
-
Wang, Jane X., et al. "Learning to reinforcement learn." arXiv preprint arXiv:1611.05763 (2016).
-
Peng, Xue Bin, et al. "Sim-to-real transfer of robotic control with dynamics randomization." arXiv preprint arXiv:1710.06537 (2017).
-
Pritzel, Alexander, et al. "Neural episodic control." arXiv preprint arXiv:1703.01988 (2017).
-
Graves, Alex, et al. "Hybrid computing using a neural network with dynamic external memory." Nature 538.7626 (2016): 471.
-
Parisotto, Emilio, and Ruslan Salakhutdinov. "Neural map: Structured memory for deep reinforcement learning." (2017).
-
Oh, Junhyuk, et al. "Control of memory, active perception, and action in minecraft." arXiv preprint arXiv:1605.09128 (2016).
изменение функции ценности MDP
изменение динамики MDP
+
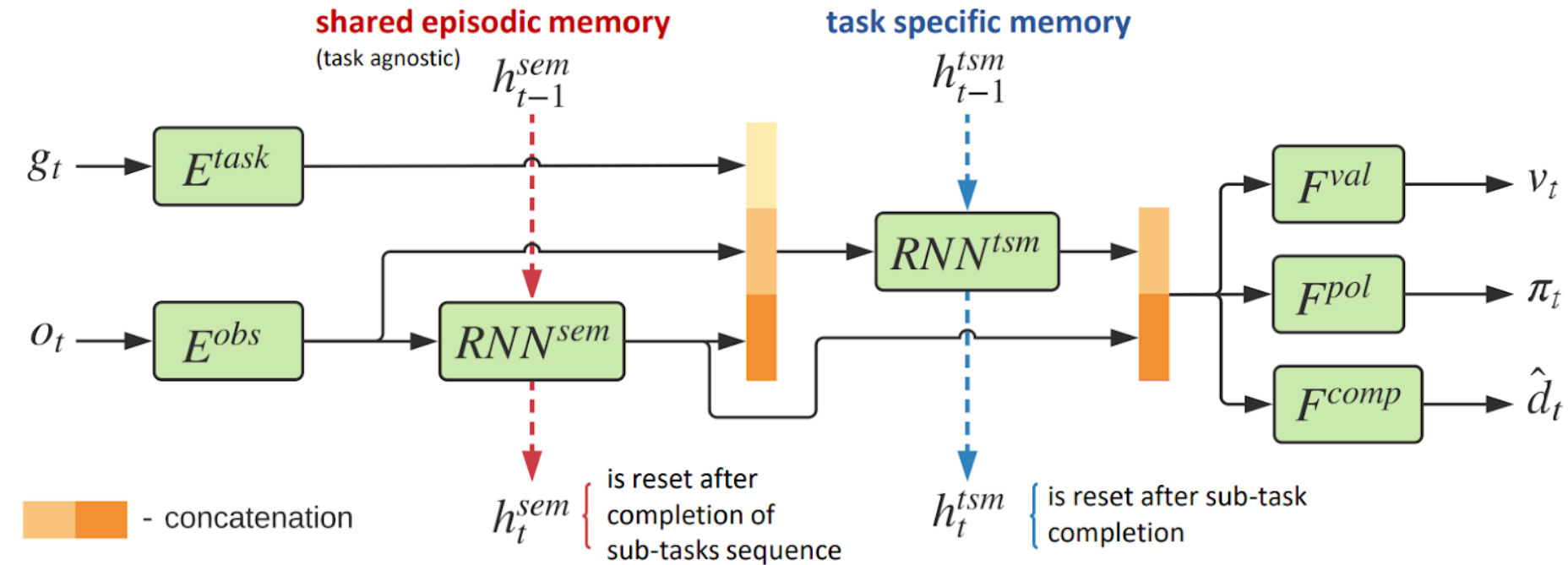
SEM: Архитектура задаче-независимой памяти
Проблема:
Агент обучается полностью перезаписывать состояние памяти при появлении новой задачи.
- A. Y. Sorokin, M. S. Burtsev., Episodic memory transfer for multi-task reinforcement learning // Biologically inspired cognitive architectures. — 2018. — т. 26. — с. 91—95.
- Sorokin, A. Y. Continual and Multi-task Reinforcement Learning With Shared Episodic Memory / A. Y. Sorokin, M. S. Burtsev // Task-Agnostic Reinforcement Learning Workshop at ICLR, New Orleans – 2019
f-LSTM: Факторизованный слой для tsm модуля
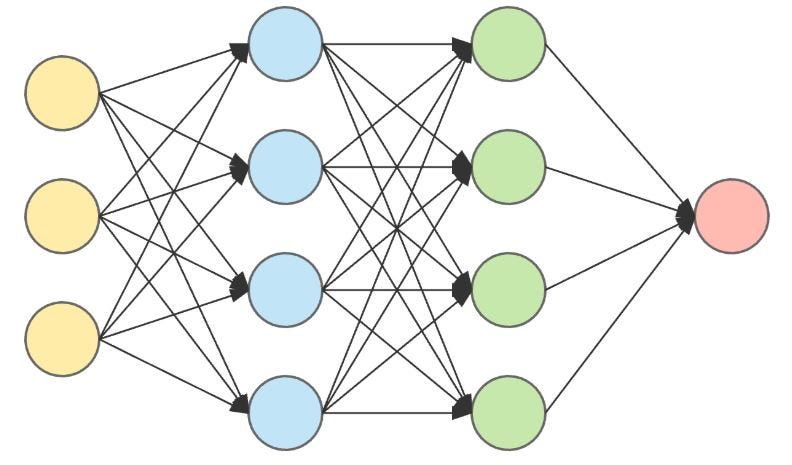
На каждом временном шаге LSTM слой вычисляет свой выходной вектор \(ℎ_𝑡\) и состояние ячейки \(c_t\), учитывая предыдущий вектор \(h_{t-1}\) , предыдущее состояние ячейки \(𝑐_{𝑡−1}\), и текущее наблюдение \(𝑥_𝑡\):
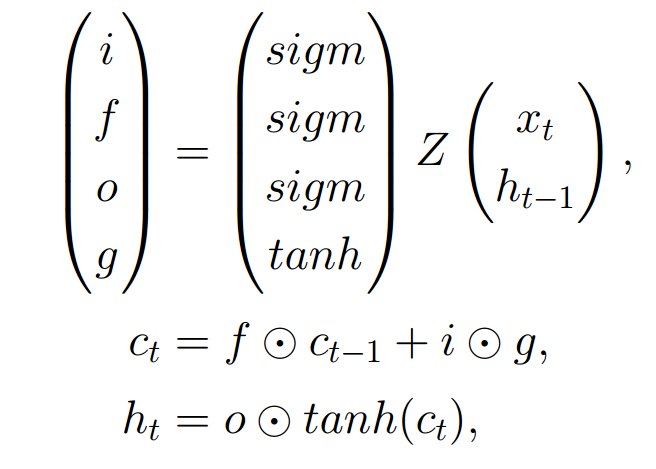
здесь \(Z\) — аффинное преобразование \(𝑍 = 𝑊 [𝑥_𝑡, ℎ_{𝑡−1}] + 𝑏\), а \((𝑖,𝑓,𝑜,𝑔)\) —«вентили» LSTM.
Для модуля RNN tsm веса LSTM \(W_{g_t}\) в задаче \(𝑔_𝑡\) вычисляются как произведение трех матриц:
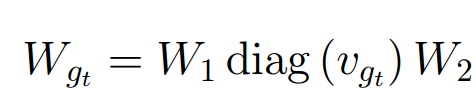
здесь \(𝑣_{𝑔_𝑡}\) — векторное представление текущей задачи \(𝑔_𝑡\). Матрицы \(𝑊_1\) и \(𝑊_2\) являются общими для всех задач, но для каждой задачи \(𝑔_𝑡\) обучается свой собственный вектор \(𝑣_{𝑔_𝑡}\)
.
- A. Y. Sorokin, M. S. Burtsev., Episodic memory transfer for multi-task reinforcement learning // Biologically inspired cognitive architectures. — 2018. — т. 26. — с. 91—95.
- Sorokin, A. Y. Continual and Multi-task Reinforcement Learning With Shared Episodic Memory / A. Y. Sorokin, M. S. Burtsev // Task-Agnostic Reinforcement Learning Workshop at ICLR, New Orleans – 2019
Эксперименты
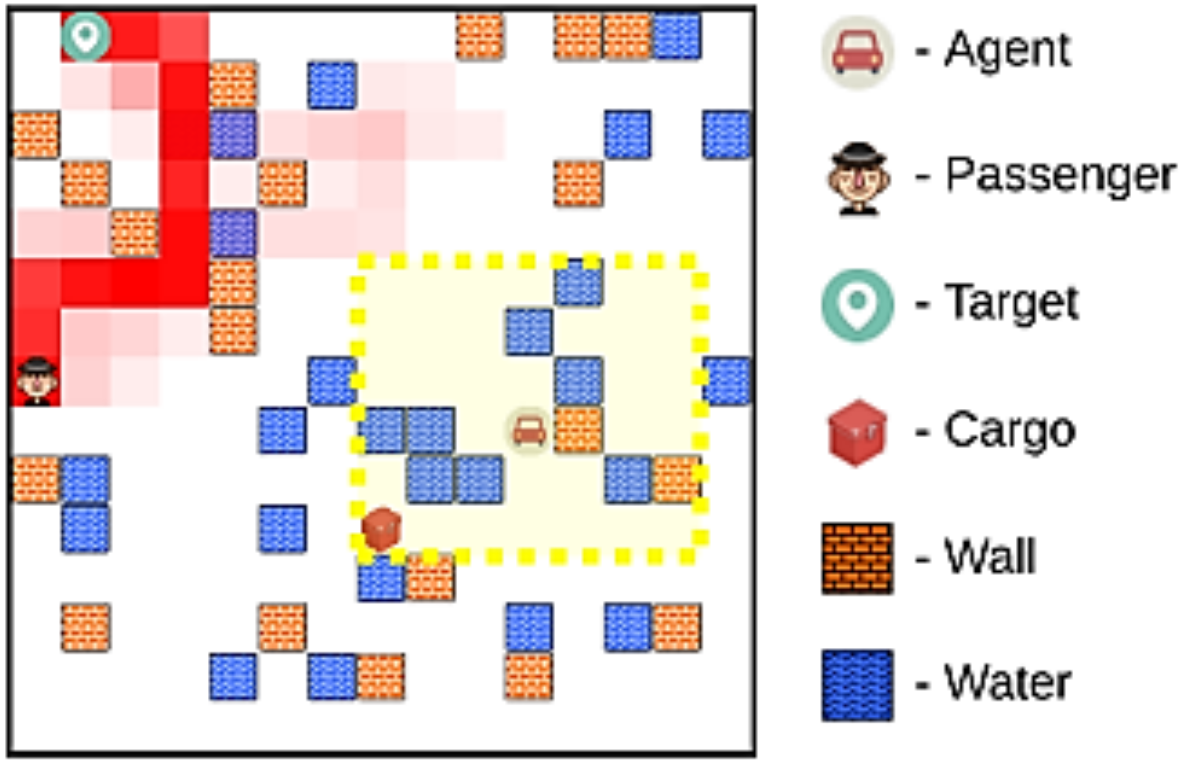
Задача Такси содержит 6 подзадачи:
- Reach (P) — добраться до пассажира по карте.
- Pickup (P) — посадить пассажира в пределах видимости в машину.
- Reach (D) — довезти пассажира до целевой локации.
- Dropoff (P) — высадить пассажира в целевой локации
- Pickup(C) — загрузить контейнер в машину.
- Deliver (C) — довезти и выгрузить контейнер в целевой локации
Детали:
- Расположение прудов и стен меняется каждые 2-3 подзадачи
- Агент видит только небольшую область 7 на 7 ячеек вокруг него
Результаты
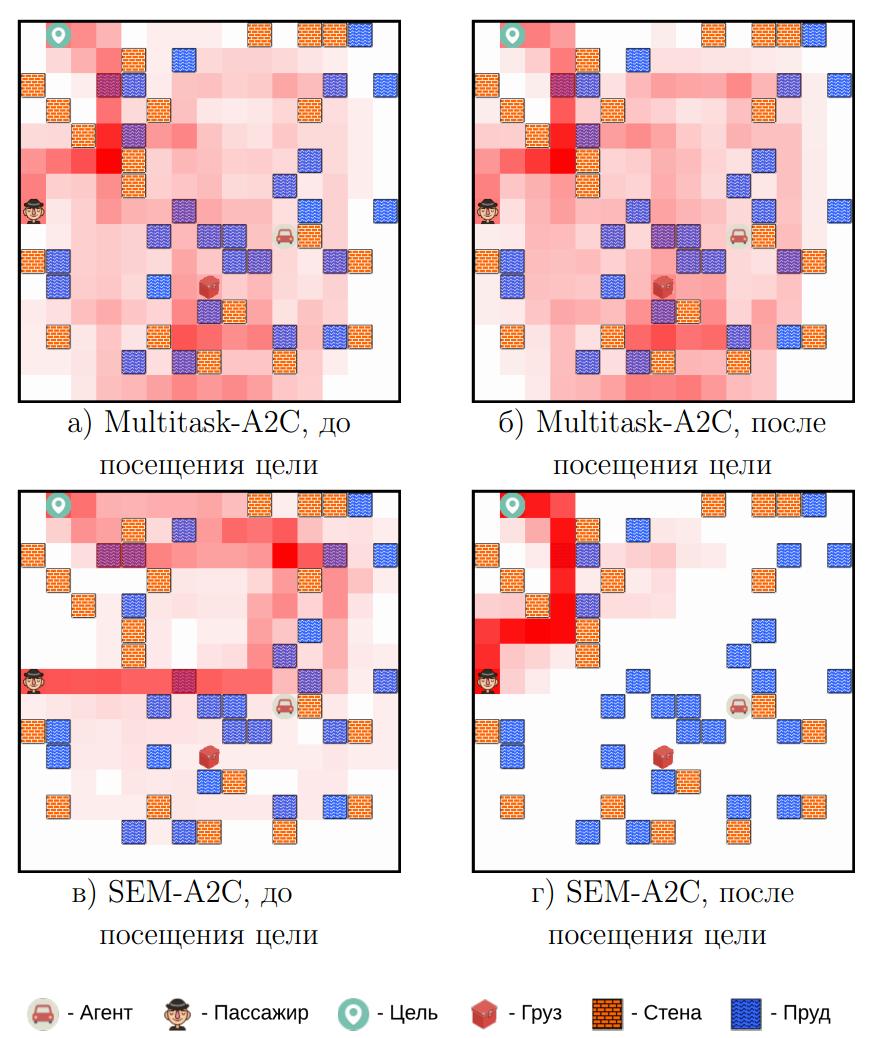
Частотная карта посещений различный локаций во время выполнения подзадачи Reach(D) для алгоритмов Multitask-A2C и SEM-A2C.
Multitask-A2C
Первая задача
SEM-A2C
Первая задача
Multitask-A2C
Вторая задача
SEM-A2C
Вторая задача
Результаты
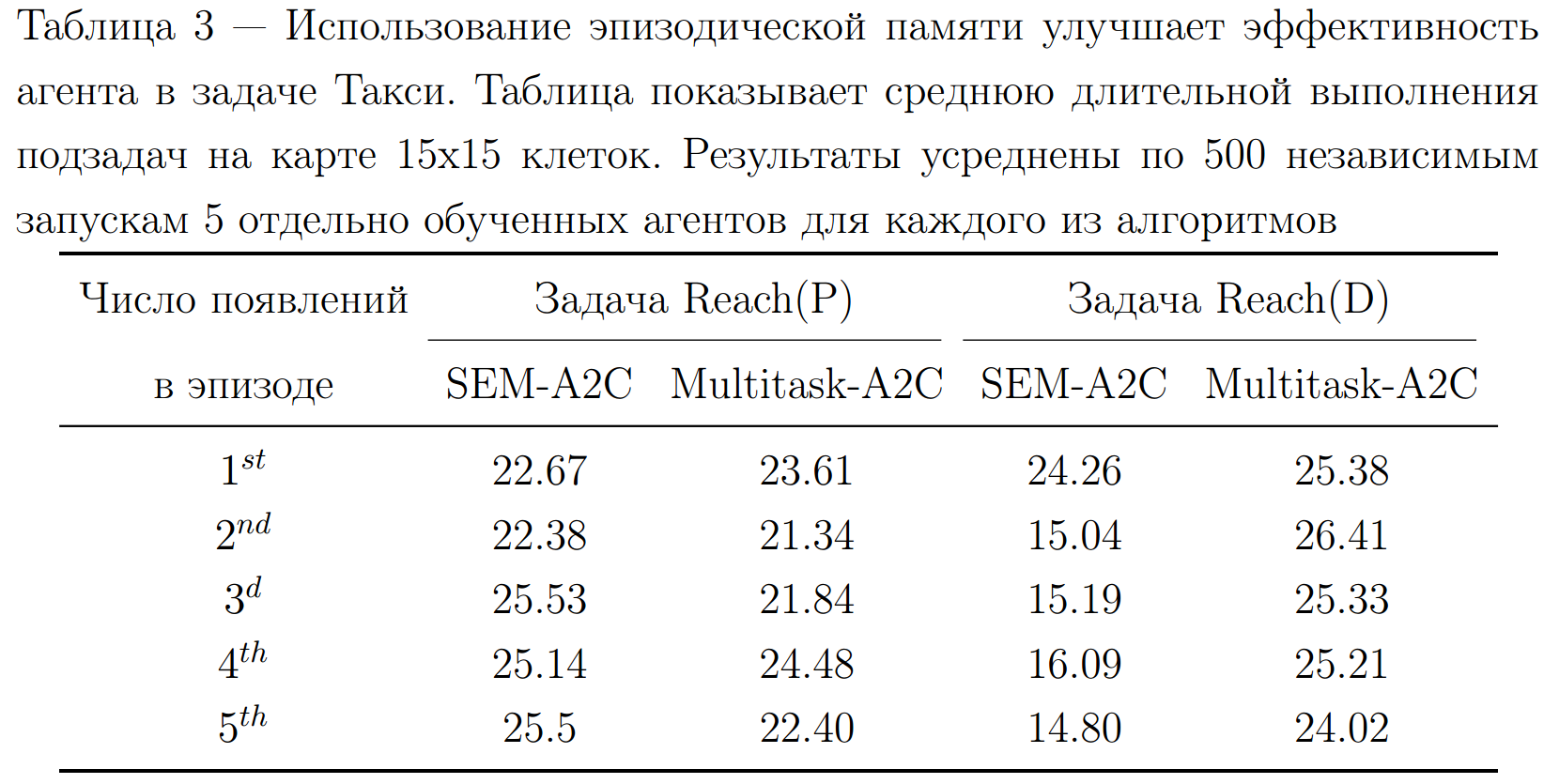
Text
Сравниваемые вариации:
- Multitask-A2C - алгоритм A2C для многозадачного обучения
- SEM-A2C - алгоритм A2C со всеми предложенными изменениям
Непрерывное обучение
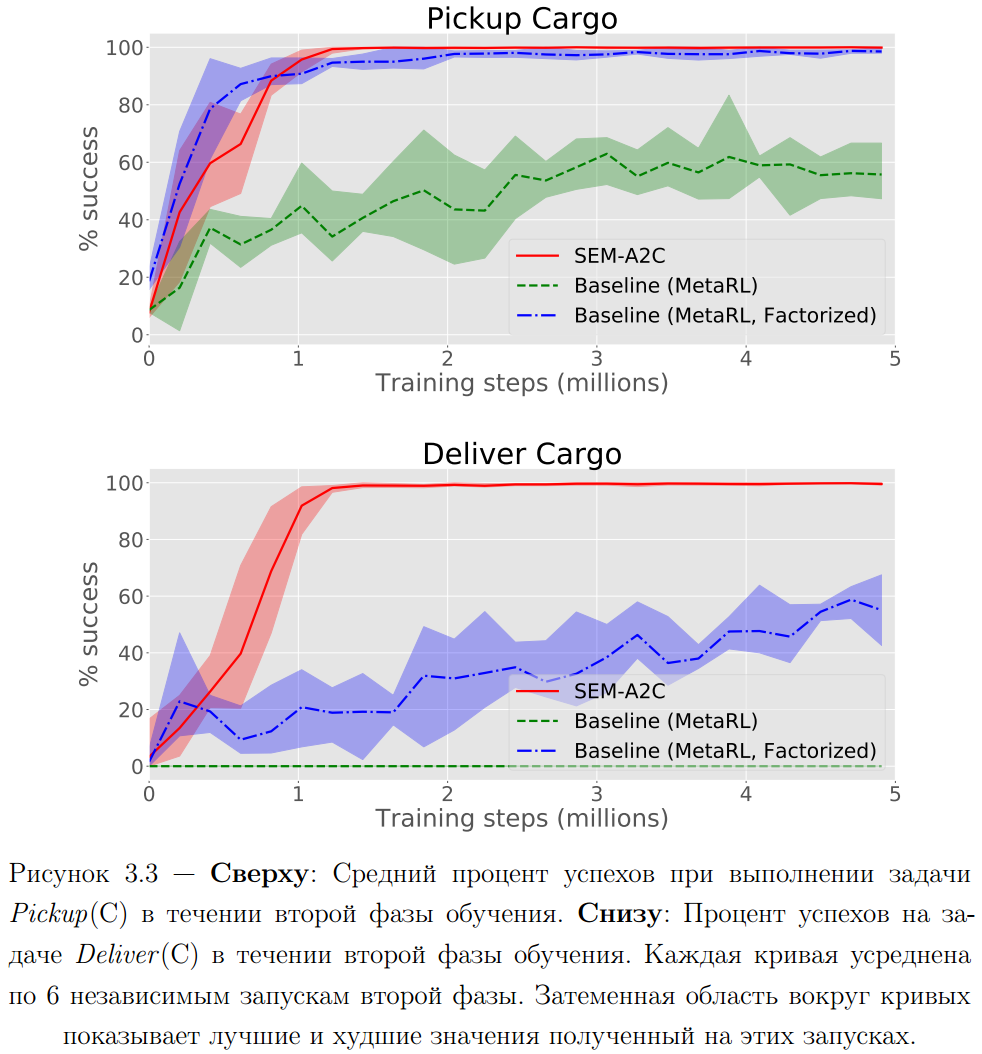
Сравниваемые вариации:
- SEM-A2C - предложенный метод
- Baseline (MetaRL) - SEM-A2C, без SEM архитектуры и f-LSTM
- Baseline (MetaRL, factorized) - SEM-A2C, без SEM архитектуры
Выводы:
- Проведенные эксперименты показывают что выделение задаче-независимой памяти улучшает качество стратегий многозадачного агента в протестированной быстро меняющейся среде.
- Разделение памяти на задаченезависимую и задачеспецифичную позволяет ускорить обучения агента на новых задачах.
- [Индексируется базой данных Scopus] A. Y. Sorokin, M. S. Burtsev., Episodic memory transfer for multi-task reinforcement learning // Biologically inspired cognitive architectures. — 2018. — т. 26. — с. 91—95.
- Sorokin, A. Y. Continual and Multi-task Reinforcement Learning With Shared Episodic Memory / A. Y. Sorokin, M. S. Burtsev // Task-Agnostic Reinforcement Learning Workshop at ICLR, New Orleans – 2019
Обучение долговременной памяти через предсказание событий высокой неопределенности
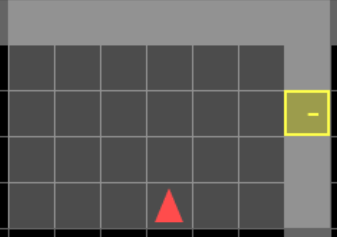
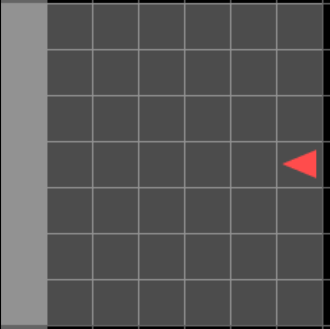
Мотивация. Пример временной зависимости

Подсказка: Хранит информацию о расположении награды
Награда
Подсказка:
- черная стена: награда находится с права
- красная стена: награда находится с лева
Агент

\(obs_{t=10}\)
\(obs_{t=12}\)
\(obs_{t=20}\)


\(act_{t=10}\)
\(act_{t=12}\)
\(act_{t=13}\)
Нам нужна эта информация
Для принятия решения в этот момент
. . .
. . .
Временная зависимость
Память: Рекурентные сети






\(act_{t=10}\)
\(act_{t=12}\)
\(act_{t=20}\)
\(h_{10}\)
. . .
. . .
\(h_9\)
\(h_{19}\)
. . .
. . .
. . .
Информация
Обратное распространение ошибки через время (TBPTT)
\(obs_{t=10}\)

\(obs_{t=12}\)
\(obs_{t=20}\)


\(act_{t=10}\)
\(act_{t=12}\)
\(act_{t=20}\)
\(h_{10}\)
. . .
. . .
\(h_9\)
\(h_{19}\)
. . .
. . .
. . .
- Пространственная сложность растет линейно с длинной TBPTT
- Проблема исчезающих градиентов (Vanishing Gradient Problem)
- Если временная зависимость не укладывается в TBPTT, она не будет выучена
Память: Окно внимания



. . .
. . .
Информация
Обратное распространение ошибки через время (TBPTT)
\(obs_{t=10}\)
\(obs_{t=12}\)
\(obs_{t=20}\)
. . .
. . .
- Для большинство Трансформеров, пространственная сложность растет квадратично с длинной окна внимания.
- Если временная зависимость не укладывается в окно внимания, она не будет выучена



\(act_{t=10}\)
\(act_{t=12}\)
\(act_{t=20}\)
Окно внимания
Проблема с RNN и Трансформерами
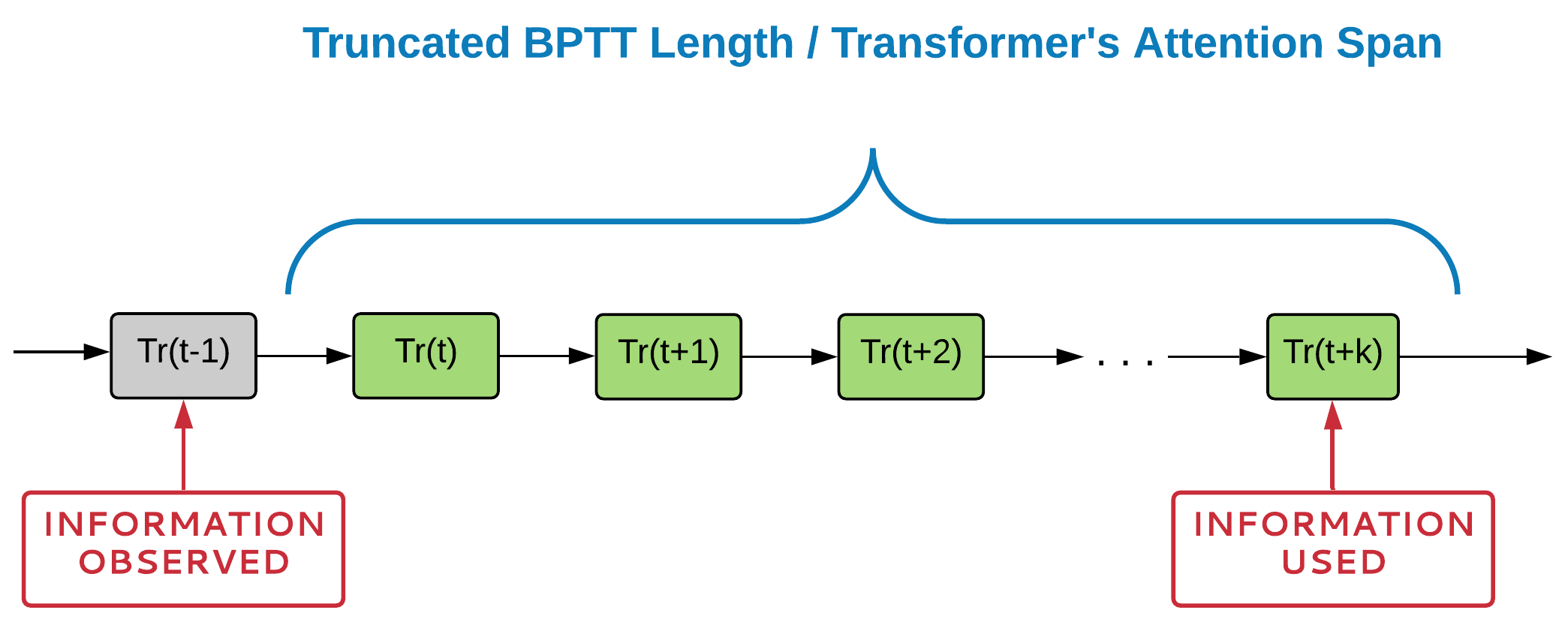
Проблема:
Нейросетевая память не сможет выучить временную зависимость, если не может обработать её целиком.
Временная зависимость должна полностью входить в TBPTT/Attention Span, чтобы нейросеть могла её использовать
Не известно между какими элементами последовательности может быть временная зависимость.
? ? ? ? ?
Что если попробовать найти временную зависимость локально?
временная зависимость между элементами t-1 и t+k
Проблема с RNN и Трансформерами

Пространственная сложность:
- Для RNN: сложность линейна от длинны раскрутки BPTT[1].
- Для Трансформеров: квадратична [2-3] в большинстве случаев [4].
Временная зависимость должна полностью входить в TBPTT/Attention Span, чтобы нейросеть могла её использовать
Не известно между какими элементами последовательности может быть временная зависимость.
? ? ? ? ?
Что если попробовать найти временную зависимость локально?
временная зависимость между элементами t-1 и t+k
- Yu, et al. "A review of recurrent neural networks: LSTM cells and network architectures." Neural computation 31, no. 7 (2019): 1235-1270.
- Vaswani, et al. "Attention is all you need." Advances in neural information processing systems 30 (2017).
- Brown, et al. (2020). Language models are few-shot learners. Advances in neural information processing systems, 33, 1877-1901.
- Zaheer, et al. (2020). Big bird: Transformers for longer sequences. Advances in Neural Information Processing Systems, 33, 17283-17297.
Проблема с RNN и Трансформерами

Temporal dependency between t-1 and t+k
- Yu, et al. "A review of recurrent neural networks: LSTM cells and network architectures." Neural computation 31, no. 7 (2019): 1235-1270.
- Vaswani, et al. "Attention is all you need." Advances in neural information processing systems 30 (2017).
- Brown, et al. (2020). Language models are few-shot learners. Advances in neural information processing systems, 33, 1877-1901.
- Zaheer, et al. (2020). Big bird: Transformers for longer sequences. Advances in Neural Information Processing Systems, 33, 17283-17297.
RNN can learn to store relevant information only if temporal dependency fit into TBPTT rollout
MemUP: Важность временной зависимости
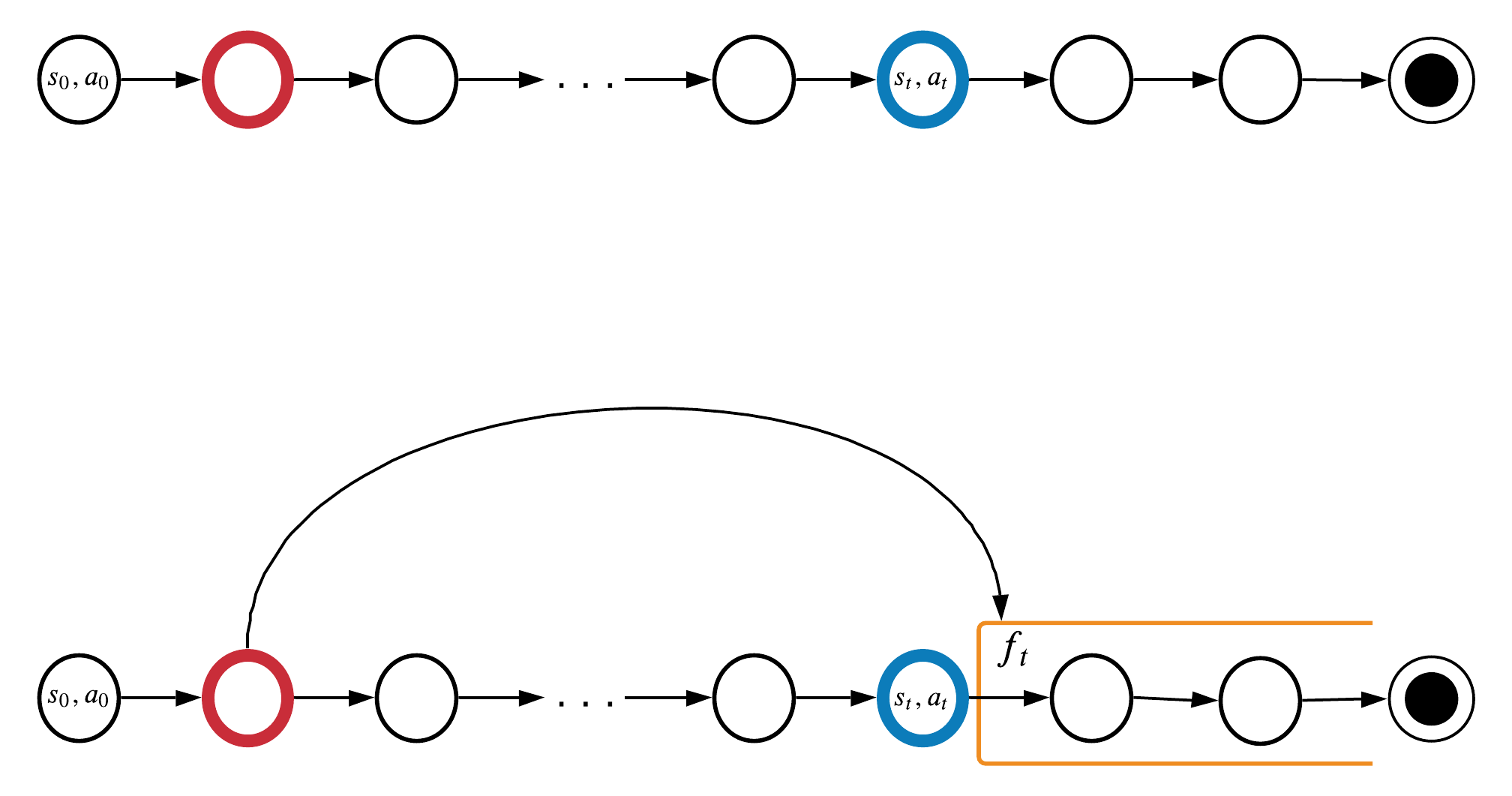
Информация с красного шага полезна на синем шаге, тогда:
Оценим силу временной зависимости (насколько важно помнить \(x_k\)):

\(y_t\) может быть Q-функцией, \(o_{t+1}\), \(r_{t+1}\), и тд.
домножили на \(P(x_{k}| x_t)\)
MemUP: Целевая функция
Обучаем модель максимизировать взаимную информацию между состоянием памяти и всеми будущими шагами:
Идея:
Вместо того, чтобы оптимизировать сумму полностью, выберем шаги когда обучение памяти может дать наибольший вклад в предсказание будущего!
Нужно обрабатывать всю последовательность для обновления \(m_t\)
Принцип Локальности:
Чем дальше во времени отдалены события тем меньше между ними временных зависимостей.
- A. Y. Sorokin, L. P. Pugachev, M. S. Burtsev., Train Long-Term Memory by Predicting High Uncertainty Events // Proceedings of MIPT. — 2021. — т. 13. — в. 4(52) — с. 39—55.
- *[Принята, Готовится к публикации] Sorokin, A., Buzun, N., Pugachev, L. and Burtsev, M., 2022. Explain My Surprise: Learning Efficient Long-Term Memory by Predicting Uncertain Outcomes. Advances in Neural Information Processing Systems 35 (NeurIPS 2022)
Потенциальная полезность памяти:
насколько важна память для предсказания \(y_t\)
Неопределенность \(y_t\) без памяти
Неопределенность \(y_t\) с идеальной памятью
Представим, что \(m^*_t\) это идеальное состояние памяти для каждого шага t!
Метрика важности памяти: Условная взаимная информация!
Локальный поиск окончания временной зависимости
Определяет конец временной зависимости
Предположим, что \(H(y_t|m^*_t, x_t) = c\) , тогда:
Для выбора шагов с наибольшим вкладом памяти в предсказания, достаточно оценивать локальную энтропию \(H(y_t|x_t)\)!
шанс выбрать шаг t
Entropy of \(y_t\) given only local information
Entropy of \(y_t\) given all available information
Imagine we have access to a perfect memory \(m^{∗}_{t}\) that stores all information from the previous inputs \(x_0, ..., x_{t}\)
How important to remember past information for predicting \(y_t\):
Локальный поиск окончания временной зависимости
Strength of temporal dependencies ending at t
If we assume that \(H(y_t|m^*_t, x_t) = c\) , then:
Valuable information from the past could make the biggest contribution at steps with the highest values of \(I(y_t; m^*_t|x_t)\)
MemUP для рекуррентных сетей
Для обучения памяти используется 3 модуля:
- Детектор Неопределенности - оценивает неопределенность \(H(y_i|x_i)\)
- Модуль памяти - обучается хранить важную информацию
- Предиктор - используется для минимизации \(H(y_i| m_t, x_i)\)
Обучение разделено на два этапа:
- Предобучение Памяти - Обучение памяти без обновления стратегии.
- Обучение Стратегии - Обучение PPO агента, который использует предобученный модуль памяти.
В RL экспериментах: \(y_t = \sum_k \gamma^k r_{t+k}\)
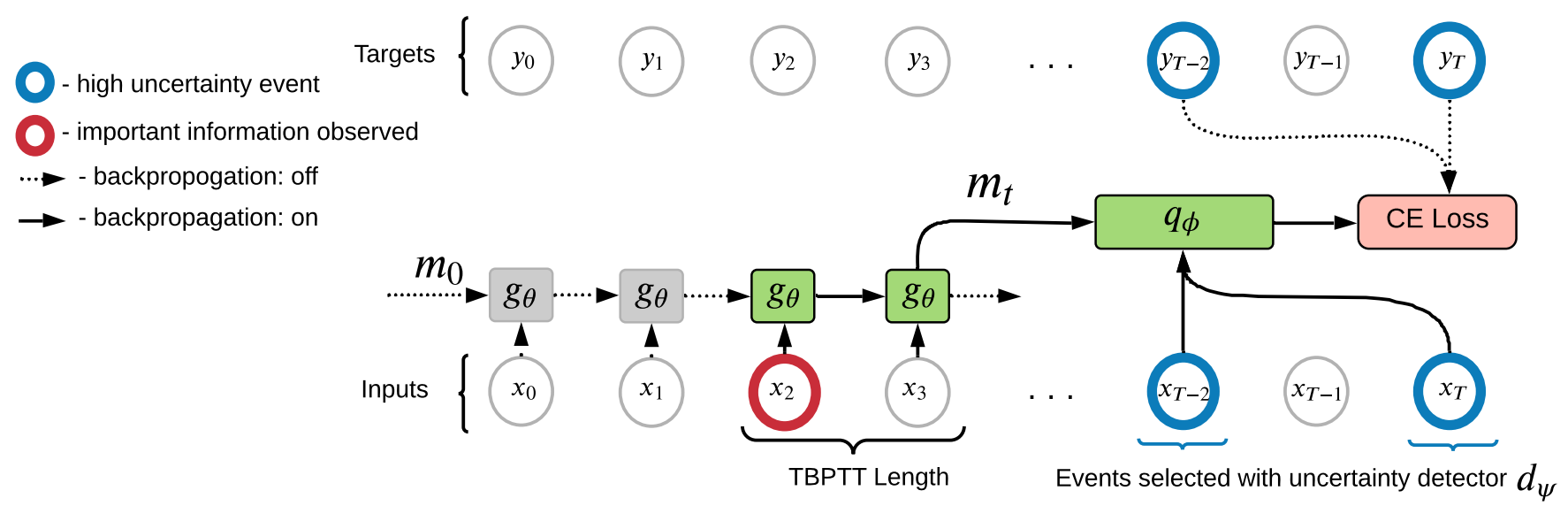
Общая схема обучения
- Учим детектор \(d_{\psi}\) предсказывать \(y_t\) на каждом шаге на основе \(x_t\). Важно уметь давать оценку неопределенности предсказаний детектора \(\hat{H}_{\psi}(y_t| x_t)\).
- Учим память \(g_{\theta}\) для каждого шага t предсказывать будущие события \(U_t\), где память может быть наиболее важна:
\(U_t\) это множество шагов, которые выбраны на основе оценки детектора \(\hat{H}_{\psi}(y_i| x_i)\); \(|U| \ll T\).
При обучении памяти мы используем информацию из будущего, которой не будем владеть во время её применения, поэтому нужна отдельная сетка для обьединения шагов k и t: предиктор
Суррогатная функция потерь
Прямая оптимизация взаимной информации может быть вычислительно сложной задачей.
Barber, Agakov (2004) доказали нижнюю оценку которую мы можем использовать для нашего случая. Для начала, введем нейросеть \(q_{\phi}\), которую назовем предиктор.
Тогда:
Т.к.
, значит
получается:
от нас не зависит
NLL loss, минимизируем её и разом обновляем \(\theta\) и \(\phi\)
хотели максимизировать
- Agakov, D. B. F. (2004). The IM algorithm: a variational approach to information maximization. Advances in neural information processing systems, 16(320), 201.
- *[Принята, Готовится к публикации] Sorokin, A., Buzun, N., Pugachev, L. and Burtsev, M., 2022. Explain My Surprise: Learning Efficient Long-Term Memory by Predicting Uncertain Outcomes. Advances in Neural Information Processing Systems 35 (NeurIPS 2022)
- Получить оценку неопределенности исхода для каждого шага последовательности.
MemUP для рекуррентных сетей
- Estimate entropy (average surprise) of the outcome for each step in the sequence.
- Select K events (steps) with probability proportional to entropy estimates.

MemUP для рекуррентных сетей
- Первый проход: Получить оценку неопределенности исхода для каждого шага последовательности.
- Первый проход: Выбрать K шагов последовательности пропорционально оценке неопределенности.
- Второй проход: Обучить модуль памяти предсказывать исходы для выбранных шагов последовательности.
MemUP для рекуррентных сетей
- A. Y. Sorokin, L. P. Pugachev, M. S. Burtsev., Train Long-Term Memory by Predicting High Uncertainty Events // Proceedings of MIPT. — 2021. — т. 13. — в. 4(52) — с. 39—55.
- *[Принята, Готовится к публикации] Sorokin, A., Buzun, N., Pugachev, L. and Burtsev, M., 2022. Explain My Surprise: Learning Efficient Long-Term Memory by Predicting Uncertain Outcomes. Advances in Neural Information Processing Systems 35 (NeurIPS 2022)
Memory via Uncertainty Prediction:
- Estimate entropy (average surprise) of the outcome for each step in the sequence.
- Select K events (steps) with probability proportional to entropy estimates.
- Train the memory module to predict outcomes for selected sequence steps.
MemUP для рекуррентных сетей

- A. Y. Sorokin, L. P. Pugachev, M. S. Burtsev., Train Long-Term Memory by Predicting High Uncertainty Events // Proceedings of MIPT. — 2021. — т. 13. — в. 4(52) — с. 39—55.
- *[Принята, Готовится к публикации] Sorokin, A., Buzun, N., Pugachev, L. and Burtsev, M., 2022. Explain My Surprise: Learning Efficient Long-Term Memory by Predicting Uncertain Outcomes. Advances in Neural Information Processing Systems 35 (NeurIPS 2022)
MemUP для рекуррентных сетей
- Первый проход: Получить оценку неопределенности исхода для каждого шага последовательности.
- Первый проход: Выбрать K шагов последовательности пропорционально оценке неопределенности.
- Второй проход: Обучить модуль памяти предсказывать исходы для выбранных шагов последовательности.
MemUP для рекуррентных сетей

- A. Y. Sorokin, L. P. Pugachev, M. S. Burtsev., Train Long-Term Memory by Predicting High Uncertainty Events // Proceedings of MIPT. — 2021. — т. 13. — в. 4(52) — с. 39—55.
- *[Принята, Готовится к публикации] Sorokin, A., Buzun, N., Pugachev, L. and Burtsev, M., 2022. Explain My Surprise: Learning Efficient Long-Term Memory by Predicting Uncertain Outcomes. Advances in Neural Information Processing Systems 35 (NeurIPS 2022)
MemUP: пространственная сложность

В SL экспериментах MemUP+LSTM сравнивался со следующими подходами:
- LSTM [1]
- SRNN [2]
- Transformer [3]
В RL экспериментах MemUP+LSTM+PPO сравнивался со следующими подходами:
- PPO-LSTM [4]
- IMPALA-ST [5]
- AMRL [6]
Эксперименты: Сравнение
Для всех экспериментов использовалось несколько версий одного и того же подхода.
Различие заключается в том насколько в ограничения на длину TBPTT/Attention Span'а при обработки последовательности.
- Greff, et al. "LSTM: A search space odyssey." IEEE transactions on neural networks and learning systems 28, no. 10 (2016): 2222-2232.
- Biswas, S., & Gall, J. Structural recurrent neural network (SRNN) for group activity analysis. In 2018 IEEE Winter Conference on Applications of Computer Vision (WACV) . IEEE.
- Vaswani, et al. (2017). Attention is all you need. Advances in neural information processing systems, 30.
- Schulman, et al. (2017). Proximal policy optimization algorithms. arXiv preprint arXiv:1707.06347.
- Parisotto, et al. (2020, November). Stabilizing transformers for reinforcement learning. In International conference on machine learning (pp. 7487-7498). PMLR.
- Beck, et al. (2019, September). Amrl: aggregated memory for reinforcement learning. In International Conference on Learning Representations.
- A. Y. Sorokin, L. P. Pugachev, M. S. Burtsev., Train Long-Term Memory by Predicting High Uncertainty Events // Proceedings of MIPT. — 2021. — т. 13. — в. 4(52) — с. 39—55.
- *[Принята, Готовится к публикации] Sorokin, A., Buzun, N., Pugachev, L. and Burtsev, M., 2022. Explain My Surprise: Learning Efficient Long-Term Memory by Predicting Uncertain Outcomes. Advances in Neural Information Processing Systems 35 (NeurIPS 2022)
Алгоритмические задачи:
- Copy Task - запомнить и повторить последовательность после задержки
- Scattered Copy Task - усложнение первой задачи
- Add Task - запомнить слагаемые и вывести сумму. Слагаемые и ответ могут располагаться в произвольных частях последовательности.
Классификация изображений:
- Sequential Permuted MNIST (pMNIST 784) - изображение разворачивается в последовательность из 784 пикселей. Ко всем изображения применяется одинаковая случайная перестановка. Задача определить класс изображения.
- pMNIST 3136 - аналогична предыдущей задаче, но используются изображения большего размера.
Эксперименты: обучение с учителем
- *[Принята, Готовится к публикации] Sorokin, A., Buzun, N., Pugachev, L. and Burtsev, M., 2022. Explain My Surprise: Learning Efficient Long-Term Memory by Predicting Uncertain Outcomes. Advances in Neural Information Processing Systems 35 (NeurIPS 2022)
Эксперименты: обучение с учителем
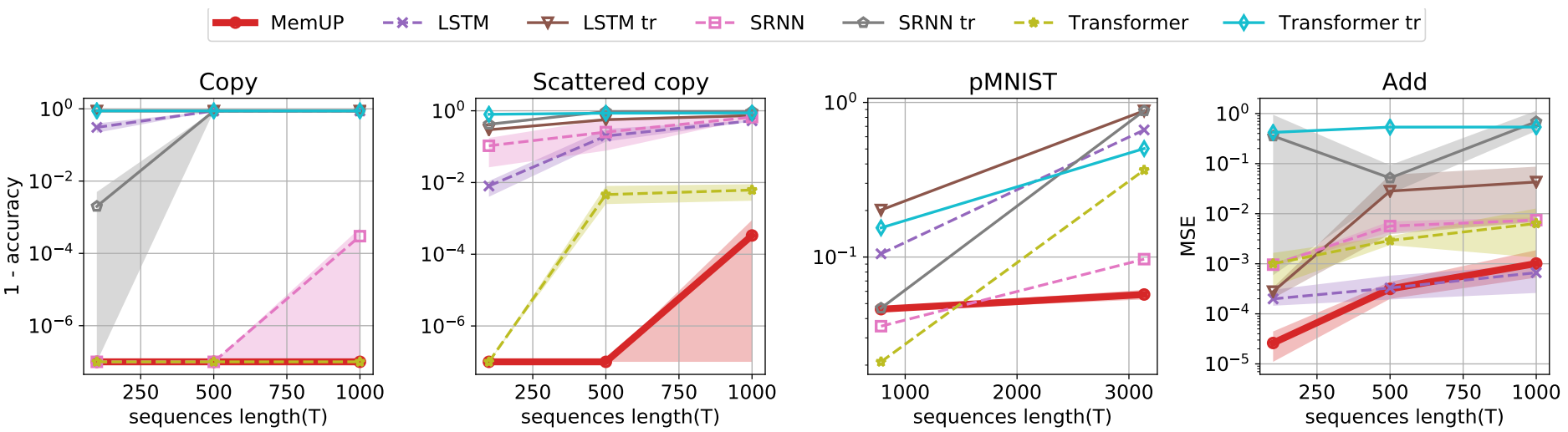
Результаты на задачах обучения с учителем. По оси X отмечается длина последовательности на которых обучались модели. Ось Y соответствует результатам модели в конце обучения. Метрики: Inverted Accuracy (1. - Accuracy) в задачах Copy, Scattered copy и pMNIST, MSE в задаче Add. Все кривые усреднены по 3 запускам.
- *[Принята, Готовится к публикации] Sorokin, A., Buzun, N., Pugachev, L. and Burtsev, M., 2022. Explain My Surprise: Learning Efficient Long-Term Memory by Predicting Uncertain Outcomes. Advances in Neural Information Processing Systems 35 (NeurIPS 2022)
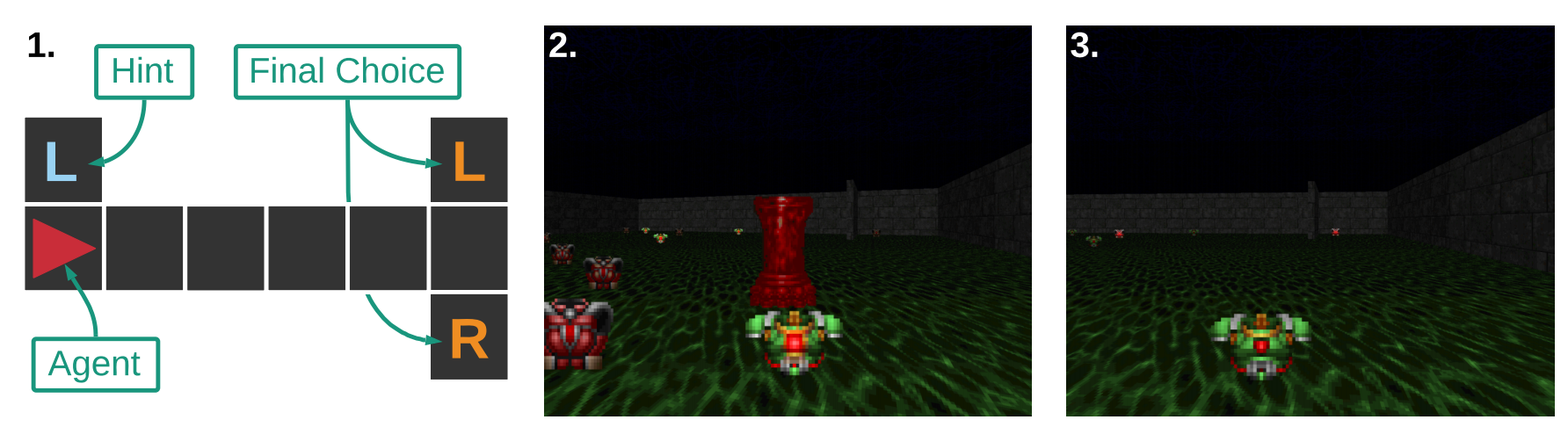
Среды для для тестирования долгосрочных временных зависимостей:
- T-maze - лабиринт в котором агент должен дойти до Т-образного перекрестка и выбрать один из поворотов (L или R). Подсказка о том, какой поворот верный предоставляется в самом начале. На каждом шаге агент может видеть только ту колонку клеток, в которой находится сам.
- Vizdoom-Two-Colors - агент находится в комнате и постоянно теряет «здоровье». Чтобы пополнять здоровье агенту нужно собирать жилеты такого же цвета, что и колона. Эпизод длится 1050 шагов, но после 45 шага колонна пропадает
Эксперименты: обучение с подкреплением
Эксперименты: T-maze
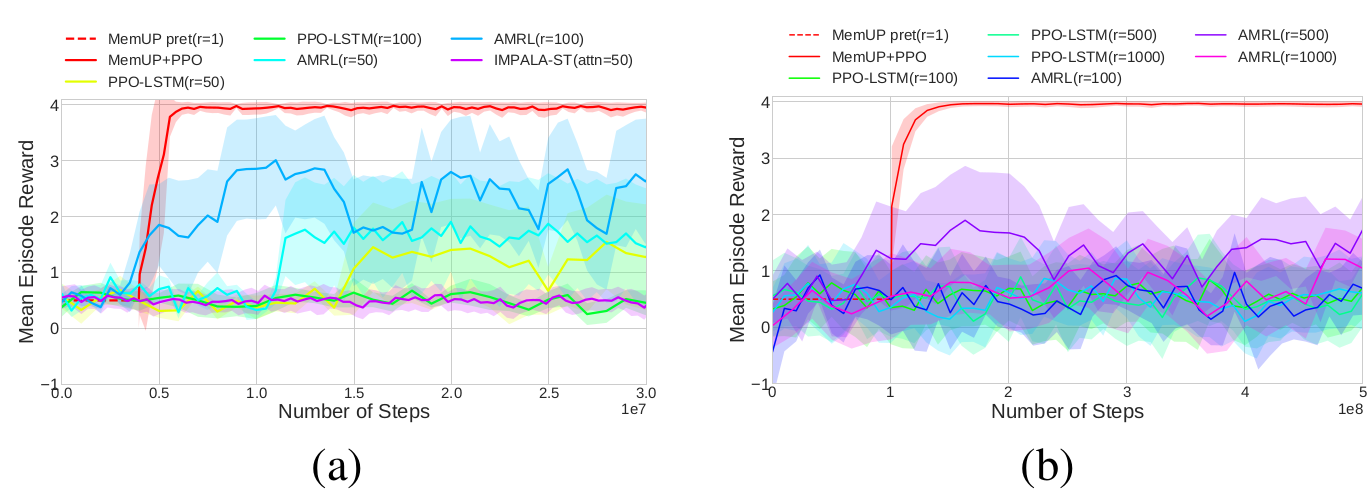
a) Кривые обучения для алгоритма MemUP и всех альтернатив в среде T-Maze-LNR-100. Все кривые являются усреднением по трем запускам с различным зерном генератора псевдослучайных чисел. Фаза предобучения памяти агента MemUP обозначена пунктирной линией.
b) Кривые обучения для среды T-Maze-LNR-1000. Кривые усреднены по трем запускам.
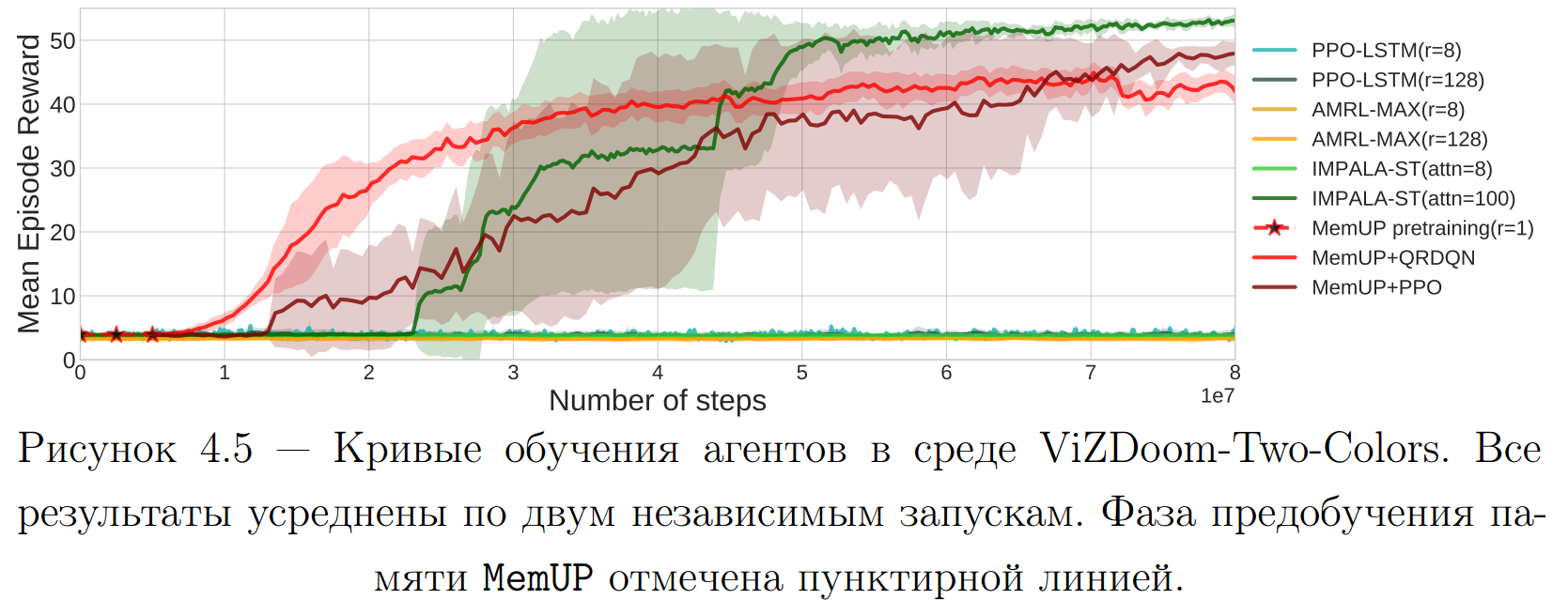
Эксперименты: ViZDoom-Two-Colors
- A. Y. Sorokin, L. P. Pugachev, M. S. Burtsev., Train Long-Term Memory by Predicting High Uncertainty Events // Proceedings of MIPT. — 2021. — т. 13. — в. 4(52) — с. 39—55.
- *[Принята, Готовится к публикации] Sorokin, A., Buzun, N., Pugachev, L. and Burtsev, M., 2022. Explain My Surprise: Learning Efficient Long-Term Memory by Predicting Uncertain Outcomes. Advances in Neural Information Processing Systems 35 (NeurIPS 2022)
Выводы:
- MemUP позволяет выучивать длинные временные зависимости, даже если вся временная зависимость не может быть обработана за один шаг градиентного спуска.
- Все альтернативные решения, демонстрирующие сопоставимые по качеству результаты требуют обработки временных зависимостей целиком.
- В большинстве случаев MemUP превосходит альтернативы, которые имели возможность работать с полными последовательностями.
- [Индексируется базой данных RSCI] A. Y. Sorokin, L. P. Pugachev, M. S. Burtsev., Train Long-Term Memory by Predicting High Uncertainty Events // Proceedings of MIPT. — 2021. — т. 13. — в. 4(52) — с. 39—55.
- *[Принята, Готовится к публикации] Sorokin, A., Buzun, N., Pugachev, L. and Burtsev, M., 2022. Explain My Surprise: Learning Efficient Long-Term Memory by Predicting Uncertain Outcomes. Advances in Neural Information Processing Systems 35 (NeurIPS 2022)
Основные результаты
-
Предложен метод объединения Сети Функциональных Систем (FSN) и обучения с подкреплением. Полученный метод эффективно обучается в графовых средах с меняющейся динамикой среды.
-
Численные исследования показали, что основное преимущество FSN по сравнению с классическими алгоритмами обучения с подкреплением, связано с использованием механизма рабочей памяти.
-
Предложена архитектура SEM, позволяющая разделять задаче-специфичную и общую рабочую память агента в многозадачном обучении с подкреплением.
- Продемонстрировано, что обособление задаче-независимой памяти (SEM) улучает эффективность многозадачного агента и ускоряет обучения на новых задачах в рандомизированной частично обозреваемой версии задачи "Такси".
-
Разработан метод обучения памяти MemUP, позволяющий выучивать временные зависимости даже если они не могут быть обработаны за один шаг градиентного спуска.
-
На задачах Add и pMNIST показано, что MemUP превосходит все рассмотренные альтернативные методы. На задаче Scattered Copy и в средах T-maze, Vizdoom-Two-Colors MemUP превосходит альтернативные методы на основе рекуррентных сетей.
Положения выносимые на защиту
-
Предложенная комбинация сети функциональных систем и обучения с подкреплением позволяет новой архитектуре быстро адаптироваться к изменениям в графовых средах.
-
Предложенный метод обучения задаченезависимой памяти в многозадачном обучении с подкреплением позволяет улучшить эффективность многозадачного агента, а так же скорость его адаптации к новым задачам.
-
Разработанный алгоритм обучения долговременной памяти за счет предсказания событий высокой неопределенности позволяет выучивать длинные временные зависимости, рассматривая во время градиентного шага лишь малое число элементов временной последовательности.
Публикации и доклады по результатам работы:
- [Доклад] Сорокин, А. Ю. Алгоритм обучения сети функциональных систем в стохастической среде // ЛОМОНОСОВ-2016. —2016. — с. 134—136
- [Индексируется базами данных Scopus] A. Y. Sorokin, M. S. Burtsev., Functional Systems Network Outperforms Q-learning in Stochastic Environment // Procedia Computer Science. — 2016. — т. 88. — с. 397—402.
- [Индексируется базой данных Scopus] A. Y. Sorokin, M. S. Burtsev., Episodic memory transfer for multi-task reinforcement learning // Biologically inspired cognitive architectures. — 2018. — т. 26. — с. 91—95.
- [Доклад] Sorokin, A. Y. Continual and Multi-task Reinforcement Learning With Shared Episodic Memory / A. Y. Sorokin, M. S. Burtsev // Task-Agnostic Reinforcement Learning Workshop at ICLR, New Orleans – 2019
- [Индексируется базой данных RSCI] A. Y. Sorokin, L. P. Pugachev, M. S. Burtsev., Train Long-Term Memory by Predicting High Uncertainty Events // Proceedings of MIPT. — 2021. — т. 13. — в. 4(52) — с. 39—55.
- *[Принята, готовится к публикации] Sorokin, A., Buzun, N., Pugachev, L. and Burtsev, M., 2022. Explain My Surprise: Learning Efficient Long-Term Memory by Predicting Uncertain Outcomes. Advances in Neural Information Processing Systems 35 (NeurIPS 2022)
Спасибо за внимание!
Ведение: Доп. Материалы
Марковский Процесс Принятия Решений
Марковский Процесс принятия Решений (MDP) - это кортеж \(<S,A,R,T>\):
- \(S\) - множество всех состояний
- \(A\) - множество всех действий
- \(R: S \times A \to \mathbb{R}\) - функция наград
- \(T: S \times A \times S \to [0,1]\) - функция переходов, где \(T(s,a,s\prime) = P(S_{t+1}=s\prime|S_t=s, A_t=a)\)
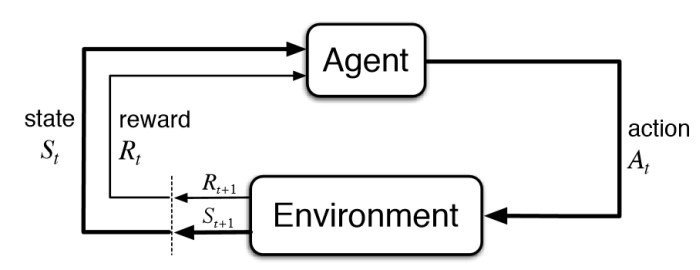
Изменения в среде:
- Изменение динамики среды, то есть функции переходов \(T(S,A,S')\)
- Изменение функции наград \(R(S,A)\)
Быстро меняющуюся среду (1 раз в эпизод) можно воспринимать, как POMDP.
Взаимодействие агента и среды
Частично обозревамый MDP
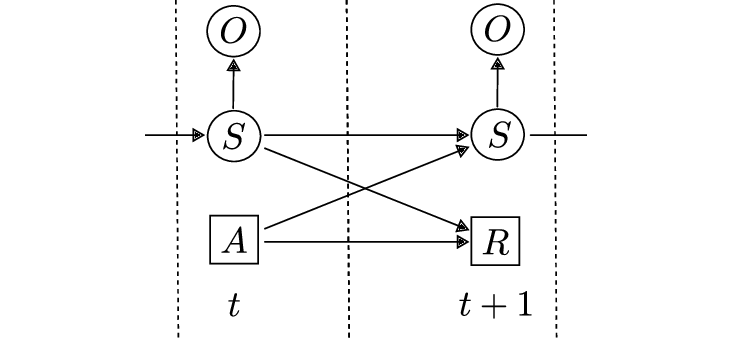
Графическая модель POMDP:
POMDP это кортеж \(<S,A,R,T,\Omega, O>\):
-
\(S\) - множество состояний
-
\(A\) - множество действий
-
\(R: S \times A \to \mathbb{R}\) - функция наград
-
\(T: S \times A \times S \to [0,1]\) - функция переходов \(T(s,a,s\prime) = P(S_{t+1}=s\prime|S_t=s, A_t=a)\)
-
\(\Omega\) - множество наблюдений
-
\(O\) это \(|S|\) множество условных распределений \(P(o|s)\)
SEM-A2C: Доп. Материалы
Мета обучение с подкреплением
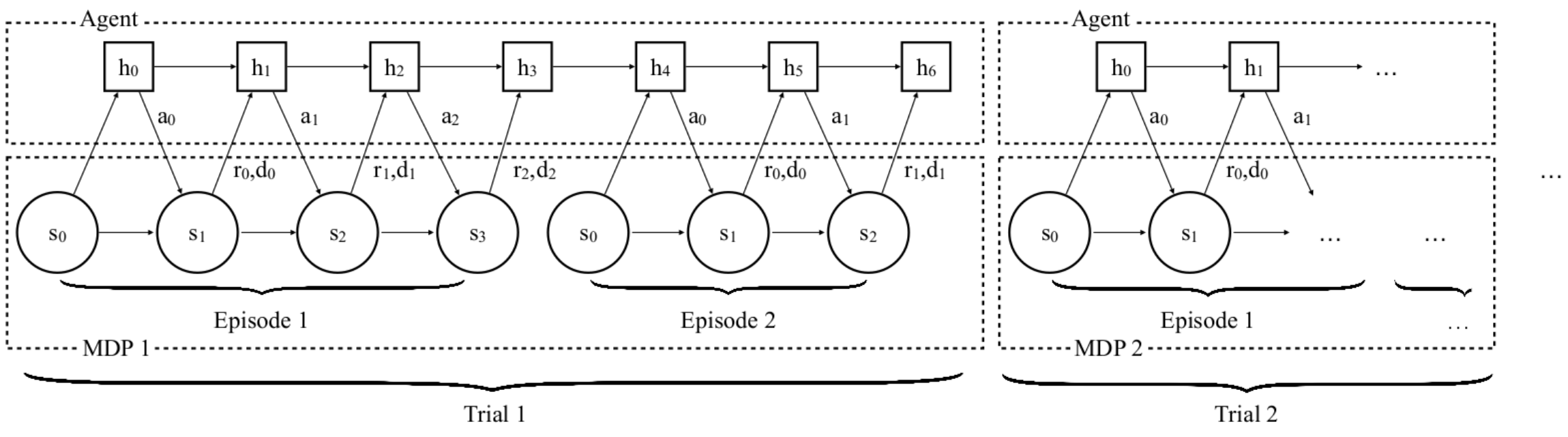
Мета обучение на основе памяти[1-3]:
-
Динамика среды меняется каждые K эпизодов
-
Состояния памяти не обнуляется пока не изменится среда
-
Агент оптимизирует награду за все K эпизодов
Мета обучение с подкреплением
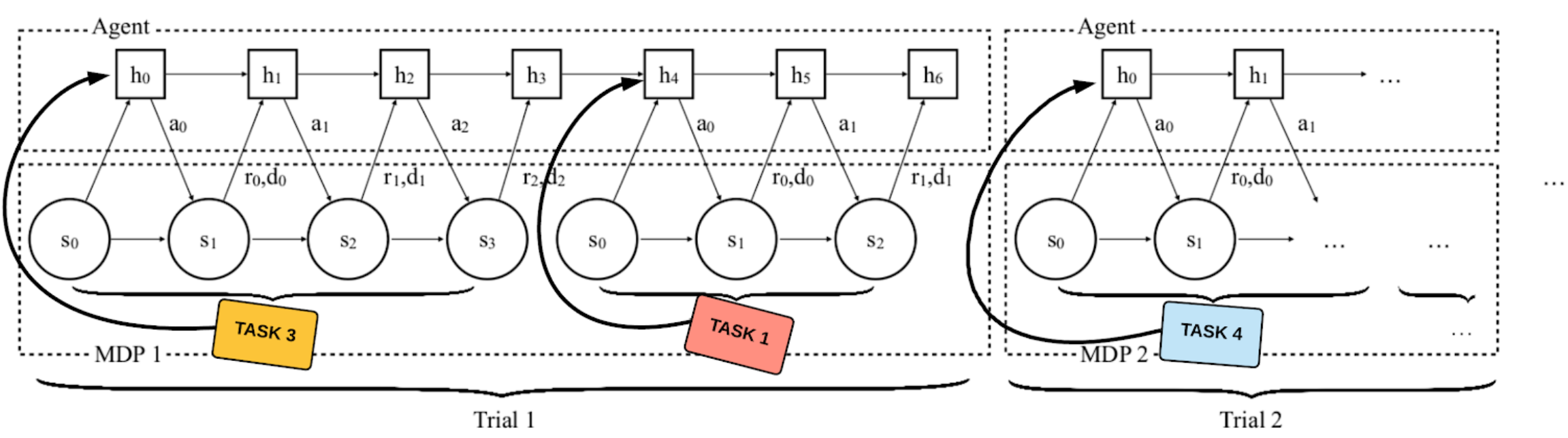
Добавим многозадачности в постановку задачи мета-обучения:
MemUP: Доп. Материалы
Детектор неопределенности: точность
- В экспериментах с Noisy T-maze лабиринтом детектор QR-DQN имеет 100% точность (вероятность выбора временных шагов, связанных с долговременной зависимостью).
- В экспериментах SL (Copy, Scattered Copy, Add) средняя точность работы детектора 80%.
- Точность детектора на задаче Vizdoom-Two-Colors измерить гораздо сложнее, так-как агент должен находиться близко к предмету, который собирается подобрать. По нашим подсчетам в ~50% случаев детектор выбирает шаг, который произошел в течение последних 5 шагов перед подбиранием предмета.
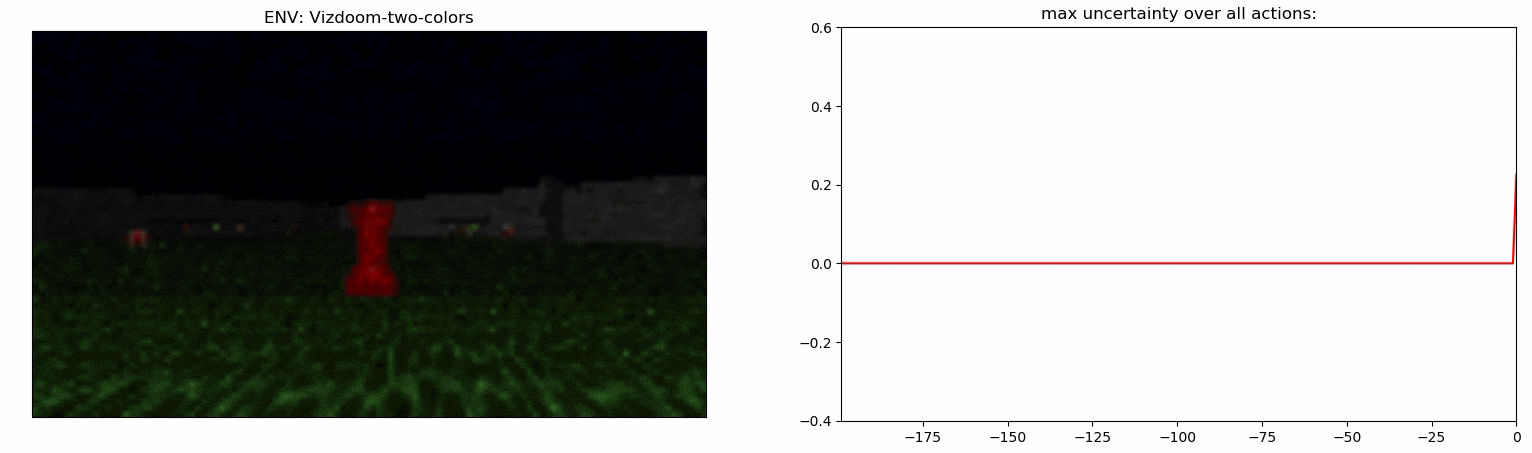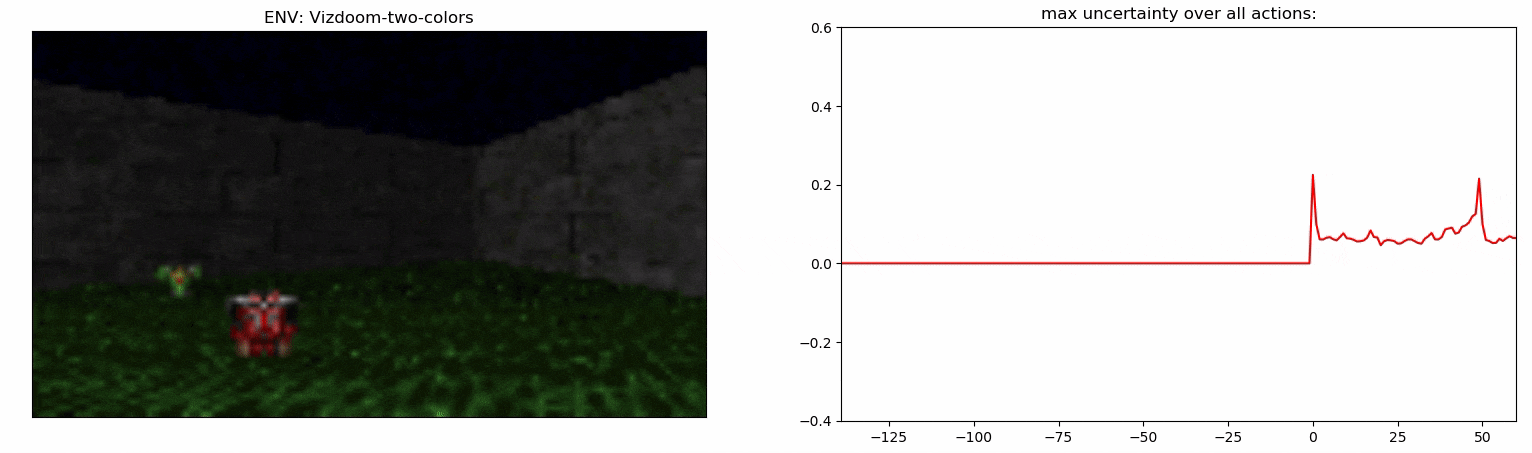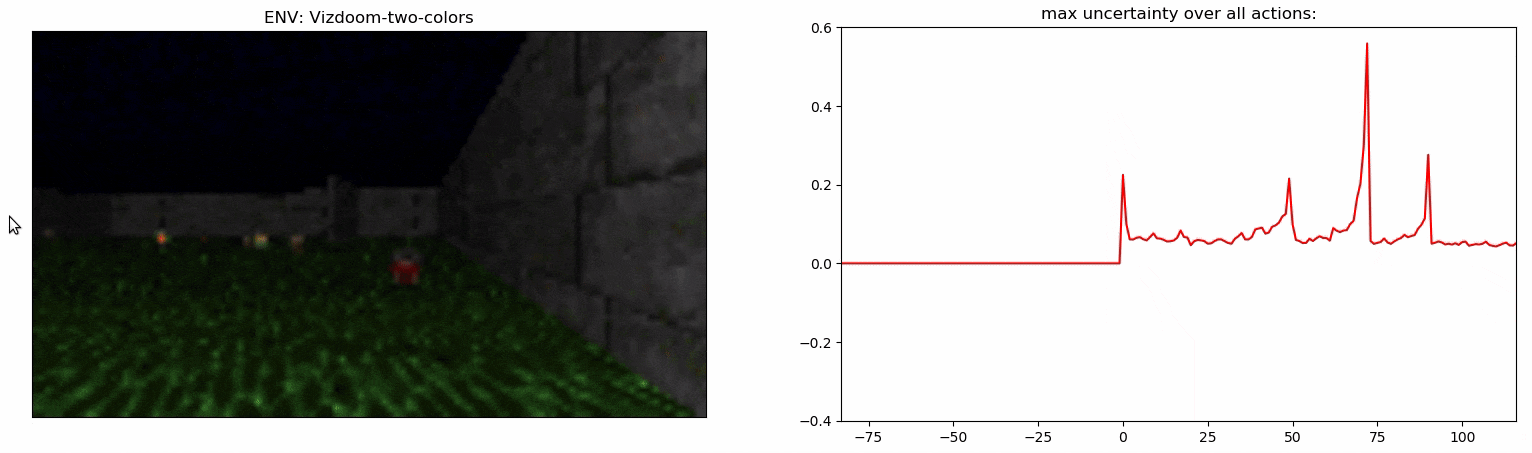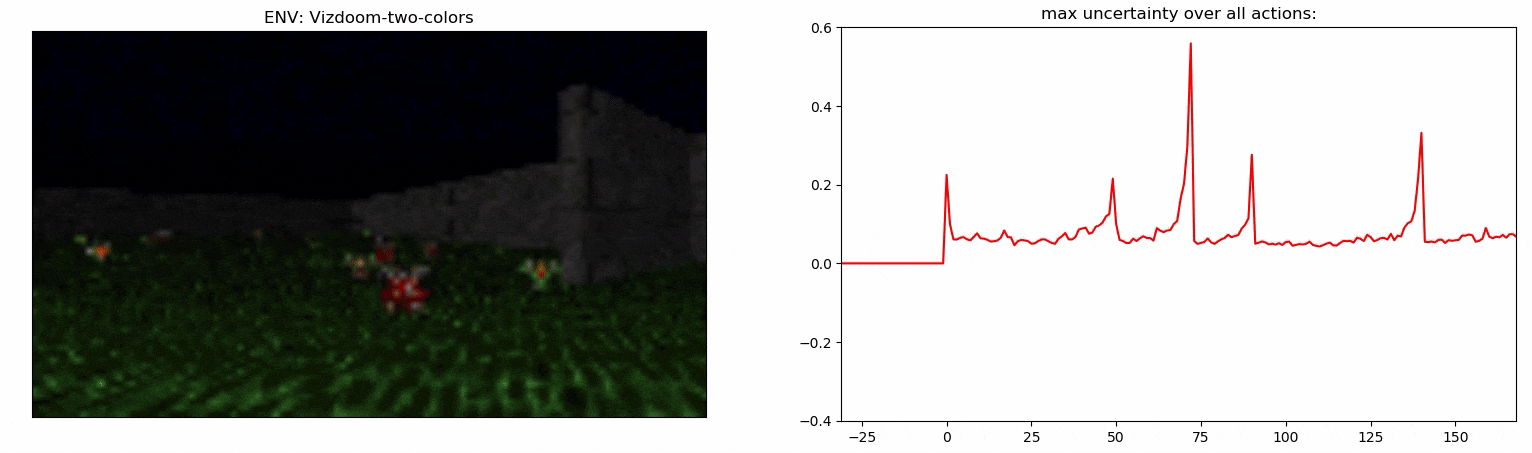
Детектор неопределенности: пример
Environment: Gym-Minigrid (Chevalier-Boisvert et al, 2018)
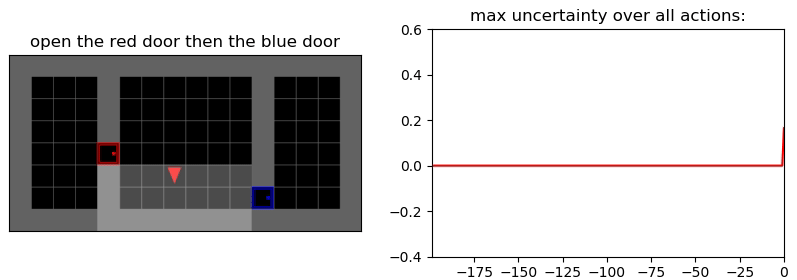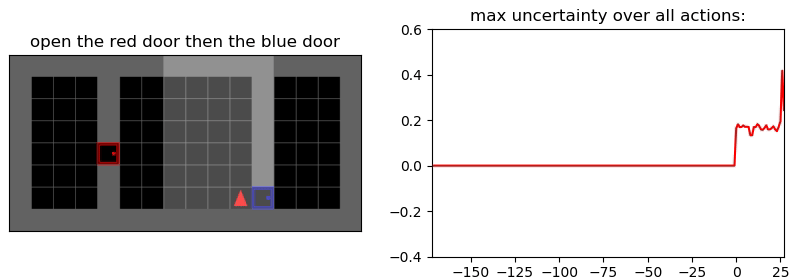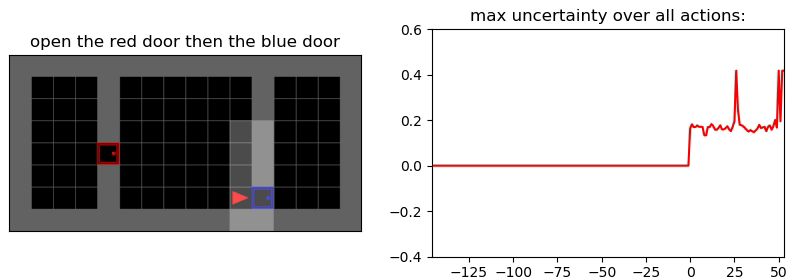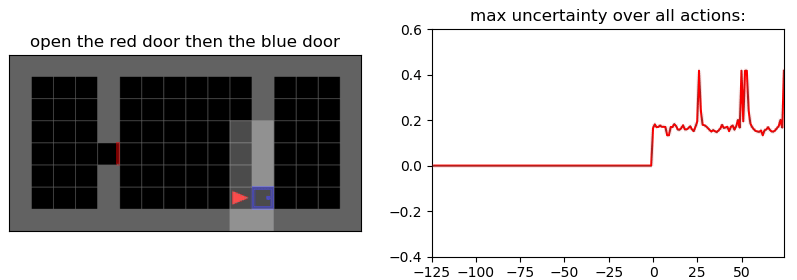
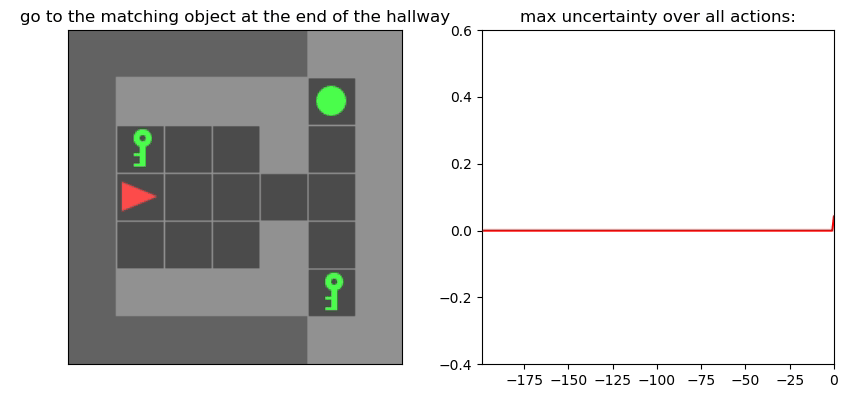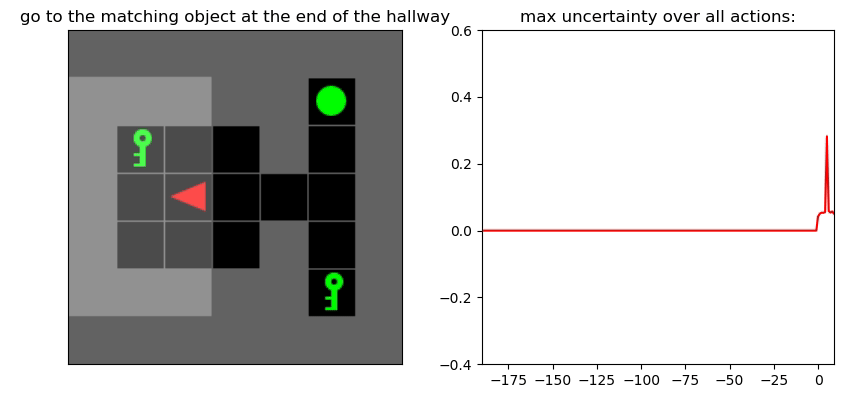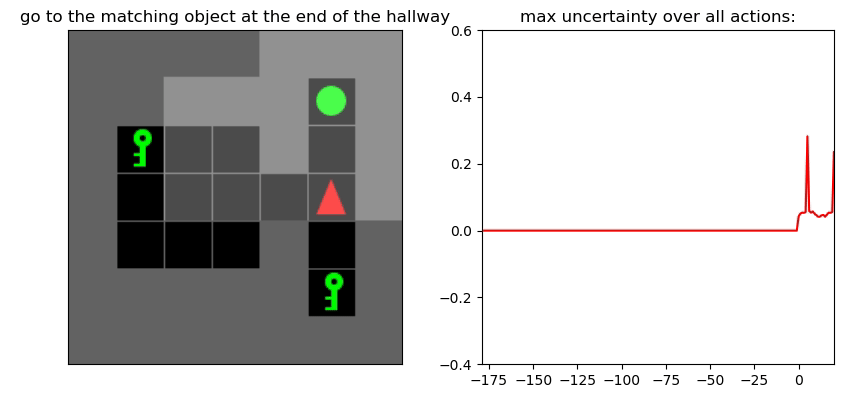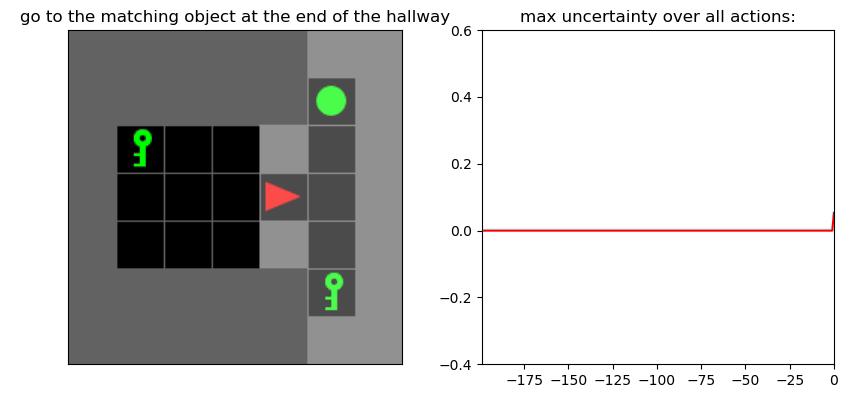
Пример работы памяти и предиктора

Эксперименты: Noisy TV Problem
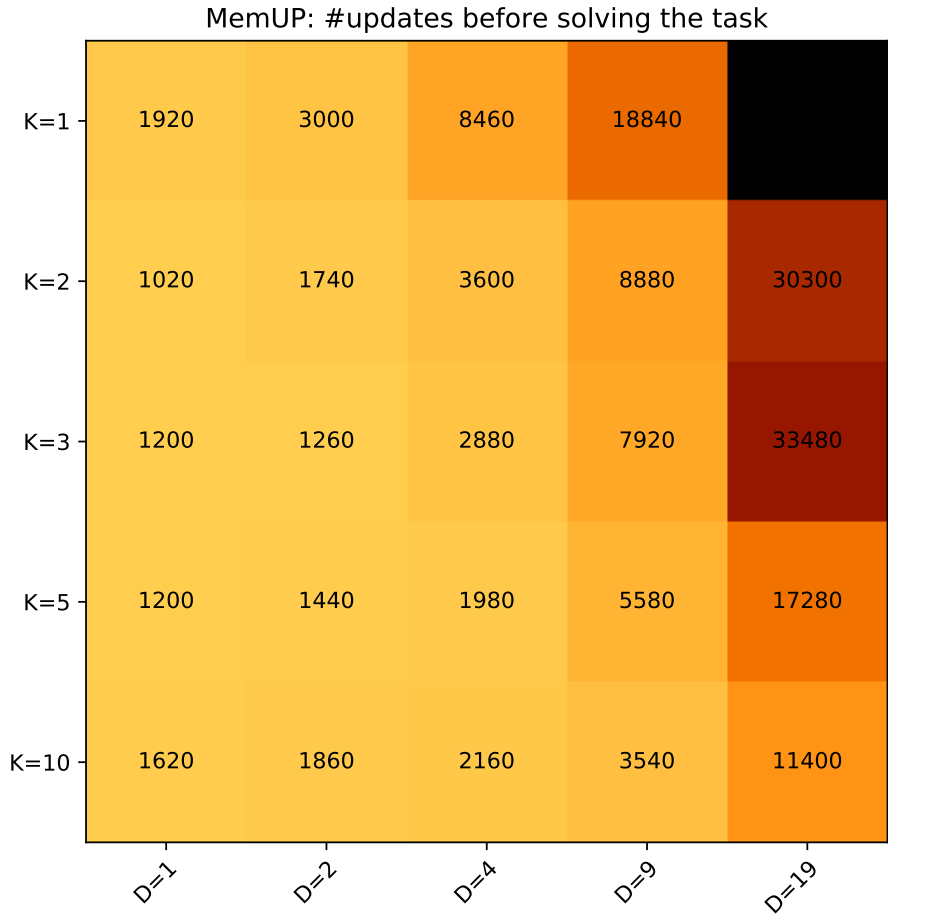
Noisy T-Maze with Distractors. В этой версии агент может получить награды +4 или -3 в \(D+1\) точках принятия решений. Точки принятия решений выбираются случайным образом на расстоянии не менее 50 шагов от подсказки. Только в 1 из \(D+1\) точек принятия решений награда зависит от действий агента и подсказки из начала эпизода. В остальных \(D\) точках награды полностью случайны.
Результат. Каждая ячейка показывает среднее количество шагов градиентного спуска, которые потребовались для решения задачи. По оси X отмечено количество непредсказуемых случайных событий в среде. По оси Y отмечен размер множеств \(U_t\). Более темные цвета означают более медленное решение.
Эксперименты: Абляционное исследование
Сравниваемые версии:
- MemUP - предложенный метод
- Rnd-Pred - отличается от MemUP только тем, что предсказывает будущие переходы, выбранные случайно и равномерно.
-
Default - отличается от MemUP и Rnd-Pred тем, что каждом шаге 𝑡
предсказывает \(y_𝑡\)
.
Детали эксперимента:
- Среда Noisy T-maze , но без обучения стратегии
- Версии сравниваются по их способности предсказать финальную награду находясь в самом конце лабиринта
Эксперименты: Абляционное исследование
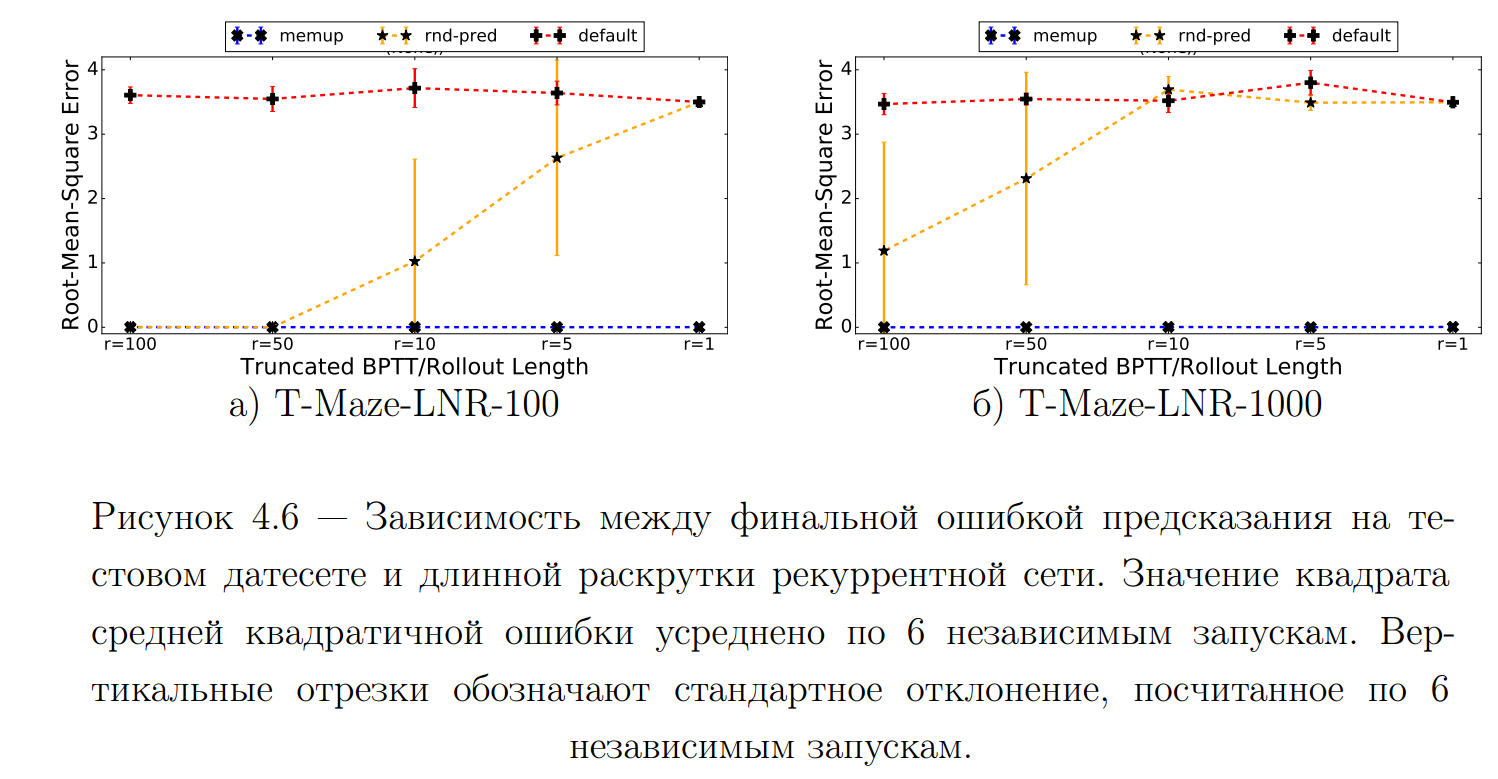
Параллельное обучение памяти и стратегии агента
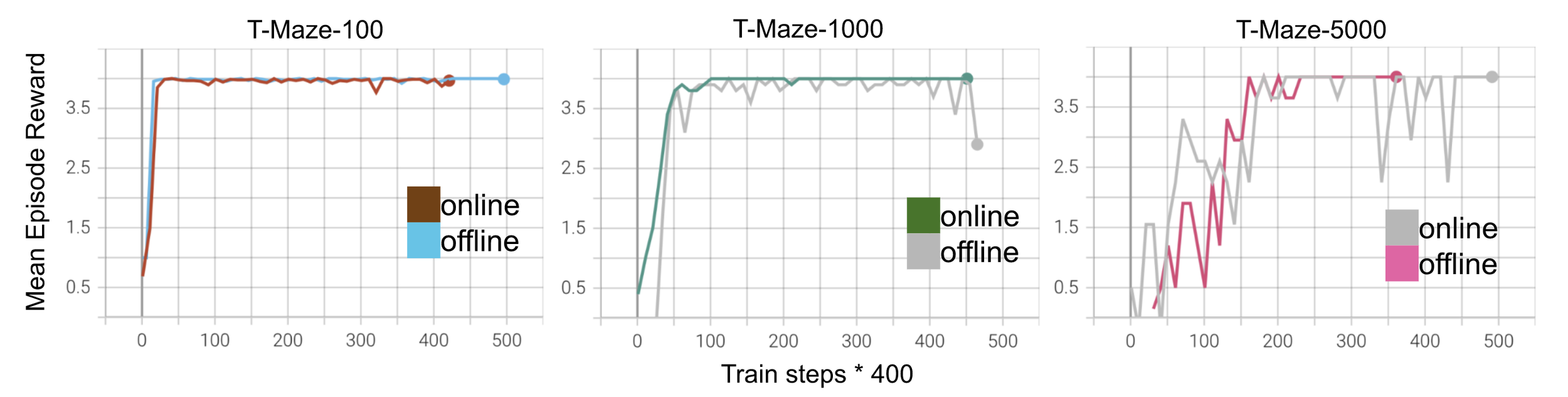
- На задаче T-maze отличий в качестве работы алгоритма с разделенным обучением (offline) и параллельным обучением стратегии и агента (online) пока не обнаружили.
- Для окончательного ответа не хватает экспериментов на других средах
Качество работы модели при занулении памяти
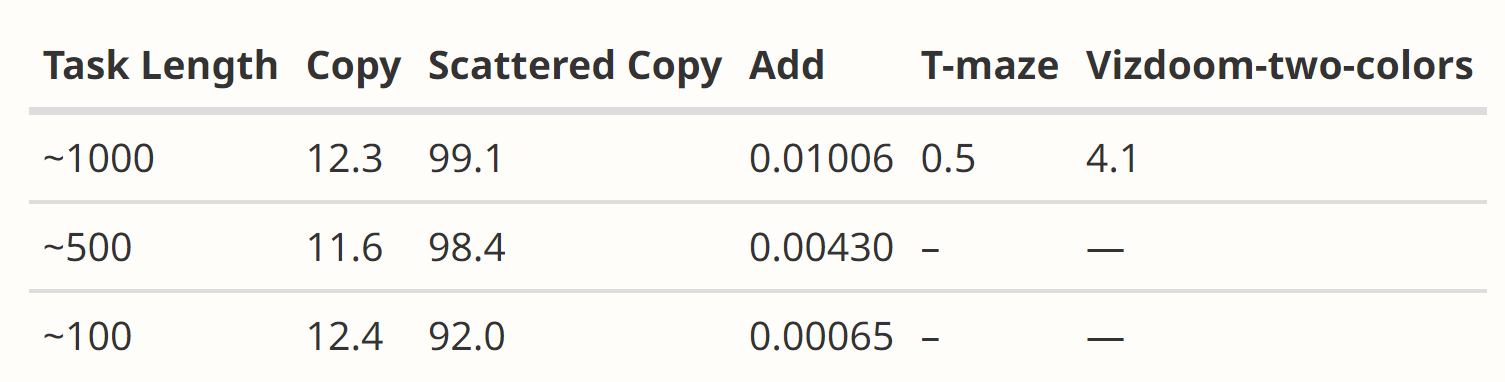
- Стоит отметить что в задачах Copy, Add, Scattered Copy используется рекуррентный контекст (\(x_t\) - это состояние другой рекурентной сети ).
- На Copy, T-maze, Vizdoom-Two-Colors качество работы модели упало до уровня необученной нейросети
- На задачах Add и Scattered Copy качество незначительно просело. Это связанно с тем, что в них минимальная длина временной зависимости равна 1.