COMP3010: Algorithm Theory and Design
Daniel Sutantyo, Department of Computing, Macquarie University
1.2 Complexity Analysis
Analysing the running time of an algorithm
1.2 - Complexity Analysis
- Which of these factors do you think affect the running time of an algorithm when we run it on a computer?
- The CPU of the computer (i3 vs i5 vs i7)
- The amount of RAM the computer has
- The memory speed of the computer (SSD vs HDD)
- The programming language used
- Multi-threading vs Single-threading
- The size of the input
- The structure of the input
Analysing the running time of an algorithm
1.2 - Complexity Analysis
- You don't measure the speed of an algorithm by just using a stopwatch
- If we want to compare two algorithms fairly, then you should run both of them in the same environment
- You definitely cannot say an algorithm is better just because you wrote it in a better language (e.g. Assembly vs Javascript)
... or can you?
... how about single-threaded vs multi-threaded algorithm?
Analysing the running time of an algorithm
1.2 - Complexity Analysis
- Generally, to compare two algorithms fairly, we need to strip down our computer to its most basic components and simplify them
- Let's assume that we have an abstract computer with a CPU, memory, and I/O. The speed doesn't matter, what matters is, what they can do.
RAM model of computation
1.2 - Complexity Analysis
- Historically, we use a hypothetical simple computer called the Random Access Machine or RAM
- Properties of RAM:
- we have primitive operations that take one time step each:
\(+\) , \( -\) , \(*\) , \(\div\) , function calls, logical tests (\(<\), \(=\), \(>\), etc) - unlimited memory (but each memory block has a size limit), memory access takes one time step
- instructions are executed one after another, i.e. no concurrency
- loops and subroutines are compositions of simple operations
- we have primitive operations that take one time step each:
- https://en.wikipedia.org/wiki/Random-access_machine if you want to find out more
RAM model of computation
1.2 - Complexity Analysis

The Art of Computer Programming
Donald E. Knuth
The imaginary MIX computer
RAM model of computation
1.2 - Complexity Analysis
-
Basically, you have a computer that can only do primitive operations, then break down your algorithm to those operations and see how many operations they need to complete the computation
-
If you can think in terms of C or Assembly (COMP2100/202), then you should have a good idea.
-
If not, think of the average Java program that you wrote back in COMP1010/125
- Problem: is it fair?
-
single-threaded vs multi-threaded
-
-
Problem: is it realistic?
-
multiplication vs addition
-
RAM model of computation
1.2 - Complexity Analysis
-
Is it perfect? No, but it allows us to have a simple model of our algorithm that we can analyse
-
The idea is, if in our simple model we see that Algorithm A is better than Algorithm B, then if we apply Algorithm A in the real world, it will probably still be better than Algorithm B

RAM model of computation
1.2 - Complexity Analysis
- In practice, you don't have to worry too much about it. It just means that when you are analysing an algorithm, you have to strip away the more complex operations, e.g
- Sorting doesn't take just one time step
- TreeMap.find(key) doesn't take just one time step
- What about computing \(2^n\) ?
- One more time: the running time or time complexity of an algorithm is the number of primitive operations that is executed by the algorithm
RAM model of computation
1.2 - Complexity Analysis
- For a rigorous example, see CLRS pg 25-27

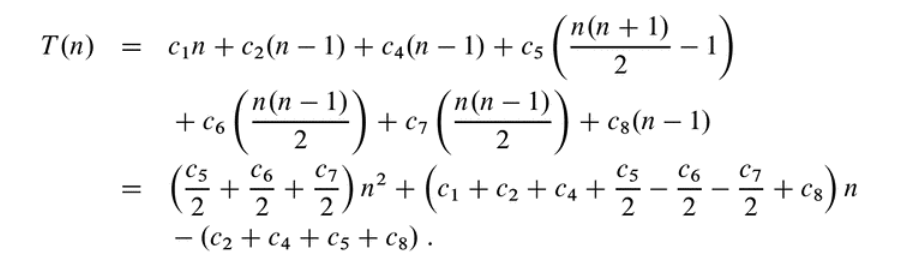
RAM model of computation
1.2 - Complexity Analysis
- Time complexity (or just complexity) of an algorithm is usually represented with the notation \(T(n)\) as seen in the example
- The good (?) news is that in this unit, we are not going to do something as rigorous as what you saw in the previous slide
- In most cases, it is enough to identify the most significant operation to derive the complexity of the algorithm
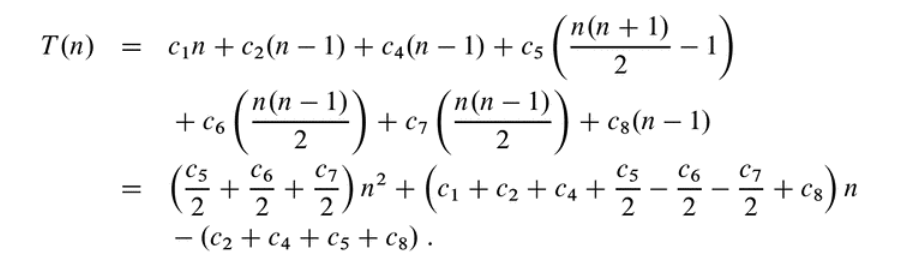
\(T(n) \approx n^2\)
Summary
1.2 - Complexity Analysis
-
Analysing an algorithm can be hard, so we need to use a simplified model
-
To analyse an algorithm, break it down to its primitive operations and count the number of operation it takes to finish