COMP3010: Algorithm Theory and Design
Daniel Sutantyo, Department of Computing, Macquarie University
1.3 Complexity Notation
From the previous video
1.3 - Complexity Notation
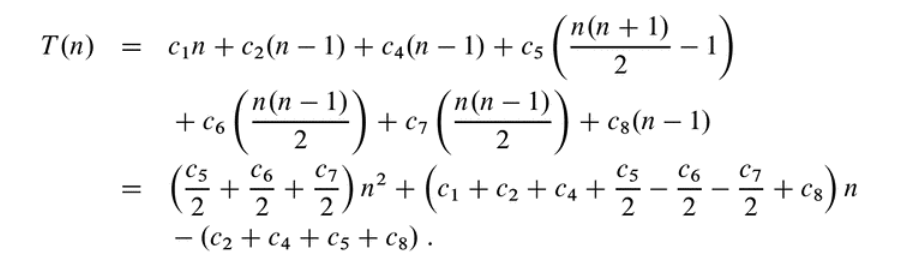
- Time complexity is represented using the notation \(T(n)\)
- To find the time complexity of an algorithm you count the number of primitive operations it needs to finish the computation when there is \(n\) input
- Great, we have a formula, now what?
- Insertion Sort time complexity (see pages 25-27 of CLRS):
- Note that \(T(n)\) is a function, so the number of operations you need to perform changes as n changes
- e.g.
- \(T(10)\) = 151 operations
- \(T(20)\) = 376 operations
- \(T(30)\) = 667 operations
- e.g.
- Now we know the growth-rate of \(T(n)\) i.e. how much more time (or space) the algorithm needs as the input size grow
- By the way, what operation are we doing in insertion sort?
1.3 - Complexity Notation
1.3 - Complexity Notation
no of operations
size of input
Algorithm A is
1.3 - Complexity Notation
\[\left(\frac{c_5}{2}+\frac{c_6}{2}+\frac{c_7}{2}\right)n^2 + \left(c_1+c_2+c_4+\frac{c_5}{2}-\frac{c_6}{2}-\frac{c_7}{2}+c_8\right)n - (c_2+c_4+c_5+c_8)\]
Algorithm B is
\[\left(c_4+c_6\right)n^2 + (c_1+c_2+c_5)n + (c_3+c_8) \]
which one is better?
1.3 - Complexity Notation
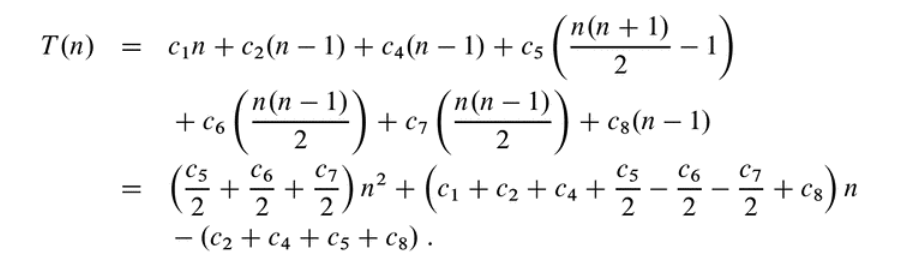
\[T(n) = c_1 n^2 + c_2 n - c_3\]
- From COMP2010/225, you know that you can ignore the lower order terms, and we say \(T(n) = O(n^2)\)
- we say that here \(n^2\) is the dominant term
- i.e. we simplify even more
- We can drop constants and lower-order terms because this does not impact our comparison of algorithms that much
- e.g. \(2^{n+3} + 21n^{20} + 43n^2 + 1729n + 17013\)
1.3 - Complexity Notation
\(n\) \(n^2\) \(n^{20}\) \(2^n\) \(2^{n+3}\)
\(100\)
\(200\)
\(1 \times 10^4\)
\(1 \times 10^{40}\)
\(1.26 \times 10^{30}\)
\(4 \times 10^4\)
\(1.05 \times 10^{46}\)
\(1.61 \times 10^{60}\)
\(300\)
\(9 \times 10^4\)
\(3.49 \times 10^{49}\)
\(2.04 \times 10^{90}\)
\(400\)
\(1.6 \times 10^5\)
\(1.10 \times 10^{52}\)
\(2.58 \times 10^{120}\)
\(1.01 \times 10^{31}\)
\(1.28 \times 10^{61}\)
\(1.63 \times 10^{91}\)
\(2.07 \times 10^{121}\)
- Actually, when we compare algorithm, we really just classify them into different classes depending on their growth rate
- by the way, we also use the term order of the function to refer to the growth rate
1.3 - Complexity Notation
1.3 - Complexity Notation
COMP1010/125
COMP2010/225
COMP3010
\[O(n)\]
\[O(n^2)\]
\[O(\log n)\]
\[O(n\log n)\]
\[O(|V||E|)\]
\[O(1)\]
\[O(|E|\log|V|)\]
\[O(2^n)\]
\[O(n!)\]
\[O(n\sqrt{n})\]
\[O(2^{\log{n}})\]
\[O(n^2\log{n})\]
\[O(\log\log{n})\]
1.3 - Complexity Notation
\(O\)-notation
- The \(O\)-notation represents the asymptotic upper bound, i.e. the growth rate of the function should not exceed this bound
- \(f(n) = O(g(n))\) means there exists a constant \(c\) such that for all \(n > n_0\), \(f(n) \le c\cdot g(n) \)
- \(f(n)\) here is the time-complexity of your algorithm
- \(g(n)\) is a polynomial (e.g. \(n, \log n, n^2\))
\(T(n) = O(n^2)\)
\(f(n)\)
\(g(n)\)
1.3 - Complexity Notation
\(O\)-notation
\(f(n) = O(g(n))\) means there exists a positive constant \(c\) such that for all \(n > n_0\), \(f(n) \le c\cdot g(n) \)
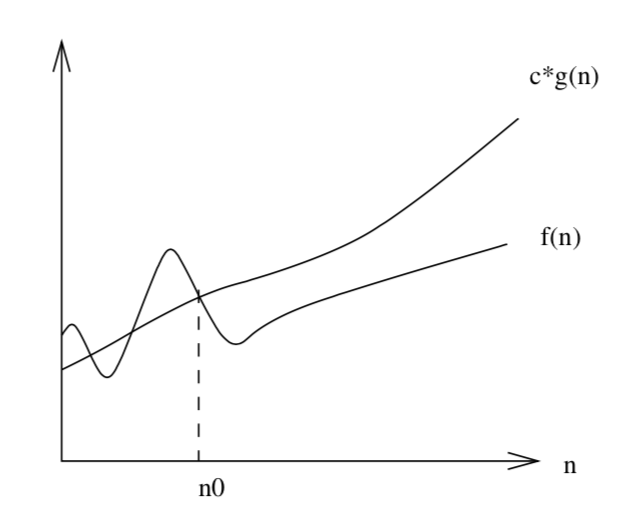
Skiena Figure 2.3, page 36
1.3 - Complexity Notation
\(O\)-notation
- Let's try to explain this using an example
- Let \(T(n) = 3n^2 + 100n + 25\)
- I claim that \(T(n) = O(n^2)\)
\(T(n)\)
\(g(n)\)
\(\le\)
\( 3n^2 + 100n + 25\)
\( n^2\)
\(f(n) = O(g(n))\) means there exists a positive constant \(c\) such that for all \(n > n_0\), \(f(n) \le c\cdot g(n) \)
\( 6\)
\(n=1\)
\(128\)
\(6\)
\(n=10\)
\(1325\)
\(600\)
\(n=100\)
\(40025\)
\(60000\)
1.3 - Complexity Notation
\(O\)-notation
- Remember, just because \(f(n) = O(g(n))\) doesn't mean that \(f(n) \le g(n)\) all the time, but \(c\cdot g(n)\) will eventually dominate \(f(n)\)
- In fact, to show \(f(n) = O(g(n))\), it is usually much simpler: just pick a big constant:
\(3n^2 + 100n + 25 \le 100n^2 + 100n^2 + 100n^2 = 300n^2\)
for all \(n \ge 1\)
i.e. use \(c = 300\) and \(n_0 = 1\)
- We will do a bit of this in the workshop
1.3 - Complexity Notation
\(O\)-notation
- Questions:
- is \(n^2 + 1000n = O(n)\)?
- is \(n = O(n^2)\)?
- is \(2^{n+1} = O(2^n)\)?
- is \(2^{2n} = O(2^n)\)?
1.3 - Complexity Notation
\(O\)-notation
- Questions:
- is \(n^2 = O(n^2)\)?
- is \(n\log n = O(n^2)\)?
- is \(n = O(n^2)\)?
- is \(\log n = O(n^2)\)?
these are all correct, but are they useful?
1.3 - Complexity Notation
\(O\)-notation
- Asymptotic analysis studies how the algorithm behaves as \(n\) tends to infinity
- We ignore lower order terms and constants because as \(n\) tends to infinity, these become insignificant (see previous table)
- We ignore constant multipliers because the growth rate is more important
- We ignore these details so that we can make comparisons between algorithms more easily
1.3 - Complexity Notation
\(\Omega\)-notation
- \(\Omega\)-notation is the asymptotic lower bound
- \(f(n) = \Omega(g(n))\) means there exists positive constants \(c\) and \(n_0\) such that for all \(n > n_0\), \(f(n) \ge c\cdot g(n) \ge 0\)
1.3 - Complexity Notation
\(\Omega\)-notation
Skiena Figure 2.3, page 36
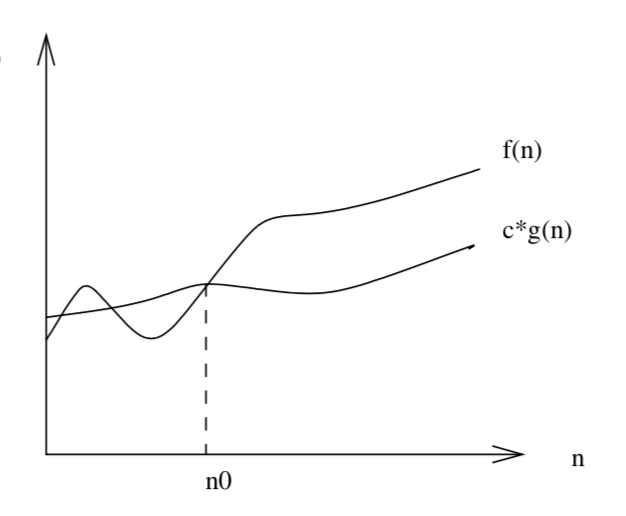
\(c\cdot g(n)\)
\( f(n)\)
1.3 - Complexity Notation
- Questions:
- is \(n^2 = \Omega(n)\)?
- is \(n\log n = \Omega(n)\)?
- is \(n = \Omega(n)\)?
- is \(\log n = \Omega(n)\)?
\(\Omega\)-notation
1.3 - Complexity Notation
\(\Theta\)-notation (Theta)
- \(\Theta\)-notation is the asymptotic tight bound
- \(f(n) = \Theta(g(n))\) means there exists positive constants \(c_1\), \(c_2\), and \(n_0\) such that for all \(n > n_0\),
\(0 \le c_1\cdot g(n) \le f(n) \le c_2\cdot g(n) \) - \(f(n) = \Theta(g(n))\) if and only if \(f(n) = \Omega(g(n))\) and \(f(n) = O(g(n))\)
- We often use \(O\)-notation to describe a tight bound, i.e. we use \(O\)-notation, when we really should be using \(\Theta\)-notation
1.3 - Complexity Notation
\(\Theta\)-notation (Theta)
Skiena Figure 2.3, page 36
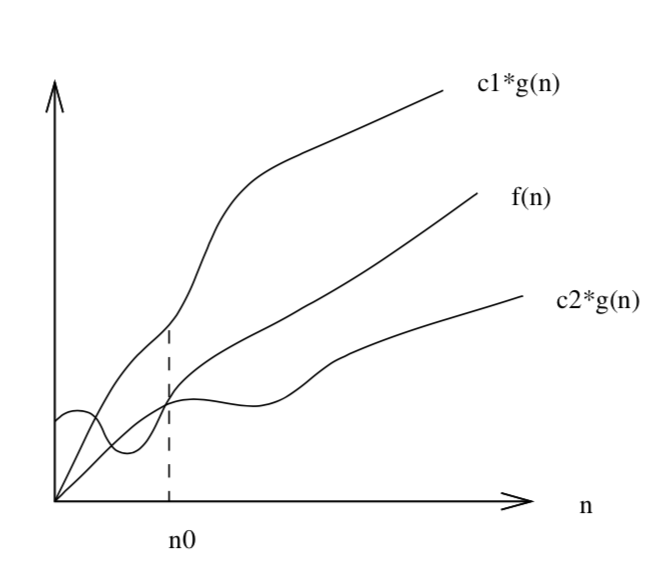
\(f(n)\)
\(c_2\cdot g(n)\)
\(c_1\cdot g(n)\)
1.3 - Complexity Notation
- Let's go back to \(T(n)\) growth rate
- e.g.
- \(T(10)\) = 151 operations
- \(T(20)\) = 376 operations
- \(T(30)\) = 667 operations
- e.g.
- Recall that \(T(n)\) is the formula for the time complexity of insertion sort (pages 25-27 of CLRS)
- If \(n = 10\), is \(T(n)\) always 151?
1.3 - Complexity Notation
- If \(n\) increases, then we expect \(T(n)\) to increase as well
- but what if \(n\) remains the same?
1.3 - Complexity Notation
Best, worst, and average-case complexity
- There can be many different inputs of size \(n\)
-
Worst-case complexity:
- the longest running time for any input of size \(n\)
- insertion sort: \(O(n^2)\) comparisons, \(O(n^2)\) swaps
-
Best-case complexity:
- the fastest running time for any input of size \(n\)
- insertion sort: \(O(n)\) comparisons, \(O(1)\) swaps
-
Average-case complexity:
- the average running time for inputs of size \(n\)
- insertion sort: \(O(n^2)\) comparisons, \(O(n^2)\) swaps
1.3 - Complexity Notation
Best, worst, and average-case complexity

Skiena, Figure 2.2, page 35
1.3 - Complexity Notation
Best, worst, and average-case complexity
- In practice, the worst-case complexity is the most useful measure (although average-case complexity can also be useful)
- In this unit we are more interested in worst-case complexity
- Why? So you can prepare for it
- Average-case complexity can be difficult to derive (need to use probability theory)
- Best-case complexity is the least useful
1.3 - Complexity Notation
Warning
- Do not confuse asymptotic notation (\(O, \Omega, \Theta\)) with best, average, or worst-case complexities
- You can express an algorithm's worst-case complexity using \(O\)-notation
- You can express an algorithm's average-case complexity using \(O\)-notation
- You can express an algorithm's best-case complexity using \(O\)-notation
- You will often see worst-case complexity expressed using the big-\(O\) notation (makes sense, right?)
- You will sometimes see the best-case complexity expressed using the \(\Omega\)-notation
1.3 - Complexity Notation
Summary
- Asymptotic notations (\(O\)-notation, \(\Omega\)-notation, \(\Theta\)-notation)
- Best-case, average-case and worst-case complexities