COMP3010: Algorithm Theory and Design
Daniel Sutantyo, Department of Computing, Macquarie University
11.0 - P vs NP
The Plan
11.0 - P vs NP
- Introduction to P vs NP
- NP-Completeness and Reduction
- Approximation Algorithms
11.0 - P vs NP
Tractable vs Intractable Problems
- In week 3, we spent a bit of time discussing brute-force methods
- the focus was to find overlapping subproblems to then construct a dynamic programming algorithm
- in the examples, we often went from \(O(2^n)\) to \(O(n^2)\)
- does this mean we can always use dynamic programming to find a polynomial-time solution to a problem?
11.0 - P vs NP
Tractable vs Intractable Problems
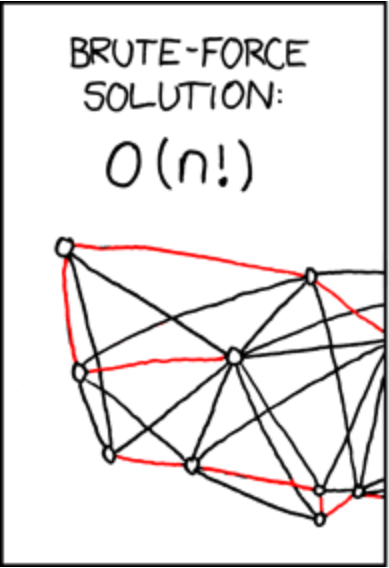


https://xkcd.com/399/
11.0 - P vs NP
Tractable vs Intractable Problems
- Tractable problems are problems that we can solve using a polynomial-time algorithm, i.e. \(O(n^k)\)
- Intractable problems are problems for which there are no known polynomial-time algorithm to solve it
- not polynomial doesn't always mean exponential, it can be factorial, i.e. \(O(n!)\), or quasi-polynomial, i.e. \(O(n^{\log n})\)
- you may have heard of P vs NP but there is also something called QP!
11.0 - P vs NP
Tractable vs Intractable Problems
- In fact there is a lot of complexity classes:
11.0 - P vs NP
Tractable vs Intractable Problems
- Although you already know the more important ones:
11.0 - P vs NP
Tractable vs Intractable Problems
- The main complexity classes you should know:
- logarithmic - \(O(\log n)\)
- linear - \(O(n)\)
- polynomial - \(O(n^k)\)
- quasi-polynomial - \(O(n^{\log n})\)
- subexponential - \(O(2^{n^\varepsilon})\) for a small \(\varepsilon > 0\), e.g. \(O(2^{\sqrt{n}})\)
- exponential - \(O(2^n)\)
- factorial - \(O(n!)\)
- double exponential - \(O(2^{2^n})\)
11.0 - P vs NP
Tractable vs Intractable Problems
- The main complexity classes you should know:
- logarithmic - \(O(\log n)\)
- linear - \(O(n)\)
- polynomial - \(O(n^k)\)
- quasi-polynomial - \(O(n^{\log n})\)
- subexponential - \(O(2^{n^\varepsilon})\) for a small \(\varepsilon > 0\), e.g. \(O(2^{\sqrt{n}})\)
- exponential - \(O(2^n)\)
- factorial - \(O(n!)\)
- double exponential - \(O(2^{2^n})\)
superpolynomial
11.0 - P vs NP
Tractable vs Intractable Problems
- polynomial - \(O(n^k)\)
- exponential - \(O(2^n)\)
11.0 - P vs NP
Tractable vs Intractable Problems
- subexponential - \(O(2^{n^\varepsilon})\)
- polynomial - \(O(n^k)\)
- exponential - \(O(2^n)\)
11.0 - P vs NP
- polynomial - \(O(n^k)\)
- exponential - \(O(2^n)\)
- subexponential - \(O(2^{n^\varepsilon})\)
- can you prove that some problems can only be done in polynomial time?
- yes
- can you prove that some problems can only be done in subexponential time?
- yes
- can you prove that some problems can only be done in exponential time?
- yes
- i.e. we can prove that this is the best that we can do
Where We Are
11.0 - P vs NP
- polynomial - \(O(n^k)\)
- exponential - \(O(2^n)\)
- subexponential - \(O(2^{n^\varepsilon})\)
- can you prove that some problems can ONLY be done in exponential time?
- can you prove that some problems can be done in exponential time?
- can you prove that some problems CANNOT be done in polynomial time?
- can you prove that some problems CANNOT be done in subexponential time?
Where We Are
11.0 - P vs NP
Where We Are
- Let's say that the only algorithm I know that can solve a problem \(Q\) is exponential in complexity
- is there absolutely NO WAY to do it in subexponential time, or am I just too stupid to work it out?
- is there absolutely NO WAY to do it in polynomial time, or am I just too stupid to work it out?
- This is the problem that scientists have:
- they cannot show that \(Q\) can be done in polynomial time
- but they also cannot show that \(Q\) cannot be done in polynomial time
11.0 - P vs NP
Where We Are
- To repeat, there are problems that are definitely exponential in complexity, but, there are also a bunch of problems where we just don't know if we can do them in polynomial time or not or subexponential complexity)
- Let \(\text{EXP}\) be the class of problems that can be solved in exponential time
- Let \(\text{P}\) be the class of problems that can be solved in polynomial time
- i.e. if a problem \(Q\) can be done in polynomial time, then usually we just say that \(Q \in P\)
- do you remember that we also defined complexity classes as sets?
- is \(Q\) also in \(\text{EXP}\)?
- Is \(\text{P} \subseteq \text{EXP}\) or \(\text{P} \subsetneq \text{EXP}\)?
11.0 - P vs NP
Where We Are
- Let's say that \(Q \in \text{P}\)
- is \(Q \in \text{EXP}\)?
- yes
- is \(Q \in \text{SUBEXP}\)?
- \(\text{SUBEXP}\) the class of problems solvable in subexponential time
- yes
- is \(Q \in \text{EXP}\)?
- Let's say that \(Q \in \text{EXP}\)
- is \(Q \in \text{P}\)?
- well, can you prove it?
- is \(Q \in \text{P}\)?
11.0 - P vs NP
The Class NP
- So far we mentioned the classes \(\text{P}\), \(\text{EXP}\), and \(\text{SUBEXP}\), and we know that
- \(\text{P} \subsetneq \text{SUBEXP} \subsetneq \text{EXP}\)
- We are going to study another class of problems called \(\text{NP}\)
- \(\text{NP}\) does NOT stand for non-polynomial
- this is a special class of problems for which there are no known polynomial time algorithm to solve them, but if you do have a solution, then it can be verified in polynomial time
- in other words, I can work out if the answer is correct or not in polynomial time, but I cannot produce the answer in polynomial time
11.0 - P vs NP
The Class NP
- Why are they so special?
- if I can verify a solution in polynomial time, does it mean that I can produce a solution in polynomial time as well?
- in practice, these problems are very similar to the problems in \(\text{P}\)
- examples:
- Shortest Path vs Longest Path
- Euler cycle vs Hamiltonian cycle
- examples:
11.0 - P vs NP
Shortest Path vs Longest Path
11.0 - P vs NP
Shortest Path vs Longest Path
11.0 - P vs NP
Shortest Path vs Longest Path
11.0 - P vs NP
Shortest Path vs Longest Path
11.0 - P vs NP
Shortest Path vs Longest Path
- If I tell you a possible solution (and assume I know what the longest path is), is it easy to check if it's correct?
11.0 - P vs NP
Euler Cycle vs Hamiltonian Cycle
- Euler Cycle: start and end at the same vertex, use every edge once
11.0 - P vs NP
Euler Cycle vs Hamiltonian Cycle
- Euler Cycle: start and end at the same vertex, use every edge once
11.0 - P vs NP
Euler Cycle vs Hamiltonian Cycle
- Euler Cycle: start and end at the same vertex, use every edge once
11.0 - P vs NP
Euler Cycle vs Hamiltonian Cycle
- Euler Cycle: start and end at the same vertex, use every edge once
- Hamiltonian Cycle: start and end at same vertex, visit every vertex once
11.0 - P vs NP
Euler Cycle vs Hamiltonian Cycle
- Euler Cycle: start and end at the same vertex, use every edge once
- Hamiltonian Cycle: start and end at same vertex, visit every vertex once
11.0 - P vs NP
Euler Cycle vs Hamiltonian Cycle
- Euler Cycle: start and end at the same vertex, use every edge once
- Hamiltonian Cycle: start and end at same vertex, visit every vertex once
11.0 - P vs NP
Euler Cycle vs Hamiltonian Cycle
- Euler Cycle: start and end at the same vertex, use every edge once
- Hamiltonian Cycle: start and end at same vertex, visit every vertex once
11.0 - P vs NP
Euler Cycle vs Hamiltonian Cycle
- Euler Cycle: start and end at the same vertex, use every edge once
- Hamiltonian Cycle: start and end at same vertex, visit every vertex once
- if I tell you a solution, is it easy to check if it's correct?
11.0 - P vs NP
The Class NP
- One more time, we don't know there if is a polynomial-time algorithm to solve the problems in \(\text{NP}\), but we know that we can verify a solution in \(\text{P}\)
- Let's make sure the setting is clear to you:
- if \(Q \in \text{NP}\), is \(Q \in \text{EXP}\)?
- yes
- if \(Q \in \text{P}\), is \(Q \in \text{NP}\)?
- yes
- if \(Q \in \text{NP}\), is \(Q \in \text{P}\)?
- well, this is what we are wondering, are these \(\text{NP}\) problems just problems in \(\text{P}\), but we don't know how to solve them yet?
- if \(Q \in \text{NP}\), is \(Q \in \text{EXP}\)?
11.0 - P vs NP
The Class NP
\(\text{P}\)
\(\text{EXP}\)
11.0 - P vs NP
The Class NP
\(\text{P}\)
\(\text{NP}\)
\(\text{EXP}\)
11.0 - P vs NP
The Class NP
\(\text{P}\)
\(\text{NP} =\)
\(\text{EXP}\)
11.0 - P vs NP
The Class NP
- The main question in the P vs NP problem is whether or not P and NP are just the same set
- that is, is every single problem in NP just a problem in P?
- for now, make sure that you are clear about the differences between P, EXP, and NP (and maybe SUBEXP)
- one question you can ask yourself:
- what do we have to do to prove that P = NP?
11.0 - P vs NP
Why Should You Care?
- Do I think that P = NP?
- No
- Are there people smarter than me who thinks that P = NP?
- Yes
- Why should you care?
- you should know that there are no efficient algorithm to solve NP problems, so don't try finding one
- you should also know that two problems can be very similar, but completely different in terms of complexity
11.0 - P vs NP
Why Should You Care?

Illustration by Stefan Szeider, https://www.ac.tuwien.ac.at/people/szeider/cartoon/
11.0 - P vs NP
Why Should You Care?
Illustration by Stefan Szeider, https://www.ac.tuwien.ac.at/people/szeider/cartoon/
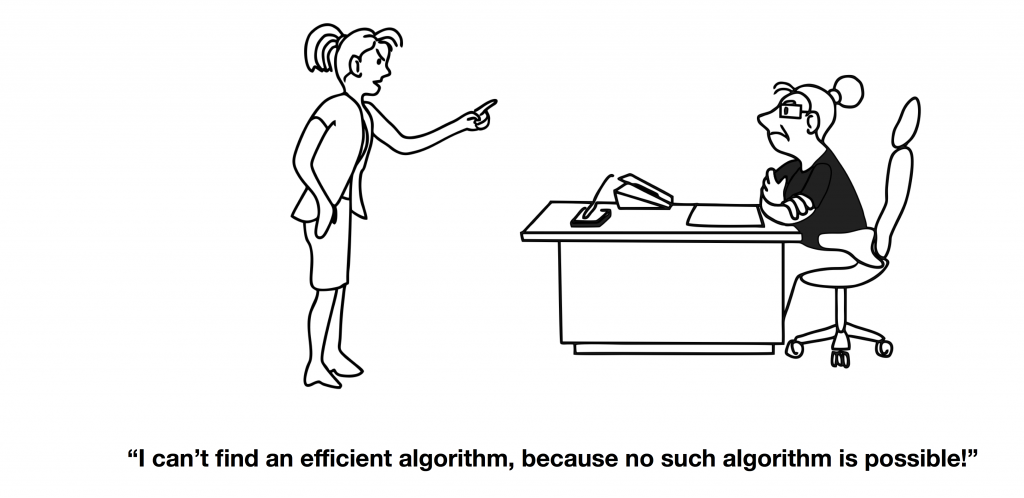
11.0 - P vs NP
Why Should You Care?
Illustration by Stefan Szeider, https://www.ac.tuwien.ac.at/people/szeider/cartoon/
