COMP3010: Algorithm Theory and Design
Daniel Sutantyo, Department of Computing, Macquarie University
3.1 Permutations and Combinations
Search space
3.1 - Permutations and Combinations
- The set of all possible solution is known as the search space or solution space
- When we are brute forcing, we simply go through all possible solution and pick the correct one
- Obviously, we need to be able to generate all possible solutions, and to do this we need to employ techniques from combinatorial mathematics (which for us is just permutations and combinations)
- references: CLRS, Appendix C, Section C.1
Rule of Sum
- The number of ways to choose one element from one or more disjoint sets is the sum of the cardinalities of the sets
- example: a character on the number plate can either be a number of a letter, how many choices do you have?
- set of 1-digit numbers: {0,1,2,3,4,5,6,7,8,9}, cardinality is 10
- set of letters: {A,B,C,…,Y,Z}, cardinality is 26
- number of choices: 26 + 10 = 36 choices
- example: a character on the number plate can either be a number of a letter, how many choices do you have?
3.1 - Permutations and Combinations
Rule of Product
- The number of ways to choose an ordered pair is the number of ways of choosing the first element multiplied by the number of ways of choosing the second element
- example: a single character followed by a one-digit integer (e.g. A9,C5,Z3), has 26∗10=260 combinations
- example: there are 100 2-digit numbers (from 00 to 99)
3.1 - Permutations and Combinations
- A permutation of a finite set S is an ordered sequenceof all elements of S such that each element appears exactly once
- example: The set {a,b,c} has six possible permutations:
- abc,acb,bac,bca,cab,cba
- example: The set {a,b,c} has six possible permutations:
- The number of permutations of a set with n elements is n!
- for the first element in the sequence, you have n choices
- for the second element, you have (n−1) choices, and so on
- hence number of choices = n∗(n−1)∗⋯∗1=n!
Permutation
3.1 - Permutations and Combinations
Permutation
- Given a set of size n, if you only want permutations of length k (called k-permutation) then:
- for the first element in the sequence, you have n choices
- for the second element, you have (n−1) choices,
- but you only want k elements, so you stop after choosing k elements
(for the last element, you have n−k+1 choices)
n∗(n−1)∗⋯∗(n−k+1)=(n−k)!n!
3.1 - Permutations and Combinations
Permutation
- Example: Given the set{a,b,c,d}, how many permutations of 3 elements?
- 4 choices for the first element, 3 choices for the second one, and 2 choices for the last, i.e. a total of 24 permutations:
- abc,acb,bac,bca,cab,cba
- abd,adb,bad,bda,dab,dba
- acd,adc,cad,cda,dac,dca
- bcd,bdc,cbd,cdb,dbc,dcb
- 4 choices for the first element, 3 choices for the second one, and 2 choices for the last, i.e. a total of 24 permutations:
3.1 - Permutations and Combinations
Combination
- Given a set S, how many combinations of unique elements in the set can you make?
- in permutation, the order matter: abc, acb, bca, bac, cab, cba are all different
- but if we just want a combination of 3 elements where ordering does not matter, then there is only one: abc
- For each combination of k elements, there are k! permutations
- so if you want the number of combinations of k elements, divide the number of permutations with k!
3.1 - Permutations and Combinations
Combination
- abc,acb,bac,bca,cab,cba
- abd,adb,bad,bda,dab,dba
- acd,adc,cad,cda,dac,dca
- bcd,bdc,cbd,cdb,dbc,dcb
- {a,b,c}
- {a,b,d}
- {a,c,d}
- {b,c,d}
- Thus, the number of combination of k elements is
k!(n−k)!n!=(kn)
3.1 - Permutations and Combinations
Combination
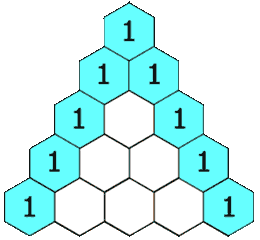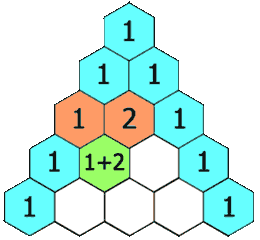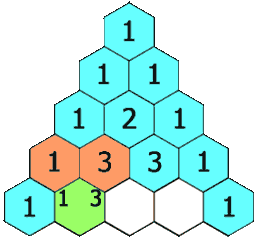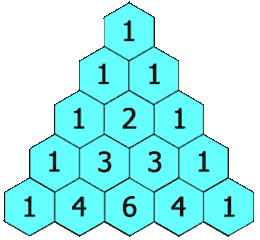
1 4 6 4 1
a b c d
a b c d
a b c
a b d
a c d
b c d
a b
a c
a d
b c
b d
c d
a
b
c
d
3.1 - Permutations and Combinations
Combination
1 4 6 4 1
1 3 3 1
23=8
1 5 10 10 5 1
25=32
24=16
a b c d
10
- The total number of combinations is always 2n because for each item, you can either choose it, or not choose it
a d
b c d
c
1 0 0 1
10
10
10
0 1 1 1
0 0 1 0
3.1 - Permutations and Combinations
Combination
(x+y)4=x4+4x3y+6x2y2+4xy3+y3
(x+y)n=k=0∑n(kn)xkyn−k
- You also use this for binomial expansion
(x+y)3=x3+3x2y+3x2y2+1y3
(x+y)2=x2+2xy+y2
3.1 - Permutations and Combinations
Example
- Question: In how many ways can you choose three distinct numbers from the set {1,2,…,99} so that their sum is even?
- Case 1: All numbers are even
- (349) possibilities since there are 49 even numbers
- Case 2: Two odd numbers, one even number
- (250)∗49
- Total answer: (349)+49∗(250)
3.1 - Permutations and Combinations
Example
- Question: How many ways can you seat n guests on a circular dining table? (assume two seatings arrangements are the same if one can be rotated from the other)
(n−1)! ways (why not n! ?)
A
B
C
D
E
A
B
C
D
E
3.1 - Permutations and Combinations
Final remarks
-
The most important takeaway from permutations and combinations is that you understand that the total number of permutation is n! and the total number of combinations is 2n
- this is where we get O(n!) and O(2n)
3.1 - Permutations and Combinations