COMP3010: Algorithm Theory and Design
Daniel Sutantyo, Department of Computing, Macquarie University
7.1 - Edit Distance
Background
7.1 - Edit Distance
- Edit distance is a the number of edits that we need to do in order to transform one string into another string
- it is used in spelling auto correct
- it is also used to compare DNA sequences (but your phones don't do that)
Background
- In modern devices, the algorithm is tailored not only to the language (and the user's dictionary) but also the keyboard
- have you ever thought about Dvorak keyboard users?
https://www.typing.com/blog/dvorak-keyboard/
7.1 - Edit Distance
Background
https://slate.com/technology/2010/07/how-your-cell-phone-s-autocorrect-software-works-and-why-it-s-getting-better.html
7.1 - Edit Distance
Background
https://arstechnica.com/tech-policy/2016/02/appeals-court-reverses-apple-v-samsung-ii-strips-away-apples-120m-jury-verdict/
"Apple lawyers didn't claim their client invented auto-correction entirely, but they alleged that Samsung had copied Apple's method of doing it."
7.1 - Edit Distance
- The idea is simple: assume the user only made a small typo, and compare what was typed to strings that are 'close enough' to it
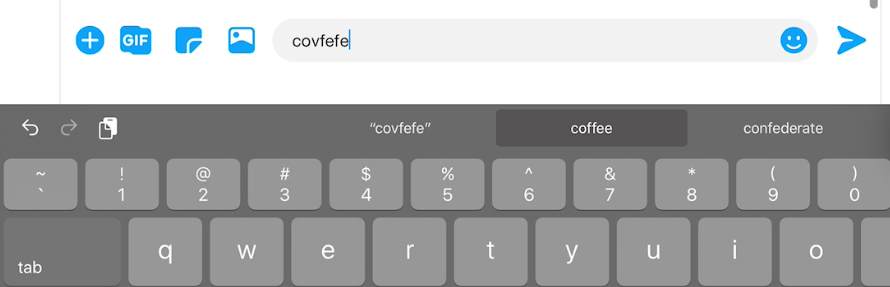
covfefe
coffee
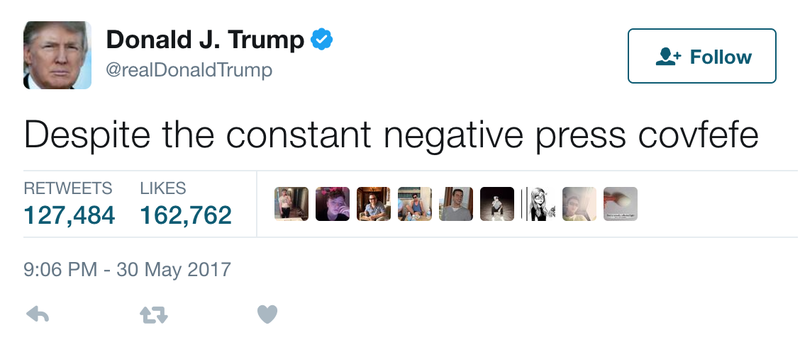
no semantics?
How does it work?
7.1 - Edit Distance
- The idea is simple: assume the user only made a small typo, and compare what was typed to strings that are 'close enough' to it
pl
pls
(but I actually wanted to type "ok" ... )
How does it work?
7.1 - Edit Distance
- The idea is simple: assume the user only made a small typo, and compare what was typed to strings that are 'close enough' to it
plsu
pls
okay
plus
plush
play
How does it work?
7.1 - Edit Distance
plsu
play
okay
plus
How does it work?
7.1 - Edit Distance
How does it work?
- We are going to cover only the basics (going back to the 60s), but please understand that the topic is huge
- you can check out the wikipedia article on approximate string matching for more information
- how about predictive text? plagiarism detector?
7.1 - Edit Distance
Levensthein Distance
- Introduced in 1965
- Levensthein suggested three simple transformations:
- insert a single character
- blck \(\rightarrow\) black
- remove a single character
- blaack \(\rightarrow\) black
- substitute a single character
- blsck \(\rightarrow\) black
- insert a single character
- Each operation is \(O(1)\)
- For this lecture, edit distance refers to the Levensthein distance (the number of operations you need to transform one string to another)
7.1 - Edit Distance
Levensthein Distance
- The discussion in CLRS (Exercise 15-5, page 406) adds a few more operations:
- twiddle: switch the order of two characters:
- balck \(\rightarrow\) black
- kill: stop processing the first string
- blackwhite \(\rightarrow\) black
- copy: copy a character
- black \(\rightarrow\) black
- in CLRS this is 5 copy operations, which is basically comparison, but we're not going to bother with this detail
- twiddle: switch the order of two characters:
7.1 - Edit Distance
Levensthein Distance
- To repeat, we are only going to use insert, remove, and substitute
- Example: kitten to sitting
- substitution:
- kitten \(\rightarrow\) sitten
- substitution:
- sitten \(\rightarrow\) sittin
- insertion:
- sittin \(\rightarrow\) sitting
- substitution:
- So the edit distance is 3
7.1 - Edit Distance
Levensthein Distance
- There are other metrics,
- Damerau-Levenshtein distance (added transposition, i.e. twiddle)
- balck \(\rightarrow\) black is one operation
- Hamming distance (how many bits are different)
- for strings of equal length
- Jaro-Winkler distance
- Damerau-Levenshtein distance (added transposition, i.e. twiddle)
7.1 - Edit Distance
The Algorithm
kitten
sitting
7.1 - Edit Distance
The Algorithm
kitten
sitting
- It is somewhat similar to LCSS
itten
sitting
kitten
itting
itten
itting
tten
sitting
kitten
tting
7.1 - Edit Distance
The Algorithm
kitten
sitting
- Do you have to decide to cut k or s?
- you don't, you just try both
itten
sitting
kitten
itting
itten
itting
tten
sitting
kitten
tting
7.1 - Edit Distance
The Algorithm
kitten
sitting
itten
sitting
kitten
itting
itten
itting
tten
sitting
kitten
tting
-
With edit distance, how do you decide if you should insert, remove, or substitute?
- you don't, you just try all three!
7.1 - Edit Distance
The Algorithm
kitten
sitting
skitten
sitting
sitten
sitting
itten
sitting
kitten
itting
itten
itting
sitten
sitting
stten
sitting
tten
sitting
- We are going to transform the first string into the second string
- i.e. transform kitten to sitting
-
At any point, we have three choices, so we try them all (brute force)
- left arrow: add a character to the start of the first string
- down arrow: substitute a character in the first string
- right arrow: remove the first character of the the first string
7.1 - Edit Distance
The Algorithm
kitten
sitting
skitten
sitting
sitten
sitting
itten
sitting
kitten
itting
itten
itting
sitten
sitting
stten
sitting
tten
sitting
- If the first characters of both string matches, then we can remove both (free operation) and we're left with the smaller subproblem
- Do you see the overlapping subproblems?
7.1 - Edit Distance
The Algorithm
lbak
black
blbak
black
bbak
black
bak
black
lbak
lack
bak
lack
ak
lack
bak
ack
aak
ack
abak
ack
aak
ack
ak
ack
lbak
lack
bak
ack
lak
lack
ak
ack
ak
lack
lak
lack
k
lack
lk
lack
lak
lack
k
lack
lk
lack
7.1 - Edit Distance
The Algorithm
k
lack
7.1 - Edit Distance
The Algorithm
k
lack
lk
lack
k
ack
ak
ack
l
lack
lack
- For the base case, if the first string is empty, then we'll say that we need to insert characters to match the second string
ack
a
ack
ack
7.1 - Edit Distance
The Algorithm
lbak
black
blbak
black
bbak
black
bak
black
lbak
lack
bak
lack
ak
lack
bak
ack
aak
ack
abak
ack
aak
ack
ak
ack
lbak
lack
bak
ack
lak
lack
ak
ack
ak
lack
lak
lack
k
lack
lk
lack
lak
lack
k
lack
lk
lack
7.1 - Edit Distance
The Algorithm
lbak
black
blbak
black
bbak
black
bak
black
lbak
lack
bak
lack
ak
lack
bak
ack
aak
ack
abak
ack
aak
ack
ak
ack
lbak
lack
bak
ack
lak
lack
ak
ack
ak
lack
lak
lack
k
lack
lk
lack
lak
lack
k
lack
lk
lack
7.1 - Edit Distance
The Algorithm
lbak
black
blbak
black
lbak
lack
bak
ack
aak
ack
aak
ack
- lbak \(\rightarrow\) blbak (bl matched)
- bak \(\rightarrow\) aak (a matched)
- ak \(\rightarrow\) ck (ck matched)
- edit distance is 3
7.1 - Edit Distance
The Algorithm
lbak
black
blbak
black
bbak
black
bak
black
lbak
lack
bak
lack
ak
lack
bak
ack
aak
ack
abak
ack
aak
ack
ak
ack
lbak
lack
bak
ack
lak
lack
ak
ack
ak
lack
lak
lack
k
lack
lk
lack
lak
lack
k
lack
lk
lack
7.1 - Edit Distance
The Algorithm
lbak
black
bbak
black
bak
lack
lak
lack
ak
ack
- lbak \(\rightarrow\) bbak (b matched)
- bak \(\rightarrow\) lak (la matched)
- k \(\rightarrow\) ck (ck matched)
- edit distance is 3 as well
7.1 - Edit Distance
The Algorithm
\(\text{EditDistance}(X,Y)\)
\(\text{EditDistance}(y_1\oplus X,Y)\)
\(\text{EditDistance}(y_1\oplus X_2,Y)\)
\(\text{EditDistance}(X_2,Y)\)
- where \(X_2 = x_2x_3\dots x_m\) and \(\oplus\) denotes string concatentation
- or more generally \(X_i\) denotes the substring of \(X\) starting at the i-th character
insert
delete
replace
- Let \(X = x_1x_2\dots x_m\) and \(Y = y_1y2\dots y_n\) be the two strings with \(x_i\) and \(y_i\) being a single character
7.1 - Edit Distance
The Algorithm
- The recursive relation is
- \(\text{EditDistance}(X,Y) = 1 + \min(\quad\text{EditDistance}(y_1\oplus X,Y)\),
- Let \(X = x_1x_2\dots x_m\) and \(Y = y_1y2\dots y_n\) be the two strings with \(x_i\) and \(y_i\) being a single character
\(\text{EditDistance}(X,Y)\)
\(\text{EditDistance}(y_1\oplus X,Y)\)
\(\text{EditDistance}(y_1\oplus X_2,Y)\)
\(\text{EditDistance}(X_2,Y)\)
insert
delete
replace
\(\text{EditDistance}(y_1 \oplus X_2,Y),\)
\(\text{EditDistance}(X_2,Y) \quad)\)
7.1 - Edit Distance
The Algorithm
- Brute-force complexity is roughly \(O(3^m)\), where \(m\) is the length of the first string
- \(1 + 3 + 9 + 27 + \cdots + 3^m\)
\(n\)
\(n\)
\(n-1\)
\(n+1\)
\(1\)
\(3\)
\(9\)
. . . . . . . . . . . . . . . . . . . . . . . . .
7.1 - Edit Distance
Bottom-up Approach
- The top-down DP implementation is quite straightforward (left as an exercise)
- it is not too hard to see the overlapping subproblems
- The bottom-up is very similar to LCSS
7.1 - Edit Distance
Bottom-up Approach
lbak
black
blbak
black
bbak
black
bak
black
lbak
lack
bak
lack
ak
lack
bak
ack
aak
ack
abak
ack
aak
ack
ak
ack
lbak
lack
bak
ack
lak
lack
ak
ack
ak
lack
lak
lack
k
lack
lk
lack
lak
lack
k
lack
lk
lack
7.1 - Edit Distance
Bottom-up Approach
lbak
black
blbak
black
bbak
black
bak
black
lbak
lack
bak
lack
ak
lack
bak
ack
lbak
lack
lak
lack
ak
lack
lak
lack
k
lack
lk
lack
- After an insertion or substitution, we are guaranteed to remove the leading characters
7.1 - Edit Distance
Bottom-up Approach
lbak
black
blbak
black
bbak
black
bak
black
lbak
lack
bak
lack
ak
lack
bak
ack
lbak
lack
lak
lack
ak
lack
lak
lack
k
lack
lk
lack
- After an insertion or substitution, we are guaranteed to remove the leading characters
- Adding a character to the first string is the same as removing a character from the second string (because we matched it)
7.1 - Edit Distance
Bottom-up Approach
lbak
black
bak
black
lbak
lack
bak
lack
ak
lack
bak
ack
ak
lack
k
lack
- After an insertion or substitution, we are guaranteed to remove the leading characters
- Adding a character to the first string is the same as removing a character from the second string (because we matched it)
7.1 - Edit Distance
Bottom-up Approach
lbak
black
bak
black
lbak
lack
bak
lack
ak
lack
bak
ack
k
lack
- After an insertion or substitution, we are guaranteed to remove the leading characters
- Adding a character to the first string is the same as removing a character from the second string (because we matched it)
lbak
ack
ak
black
k
black
7.1 - Edit Distance
Bottom-up Approach
lbak
black
bak
black
lbak
lack
bak
lack
ak
lack
bak
ack
k
lack
- After an insertion or substitution, we are guaranteed to remove the leading characters
- Adding a character to the first string is the same as removing a character from the second string (because we matched it)
lbak
ack
ak
black
k
black
ak
ack
7.1 - Edit Distance
Bottom-up Approach
lbak
black
bak
black
lbak
lack
bak
lack
ak
lack
bak
ack
k
lack
- After an insertion or substitution, we are guaranteed to remove the leading characters
- Adding a character to the first string is the same as removing a character from the second string (because we matched it)
lbak
ack
ak
black
k
black
ak
ack
black
lack
7.1 - Edit Distance
Bottom-up Approach
| lbak | bak | ak | k | ||
| black | 5 | ||||
| lack | 4 | ||||
| ack | 3 | ||||
| ck | 2 | ||||
| k | 1 | ||||
| 4 | 3 | 2 | 1 | 0 |
7.1 - Edit Distance
Bottom-up Approach
| lbak | bak | ak | k | ||
| black | 5 | ||||
| lack | 4 | ||||
| ack | 3 | ||||
| ck | 2 | ||||
| k | 0 | 1 | |||
| 4 | 3 | 2 | 1 | 0 |
7.1 - Edit Distance
Bottom-up Approach
| lbak | bak | ak | k | ||
| black | 4 | 5 | |||
| lack | 3 | 4 | |||
| ack | 2 | 3 | |||
| ck | 1 | 2 | |||
| k | 3 | 2 | 1 | 0 | 1 |
| 4 | 3 | 2 | 1 | 0 |
7.1 - Edit Distance
Bottom-up Approach
| lbak | bak | ak | k | ||
| black | 4 | 5 | |||
| lack | 3 | 4 | |||
| ack | 2 | 3 | |||
| ck | 1 | 2 | |||
| k | 3 | 2 | 1 | 0 | 1 |
| 4 | 3 | 2 | 1 | 0 |
ak
k
k
k
ak
ck
k
ck
7.1 - Edit Distance
Bottom-up Approach
| lbak | bak | ak | k | ||
| black | 4 | 5 | |||
| lack | 3 | 4 | |||
| ack | 2 | 3 | |||
| ck | 1 | 1 | 2 | ||
| k | 3 | 2 | 1 | 0 | 1 |
| 4 | 3 | 2 | 1 | 0 |
ak
k
k
k
ak
ck
k
ck
7.1 - Edit Distance
Bottom-up Approach
| lbak | bak | ak | k | ||
| black | 4 | 5 | |||
| lack | 3 | 4 | |||
| ack | 1 | 2 | 3 | ||
| ck | 1 | 1 | 2 | ||
| k | 3 | 2 | 1 | 0 | 1 |
| 4 | 3 | 2 | 1 | 0 |
ak
ck
k
ck
ak
ack
k
ack
7.1 - Edit Distance
Bottom-up Approach
| lbak | bak | ak | k | ||
| black | 3 | 4 | 5 | ||
| lack | 2 | 3 | 4 | ||
| ack | 1 | 2 | 3 | ||
| ck | 1 | 1 | 2 | ||
| k | 3 | 2 | 1 | 0 | 1 |
| 4 | 3 | 2 | 1 | 0 |
7.1 - Edit Distance
Bottom-up Approach
| lbak | bak | ak | k | ||
| black | 2 | 3 | 4 | 5 | |
| lack | 2 | 2 | 3 | 4 | |
| ack | 2 | 1 | 2 | 3 | |
| ck | 2 | 1 | 1 | 2 | |
| k | 3 | 2 | 1 | 0 | 1 |
| 4 | 3 | 2 | 1 | 0 |
7.1 - Edit Distance
Bottom-up Approach
| lbak | bak | ak | k | ||
| black | 3 | 2 | 3 | 4 | 5 |
| lack | 2 | 2 | 2 | 3 | 4 |
| ack | 3 | 2 | 1 | 2 | 3 |
| ck | 3 | 2 | 1 | 1 | 2 |
| k | 3 | 2 | 1 | 0 | 1 |
| 4 | 3 | 2 | 1 | 0 |
7.1 - Edit Distance