COMP333 Algorithm Theory and Design - W3 2019

COMP333

Algorithm Theory and Design

Daniel Sutantyo

Department of Computing

Macquarie University

Lecture slides adapted from lectures given by Frank Cassez, Mark Dras, and Bernard Mans

Summary of Week 1 & 2

Problems
- definition (input and output), types of problems
- tractable vs intractable
Algorithms
- complexity analysis (asymptotic notation)
- recurrence equation, recursion-tree
Algorithm correctness
- induction (recursive algorithms)
- loop invariants

void selection_sort(int arr[]){
  for (int i = 0; i < n-1; i++){
    int min_index = i;
    for (int j = i+1; j < n; j++){
      if (arr[j] < arr[min_index])
        min_index = j;
    }
    swap(i,min_index);
  }
}

"The subarray A[0 .. i-1] is in sorted order and all the values in A[0 .. i-1] are smaller than or equal to the values in A[i..n-1]"

Loop invariant

selection sort

void selection_sort(int arr[]){
  int n = arr.length; // added this line
  for (int i = 0; i < n-1; i++){
    int min_index = i;
    for (int j = i+1; j < n; j++){
      if (arr[j] < arr[min_index])
        min_index = j;
    }
    swap(i,min_index);
  }
}

A[0 .. i-1] is in sorted order
Values in A[0 .. i-1] are less than or equal to the values in A[i..n-1]

Input: [ 17 41 15 33 66 24 91 60 ]

Initialisation: i = 0

The subarray A[0 .. -1] is an empty array, so it is trivially in sorted order (by convention, we say an empty array is sorted)
The subarray A[0 .. -1] is an empty array, so all the values in this subarray are $\le$ the values in A[0 .. n-1]

void selection_sort(int arr[]){
  int n = arr.length; // added this line
  for (int i = 0; i < n-1; i++){
    int min_index = i;
    for (int j = i+1; j < n; j++){
      if (arr[j] < arr[min_index])
        min_index = j;
    }
    swap(i,min_index);
  }
}

A[0 .. i-1] is in sorted order
Values in A[0 .. i-1] are less than or equal to the values in A[i..n-1]

Array: [ 15 41 17 33 66 24 91 60 ]

To convince yourself (or others), you may want to show that the loop invariant is still correct after we perform the 1st of the loop (i.e. i = 1)

the inner loop (line 4-8) finds the smallest value in A[0 .. n-1] and then swap it with A[0]
at the end of the iteration i is incremented by 1
the subarray A[0 .. 0] contains one element, so it is sorted
the subarray A[0 .. 0] contains the smallest value in A[0 .. n-1], so obviously it is $\le$ all the values in A[1 .. n-1]

A[0 .. i-1] is in sorted order
Values in A[0 .. i-1] are less than or equal to the values in A[i..n-1]

Array: [ 15 17 24 33 66 41 91 60 ]

Maintenance: assume the loop invariant is true when i = k

show the loop invariant is true when i = k + 1

in the loop:
- the inner loop (line 4-8) finds the smallest value in A[k .. n-1] and then swap the smallest value with A[k]
- i is incremented by 1
at end of iteration i = k+1:
- the subarray A[0 .. k] is sorted because A[k] was a value in A[k .. n-1], and by our assumption, it is $\ge$ integers in A[ 0 .. k-1]
- if follows that the values in A[k+1 .. n-1] are $\ge$ values in A[0 .. k]

we assume:
- the subarray A[0 .. k-1] is in sorted order
- the values in A[0 .. k-1] are less than or equal to the values in A[k .. n-1]

A[0 .. i-1] is in sorted order
Values in A[0 .. i-1] are less than or equal to the values in A[i..n-1]

Array: [ 15 17 24 33 41 60 66 91 ]

Termination: loop guard is i < n-1, hence at termination i = n-1

from the previous slide (maintenance), we have shown that the loop invariant is maintained, and so when i = n-1
- the subarray A[0 .. n-2] is in sorted order
- the values in A[0 .. n-2] are less than or equal to the value in A[n-1 .. n-1]

void selection_sort(int arr[]){
  int n = arr.length; // added this line
  for (int i = 0; i < n-1; i++){
    int min_index = i;
    for (int j = i+1; j < n; j++){
      if (arr[j] < arr[min_index])
        min_index = j;
    }
    swap(i,min_index);
  }
}

A[0 .. i-1] is in sorted order
Values in A[0 .. i-1] are less than or equal to the values in A[i..n-1]

Array: [ 15 17 24 33 41 60 66 91 ]

Proving the code is correct:
- the subarray A[0 .. n-2] is in sorted order
- the values in A[0 .. n-2] are less than or equal to the value in A[n-1 .. n-1]
From the above two points, we can infer that the array A[0 .. n-1] is sorted
- note that the loop invariant doesn't actually say that A[0 .. n-1] is sorted
- you also need to show that the loop terminates

void selection_sort(int arr[]){
  int n = arr.length; // added this line
  for (int i = 0; i < n-1; i++){
    int min_index = i;
    for (int j = i+1; j < n; j++){
      if (arr[j] < arr[min_index])
        min_index = j;
    }
    swap(i,min_index);
  }
}

int eval(int[] c, int x) {
  int y = 0, t = 1, n = c.length-1;
  for (int i = 0; i <= n; i++) {
    y = y + t * c[i];
    t = t * x;
  }
  return y;
}

$ i = 0\quad\rightarrow\quad y = c_0$

Loop invariant

polynomial evaluation

\[ f(x) = c_nx^n + c_{n-1}x^{n-1} + \cdots +c_1x + c_0 \]

$ i =1\quad\rightarrow\quad y = c_0 + c_1x$

$ i =2\quad\rightarrow\quad y = c_0 + c_1x + c_1x^2$

in the end, will we have $ y = c_0 + c_1x + c_1x^2 + \cdots + c_nx^n$?

The loop invariant holds at initialisation (we consider an empty sum to be 0)

int eval(int[] c, int x) {
  int y = 0, t = 1, n = c.length-1;
  for (int i = 0; i <= n; i++) {
    y = y + t * c[i];
    t = t * x;
  }
  return y;
}

\[ y = \sum_{j = 0}^{i-1} c_jx^j = c_0 + c_1x + \cdots + c_{i-1}x^{i-1}\]

Loop invariant:

\[ i = 0\quad\rightarrow\quad y = \sum_{j = 0}^{-1} c_jx^j = 0, t = x^0 = 1 \]

Initialisation: i = 0, t = 1, y = 0

\[t = x^i\]

int eval(int[] c, int x) {
  int y = 0, t = 1, n = c.length-1;
  for (int i = 0; i <= n; i++) {
    y = y + t * c[i];
    t = t * x;
  }
  return y;
}

\[ i = 1\quad\rightarrow\quad y = \sum_{j = 0}^{0} c_jx^j = c_0, t = x \]

As before, you may want to check if the loop invariant holds when i = 1 (after we perform the first iteration)
- we multiply $t = 1$ with $c_0$, and add this to $y$, thus $y = c_0$
- we multiply $t$ by $x$, thus $t = x$
- we increment i by 1

\[ y = \sum_{j = 0}^{i-1} c_jx^j = c_0 + c_1x + \cdots + c_{i-1}x^{i-1}\]

Loop invariant:

\[t = x^i\]

Maintenance: assume the loop invariant is true when i = k

show the loop invariant is true when i = k + 1

in the loop:
- we multiply $t = x^i$ with $c_k$, and add this to $y$
  - thus $y = c_0 + c_1x + \cdots + c_{k-1}x^{k-1} + c_kx^k$
- we multiply $t$ by $x$, thus $t = x^{k+1}$
- we increment i by 1
thus the loop invariant is true at the end of the iteration when i = k+1

at the start of the iteration i = k, we assume

\[ y = \sum_{j = 0}^{k-1} c_jx^j = c_0 + c_1x + \cdots + c_{k-1}x^{k-1}, \qquad t = x^k\]

\[ y = \sum_{j = 0}^{i-1} c_jx^j = c_0 + c_1x + \cdots + c_{i-1}x^{i-1}\]

Loop invariant:

\[t = x^i\]

int eval(int[] c, int x) {
  int y = 0, t = 1, n = c.length-1;
  for (int i = 0; i <= n; i++) {
    y = y + t * c[i];
    t = t * x;
  }
  return y;
}

\[ i = n+1\quad\rightarrow\quad y = \sum_{j = 0}^{n} c_jx^j = c_0 + c_1x + \cdots + c_nx^n, t = x^{n+1} \]

\[ y = \sum_{j = 0}^{i-1} c_jx^j = c_0 + c_1x + \cdots + c_{i-1}x^{i-1}\]

Loop invariant:

\[t = x^i\]

Termination: the loop guard is i <= n, hence at termination, i = n+1

from the previous slide, we proved that the loop invariant is true at termination of the loop, and so we have

the correctness of the algorithm follows immediately from the loop invariant

Exhaustive Search

exhaustive search

complete search

generate and test

brute-force algorithms

Exhaustive search

Tractable vs intractable problem
Search space, search space tree
Recursive backtracking
Pruning

Why study algorithms?

Obvious solutions are not always tractable
- tractable: can be solved in polynomial time, i.e. 'easy'
Tractable solutions can be improved
Recognise hard problems
- prevents us from wasting time looking for an efficient solution

We consider problems that can be solved by a polynomial-time algorithm as being tractable (or easy)
If a problem has no known polynomial-time algorithm that can be used to solve it, then we call them intractable (or hard)
- or if the problem can only be solved using superpolynomial-time algorithms
- think $O(2^n)$ or $O(n!)$

Why study algorithms

intractable vs tractable problems

Just because a problem is hard, it does not mean that it is hard to come up with a solution for it
Coming up with an efficient solution for a tractable problem can be difficult
Coming up with a solution for a tractable or intractable problem is generally not that difficult
Tractable/intractable solution?

😎

Why study algorithms

intractable vs tractable problems

😎

Why study algorithms

intractable vs tractable problems

intractable solution
for
a tractable problem

intractable solution
for
intractable problem

Assuming the problem can be solved, you should always be able to find a brute-force solution
- aside: are there problems that cannot be solved?
In fact, for most problems, our first solution is often going to be the exhaustive search or brute-force search
An exhaustive search is a problem-solving technique where we enumerate all possible candidates for the solution, and then choose the best one

Why study algorithms

intractable vs tractable problems

It is a good starting point
- it is easy to write
- by doing a brute force solution you can find patterns in the solution which can lead to a better algorithm
Sometimes it is the only solution

Why brute force?

The set of all possible solution is known as the search space or solution space
To generate all possible combinations in the search space, we have to employ techniques from combinatorial math (often just permutations and combinations)
Let's do a quick review

Search space

Rule of sum: the number of ways to choose one element from one or two disjoint sets is the sum of the cardinalities of the sets
- example: a character on the number plate can either be a number of a letter, how many choices do you have?
  - set of 1-digit numbers: $\{0,1,2,3,4,5,6,7,8,9\}$, cardinality is 10
  - set of letters: $\{A,B,C,\dots,Y,Z\}$, cardinality is 26
  - number of choices: 26 + 10 = 36 choices

Search space

permutations and combinations

(references: CLRS, Appendix C, Section C.1)

Rule of product: number of ways to choose an ordered pair is (the number of ways of choosing the first element) multiplied by (the number of ways of choosing the second element)
- example: a single character followed by a one-digit integer (e.g. $A9, C5, Z3$), has $26 * 10 = 260$ combinations
- example: there are 100 2-digit numbers (from 00 to 99)

Search space

permutations and combinations

(references: CLRS, Appendix C, Section C.1)

Permutation: a permutation of a finite set $S$ is an ordered sequence of all elements of $S$ such that each element appears exactly once
- example: The set $\{a,b,c\}$ has six possible permutations:
  - $abc, acb, bac, bca, cab, cba$
The number of permutations of a set with $n$ elements is $n!$
- for the first element in the sequence, you have $n$ choices
- for the second element, you have $(n-1)$ choices, and so on
- hence number of choices = $n*(n-1)*\cdots*1 = n!$

Search space

permutations and combinations

(references: CLRS, Appendix C, Section C.1)

Given a set of size $n$, if you only want permutations of length $k$ (called $\text{$k$-permutation}$) then:
- for the first element in the sequence, you have $n$ choices
- for the second element, you have $(n-1)$ choices,
- but you only want $k$ elements, so you stop after choosing $k$ elements
  
  (for the last element, you have $n-k+1$ choices)

Search space

permutations and combinations

(references: CLRS, Appendix C, Section C.1)

\[n * (n-1) * \cdots * (n-k+1) = \frac{n!}{(n-k)!}\]

Search space

permutations and combinations

(references: CLRS, Appendix C, Section C.1)

Example: Given the set$\{a,b,c,d\}$, how many permutations of 3 elements?
- 4 choices for the first element, 3 choices for the second one, and 2 choices for the last, i.e. a total of 24 permutations:
  - $abc,acb,bac,bca,cab,cba$
  - $abd,adb,bad,bda,dab,dba$
  - $acd,adc,cad,cda,dac,dca$
  - $bcd,bdc,cbd,cdb,dbc,dcb$

Search space

permutations and combinations

(references: CLRS, Appendix C, Section C.1)

Given a set $S$, how many combinations of unique elements in the set can you make?
- in permutation, the order matter: $abc$, $acb$, $bca$, $bac$, $cab$, $cba$ are all different
- but if we just want a combination of 3 elements where ordering does not matter, then there is only one: $abc$
For each combination of $k$ elements, there are $k!$ permutations
- so if you want the number of combinations of $k$ elements, divide the number of permutations with $k!$

Search space

permutations and combinations

(references: CLRS, Appendix C, Section C.1)

$abc,acb,bac,bca,cab,cba$
$abd,adb,bad,bda,dab,dba$
$acd,adc,cad,cda,dac,dca$
$bcd,bdc,cbd,cdb,dbc,dcb$

$\{a,b,c\}$
$\{a,b,d\}$
$\{a,c,d\}$
$\{b,c,d\}$

Thus, the number of combination of $k$ elements is

\[\frac{n!}{k!(n-k)!} = \binom{n}{k}\]

Search space

permutations and combinations

(references: CLRS, Appendix C, Section C.1)

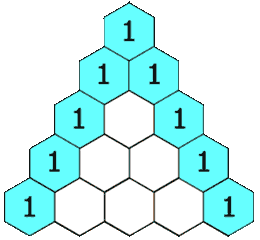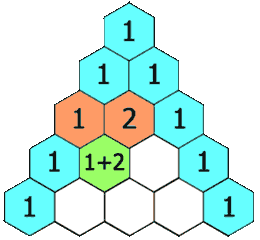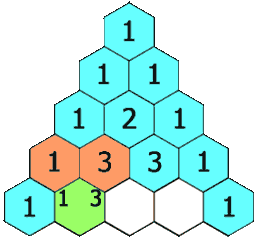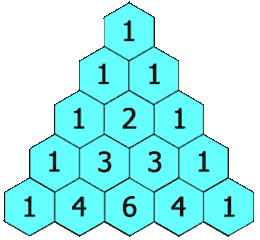
Search space

permutations and combinations

(references: CLRS, Appendix C, Section C.1)

1 4 6 4 1

a b c d

a b c

a b d

a c d

b c d

a b

a c

a d

b c

b d

c d

Search space

permutations and combinations

(references: CLRS, Appendix C, Section C.1)

1 4 6 4 1

$2^4 = 16$

1 5 10 10 5 1

$2^5 =32$

1 3 3 1

$2^3 = 8$

a b c d

$\frac{0}{1}$

The total number of combinations is always $2^n$ because for each item, you can either choose it, or not choose it

a d

b c d

1 0 0 1

$\frac{0}{1}$

0 1 1 1

0 0 1 0

Search space

permutations and combinations

(references: CLRS, Appendix C, Section C.1)

\[(x+y)^4 = x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^3\]

\[(x+y)^n = \sum_{k=0}^n \binom{n}{k} x^ky^{n-k}\]

Search space

permutations and combinations

(references: CLRS, Appendix C, Section C.1)

Question: In how many ways can you choose three distinct numbers from the set $\{1,2,\dots,99\}$ so that their sum is even?

Case 1: All numbers are even
- $\binom{49}{3}$ possibilities since there are 49 even numbers
Case 2: Two odd numbers, one even number
- $\binom{50}{2} * 49$
Total answer: $\binom{49}{3} + 49 * \binom{50}{2}$

Search space

permutations and combinations

(references: CLRS, Appendix C, Section C.1)

Question: How many ways can you seat $n$ guests on a circular dining table? (assume two seatings arrangements are the same if one can be rotated from the other)

$(n-1)!$ ways (why not $n!$ ?)

Let us use an example to illustrate

Search space

We have a bunch of metallic bars with known lengths. Sometimes we need to produce a bar of a certain length from the bars that we have.

We are not allowed to cut up any metallic bar, but we can solder any two rods together to create a longer bar.

Search space

We have a bunch of metallic bars with known lengths. Sometimes we need to produce a bar of a certain length from the bars that we have.

We are not allowed to cut up any metallic bar, but we can solder any two rods together to create a longer bar.

The input is the lengths of the metallic bars that we have, and the length of the metallic bar that we want to make
- e.g. bars = [ 10, 12, 5, 7, 11 ], target = 25
The output is 'yes' if we are able to make a bar of the given length, and 'no' otherwise

Search space

We have a bunch of metallic bars with known lengths. Sometimes we need to produce a bar of a certain length from the bars that we have

We are not allowed to cut up any metallic bar, but we can solder any two rods together to create a longer bar

Input: The array $B = \{b_1, b_2, \dots, b_n\}$ containing the lengths of the bars and an integer $L \ge 0$
Output: True if there is a subarray $\{b_{i_0}, b_{i_1}, \dots, b_{i_k}\}, 1 \le i_j \le n$ such that

\[\sum_{j=0}^k b_{i_j} = L\]

Search space

Sample input: [10, 12, 5, 7, 11]
- L = 25, there is no solution
- L = 22, there are multiple solutions
We know that there are $2^5 = 32$ combinations, but how do we actually enumerate them?

for (int i = 0; i < b.length; i++){
  for (int j = 0; j < b.length; j++){
    for (int k = 0; k < b.length; k++){
      for (int l = 0; l < b.length; l++){
         for (int m = 0; m < b.length; m++){
            ...
}}}}}

Search space

Given [10, 12, 5, 7, 11], can we make 25?
- reduce the problem to subproblems
  - if you pick 10, then, we still need to make 15
  - if you do not pick 10, then we still need to make 25

Search space

public static boolean solve(int[] b, int i, int L) {
  // if L == 0, we are done
  if (L == 0){
    return true;
  }
  // if we get to the end of array but still can't make the sum, 
  // return false
  if (i >= b.length) {
    return false;
  }
  // else keep on going with the remaining sum
  return solve(b,i+1,L-b[i]) || solve(b,i+1,L);
}

if (L == 0), we are done since we managed to make the sum earlier, so stop the program
solve(b,index+1,L-b[index]): pick the current element, keep going
solve(b,index+1,L): don't pick the current element, keep going

Search space

[10,12,5,7,11] L = 25

[12,5,7,11] L = 15

[12,5,7,11] L = 25

don't pick 10

pick 10

[5,7,11] L = 3

[5,7,11] L = 15

[5,7,11] L = 25

don't pick 12

pick 12

don't pick 12

[7,11] L = -2

[11] L = -9

pick 5

pick 7

...

[7,11] L = 15

[11] L = 8

pick 7

don't pick 5

...

don't pick 7

...

[11] L = 15

[7,11] L = 15

pick 5

...

Search space

Another example: produce all possible combinations of three unique letters in the English alphabet
- e.g. abc, abd, abe, ..., ayz, bcd, bce, ..., xyz

Search space

"a"

"ab"

"a"

"b"

"abc"

"ab"

"ac"

"a"

"bc"

"b"

"c"

a ?

b ?

c ?

d ?

"abd"

"ab"

"bcd"

"bc"

"d"

... ...

(and so on)

Search space

The search space is actually a tree
- here I am going to refer to it as the decision tree or search tree

Is it always a binary tree?

Search space

Is it always a binary tree?
Problem: generate all possible license plate

Search space

Is it always a binary tree?
Problem: generate all possible license plate

"a" "b" "c" ..... "9" "0"

Search space

If your search space is a tree, then how do you traverse through a tree (or more generally, how do you traverse a graph)?
You can use either DFS or BFS

public static boolean solve(int[] b, int i, int L) {
  // if L == 0, we are done
  if (L == 0){
    return true;
  }
  // if we get to the end of array but still can't make the sum, 
  // return false
  if (i >= b.length) {
    return false;
  }
  // else keep on going with the remaining sum
  return solve(b,i+1,L-b[i]) || solve(b,i+1,L);
}

Search space

DFS or BFS

[10,12,5,7,11] L = 25

[12,5,7,11] L = 15

[12,5,7,11] L = 25

don't pick 10

pick 10

[5,7,11] L = 3

[5,7,11] L = 15

[5,7,11] L = 25

don't pick 12

pick 12

don't pick 12

[7,11] L = -2

[11] L = -9

pick 5

pick 7

...

[7,11] L = 15

[11] L = 8

pick 7

don't pick 5

...

don't pick 7

...

[11] L = 15

[7,11] L = 15

pick 5

...

Search space

DFS or BFS

"a"

"ab"

"a"

"b"

"abc"

"ab"

"ac"

"a"

"bc"

"b"

"c"

a ?

b ?

c ?

d ?

"abd"

"ab"

"bcd"

"bc"

"d"

... ...

(and so on)

Search space

DFS or BFS

You will be using DFS almost all the time because this is the natural way to think when writing a recursive algorithm
- our task is often to produce all bitstrings of length n
- we build our solution incrementally
  - 0 -> 01 -> 011 -> 0110 -> 01101 etc
  - when we backtrack, we do so in a way that minimises the work we have to do
    - to build 01100 from 01101, it is easiest to backtrack to 0110

Search space

recursive backtracking

"a"

"ab"

"a"

"b"

"abc"

"ab"

"ac"

"a"

"bc"

"b"

"c"

a ?

b ?

c ?

d ?

"abd"

"ab"

"bcd"

"bc"

"d"

... ...

backtrack

(and so on)

Recursive backtracking

Recursive backtracking (or just backtracking) is a technique to produce a solution by iterating through all possible configurations of the search space
- i.e. what we have been doing in the last few slides
At each node of the search tree we check if we have the solution:
- if yes, great (unless we have to find more)
- if not, then we can try to extend our solution
- if we cannot go anywhere else, then we backtrack, going to a more 'primitive' solution and starting again from there

Recursive backtracking is essentially just a DFS traversal on the search tree
Can you do BFS instead?
- Problem: generate all combinations of 3 unique letters
  - DFS: a -> ab -> abc (backtrack) abd (backtrack) abe
  - BFS:
    - generate a, b, c, d, e, ..., z
    - generate ab, ac, ad, ae, ... az, ba, ..., yz

Recursive backtracking

Some literature make a distinction between backtracking and branch-and-bound (or pruning)
The idea is the same, you perform a DFS on the search tree, and at every node, you can make the decision to stop and backtrack
- backtracking is a more general, you generally keep on going until it is no longer feasible (e.g. searching problem)
- branch-and-bound adds an additional stopping constraint: if you have found a better solution (e.g. optimisation problem)

Recursive backtracking

branch and bound

With branch-and-bound method, we can apply a bounding function at every node to see if there is any point in doing further recursion
If there is no point in doing further recursions, then we can prune the search tree, reducing the number of cases that we need to evaluate
- I have also seen 'pruning function' and 'feasibility function' being used instead of 'bounding function'

Recursive backtracking

branch and bound

We have a bunch of metallic bars with known lengths. Sometimes we need to produce a bar of a certain length from the bars that we have.

We are not allowed to cut up any metallic bar, but we can solder any two rods together to create a longer bar.

Recursive backtracking

branch and bound

Example: Given [ 50, 2, 18, 11, 9, 23, 5, 10, 30, 6, 17 ]
- can we make 27?

Recursive backtracking

branch and bound

[ 50, 2, 18, 11, 9, 23, 5, 10, 30, 6, 17 ] L = 27

[2, 18, 11, ..., 17 ] L = -23

[2, 18, 11, ..., 17 ] L = 27

don't pick 50

pick 50

[18, 11, ... , 17] L = -25

don't pick 2

pick 2

don't pick 2

...

[18, 11, ... , 17] L = -23

[18, 11, ... , 17] L = 25

[18, 11, ... , 17] L = 27

...

Recursive backtracking

branch and bound

Once we hit a negative sum, there is no point in going on since (i.e. we can prune that path)

public static boolean solve(int[] b, int i, int L) {
  // if L == 0, we are done
  if (L == 0){
    return true;
  }
  // if L is negative or we get to the end of the array
  // return false
  if (i >= b.length || L < 0) {
    return false;
  }
  // else keep on going with the remaining sum
  return solve(b,i+1,L-b[i]) || solve(b,i+1,L);
}

Example: Given [50, 2, 18, 11, 9, 23, 5, 10, 30, 6, 17 ]
- can we make 27?

Recursive backtracking

branch and bound

Can you suggest a small change that will make the search tree smaller?
- note that this algorithm is $O(2^n)$, so you can do whatever you want with the data and it probably won't make that much of a difference

Example: Given [ 50, 2, 18, 11, 9, 23, 5, 10, 30, 6, 17 ]
- can we make 27? Yes, [2, 11, 9, 5]

Recursive backtracking

branch and bound

If you sort the input in descending order, we can prune earlier:
- [ 50, 2, 18, 11, 9, 23, 5, 10, 30, 6, 17 ] L = 27
  - we are going to try a lot of combinations starting with 2
- [ 50, 30, 23, 18, 17, 11, 10, 9, 6, 5, 2 ] L = 27
  - we pretty much ignore the first 2 entries
  - we get our answer quite early

Recursive backtracking

branch and bound

Be careful not to write an inefficient pruning function
- our pruning function in the previous example is just an integer comparison, so it is O(1)
- can you think of a bad pruning function?

public static boolean solve(int[] b, int i, int L) {
  // if L == 0, we are done
  if (L == 0){
    return true;
  }
  // if L is negative or we get to the end of the array
  // return false
  if (i >= b.length || L < 0) {
    return false;
  }
  // else keep on going with the remaining sum
  return solve(b,i+1,L-b[i]) || solve(b,i+1,L);
}

Recursive backtracking

branch and bound

public static boolean solve(int[] b, int i, int L) {
  // if L == 0, we are done
  if (L == 0){
    return true;
  }
  // if L is negative or we get to the end of the array
  // return false
  if (i >= b.length || L < 0 || sum(b,i) < L) {
    return false;
  }
  // else keep on going with the remaining sum
  return solve(b,i+1,L-b[i]) || solve(b,i+1,L);
}

Recursive backtracking

branch and bound

[ 50, 2, 18, 11, 9, 23, 5, 10, 30, 6, 17 ] L = 27
[ 50, 30, 23, 18, 17, 11, 10, 9, 6, 5, 2 ] L = 27
If the problem is an optimisation problem then we can add another criteria for pruning
- the optimal answer is (18 + 9) or (17 + 10)
- once we know the optimal answer only takes 2 bars, we can stop recursing every time we have evaluated any 2 bars, this is our bounding function

Recursive backtracking

branch and bound

Ideally, we want our pruning function to exit as early as possible, thus reducing the size of the search tree
In this example, it can be achieved by sorting the input data in descending order
- is this something that we should always do?

Recursive backtracking

heuristics

[ 50, 30, 23, 18, 17, 11, 10, 9, 6, 5, 2 ]
[ 50, 2, 18, 11, 9, 23, 5, 10, 30, 6, 17 ]
L = 27, which input gives you the smaller search tree?
L = 12, which input gives you the smaller search tree?
we cannot be sure that sorting the input in descending order will always give the best performance
- but it probably is a good idea
- this is a form of heuristics

Recursive backtracking

heuristics

"Heuristic search algorithms have an air of voodoo about them" - Skiena, page 247
A heuristic is a problem solving approach that is practical, but not guaranteed to be optimal (or even rational)
- educated guess, rule of thumb, common sense, experience
- the most fundamental form of heuristic is trial and error
- you can read more about heuristics in Chapter 7 of Skiena

Recursive backtracking

heuristics

Example of using heuristics:
- what should be your bounding function?
  - random sampling
  - greedy method
  - prior knowledge / experience
- how should you pick your next case
  - greedy method
  - random
  - local search

L = 48 [ 18, 11, 10, 6 ]

[ 17, 11, 10, 9 ]

Recursive backtracking

heuristics methods

Random sampling
Local search
Simulated annealing

Recursive backtracking

general tips

Prune early
Use precomputation
See if you can work backward
- these are my input, what kind of solution space do I have?
- this is the solution space, which input can produce this?

Recursive backtracking

general tips

Use an efficient data structure

// this here is a C++ code
// n is the size of the array
for (i = 0; i < (1 << n); i++){
  sum = 0;
  for (int j = 0; j < n; j++)
     if (i & (1 << j))
        sum = sum + b[j];
}

i : 0 to $2^n$

i : 110000010

j : 100000000

j : 010000000

j : 000000010

pick b[8]

pick b[7]

pick b[1]

Summary

exhaustive search

Permutation and combination
Brute force:
- use starting point or to find patterns in solutions
- sometimes it is the only solution
Search space, search tree, DFS
- recursive backtracking (pruning function)
- branch and bound (bounding function)
Heuristics

Summary

Algorithm complexity (running time, recursion tree)
Algorithm correctness (induction, loop invariants)
Problem solving methods:
- exhaustive search
- dynamic programming
- greedy method
- divide-and-conquer
- probabilistic method
- algorithms involving strings
- algorithms involving graphs