COMP333
Algorithm Theory and Design
Daniel Sutantyo
Department of Computing
Macquarie University
Lecture slides adapted from lectures given by Frank Cassez, Mark Dras, and Bernard Mans
Summary
- Algorithm complexity (running time, recursion tree)
- Algorithm correctness (induction, loop invariants)
-
Problem solving methods:
- exhaustive search
- dynamic programming
- greedy method
- divide-and-conquer
- probabilistic method
- algorithms involving strings
- algorithms involving graphs
Summary
- Exhaustive search:
- Problems and subproblems, search tree, backtracking
- Dynamic programming:
- Optimal substructure
- Overlapping subproblems
public static int fib(int n) {
if (n <= 2)
return 1;
else return fib(n-1) + fib(n-2);
}Fibonacci
(the obligatory dynamic programming example)
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...
public static int fib(int n) {
if (n <= 2)
return 1;
else return fib(n-1) + fib(n-2);
}Fibonacci
fib(10)
fib(9)
fib(8)
fib(8)
fib(7)
fib(7)
fib(6)
fib(6)
fib(6)
fib(5)
fib(6)
fib(5)
fib(5)
fib(4)
fib(7)
fib(6)
fib(5)
...
...
...
...
Fibonacci
number recursive calls
public static int fib(int n) {
if (n <= 2)
return 1;
else return fib(n-1) + fib(n-2);
}| n | fib(n) | no. of recursive calls |
|---|---|---|
| 10 | 55 | 109 |
| 20 | 6,765 | 13,529 |
| 30 | 832,040 | 1,664,079 |
| 40 | 102,334,155 | 204,668,309 |
| 50 | 12,586,269,025 | 25,172,538,049 |
| 60 | ??? | ??? |
Fibonacci
top down dynamic programming
(memoisation)
public static long table[] = new long[1000];
public static int fib(int n) {
if (table[n] != 0)
return table[n];
else {
table[n] = fib2(n-1) + fib2(n-2);
return table[n];
}
}Fibonacci
top down dynamic programming
(tabulation)
fib(10)
fib(9)
fib(8)
fib(8)
fib(7)
fib(6)
fib(6)
fib(5)
fib(7)
...
Fibonacci
bottom-up dynamic programming
public static long fib(int n) {
long a = 0;
long b = 1;
for (int i = 0; i < n; i++) {
b = a + b;
a = b - a;
}
return a;
}
recursion
top-down
DP
bottom-up
DP
???
Dynamic Programming
dynamic programming vs divide-and-conquer
- We are going to discuss divide-and-conquer strategy in Week 6
- However, you should already understand how divide-and-conquer strategy works (from COMP125 and COMP225):
- Divide the problem into smaller subproblems
- Conquer the subproblems
- Combine the solutions to the subproblem into the solution for the original problem
Dynamic Programming
dynamic programming vs divide-and-conquer
- Questions:
- is the first version of recursive fibonacci algorithm a divide-and-conquer algorithm?
- is binary search a divide-and-conquer algorithm?
- is linear search a divide-and-conquer algorithm?
- is the first version of recursive fibonacci algorithm a divide-and-conquer algorithm?
public static int fib(int n) {
if (n <= 2)
return 1;
else return fib(n-1) + fib(n-2);
}Dynamic Programming
dynamic programming vs divide-and-conquer
fib(n)
fib(n-1)
fib(n-2)
linear_search(0,n)
linear_search(0,0)
linear_search(1,n)
binary_search(0,n)
binary_search(0,n/2)
binary_search(n/2+1,n)
Dynamic Programming
dynamic programming vs divide-and-conquer
fib(n)
fib(n-1)
fib(n-2)
merge_sort(0,n)
merge_sort(0,n/2)
merge_sort(n/2+1,n)
Dynamic Programming
dynamic programming vs divide-and-conquer
fib(n)
fib(n-1)
fib(n-2)
m_sort(0,n)
m_sort(0,n/2)
m_sort(n/2+1,n)
fib(n-2)
fib(n-3)
fib(n-3)
fib(n-4)
m_sort(0,n/4)
m_sort(n/4+1,n/2)
m_sort(n/2+1,3n/4)
m_sort(3n/4+1,n)
Dynamic Programming
dynamic programming vs divide-and-conquer
fib(n)
fib(n-1)
fib(n-2)
fib(n-2)
fib(n-3)
fib(n-3)
fib(n-4)
-
Overlapping subproblems: the subproblems share subsubproblems
- computing this subsubproblem twice (or more) is a waste!
Dynamic Programming
dynamic programming vs divide-and-conquer
- Dynamic programming is a divide-and-conquer approach
- think of it as a 'smarter' recursive backtracking
- The main difference is that some problems have overlapping subproblems
- if there are overlapping subproblems, we only need to compute said subproblem once and store the result
- Dynamic programming is typically used to solve optimisation problems and counting problems
Dynamic Programming
optimal substructure
- For us to be able to use dynamic programming, the problem also needs to exhibit optimal substructure:
- the optimal solution to the problem can be constructed using optimal solutions to the subproblems
- Does the fibonacci problem have the optimal substructure property?
- does the (optimal) solution to the problem contains the (optimal) solution to the subproblem?
- how do you construct the (optimal) solution to the problem using the (optimal) solutions to the subproblems
Optimal Substructure
We have a bunch of metallic bars with known lengths. Sometimes we need to produce a bar of a certain length from the bars that we have.
We are not allowed to cut up any metallic bar, but we can solder any two bars together to create a longer bar.
- Example: Given [ 50, 2, 18, 11, 9, 23, 5, 10, 30, 6, 17 ]
- can we make 27?
- what is the minimum number of bars that we need?
[ 50, 2, 18, 11, 9, 23, 5, 10, 30, 6, 17 ] L = 27
[ 2, 18, 11, ..., 17 ] L = -23
[ 2, 18, 11, ..., 17 ] L = 27
don't pick 50
pick 50
[18, 11, ... , 17] L = -25
don't pick 2
pick 2
pick 2
don't pick 2
...
...
...
...
...
...
[18, 11, ... , 17] L = -23
[18, 11, ... , 17] L = 25
[18, 11, ... , 17] L = 27
...
...
Optimal Substructure
[ 50, 2, 18, 11, 9, 23, 5, 10, 30, 6, 17 ] L = 27
[ 2, 18, 11, 9, 23, ..., 17 ] L = -23
pick 50
[ 50, 18, 11, 9, 23, ..., 17 ] L = 25
pick 2
[ 50, 2, 11, 9, 23, ..., 17 ] L = 7
[ 50, 2, 18, 9, 23, ..., 17 ] L = 16
pick 18
pick 11
[ 50, 2, 18, 11, 9, 23, ..., 6 ] L = 10
pick 17
pick 9
[ 50, 2, 18, 11, 23, ..., 17 ] L = 16
...
...
...
Optimal Substructure
subproblems
subproblem: [ 50, 2, 18, 11, 9, 23, 5, 30, 6, 17 ] L = 17
optimal solution: 1 number (pick 17)
non-optimal solutions: 2 numbers (pick 11, 6)
pick 2
pick 10
subproblem: [ 50, 2, 18, 11, 9, 23, 5, 10, 30, 6 ] L = 25
optimal solution: 3 (pick 11, 9, 5)
problem: [ 50, 2, 18, 11, 9, 23, 5, 10, 30, 6, 17 ] L = 27
optimal solution: 2 (pick 17 and 10)
the optimal solution to the problem contains
the optimal solution to the subproblem
...
...
...
Optimal Substructure
subproblems
subproblem: [ 50, 2, 18, 11, 9, 23, 5, 30, 6, 17 ] L = 17
optimal solution: 1 number (pick 17)
non-optimal solutions: 2 numbers (pick 11, 6)
problem: [ 50, 2, 18, 11, 9, 23, 5, 10, 30, 6, 17 ] L = 27
optimal solution: 2 (pick 17 and 10)
How do you construct the optimal solution to the problem using the optimal solutions of the subproblems?
Optimal substructure (informally): The optimal solution is 1 + the best among the optimal solutions of the subproblems
Optimal Substructure
subproblems
We have a bunch of metallic bars with known lengths. Sometimes we need to produce a bar of a certain length from the bars that we have.
We are not allowed to cut up any metallic bar, but we can solder any two bars together to create a longer bar.
- Can we use dynamic programming to solve this problem?
- Yes, you do have overlapping subproblems and optimal substructure
- However, it may not be worth it
Optimal Substructure
We have metallic bars with known lengths as before, but for each length, you now have an infinite number of bars with that length.
We need to produce a bar of a certain length from the bars that we have. As before, you cannot cut up any metallic bar, but can solder any two bars together to create a longer bar.
- Example: Given [ 100, 50, 25, 10, 5, 1 ]
- can we make 374?
- what is the minimum number of bars that we need?
Optimal Substructure
[ 100, 50, 25, 10, 5, 1 ] L = 374
pick 100
pick 50
pick 25
pick 10
[ 100, 50, 25, 10, 5, 1 ] L = 373
pick 1
pick 5
[ 100, 50, 25, 10, 5, 1 ] L = 274
[ 100, 50, 25, 10, 5, 1 ] L = 369
[ 100, 50, 25, 10, 5, 1 ] L = 364
[ 100, 50, 25, 10, 5, 1 ] L = 349
[ 100, 50, 25, 10, 5, 1 ] L = 324
Optimal Substructure
[ 100, 50, 25, 10, 5, 1 ] L = 374
pick 100
pick 50
pick 25
pick 10
[ 100, 50, 25, 10, 5, 1 ] L = 373
pick 1
pick 5
[ 100, 50, 25, 10, 5, 1 ] L = 274
[ 100, 50, 25, 10, 5, 1 ] L = 369
[ 100, 50, 25, 10, 5, 1 ] L = 364
[ 100, 50, 25, 10, 5, 1 ] L = 349
[ 100, 50, 25, 10, 5, 1 ] L = 324
Do you have overlapping subproblems?
Optimal Substructure
[ 100, 50, 25, 10, 5, 1 ] L = 374
Do you have overlapping subproblems?
Pick 100 : subproblem [ 100, 50, 25, 10, 5, 1 ] L = 274
Pick 50 twice : subproblem [ 100, 50, 25, 10, 5, 1 ] L = 274
Pick 25 four times : subproblem [ 100, 50, 25, 10, 5, 1 ] L = 274
Pick 1, 1, 1, 1, 1, 5, 5, 5, 5, 25, 25, 5, 5, 5, 5, then pick 5 :
subproblem [ 100, 50, 25, 10, 5, 1 ] L = 274
Optimal Substructure
[ 100, 50, 25, 10, 5, 1 ] L = 374
pick 100
pick 50
pick 25
pick 10
[ 100, 50, 25, 10, 5, 1 ] L = 373
pick 1
pick 5
[ 100, 50, 25, 10, 5, 1 ] L = 274
[ 100, 50, 25, 10, 5, 1 ] L = 369
[ 100, 50, 25, 10, 5, 1 ] L = 364
[ 100, 50, 25, 10, 5, 1 ] L = 349
[ 100, 50, 25, 10, 5, 1 ] L = 324
Do you have optimal substructure?
Optimal Substructure
[ 100, 50, 25, 10, 5, 1 ] L = 374
pick 100
pick 50
pick 25
pick 10
[ 100, 50, 25, 10, 5, 1 ] L = 373
pick 1
pick 5
[ 100, 50, 25, 10, 5, 1 ] L = 274
[ 100, 50, 25, 10, 5, 1 ] L = 369
[ 100, 50, 25, 10, 5, 1 ] L = 364
[ 100, 50, 25, 10, 5, 1 ] L = 349
[ 100, 50, 25, 10, 5, 1 ] L = 324
Optimal Substructure
How do you construct the optimal solution to the problem using the optimal solutions of the subproblems?
Optimal substructure (informally): the optimal solution is 1 + the best among the optimal solutions of the subproblems
- Do problems always have optimal substructure property?
- Shortest path (Dijkstra)
- Minimum spanning tree
- What about the hard problems?
- Knapsack?
- Travelling salesman?
- Minimum vertex cover?
Optimal Substructure
- Travelling salesman: find the shortest route to visit every city and then return to the origin city
- Let \(A\) be the starting city
- Problem: \(A \rightarrow \text{(every other city)} \rightarrow A\)
- Subproblem:
- \(A \rightarrow B\)
- \(B \rightarrow \text{(every other city)} \rightarrow A\)
- Does this mean you can use dynamic programming to solve the travelling salesman problem?
Optimal Substructure
problems with optimal substructure
- Does this mean you can use dynamic programming to solve the travelling salesman problem EFFICIENTLY?

Optimal Substructure
problems with optimal substructure
- Does this mean you can use dynamic programming to solve the travelling salesman problem EFFICIENTLY?
- Longest path problem
- find the longest path between two vertices without visiting any vertices twice
5
4
1
3
2
Optimal Substructure
problems without optimal substructure
- Longest path problem
- what is the longest path between 1 and 5?
- does it has optimal substructure?
5
4
1
3
2
Optimal Substructure
problems without optimal substructure
- Subproblems of longest path between 1 and 5:
- what is the longest path between 1 and 3?
- what is the longest path between 3 and 5?
5
4
1
3
5
1
3
2
Optimal Substructure
problems without optimal substructure
- Why does it matter to have an optimal substructure?
- We want to find an optimal solution to a problem
- We want to break down our problem into smaller subproblems (because it is easier to do smaller problems, and there can be overlaps)
- We want to apply the SAME algorithm to the subproblem (this means we will also get the optimal solution to that subproblem)
Optimal Substructure
why does it matter
- If the optimal solution to the subproblem does not help in finding the optimal solution to the problem, then you cannot recursively perform divide-and-conquer
Optimal Substructure
why does it matter
Dynamic Programming
can we solve it?
- Does the problem have overlapping subproblems?
- Does the problem have the optimal substructure property?
- If the answer to these two questions is yes, then we can use dynamic programming to solve the problem
Dynamic Programming
developing a DP algorithm
- In developing a dynamic-programming solution, we follow a sequence of four steps (from CLRS, page 359)
- Characterise the structure of an optimal solution
- Recursively define the value of an optimal solution
- Compute the value of an optimal solution
- (optional) Construct an optimal solution from computed information
Dynamic Programming
developing a DP algorithm
- Informally:
- Show that there is an optimal substructure
- Show the recursive relation that gives optimal solution
- Compute the value of an optimal solution
- (optional) Construct an optimal solution from computed information
Rod Cutting
- We have one piece of rod that we can cut into smaller pieces. Suppose that cutting a rod is free and we can sell a rod of length \(i\) for \(p_i\). Given a rod of length \(n\), how should we cut it up to maximise our revenue?
\(i\)
\(p_i\)
1 2 3 4 5 6 7 8 9 10
1 5 8 9 10 17 17 20 24 30
\(i\)
\(p_i\)
1 2 3 4 5 6 7 8 9 10
1 5 8 9 10 17 17 20 24 30
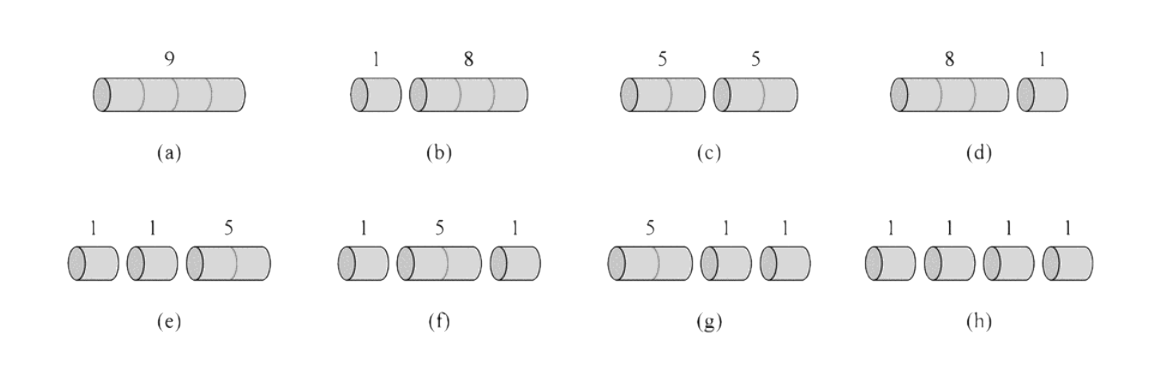
Rod Cutting

Rod Cutting
brute force
4
1+3
2+2
1+1+2
3+1
1+2+1
2+1+1
1+1+1+1
Rod Cutting
brute force
5,
4+1, 3+2, 2+3, 1+4
3+1+1, 1+3+1, 1+1+3, 2+2+1, 2+1+2, 1+2+2
1+1+1+2, 1+1+2+1, 1+2+1+1, 2+1+1+1
1+1+1+1+1
Rod Cutting
brute force
- no cut: \(\binom{4}{0}\) = 1 way
- cut in 1 place: \(4 \choose 1\) = 4 ways
- cut in 1 place: \(4 \choose 2\) = 6 ways
- cut in 1 place: \(4 \choose 3\) = 4 ways
- cut in 1 place: \(4 \choose 4\) = 1 way
\(c_1\)
\(c_2\)
\(c_3\)
\(c_4\)
Rod Cutting
brute force
- If n = 5, you have 4 possible places to cut
- In total, there are \(2^{n-1}\) possible combinations
- hence the brute-force approach is \(O(2^n)\)
\(c_1\)
\(c_2\)
\(c_3\)
\(c_4\)
Rod Cutting
overlapping subproblems
- Once we make a cut, we have a smaller problem of the same type, but with smaller \(n\)
- Can you spot the overlapping subproblems?

Rod Cutting
overlapping subproblems
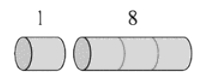
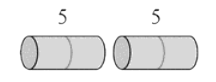
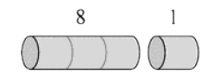
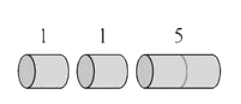
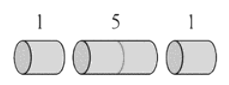
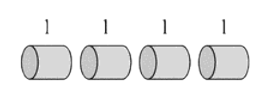

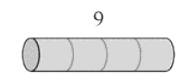







Rod Cutting
overlapping subproblems













- Rule: after each cut, don't cut the left part any further
- Is this still brute force?
Rod Cutting
optimal substructure
- Does the problem exhibit optimal substructure?
- You have to show that the optimal solution to the problem contains the optimal solutions to the subproblems

Rod Cutting
Step 1: show that there is an optimal substructure
- To solve the problem, you have to make a choice





Rod Cutting
Step 1: show that there is an optimal substructure
- The choice you make results in more subproblems













Rod Cutting
Step 1: show that there is an optimal substructure
- Imagine that you have the optimal solution the problem by picking one path (i.e. you know which subproblem to do next)
- you already have the optimal solution, so obviously you have the solution to the subproblem
- is the solution to the subproblem optimal?
Rod Cutting
Step 1: show that there is an optimal substructure
- Suppose that you have the optimal solution to the problem of cutting a rod of length \(n\)
- Suppose that this optimal solution requires you to cut the rod into two pieces, of length \(r\) and \((n-r)\)
- this means you have the subproblem of cutting a rod of length \((n-r)\)
- the solution to this subproblem must be optimal
- why?
Rod Cutting
Step 1: show that there is an optimal substructure
- Suppose that the solution to the subproblem of cutting a rod of length \((n-r)\) gives you \(y\) dollars
- Suppose that the optimal solution to the problem of cutting a rod of length \(n\) gives you \((x+y)\) dollars
$10
$1 + $8
$8 + $1
$9+$0




$10
Rod Cutting
Step 1: show that there is an optimal substructure
- If the solution to the subproblem is NOT optimal, then you would be able to find a better solution that gives you \(z > y\) dollars
- but this means the optimal solution to the problem is \((x + z)\) dollars, not \((x+y)\) dollars
$11
$1 + $8
$8 + $1
$9+$0




$11
Rod Cutting
Step 1: show that there is an optimal substructure
- Therefore, for the rod cutting problem, the optimal solution to the problem must contain the optimal solution to the subproblem
- It has the optimal substructure property!
- To show the existence of optimal substructure, you always follow the same steps
- Show that the optimal solution requires you to solve one or more subproblems and assume that you have the optimal solution
- You argue that the solution to the subproblems must also be optimal
- otherwise, you can construct a better solution for the problem using cut-and-paste technique
- but this is a contradiction: we assumed we have the optimal solution!
Optimal Substructure
showing optimal substructure
- Cut-and-paste technique:
- cut the non-optimal solution and paste in the optimal solution
- Refer to CLRS page 379 if you want a more detailed breakdown of these steps
Optimal Substructure
showing optimal substructure
Rod Cutting
Step 2: show the recursive relation that gives optimal solution
- We have shown that the rod cutting problem has an optimal substructure
- How do we choose which subproblem gives you the optimal answer?





Rod Cutting
Step 2: show the recursive relation that gives optimal solution
- Let \(p_i\) be the price of a rod of length \(i\), \(1 \le i \le n\)
- \(p_n\) is the price of the whole rod (i.e. don't make any cut)
- Let \(r_i\) be the maximum revenue that we can obtain from a rod of length \(i\), \(1 \le i \le n\)





Rod Cutting
Step 2: show the recursive relation that gives optimal solution
- The possible revenues for cutting a rod of length \(n\) are:
- \(p_n\)
- \(p_{n-1} + r_1\)
- \(p_{n-2} + r_2 \)
- ...
- \(p_2+r_{n-2}\)
- \(p_1+r_{n-1}\)
- All cases except for the first one creates an additional subproblem
Rod Cutting
Step 2: show the recursive relation that gives optimal solution
- The recursive relation for the rod cutting problem is
- i.e. go through all the subproblems, and find one that will maximise the revenue
- now you know how to code this!
\[r_n = \max_{1\le i \le n} (p_i + r_{n-i}) \]
Rod Cutting
Step 3: compute the value of an optimal solution
\[r_n = \max_{1\le i \le n} (p_i + r_{n-i}) \]
// assume p[i] gives price of rod of length i
public static int cut(int n) {
if (n == 0)
return 0;
int answer = Integer.MIN_VALUE;
for (int i = 1; i <= n; i++) {
answer = Math.max(answer, p[i] + cut(n-i));
}
return answer;
}Rod Cutting
Step 3: compute the value of an optimal solution
static int[] p = {0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30,
33, 36, 40, 42, 45, 50, 52, 58, 58, 60,
62, 65, 66, 72, 80, 82, 83, 85, 87, 88};
public static int cut(int n) {
if (n == 0)
return 0;
int answer = Integer.MIN_VALUE;
for (int i = 1; i <= n; i++) {
answer = Math.max(answer, p[i] + cut(n-i));
}
return answer;
}| n | optimal answer | no. of recursive calls |
|---|---|---|
| 10 | 30 | 1,024 |
| 15 | 45 | 33,792 |
| 20 | 63 | 1,082,368 |
| 25 | 80 | 34,636,800 |
| 30 | 94 | 1,108,378,624 |

static int[] p = {0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30,
33, 36, 40, 42, 45, 50, 52, 58, 58, 60,
62, 65, 66, 72, 80, 82, 83, 85, 87, 88};
public static int cut(int n) {
if (n == 0)
return 0;
int answer = Integer.MIN_VALUE;
for (int i = 1; i <= n; i++) {
answer = Math.max(answer, p[i] + cut(n-i));
}
return answer;
}public static int cut(int n) {
if (r[n] != 0) return r[n]; // memoise
if (n == 0)
return 0;
int answer = Integer.MIN_VALUE;
for (int i = 1; i <= n; i++) {
answer = Math.max(answer, p[i] + cut(n-i));
}
return r[n] = answer; // store the result
}Rod Cutting
Step 3: compute the value of an optimal solution
public static int cut(int n) {
if (r[n] != 0) return r[n]; // memoise
if (n == 0)
return 0;
int answer = Integer.MIN_VALUE;
for (int i = 1; i <= n; i++) {
answer = Math.max(answer, p[i] + cut(n-i));
}
return r[n] = answer; // store the result
}| n | optimal answer | no. of recursive calls |
|---|---|---|
| 10 | 30 | 56 |
| 15 | 45 | 122 |
| 20 | 63 | 213 |
| 25 | 80 | 329 |
| 30 | 94 | 470 |

recursion
top-down
DP
bottom-up
DP
???
Rod Cutting
Step 3: compute the value of an optimal solution
public static int cut_bottom_up(int n) {
r[0] = 0;
for (int j = 1; j <= n; j++) {
int answer = Integer.MIN_VALUE;
for (int i = 1; i <= j; i++) {
answer = Math.max(answer, p[i] + r[j-i]);
}
r[j] = answer;
}
return r[n];
}Rod Cutting
Step 3: compute the value of an optimal solution
public static int cut_bottom_up(int n) {
r[0] = 0;
for (int j = 1; j <= n; j++) {
int answer = Integer.MIN_VALUE;
for (int i = 1; i <= j; i++) {
answer = Math.max(answer, p[i] + r[j-i]);
}
r[j] = answer;
}
return r[n];
}- To compute \(r_n\), we need \(r_1\), \(r_2\), \(\dots\), \(r_{n-1}\)
- Compute \(r_j\) for \(j = 1, 2, \dots, n\)
- \(r_1 = p_1\)
- \(r_2 = \max\{p_2,p_1+r_1\}\)
- \(r_3 = \max\{p_3,p_2+r_1,p_1+r_2\}\)
Rod Cutting
Step 4: construct an optimal solution from computed information
public static int cut_bottom_up(int n) {
r[0] = 0;
for (int j = 1; j <= n; j++) {
int answer = Integer.MIN_VALUE;
for (int i = 1; i <= j; i++) {
if (answer < p[i] + r[j-i]) {
answer = p[i] + r[j-i];
s[j] = i;
}
}
r[j] = answer;
}
return r[n];
}- Create an array \(s\) where \(s[j]\) holds the optimal size of the first piece (i.e. the piece that you do not cut any further) when solving a subproblem of size \(j\)
Rod Cutting
Step 4: construct an optimal solution from computed information
\(i\)
\(p_i\)
1 2 3 4 5 6 7 8 9 10
1 5 8 9 10 17 17 20 24 30
\(s_i\)
1 2 3 2 2 6 1 2 3 10
- For \(i = 10\), the optimal cut is 10 and 0
- optimal solution is 30, just use 10
- For \(i = 9\), the optimal cut is 3 and 6
- For \(i = 6\), the optimal cut is 6 and 0
- optimal solution is 3 and 6
Rod Cutting
Step 4: construct an optimal solution from computed information
\(i\)
\(p_i\)
1 2 3 4 5 6 7 8 9 10
1 5 8 9 10 17 17 20 24 30
\(s_i\)
1 2 3 2 2 6 1 2 3 10
public static String construct_solution(int n) {
String ans = "";
while (n > 0) {
ans = ans + s[n] + " ";
n = n - s[n];
}
return ans;
}Rod Cutting
Step 4: construct an optimal solution from computed information
static int[] p = {0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30,
33, 36, 40, 42, 45, 50, 52, 58, 58, 60,
62, 65, 66, 72, 80, 82, 83, 85, 87, 88};| n | optimal answer | optimal cuts |
|---|---|---|
| 10 | 30 | 10 |
| 15 | 45 | 2 and 13 |
| 20 | 63 | 2 and 18 |
| 25 | 80 | 25 |
| 30 | 94 | 12 and 18 |
Rod Cutting
final words
- Bottom-up dynamic programming solution can be difficult to construct
- In this lecture, you are not learning how to write a code to a DP problem
- You are learning how to recognise the situation when you can apply the DP method:
- find optimal substructure and overlapping subproblems
- find the recursive relationship to find the optimal answer
Longest Common Subsequence
definition
- Given two sequences \(X\) and \(Y\), find the longest common subsequence of \(X\) and \(Y\)
- example from CLRS 15.4 (page 390)
- e.g. \(X = \{ A,B,C,B,D,A,B \}\)
\(Y = \{ B,D,C,A,B,A \} \)
the sequence \(\{ B,D,A,B \}\) and \(\{ B,C,B,A \}\) are two
possible solutions
- What is the brute-force solution?
- Example:
- \(X = \{ A,B,C,B,D,A,B \}\)
- \(Y = \{ B,D,C,A,B,A \} \)
- Brute force solution:
- Generate all subsequences of \(X\)
- Generate all subsequence of \(Y\)
- For each subsequence of \(X\), compare it with a subsequence of \(Y\)
- \(O(2^n)\) where \(n\) is the total length of the sequences \(X\) and \(Y\)
Longest Common Subsequence
brute force
- Example:
- \(X = \{ A,B,C,B,D,A,B \}\)
- \(Y = \{ B,D,C,A,B,A \} \)
- Can you improve the brute force approach?
- do you need to compare all these?
- A,B,C,B with B,D,C
- A,B,C,B with B,D
- A,B,C,B with D,C
- A,B,C,B with B,C
- do you need to compare all these?
Longest Common Subsequence
brute force
- Example:
- \(X = \{ A,B,C,B,D,A,B \}\)
- \(Y = \{ B,D,C,A,B,A \} \)
- Let's get some intuition:
- A,B,C,B with B,D,C
- A,B,C,B with B,D
- A,B,C,B with D,C
- A,B,C,B with B,C
- Intution 1: Why do we keep on comparing A? Can we drop it?
Longest Common Subsequence
brute force
- Example:
- \(X = \{ A,B,C,B,D,A,B \}\)
- \(Y = \{ B,D,C,A,B,A \} \)
- Let's get some intuition:
- A,B,C,B with B,D,C
- A,B,C,B with B,D
- A,B,C,B with D,C
- A,B,C,B with B,C
- Intuition 2: Why do we keep on comparing B? Can we drop it?
Longest Common Subsequence
brute force
-
Example:
- \(X = \{ A,B,C,B,D,A,B \}\)
- \(Y = \{ B,D,C,A,B,A \} \)
- Is there some sort of structure that we can exploit?
- Optimal substructure:
- does the longest common subsequence problem have an optimal substructure?
Longest Common Subsequence
brute force
- \(X = \{ x_1, x_2, x_3, \dots, x_m \} \)
- \(Y = \{ y_1, y_2, y_3, \dots, y_n \} \)
- Let \(Z = \{ z_1, z_2, z_3, \dots, z_k \} \) be the LCSS of \(X\) and \(Y\)
- If \(x_1 = y_1\), then Z should contain \(x_1 = y_1\), i.e. \(z_1 = x_1 = y_1\), and \(Z_2 = \{z_2,z_3,\dots,z_k\}\) is the LCSS of \(X_2\) and \(Y_2\)
Case A:
Case B:
Longest Common Subsequence
optimal substructure
- If \(x_1 \ne y_1\), then Z is either
- the LCSS of \(X_2 =\{x_2,x_3,\dots,x_m\}\), and \(Y=\{y_1,y_2,\dots,y_n\}\), or
- the LCSS of \(X = \{x_1,x_2,\dots,x_m\}\) and \(Y_2 =\{y_2,y_3,\dots,y_n\}\)
Longest Common Subsequence
optimal substructure
A B C B D A B
B D C A B A
B C B D A B
B D C A B A
A B C B D A B
D C A B A
- If \(x_1 \ne y_1\), then Z is either
- the LCSS of \(X_2 =\{x_2,x_3,\dots,x_m\}\), and \(Y=\{y_1,y_2,\dots,y_n\}\), or
- the LCSS of \(X = \{x_1,x_2,\dots,x_m\}\) and \(Y_2 =\{y_2,y_3,\dots,y_n\}\)
Case A:
Longest Common Subsequence
optimal substructure
Proof (by contradiction):
- \(Z\) is the LCSS of \(X\) and \(Y.\)
- If Z is NOT the LCSS of \(X_2\) and \(Y\), that means they have a longer common subsequence than \(Z\), say \(Z^*\).
- This means \(Z^*\) is the LCSS of \(X\) and \(Y\), a contradiction!
- Proof is symmetrical for the case \(X\) and \(Y_2\)
- If \(x_1 \ne y_1\), then Z is either
- the LCSS of \(X_2 =\{x_2,x_3,\dots,x_m\}\), and \(Y=\{y_1,y_2,\dots,y_n\}\), or
- the LCSS of \(X = \{x_1,x_2,\dots,x_m\}\) and \(Y_2 =\{y_2,y_3,\dots,y_n\}\)
Case A:
Longest Common Subsequence
optimal substructure
B C B D A B
B D C A B A
C B D A B
B D C A B A
B C B D A B
D C A B A
Case B:
C B D A B
D C A B A
- If \(x_1 = y_1\), then Z should contain \(x_1 = y_1\), i.e. \(z_1 = x_1 = y_1\), and \(Z_2 = \{z_2,z_3,\dots,z_k\}\) is the LCSS of \(X_2\) and \(Y_2\)
Longest Common Subsequence
optimal substructure
Case B:
Proof (by contradiction):
- if \(Z\) does not contain \(x_1\), then we can always append \(x_1\) to it, making a longer common subsequence
- if \(Z_2\) is not the LCSS of \(X_2\) and \(Y_2\), then there is another common subsequence \(Z^*\) that is longer. If we append \(x_1\) to \(Z^*\), \(Z^*\) would be longer than \(Z\), a contradiction!
- If \(x_1 = y_1\), then Z should contain \(x_1 = y_1\), i.e. \(z_1 = x_1 = y_1\), and \(Z_2 = \{z_2,z_3,\dots,z_k\}\) is the LCSS of \(X_2\) and \(Y_2\)
Longest Common Subsequence
recursive relation
\(x_1\ x_2\ x_3 \dots x_m\)
\(y_1\ y_2\ y_3\dots y_n\)
\(x_2\ x_3 \dots x_m\)
\(y_1\ y_2\ y_3\dots y_n\)
\(x_1\ x_2\ x_3 \dots x_m\)
\(y_2\ y_3\dots y_n\)
\(x_2\ x_3 \dots x_m\)
\(y_2\ y_3\dots y_n\)
\(x_1 = y_1\)
\(x_1 \ne y_1\)
\(x_1 \ne y_1\)
Longest Common Subsequence
recursive relation
\[ \text{LCSS}(X,Y) = \begin{cases} 0 & \text{if \(X\) or \(Y\) is empty}\\1 + \text{LCSS}(X_2,Y_2) & \text{if $x_1 = y_1$}\\\max\left(\text{LCSS}(X_2,Y_1),\text{LCSS}(X_1,Y_2)\right) & \text{if $x_1 \ne y_2$}\end{cases} \]
\(x_1\ x_2\ x_3 \dots x_m\)
\(y_1\ y_2\ y_3\dots y_n\)
\(x_2\ x_3 \dots x_m\)
\(y_1\ y_2\ y_3\dots y_n\)
\(x_1\ x_2\ x_3 \dots x_m\)
\(y_2\ y_3\dots y_n\)
\(x_2\ x_3 \dots x_m\)
\(y_2\ y_3\dots y_n\)
\(x_1 = y_1\)
\(x_1 \ne y_1\)
\(x_1 \ne y_1\)
Longest Common Subsequence
top-down solution
public static int lcss_top_down(String x, String y) {
int i = x.length()-1, j = y.length()-1;
if (x.length() == 0 || y.length() == 0)
return 0;
if (lcss[i][j] != -1)
return lcss[i][j];
else if (x.charAt(0) == y.charAt(0))
return lcss[i][j] = i=1 + lcss_top_down(x.substring(1),y.substring(1));
else
return lcss[i][j] = Math.max(lcss_top_down(x.substring(1),y), lcss_top_down(x,y.substring(1)));
}Longest Common Subsequence
bottom-up solution
for (int i = 0; i < n+1; i++) lcss[m][i] = 0;
for (int i = 0; i < m+1; i++) lcss[i][n] = 0;
for (int i = m-1; i > -1; i--){
for (int j = n-1; j > -1; j--){
// if character matches, then go diagonally
if(a.charAt(i) == b.charAt(j))
lcss[i][j] = 1 + lcss[i+1][j+1];
// else, compare the cell to your right and to your bottom,
// and pick the larger one
else
lcss[i][j] = Integer.max(lcss[i][j+1], lcss[i+1][j]);
}
}