COMP333 Algorithm Theory and Design - W6 2019

COMP333

Algorithm Theory and Design

Daniel Sutantyo

Department of Computing

Macquarie University

Lecture slides adapted from lectures given by Frank Cassez, Mark Dras, and Bernard Mans

Summary

Algorithm complexity (running time, recursion tree)
Algorithm correctness (induction, loop invariants)
Problem solving methods:
- exhaustive search
- dynamic programming
- greedy method
- divide-and-conquer
- probabilistic method
- algorithms involving strings
- algorithms involving graphs

Divide the problem into subproblems which are smaller instances of the same problem
Conquer the subproblems by solving them recursively, until it is small enough to solve trivially
Combine the solutions to the subproblems into a solution for the original problem

Divide and Conquer

We have already seen a lot of divide-and-conquer algorithms:
- remember our discussion about brute force, divide and conquer, and dynamic programming?
Is binary search a divide-and-conquer algorithm?
Is linear search a divide-and-conquer algorithm?

Divide and Conquer

The focus this week is not about how to write a divide-and-conquer algorithm
- you already know how to do this
Our focus is on the analysis of the running time of divide-and-conquer algorithms

Divide and Conquer

We characterise the running times of divide-and-conquer algorithms using a recurrence equation (or recurrence)
Formally, if $T(n)$ is the running time of the algorithm:

Divide and Conquer

$T(n) = \begin{cases} \Theta(1) &\text{if $n \le c$}\\ aT(n/b) + D(n) + C(n) &\text{otherwise} \end{cases}$

where

$D(n)$ is the cost of dividing the problem into subproblems
$C(n)$ is the cost of combining solutions of the subproblems to create a solution for the problem

Linear Search

divide and conquer method

public static int linearSearch(int[] a, int i, int j, int target){
    if (i > j)
        return -1;
    if (a[i] == target)
    	return i;
    return linearSearch(a,i+1,j,target);
}

public static int linearSearch(int[] a, int i, int j, int target){
    if (i > j)
        return -1;
    if (a[i] == target)
    	return i;
    return linearSearch(a,i+1,j,target);
}

public static int linearSearch(int[] a, int i, int j, int target) {
	if (i > j) 
		return -1;
	int m = (i+j)/2;
	if (a[m] == target)
		return m;
	return Math.max(linearSearch(a,i,m-1,target), linearSearch(a,m+1,j,target));
}

Linear Search

divide and conquer method

Linear Search

recursive relation between a problem and its subproblems

linearSearch(a[], 0, 8, target)

linearSearch(a[], 0, 3, target)

linearSearch(a[], 5, 8, target)

linearSearch(a[], i, j, target) = max(

linearSearch(a[],i,(i+j)/2-1,target),

linearSearch(a[],(i+j)/2+1,j,target)

)

Linear Search

recursive relation between a problem and its subproblems

linearSearch(a[], 0, 8, target)

linearSearch(a[], 0, 3, target)

linearSearch(a[], 5, 8, target)

$n$

\[\frac{n}{2}\]

Linear Search

recurrence

$T(n) = \begin{cases} \Theta(1) &\text{if $n \le c$}\\ aT(n/b) + D(n) + C(n) &\text{otherwise} \end{cases}$

$T(n) = \begin{cases} \Theta(1) &\text{if $n \le 1$}\\ 2T(n/2) + \Theta(1)&\text{otherwise} \end{cases}$

Linear Search

recurrence

$T(n) = \begin{cases} \Theta(1) &\text{if $n \le 1$}\\ 2T(n/2) + \Theta(1)&\text{otherwise} \end{cases}$

$T(n) = \begin{cases} \Theta(1) &\text{if $n \le 1$}\\ 3T(n/3) + \Theta(1)&\text{otherwise} \end{cases}$

If we divide the array into two parts:

If we divide the array into three parts:

Note that we can be a bit sloppy about the details

Linear Search

recurrence

Note that we can be a bit sloppy about the details

A[ 0 .. 8 ]

A [ 0 .. 3 ]

A [ 5 .. 8 ]

$n$

$\lfloor (n-1)/2 \rfloor $

$\lfloor n/2 \rfloor $

Linear Search

recurrence

We will keep it simple!

$n$

\[\frac{n}{2}\]

$n$

\[\frac{n}{3}\]

Divide and Conquer

solving recurrence to obtain bound for time complexity

Once we have the recurrence equation, we can work out the running time of the code
Remember, our goal is to find the asymptotic notation for $T(n)$
- e.g. $T(n) = O(g(n))$
- have to show $T(n) \le c\cdot g(n)$ for $c > 0, n > n_0 >0$

Divide and Conquer

solving recurrence to obtain bound for time complexity

There are three main methods for obtaining the asymptotic running time:
- using master method
- using substitution method
- using a recursion tree
You need to understand all three methods
- if an exam question asks you to derive the algorithm running time using the substitution method, then you cannot just use the master theorem

Master method

master theorem

The master theorem is a formula the describes the running time of some divide-and-conquer algorithms
- The algorithm must be of the form
  - $T(n) = aT(n/b) + f(n)$
- where $a \ge 1$, $b > 1$, and $f(n) > 0$
First presented by Bentley, Haken, and Saxe in 1980
- the term 'master theorem' was popularised by CLRS
- there is a proof in CLRS, but we won't go through it

Master method

master theorem

Given a recurrence of the form

$T(n) = aT(n/b) + f(n) $

if $f(n) = O(n^{\log_b a-\epsilon})$ for some constant $\epsilon > 0$ then
- $T(n) =\Theta(n^{\log_b a})$
if $f(n) = \Theta(n^{\log_b a})$ then
- $T(n) = \Theta(n^{\log_b a}\log n)$
if $f(n) = \Omega(n^{\log_b a + \epsilon})$ for some constant $\epsilon > 0$, and if $a f(n/b) \le cf(n)$ for some $c < 1$ then
- $T(n) = \Theta(f(n))$

$T(n) = aT(n/b) + f(n) $

$f(n) = O(n^{\log_b a-\epsilon})$

$f(n) = \Theta(n^{\log_b a})$

$f(n) = \Omega(n^{\log_b a + \epsilon})$

$T(n) = aT(n/b) + cn^k $

So we can write $f(n) = cn^k$

Master method

master theorem (simplification)

Master method

master theorem (simplification)

$T(n) = aT(n/b) + cn^k $

if $f(n) = O(n^{\log_b a-\epsilon})$ for some constant $\epsilon > 0$
- i.e.

$ k = \log_b a - \epsilon$

$ b^k = a - b^\epsilon$

(take both sides to the power of $b$)

$b^k < a$

in other words:

Master method

master theorem (simplification)

Given a recurrence of the form $T(n) = aT(n/b) + f(n) $
if $f(n) = O(n^{\log_b a-\epsilon})$ for some constant $\epsilon > 0$
- $T(n) =\Theta(n^{\log_b a})$

Given a recurrence of the form $T(n) = aT(n/b) + cn^k $ whenever $n$ is a power of $b$
if $b^k < a$ for some constant $\epsilon > 0$
- $T(n) =\Theta(n^{\log_b a})$

Master method

linear search

$T(n) = \begin{cases} \Theta(1) &\text{if $n \le 1$}\\ 2T(n/2) + \Theta(1)&\text{otherwise} \end{cases}$

$T(n) = \begin{cases} \Theta(1) &\text{if $n \le 1$}\\ 3T(n/3) + \Theta(1)&\text{otherwise} \end{cases}$

Linear search, divide into two parts:

Linear search, divide into three parts:

Master method

linear search

Given a recurrence of the form $T(n) = aT(n/b) + cn^k $ whenever $n$ is a power of $b$
- we have $T(n) = 2T(n/2) + \Theta(1)$
if $b^k < a$ for some constant $\epsilon > 0$
- we have $k = 0, b=2, a=2$, so $b^0 < a$
then $T(n) =\Theta(n^{\log_b a})$
- we have $T(n) = \Theta(n)$

Master method

linear search

Given a recurrence of the form $T(n) = aT(n/b) + cn^k $ whenever $n$ is a power of $b$
- we have $T(n) = 3T(n/3) + \Theta(1)$
if $b^k < a$ for some constant $\epsilon > 0$
- we have $k = 0, b=3, a=3$, so $b^0 < a$
then $T(n) =\Theta(n^{\log_b a})$
- we have $T(n) = \Theta(n)$

Master method

master theorem (simplification)

$T(n) = aT(n/b) + cn^k $

if $f(n) = O(n^{\log_b a})$
- i.e. $k = \log_b a \quad\rightarrow\quad b^k = a$
then you have $T(n) = \Theta(n^{\log_b a}\log n) = \Theta(n^{k}\log n)$

if $f(n) = O(n^{\log_b a+\epsilon})$
- i.e. $k > \log_b a \quad\rightarrow\quad b^k > a$
then you have $T(n) = \Theta(f(n)) = \Theta(n^{k})$

Master method

master theorem (simplification)

\[T(n)=\begin{cases}\Theta(n^{\log_b a}),&\text{if $f(n) = O(n^{\log_b a - \epsilon})$ for $\epsilon > 0$}\\\Theta(n^{\log_ba}\log n),&\text{if $f(n)=\Theta(n^{\log_b a})$}\\\Theta(f(n)),&\text{if $f(n) = \Omega(n^{\log_ba+\epsilon})$ for $\epsilon > 0$}\end{cases}\]

\[T(n) = aT(n/b) + f(n) \]

\[T(n)=\begin{cases}\Theta(n^{\log_ba}),&\text{if $a > b^k$ }\\\Theta(n^{\log_ba}\log n),&\text{if $a = b^k$}\\\Theta(n^k),&\text{if $a < b^k$}\end{cases}\]

\[T(n) = aT(n/b) + cn^k \]

Master method

examples

\[T(n) = aT(n/b) + cn^k\]

\[T(n)=\begin{cases}\Theta(n^{\log_ba}),&\text{if $a > b^k$ }\\\Theta(n^{\log_ba}\log n),&\text{if $a = b^k$}\\\Theta(n^k),&\text{if $a < b^k$}\end{cases}\]

$T(n) = \begin{cases} \Theta(1) &\text{if $n \le 1$}\\ 2T(n/2) + \Theta(n)&\text{otherwise} \end{cases}$

$a = 2, b = 2, k = 1 \quad\rightarrow\quad T(n) = \Theta(n\log n)$

Master method

examples

$T(n) = \begin{cases} \Theta(1) &\text{if $n \le 1$}\\ T(n/2) + \Theta(1)&\text{otherwise} \end{cases}$

$a = 1, b = 2, k = 0 \quad\rightarrow\quad T(n) = \Theta(\log n)$

\[T(n) = aT(n/b) + cn^k\]

\[T(n)=\begin{cases}\Theta(n^{\log_ba}),&\text{if $a > b^k$ }\\\Theta(n^{\log_ba}\log n),&\text{if $a = b^k$}\\\Theta(n^k),&\text{if $a < b^k$}\end{cases}\]

Master method

examples

$T(n) = \begin{cases} \Theta(1) &\text{if $n \le 1$}\\ 4T(n/2) + \Theta(n)&\text{otherwise} \end{cases}$

$a = 4, b = 2, k = 1 \quad\rightarrow\quad T(n) = \Theta(n^{2})$

\[T(n) = aT(n/b) + cn^k\]

\[T(n)=\begin{cases}\Theta(n^{\log_ba}),&\text{if $a > b^k$ }\\\Theta(n^{\log_ba}\log n),&\text{if $a = b^k$}\\\Theta(n^k),&\text{if $a < b^k$}\end{cases}\]

Master method

examples

$T(n) = \begin{cases} \Theta(1) &\text{if $n \le 1$}\\ 3T(n/2) + \Theta(n)&\text{otherwise} \end{cases}$

$a = 3, b = 2, k = 1 \quad\rightarrow\quad T(n) = \Theta(n^{\log_2 3})$

\[T(n) = aT(n/b) + cn^k\]

\[T(n)=\begin{cases}\Theta(n^{\log_ba}),&\text{if $a > b^k$ }\\\Theta(n^{\log_ba}\log n),&\text{if $a = b^k$}\\\Theta(n^k),&\text{if $a < b^k$}\end{cases}\]

Master method

examples

$T(n) = \begin{cases} \Theta(1) &\text{if $n \le 1$}\\ T(n/2) + \Theta(n)&\text{otherwise} \end{cases}$

$a = 1, b = 2, k = 1 \quad\rightarrow\quad T(n) = \Theta(n)$

\[T(n) = aT(n/b) + cn^k\]

\[T(n)=\begin{cases}\Theta(n^{\log_ba}),&\text{if $a > b^k$ }\\\Theta(n^{\log_ba}\log n),&\text{if $a = b^k$}\\\Theta(n^k),&\text{if $a < b^k$}\end{cases}\]

Master method

Master method can only be applied to recurrences of a specific form
- however, most algorithms you encounter in 333 is going to have this form (and probably most algorithms you encounter in life)
You can use master method to get some idea on the complexity of the algorithm
However, if you are asked to use ANOTHER method in a question, then DO NOT USE the master method (although you can cheat a bit: use master method as a guide to tell you what the answer is)

Recursion-Tree Method

To find the time complexity of an algorithm we can draw the recursion tree

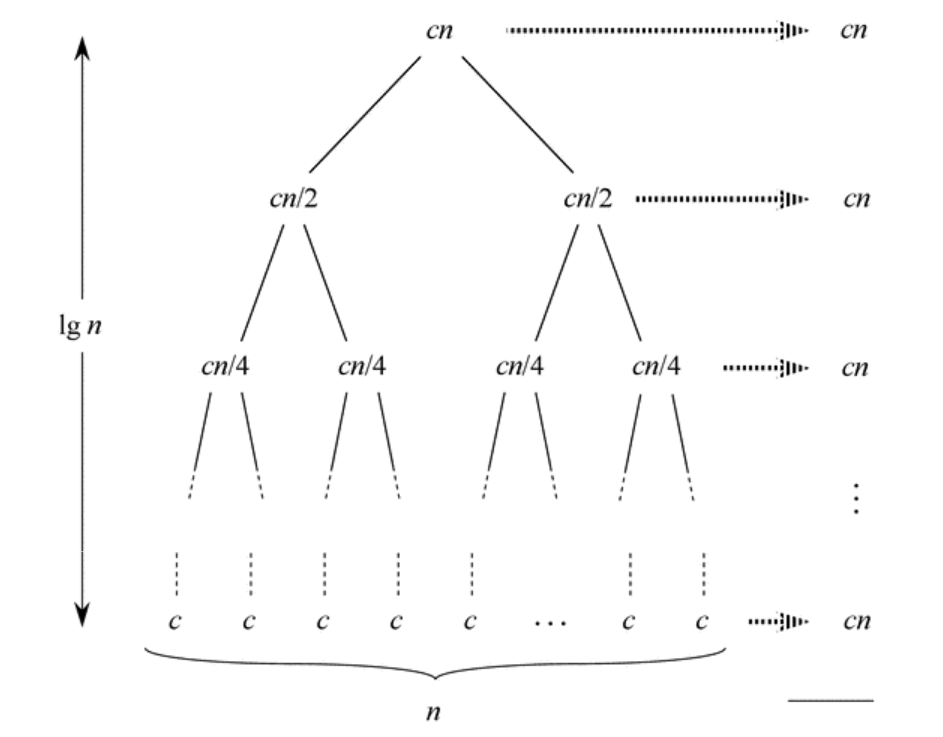
Recursion-Tree Method

The recursion-tree method has the following steps:
1. draw the tree until you can see a pattern (2-3 levels should be enough)
2. determine the number of operations on each level
3. determine the height of the tree
4. hence determine the total number of operation:
  - height of tree $\times$ number of operation on each level

Recursion-Tree Method

The recursion-tree method has the following steps:
- draw the tree until you can see a pattern (2-3 levels should be enough)
- count the number of operations on each level
- determine the height of the tree
- hence determine the total number of operation:
  - height of tree $\times$ number of operation on each level

Recursion-Tree Method

example: merge sort

\[T(n) = 2T(n/2) + \Theta(n)\]

assume $n$ is a power of 2 to simplify the discussion
assume we are doing $cn$ operations on each recursion
assume we are doing 1 operation at the leaves

$T(n) = \begin{cases} \Theta(1) &\text{if $n = 1$}\\ 2T(n/2) + cn &\text{if $n > 1$} \end{cases}$

Recursion-Tree Method

step 1: draw the tree

$T(n) = \begin{cases} \Theta(1) &\text{if $n = 1$}\\ 2T(n/2) + cn &\text{if $n > 1$} \end{cases}$

$cn$

\[\frac{cn}{2}\]

Recursion-Tree Method

step 1: draw the tree

$cn$

\[\frac{cn}{2}\]

\[\frac{cn}{4}\]

\[\frac{cn}{2}\]

\[\frac{cn}{4}\]

. . .

Recursion-Tree Method

step 2: count the number of operations on each level

$cn$

\[\frac{cn}{2}\]

\[\frac{cn}{4}\]

\[\frac{cn}{2}\]

\[\frac{cn}{4}\]

. . .

\[n\]

Recursion-Tree Method

step 3: determine the height of the tree

$cn$

\[\frac{cn}{2}\]

\[\frac{cn}{4}\]

\[\frac{cn}{2}\]

\[\frac{cn}{4}\]

. . .

\[n\]

Recursion-Tree Method

step 3: determine the height of the tree

On each level we divide the problem size by 2
The subproblem sizes:
- $n \quad\rightarrow \quad n/2 \quad\rightarrow\quad n/4 \quad\rightarrow\quad\cdots\quad\rightarrow\quad n/2^i$
The final level is when $n /2^i = 1$
- i.e. when $2^i = n \quad\rightarrow\quad i = \log_2n$
Level $i$ has $2^i$ nodes, so the final level has $2^{\log_2 n}$ nodes = $n$ nodes (as we expected)

Recursion-Tree Method

step 4: determine the total number of operations

Number of levels: $\log_2 n$
Number of operations on each level: $n$
Total number of operations: $n \log n$

$T(n) = O(n \log n)$

Recursion-Tree Method

example: linear search

$T(n) = \begin{cases} \Theta(1) &\text{if $n \le 1$}\\ 2T(n/2) + \Theta(1)&\text{otherwise} \end{cases}$

assume $n$ is a power of 2 to simplify the discussion
assume we are doing 1 operation at each node

Recursion-Tree Method

example: linear search

$cn$

\[\frac{cn}{2}\]

\[\frac{cn}{4}\]

\[\frac{cn}{2}\]

\[\frac{cn}{4}\]

. . .

\[n\]

Recursion-Tree Method

example: linear search

$1$

. . .

\[4\]

\[2\]

\[1\]

\[???\]

Recursion-Tree Method

example: linear search

As before, the final level is when $n /2^i = 1$
- i.e. when $2^i = n \quad\rightarrow\quad i = \log_2n$
Level $i$ has $2^i$ nodes, so the final level has $2^{\log_2 n}$ nodes = $n$ nodes
Note that we are being a bit sloppy here: you will not get a nice balanced tree if $n$ is not a power of 2

Recursion-Tree Method

example: linear search

. . .

\[4\]

\[2\]

\[1\]

\[2^{\log_2 n} = n\]

Recursion-Tree Method

example: linear search

To find the total number of operation, we need to find the sum of

\[ 1 + 2 + 4 + \cdots + n \]

\[ = 2^0 + 2^1 + 2^2 + \cdots + 2^{\log_2 n} \]

\[ = \sum_{k=0}^{\log_2 n} 2^k \]

We need the formula for geometric series
- see CLRS Appendix A

\[\sum_{k=0}^m x^k = 1 + x + x^2 + \cdots + x^m = \frac{x^{m+1}-1}{x-1}\]

Recursion-Tree Method

example: linear search

\[\sum_{k=0}^{\log_2 n} x^k = 1 + 2 + 2^2 + \cdots + 2^{\log_2 n}= \frac{2^{\log_2 n+1}-1}{2-1} = 2n - 1\]

\[\sum_{k=0}^m x^k = 1 + x + x^2 + \cdots + x^m = \frac{x^{m+1}-1}{x-1}\]

from here we can see that linear search is $O(n)$

$T(n) = \begin{cases} \Theta(1) &\text{if $n \le 1$}\\ 3T(n/3) + \Theta(1)&\text{otherwise} \end{cases}$

assume $n$ is a power of 3 to simplify the discussion
assume we are doing 1 operation at each node

Recursion-Tree Method

example: linear search (3 partitions)

Recursion-Tree Method

example: linear search (3 partitions)

. . .

\[9\]

\[3\]

\[1\]

\[3^{\log_3 n} = n\]

To find the total number of operation, we need to find the sum of

\[ 1 + 3 + 9 + \cdots + n \]

\[ = 3^0 + 3^1 + 3^2 + \cdots + 3^{\log_3 n} \]

\[ = \sum_{k=0}^{\log_3 n} 3^k \]

Another geometric series:

\[\sum_{k=0}^m x^k = 1 + x + x^2 + \cdots + x^k = \frac{x^{m+1}-1}{x-1}\]

Recursion-Tree Method

example: linear search (3 partitions)

\[\sum_{k=0}^{\log_2 n} x^k = 1 + 3 + 3^2 + \cdots + 3^n = \frac{3^{\log_3 n+1}-1}{3-1} = \frac{3n-1}{2}\]

\[\sum_{k=0}^m x^k = 1 + x + x^2 + \cdots + x^k = \frac{x^{m+1}-1}{x-1}\]

and this version of linear search is also $O(n)$, as expected

Recursion-Tree Method

example: linear search (3 partitions)

Recursion-Tree Method

another example

\[T(n) = 3T(n/4) + \Theta(n^2)\]

assume $n$ is a power of 4 to simplify the discussion
assume we are doing $cn^2$ operations on each recursion

$T(n) = \begin{cases} \Theta(1) &\text{if $n = 1$}\\ 3T(n/4) + cn^2 &\text{if $n > 1$} \end{cases}$

$cn^2$

\[\frac{cn^2}{16}\]

Recursion-Tree Method

step 1: draw the tree

Recursion-Tree Method

step 1: draw the tree

$cn^2$

\[\frac{cn^2}{16}\]

\[\frac{cn^2}{256}\]

. . . . . . . . . . . . . . . . . . . . .

$cn^2$

\[\frac{cn^2}{16}\]

\[\frac{cn^2}{256}\]

. . . . . . . . . . . . . . . . . . . . .

\[\frac{cn^2}{256}\]

$cn^2$

\[\frac{3}{16}cn^2\]

\[\frac{9}{256}cn^2\]

???

Recursion-Tree Method

step 2: count number of operations on each level

Recursion-Tree Method

step 3: determine the height of the tree

On each level we divide the problem size by 4
The subproblem sizes:
- $n \quad\rightarrow \quad n/4 \quad\rightarrow\quad n/16 \quad\rightarrow\quad\cdots\quad\rightarrow\quad n/4^i$
The final level is when $n /4^i = 1$
- i.e. when $4^i = n \quad\rightarrow\quad i = \log_4 n$
Level $i$ has $3^i$ nodes, so the final level has $3^{\log_4 n}$ nodes

$cn^2$

\[\frac{cn^2}{16}\]

\[\frac{cn^2}{256}\]

. . . . . . . . . . . . . . . . . . . . .

\[\frac{cn^2}{256}\]

$cn^2$

\[\frac{3}{16}cn^2\]

\[\frac{9}{256}cn^2\]

$3^{\log_4 n}$

Recursion-Tree Method

step 3: determine the height of the tree

Recursion-Tree Method

step 4: determine the total number of operations

Finding the total number of operations is not that simple
- you need to find the sum the number of operations on each level:

\[cn^2 + \frac{3}{16}cn^2 + \frac{9}{256}cn^2+\cdots+ 3^{\log_4 n}\]

\[cn^2 + \frac{3}{16}cn^2 + \left(\frac{3}{16}\right)^2cn^2+\cdots+ \left(\frac{3}{16}\right) ^{\log_4 n - 1}cn^2+ 3^{\log_4 n}\]

\[\left(\frac{3}{16}\right)^i\]

each term has

$i$ goes from 0 to $\log_4 n - 1$

We need to use the sum to the geometric progression formula again:

\[\sum_{k=0}^n x^k = 1 + x + x^2 + \cdots + x^n = \frac{x^{n+1}-1}{x-1}\]

\[cn^2 + \frac{3}{16}cn^2 + \left(\frac{3}{16}\right)^2cn^2+\cdots+ \left(\frac{3}{16}\right) ^{\log_4 n - 1}cn^2+ 3^{\log_4 n}\]

\[cn^2\sum_{i=0}^{\log_4n-1}\left(\frac{3}{16}\right)^i+ 3^{\log_4 n}\]

\[= \frac{(3/16)^{\log_4 n}-1}{(3/16)-1}cn^2+ 3^{\log_4 n}\]

Recursion-Tree Method

step 4: determine the total number of operations

\[\sum_{k=0}^\infty x^k = \frac{1}{1-x}\]

this is ugly ...
but here we can be a bit sloppy again:
- use geometric sum of an infinite series, with $|x| < 1$

\[cn^2\sum_{i=0}^{\log_4n-1}\left(\frac{3}{16}\right)^i + 3^{\log_4 n}\]

\[= \frac{(3/16)^{\log_4 n}-1}{(3/16)-1}cn^2+ 3^{\log_4 n}\]

Recursion-Tree Method

step 4: determine the total number of operations

\[\sum_{k=0}^n x^k <\sum_{k=0}^\infty x^k = \frac{1}{1-x}\]

therefore

\[\sum_{i=0}^{\log_4n-1}\left(\frac{3}{16}\right)^i cn^2+ 3^{\log_4 n}\]

Recursion-Tree Method

step 4: determine the total number of operations

if $|x| < 1$ and each term is positive:

\[< \sum_{i=0}^{\infty}\left(\frac{3}{16}\right)^i cn^2+ 3^{\log_4 n}\]

\[=\frac{1}{1-(3/16)} cn^2+ 3^{\log_4 n}\]

Recursion-Tree Method

step 4: determine the total number of operations

\[\frac{1}{1-(3/16)} cn^2+ 3^{\log_4 n} = \frac{16}{13}cn^2 + 3^{\log_4 n}\]

One more rule that may be useful:
Hence:

\[ 3^{\log_4 n} = n^{\log_4 3}\]

\[T(n) \le \frac{16}{13}cn^2 + n^{\log_43}\]

\[T(n) = O(n^2)\]

Recursion-Tree Method

using master method

$T(n) = \begin{cases} \Theta(1) &\text{if $n \le 1$}\\3 T(n/4) + \Theta(n^2)&\text{otherwise} \end{cases}$

$a = 3, b = 4, k = 2 \quad\rightarrow\quad T(n) = \Theta(n^2)$

\[T(n) = aT(n/b) + cn^k\]

\[T(n)=\begin{cases}\Theta(n^{\log_ba}),&\text{if $a > b^k$ }\\\Theta(n^{\log_ba}\log n),&\text{if $a = b^k$}\\\Theta(n^k),&\text{if $a < b^k$}\end{cases}\]

Substitution Method

The substitution method has two steps:
- Guess the time complexity
- Use mathematical induction to find the constants and show that the time complexity we guessed is correct

Substitution Method

example

$T(n) = \begin{cases} 1 &\text{if $n \le 1$}\\ 2T(\lfloor n/2\rfloor) + n&\text{otherwise} \end{cases}$

Assume integer division, i.e. $\lfloor n/2\rfloor$
Step 1: Guess a solution
- draw the recursion tree and estimate the number of operations
- try different bounds and see which one works (e.g. try $n^2$, then $n$, then $n \log n$
- gain experience: as you learn more algorithms, you can have a good feel on an algorithm's complexity

Substitution Method

example

Guess: $T(n) = O(n\log n)$ (use log base 2 this time)
Step 2: use induction to prove the correctness of our guess

$T(n) = \begin{cases} 1 &\text{if $n \le 1$}\\ 2T(\lfloor n/2\rfloor) + n&\text{otherwise} \end{cases}$

Substitution Method

example

Guess: $T(n) = O(n\log n)$
Step 2: use induction to prove the correctness of our guess

Prove: $T(n) = O(n\log n)$
- i.e. prove there exists $c > 0$ and $n_0 > 0$ such that $T(n) \le cn\log n$ for all $n > n_0$

$T(n) = \begin{cases} 1 &\text{if $n \le 1$}\\ 2T(\lfloor n/2\rfloor) + n&\text{otherwise} \end{cases}$

Substitution Method

example

Prove $T(n) \le cn\log n$ for all $n > n_0$ for some $c > 0$ and $n_0 > 0$

Base case: $n = 1$
- LHS: $T(1) = 1$
- RHS: $cn\log n = c * \log 1 = 0$

Substitution Method

example

Prove $T(n) \le cn\log n$ for all $n > n_0$ for some $c > 0$ and $n_0 > 0$

We don't have to start from 1!
Base case:
- $n = 2$
  - LHS: $T(2) = 2*T(1)+2 = 4$
  - RHS: $cn\log n =2c * \log 2$
- $n = 3$
  - LHS: $T(3) = 2*T(1)+3 = 5$
  - RHS: $cn\log n =3c * \log 3$

Substitution Method

example

$n = 4$
- LHS: $T(4) = 2*T(2)+4 = 12$
- RHS: $cn\log n =4c * \log 4$
$n = 5$
- LHS: $T(5) = 2*T(2)+5 = 13$
- RHS: $cn\log n =5c * \log 5$
$n = 6$
- LHS: $T(6) = 2*T(3)+6 = 16$
- RHS: $cn\log n =6c * \log 6$

Substitution Method

example

Prove $T(n) \le cn\log n$ for all $n > n_0$ for some $c > 0$ and $n_0 > 0$

Base case:
- $n = 2$
  - LHS: $T(2) = 2*T(1)+2 = 4$
  - RHS: $cn\log n =2c * \log 2$
- $n = 3$
  - LHS: $T(3) = 2*T(1)+3 = 5$
  - RHS: $cn\log n =3c * \log 3$
- True for $c \ge 2$ (we are using log base 2)

Substitution Method

example

Prove $T(n) \le cn\log n$ for all $n > n_0$ for some $c > 0$ and $n_0 > 0$

Induction step:
- Induction hypothesis: assume $T(k) \le ck\log k$ for some $k > 1$
- Prove: $T(2k)\le 2ck\log 2k$

$T(2k) = 2*T(k) + 2k$

$\le 2ck\log k + 2k$

(from the recurrence)

(from the induction hypothesis)

$\le 2ck\log 2k + 2k$

Substitution Method

example

$T(2k)\le 2ck\log 2k + 2k$

$T(2k) \le 2ck\log 2k$

we can prove that:

but this not the same as proving:

because it could be the case that
- $2ck\log 2k \le T(2k) \le 2ck\log 2k + 2k$

Substitution Method

example

Prove $T(n) \le cn\log n$ for all $n > n_0$ for some $c > 0$ and $n_0 > 0$

Induction step:
- Induction hypothesis: assume $T(\lfloor k/2\rfloor) \le c(\lfloor k/2 \rfloor)\log (\lfloor k/2\rfloor)$ for some $k > 3$
- Prove: $T(k)\le ck\log k$

$T(k) = 2T(\lfloor k/2 \rfloor) + k $

$\le c(\lfloor k/2 \rfloor )\log(\lfloor k/2\rfloor) + k $

$\le ck\log(k/2 ) + k$

$= ck\log k - ck\log 2 + k$

$\le ck\log k$

Substitution Method

example

$T(k) = 2T(k/2) + k $

The proof works this time because $ck\log_2 2 = ck > k$ as long as $c > 1$
- and we used $c \ge 2$

$\le c(\lfloor k/2 \rfloor )\log(\lfloor k/2\rfloor) + k $

$\le ck\log(k/2 ) + k$

$= ck\log k - ck\log 2 + k$

$\le ck\log k$

Substitution Method

final words

Remember that if you have the wrong induction hypothesis, then you will end up with a wrong proof
- what would happen if you guessed $O(n)$ in the previous example?
Be careful of the pitfall mentioned:
- $T(n) \le cn + d \quad\rightarrow\quad T(n) = O(n)$?
Read CLRS page 85-86 for more discussion on this

Integer Multiplication

$x = x_1B^m + x_0$

$y = y_1B^m + y_0$

$x_0 < B^m$

$y_0 < B^m$

$xy = (x_1B^m + x_0)(y_1B^m+y_0)$

$= (x_1y_1)B^{2m} + (x_1y_0+x_0y_1)B^m + x_0y_0$

Integer Multiplication

$x = x_1B^m + x_0$

$y = y_1B^m + y_0$

$xy = (x_1y_1)B^{2m} + (x_1y_0+x_0y_1)B^m + x_0y_0$

$12345678 = 1234*10^4 + 5678$

$87654321 = 8765*10^4 + 4321$

$\begin{aligned}12345678 * 87654321 =\ &(1234*8765)10^{8}\\ &+ (1234*4321+5678*8765)10^4 \\&+ (5678*4321)\end{aligned}$

Integer Multiplication

$\text{mul}(1234,8765)$

$\text{mul}(12345678,87654321)$

$\begin{aligned}12345678 * 87654321 =\ &(1234*8765)10^{8}\\ &+ (1234*4321+5678*8765)10^4 \\&+ (5678*4321)\end{aligned}$

$\text{mul}(5678*8765)$

$\text{mul}(1234*4321)$

$\text{mul}(5678*4321)$

Integer Multiplication

$\text{mul}(1234,8765)$

$\text{mul}(12345678,87654321)$

$\text{mul}(5678,8765)$

$\text{mul}(1234,4321)$

$\text{mul}(5678,4321)$

$\text{mul}(12,87)$

$\text{mul}(12,65)$

$\text{mul}(34,87)$

$\text{mul}(34,65)$

$\text{mul}(1,8)$

$\text{mul}(1,7)$

$\text{mul}(2,8)$

$\text{mul}(2,7)$

we can use precomputation to speed this up
in reality, we will be doing this in base 2, and multiplying by the base is 'free'

Integer Multiplication

recurrence equation

$x = x_1B^m + x_0$

$y = y_1B^m + y_0$

$xy = (x_1y_1)B^{2m} + (x_1y_0+x_0y_1)B^m + x_0y_0$

$T(n) = \begin{cases} O(1) &\text{if $n \le 1$}\\ 4T(n/2) + O(n) &\text{otherwise} \end{cases}$

Integer Multiplication

master method

$T(n) = \begin{cases} 1&\text{if $n \le 1$}\\ 4T(n/2) +cn &\text{otherwise} \end{cases}$

\[T(n)=\begin{cases}\Theta(n^{\log_ba}),&\text{if $a > b^k$ }\\\Theta(n^{\log_ba}\log n),&\text{if $a = b^k$}\\\Theta(n^k),&\text{if $a < b^k$}\end{cases}\]

$a = 4, b = 2, k = 1 \quad \rightarrow \quad T(n) = \Theta(n^2)$

Integer Multiplication

recursion tree method

\[cn\]

\[\frac{cn}{2}\]

\[\frac{cn}{4}\]

\[\frac{cn}{2}\]

\[\frac{4cn}{2} = 2cn\]

\[cn\]

The number of operation:
The final level is when $i = \log_2 n$
$T(n) = cn(1 + 2 + 4 + \cdots + 2^{\log_2 n}) =cn(2n-1) = O(n^2)$

\[\frac{16cn}{4} = 4cn\]

\[\frac{4^icn}{2^i} = 2^icn\]

\[\frac{cn}{4}\]

Integer Multiplication

substitution method

Guess: $T(n) = O(n^2)$
- we want to prove that $T(n) \le cn^2$ for some $c >0, n \ge n_0 > 0$

Base case: $n = 1 \quad\rightarrow\quad T(1) = 1 \le 1^2$, so $T(n) \le n^2$

Induction step:
- Induction hypothesis: we assume $T(k/2) \le ck^2/4$ for $k > 1$

$T(k) = 4T(k/2) + ck$

$\le 4ck^2/4 + ck = ck^2 + ck$

$T(k) = O(k^2)$

Integer Multiplication

substitution method

One more time:
- you can say $T(k) = O(k^2)$ if $T(k) \le ck^2$,
  - but we only showed that $T(k) \le ck^2 + ck$
  - it could the case that
    - $ck^2 < T(k) \le ck^2 + ck$
- so don't try to show that $T(n) \le cn^2$
  - instead we try to prove that $T(n) \le cn^2 - n$
  - if $T(n) \le cn^2 -n$ we still have $T(n) = O(n^2)$
    - i.e. we subtract lower order term

Integer Multiplication

substitution method

Guess: $T(n) = O(n^2)$
- we want to prove that $T(n) \le cn^2-n$ for some $c >0, n \ge n_0 > 0$
Base case:
- $n = 1$ : $T(1) = 1 \le 2 - 1$ ,
- thus when $n=1$, $T(n) \le cn^2-n$ for $c \ge 2$
Induction step:
- induction hypothesis: assume $T(k/2) \le ck^2/4-k/2$
- proof:

$T(k) = 4T(k/2) + ck$

$\le 4(ck^2/4-k/2) + ck$

$\le ck^2 -2k + ck$

$\le ck^2$

(from recurrence)

(from induction hypothesis)

(if $c \le 2$)